Open Access Article
Open Access ArticleRIDME spectroscopy on high-spin Mn2+ centers†
D.
Akhmetzyanov‡
a,
H. Y. V.
Ching‡
b,
V.
Denysenkov
a,
P.
Demay-Drouhard
cd,
H. C.
Bertrand
cd,
L. C.
Tabares
b,
C.
Policar
cd,
T. F.
Prisner
*a and
S.
Un
*b
aGoethe-University Frankfurt am Main, Institute of Physical and Theoretical Chemistry and Center for Biomolecular Magnetic Resonance, Max von Laue Str. 7, 60438 Frankfurt am Main, Germany. E-mail: prisner@chemie.uni-frankfurt.de
bInstitute for Integrative Biology of the Cell (I2BC), Department of Biochemistry, Biophysics and Structural Biology, Université Paris-Saclay, CEA, CNRS UMR 9198, Gif-sur-Yvette, F-91198, France. E-mail: sun.un@cea.fr
cDépartement de Chimie, Ecole Normale Supérieure, PSL Research University, UPMC Univ Paris 06, CNRS, Laboratoire des Biomolécules (LBM), 24 rue Lhomond, 75005 Paris, France
dSorbonne Universités, UPMC Univ Paris 06, Ecole Normale Supérieure, CNRS, Laboratoire des Biomolécules (LBM), 24 rue Lhomond, 75005 Paris, France
First published on 13th October 2016
Abstract
Pulsed EPR dipolar spectroscopy is a powerful tool for determining the structure and conformational dynamics of biological macromolecules, as it allows precise measurements of distances in the range of 1.5–10 nm. Utilization of high-spin Mn2+ species as spin probes for distance measurements is of significant interest, because they are biologically compatible and endogenous in numerous biological systems. However, to date dipolar spectroscopy experiments with this kind of species have been underexplored. Here we present pulsed electron electron double resonance (PELDOR also called DEER) and relaxation-induced dipolar modulation enhancement (RIDME) experiments, which have been performed at W-band (94 GHz) and J-band frequencies (263 GHz) on a bis-MnDOTA (DOTA = 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetate) model system. The distances obtained from these experiments are in good agreement with predictions. RIDME experiments reveal a significantly higher modulation depth compared to PELDOR, which is an important consideration for biological samples. These experiments also feature higher harmonics of the dipolar coupling frequency due to effective multiple-quantum relaxation of high-spin Mn2+ as well as the multiple-component background function. Harmonics of the dipolar coupling frequency were taken into account by including additional terms in the kernel function of Tikhonov regularization analysis.
Introduction
Pulsed electron paramagnetic resonance (EPR) dipolar spectroscopy, which can precisely measure distances in the range of 1.5–10 nm, has become a valuable tool for structural biology by providing important information about tertiary structures, conformational flexibilities and intermolecular interactions of biomacromolecules.1–3 Pulsed electron–electron double resonance (PELDOR,4 also called DEER5,6) is the most commonly used of such EPR techniques, where the distances are measured by determining the magnitude of the magnetic dipolar coupling (ωdd) between pairs of spin probes, which in the weak coupling regime is given by the formula (1)6: | (1) |
Compared to nitroxide and other organic radicals, Mn2+ is a more complicated spin system with an electron spin of S = 5/2. Thus, the EPR spectrum of Mn2+ complexes with non-zero quadrupole Zero-Field Splitting (ZFS) parameters reveals a fine structure, consisting of five resonance lines |mS〉 → |mS ± 1〉, where mS is the projection of the electron spin vector to the magnetic field vector. Each of these is further split into a sextet of hyperfine lines, arising from the 55Mn nuclear spin (I = 5/2, 100% abundant). In disordered samples, the total width of the EPR spectrum is defined to a large extent by the ZFS and 55Mn hyperfine coupling.21,22 The individual widths of the six hyperfine lines corresponding to the central |−1/2,mI〉 → |1/2,mI〉 transition, where mI is the projection of the 55Mn nuclear spin vector to the magnetic field vector, do not depend on ZFS in first order perturbation theory and hence these lines are very sharp. The other electron spin transitions have a first order ZFS dependency and are typically broad and featureless.
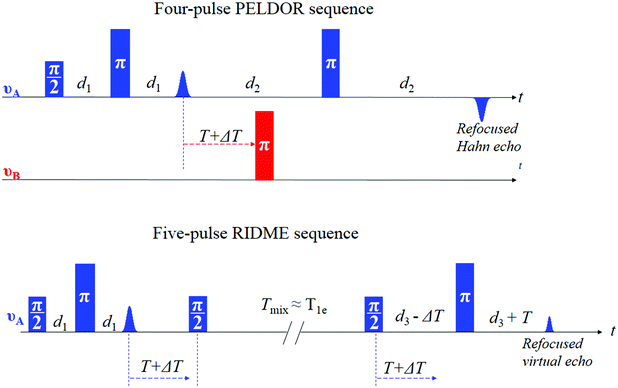
One of the important properties that governs the sensitivity of PELDOR experiments is the dipolar modulation depth. It is defined by the fraction of spins (referred to as B spins in the following) that are inverted by the applied pump pulse at the second microwave frequency, νB (see Fig. 1). The fraction of spins that are detected (referred to as A spins that are in resonance with the pulses at the microwave frequency of νA) is also an important parameter for sensitivity, since it contributes to the echo amplitude. For Mn2+ centers only a part of one of the six hyperfine lines of the central |−1/2,mI〉 → |1/2,mI〉 transition can be excited by the pump pulse, leading to low modulation depths of about 0.5 to 2%.13–15,23
As has been shown for Gd3+ complexes,24,25 one way to improve on this low modulation depth condition is to use the relaxation-induced dipolar modulation enhancement (RIDME)26,27 experiment instead of PELDOR. Unlike PELDOR, where the single-quantum electron spin transition of the B spin is driven coherently by a microwave pulse, in RIDME the B spin transition is driven incoherently by electron spin longitudinal relaxation, which is characterized by the time constant T1e. Experimentally it is achieved by replacing the pump pulse at the second microwave frequency νB by a mixing block, composed of two π/2 pulses, applied at the detection frequency νA (Fig. 1).27 In this case, the dipolar modulation depth is defined by the formula (2):
 | (2) |
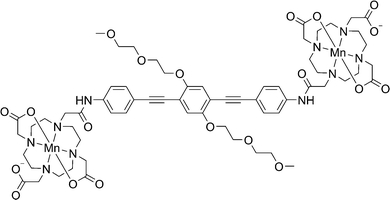
In the current work we describe the RIDME experiments on the bis-Mn2+ complex23 shown in Fig. 2 at W-band (94 GHz, 3.3 T) and J-band (263 GHz, 9.4 T) microwave frequencies. We examined how the multiple quantum components affect the RIDME measurements and compared the performance of these experiments with PELDOR.
Experimental results and discussion
Pulsed EPR spectroscopy
 | ||
| Fig. 4 The 6 K, W-band PELDOR experiments of complex 1 in a deuterated solvent, recorded at different pump–probe frequency offsets and resonance positions in the EPR spectrum (see Fig. 3). (A) The experimental time traces (black) with corresponding mono-exponential background-functions (orange). (B) The background-divided time traces (black) with corresponding fits (red) based on Tikhonov regularization analysis using a regularization parameter of 10. (C) The distance distributions obtained using Tikhonov regularization in the DeerAnalysis36 toolbox. For better visualization, the PELDOR time traces (A and B) and distance distributions (C) have been vertically offset. | ||
| Experiment | Parameter | R max [nm] | ΔR (fwhm) [nm] | λ | SNR/ [h−0.5] |
|---|---|---|---|---|---|
| a Obtained by Tikhonov regularization with kernel function (eqn (4)). b Obtained by Tikhonov regularization with kernel function (eqn (5)). | |||||
| PELDOR | 70 MHz | 2.6 | 0.6 | 0.016 | 60 |
| 150 MHz | 2.6 | 0.6 | 0.017 | 50 | |
| −252 MHz | 2.5 | 0.6 | 0.012 | 70 | |
| RIDME | W-band, 20 μs | 2.5a | 0.6a | 0.308 | 210 |
| W-band, 80 μs | 2.6b | 0.6b | 0.547 | 150 | |
| J-band | 2.5b | 0.6b | 0.373 | 50 | |
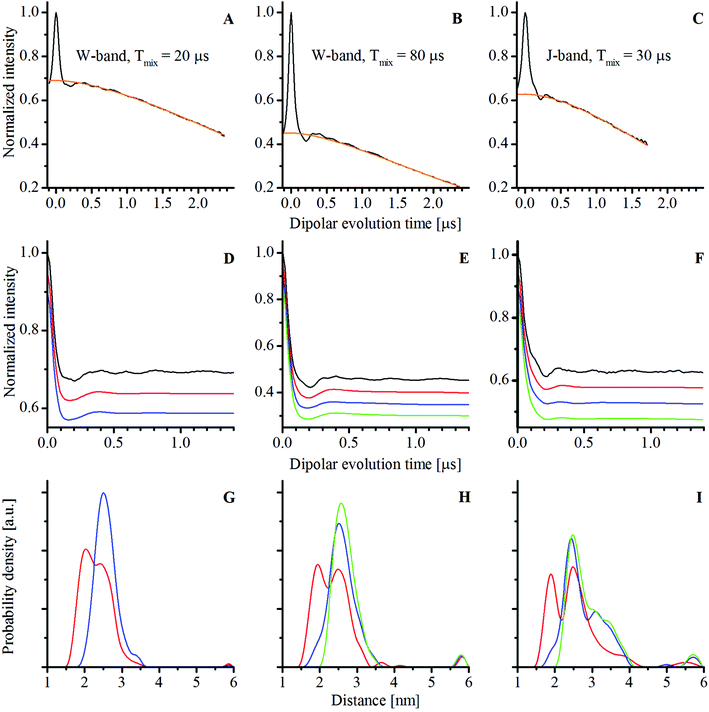
The distance distributions obtained by Tikhonov regularization analysis by the DeerAnalysis36 toolbox are shown in Fig. 4C. The most probable distances were about 2.5–2.6 nm with a full width at half maximum of about 0.6 nm for each PELDOR time trace. The distance distributions were in agreement with the structural predictions.23
The experimental W- and J-band RIDME time traces of complex 1 in a deuterated solvent with corresponding fitted background functions (analytic functions are given in Table S1, ESI†) as well as background-divided time traces are shown in Fig. 6. The W-band time traces were obtained with two different mixing times: 20 μs corresponding roughly to 3 times Tme (left column, Fig. 6) and 80 μs corresponding approximately to the T1e relaxation time at 94 GHz (middle column, Fig. 6). For a shorter mixing time, the dipolar modulation depth was about 30% (Fig. 6D) and for a longer mixing time it was about 55% (Fig. 6E). The experimental modulation depths were larger than the theoretical values (about 10 and 30%, respectively) obtained using eqn (2).27 The higher experimental modulation depths might indicate the influence of the high electron spin of the Mn2+ ion. By comparison, the modulation depth at the J-band was about 37%, while the calculated value was about 30% (with T1e of 30 μs at this frequency).
Analysis of the background-divided RIDME time traces was performed with Tikhonov regularization (see the Experimental section). The distance distributions and back-calculated dipolar evolution functions, based on the Tikhonov analysis with the conventional kernel function (identical to that used in the DeerAnalysis toolbox), given as:
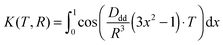 | (3) |
The distance distributions obtained from the RIDME measurements all showed two resolved maxima rather than the one found by PELDOR. Similar complex distance distributions have been reported for RIDME experiments with Gd3+ ions (S = 7/2)24,25 and for the Mn2+ – bis-nitroxide complex.28 This apparent increase in the complexity of the distance distributions has been attributed to multi-quantum longitudinal relaxation of high-spin systems.
The W-band RIDME time trace with a 20 μs mixing time and its analysis are depicted in Fig. 6A, D and G. The peak at about 2.5 nm obtained from Tikhonov regularization analysis with the conventional kernel function (eqn (3)) corresponded to the expected interspin distance.23 The 2.0 nm peak corresponded to the contribution from the second harmonic of the dipolar coupling frequency. In order to test this, the second harmonic of the dipolar coupling frequency was explicitly added to the kernel function for the Tikhonov regularization:
 | (4) |
The W-band RIDME time trace with a 80 μs mixing time (approximately T1e at this frequency) and the analysis based on Tikhonov regularization are shown in Fig. 6B, E and H. As above, the expected 2.5 nm distance is found by Tikhonov analysis with the conventional kernel function (Fig. 6H). Assuming that the first and second harmonics of dipolar coupling frequency are equally weighted, as was the case for the experiment with a 20 μs mixing time, the peak at 2.0 nm again disappeared from the distance distribution when the modified kernel function (eqn (4)) was used (Fig. 6E and H in blue). However unlike for the measurement with a shorter mixing time, there was an additional small shoulder at about 1.8 nm in the distance distribution. To test whether this feature was due to the buildup of a triple quantum relaxation component, a kernel function having an explicit third harmonic contribution given by
 | (5) |
Reduced phase memory time at the J-band with respect to W-band frequencies led to a decrease in sensitivity for RIDME experiments on compound 1. The distance distribution from the 30 μs mixing time J-band RIDME measurements using the conventional (eqn (3)) and modified kernels (eqn (4) and (5)) is shown in Fig. 6F and I (for more detailed analysis of the dependence of the distance distribution on the weight of 2ωdd and 3ωdd components see Section 7.3 of the ESI†). They were similar to the one obtained from 80 μs mixing time W-band measurements, with the most probable distance being consistent with expectations. However, Tikhonov regularization analysis using the conventional kernel function gave a wing that extended from 3 to 4 nm (red curve in Fig. 6I), which was not present in neither of the W-band RIDME measurements. Tikhonov analysis with the modified kernels (eqn (4) and (5)) enhanced the intensity of this wing (blue and green curves in Fig. 6I). A possible cause of this peak might have been the incomplete cancellation of the moving Hahn echo arising from the last two pulses (see the RIDME pulse sequence in Fig. 1) and the refocused stimulated echo due to imperfect phases of the microwave pulses in the 8-step phase cycle. The correction procedure of the J-band time trace is given in Section 8 of the ESI,† the corrected time trace and the Tikhonov regularization analysis are presented in Fig. S29 (ESI†). As can be seen from this figure, when imperfect phases are accounted for, the wing in the distance distribution was nearly completely suppressed.
It is worth noting that all three RIDME time traces had small amplitude oscillations (see Fig. 6D–F). The Fourier transforms of the differences between the experimental RIDME time traces and back calculations revealed multiple peaks in the frequency domain (see Fig. S12, S16, S19, S24 and S27, ESI†). However, the amplitudes of these oscillations were not more than 3% of the amplitude of the dipolar oscillations. These oscillations remained when the long mixing-time W-band RIDME time trace was divided by the short mixing-time one (see Fig. S30, ESI†). This indicated that the amplitude of these oscillations built up with an increasing mixing time. A more detailed analysis of these oscillations is given in Section 7 of the ESI,† where differences in the background-divided RIDME time traces and back-calculations, based on Tikhonov analysis with different kernel functions, are shown (Fig. S11, S15, S18, S23 and S26, ESI†). Measurements on the mono-MnDOTA complex (chemical structure is shown in Fig. S1, ESI†) also had a small amplitude oscillation (see Section 5 of the ESI,† Fig. S6) but with a distinct single frequency of about 1.7 MHz. This frequency corresponded to the 14N hyperfine coupling14 and likely arose from non-coherent ESEEM effects.37 Importantly, the oscillations seen in RIDME (Fig. 6D–F) were so small in amplitude that they did not affect the Tikhonov analysis in any substantive way.
However, RIDME measurements on Mn2+ centers have some disadvantages with respect to PELDOR. Determination of the background function for PELDOR experiments is already a non-trivial task, especially for flexible molecules, which have dipolar oscillations that dampen very quickly. But even in such cases, the PELDOR background functions have only a single component, namely inter-molecular dipolar couplings, which for randomly distributed molecules can be accurately approximated with a mono-exponential function.4,6 By contrast, the background functions of RIDME measurements are more complex, having several different contributions which, as in previous studies,24,25,27 appear to be adequately modeled with a stretched exponential function (analytical functions for the backgrounds are given in Table S1, ESI†). Comparisons of the RIDME and PELDOR background functions are shown in Fig. 6A–C and 4A. One can also see that the RIDME background functions strongly depend on whether the solvent is protonated or deuterated (see Fig. 4). This indicated a strong dependence on the transverse relaxation of the Mn2+ spin. Whereas the RIDME background definition is relatively robust in the case of a deuterated solvent (see Section 14 of the ESI† for the analysis of the influence of differently defined backgrounds on the modulation depth and the results of Tikhonov regularization analysis), a more detailed theoretical understanding of how to model the RIDME background function would be important to minimize the uncertainty in the background-correction procedure, especially for the cases where exchange of the solvent is not possible.
In contrast to PELDOR, RIDME exploits longitudinal relaxation to change the mS state of one of the spins in the pair. In high-spin systems relaxation can effectively change mS not only by ±1, but also by ±2 and higher. This creates additional harmonics of the dipolar coupling frequency in the experimental time trace that can be seen in the distance distribution. For model systems studied previously24,25,28 and in this study (see Fig. 6G–I), the distance can still be precisely extracted from Tikhonov analysis with a conventional kernel function (eqn (3)). However, for more flexible systems, a not uncommon case for biomolecules, these peaks cannot be so easily distinguished. Thus, the Tikhonov analysis with the conventional kernel function can lead to the distance distribution that deviates from the real one, even assuming that the background function has been determined correctly (see Section 12 and Fig. S34 of the ESI,† where this situation is modelled). But this analysis can still be used to make an adequate estimation of the distance, since for flexible systems the distance is initially not well defined. For more precise determination of the distance the Tikhonov regularization with the modified kernel can be of interest. As can be seen from Fig. 6G–I, with this approach the unwanted contributions from the harmonics of the dipolar-coupling frequency can be removed from the distance distributions. However, the weights of the different components vary, depending on the sample and experimental conditions,24–25,28 leading to additional parameters that must be accounted for in the data analysis. Moreover, the more complex background function of RIDME can complicate the analysis of the harmonics contributions of the dipolar coupling, as has been shown in RIDME on a protein labelled with Gd3+ centers.25 Such peculiarities associated with the complex background function and harmonics of the dipolar coupling frequency in RIDME experiments with Mn2+ can make it difficult to obtain meaningful information particularly in flexible biological systems. However, for systems with a relatively rigid structure, where dipolar oscillations are easily seen, RIDME measurements can be quantitatively interpreted and have higher sensitivity compared to PELDOR.
These considerations suggest that Mn2+ – based RIDME measurements are best suited for cases where accurate distances are not required, for example for determining the quaternary structures of proteins or for optimizing labelling conditions. Such applications can be performed more quickly due to the higher sensitivity and relative simplicity of setting up the RIDME experiment. For the cases where accurate distances are needed, RIDME can be complemented with PELDOR, which requires longer measurement times.
Experimental
The concentration of compound 1 was 50 μM in D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol-d8 or H2O
glycerol-d8 or H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol, 4
glycerol, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v
1, v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v with 100 mM HEPES at pD or pH 8. The detailed synthesis of the compound and initial characterization are presented in another study.23 RIDME and PELDOR experiments were performed in a deuterated solvent with the exception of some RIDME time traces shown in Fig. 4.
v with 100 mM HEPES at pD or pH 8. The detailed synthesis of the compound and initial characterization are presented in another study.23 RIDME and PELDOR experiments were performed in a deuterated solvent with the exception of some RIDME time traces shown in Fig. 4.
W-band pulsed EPR measurements
Pulsed EPR experiments at W-band frequencies were performed on a Bruker Elexsys E680 EPR spectrometer, equipped with a Bruker ‘‘power upgrade 2’’ and an Oxford Instruments CF935 flow cryostat. The Hahn echo-detected field-swept EPR spectrum was obtained with 10 and 20 ns pulses, an interpulse delay of 400 ns, 1 shot per point, a pulse repetition time of 11 ms, a sweep width of 0.1 T at a temperature of 25 K.All RIDME experiments were performed with a deadtime-free five pulse sequence at a sample temperature of 25 K.27
The W-band RIDME experiment with a mixing time of 20 μs was conducted with 10 ns and 20 ns π/2 and π pulses, respectively. This short mixing time was about 3Tme time in order to eliminate the transversal component of the magnetization. Hence, the unnecessary echo signals originating from the π/2 pulses of the mixing block and other pulses in the sequence, and, therefore, distortions in the RIDME time traces, are removed. Initial delay between pulses (d1 in Fig. 1) was 400 ns. The initial time position for the mixing block (position of the first π/2 pulse in the block) was 300 ns after the first π pulse. The time delay between the second π/2 in the block and the last π pulse (d3 in Fig. 1) was 2.5 μs. The sequence can be represented: 10 ns-400 ns-20 ns-(300 ns + ΔT)-10 ns-20μs-10 ns-(2.5 μs − ΔT)-20 ns-2.4 μs-echo. The time increment ΔT was 16 ns with 156 number of points. A shot repetition time was 1 ms and the number of shots per point was 100. The 8-step phase cycle protocol27 for the π/2 pulses was used. 55 scans were taken corresponding to a total accumulation time of about 2 hours. For the RIDME experiments with a mixing time of 80 μs on compound 1 in a deuterated solvent, 371 scans were taken corresponding to a total accumulation time of about 14.23 hours. For analogous measurements in a protonated solvent, 507 scans were taken corresponding to a total accumulation time of about 16 hours. All W-band RIDME measurements were performed with the resonance position of the pulses set to the highest field hyperfine line of the central transition.
W-band PELDOR measurements were performed at 6 K using the standard four-pulse, deadtime-free PELDOR/DEER sequence,1,6 with a four-step two-phase cycle.38 The initial interpulse delay (between detection π/2 and π pulses) was 544 ns and the dipolar evolution window was 2226 ns. The initial time delay between the detection π pulse and the pump pulse was 364 ns which was incremented by 16 ns with 100 number of points. The shot repetition time was 800 μs with 100 shots per point. For measurements with a pump–probe frequency offset of 70 MHz, the pump pulse duration was 24 ns and the duration of the π/2 and π detection pulses was 12 and 24 ns. The number of scans was 256 resulting in a total accumulation time of about 2.34 hours. For measurements with a pump–probe frequency offset of 150 MHz, the pump pulse duration was 24 ns and the duration of the π/2 and π detection pulses was 36 and 72 ns. The number of scans was 363 resulting a total accumulation time of about 3.32 hours. For measurements with a pump–probe frequency offset of −252 MHz, the pump pulse duration was 58 ns and the duration of the π/2 and π detection pulses was 30 and 58 ns. The number of scans was 243 resulting in a total accumulation time of about 2.22 hours.
J-band pulsed EPR measurements
J-band RIDME experiments were performed on a 263 GHz Bruker Elexsys E780 pulsed EPR spectrometer. The system is equipped with a 9.4 T superconducting magnet, with a quasi-optical front-end with a microwave power of about 15 mW and an arbitrary waveform generator (AWG). The J-band RIDME experiment with a mixing time of 30 μs was conducted with 18 ns and 32 ns π/2 and π pulses, respectively. Initial delay between pulses (d1 in Fig. 1) was 400 ns. The initial time position for the mixing block (the position of the first π/2 pulse in the block) was 300 ns after the first π pulse. The time delay between the second π/2 in the block and the last π pulse (d3 in Fig. 1) was 2.0 μs. The sequence can be represented: 18 ns-400 ns-32 ns-(300 ns + ΔT)-18 ns-30 μs-18 ns-(2.0 μs − ΔT)-32 ns-1.9 μs-echo. The time increment ΔT was 16 ns with 115 number of points. The shot repetition time was 0.5 ms and the number of shots per point was 100. A 8-step phase cycle protocol27 for the π/2 pulses was used. 930 scans were taken corresponding to a total accumulation time of about 12.95 hours.The J-band RIDME time trace on compound 1 in a protonated solvent (Fig. 4) was obtained with 16 ns and 30 ns π/2 and π pulses, respectively, and a mixing time of 25 μs. All the other parameters were identical to those in the previous case. The number of scans was 1133 resulting to a total acquisition time of about 18 hours. All J-band RIDME time traces were obtained with the resonance position of the pulses set to the lowest field hyperfine line of the central transition. No change in the time traces upon changing the resonance position of the pulses to the highest field hyperfine line was observed.
Tikhonov regularization analysis
The Tikhonov program used in our analysis closely followed the one found in DeerAnalysis.36 This implementation was faster and more flexible with regard to the use of non-conventional kernels. Our implementation was validated by comparing the results against those obtained using DeerAnalysis for a set of PELDOR measurements.Our Fortran-90 program was an adaption of the program FTIKREG39 which minimizes a functional:
| G(P) = ∥KP − F∥2 +λ∥LP∥, | (6) |
| F(T) = K(T,R)P(R) | (7) |
Conclusion
RIDME and PELDOR experiments were performed on a model compound, containing two dipolar-coupled Mn2+ ions. RIDME experiments were performed at W- and J-band microwave frequencies. For the studied system, where the ligand for Mn2+ ion is DOTA, it is advantageous to perform the experiments at W-band frequency, due to a higher electron spin phase memory time at this frequency. A significant influence of the solvent deuteration on the background function was observed for RIDME experiments at both frequencies.Both types of EPR dipolar spectroscopy experiments, RIDME and PELDOR, yielded a distance of 2.5–2.6 nm in good agreement with predictions. RIDME gave a significantly larger modulation depth (up to 55%) with respect to PELDOR (up to 1.7%) that led to a significant gain in sensitivity. In general, RIDME is instrumentationally less demanding than PELDOR, since it does not require a second microwave frequency and an associated increased spectrometer bandwidth. The complex background function and contributions from harmonics of the dipolar coupling frequency can reduce the accuracy of distances determined using RIDME especially in cases where systems are flexible. The harmonic contributions can be accounted for by using a kernel that includes such terms in the Tikhonov analysis, but at the price of increased complexity in interpretation. Based on this, we concluded that the RIDME technique is best suited for the quantitative analysis of relatively rigid systems or cases where accurate distances are less important and sensitivity is of highest priority.
Acknowledgements
This work was supported by a joint ANR/DFG project (MnHFPELDOR, ANR-DFG Chemistry 2011-INTB-1010-01) and DFG (PR 294/14-1), the French Infrastructure for Integrated Structural Biology (FRISBI, ANR-10-INSB-05-01), the CNRS ‘‘Interface PCB’’ program, the DFG Priority Program 1601 (New Frontiers in Sensitivity for EPR Spectroscopy). The W-band EPR spectrometer was funded by the Region Ile-de-France ‘‘Sesame’’ program, the CEA, and CNRS and the J-band EPR spectrometer by the Cluster of Excellence Frankfurt (CEF) Macromolecular Complexes.References
- M. Pannier, S. Veit, A. Godt, G. Jeschke and H. W. Spiess, J. Magn. Reson., 2000, 142, 331 CrossRef CAS PubMed
.
- G. Jeschke, Annu. Rev. Phys. Chem., 2012, 63, 419 CrossRef CAS PubMed
.
- O. Schiemann and T. F. Prisner, Q. Rev. Biophys., 2007, 40, 1 CrossRef CAS PubMed
.
- A. D. Milov, K. M. Salikhov and M. D. Shchirov, Phys. Solid State, 1981, 23, 565 Search PubMed
.
- R. G. Larsen and D. J. Singel, J. Chem. Phys., 1993, 98, 5134 CrossRef CAS
.
- R. E. Martin, M. Pannier, F. Diederich, V. Gramlich, M. Hubrich and H. W. Spiess, Angew. Chem., Int. Ed., 1998, 37, 2833 CrossRef
.
- W. L. Hubbell, A. Gross, R. Langen and M. Lietzow, Curr. Opin. Struct. Biol., 1998, 8, 649 CrossRef CAS PubMed
.
- W. L. Hubbell, C. J. López, C. Altenbach and Z. Yang, Curr. Opin. Struct. Biol., 2013, 23, 725 CrossRef CAS PubMed
.
- G. E. Fanucci and D. S. Cafiso, Curr. Opin. Struct. Biol., 2006, 16, 644 CrossRef CAS PubMed
.
- I. Krstic, B. Endeward, D. Margraf, A. Marko and T. F. Prisner, Top. Curr. Chem., 2012, 321, 159 CrossRef CAS PubMed
.
- S. A. Shelke and T. T. Sigurdsson, Eur. J. Org. Chem., 2012, 2291 CrossRef CAS
.
- A. Raitsimring, C. Gunanathan, A. Potapov, I. Efremenko, J. Martin, D. Milstein and D. Goldfarb, J. Am. Chem. Soc., 2007, 129, 14138 CrossRef CAS PubMed
.
- D. Banerjee, H. Yagi, T. Huber, G. Otting and D. Goldfarb, J. Phys. Chem. Lett., 2012, 3, 157 CrossRef CAS
.
- H. Y. V. Ching, P. Demay-Drouhard, H. C. Bertrand, C. Policar, L. C. Tabares and S. Un, Phys. Chem. Chem. Phys., 2015, 17, 23368 RSC
.
- A. Martorana, Y. Yang, Y. Zhao, Q.-F. Li, X.-C. Su and D. Goldfarb, Dalton Trans., 2015, 44, 20812 RSC
.
- H. Y. V. Ching, F. C. Mascali, H. C. Bertrand, E. M. Bruch, P. Demay-Drouhard, R. M. Rasia, C. Policar, L. C. Tabares and S. Un, J. Phys. Chem. Lett., 2016, 7, 1072 CrossRef CAS PubMed
.
- K. Wieghardt, Angew. Chem., Int. Ed., 1989, 28, 1153 CrossRef
.
-
G. Reed and G. Markham, in Biological Magnetic Resonance, ed. L. Berliner and J. Reuben, 1984, vol. 6, p. 73 Search PubMed
.
- T. Schweins, K. Scheffzek, R. Aßheuer and A. Wittinghofer, J. Mol. Biol., 1997, 266, 847 CrossRef CAS PubMed
.
- C. W. Bock, A. K. Katz, G. D. Markham and J. P. Glusker, J. Am. Chem. Soc., 1999, 121, 7360 CrossRef CAS
.
- G. L. Bir and L. S. Sochava, Phys. Solid State, 1964, 5, 2637 Search PubMed
.
- G. L. Bir, Phys. Solid State, 1964, 5, 1628 Search PubMed
.
- P. Demay-Drouhard, H. Y. V. Ching, D. Akhmetzyanov, R. Guillot, L. C. Tabares, H. C. Bertrand and C. Policar, ChemPhysChem, 2016, 17, 2066 CrossRef CAS PubMed
.
- S. Razzaghi, M. Qi, A. I. Nalepa, A. Godt, G. Jeschke, A. Savitsky and M. Yulikov, J.
Phys. Chem. Lett., 2014, 5, 3970 CAS
.
- A. Collauto, V. Frydman, M. D. Lee, E. H. Abdelkader, A. Feintuch, J. D. Swarbrick, B. Graham, G. Otting and D. Goldfarb, Phys. Chem. Chem. Phys., 2016, 18, 19037 RSC
.
- L. V. Kulik, S. Dzuba, I. Grigoryev and Y. D. Tsvetkov, Chem. Phys. Lett., 2001, 343, 315 CrossRef CAS
.
- S. Milikisyants, F. Scarpelli, M. G. Finiguerra, M. Ubbink and M. Huber, J. Magn. Reson., 2009, 201, 48 CrossRef CAS PubMed
.
- A. Meyer and O. Schiemann, J. Phys. Chem. A, 2016, 120, 3463 CrossRef CAS PubMed
.
- I. Kaminker, I. Tkach, N. Manukovsky, T. Huber, H. Yagi, G. Otting, M. Bennati and D. Goldfarb, J. Magn. Reson., 2013, 227, 66 CrossRef CAS PubMed
.
- M. R. Cohen, V. Frydman, P. Milko, M. Iron, E. H. Abdelkader, M. D. Lee, J. D. Swarbrick, A. Raitsimring, G. Otting, B. Graham, A. Feintuch and D. Goldfarb, Phys. Chem. Chem. Phys., 2016, 18, 12847 RSC
.
- P. E. Spindler, S. J. Glaser, T. E. Skinner and T. F. Prisner, Angew. Chem., Int. Ed., 2013, 52, 3425 CrossRef CAS PubMed
.
- A. Doll, S. Pribitzer, R. Tschaggelar and G. Jeschke, J. Magn. Reson., 2013, 230, 27 CrossRef CAS PubMed
.
- A. Doll, M. Qi, N. Wili, S. Pribitzer, A. Godt and G. Jeschke, J. Magn. Reson., 2015, 259, 153 CrossRef CAS PubMed
.
- A. Doll, M. Qi, S. Pribitzer, N. Wili, M. Yulikov, A. Godt and G. Jeschke, Phys. Chem. Chem. Phys., 2015, 17, 7334 RSC
.
- P. E. Spindler, I. Waclawska, B. Endeward, J. Plackmeyer, C. Ziegler and T. F. Prisner, J. Phys. Chem. Lett., 2015, 6, 4331 CrossRef CAS PubMed
.
- G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. Timmel, D. Hilger and H. Jung, Appl. Magn. Reson., 2006, 30, 473 CrossRef CAS
.
- L. V. Kulik, E. S. Salnikov and S. Dzuba, Appl. Magn. Reson., 2005, 28, 1 CrossRef CAS
.
- E. Matalon, T. Huber, G. Hagelueken, B. Graham, V. Frydman, A. Feintuch, G. Otting and D. Goldfarb, Angew. Chem., Int. Ed., 2013, 52, 11831 CrossRef CAS PubMed
.
- J. Weese, Comput. Phys. Commun., 1992, 69, 99 CrossRef
.
- G. Jeschke, G. Panek, A. Godt, A. Bender and H. Paulsen, Appl. Magn. Reson., 2004, 26, 223 CrossRef CAS
.
- Y.-W. Chiang, P. P. Borbat and J. H. Freed, J. Magn. Reson., 2005, 172, 279 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp05239h |
| ‡ Authors contributed equally to the work. |
| This journal is © the Owner Societies 2016 |