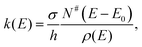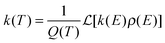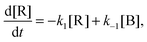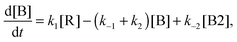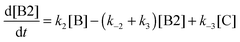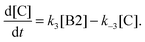Gas phase vibrational spectroscopy of the protonated water pentamer: the role of isomers and nuclear quantum effects

Abstract

We use cryogenic ion trap vibrational spectroscopy to study the structure of the protonated water pentamer, H⁺(H₂O)₅, and its fully deuterated isotopologue, D⁺(D₂O)₅, over nearly the complete infrared spectral range (220–4000 cm⁻¹) in combination with harmonic and anharmonic electronic structure calculations as well as RRKM modelling. Isomer-selective IR–IR double-resonance measurements on the H⁺(H₂O)₅ isotopologue establish that the spectrum is due to a single constitutional isomer, thus discounting the recent analysis of the band pattern in the context of two isomers based on AIMD simulations 〈W. Kulig and N. Agmon, Phys. Chem. Chem. Phys., 2014, 16, 4933–4941〉. The evolution of the persistent bands in the D⁺(D₂O)₅ cluster allows the assignment of the fundamentals in the spectra of both isotopologues, and the simpler pattern displayed by the heavier isotopologue is consistent with the calculated spectrum for the branched, Eigen-based structure originally proposed 〈J.-C. Jiang, et al., J. Am. Chem. Soc., 2000, 122, 1398–1410〉. This pattern persists in the vibrational spectra of H⁺(H₂O)₅ in the temperature range from 13 K up to 250 K. The present study also underscores the importance of considering nuclear quantum effects in predicting the kinetic stability of these isomers at low temperatures.

---

Introduction

How ions are hydrated has intrigued chemists since the birth of the field of Physical Chemistry.¹ Proton hydration, in particular, is of fundamental importance in chemical, biological and atmospheric processes, but the molecular level interpretation of the anomalously high mobility of protons in aqueous solutions remains hotly debated.² Size-selected protonated water clusters, H⁺(H₂O)_n, isolated in the gas phase, play an important role in clarifying the spectroscopic markers that encode the collective mechanics involved in long range proton translocation. The advantage of isolated clusters is that they allow direct spectroscopic characterization of key local hydration motifs that are metastable in solution, but can occur naturally in the size- and temperature-dependent structures of the gas-phase clusters. Since protonated water clusters can be characterized experimentally with high selectivity and sensitivity and are also amenable to higher level quantum chemical calculations, such measurements deliver stringent benchmarks for evaluating the validity of approximations necessary for treating ions in extended solvation environments. However, the widely accepted structural assignment of small protonated water clusters, in particular that of the protonated water tetramer and pentamer, has recently been drawn into question based on the implications of ab initio molecular dynamics (AIMD) simulations.^3,4

In this study, we characterize the gas phase vibrational spectroscopy of the protonated water pentamer over nearly the complete IR spectral range and show experimentally, using an isomer-specific, double resonance technique as well as temperature-dependent measurements (13–250 K), that the observed IR transitions are due to a single spectroscopically unique species. We then address the assignments of the strong bands in the cold spectrum to fundamentals expected for the branched structure originally proposed by Jiang et al.⁵ with the aid of anharmonic spectra from electronic structure calculations. Finally, we use RRKM theory to explore the kinetic stability of the isomers at low temperatures, highlighting the importance of considering nuclear quantum effects.

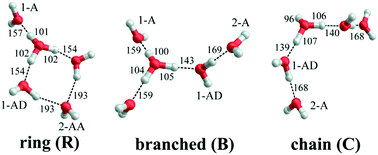
The vibrational spectroscopy of the protonated water pentamer has been studied by several groups. Jiang et al.⁵ measured the infrared photodissociation (IRPD) spectrum of H⁺(H₂O)₅ in the O–H stretching region (2700–3900 cm⁻¹) at an estimated temperature of 170 K. Aided by harmonic vibrational frequencies and intensities from electronic structure calculations, they identified an acyclic, branched isomer (labelled B in Fig. 1) as the signal carrier in the IRPD spectrum. Temperature-dependent measurements confirmed that the IRPD spectrum was free of contributions from other isomers. Subsequently, Headrick et al.⁶ probed colder clusters using argon-tagging. They measured IRPD spectra down into the fingerprint region (1000–3900 cm⁻¹), identifying the evolution of the spectral signature of the hydrated proton with cluster size. These studies confirmed the assignment to the branched isomer B.⁶ The effect of messenger-tagging on the IRPD spectra of protonated water clusters was systematically studied by Mizuse et al. also confirming the presence of a single isomer (B).⁷ Tagging with H₂, Ar and Ne leads to sharper vibrational features due to colder clusters but hardly perturbs the IRPD spectrum. Douberly et al. then studied the effect of deuteration on the band pattern in the IRPD spectrum in the O–D stretching region (2300–2900 cm⁻¹).⁸ They found that the spectra of H⁺(H₂O)₅·Ar and D⁺(D₂O)₅·Ar both agree best with the predicted harmonic spectrum of the branched isomer B and that the contribution from other isomers was insignificant. This is particularly remarkable, since their electronic structure calculations predict that B is not the global minimum energy structure.⁸

Fig. 1 B3LYP-D3/aug-cc-pVTZ minimum-energy structures of the three constitutional isomers discussed in the text. Intramolecular hydronium ion O–H and intermolecular hydrogen bond lengths are reported in pm. Water molecules are classified according to their location in the first (1) or second (2) hydration shell of H₃O⁺, and their function as hydrogen bond acceptor (A) or donor (D).

Electronic structure calculations^3,5,8–13 (Monte Carlo, DFT and MP2) of bare H⁺(H₂O)₅ consistently predicted a cyclic four-member ring with an Eigen core (labelled R in Fig. 1) as the global minimum-energy structure, closely followed by two non-cyclic Eigen isomers: one branched (B: +3.7 kJ mol⁻¹)¹³ and the other non-branched (C: +17 kJ mol⁻¹).¹³ When zero-point energy (ZPE) is considered, the energetic ordering changes and B is found to be 0.3 kJ mol⁻¹ more stable than R.⁸ Such a change in ordering is not found for the perdeuterated analogue because its ZPE is smaller. In both cases, however, B is favoured by entropy and it represents the global minimum above 50 K in terms of free energy.⁸ The comparison of the computed harmonic spectra with the experimental IR spectra, in particular in the O–H (O–D) stretching region, supports the assignment of the protonated water pentamer and of its fully deuterated isotopologue to the branched isomer B.^5–8 The agreement is less satisfactory in the fingerprint region, namely for the Eigen core O–H stretching mode, which involves a displacement towards the single acceptor–single donor (1-AD) H₂O. It is predicted by MP2 calculations to occur about 460 cm⁻¹ above the experimentally observed band at 1885 cm⁻¹.⁶ However, Vibrational Self-Consistent Field calculations (VSCF) accurately recover the red shift of this band, thus supporting the assignment to isomer B.⁶ The complexity of this assignment is apparent, however, by the fact that application of the VPT2 perturbative treatment supports the assignment of a previously unassigned, relatively strong feature at 1470 cm⁻¹ (labelled a₉ in Fig. 3) to the key OH stretching band of the embedded H₃O⁺ moiety.¹⁴ The appearance of such unassigned “extra features” (i.e., those not readily assignable to fundamentals)^6,14 has, in fact raised the spectre that distinct isomers may be in play, and indeed the assignment of the vibrational spectrum to the branched isomer B has recently been challenged by Kulig and Agmon, based on insights derived from AIMD simulations.³ These authors suggest that two other isomers contribute to the observed spectrum: the cyclic Eigen isomer R and the higher energy chain isomer C. A major motivation for the present study was, therefore, to address the heterogeneity in the spectrum of the light isotopologue and to follow how the bands evolve with increasing temperature as well as upon isotopic substitution.

Experimental

IRPD experiments are conducted using a 6 K ion-trap triple mass spectrometer described previously.^15,16 Clusters are produced in a nanospray ion-source using a 10 mM H₂SO₄ in CH₃OH/H₂O (1 : 1, v : v) solution and D₂SO₄ in a CD₃OD/D₂O (2 : 1, v : v) solution for the all-H and all-D isotopologues, respectively. The ions of interest are thermalized at room temperature in a gas-filled ion guide and then mass-selected using a quadrupole mass filter and focused in a radio-frequency (RF) ring-electrode ion-trap. The trap, filled with pure D₂ buffer gas, is cooled with a closed-cycle He cryostat and held at temperatures between 13 K and 250 K. Many collisions of the trapped ions with the buffer gas provide gentle cooling of the internal degrees of freedom close to the ambient temperature and typically avoid the production of kinetically trapped species. At sufficiently low ion-trap temperatures, ion-messenger complexes are formed via three-body collisions.^17,18 All ions are extracted either every 100 ms or 200 ms, depending on the lasers used, and focused both temporally and spatially into the centre of the extraction region of an orthogonally mounted reflectron time-of-flight (TOF) tandem photofragmentation mass spectrometer. Here, the ions are irradiated with a counter-propagating IR laser pulse produced either by one of the two OPO/OPA/AgGaSe₂ IR laser systems¹⁹ (700–4500 cm⁻¹) or by the FHI-FEL (210–3000 cm⁻¹).²⁰ All parent and photofragment ions are then accelerated towards an MCP detector. An IRPD spectrum is recorded by averaging over 50–200 TOF mass spectra per wavelength and scanning the wavelength of the laser pulse. The photodissociation cross section σ_IRPD is determined as described previously.^15,16

The covered spectral range from 220–4000 cm⁻¹ requires the use of three different laser configurations. The individual spectra covering these overlapping spectral regions (200–1000 cm⁻¹, 900–2300 cm⁻¹ and 2000–4000 cm⁻¹) are then scaled in intensity such that the intensity of common peaks match, in order to correct for changes in laser beam/ion cloud overlap.

Alternatively, isomer-specific IR²MS² double resonance measurements^21–23 can be performed using an analogous setup, employing two IR laser pulses.^24,25 The first laser pulse generates a set of photofragment ions, which are separated from parent ions in the 180° reflectron stage of the tandem TOF mass-spectrometer, where they separate in time and space according to their mass-to-charge ratio. They are then refocused between the extraction plates, and the parent ion packet is irradiated with a second, properly timed laser pulse to generate a second set of photofragment ions. All ions located between the acceleration plates are then reaccelerated and mass analysed using the linear TOF stage.^15,16

We used two ways to measure IR²MS² spectra, which differ in the sequence of the probe and scan laser pulses. If the probe pulse (fixed wavelength) interacts with the ions after the scan pulse (tuneable wavelength), the IR²MS² spectrum manifests itself in the form of dips in the otherwise constant fragment ion signal from the probe pulse (ion-dip technique). If the scanned pulse is applied after the probe pulse, then two TOF spectra are acquired, one with and the other without the probe pulse using an additional mechanical chopper (a population-modulation or hole-burning technique). In this case, the IR²MS² spectrum is obtained by subtracting these two TOF spectra. Probe laser pulses with wavenumbers larger than 2300 cm⁻¹ are typically generated with one of the OPO/OPA systems while those at smaller wavenumbers (<2300 cm⁻¹) are produced by the FHI FEL. The macropulse duration of the IR FEL pulses (∼10 μs) requires that the FEL laser beam is aligned counter-propagating to the ion cloud extracted from the trap and prior to acceleration into the tandem TOF mass spectrometer to ensure a sufficient temporal overlap. Hence, the FHI FEL laser pulse always needs to be timed prior to the laser pulse from the OPO/OPA system, which is sufficiently short in duration (∼7 ns) that the fast (few keV) ions can be efficiently irradiated.

Computational methods

Quantum chemistry

Electronic structure calculations were performed using the Gaussian 09 rev. D.01 software package.²⁶ We optimized geometries of a number of energetically low-lying isomers using density functional theory (DFT), in particular, the B3LYP functional²⁷ in combination with the 6-311++G(3df,3pd) and the aug-cc-pVTZ basis sets.^28–31 Additionally, we checked the influence of dispersion interactions by using the D3 version of Grimme's dispersion correction.³² Tight convergence criteria and the “superfine” grid option are employed. We identified transition states (TS) of the unimolecular isomerization reactions by locating first-order saddle points along the reaction coordinate. The reaction paths were followed using the intrinsic reaction coordinate (IRC) method.^33,34 Vibrational harmonic frequencies of minima and TS configurations were computed at the same level of theory. To account for anharmonic effects as well as systematic errors on the harmonic force constants, we determined scaling factors on the basis of a comparison of the IRPD spectra with harmonic spectra of isomer B for both the all-H and all-D isotopologues. Two scaling factors for each method (see Table S4, ESI†), one for the spectral region below 1500 cm⁻¹ (1100 cm⁻¹ for the perdeuterated complex) and one for the higher energy region, were calculated with a least-squares procedure by minimizing the residuals as proposed by Scott and Radom.³⁵ Additionally, we performed anharmonic frequency calculations using the Second-order Vibrational Perturbation Theory (VPT2) method as implemented by Bloino and Barone.³⁶ To obtain more reliable electronic energies and further improve the energetic description of the isomers, we performed CCSD(T)/aug-cc-pVTZ single point calculations at the DFT geometries. Optimized geometries, energies, vibrational spectra, IRC paths and scaling factors are reported in the ESI† (Fig. S1, S2, S4 and S5; Tables S1–S13, ESI†).

RRKM rate constants and kinetics

Microcanonical isomerization rate constants of the protonated water pentamer k(E), where E refers to the internal energy of the system, were calculated using RRKM theory.³⁷ The sequential kinetic scheme consisting of three isomerization equilibria is depicted in Fig. 2. We used CCSD(T) energies of the B3LYP-D3 structures plus the B3LYP-D3 ZPEs, derived from scaled harmonic wavenumbers. To obtain the rate constants, we used the code written by Zhu and Hase,³⁸ using the standard formula:³⁷
where σ is the reaction path degeneracy, E₀ is the unimolecular threshold, N^#(E − E₀) is the TS sum of states and ρ(E) the reactant density of states. N^#(E − E₀) and ρ(E) refer only to active degrees of freedom. The reaction path is doubly degenerate for all isomerizations considered. Note, the contribution from rotational excitation was neglected, since the minima and TS configurations have very similar moments of inertia and thus cancelled out. Indeed, test calculations with different J values provided consistent results. Classical RRKM rate constants were calculated disregarding quantization of vibrational modes with classical state counting. In contrast, to obtain the quantum rate constants, ZPEs were taken into account and state counting was performed with the direct count method using the Beyer–Swinehart algorithm.³⁹

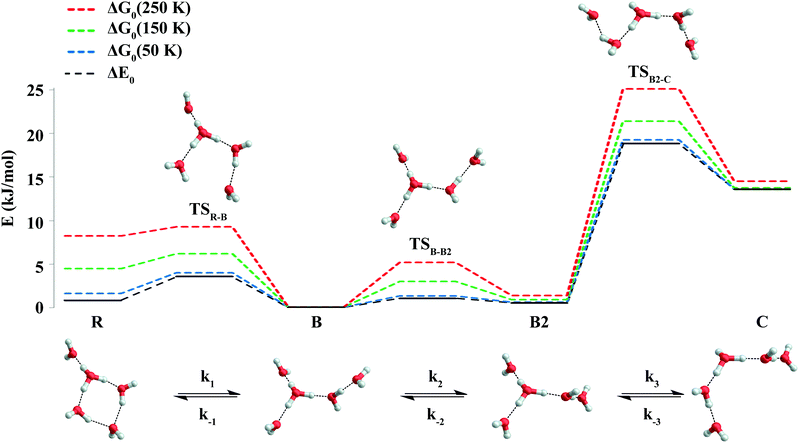Fig. 2 B3LYP-D3/aug-cc-pVTZ minimum-energy and TS structures of the protonated water pentamer discussed in the text. The energy diagram reports relative energies ΔE₀, determined from CCSD(T) energies plus DFT ZPEs, and relative Gibbs free energies (ΔG₀), determined from CCSD(T) energies plus thermal corrections to Gibbs free energies at 50, 150 and 250 K. All energies are given in kJ mol⁻¹ (see Table 2). The bottom panel illustrates the sequence of the equilibrium reactions assumed for the RRKM calculations.

From microcanonical rate constants and densities of states, the canonical rate constants can be expressed as⁴⁰

where is the Laplace transform operator and Q(T) is the partition function, which can be expressed as the Laplace transform of density of states, .

We then solved the four kinetic differential equations associated with the system for different initial conditions to study the kinetic stability of the four isomers:

and

The kinetic constants k₁, k₋₁, k₂, k₋₂, k₃ and k₋₃ of the isomerization reactions considered are defined in Fig. 2. The system of differential equations was numerically solved using the ODE45 solver as implemented in Matlab^41,42 and yields the time evolution of the relative isomer populations.

Results and discussion

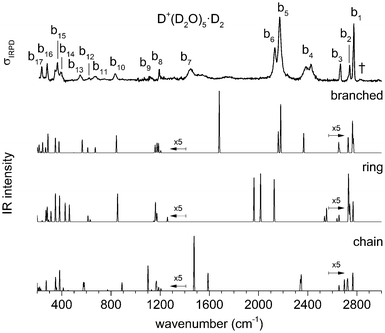
Fig. 3 shows a comparison of the IRPD spectra of the D₂-tagged protonated water pentamer and its fully perdeuterated isotopologue from 210 cm⁻¹ to 4000 cm⁻¹. Band positions are listed in Table 1. For better comparability, a scaling factor (1/1.36) is used for the alignment of the two wavenumber scales, which brings the sharp water bending fundamentals of the two isotopologues (a₈ and b₈) into alignment. The scaling factor is close to the theoretical value of 1/1.37 that is expected for isolated O–H vs. O–D oscillators. The spectra are in good agreement with previous measurements (1000–4000 cm⁻¹ for H⁺(H₂O)₅ and 2300–2900 for D⁺(D₂O)₅) considering the different experimental setups.^5–8 Additionally, the D₂-tagged IRPD spectrum of D⁺(D₂O)₅ (1000–3000 cm⁻¹) measured at the Yale photofragmentation mass spectrometer⁴³ confirms the reproducibility of the experimental results presented here (see Fig. S3, ESI†). The striking resemblance of the two spectra shown in Fig. 3 provides unambiguous evidence that both spectra probe signal carriers with similar structures and, in particular, identical connectivity. Note that the absorption near the key a₉ feature is substantially less intense in the spectrum of the perdeuterated species, as are the weaker features that appear higher in energy, labelled by * and †. Such selectivity in the affected bands could arise from the appearance of a second isomer in the all-H isotopologue, or from the suppression of anharmonic bands in the heavy isotopologue. As mentioned above, Kulig and Agmon³ have recently invoked an assignment scheme for the H⁺(H₂O)₅ based on two isomers (R and C in Fig. 2) and not involving isomer B. We address these key issues of isomeric composition and temperature dependence in the next two sections.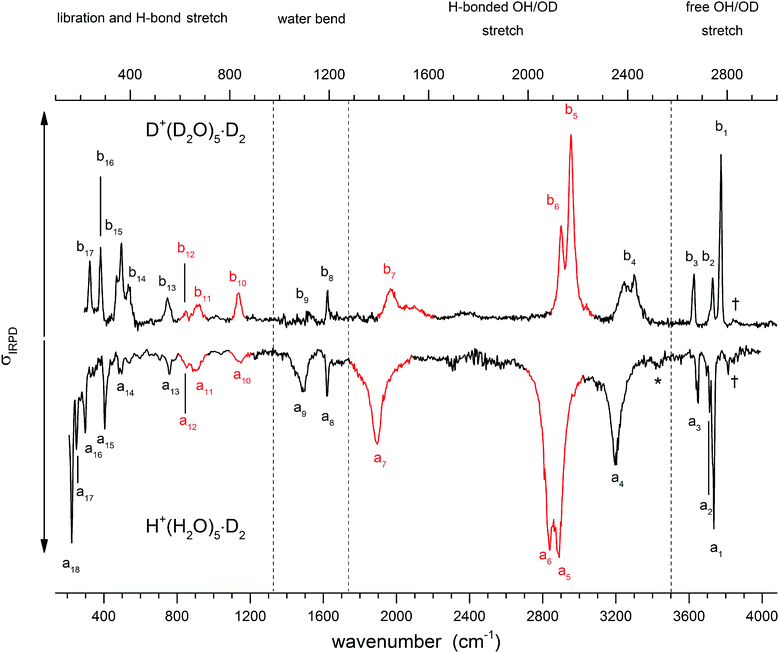

Fig. 3 IRPD spectra of D₂-tagged isotopologues of the protonated water pentamer: D⁺(D₂O)₅ (top) and H⁺(H₂O)₅ (bottom). For better comparability the spectra are plotted against opposing ordinates and the abscissa of the top spectrum has been scaled by 1.36 (see text). Bands coloured red indicate modes assigned to the hydronium ion. See Table 1 for band assignments.

Table 1 Experimental band positions, scaled harmonic vibrational wavenumbers (both in cm⁻¹) and assignments of the features observed in the IRPD of D₂-tagged H⁺(H₂O)₅ and D⁺(D₂O)₅ shown in Fig. 3

Label all-H	Label all-D	Exp. all-H^a	Exp. all-D^a	Theory harm. all-H^b	Theory VPT2 all-H^c	Theory harm. all-D^b	Theory VPT2 all-D^c	Assignment
a Bands position are given with an error of ±5 cm^−1. b B3LYP-D3/aug-cc-pVTZ harmonic wavenumbers of the all-H (all-D) isotopologue, scaled by 0.962 (0.973) above and 0.908 (0.927) below 1500 cm^−1 (1100 cm^−1). c Anharmonic VPT2/B3LYP/6-311++G(3df,3pd). d Only combination bands with intensities higher than 2 km mol^−1 are considered. e Tentative assignment.
†	†	3814	2824		3823, 3825, 3850		2808, 2808, 2810	Combination bands^d (see text)
a1	b1	3732	2775	3737	3694, 3722, 3723	2772	2764, 2759, 2759	Free O–H antisym. H2O stretch (2-A-H2O)
				3727, 3727		2765, 2764		Free O–H antisym. H2O stretch (1-A-H2O)
a2	b2	3710	2741	3703	3748	2729	2720	Free O–H stretch (1-AD-H2O)
a3	b3	3647	2667	3648	3629, 3640, 3639	2658	2657, 2654, 2653	Free O–H sym. H2O stretch (2-A-H2O)
				3640, 3639		2653, 2652		Free O–H sym. H2O stretch (1-A-H2O)
*		3420			3457, 3406			Combination band (see text)
a4	b4	3200	2407	3220	3263	2367	2350	H-bonded O–H stretch (1-AD-H2O)
a5	b5	2883	2175	2973	2862	2180	2115	H-bonded O–H H3O^+ stretch (1-A-H2O)
a6	b6	2837	2133	2908	2826	2161	2097	H-bonded O–H H3O^+ stretch (1-A-H2O)
a7	b7	1889	1446	2238	1548	1681	1328	H-bonded O–H H3O^+ stretch (H3O^+⋯1-AD-H2O)^e
a8	b8	1618	1194	1649, 1627, 1586, 1576, 1568	1598, 1537, 1574, 1583, 1581	1205, 1187, 1175, 1169, 1159	1173, 1160, 1165, 1171, 1158	A-H2O bend
a9	b9	1470	1115	1560	1564	1152	1131	Combination bands and 1-AD-H2O bend^e
a10	b10	1150	836	1134	1126	844	821	H3O^+ umbrella
a11	b11	895	672	913	910	672	686	H3O^+ libration
a12	b12	850	621	834	856	611	627	H3O^+ libration
a13	b13	760	550	768	743	566	567	1-AD-H2O libration
a14	b14	490	392	494	457	377	406	1-AD-H2O libration
a15	b15	405	365	377	397	348	365	HB stretch (1-AD-H2O⋯H3O^+)
a16	b16	298	281	345, 319	326, 307	287, 268	258, 257	HB stretch (1-A-H2O⋯H3O^+)
								1-A-H2O libration^e
a17	b17	248	237	297, 274	261, 304	244, 232	230, 223	HB stretch (1-A-H2O⋯H3O^+)
								1-A-H2O libration^e
a18		226		254, 238	183, −83			HB stretch (1-A-H2O⋯2-A-H2O)
								1-AD-H2O libration^e

---

Double resonance IR²MS² measurements: identifying the number of spectroscopically unique species

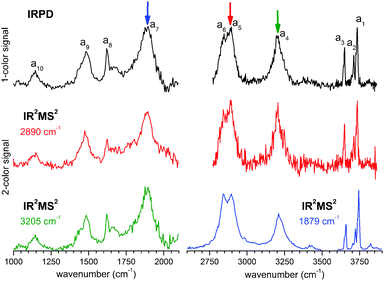
In order to assess how many different isomers contribute to the IRPD spectra of the D₂-tagged protonated water pentamer, we performed isomer-specific IR²MS² measurements.^21–23 More precisely, the method is sensitive to laser-induced population changes that are maintained longer than the delay between the two IR laser pulses (∼10⁻⁵ s). Hence, the IR spectra of more quickly interconverting isomers cannot be isolated using this double resonance technique, but their presence may be indicated by broadening of spectral features (see below).

The results of the IR²MS² experiments are shown in Fig. 4, along with the IRPD spectrum of H⁺(H₂O)₅·D₂ (top trace). The IR²MS² traces are colour-coded to easily identify the probe wavenumber (green: a₄, 3205 cm⁻¹; red: a₅, 2890 cm⁻¹; blue: a₇, 1879 cm⁻¹), which is also indicated by coloured arrows. The choices of the probe wavenumbers were motivated by a previous assignment of these bands to isomers C (a₄ and a₇) and R (a₅) based on AIMD simulations.³ Depending on the laser used for the probe pulse (either OPO/OPA or FEL) we applied different experimental schemes to obtain the isomer specific spectra (see Experimental section), explaining the differences in the signal-to-noise ratios of the traces in Fig. 4. The measured spectra show no distinct differences, thus providing strong evidence for the presence of a single, spectroscopically unique species and hence a single constitutional isomer under the present experimental conditions.

Fig. 4 IRPD (top row) and IR²MS² (middle and bottom row) spectra of D₂-tagged H⁺(H₂O)₅ from 1000 to 2100 cm⁻¹ and from 2600 to 3900 cm⁻¹. Probe energies are indicated by vertical coloured arrows and IR²MS² traces are coloured accordingly.

Empirical band assignments based on isomer B

The persistent bands across both isotopologues are readily assigned in the context of those expected for isomer B. Three sharp peaks with characteristic spacing and relative intensities (a₁–a₃/b₁–b₃) are found at highest energy in the free O–H/O–D stretch region. Further to the red, the next four features (a₄–a₇/b₄–b₇) are attributed to hydrogen-bonded (H-bonded) O–H/O–D stretches and appear broader, as is typical for modes that contain embedded OH groups. The sharp transitions (a₈/b₈) are associated with the water bending modes. Characteristic triplets (a₁₀, a₁₁, a₁₃/b₁₀, b₁₁, b₁₃) emerge in the high energy part of the libration region, of which band a₁₀/b₁₀ corresponds to the umbrella mode of the Eigen core (see Table 1). Interestingly, the peaks at lowest energy, i.e. a₁₅–a₁₈/b₁₅–b₁₇, are among the sharpest in the IR spectrum, similar to the corresponding bands observed in the IRPD spectrum of H⁺(H₂O)₆.²² The weak features just above the highest energy free O–H (O–D) stretches (see † band in Fig. 5) are often observed in cationic water clusters. They originate from excitation of the frustrated rotations of the single acceptor water molecules in combination with the antisymmetric O–H stretch.⁴⁴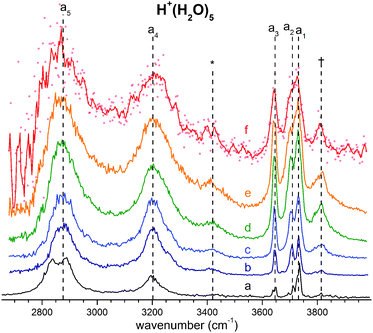

Fig. 5 (b–f) Temperature-dependent IRMPD spectra of H⁺(H₂O)₅ in the O–H stretching region recorded by varying the trap temperature in 50 K steps from 50 to 250 K. (a) The D₂-predissociation spectrum at 13 K is reported for comparison. See Table 1 for band labels and assignments.

The strongly isotope-dependent feature, the a₉/b₉ pair near 1400 cm⁻¹, is much more intense in the all-H isotopologue. This is important because, as mentioned above, the assignment of a₇ and a₉ has been controversial, with VSCF theory supporting the assignment of a₇ to the OH stretch of the embedded Eigen motif⁶ in B, while a VPT2 treatment¹⁴ suggested that a₉ was a more likely candidate. In either case, one of these features remains unassigned. The persistence of the a₇/b₇ pair, however, strongly argues for that feature as the bonded OH stretch, because it appears with the shift and intensity expected for an anharmonic fundamental, while b₉ is much weaker in the spectrum of the heavy isotope. This suggests that the transitions contributing to band a₉ predominantly arise from anharmonicities that are suppressed as the range of the vibrational zero-point wavefunction is reduced upon deuteration. The reduction of anharmonicities is also reflected by the difference in the scaling factors obtained for the two isotopologues (See Table 1 and Table S4, ESI†). When comparing the calculated values at the same level of theory for the two species, the method-related contributions to the scaling factor cancel out. The result is an evaluation of the change in anharmonicity upon deuteration, which amounts to ∼20–30% smaller anharmonicities in the heavier isotopologue.

Temperature-dependent IRMPD spectra: the role of entropy

In order to probe how the anharmonicity-induced bands respond to temperature, we measured vibrational spectra at five ion trap temperatures in-between 50 and 250 K. Fig. 5 shows the temperature-dependent infrared multiple photon photodissociation (IRMPD) spectra of H⁺(H₂O)₅ in the O–H stretching region (2650–4000 cm⁻¹). The IRMPD spectrum measured at 50 K is similar to the IRPD spectrum of D₂-tagged H⁺(H₂O)₅ obtained at 13 K, confirming that the D₂-tag has a minor influence on the vibrational spectrum as well as the energetic ordering of the lowest-lying isomers. At higher temperatures, band broadening due to thermal rotational and low-energy vibrational excitation is observed leading, for example, to a coalescence of bands a₁ and a₂ above 150 K. Interestingly, the combination bands, labelled with an asterisks and a dagger in Fig. 5, gain substantially in relative intensity with increasing temperature, which is consistent with their oscillator strengths being derived from large amplitude displacements. Here, increasing temperature plays a role analogous to that attributed to isotopic modulation of the displacements available in the vibrational ground state. Besides these minor temperature effects, the overall appearance of the IRMPD spectra remain quite similar up to 250 K, providing no clear experimental indication for a significant change in relative isomer populations up to 250 K. Hence, we find no experimental evidence for the presence of multiple isomers, in agreement with all previous spectroscopic studies.^5–8

Assignment of the vibrational spectrum of D⁺(D₂O)₅·D₂

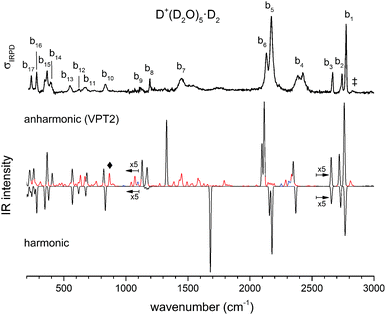
Much of the confusion regarding the assignment of the vibrational spectra of protonated water clusters arises from the fact that standard quantum computational approaches, due to their approximate nature, do not fully recover the pronounced anharmonic effects in these systems.⁴⁵ With this in mind, we first evaluate which single isomer yields the best fit vibrational spectrum before discussing the remaining discrepancies, and then assess if this is a reasonable choice regarding its thermodynamic and kinetic stability.

The vibrational spectrum of the protonated water pentamer has been extensively discussed in the literature.^5–8 Therefore, we focus on the description of the IRPD spectrum of the fully deuterated isotopologue here. Fig. 6 shows a comparison of the IRPD spectrum of the D₂-tagged perdeuterated water pentamer (top trace) with the B3LYP-D3/aug-cc-pVTZ harmonic vibrational spectra of the B, R and C isomers (see Fig. 1) in the range from 215 to 3000 cm⁻¹. The experimental spectrum shows seventeen distinct absorption features labelled with b₁ to b₁₇. Band positions and assignments are summarized in Table 1. The calculated harmonic spectrum of B provides the best fit, reproducing nearly all the main features observed in the experiment, in particular the new experimental data in the far IR region (see also Fig. 8). Three sharp peaks, b₁, b₂ and b₃, are found at the high energy end of the spectrum, in the free O–D stretching region. The band positions and relative intensities of these modes are very sensitive to the environment of a particular water molecule. With this in mind, it is worth noting that the calculated harmonic spectrum of B is the only one that reproduces the characteristic spectral pattern of these bands. Features b₄, b₅, b₆ and b₇ correspond to the hydrogen-bonded O–D stretches. b₄ arises from the O–D stretch of the 1-AD water. The symmetric and antisymmetric combination of the two O–D stretches of the D₃O⁺ core towards the 1-A waters are responsible for peaks b₅ and b₆. b₇ corresponds to the third O–D stretch of the D₃O⁺ core (towards 1-AD-D₂O) and shows the largest deviation (+235 cm⁻¹) from the experiment. Once again, this discrepancy highlights the fact that the structure associated with these motions is not well described within either the harmonic approximation or the VPT2 approach (vide infra). The sharp feature b₈ is assigned to D₂O and D₃O⁺ bending modes, although the calculated spectrum does not reproduce the relative intensities very well. b₉ is most strongly affected by isotopic substitution and only a weak feature remains in the all-D spectrum, which we tentatively attribute to the AD-D₂O bend. Band b₁₀, which spans the range from 810 to 855 cm⁻¹, arises from the umbrella motion of the hydronium core. In the libration region, features b₁₁/b₁₂ and b₁₃/b₁₄ correspond to frustrated rotations of D₃O⁺ and AD-D₂O, respectively. The sharp features b₁₅ and b₁₇ are assigned to hydrogen bond stretches involving D₃O⁺ coupled to terminal water librations.

Fig. 6 IRPD spectra of D₂-tagged D⁺(D₂O)₅ in the region from 215 to 3000 cm⁻¹ compared to the scaled (0.922 below 1100 cm⁻¹ and 0.974 above) B3LYP-D3/aug-cc-pVTZ harmonic spectra for the three isomers B (branched), R (ring) and C (chain) discussed in the text. Traces below 1400 cm⁻¹ and above 2580 cm⁻¹ are shown with a vertical magnification of ×5 for better visibility.

Fig. 7 shows a comparison of the IRPD spectrum (top trace) with the VPT2/B3LYP/6-311++G(3df,3pd) vibrational spectrum (anharmonic) of D⁺(D₂O)₅ (middle trace) and the scaled harmonic one obtained at the corresponding level of theory (bottom trace). Anharmonic combination bands and overtones are colour coded in red and blue, respectively. The feature recorded at 2824 cm⁻¹ and labelled with a dagger arises from combination bands of the O–D antisymmetric stretching modes of the 1-A-D₂O molecules with two terminal D₂O librations (50 and 54 cm⁻¹). The additional structure observed for band b₄ is rather well reproduced by the VPT2 calculation, revealing substantial contribution from combination bands. Note, the four hydrogen-bonded O–D stretching modes are consistently computed too low in energy. In particular the strong red shift of the hydrogen-bonded O–D stretch of the D₃O⁺ towards the 1-AD-D₂O (b₇) is overestimated by about 120 cm⁻¹. Several combination bands account for the broad and weak structure to the blue of band b₇. The position of the two water bend peaks, b₈ and b₉, is also improved by including anharmonic effects. The combination of a libration mode of the 1-AD water molecule with the hydrogen bond stretch involving the same water molecule and D₃O⁺ gives rise to a calculated peak at 867 cm⁻¹ (labelled ◆ in Fig. 7) which is not observed in the experimental spectrum. Finally, the positions and relative intensities of bands b₁₄, b₁₅, b₁₆ and b₁₇ are better reproduced by the anharmonic calculations. Summarizing, the anharmonic calculations support our spectral assignments based on the presence of a single constitutional isomer and provide further insight into some of the details of the vibrational spectrum of D⁺(D₂O)₅. However, besides overestimating the exceptional red shift of band b₇, two low energy fundamental modes, as well as their overtones and combination bands, are predicted to have negative energy. Furthermore, the obtained intensities of two other low energy modes are unreasonably high (on the order of 200 000 km mol⁻¹). The VPT2 calculation showed poorer performance when applied to the light isotopologue or employing the aug-cc-pVTZ basis set, resulting in additional negative energy and high intensities. The a₇ mode is most unstable with respect to correction at the VPT2 level, raising the possibility that the levels involving this motion require inclusion of higher order terms in the potential to converge on the experimentally observed band location. A comparison of the harmonic and VPT2 anharmonic frequencies and intensities obtained with the two basis sets is reported in Tables S5 and S6 (ESI†).

Fig. 7 IRPD spectrum of D₂-tagged D⁺(D₂O)₅ in the region 215 to 3000 cm⁻¹ (top trace) compared to the anharmonic (middle trace) and the scaled (0.92/0.97) harmonic spectrum (bottom trace) of the branched isomer B calculated at the B3LYP/6-311++G(3df,3pd) level of theory. Combination bands and overtones in the VPT2 spectrum are coloured in red and blue, respectively. Traces below 1085 cm⁻¹ and above 2600 cm⁻¹ are shown with a vertical magnification of ×5 for better visibility.

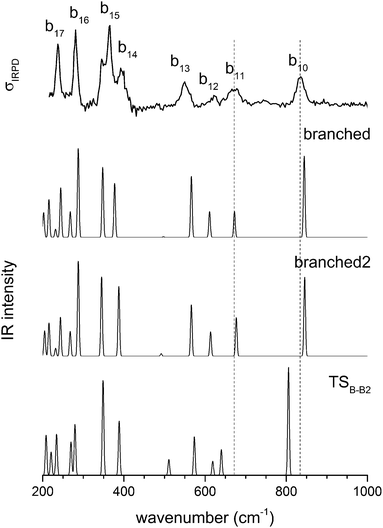
A conformational isomer of B, referred to as B2, with an almost identical vibrational spectrum (see Fig. 8), is obtained by rotating the 1-AD/2-A waters by roughly 180 degrees around an axis parallel to the hydrogen bond between the D₃O⁺ and the 1-AD water (see Fig. 2). The two branched rotamers are approximately isoenergetic and the low barrier between them can easily be overcome, even at the low temperatures of the experiment, as is supported by the kinetic model (see below). The system is thus expected to be so fluxional that it can explore all the configurations connecting the two structures. This fluxionality is likely the cause of the broadening of bands b₁₀ and b₁₁. The corresponding vibrational modes show a shift in wavenumber of 39 and 37 cm⁻¹, respectively, upon isomerization viaTS_B-B2 (see Fig. 8). We thus refine our assignment of the structure of D⁺(D₂O)₅ and note the fluxional character of the branched structure.

Fig. 8 IRPD spectrum of D₂-tagged D⁺(D₂O)₅ in the region 215 to 1000 cm⁻¹ compared to the scaled B3LYP-D3/aug-cc-pVTZ harmonic spectra for the two versions of the branched isomer and the TS between them.

The assignments of the fundamentals in the all-D isotopologue spectrum are useful in unravelling the origin of the more complex band patterns in the all-H system. Because all of the bands in the latter are demonstrated by IR²MS² to arise from the same carrier, the “extra” bands in the light isotopologue must be due to overtone and combination bands induced by anharmonic coupling. For example, the feature labelled with an asterisk denotes a combination band and, as mentioned above, is present only in the IRPD spectrum of H⁺(H₂O)₅·D₂. Anharmonic VPT2 calculations on the all-H isotopologue predict several active combination bands in this region. The main contribution stems from the combination of the hydrogen-bonded O–H stretch 1-AD-H₂O (a₄) with two low energy modes. One of these is the frustrated rotation of a 1-A-H₂O combined with the hydrogen bond stretch between the 1-AD and the 2-A water molecules and the second is the frustrated rotation of the 2-A water. In the spectrum of the perdeuterated species only the latter combination band has some IR intensity but falls under the broad feature b₄.

RRKM calculations and kinetic modelling

The relative B3LYP and CCSD(T) energies of the three lowest energy isomers of the protonated water pentamer B, R and C and the first-order transition states TS_R-B and TS_B-C, connecting the corresponding potential minima, are listed in Table 2 (see also Table S1, ESI†). For the branched isomer, two nearly isoenergetic structures, labelled B and B2 in Fig. 2 and Table 1, exist, separated by a shallow barrier (TS_B-B2: 1.0 kJ mol⁻¹). As we show later, only these conformational isomers B and B2 are predicted to be kinetically stable at low temperature, while the constitutional isomers R and C are not.

Table 2 Relative B3LYP and CCSD(T) electronic energies (in kJ mol⁻¹) without ZPE (ΔE), CCSD(T) electronic energies with ZPE (ΔE₀), and Gibbs free energies (ΔG₀) of the B3LYP-D3/aug-cc-pVTZ minimum energy and first order transition state structures considered in this work

Species	ΔE (B3LYP)	ΔE (CCSD(T))	ΔE0 (H, harm)^a	ΔG0 (H, 150 K)^b	ΔE0 (D, harm)	ΔG0 (D, 150 K)^b
a ZPE is calculated using scaled harmonic B3LYP-D3/aug-cc-pVTZ wavenumbers. b The thermal energy contributions are calculated at 0.001 atm and with a vibrational scaling factor of 0.962 (0.973) for the all-H (all-D) isotopologue. Note the different scaling below 1500 in Table 1.
R	0.0	0.0	+0.8	+4.5	0.0	+3.5
B	+4.6	+4.5	0.0	0.0	+0.5	0.0
B2	+4.5	+4.4	+0.5	+0.9	+0.9	+0.8
C	+18.0	+19.9	+13.6	+13.7	+14.7	+14.6
TSR-B	+7.0	+6.5	+3.5	+6.2	+3.6	+5.9
TSB-B2	+5.9	+5.9	+1.0	+3.0	+1.6	+3.1
TSB2-C	+22.4	+23.3	+18.8	+21.4	+18.9	+21.9

---

R represents the global minimum energy structure on both the B3LYP and presumably the CCSD(T) potential energy hypersurfaces (see Table 2). However, B is stabilized relative to R, when (harmonic) ZPE is taken into account reducing the energy difference to less than 1 kJ mol⁻¹, making them nearly isoenergetic. While the level of theory used here is not sufficiently accurate to predict the energetic ordering of B and R at 0 K, it is apparent that B is entropically favoured over R at higher temperatures (see Gibbs free energies ΔG₀, equilibrium constants K₀ and Boltzmann weighted populations P₀ in Table 2 and Tables S2, S3, ESI†). Moreover, the free energy difference between B and C remains nearly constant and larger than 10 kJ mol⁻¹, indicating that C can only be spectroscopically probed at low temperature if it is kinetically trapped behind the ∼5 kJ mol⁻¹ barrier.

The RRKM canonical rate constants are shown in Fig. 9: panel (a) depicts the results obtained from the quantum treatment (i.e. quantum density and sum of vibrational states and inclusion of ZPE) while panel (b) displays the ones from the classical approach (i.e. classical density and sum of rovibrational states and no inclusion of ZPE). In particular, rate constants are reported as a function of the temperature for the forward and backward elementary reactions of the three isomerization pathways considered (see Fig. 2). Microcanonical rate constants are reported in Fig. S6 (ESI†). First, we analyse the quantum case. It is helpful to compare the two rate constants for opposite directions of the same isomerization process at the same temperature. For example, the fact that k₁ exceeds k₋₁ by one to three orders of magnitude indicates a preference for the branched isomer B over the ring isomer R across the entire energy range considered. On the other hand, similar values for k₂ and k₋₂ suggest that the conformational isomers B and B2 will rapidly interconvert. k₃ and k₋₃ show the largest difference, in particular at low energies (or temperature), revealing that the chain isomer C will convert nearly completely to the branched conformers B and B2. The main difference between the classical and the quantum treatment is found in the low temperature region, where the classical rate constants are smaller. As expected, the values of the classical and quantum rate constants approach each other with increasing temperature.

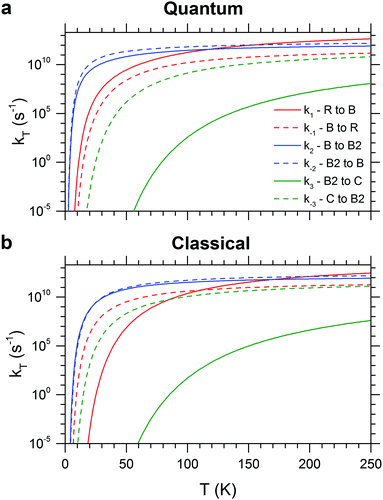Fig. 9 Quantum (a) and classical (b) canonical rate constants obtained with RRKM calculations for the forward and backward elementary reactions of the three isomerization pathways considered (see Fig. 2).

The most striking difference between the classical and quantum RRKM calculations manifests itself in the rate constants for the R/B isomerization reaction, which leads to a qualitatively different kinetic stability at low energies (temperatures). In the absence of ZPE R, the global minimum energy structure, is also the kinetically preferred isomer, which is reflected in a larger isomerization rate constant for the back reaction (k₋₁ > k₁) forming R at low energies (temperatures). The rate constants are equal at 40 kJ mol⁻¹ (111 K) and above this energy (temperature) the forward reaction leading to B is preferred (k₁ > k₋₁).

The kinetic stability of each isomer at 50 K is evaluated in Fig. 10 for the quantum (upper row) and the classical case (lower row). Independent of the initially prepared constitutional isomer, R (left column), B/B2 (center column) or C (right column) the thermodynamic limit is reached within a few tens of nanoseconds with the exception of the quantum case for isomer C, where it is reached in several microseconds. B/B2 are predominantly formed for the quantum case, while interconversion to R is dominant in the classical case.

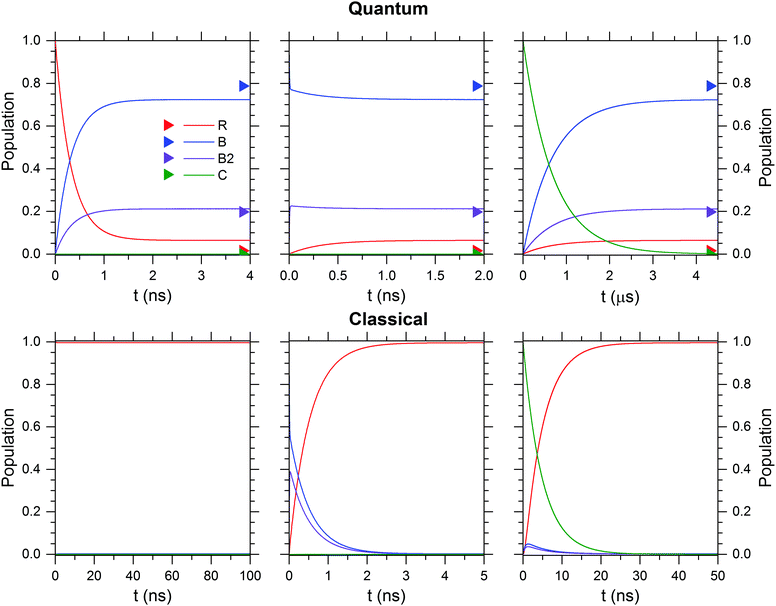Fig. 10 The kinetic stability of the isomers R, B, B2 and C is tested with a kinetic model that uses either quantum (top row) or classical (bottom row) rate constants obtained from RRKM calculations at 50 K. Boltzmann weighted populations at 50 K obtained from relative Gibbs free energies (see Table S2, ESI†) are indicated by colour-coded triangles.

We also tested the effect of the quality of the potential energy surface on the RRKM calculation by using the energies obtained without dispersion correction or with different basis sets (e.g. 6-311++G(3df,3pd)). This leads to small changes in the relative energies and thus the respective equilibrium constants, which in return can lead to slightly larger numbers for the population of R in the quantum case. The equilibration times are also affected, but overall the results remain in qualitative agreement. A more thorough description of the details and the results of the RRKM calculations, also involving higher energy isomerization reactions, lies outside the scope of the present study and will be part of a separate publication.

Summarizing, the results of the RRKM calculations lead to two important insights. First, the kinetic stability of the considered isomers below 100 K changes dramatically, when nuclear quantum effects in the form of ZPE are considered. Second, isomer C is not kinetically stable (on a microsecond timescale) at 50 K.

Summary and conclusions

We have shown that the IRPD spectra of the D₂-tagged protonated water pentamer and its fully deuterated isotopologue probe the same spectroscopic species that is most consistent with a branched structure, consisting of two conformational isomers that interconvert readily on the time scale of the experiment.

Harmonic DFT calculations of the branched isomer B reproduce the IRPD spectra of the D₂-tagged H⁺(H₂O)₅ and D⁺(D₂O)₅ with reasonable agreement, with the exception of bands a₇/b₇ and a₉/b₉. The strong feature a₉ just below the intramolecular HOH bending mode in H⁺(H₂O)₅, previously attributed to an H-bonded OH fundamental of the Eigen core,¹⁴ is dramatically suppressed in the perdeutero isotopologue, indicating that it contains significant contributions arising from anharmonic coupling, while the higher energy feature (a₇/b₇) is the fundamental associated with this oscillator. Anharmonic VPT2 calculations accurately account for most of the features across the D⁺(D₂O)₅ spectrum. However, this approach overestimates the pronounced red shift of mode b₇. It also performs considerably worse in reproducing the H⁺(H₂O)₅ spectrum, since anharmonic effects are more pronounced here as a result of the larger displacements in both the ground and excited vibrational states. In summary, higher level anharmonic calculations are necessary to achieve satisfactory convergence between experiment and theory for the IR spectra of the protonated water pentamer, similar to the archetypal case of H₅O₂⁺.⁴⁵

A simple kinetic treatment shows that for a reliable understanding of the equilibrium dynamics between the various isomers of the protonated water pentamer, nuclear quantum effects must be taken into account at low temperature. Hence, conclusions derived from standard AIMD simulations, which make use of quantum mechanics (at the DFT level) for the electronic structure, but treat nuclear motion in a pure Newtonian way, can be unreliable when dealing with (i) effects that result from the quantum nature of protons and/or (ii) kinetically unstable isomers. A step closer to convergence between experiment and theory could certainly be achieved by the application of path integral molecular dynamics simulations (as well as related methods)^46–50 to the present system, thus including the quantum dynamics of the nuclei.

Acknowledgements

This research is supported by the Collaborative Research Center 1109 of the German Research Foundation DFG. MAJ thanks the U.S. Department of Energy under grant DE-FG02-06ER15800.

References

1. S. Arrhenius, Z. Phys. Chem., 1887, 1, 631–649.
2. M. Thamer, L. De Marco, K. Ramasesha, A. Mandal and A. Tokmakoff, Science, 2015, 350, 78–82.
3. W. Kulig and N. Agmon, Phys. Chem. Chem. Phys., 2014, 16, 4933–4941.
4. W. Kulig and N. Agmon, J. Phys. Chem. B, 2014, 118, 278–286.
5. J.-C. Jiang, Y.-S. Wang, H.-C. Chang, S. H. Lin, Y. T. Lee, G. Niedner-Schatteburg and H.-C. Chang, J. Am. Chem. Soc., 2000, 122, 1398–1410.
6. J. M. Headrick, E. G. Diken, R. S. Walters, N. I. Hammer, R. A. Christie, J. Cui, E. M. Myshakin, M. A. Duncan, M. A. Johnson and K. D. Jordan, Science, 2005, 308, 1765–1769.
7. K. Mizuse and A. Fujii, J. Phys. Chem. A, 2012, 116, 4868–4877.
8. G. E. Douberly, R. S. Walters, J. Cui, K. D. Jordan and M. A. Duncan, J. Phys. Chem. A, 2010, 114, 4570–4579.
9. G. Corongiu, R. Kelterbaum and E. Kochanski, J. Phys. Chem., 1995, 99, 8038–8044.
10. M. P. Hodges and D. J. Wales, Chem. Phys. Lett., 2000, 324, 279–288.
11. J.-L. Kuo and M. L. Klein, J. Chem. Phys., 2005, 122, 024516.
12. A. Bankura and A. Chandra, Chem. Phys., 2011, 387, 92–102.
13. R. A. Christie and K. D. Jordan, J. Phys. Chem. A, 2001, 105, 7551–7558.
14. J. A. Fournier, C. T. Wolke, M. A. Johnson, T. T. Odbadrakh, K. D. Jordan, S. M. Kathmann and S. S. Xantheas, J. Phys. Chem. A, 2015, 119, 9425–9440.
15. N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2015, 34, 1–34.
16. N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2016, 35, 507.
17. M. Brümmer, C. Kaposta, G. Santambrogio and K. R. Asmis, J. Chem. Phys., 2003, 119, 12700–12703.
18. D. J. Goebbert, T. Wende, R. Bergmann, G. Meijer and K. R. Asmis, J. Phys. Chem. A, 2009, 113, 5874–5880.
19. W. R. Bosenberg and D. R. Guyer, J. Opt. Soc. Am. B, 1993, 10, 1716–1722.
20. W. Schöllkopf, S. Gewinner, H. Junkes, A. Paarmann, G. von Helden, H. Bluem and A. M. M. Todd, Proc. SPIE, 2015, 9512, 95121L.
21. B. M. Elliott, R. A. Relph, J. R. Roscioli, J. C. Bopp, G. H. Gardenier, T. L. Guasco and M. A. Johnson, J. Chem. Phys., 2008, 129, 094303.
22. N. Heine, M. R. Fagiani, M. Rossi, T. Wende, G. Berden, V. Blum and K. R. Asmis, J. Am. Chem. Soc., 2013, 135, 8266–8273.
23. N. Heine, M. R. Fagiani and K. R. Asmis, J. Phys. Chem. Lett., 2015, 6, 2298–2304.
24. D. J. Goebbert, G. Meijer and K. R. Asmis, AIP Conf. Proc., 2009, 1104, 22–29.
25. D. J. Goebbert, E. Garand, T. Wende, R. Bergmann, G. Meijer, K. R. Asmis and D. M. Neumark, J. Phys. Chem. A, 2009, 113, 7584–7592.
26. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, USA, 2009.
27. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
28. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
29. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
30. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
31. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
32. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
33. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
34. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
35. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513.
36. J. Bloino and V. Barone, J. Chem. Phys., 2012, 136, 124108.
37. T. Baer and W. L. Hase, Unimolecular Reaction Dynamics. Theory and Experiments, Oxford University Press, New York, 1996.
38. L. Zhu and W. L. Hase, QCPE bulletin, 1994, 644.
39. T. Beyer and D. F. Swinehart, Commun. ACM, 1973, 16, 379.
40. W. Forst, J. Phys. Chem., 1982, 86, 1771–1775.
41. L. Shampine and M. Reichelt, SIAM J. Sci. Comput., 1997, 18, 1–22.
42. MATLAB version 8.4 (R2014b), The MathWorks, Inc., Natick, Massachusetts, 2014.
43. A. B. Wolk, C. M. Leavitt, E. Garand and M. A. Johnson, Acc. Chem. Res., 2014, 47, 202–210.
44. P. D. Carnegie, A. B. McCoy and M. A. Duncan, J. Phys. Chem. A, 2009, 113, 4849–4854.
45. O. Vendrell, F. Gatti and H.-D. Meyer, Angew. Chem., Int. Ed., 2007, 46, 6918–6921.
46. S. D. Ivanov, I. M. Grant and D. Marx, J. Chem. Phys., 2015, 143, 124304.
47. S. D. Ivanov, A. Witt and D. Marx, Phys. Chem. Chem. Phys., 2013, 15, 10270–10299.
48. J. M. Bowman, B. J. Braams, S. Carter, C. Chen, G. Czakó, B. Fu, X. Huang, E. Kamarchik, A. R. Sharma, B. C. Shepler, Y. Wang and Z. Xie, J. Phys. Chem. Lett., 2010, 1, 1866–1874.
49. D. Marx and M. Parrinello, J. Chem. Phys., 1996, 104, 4077–4082.
50. O. Vendrell, M. Brill, F. Gatti, D. Lauvergnat and H.-D. Meyer, J. Chem. Phys., 2009, 130, 234305.

---

Footnotes

† Electronic supplementary information (ESI) available: A PDF file with Fig. S1–S6 and Tables S1–S13. See DOI: 10.1039/c6cp05217g

‡ Present address: Chemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA.

---