Excited-state relaxation of the solar cell dye D49 in organic solvents and on mesoporous Al₂O₃ and TiO₂ thin films

Abstract

We present an ultrafast UV-Vis-NIR transient absorption study of the donor–acceptor solar-cell dye D49 in diisopropyl ether, THF and acetonitrile, as well as on mesoporous Al₂O₃ and TiO₂ thin films. Photoexcitation at 505 nm initially populates the first electronically excited state of the dye having significant intramolecular charge transfer character (“S₁/ICT”). On Al₂O₃ and in the three organic solvents, the dynamics are fully explained in terms of S₁/ICT stabilisation (by reorientation of adjacent solvent or D49 molecules and collisional cooling), intramolecular vibrational redistribution and S₁/ICT → S₀ electronic decay. A substantial decrease of the S₁/ICT lifetime is observed with increasing polarity of the surrounding medium suggesting an acceleration of internal conversion. In agreement with these results, the addition of the nonpolar co-adsorbent deoxycholic acid (DCA) to the Al₂O₃ surface leads to a substantial increase of the S₁/ICT lifetime. DCA spacers reduce the local polarity around the dye molecules, thus interrupting D49 “self-solvation”. These results are in contrast to a recent experimental study for the indoline dye D131 on Al₂O₃, where charge transfer from electronically excited D131 to adjacent dye molecules was proposed (Cappel et al., Sci. Rep., 2016, 6, 21276). We do not see evidence for charge transfer processes between D49 molecules and also not for electron injection from D49 into Al₂O₃ trap states. Charge separation is only observed for D49 bound to TiO₂ thin films, with efficient injection of electrons into the conduction band of the semiconductor via formation of a [D49˙⁺⋯e⁻] complex and a transient Stark effect signalling the formation of mobile electrons upon dissociation of the complex.

---

1. Introduction

Efficient photoinduced electron injection from appropriate dyes into mesoporous TiO₂ or ZnO semiconductor oxide thin films is the key step for initial charge separation in dye-sensitised solar cells (DSCs).¹ Frequently, metal-free organic donor–acceptor dyes, such as substituted indolines^2–4 or triarylamine–thiophenylcyanoacrylic acids,^5,6 are employed as photosensitisers. The dynamics of the initial charge separation event is conveniently followed by transient absorption spectroscopy. From such data one obtains timescales for electron injection and migration as well as the spectra of the transient species involved.^7–18

Mesoporous thin films of large band-gap oxide materials, such as Al₂O₃, have been employed as reference systems for studying the dynamics of solar cell dyes under “non-injecting” conditions.^{16,17,19–21} For instance, the results of transient absorption experiments suggest that triarylamine–benzothiazole sensitisers inject electrons into Al₂O₃ surface trap states.¹⁷ Very recently, Cappel et al. proposed a mechanism, in which photoexcited D131 indoline dyes bound to Al₂O₃ exhibit efficient charge transfer to neighbouring D131 molecules. The formation of a D131˙⁺ radical cation and a D131˙⁻ radical anion with an efficiency of up to 80% at high surface concentrations of the dye was claimed, yet no fingerprints of the radical anion have been found in the transient spectra.²² Such a process may be regarded as a special type of hole transfer event relevant to the understanding of dye regeneration processes in DSCs.

Here, we present a broadband (350–1600 nm) transient absorption study of the donor–acceptor dye D49 (Fig. 1) in organic solvents, on Al₂O₃ thin films (with or without the co-adsorbent deoxycholic acid (3α,12α-dihydroxy-5β-cholan-24-oic acid = “DCA”, Fig. 1)) and on mesoporous TiO₂ surfaces. Investigations in diisopropyl ether, THF and acetonitrile clarify the polarity-dependent spectra and relaxation time constants of the isolated electronically excited dye. These data then serve as a basis to understand the photoinduced dynamics observed on the Al₂O₃ and TiO₂ thin films.

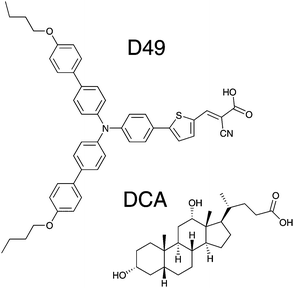Fig. 1 Chemical structures of the donor–acceptor dye D49 and the co-adsorbent 3α,12α-dihydroxy-5β-cholan-24-oic acid (DCA).

2. Experimental

2.1 Chemicals and preparation of thin films

The dye D49 ((E)-3-(5-(4-(bis(4′-butoxy-[1,1′-biphenyl]-4-yl)amino)phenyl)thiophen-2-yl)-2-cyanoacrylic acid) was purchased from Dyenamo. Additional D49 samples for the measurements, synthesised by E. Gabrielsson and L. Sun (KTH Stockholm, Sweden), were kindly provided by G. Boschloo (University of Uppsala).²³ Mesoporous Al₂O₃ and TiO₂ thin films with a thickness of ca. 2 μm (ca. 500 nm for the spectroelectrochemistry experiments on TiO₂) were prepared on microscope glass slides (BMS) or fluorine doped tin oxide (FTO) glass (Solaronix, TCO10-10) as described in our previous publications.^13–15 Thin films were sensitised by placing them in a 50 μM solution of D49 in acetonitrile until the desired optical density (OD) was reached, followed by rinsing with acetonitrile to remove free D49.

In additional experiments, the ratio of the D49 sensitiser and the co-adsorbent DCA was varied. Two different methods were employed: in the “two-step” method, the thin films were first saturated with the co-adsorbent by placing them in a 5.0 × 10⁻³ M solution of DCA in i-propanol for two days. Afterwards, DCA-coated thin films were dipped into a 2.7 × 10⁻⁵ M solution of D49 in i-propanol until the desired OD of D49 was reached. In the “one-step” method, thin films were dipped into solutions of either i-propanol or acetonitrile/tert-butanol (1 : 1 by volume) containing specific DCA : D49 mole ratios between 0 : 1 and 400 : 1 for 30–180 min, with the D49 concentration in the range (2.5–11) × 10⁻⁵ M.

The substances diisopropyl ether (Merck, p.a., 99.0%), THF (Merck, Uvasol, 99.9%), acetonitrile (Fisher, HPLC gradient grade, 99.99%), i-propanol (Fisher, analytical reagent grade, 99.97%), tert-butanol (Alfa Aesar, 99.5%, anhydrous), acetic acid (Th. Geyer, p.a., 99.5%) and ferrocene (Alfa Aesar, high purity, 99.5%) were used as received.

2.2 Pump – supercontinuum probe (PSCP) spectroscopy

Ultrafast UV-Vis-NIR transient absorption spectra were recorded at 920 Hz repetition frequency on three different setups employing the PSCP technique.^{13,14,24–27} In the first setup,^27,28 a multifilament Vis-NIR supercontinuum covering the wavelength range 500–920 nm was generated in a translating 2 mm thick CaF₂ plate using a noncollinearly phase-matched optical parametric amplifier (NOPA) running at 630 nm (12 μJ pulse⁻¹). The NOPA was driven by a regeneratively amplified titanium:sapphire system (Spectra-Physics Hurricane, 780 nm, 90 fs, 1 mJ pulse⁻¹).

In the second PSCP setup,^29–32 a UV-Vis multifilament supercontinuum spanning a wavelength range of 260–660 nm was generated in a translating 2 mm thick CaF₂ plate from the second harmonic (400 nm, 12 μJ pulse⁻¹) of the fundamental beam of a regeneratively amplified titanium:sapphire system (Coherent Libra USP-HE, 800 nm, 50 fs, 3.5 mJ pulse⁻¹).

In the third, a newly-established PSCP setup, a multifilament supercontinuum spanning a wavelength range of 820–1600 nm was generated in a 2 mm thick sapphire plate using 800 nm radiation (20 μJ pulse⁻¹) from the same regeneratively amplified titanium:sapphire system used for UV-Vis supercontinuum generation.

In each setup, the supercontinuum was split up into a reference and probe beam path. Pump pulses at 505 nm (typical fluences: 0.45 mJ cm⁻² for solvent experiments and 0.07–0.10 mJ cm⁻² for thin film measurements) were generated using a NOPA and chopped at a frequency of 460 Hz. Pump and probe beams were polarised at a magic angle (54.7°). The cross-correlation was typically ca. 80 fs, and the determination of zero time delay was accurate within ca. 20 fs.

The pump and probe pulses were focused into a home-built contact cell¹⁵ accommodating the sensitised thin film in contact with nitrogen (Messer, 4.6). During the experiment, the contact cell was constantly moved in a plane perpendicular to the propagation axis of the probe beam (scanning area 2 × 2 mm²). For experiments in organic solvents, 10–15 mL of a nitrogen-saturated solution of D49 in diisopropyl ether, THF or acetonitrile was circulated through a flow cell with a path length of 1 mm, so that the sample volume was exchanged between subsequent pump–probe cycles. Solutions with a typical OD of 0.1 (at 505 nm, 1 mm path length) were used.

In both setups, the reference and probe beams were imaged onto the entrance slits of separate grating spectrographs and detected by 512 element Si or InGaAs photodiode array detectors. Single-shot baseline corrections were applied. Unless otherwise stated, a transient spectrum represents the average of three independent scans, each typically consisting of 1000 pump–probe cycles per delay time.

Steady-state absorption and fluorescence spectra were recorded on Varian Cary 5000 and Agilent Cary Eclipse spectrometers, respectively. For fluorescence measurements, the samples were excited at 454 nm. A small amount (≤0.2 vol%) of acetic acid was added to the solutions to avoid any deprotonation of D49. We carefully checked that this small amount had no influence on the absorption/fluorescence properties of the neutral dye. Slit widths for excitation/emission were 2.5 or 5.0 nm.

2.3 PSCP data treatment and global kinetic analysis

The PSCP spectra were chirp-corrected using the coherent response of pure solvents or thin films. In organic solvents, the UV-Vis coherent signals were subtracted from the transient absorption data of D49 to obtain the pure dynamics of the dye. Solvent contributions in the NIR and thin film contributions over the whole spectral range were so weak that they were neglected during analysis.

UV-Vis and NIR PSCP data sets were subjected to a global modelling procedure^13,26,33 employing the kinetic schemes discussed below. Species-associated spectra were parametrised by a sufficient number of Gaussian functions, including a possible time dependence of the parameters, e.g. to describe continuous solvation band shifts. The lifetimes as well as the position, width and height of the Gaussian functions were optimised simultaneously to arrive at the best fit, which included convolution with the experimental time response. The latter one was determined from the transient absorption signal of the pure solvents or thin films.

2.4 Spectroelectrochemistry

Details of our setup for spectroelectrochemistry employing a Metrohm Autolab PGSTAT 101 potentiostat were described previously.¹⁴ The oxidation of D49 was investigated on TiO₂ thin films deposited on FTO glass in contact with nitrogen-purged acetonitrile containing 100 mM tetrabutylammonium perchlorate as the supporting electrolyte. A newly developed spectroelectrochemical cell was used. It consisted of a 10 mm × 10 mm quartz cuvette, covered by a polyether ether ketone (PEEK) cap with feedthroughs. A brass clamp attached to the cap accommodated the dye-sensitised mesoporous TiO₂ film on FTO glass as the working electrode. A platinum wire coiled up on a stainless steel bar served as the counter-electrode and a silver wire was used as the pseudoreference electrode.

2.5 DFT/TDDFT calculations

Calculations for neutral D49, the radical cation D49˙⁺ and the radical anion D49˙⁻ were carried out using procedures described in our previous publications:^14,15 briefly, the structure of each ground electronic state was optimised using DFT employing the B3LYP functional and a 6-31G(d) basis set. Energies of the excited states (vertical excitation) were determined by TDDFT using the MPW1K functional and a 6-31+G(d) basis set. The MPW1K functional was chosen because it provides reasonable accuracy for the excited state transitions of solar cell donor–acceptor dyes.^13,14,34 The PCM solvent model was employed for acetonitrile.

3. Results and discussion

3.1 Steady-state spectra

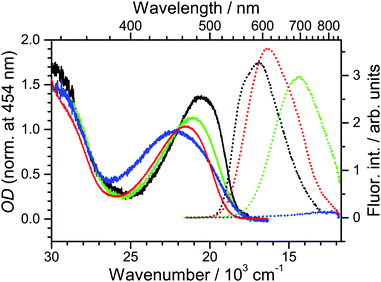
Steady-state absorption and fluorescence spectra of D49 are presented in Fig. 2 for the solvents n-hexane, diisopropyl ether, THF and acetonitrile. Deprotonation of the dye in the low-concentration solutions used in the fluorescence experiments was suppressed by adding a small amount of acetic acid (Fig. S1 and S2, ESI†). Also, we did not find any indications for dye aggregation (Fig. S2, ESI†). The Stokes shift of D49 increases drastically with increasing polarity (3600, 5200, 6700 and 9800 cm⁻¹). This suggests a strong intramolecular charge transfer (ICT) character in the first excited electronic state of D49, and therefore we denote it as S₁/ICT. A similar behaviour was found previously by us for the related dye D35. In that case, DFT/TDDFT calculations showed that electron density moves from the triarylamine donor to the thiophenylcyanoacrylic acid acceptor upon photoexcitation.¹⁴

Fig. 2 Steady-state absorption (solid lines) and fluorescence spectra (dotted lines) of D49 in different solvents; (black) n-hexane, (red) diisopropyl ether, (green) THF, (blue) acetonitrile. The fluorescence excitation wavelength in all cases is 454 nm. The area under each fluorescence spectrum reflects the absolute fluorescence intensity for identical absorbance at the excitation wavelength.

In addition, the fluorescence intensity in acetonitrile drops considerably (shown by the blue dotted line). Assuming an only weakly solvent-dependent radiative rate constant, this suggests a strong reduction of the excited-state lifetime in highly polar solvents due to accelerated intramolecular nonradiative relaxation. The transient absorption experiments reported in Section 3.2 indeed find a fast IC channel S₁/ICT → S₀.

Fig. 3 contains steady-state absorption and fluorescence spectra of Al₂O₃ for different DCA : D49 ratios. Samples were prepared using the “two-step” method (Section 2.1) which provides much better spectral reproducibility than the “one-step” route (see ESI†). Starting from a DCA-saturated mesoporous Al₂O₃ thin film, the absorbance and fluorescence intensities of the samples increase from 1 to 60 min dipping time (black to green lines). D49 binds to the surface by adsorbing to empty places in between DCA or by exchange. Saturation of the absorbance signal is reached after three days (red line), accompanied by a reduction of the fluorescence signal for high-OD films. As will be shown below, the reduction of fluorescence is also due to polarity-induced acceleration of D49 nonradiative decay, in this case because of increased D49–D49 interactions at higher surface concentrations. Still, the main contribution to the fluorescence signal stems from D49 surrounded by DCA.

Fig. 3 Steady-state absorption spectra (solid lines) and fluorescence spectra (dotted lines) of D49 with co-adsorbent DCA on Al₂O₃. Sensitisation with D49 was carried out using a DCA-saturated Al₂O₃ film. D49 sensitisation times from (black) to (red): 1, 2, 4, 10, 20, 60 min and three days. The fluorescence excitation wavelength in all cases is 454 nm.

A cyclic voltammogram of D49 on mesoporous TiO₂ is shown in Fig. S3 (ESI†), yielding an oxidation potential of 1.14 V vs. NHE. In Fig. 4 we display steady-state absorption spectra in the 600–1700 nm region obtained upon oxidation of D49 on TiO₂/FTO (black line). A characteristic absorption band with a peak at 1145 nm is observed. It is assigned to the D₀ → D₁ transition of the radical cation D49˙⁺.¹⁵ The corresponding spectrum for D49˙⁺ in acetonitrile is shown for comparison. Here, the spectrum peaks at 1046 nm.¹⁵ The spectral shift is likely due to changes in the electronic structure arising from the different types of carboxyl functions and “solvent” environments. The full width at half maximum (FWHM) of the spectrum on TiO₂ is 3190 cm⁻¹ and thus larger than that in acetonitrile (2590 cm⁻¹). It is likely that different binding sites on the surface lead to a larger inhomogeneous broadening of the spectrum.

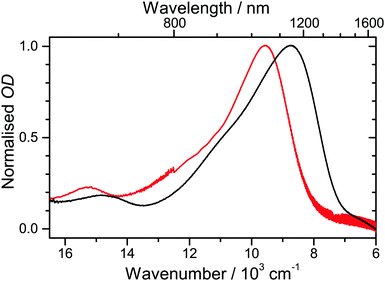Fig. 4 Comparison of radical cation spectra from spectroelectrochemistry: (black) D49˙⁺ on TiO₂/FTO and (red) D49˙⁺ in acetonitrile (adapted from ref. 15).

3.2 Ultrafast photoinduced dynamics of D49 in organic solvents and on mesoporous Al₂O₃ and TiO₂ thin films

UV-Vis-NIR broadband transient absorption spectra obtained after laser excitation at 505 nm (S₀ → S₁/ICT) in the organic solvents diisopropyl ether, THF and acetonitrile and on mesoporous Al₂O₃, Al₂O₃/DCA and TiO₂ are shown in Fig. 5(A–F) as contour plots. The corresponding sets of broadband PSCP spectra can be found in Fig. S4–S9 (ESI†). The results of global modelling are summarised in Table 1. A comparison of transient spectra and selected kinetic traces including fit lines is shown in Fig. 6. We commence with the dynamics of D49 in organic solvents and discuss its transient spectra on thin films afterwards.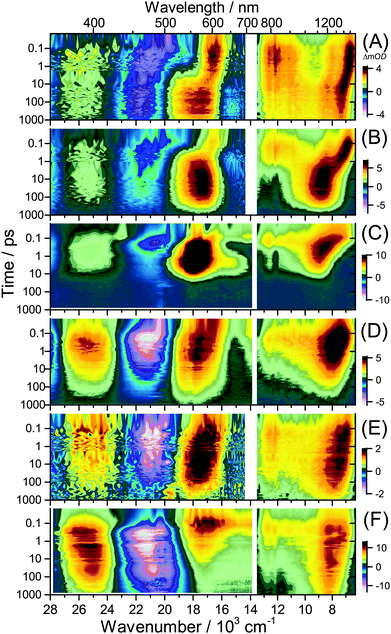

Fig. 5 Contour plots of PSCP spectra for D49. (A) Diisopropyl ether, (B) THF, (C) acetonitrile, (D) Al₂O₃, (E) Al₂O₃/DCA, and (F) TiO₂.

Table 1 Parameters from global kinetic analysis for the solar cell dye D49 in different environments after excitation at 505 nm

Solvent/thin film	Δf^a	τ(ICT)^b (ps)	τ(S1)^b (ps)	Φ (S1)^c	τ av (ps)	τ 1 (ps)	τ 2 (ps)
a Solvent dipolarity Δf = R(ε) − R(n) = (ε − 1)/(ε + 2) − (n^2 − 1)/(n^2 + 2); ε = dielectric constant, n = refractive index. Δf values are taken from ref. 32. b τ(S1) and τ(ICT) represent the lifetime of the S1 and ICT species, respectively. For diisopropyl ether and THF there is no experimental indication for separate S1 and ICT species. Therefore we assume a single S1/ICT state with a lifetime τ(S1/ICT). c Quantum yield for initial formation of the S1 species. For the thin films, the biexponential character might also reflect site-specific polarity. d Average relaxation time τav = Φ(S1)·τ(S1) + (1 − Φ(S1))·τ(ICT). e Time constants describing band shape changes mainly due to solvation and also intramolecular vibrational redistribution. Components with time constants of several ps likely also reflect collisional cooling. Values for acetonitrile are taken from ref. 36, see Section 3.4. f Time constants τComplex for separation of the initially formed radical cation–electron complex [D49˙^+⋯e^−] and its intramolecular vibrational redistribution τIVR. τComplex also describes spectral changes due to the transient Stark effect which indicates formation of mobile electrons in the TiO2 conduction band. g Lifetime τCat of the radical cation D49˙^+ and slower band shape changes due to the transient Stark effect described by τStark.
Diisopropyl ether	0.28	2900		—	2900	5.0	34
THF	0.44	350		—	350	0.60	3.3
Acetonitrile	0.71	8.8	1200	0.05	72	0.089	0.630
Al2O3	—	94	1700	0.25	490	0.56	9.0
Al2O3/DCA	—	600	2800	0.48	1700	0.30	31

---

		τ Complex (ps)	τ IVR (ps)	τ Cat (ps)	τ Stark (ps)
TiO2		3.1	0.13	3200	210

---

Fig. 6 (A) Scaled UV-Vis-NIR transient absorption spectra of D49 at 5 ps for diisopropyl ether (black), Al₂O₃/DCA (red), Al₂O₃ (blue), THF (green) and acetonitrile (magenta). (B) Kinetic traces at 9720 cm⁻¹ (1030 nm) for the same solvents/thin films including fit lines from global kinetic analysis.

Diisopropyl ether (A). Early on, we observe the appearance of the S₀ → S₁/ICT ground state bleach (GSB) at 490 nm and excited-state absorption (ESA) features at 400, 600, 830 and 1500 nm which are assigned to the S₁/ICT → S_n transitions. Later on, we find characteristic spectral changes indicative of solvation dynamics: a blue-shift of the Vis and NIR ESA bands and the appearance of a weak negative signal at 650 nm which arises from red-shifting stimulated emission (SE). Assuming an only weakly solvation-dependent energy of the upper state in the ESA transition, the ESA blue-shift can be explained by the progressive stabilisation of S₁/ICT by solvent reorientation, which increases the S₁/ICT-S_n energy difference, resulting at the same time in a reduction of the S₁/ICT-S₀ energy gap (red shift of SE).³⁵ Afterwards, the whole spectrum decays slowly. This is assigned to the process S₁/ICT → S₀ consisting of radiative and nonradiative contributions. The dynamics are successfully modelled globally by the process S₁/ICT → S₀. To describe the solvation-induced transient shifts and changes in the width of ESA and SE bands, the S₁/ICT spectrum was assumed to be time-dependent. For these processes, mainly involving dynamic solvation and also collisional relaxation, we obtain time constants of 5.0 and 34 ps. The decay to S₀ is slow and cannot be fully captured in our time window of 2 ns. We estimate a lifetime of 2.9 ns.

THF (B). The dynamics in THF is qualitatively similar to diisopropyl ether, with three distinct differences: the amplitude ratio of ESA at 575 nm and GSB at 465 nm is higher, and the blue-shift of the ESA band in NIR is more pronounced, compare using Fig. 5(A). In addition, the time constants for the band shift are different. Also, the IC process S₁/ICT → S₀ accelerates markedly (Table 1). From the global kinetic analysis, we obtain time constants for the transient band shift/broadening of 0.60 and 3.3 ps. These time constants are compatible with solvation dynamics, yet for THF they appear to be somewhat slower compared to the values obtained using typical solvation probes, such as Coumarin 153.³⁶ This might again be an indication for superimposed collisional relaxation processes in S₁/ICT. The S₁/ICT lifetime is 350 ps and thus much shorter than in the less polar diisopropyl ether.

Acetonitrile (C). The ESA : GSB band ratio increases even further, in agreement with the higher solvent polarity. The shift and broadening dynamics of the S₁/ICT band also accelerate; for a detailed analysis of the solvation contribution see Section 3.4. The decay time is 8.8 ps, and thus even shorter than in THF. We observe a 5% contribution of a second, long-lived component. Therefore, our global modelling for acetonitrile involves an initial branching into ICT and S₁ species decaying independently to S₀. The most likely explanation is a polarity-dependent barrier between S₁ and ICT, which leads to initial trapping of a small part of the population in the long-lived higher-energy S₁ part of the excited-state potential, with an estimated S₁ lifetime of ca. 1200 ps.

Al₂O₃ (D). All bands observed in the transient spectra of the organic solvents are also present for D49 bound to Al₂O₃. One observes a similar blue-shift of the NIR ESA band with time, but it occurs on a much narrower energy scale. We assign this process to “restricted self-solvation” of D49 on the film: because the dye molecules are chemically anchored onto the surface and are closely packed, reorientational response to stabilise the excited-state dipole of D49 will be hampered considerably. Two time constants of 0.56 and 9.0 ps are assigned to this weak band-shift. The excited-state decay is modelled by two time constants. The ICT part decays with 94 ps, whereas the estimated value for the S₁ part is 1700 ps. Deviation from single exponential behaviour might also arise from the distribution of different binding motifs and solvation environments on the film. Such heterogeneity will lead to site-specific polarity resulting in the distribution of excited-state lifetimes.

Al₂O₃/DCA (E). If the local surface polarity of the Al₂O₃ thin film in (D) is the key effect, addition of the low-polarity bile acid co-adsorbent DCA (Fig. 1) should slow down the excited-state decay of D49, compared to e.g. the 2.9 ns lifetime of D49 in diisopropyl ether (A). This is indeed the case, as shown by the results in (E). Therefore direct D49–D49 interactions are largely reduced compared with (D) where the D49 molecules are closely packed. The slight transient blue-shift of the NIR ESA band is assigned to “surface solvation” by DCA molecules surrounding D49. Most importantly, the lifetime of D49 increases considerably, in agreement with the reduced local polarity. We obtain time constants of 600 ps (ICT) and ca. 2.8 ns (S₁).

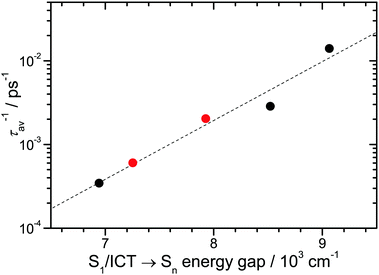
The correlation of the S₁/ICT lifetime with polarity may be quantified in terms of the “energy gap law” of radiationless transitions:^37–39 the lifetime should decrease with increasing polarity because of the decreasing S₁/ICT–S₀ energy gap. We already noted that this decrease is accompanied by a corresponding increase of the energy gap between S₁/ICT and the upper state S_n of the NIR ESA transition. This is underlined by the blue-shift of this peak in Fig. 6(A). According to the energy gap law, the average rate constant (= inverse average lifetime) should show a dependence of the type log₁₀(k_av) = log₁₀(τ_av⁻¹) = A + B·E, where E is the energy gap, and A and B are fit parameters.^37–39Fig. 7 shows such an energy gap law correlation for D49. Here we employed the NIR peak positions from Fig. 6(A) and average lifetimes τ_av = Φ(S₁)·τ(S₁) + (1 − Φ(S₁))·τ(ICT) (Table 1), with Φ(S₁) being the quantum yield for forming S₁. The average lifetime should give the best representation of the overall excited-state decay. All data points are well described by the energy gap law expression (dashed line). According to the correlation, the average local polarity for closely-packed D49 on Al₂O₃ is smaller than for D49 in THF. The addition of DCA reduces the local polarity further and brings τ_av closer to the value for D49 in diisopropyl ether. This is reasonable considering the chemical structure of DCA (Fig. 1).

Fig. 7 Correlation of the inverse average lifetime τ_av⁻¹ for S₁/ICT of D49 with the S₁/ICT → S_n energy gap. From left to right: diisopropyl ether, Al₂O₃/DCA, Al₂O₃, THF and acetonitrile. The dashed line is the best fit to the data points: log₁₀(τ_av⁻¹) = −8.35 + 7.04 × 10⁻⁴·E, where E is the energy gap in cm⁻¹. Note the logarithmic scale on the ordinate.

TiO₂ (F). The dynamics of D49 on mesoporous TiO₂ in Fig. 5(F) differs markedly from those observed for the other systems in (A–E). An initially formed “S₁/ICT-type” band centred at 575 nm decays up to ca. 3 ps, and we see persistent absorption around 1200 nm and 400 nm afterwards. In addition, the ESA band at 400 nm and the GSB slowly shift to a larger wavelength up to the nanosecond timescale. We interpret these spectral features as clear indications for electron injection from D49 into the TiO₂ thin film and the early stages of electron delocalisation inside TiO₂.

The PSCP spectra suggest the following series of events: photoexcitation generates instantaneously (within our time resolution) a close radical cation–electron complex [D49˙⁺⋯e⁻](TiO₂). Although initial charge separation has therefore already happened, the broadened spectrum still resembles that of the S₁/ICT state observed in organic solvents and on Al₂O₃. Afterwards, the electron separates from the radical cation core and becomes a “mobile” conduction band electron in TiO₂: [D49˙⁺⋯e⁻](TiO₂) → D49˙⁺ + e⁻ (TiO₂), see e.g. the spectra at 0.5–6 ps in Fig. S9 (ESI†). The dynamics involves a slight blue-shift of the NIR absorption band, a decay of absorption in the 550–1000 nm range and a red-shift of the GSB. The spectrum above 600 nm at 6 ps already resembles the D49˙⁺ spectrum from spectroelectrochemistry (Fig. 4), with a characteristic NIR peak and a long tail toward the visible region. According to the global kinetic analysis, the lifetime of the [D49˙⁺⋯e⁻] complex is τ_Complex = 3.1 ps. We assign an additional superimposed ultrafast change in the band shape to intramolecular vibrational redistribution (IVR) inside the complex with a time constant τ_IVR = 0.13 ps (Table 1).

From 20 ps onward, the amplitude of the bleach feature at 485 nm and of the absorption band at 400 nm decreases (Fig. S9 (ESI†), third panel). At the same time the 400 nm band and the GSB are continuously shifting to the red. We ascribe these pronounced dynamics in the GSB region of the spectrum to a transient Stark effect (=electrochromism):^{13–15,40,41} as the mobile electrons separate further from the stationary radical cations over time, the resulting electric field between D49˙⁺ and e⁻(TiO₂) exerted on neighbouring ground state D49 molecules changes and also slowly decreases because the electrons are progressively screened inside the semiconductor. As shown previously by Cappel et al., the transient spectrum of the GSB region in the presence of a Stark shift should largely resemble the first derivative of the inverted steady-state absorption spectrum.⁴⁰ The bottom panel of Fig. S9 (ESI†) shows that this is indeed the case (compare the green spectrum at 900 ps and the magenta dashed scaled derivative in the 450–550 nm range). The amplitude of the derivative-like feature is proportional to the amplitude of the electric field across the thin film.⁴⁰ The decay of these spectral features and the slight red-shift of the UV-Vis ESA and GSB bands from 20 ps onward seen in Fig. 5(F) and Fig. S9 (ESI†) (third and fourth panels) must therefore arise from a decrease of the electric field strength due to electron screening. Global kinetic modelling provides a time constant of τ_Stark = 210 ps for this process (Table 1). We note that the transient D49˙⁺ spectrum in the NIR at 1800 ps is slightly red-shifted compared with the spectrum from spectroelectrochemistry. This is likely due to the fact that the Stark effect also induces a weak shift of the radical cation D₀ → D₁ absorption. Our experiments suggest that the transient Stark effect is a sensitive spectral indicator for the initial formation of mobile electrons and the subsequent delocalisation of the conduction band electrons in TiO₂. “Transient absorption Stark effect spectroscopy” therefore provides valuable information on electron relaxation timescales at the dye-semiconductor interface which is complementary to data from time-resolved THz techniques.¹²

Electron–cation recombination occurs on much slower timescales and we estimate a radical cation lifetime of τ_Cat = 3.2 ns for this process from the slow decay of the spectrum above 1 ns (Table 1).

3.3 No evidence for D49–D49 charge transfer on Al₂O₃

The data presented so far suggest that D49 in organic solvents and bound to an Al₂O₃ thin film only exhibits S₁/ICT excited-state “solvation”, collisional relaxation and fluorescence/IC. We do not see photoinduced charge separation processes like on TiO₂, in contrast to what was suggested previously for the indoline dye D131 on Al₂O₃.²² To further support this interpretation, we carried out DFT/TDDFT calculations for different dye species. The PCM solvent model was employed for acetonitrile. Calculated values are summarised in Table S1 (ESI†), and additional gas-phase results for D49 and D49˙⁺ can be found in our previous study.¹⁵ The transitions and their oscillator strengths (gas-phase values) are shown in Fig. 8 as stick spectra for D49 (black), D49˙⁺ (red) and D49˙⁻ (green). The positions of the experimentally determined S₀ → S₁/ICT band of D49 (Fig. 2) and the D₀ → D₁ band of D49˙⁺ (Fig. 4) are very well reproduced. According to the calculations, one would expect that any spectral contributions of the radical anion D49˙⁻, produced via the hypothetical charge transfer process D49(S₁/ICT) + D49(S₀) → D49˙⁺ + D49˙⁻,²² would show up as a strong band around 510 nm in the PSCP spectra. At the same time, this charge transfer step would bleach additional D49(S₀) molecules and remove S₁/ICT population. Assuming e.g. 80% efficiency of this process claimed for indoline D131 on Al₂O₃ at “full coverage”,²² this should increase the amplitude of the GSB around 480 nm by about a factor of two, and the S₁/ICT ESA band at 580 nm should disappear almost completely. All of this should happen with an expected time constant of >7 ps.²² There is clearly no indication for such a process in our PSCP spectra. We therefore conclude that an intermolecular D49–D49 charge transfer channel is not operative on mesoporous Al₂O₃. Instead the spectral changes are fully explained by intramolecular S₁/ICT excited state dynamics of the dye under the influence of the solvent environment.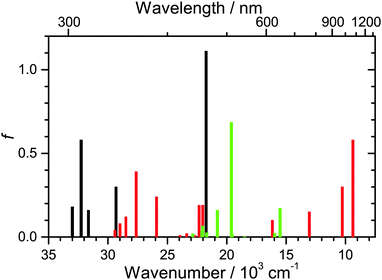

Fig. 8 Oscillator strengths f (gas-phase values) for the five energetically lowest S₀ → S_n transitions of neutral D49 (black), the fifteen energetically lowest D₀ → D_n transitions of the radical cation D49˙⁺ (red), and the ten energetically lowest D₀ → D_n transitions of the radical anion D49˙⁻ (green). Values for D49 and D49˙⁺ are taken from ref. 15.

3.4 A closer look at the solvation dynamics of D49

Solvation dynamics of dye molecules in their excited state is usually monitored by ultrafast fluorescence techniques, such as broadband fluorescence up-conversion spectroscopy (FLUPS), where the time-resolved fluorescence response of the sample is detected by optical gating.^42,43 Transient shifts of SE or ESA bands in broadband transient absorption spectra carry the same information, however their evaluation often becomes complicated due to the presence of overlapping ESA bands. This requires careful deconvolution of the time-resolved spectra.^35,44

Here we demonstrate that the problem of spectral overlap can be resolved by monitoring the dynamics of the lowest-energy ESA transition located in the NIR region which is well separated from the rest of the electronic spectrum. As an example, Fig. 9(A) contains a set of PSCP spectra for the spectral development of the NIR ESA transition of D49 in acetonitrile between 0.10 and 19.9 ps. The initially broad and asymmetric electronic band moves to shorter wavelengths, narrows and becomes more symmetric. For the analysis of this solvation dynamics we fit the transient bands to a log-normal function, resulting in the respective solid fit lines.^36,45

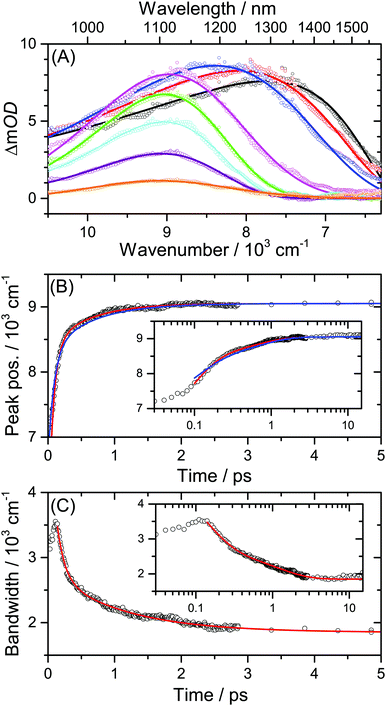Fig. 9 Solvation dynamics of the solar cell dye D49 in acetonitrile. (A) NIR PSCP spectra at 0.10, 0.15, 0.20, 1.0, 2.5, 4.9, 9.9 and 19.9 ps (from right to left) including log-normal fits. (B) Blue-shift of the NIR ESA band peak with time. Solid lines are biexponential fits from this work (red line) and Horng et al. for Coumarin 153/acetonitrile from ref. 36 (blue line). (C) Change of the bandwidth of the NIR ESA band with time including a biexponential fit (red line). The insets in (B) and (C) show the dynamics on a logarithmic timescale up to 15 ps.

The temporal changes of the peak frequency and bandwidth are plotted in panels (B) and (C). We describe these by biexponential fits starting from 0.10 ps, as it is usually practiced in the evaluation of solvation dynamics experiments.^45,46 In (B), the blue line corresponds to a constrained fit employing the time constants and amplitudes from the work of Horng et al. for Coumarin 153 in acetonitrile (τ₁ = 0.089 ps, A₁ = 0.686, τ₂ = 0.630 ps, A₂ = 0.314).³⁶ The agreement is very good, especially considering the fact that there could be small differences in the measured solvation times due to the different molecular structure of the solvation probe.⁴⁶ Using a free biexponential fit (red line) we obtain similar time constants and amplitudes: τ₁ = 0.07 ps (A₁ = 0.82) and τ₂ = 0.58 ps (A₂ = 0.18).

In (C), the initial increase of the width of the ESA band on a 100 fs timescale is likely due to IVR in the S₁/ICT state of D49.^36,45 The decrease of the bandwidth at later times is well described by a biexponential function. We obtain the values τ₁ = 0.12 ps (A₁ = 0.74) and τ₂ = 1.1 ps (A₂ = 0.26). The underlying processes are also dominated by IVR, with the slower component containing contributions of cooling processes in the excited state.⁴⁵

This example suggests that the NIR band-shift and broadening dynamics of D49 in organic solvents and on Al₂O₃ are dominated by solvation processes superimposed by contributions of IVR and collisional cooling. Such background-free transient absorption spectroscopy of ESA transitions in the NIR range turns out to be a powerful tool for studying solvation dynamics of molecular probes, complementary to broadband fluorescence up-conversion spectroscopy.

4. Conclusions

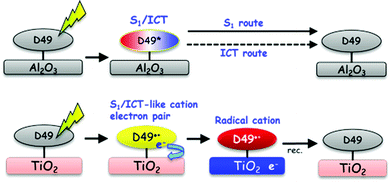
Our investigations of the excited-state dynamics of the solar cell dye D49 by UV-Vis-NIR transient absorption spectroscopy revealed the following photoinduced processes:

In organic solvents and on Al₂O₃, relaxation arises from the S₁/ICT → S₀ electronic decay, with contributions from radiative (fluorescence) and nonradiative (IC) channels. As the polarity of the dye's surrounding increases, nonradiative decay by IC strongly accelerates. This behaviour is successfully modelled in terms of an energy gap law approach. Biexponential decays of D49 observed in polar environments suggest that the S₁ and ICT populations decay independently (i.e. S₁ → S₀ and ICT → S₀). This is likely due to a sufficiently high energy barrier suppressing interconversion between the S₁ and ICT species, as known from other molecular systems, such as all-trans retinal.³² The biexponential decay observed for D49 on Al₂O₃ also contains contributions from surface inhomogeneity resulting in a range of adsorption sites of different local polarity. The local polarity around the dye on Al₂O₃ is efficiently reduced by introducing nonpolar DCA spacer molecules. We observe solvation dynamics of the dye in all organic solvents and on Al₂O₃. As an example, the solvation time constants and amplitudes in acetonitrile are in very good agreement with those obtained for the “gold standard”⁴⁷ solvation probe Coumarin 153. On Al₂O₃, “self-solvation” of D49 is observed and arises from the restricted movements of adsorbed dye or DCA spacer molecules. We do not see any evidence for charge transfer processes between D49 molecules and also no indication for electron injection into Al₂O₃ trap states. Based on our current findings for D49, the intermolecular charge-transfer mechanism between adjacent indoline D131 dye molecules proposed in ref. 22 should be re-examined, as there might be an alternative explanation based on the mechanism shown in Fig. 10 (top).

Fig. 10 Relaxation mechanisms of D49 on different thin films. (Top) On Al₂O₃ and in organic solvents, photoexcited D49 shows no charge separation. Only S₁/ICT excited-state relaxation to S₀ occurs. This is accompanied by solvation and collisional relaxation (not shown). (Bottom) Photoexcitation of D49 on TiO₂ results in instantaneous formation of a [D49˙⁺⋯e⁻] pair which dissociates into the radical cation D49˙⁺ and a “mobile” electron in the conduction band of TiO₂. Recombination occurs on a much longer timescale. The formation of “mobile” electrons is accompanied by a transient Stark shift in transient absorption spectra (not shown).

The UV-Vis-NIR coverage of the transient absorption spectra provides a detailed picture of the ultrafast electron injection mechanism of D49 into the conduction band of TiO₂. An immediately formed radical cation–electron complex separates into D49˙⁺ and mobile electrons. The appearance of mobile electrons is tracked by the transient Stark effect signalling the build-up of an electric field at the interface which induces characteristic shifts of the ground state D49 and radical cation spectra on picosecond timescales. This completely different behaviour of D49 on “injecting” TiO₂ and “non-injecting” Al₂O₃ thin films is summarised by the illustration in Fig. 10.

Acknowledgements

K. O. and T. L. thank the German Science Foundation (DFG) for financial support of this work through grants OU 58/10-1 and LE 926/11-1. We acknowledge G. Boschloo, E. Gabrielsson and L. Sun (University of Uppsala) for providing a high purity D49 sample for the current experiments. We thank J. Weber and J. Schmedt auf der Günne (University of Siegen) for providing the oven for sintering the mesoporous Al₂O₃ and TiO₂ layers. We also thank N. P. Ernsting (Humboldt University Berlin, Germany) and J. L. Pérez Lustres (University of Santiago de Compostela, Spain) as well as J. Troe, K. Luther, J. Schroeder, D. Schwarzer and A. M. Wodtke (Georg August University Göttingen, Germany) for their continuous support and advice.

References

1. A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595.
2. T. Horiuchi, H. Miura and S. Uchida, Chem. Commun., 2003, 3036.
3. T. Horiuchi, H. Miura, K. Sumioka and S. Uchida, J. Am. Chem. Soc., 2004, 126, 12218.
4. S. Ito, S. M. Zakeeruddin, R. Humphry-Baker, P. Liska, R. Charvet, P. Comte, M. K. Nazeeruddin, P. Péchy, M. Takata, H. Miura, S. Uchida and M. Grätzel, Adv. Mater., 2006, 18, 1202.
5. S. M. Feldt, E. A. Gibson, E. Gabrielsson, L. Sun, G. Boschloo and A. Hagfeldt, J. Am. Chem. Soc., 2010, 132, 16714.
6. D. P. Hagberg, X. Jiang, E. Gabrielsson, M. Linder, T. Marinado, T. Brinck, A. Hagfeldt and L. Sun, J. Mater. Chem., 2009, 19, 7232.
7. R. Huber, J.-E. Moser, M. Grätzel and J. Wachtveitl, J. Phys. Chem. B, 2002, 106, 6494.
8. G. Benkö, J. Kallioinen, J. E. I. Korppi-Tommola, A. P. Yartsev and V. Sundström, J. Am. Chem. Soc., 2002, 124, 489.
9. A. Furube, R. Katoh, K. Hara, S. Murata, H. Arakawa and M. Tachiya, J. Phys. Chem. B, 2003, 107, 4162.
10. A. Furube, R. Katoh, T. Yoshihara, K. Hara, S. Murata, H. Arakawa and M. Tachiya, J. Phys. Chem. B, 2004, 108, 12583.
11. B. Wenger, M. Grätzel and J.-E. Moser, J. Am. Chem. Soc., 2005, 127, 12150.
12. H. Nemec, J. Rochford, O. Taratula, E. Galoppini, P. Kuzel, T. Polívka, A. Yartsev and V. Sundström, Phys. Rev. Lett., 2010, 104, 197401.
13. K. Oum, P. W. Lohse, O. Flender, J. R. Klein, M. Scholz, T. Lenzer, J. Du and T. Oekermann, Phys. Chem. Chem. Phys., 2012, 14, 15429.
14. K. Oum, P. W. Lohse, J. R. Klein, O. Flender, M. Scholz, A. Hagfeldt, G. Boschloo and T. Lenzer, Phys. Chem. Chem. Phys., 2013, 15, 3906.
15. K. Oum, O. Flender, P. W. Lohse, M. Scholz, A. Hagfeldt, G. Boschloo and T. Lenzer, Phys. Chem. Chem. Phys., 2014, 16, 8019.
16. O. Flender, P. W. Lohse, J. Du, T. Oekermann, M. Scholz, K. Oum and T. Lenzer, Z. Phys. Chem., 2015, 229, 1907.
17. M. Fakis, P. Hrobárik, O. Yushchenko, I. Sigmundová, M. Koch, A. Rosspeintner, E. Stathatos and E. Vauthey, J. Phys. Chem. C, 2014, 118, 28509.
18. E. Rohwer, I. Minda, G. Tauscher, C. Richter, H. Miura, D. Schlettwein and H. Schwoerer, ChemPhysChem, 2015, 16, 943.
19. C. Martín, M. Ziółek, M. Marchena and A. Douhal, J. Phys. Chem. C, 2011, 115, 23183.
20. M. Fakis, E. Stathatos, G. Tsigaridas, V. Giannetas and P. Persephonis, J. Phys. Chem. C, 2011, 115, 13429.
21. M. Wielopolski, J.-H. Kim, Y.-S. Jung, Y.-J. Yu, K. Y. Kay, T. W. Holcombe, S. M. Zakeeruddin, M. Grätzel and J.-E. Moser, J. Phys. Chem. C, 2013, 117, 13805.
22. U. B. Cappel, D. Moia, A. Bruno, V. Vaissier, S. A. Haque and P. R. F. Barnes, Sci. Rep., 2016, 6, 21276.
23. Y. Hao, E. Gabrielsson, P. W. Lohse, W. Yang, E. M. J. Johansson, A. Hagfeldt, L. Sun and G. Boschloo, Adv. Sci., 2015, 2, 1500174.
24. A. L. Dobryakov, S. A. Kovalenko, A. Weigel, J. L. Pérez Lustres, J. Lange, A. Müller and N. P. Ernsting, Rev. Sci. Instrum., 2010, 81, 113106.
25. P. W. Lohse, J. Kuhnt, S. I. Druzhinin, M. Scholz, M. Ekimova, T. Oekermann, T. Lenzer and K. Oum, Phys. Chem. Chem. Phys., 2011, 13, 19632.
26. K. Golibrzuch, F. Ehlers, M. Scholz, R. Oswald, T. Lenzer, K. Oum, H. Kim and S. Koo, Phys. Chem. Chem. Phys., 2011, 13, 6340.
27. T. Lenzer, S. Schubert, F. Ehlers, P. W. Lohse, M. Scholz and K. Oum, Arch. Biochem. Biophys., 2009, 483, 213.
28. J. R. Klein, O. Flender, M. Scholz, K. Oum and T. Lenzer, Phys. Chem. Chem. Phys., 2016, 18, 10800.
29. K. Oum, T. Lenzer, M. Scholz, D. Y. Jung, O. Sul, B. J. Cho, J. Lange and A. Müller, J. Phys. Chem. C, 2014, 118, 6454.
30. L. F. Tietze, B. Waldecker, D. Ganapathy, C. Eichhorst, T. Lenzer, K. Oum, S. O. Reichmann and D. Stalke, Angew. Chem., Int. Ed., 2015, 54, 10317.
31. O. Flender, J. R. Klein, T. Lenzer and K. Oum, Phys. Chem. Chem. Phys., 2015, 17, 19238.
32. O. Flender, M. Scholz, J. Hölzer, K. Oum and T. Lenzer, Phys. Chem. Chem. Phys., 2016, 18, 14941.
33. T. Lenzer, F. Ehlers, M. Scholz, R. Oswald and K. Oum, Phys. Chem. Chem. Phys., 2010, 12, 8832.
34. M. Pastore, E. Mosconi, F. De Angelis and M. Grätzel, J. Phys. Chem. C, 2010, 114, 7205.
35. J. Ruthmann, S. A. Kovalenko, N. P. Ernsting and D. Ouw, J. Chem. Phys., 1998, 109, 5466.
36. M. L. Horng, J. A. Gardecki, A. Papazyan and M. Maroncelli, J. Phys. Chem., 1995, 99, 17311.
37. R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145.
38. V. Chynwat and H. A. Frank, Chem. Phys., 1995, 194, 237.
39. F. Ehlers, D. A. Wild, T. Lenzer and K. Oum, J. Phys. Chem. A, 2007, 111, 2257.
40. U. B. Cappel, S. M. Feldt, J. Schöneboom, A. Hagfeldt and G. Boschloo, J. Am. Chem. Soc., 2010, 132, 9096.
41. S. Ardo, Y. Sun, A. Staniszewski, F. N. Castellano and G. J. Meyer, J. Am. Chem. Soc., 2010, 132, 6696.
42. X.-X. Zhang, C. Würth, L. Zhao, U. Resch-Genger, N. P. Ernsting and M. Sajadi, Rev. Sci. Instrum., 2011, 82, 063108.
43. M. Gerecke, G. Bierhance, M. Gutmann, N. P. Ernsting and A. Rosspeintner, Rev. Sci. Instrum., 2016, 87, 053115.
44. M. Sajadi, T. Obernhuber, S. A. Kovalenko, M. Mosquera, B. Dick and N. P. Ernsting, J. Phys. Chem. A, 2009, 113, 44.
45. M. Sajadi and N. P. Ernsting, J. Phys. Chem. B, 2013, 117, 7675.
46. M. Sajadi, M. Weinberger, H.-A. Wagenknecht and N. P. Ernsting, Phys. Chem. Chem. Phys., 2011, 13, 17768.
47. M. Maroncelli, X.-X. Zhang, M. Liang, D. Roy and N. P. Ernsting, Faraday Discuss., 2012, 154, 409.

---

Footnotes

† Electronic supplementary information (ESI) available: Concentration-dependent steady-state absorption spectra of D49; cyclic voltammetry of D49; UV-Vis-NIR broadband transient absorption spectra of D49; comparison of D49-sensitised Al₂O₃ thin films with and without prior DCA saturation; one-step co-adsorption of D49 and DCA on Al₂O₃ thin films; results of DFT/TDDFT calculations for D49, D49˙⁻ and D49˙⁺. See DOI: 10.1039/c6cp05167g

‡ These authors contributed equally to this work.

---