Chiral recognition by fullerenes: CHFClBr enantiomers in the C₈₂ cage

Abstract

Density-functional theory and symmetry-adapted perturbation theory calculations on complexes of the enantiomers of CHFClBr with the most stable isomer of C₈₂-3 fullerene show that despite the guests being too large for the host cage, they are nevertheless stabilized by electrostatic interactions. The complexation leads to considerable strain on the cage and the guests accompanied by compression of the bonds of the guest molecule, resulting in considerable complexation-induced changes in the infrared (IR), vibrational circular dichroism (VCD), nuclear magnetic resonance (NMR), and UV-vis spectra. The effect of chiral recognition is pronounced only for the ¹⁹F signal in the NMR spectra and in a sign reversal of the rotational strength of the ν_CH stretching vibration of S-CHFClBr@C₈₂-3 in the VCD spectrum as compared to that of the free guest, making the sign of this band for the C₈₂ complexes with the S- and R-guest enantiomers the same. This is a surprising result since vibrational circular dichroism is considered a reliable method for determining the absolute chirality of small molecules and for establishing dominant conformations in biopolymers.

---

1. Introduction

Fullerenes display fascinating electrochemical,¹ magnetic,² optical,^3,4 and other properties.^5–8 In the early fullerene days in the 1990s, the proposals of their applications abounded.⁹ They encompassed, among others, the use of doped C₆₀ as a superconductor, perfluorinated C₆₀F₆₀ as the ideal lubricant and even C₆₀ with a door and a guest drug inside (released at a suitable place and time into the organism through the opened door) as a drug carrier.¹⁰ Some fullerene applications in medicine have also been proposed.^11,12 Nevertheless, with the exception of using C₆₀ as an AFM tip,¹³ to our best knowledge no applications of pure endohedral fullerene complexes have been reported. The most exciting prospects for using fullerene derivatives (among which phenyl-C61-butyric acid methyl ester – PCBM – is the most popular) is in quantum computing^14,15 and solar cells,¹⁶ whereas the applications proposed for use in hydrogen storage appear to be mostly misleading.¹⁷

Most studies of endohedral fullerene complexes focus on metallic guest(s) inside the cage because of their availability and their interesting properties. These complexes are untypical salts since, upon inclusion, the guest becomes a cation, transferring its electron(s) to the host cage. Extending this notion to small polar guest molecules, their encapsulation offers a unique possibility of studying subtle effects on e.g. translational–rotational–vibrational motions caused by the reduced mobility of the small guest molecule, the lowering of the high cage symmetry of the host due to perturbations from the guest, or the interconversion of the ortho and para spin isomers of the guests. Such studies, performed mostly using IR, far-IR, NMR or inelastic neutron scattering spectroscopy, have been carried out for complexes such as H₂@C₆₀^18–20 or H₂O@C₆₀,^21,22 and were predicted theoretically for CO@C₆₀.²³ Although such studies do not lead to immediate applications, they are nonetheless enlightening from the theoretical point of view, allowing one to analyze the predictive power of the calculations for complexes where subtle interactions are dominant.

It should be emphasized that encapsulation of a guest inside a host molecule can lead to spectacular changes in the properties. Exciting examples are the creation of a stable cyclobutadiene inside a hemicarcerand cage synthesized by Cram and coworkers,²⁴ the production of negative alkaline ions in alkalides,²⁵ the stability of white phosphorus in air within a self-assembled capsule²⁶ and an isolated nitrogen atom incarcerated inside the C₆₀ fullerene cage.²⁷ In all these cases, the properties of the guest molecule or ion dramatically change upon complexation.

Other molecular properties that can be affected by encapsulation arise from the chirality of the host and the guest. Chirality is an important property of molecules that are not superimposable on their mirror image²⁸ and chiral recognition refers to the differentiation of these enantiomers by a third chiral agent. It is an important property since the majority of organic molecules, from which living creatures are built, are chiral. Moreover, drug chirality is an important issue for the pharmaceutical industry in view of different, sometimes dangerous, biological activity of drug enantiomers. Due to their high symmetry, C₆₀ and C₇₀ are achiral but higher fullerenes are usually a mixture of chiral and achiral isomers. The lowest stable fullerene having a pair of chiral isomers, C₇₆, was resolved into enantiomers more than 20 years ago.²⁹

The present study of chiral recognition by a fullerene cage was carried out as a continuation of our calculations on endohedral fullerene complexes.^30–33 We have shown that C₆₀ can host only one hydrogen molecule whereas for C₇₀ we demonstrated the possible existence of both complexes with one or two H₂ guests,³⁴ the calculated energy difference between them, partly accidentally, was equal to a later determined experimental result.³⁵ One of the present authors (HD) postulated as early as in 2001 that for applications of endohedral fullerene complexes, efficient synthetic and purification procedures for higher fullerenes are needed.³⁰

Except the methyl halides involving hydrogen isotopes (CHDTX and CHDXY, etc., X, Y = halides), CHFClBr (1a/1b) is the smallest chiral molecule with a chiral center. Therefore, it was chosen as the guest for studying chiral recognition by fullerene cages. The molecule was separated into enantiomers^36,37 and their absolute configuration was determined.³⁸ Interestingly, 1a/1b has been considered to be of importance for studies of parity violation.^39,40

Except for some chiral stationary phases involving cyclodextrins, 1a/1b has been found to be complexed only by a few cryptophanes capable of differentiating the two enantiomers.^41,42 The ¹H and ¹⁹F NMR signals in this molecule have been reported together with the spectra of the cryptophane complexes.

The smallest fullerene capable of forming complexes with 1a/1b is C₈₂. This higher fullerene seems to be of importance in view of the ease of formation of its complexes with metallic guests,⁴³ anticancer activity of its polyol derivative with a gadolinium guest^44,45 and other applications of the endohedral complexes in medicine.⁴⁶ Of interest are also a C₈₂ complex with an unusual guest structure,⁴⁷ a non-IPR (non-Isolated Pentagon Rule) isomer of the endohedral complex involving C₈₂,⁴⁸ and the so-called peapods – that is, nanotubes with Ga@C₈₂ inside.^49–53

Of the 9 IPR isomers of C₈₂, only three (isomers 1, 3, and 5 of C₂ symmetry; see The Atlas of Fullerenes⁵⁴ for the nomenclatures) are chiral (Fig. 1).⁵⁴ Kikuchi et al. showed that three isomers of C₂, C_2v and C_3v symmetry are formed in the C₈₂ manufacturing, with the first one prevailing with more than 80% abundance.⁵⁵ The most stable isomer 3 of C₂ symmetry was isolated and its structure determined mainly on the basis of the comparison between the measured and calculated NMR spectra.^56,57 Marcelli et al.⁵⁸ synthesized C₂ and C_2v isomers of C₈₂ and characterized them. Some endohedral metallofullerenes in which there is a strong interaction between the host cage and the guest were shown to have C_2v symmetry, in which the cage corresponded to the chiral isomer 9.^58,59 Several calculations for C₈₂ were carried out, all showing that isomer 3 has the lowest energy.^57,60,61 Khamatgalimov and Kovalenko carried out calculations for all 9 isomers by DFT using the B3LYP functional and the 6-31G, 6-31G*, and 6-31+G* basis sets⁶⁰ and found isomer 3 to be the most stable for all basis sets used. However, contrary to the experimental finding,⁵⁵ the energy of all isomers of C₂ symmetry was calculated to be lower than those of other symmetries. Gao and coworkers⁶² calculated UPS, NEXAFS, XPS, and RIXS spectra for isomers 3, 6 and 9 of C₂, C_s and C_2v symmetry, respectively. They found a strong dependence of the spectra on the isomers and claimed agreement with experimental data. Sun and Kertesz carried out calculations for all IPR isomers with a nonvanishing HOMO–LUMO gap at the B3LYP/6-31G* level (isomers 1–6). By comparing their calculated NMR spectra with experiment, they concluded, in agreement with experimental finding by Kikuchi et al.,⁵⁵ that isomer 3 prevails.

Fig. 1 The guest (CHFClBr) enantiomers 1a and 1b, one enantiomer of the fullerene C₈₂-3 2, and the 3a and 3b complexes R- and S-CHFClBr@C₈₂-3.

As mentioned above, preliminary calculations have shown that C₈₂ is the smallest fullerene cage capable of hosting the CHFClBr guest. We have therefore carried out calculations of the energy, infrared (IR), vibrational circular dichroism (VCD), UV-vis and nuclear magnetic resonance (NMR) spectra of one enantiomer of the C₈₂ fullerene, the guests and complexes of one host enantiomer with the S and R guest enantiomers, with the goal of studying the chiral recognition of the fullerene cage and its manifestations on the spectra.

2. Computational methods

The optimized geometries for isomers of C₈₂, for an isolated CHFClBr molecule and the endohedral complexes CHFClBr@C₈₂ were obtained by density-functional theory (DFT), using the B97D functional⁶³ and the 6-31G(d) basis set.⁶⁴ It should be emphasized that the size of the species studied prevented us from using larger basis sets. However, several studies have confirmed that the geometries provided by this combination of method and the basis set are sufficient.⁶⁵ Noteworthily, the B97D functional includes dispersion corrections, so it should give reliable results for the dispersion-bound intermolecular complexes. However, in contrast to the previous guests we have studied,^31–33 in this case not only dispersion but also electrostatic interactions with the labile π-electron systems are of importance. The stationary points resulting from the B97D/6-31G(d) optimization were verified to correspond to minima on the potential energy surface by performing a harmonic frequency analysis at the same level of theory. These frequencies were later used to calculate the zero-point vibrational energy (ZPVE) for the molecules studied here.

Because we in this work are focused on chiral recognition, only chiral IPR (Isolated Pentagon Rule) isomers, i.e. isomers 1, 3, and 5 according to The Atlas of Fullerenes,⁵⁴ were taken into account and structurally optimized. The insertion of the R or S enantiomers of the guest into one of the host enantiomers thus resulted in six distinct complexes, denoted in the following by the guest chirality as 1R, 1S, 3R, 3S, 5R and 5S, irrespective of the cage chirality. Such a procedure enabled us to define all diastereomeric complexes. The optimized geometric structures were then utilized in all subsequent calculations.

In agreement with the supermolecular approach which we applied previously,^31–33 the interaction energy is defined as

E_int(A@B) = E(A@B) − (E(A) + E(B)), (1)

where the geometries of A and B were the same as in the complex. The interaction energy was calculated either by the supermolecular (DFT, MP2) or by the perturbational approach. In previous studies,^31–33eqn (1) was utilized with the three energies calculated by either DFT using the B97D or PBE + D3(BJ) functional,^66,67 MP2, or the spin-component-scaled MP2 (SCS-MP2).⁶⁸ For all supermolecular calculations, the Boys-Bernardi counterpoise scheme⁶⁹ was applied in order to reduce the basis-set superposition errors (BSSE), i.e. both A and B were calculated in the A@B orbital basis set. The MP2 method is known to overestimate the stabilization for systems involving conjugated bonds, SCS-MP2 often correcting this behavior of MP2. For this reason, we have tested whether the SCS-MP2 approach can produce reliable results for the endohedral complexes studied here. In these calculations, the def2-TZVP basis set⁷⁰ was utilized. In addition, some calculations were repeated in a larger def2-QZVP basis set in order to estimate the saturation of the results with the basis set size.

As an alternative perturbational approach, the symmetry-adapted perturbation theory (SAPT) with a DFT description of the constituent molecules was applied^71–73 using the PBE functional (with the asymptotic correction of Grüning et al.⁷⁴) to account for the intramolecular electron correlation. The energies of the highest occupied molecular orbitals of the host and the guest were calculated using the PBE functional and the same basis set as in the main SAPT calculations. Ionization potentials (IPs) were either calculated at the PBE/def2-QZVP level (for C₈₂) or taken from experiment (for CHFClBr).⁷⁵ The calculated energies were 6.52, 6.67, and 6.76 eV for the 1, 3, and 5 isomers of C₈₂, respectively, while the experimental IP value for the guest amounts to 11.15 eV. The latter value is close to 10.67 eV obtained using the same computational method as that used for C₈₂. The asymptotic correction for the guest molecule was set to 0.142 hartree. Since the HOMO energies of the three isomers of C₈₂ were shifted according to the IP values, it turned out that the asymptotic corrections for all three cage types were the same and equal to 0.05 hartree.

The SAPT interaction energy was obtained in the form of a sum of several components, such as the electrostatic, induction, dispersion terms and their exchange counterparts, resulting from imposing an antisymmetry condition on the approximate wave functions. Higher-order terms were estimated through the so-called delta Hartree–Fock term (δE_HF).⁷⁶ Summarizing, the SAPT interaction energy is obtained using the equation:

E_int(SAPT) = E⁽¹⁾_elst + E⁽²⁾_ind + E⁽²⁾_disp + E⁽¹⁾_exch + E⁽²⁾_exch-ind + E⁽²⁾_exch-disp + δE_HF. (2)

It should be noted that this natural decomposition of the interaction energy allows the main driving force of the complex formation to be interpreted.

The stability of the complex is best described through the stabilization energy, which accounts for the deformation of the constituent molecules forming a complex, E_def(X), and for the zero-point vibration energy differences, ΔZPVE, of the complex A@B and molecules A and B,

E_stab = E_int(A@B) + E_def(A) + E_def(B) + ΔZPVE (3)

The deformation energies and ΔZPVE were available from the optimization calculations. The E_int(A@B) energies were taken from eqn (2).

Most SAPT(DFT) calculations have been performed using the def2-TZVP basis set. However, since the dispersion energy is known to be difficult to saturate with respect to the basis set size, we additionally calculated this energy in a larger def2-QZVP basis set. From the values of E⁽²⁾_disp in both basis sets, one can further estimate the complete-basis set (CBS) limit for this energy component. Since the dispersion energy is a pure electron-correlation contribution, a suitable formula for the CBS limit can be found e.g. in ref. 77:

E⁽²⁾_disp(CBS) = E⁽²⁾_disp[X] + C/X³, (4)

where X denotes the “cardinal number” of the basis set, taken here as 3 for def2-TZVP and 4 for def2-QZVP, in accordance with ref. 78. The contribution E⁽²⁾_disp(CBS)−E⁽²⁾_disp[def2-TZVP] is in this case about 70% larger (in absolute value) than the difference E⁽²⁾_disp[def2-QZVP]−E⁽²⁾_disp[def2-TZVP].

Geometry optimizations, single-point calculations of the interaction energies with DFT, MP2, and SCS-MP2, as well as the TD-DFT calculations with the CAM-B3LYP functional were performed using the Gaussian (G09) program package.⁷⁹ The SAPT(DFT) calculations and the calculations of the C₈₂ ionization potential with unrestricted DFT were performed using the Molpro package.⁸⁰

Another energy parameter describing the stability of the complex is the binding energy. Binding energy is defined as the difference between the energies at the optimized geometries for A@B and the sum of the energies of the isolated A and B molecules. In order to avoid estimating the BSSE, the binding energy is calculated from the following formula:

E_bind = E_int(A@B) + E_def(A) + E_def(B), (5)

where E_int(A@B) is the interaction energy for the A@B complex and E_def(X) is the deformation energy, i.e. the difference between the energy of molecule X in the complex and in the isolated state. The latter energy is always positive since the positions of atom X in the complexes are not optimal for the isolated molecule. To the energy obtained from eqn (4) one usually adds the ZPVE difference between the complex and the sum of the contributions for the constituent molecules (ΔZPVE) in order to approximately take into account the total (electronic and nuclear) stabilization of the complex. For conventional (non-endohedral) complexes, the latter quantity can be identified as the negative of the dissociation energy. However, for the endohedral case one needs to break the cage in order to free the guest molecule, so we prefer to use the notion of stabilization energy instead:

E_stab = E_bind + ΔZPVE (6)

The 10 lowest electronic excited states of the 3R, 3S complexes and the empty C₈₂-3 cage were calculated using TD-DFT^81–83 with the CAM-B3LYP functional, using a modified exact exchange ratio.⁸⁴ The def2-TZVP basis set was used in these calculations. It should be noted that the CAM-B3LYP functional has been developed for use in the context of TD-DFT in order to correctly reproduce excited states with some charge-transfer character.

The infrared (IR) and vibrational circular dichroism (VCD) spectra of the complexes were obtained within the harmonic approximation using the B97D/6-31G(d) approach. Although the absolute values of the frequencies obtained in this way differ from experiment, they should allow us to evaluate trends of frequency shifts upon complexation and eventually reveal manifestations of chiral recognition of the CHFClBr enantiomers by the chiral C₈₂ cage. Since the resulting identical sign of the rotatory strength of the stretching C–H vibration mode of both the S and R guest enantiomers in the C₈₂-3 host is unusual, we performed additional calculations of this property using the B97D functional and the SVP and 6-311G(d,p) basis sets, as well as using one more functional (PBE) and the same basis set (6-31G(d)). The results show that the rotatory strength of the C–H stretching mode is negative for all combinations of functionals and basis sets, and that the S enantiomer always has a higher rotatory strength than the R one.

The nuclear magnetic resonance (NMR) spectra are particularly sensitive to the environment. NMR chemical shifts were calculated using the spin–orbit zero-order regular approximation (SO-ZORA)^85,86 as implemented in the Amsterdam Density Functional (ADF) program.⁸⁷ We used the PBE functional including Grimme's dispersion correction (PBE-D3)^66,67,88 and the relativistically optimized all-electron TZ2P basis set.⁸⁹ Solvent effects were accounted for by using chloroform in a conductor-like screening model (COSMO)⁹⁰ as implemented in ADF. The chemical shifts of the carbon atoms of the cage relative to tetramethylsilane (TMS) (in ppm) were obtained by using benzene as the secondary reference as given in the following equation:

δ(C_i, C₈₂) = [σ(C, C₆H₆) − σ(C_i, C₈₂) + 128.5] (7)

where δ(C_i, C₈₂) is the chemical shift of the ith carbon atom of C₈₂ and its complexes, σ(C, C₆H₆) is the calculated absolute shielding constant of a benzene carbon atom, σ(C_i, C₈₂) is the calculated absolute shielding constant of the ith carbon atom of C₈₂ and its complexes, and 128.5 ppm is the chemical shift of benzene relative to TMS. This method has been shown to give reliable chemical shifts for similar molecular systems.^91–93

3. Results and discussion

3.1. Energies and geometries of the complexes

As already mentioned, there are 9 IPR isomers of C₈₂, and among these, isomer 3 was determined to prevail both experimentally⁵⁵ and theoretically (see ref. 57, 60, 62 and references cited therein). Kikuchi et al.⁵⁵ observed three isomers of the fullerene: 80% of the prevailing isomer 3, and the rest arising from achiral isomers of C_2v and C_3v symmetry.

As in all previous calculations,^57,60,62 the analysis of the free energies under normal conditions and total electronic energies confirms that the most stable isomer of the isolated C₈₂ is the chiral isomer 3. Only isomer 3 and the less stable isomers 1 and 5 (all of C₂ symmetry) of all possible IPR isomers of C₈₂ are chiral. Therefore, we will in the following focus on these isomers and their complexes. The calculated differences between the free energy ΔG under standard (298.15 K, 1 atm) conditions and the total electronic energy ΔE of the isomers 1, 3 and 5 of C₈₂ with respect to the most stable isomer 3 calculated at the B97D/6-31G(d), B97D/6-311G(d,p) (in parentheses) and PBE-D3(BJ)/6-31G(d) [in brackets] levels are collected in Table S1 in the ESI.† The ΔG energy differences between the isomers relative to that of isomer 3 are larger than 4 kcal mol⁻¹ for isomers 1 and 5, whereas the corresponding ΔE values are larger than 6 kcal mol⁻¹ for all functionals and basis sets used. Thus, in agreement with the experimental finding of Kikuchi et al.,⁵⁵ the population of the other chiral isomers (1 and 5) should be negligible at room temperature.

The calculated energies of the diastereomeric complexes of the chiral isomers with both enantiomers of the CHFClBr guest is collected in Table 1 and indicate that stable complexes should be formed only with the most stable isomer 3, and that the complex with the S enantiomer should be more stable than that with the R enantiomer by ca. 0.5 kcal mol⁻¹. To allow future experimental investigations to verify this prediction, the IR, VCD, UV-vis and NMR spectra of both complexes, i.e. R-CHFClBr@C₈₂ and S-CHFClBr@C₈₂, have been calculated.

Table 1 Free energy differences ΔG at standard (298.15 K, 1 atm) conditions and the total electronic energy ΔE differences (in kcal mol⁻¹) of the complexes with isomers 1, 3 and 5, calculated using B97D/6-31G(d) and B97D/6-311G(d,p) (in parentheses) with respect to 3S

CHFClBr@C82	ΔG	ΔE
1R	3.7 (3.7)	3.4 (3.6)
1S	7.1 (6.8)	7.0 (6.7)
3R	0.4 (0.7)	0.9 (1.0)
3S	0.0 (0.0)	0.0 (0.0)
5R	13.4 (12.8)	15.0 (14.3)
5S	12.2 (11.7)	13.5 (13.2)

---

Interestingly, the energy ordering of the complexes involving isomers 1 and 5 changes upon complexation. The 1R complex gains the most with respect to isomer 3, i.e. the difference between 1R and 3S or 3R is about 4 kcal mol⁻¹ less than for the isolated C₈₂-1. On the other hand, isomer 5 increases its relative energy upon complexation (the difference between isolated isomer 5 and 3 amounts to 6 kcal mol⁻¹, whereas for the 5S and 5R complexes it is more than two times larger). However, the 3R and 3S complexes are more stable than those with 1 and 5 cage isomers by more than 3 kcal mol⁻¹, and the 3S complex is more stable than the 3R one by 0.4 kcal mol⁻¹.

DFT calculations of the complexes reveal that the guests are too large for the cage, since the distances between their substituents and the closest carbon cage atom d_XC are smaller than the sums of the van der Waals radii of the corresponding atoms by approximately 0.4–0.6 Å (Table 2). The Δ values are smaller for the more electronegative halogen substituent (as expressed by Pauling electronegativity).^94,95 It should be stressed that such a short distance between the atoms is associated with strong repulsion, resulting in a considerable strain to which both the host and guests are exposed. Interestingly, only the smallest distances to the hydrogen atom show a large chiral recognition effect of ca. 0.1 Å, for all other distances the differences between the enantiomeric guests atoms and the cage are insignificant.

Table 2 The distances of the guest substituents to the closest carbon atoms of the C₈₂-3 cage d_XC in the complexes with the R and S enantiomers of CHFClBr guest calculated using B97D/6-31G(d) and B97D/6-311G(d,p) (in parentheses), the van der Waals radii of the guest atoms,⁹⁶ the sum of van der Waals distances of a guest atom and that of the carbon atom of the cage and the difference between the sum of the radii and the distance to the nearest carbon atom Δ (all in Å)

Nonbonding distance	van der Waals radii		Distances to the nearest carbon dXC and the Δ values
	Of the substituent	Sum of the radii of the carbon cage atom (1.70 Å) and of the substituent	d XC(R)	Δ(R)	d XC(S)	Δ(S)
H⋯C82	1.20	2.90	2.42 (2.40)	−0.48 (−0.50)	2.33 (2.30)	−0.57 (−0.60)
F⋯C82	1.47	3.17	2.57 (2.56)	−0.60 (−0.61)	2.59 (2.58)	−0.58 (−0.59)
Cl⋯C82	1.75	3.45	3.01 (2.98)	−0.56 (−0.53)	3.02 (3.00)	−0.57 (−0.55)
Br⋯C82	1.85	3.65	3.10 (3.13)	−0.45 (−0.42)	3.09 (3.12)	−0.44 (−0.43)

---

Too large guests inserted inside the cage lead to its considerable distortion: a reduction of some bond lengths and considerable changes in bond angles (Table 3). They raise the question to the origin of the stability of the complexes (vide infra). The CBr bond of the guest displays the largest compression (by almost 0.1 Å) upon complex formation, the CCl bond a somewhat smaller compression and the smallest reduction in bond length is observed for the bond with the largest polarity, the CF bond. Interestingly, also in this case the Δ values of the reduced C–halogen bond lengths correlate with the decrease in the Pauling electronegativity parameter of the halogen substituent. All guest bond angles involving the hydrogen atom in the complexes are increased in comparison to the values for the free guest, whereas the angles involving only the heavier atoms are reduced. The maximum values of the change (of ca. 4°) are obtained for the HCBr angle. No significant changes in the bond lengths or bonds of the guests that could be related to chiral recognition are found, except, perhaps the ∠FCBr bond angle. For obvious reasons, the distortions of bond lengths and bond angles of the C₈₂ cage are much smaller than those observed for the guests since they are spread over a much larger structure.

Table 3 Bond lengths (Å) and angles (degrees) in CHFClBr calculated using B97D/6-31G(d) and B97D/6-311G(d,p) (in parentheses) and the difference Δ between the values in the free guest and the R- and S-complexes

	Guest R/S	R@C82		S@C82
		d CX/∠XCY	Δ	d CX/∠XCY	Δ
C–H	1.095 (1.092)	1.087 (1.085)	−0.008 (−0.007)	1.087 (1.084)	−0.008 (−0.008)
C–F	1.350 (1.351)	1.347 (1.345)	−0.003 (−0.006)	1.346 (1.344)	−0.004 (−0.007)
C–Cl	1.797 (1.794)	1.734 (1.728)	−0.063 (−0.066)	1.732 (1.726)	−0.065 (−0.068)
C–Br	1.990 (1.991)	1.893 (1.884)	−0.097 (−0.107)	1.896 (1.888)	−0.094 (−0.103)
∠HCF	110.7 (110.3)	111.6 (111.4)	0.9 (1.1)	111.5 (111.2)	0.8 (0.9)
∠HCCl	108.6 (108.4)	111.2 (111.1)	2.6 (2.7)	111.7 (111.5)	3.1 (3.3)
∠HCBr	106.6 (106.7)	111.0 (111.3)	4.4 (4.6)	110.4 (110.8)	3.8 (4.1)
∠FCCl	109.9 (109.7)	107.7 (107.9)	−2.2 (−1.8)	107.0 (107.3)	−2.9 (−2.4)
∠FCBr	109.3 (109.3)	106.2 (106.2)	−3.1 (−3.1)	107.4 (107.2)	−1.9 (−2.1)
∠ClCBr	111.8 (112.4)	108.9 (108.7)	−2.9 (−3.7)	108.7 (108.6)	−3.1 (−3.8)

---

The sum of NBO⁹⁷ charges on the guests and host in the complexes calculated using B97D/6-31G(d) and B97D/6-311G(d,p) (in parentheses) and those calculated using B97D/6-31G(d) applying the QTAIM⁹⁸ method are collected in Table S2 (ESI†). They show very small net charges on the host and guest, with considerably larger values calculated by QTAIM.

As mentioned in the previous section, factors influencing the stability of the complexes with respect to the constituent molecules were determined by calculating the interaction energies using several methods. The binding energies were obtained by adding the deformation energies of the constituent molecules of the complex to the interaction energies (see Computational methods section for details), and the stabilization energies by additionally correcting the binding energy with the ZPVE of the nuclear motion. The results of these calculations are listed in Table 4.

Table 4 Interaction energy E_int for six endohedral complexes CHFClBr@C₈₂ obtained with various methods and the deformation and stabilization energy calculated from eqn (5) with the SAPT interaction energy (the last column) in kcal mol⁻¹

Complex	SAPT (DFT)^a def2-TZVP/QZVP	B97D def2-TZVP	B97D def2-QZVP	PBE + D3 def2-TZVP	PBE + D3 def2-QZVP	MP2 def2-TZVP	SCS-MP2 def2-TZVP	ΔZPVE	E def	E stab
a The SAPT(DFT) results in parenthesis are obtained from the CBS extrapolation of the E^(2)disp energy (def2-TZVP → def2-QZVP), see Computational details. The results without parenthesis are obtained by a simple replacement of the E^(2)disp(def2-TZVP) value in the SAPT(DFT)/def2-TZVP energy by the E^(2)disp(def2-QZVP) result.
1R	−5.3 (−8.5)	−3.7	−5.3	0.8	−0.1	−37.3	−14.7	1.1	5.5	1.3 (−1.9)
1S	−3.3 (−6.8)	−0.8	−2.4	2.9	1.8	−35.1	−12.3	1.0	5.5	3.3 (−0.3)
3R	−4.0 (−7.6)	−0.4	−2.0	2.5	1.5	−35.1	−12.7	0.5	6.6	3.1 (−0.6)
3S	−4.3 (−7.8)	−0.9	−2.5	2.2	1.1	−35.5	−13.1	0.7	6.2	2.7 (−0.9)
5R	−2.3 (−6.0)	3.4	1.8	4.3	3.3	−33.1	−10.8	0.3	9.3	7.3 (+3.6)
5S	−2.3 (−6.1)	3.2	1.6	4.4	3.4	−33.5	−11.0	0.4	8.3	6.4 (+2.6)

---

As can be seen from Table 4, the MP2 and SCS-MP2 interaction energies are unphysically large in absolute values. The MP2 overbinding is well known for stacked conjugated systems⁹⁹ and apparently this effect is here amplified by the electron-rich guest. The SCS-MP2 approach, which is known to correct MP2 in many cases,⁶⁸ also gives unsatisfactory results in the present case. Both sets of results are presented here only as a warning that in some cases the MP2 (and SCS-MP2) methods are unable to give reliable interaction energies in supermolecular calculations. A similar huge overestimation of the binding energy by the MP2 and SCS-MP2 methods has recently been observed in ref. 100 where large intermolecular complexes involving a fullerene with a buckycatcher molecule were studied.

The PBE + D3 method produces a slightly negative energy for the 1R case in the largest basis set. It should be emphasized that in this case, the pure PBE contribution to the energy is large and positive, and the dispersion “correction” is as large in absolute value as the PBE interaction energy, but of the negative sign, almost canceling each other. This casts some doubts on the reliability of the PBE + D3 interaction energies for systems of interacting nonpolar molecules, bound mostly by dispersion. On the other hand, the B97D functional as well as SAPT(DFT) gives reasonable values for the interaction energies. The CBS estimate of the dispersion energy (see the Computational methods section for details) enhances the attraction energy by about 3 to 4 kcal mol⁻¹ compared to the non-CBS results. The stabilization energies computed with the CBS-extrapolated energy give slightly negative (attractive) results for four of the six complexes. It should be noted that the CBS procedure turns out to be indispensable. This is due to a well-known feature of the dispersion energy of intermolecular interactions (see, e.g.ref. 100 for an analysis of complexes of a similar size to the present case), being very sensitive to the quality of the orbital basis set. The dispersion energy calculated in a triple or even quadruple-zeta basis is thus often still far from saturated. Nevertheless, these values are of sufficient quality to estimate the CBS limit.

When comparing the energy ordering resulting from the ΔE values in Table 1 with that of the binding energies from eqn (5) in Table 4, one should keep in mind that their ordering will only be identical for the ideal case when both quantities are calculated using the same method in the complete basis set limit. Because the 6-31G(d) basis set is very far away from the CBS, the BSSE is quite large (in fact, it is of the order of the binding energy itself), and irregularities in the energy ordering can appear. However, some trends can be seen in both tables, i.e. for the same C₈₂ isomer, the energetic ordering of the R and S guest isomers of the complex is the same.

According to all methods used, the largest stabilization upon complexation is obtained for the 1R complex, and the next is the 3S complex as far as the interaction energies are concerned. The third most stable complex according to the interaction energies is the 3R complex when using SAPT(DFT), and 1S using B97D, but the energy differences are in this case small. Finally, the 5S and 5R complexes are the least stabilized. The deformation energies are quite substantial in view of the smallness of the interaction energies, and the final values for the stabilization energies are thus the result of a delicate balance between the attractive interaction energy and the repulsive deformation energy (with a small additional contribution from the nuclear motion).

Although the 1R complex has the largest stabilization energy (Table 4), it is isomer 3 that is the most abundant according to both the calculations and experimental results. Thus, the complexes of this isomer with CHFClBr should be observable. We therefore present in the next section their IR, VCD, UV-vis, and NMR spectra to enable a future observation.

3.2 IR and VCD spectra

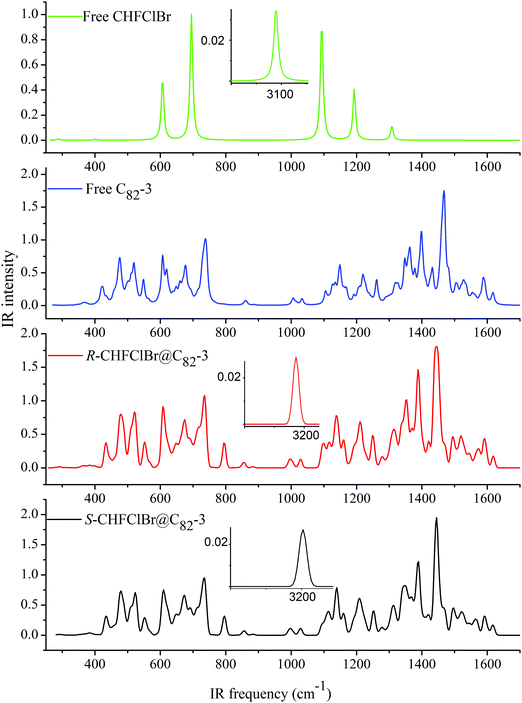
The calculated IR spectra of the free host and guest and their complexes are shown in Fig. 2 (a full list of the normal frequencies is presented in Table S3 of the ESI†) and reveal a strong influence of both the complexation and the guest chirality on the calculated spectra. Not unexpectedly, the most prominent effect is seen on the ν_CH stretching vibration band. However, in contrast to the usual IR manifestations of hydrogen bonding, the bands are shifted to higher frequencies by more than 100 cm⁻¹. This is due to the considerable shortening of the CH bonds upon the formation of the complex (Table 3). The calculated effects of chiral recognition on the vibrational frequencies are quite sensitive to the method of calculation. Because CH stretching vibration is a well-localized characteristic vibration, the IR spectra could in this case be used as a marker for both molecular and chiral recognition. On the other hand, the region below 1650 cm⁻¹ contains numerous nonlocalized vibrations of the C₈₂ cage, which are likely to appear together with guest vibrations and vibrational overtones. For instance, the bands at 1093 cm⁻¹, 1101 cm⁻¹, and 1107 cm⁻¹ contain a significant contribution from the ν_CF of the guest and of the cage vibrations whereas for the bands at 695 cm⁻¹, 795 cm⁻¹, and 796 cm⁻¹, the contribution of ν_CCl of the guest as well as cage vibrations is considerable, and they are also likely to be influenced by Fermi resonances in the experiment. Thus, although one can see clear differences in the spectra of the host, guest, and the complexes in the region below 1650 cm⁻¹, they are of a negligible diagnostic value.

Fig. 2 The IR spectra of free host and guest and the complexes calculated using B97D/6-31G(d).

VCD is one of the most important methods for determining the absolute configuration of organic molecules and for establishing the dominant conformations in biopolymers.^101–104 The rotational strengths of the vibrational bands of free guests 1 and host 2 and complexes 3a and 3b were therefore calculated.

The rotational strengths calculated for the stretching CH vibrations for 3a and 3b (Fig. 3 and Table 5 contain results obtained using several functionals and basis sets) show that both the ν_CH frequencies and the rotational strengths depend on the functionals and basis sets used. However, in all cases the rotational strengths for both complexes with the R- and the S-guest enantiomers have the same sign. Such a sign reversal for the ν_CH band for the complex with the S guest enantiomer relative to the free molecule, independently of the choice of the exchange–correlation functional and the basis set used, has not been previously reported for diastereomeric complexes.^101–104

Fig. 3 VCD spectra of 1a and 1b (top), 2 (middle) and 3a and 3b (bottom), calculated using B97D/6-31G(d). The inset depicts the VCD band of the ν_CH stretching mode of 1.

Table 5 Vibrational frequency (cm⁻¹) and rotational strength (10⁻⁴⁴ esu² cm²) of the CHFClBr enantiomers and R-CHFClBr@C₈₂-3 and S-CHFClBr@C₈₂-3 complexes calculated at the B97D/6-31G(d), B97D/SVP, PBE/6-31G(d) and B97D/6-311G(d,p) levels for the stretching CH vibrations. Note that independently of the calculation method used, the S complex has a lower energy than the R complex

Molecule	Vibrational frequency	Rotational strength
B97D/6-31G(d)
R-CHFClBr/S-CHFClBr	3089.4	−1.30/+1.30
R-CHFClBr@C82-3	3185.9	−2.03
S-CHFClBr@C82-3	3202.6	−1.00
B97D/6-311G(d,p)
R-CHFClBr/S-CHFClBr	3080.1	−0.92/+0.92
R-CHFClBr@C82-3	3178.3	−2.35
S-CHFClBr@C82-3	3174.7	−0.81
B97D/SVP
R-CHFClBr/S-CHFClBr	3060.0	−0.54/+0.54
R-CHFClBr@C82-3	3161.2	−4.15
S-CHFClBr@C82-3	3170.3	−1.00
PBE/6-31G(d)
R-CHFClBr/S-CHFClBr	3093.7	−1.26/+1.26
R-CHFClBr@C82-3	3143.2	−1.46
S-CHFClBr@C82-3	3146.5	−0.96

---

3.3. NMR spectra

The complexes contain several nuclei that are sensitive to their environment. Therefore, predicting changes in e.g. chemical shifts can be useful for the future detection of S or R isomers of the endohedral complexes with C₈₂. We have therefore calculated ¹H, ¹³C, ¹⁹F, ³⁵Cl, and ⁷⁹Br chemical shifts for the complexes and for the free host and guest. In view of the numerous close-lying carbon signals of the host cage, only signals pertaining to the guest are collected in Table 6 and discussed in the following. First, it should be mentioned that the negative values for the fluorine chemical shifts as opposed to the positive values for all other nuclei are caused by the choice of reference for this nucleus in the experimental work.¹⁰⁵ The proton, carbon, and fluorine guest signals will be discussed first since for these nuclei the experimental values have been reported. The calculated chemical shift of the carbon nucleus differs considerably from the reported experimental value, highlighting the challenge for DFT of calculating properties of even small molecules with electron-rich substituents. However, because the chemical shifts of CHFClBr for the different nuclei are determined in separate experiments and because the chemical shift of the carbon atom of the guest is well separated from the signals of the cage atoms, we can nevertheless draw some qualitative conclusions from the calculations.

Table 6 Chemical shifts of the guest nuclei (δ in ppm) calculated in chloroform using SO-ZORA/PBE-D3/TZ2P for the free CHFClBr and those in the complexes, together with the differences between the experimental and calculated values for the free guest (Δδ_exp-calc = δ_exp − δ_calc), differences between chemical shifts of free guest and those in the complexes (Δδ_free-complex); and the differences between the chemical shift of guest atoms in the complex with R enantiomer and that of the S enantiomer (Δδ = δR − δS)

	Free CHFClBr			R-CHFClBr@C82-3		S-CHFClBr@C82-3		Δδ
	δ exp	δ calc	Δδexp-calc	δR	Δδfree-complex	δS	Δδfree-complex
a Chemical shifts of the guest atoms referenced to TMS.^41 (Other ^1H for the free guest reported by Doyle and Vogl^37 is 7.62 ppm). b Chemical shifts of the guest atoms referenced to CFCl3. c Chemical shifts of the guest atoms referenced to NaCl. d Chemical shifts of the guest atoms referenced to NaBr. e Average values of ^13C signals taken from ref. 37. f Ref. 41.
^1H^a	7.65^f	8.15	−0.50	2.85	5.30	2.73	5.42	0.12
^13C^a	91.4^e	116.5	−25.1	100.5	16.0	100.5	16.0	0.0
^19F^b	−80.1^f	−92.8	12.7	−103.1	10.3	−107.0	14.2	3.9
^35Cl^c	—	608	—	591	17	597	11	−6
^79Br^d	—	1572	—	1518	54	1506	66	12

---

An inspection of the data collected in Table 6 reveals that (a) all guest signals are considerably shifted upon complexation with a very large value for the proton and carbon shifts; (b) the fluorine, and to a lesser extent, the proton signals, are sensitive to the guest chirality. On the other hand, differences in chemical shifts of the guest carbon, chlorine and bromine nuclei in the spectra of the 3R and 3S complexes lie within the experimental error bars.

The signals of the cage carbon atoms are collected in Table S4 of the ESI.† Interestingly, the differences between the experimental and calculated values are reasonably small, not exceeding 2 ppm. The complexation shifts for the cage carbon atoms are also usually small; they only exceed 2 ppm for three signals of the 3R complex and for one signal of the 3S complex. The differences in ΔδC_cage between the chemical shifts of the diastereomeric 3R and 3S complexes pertaining to chiral recognition are also too small to be significant.

To summarize, all guest signals (except the ³⁵Cl signals) exhibit considerable complexation shifts. However, only the signals of the fluorine nucleus are suitable for the detection of chiral recognition of the CHFClBr enantiomers by the C₈₂ cage by NMR.

3.4. Electronic spectra

The calculated vertical excitation energies (in eV) and oscillator strengths (f) for the 10 lowest singlet excited states of the empty C₈₂-3 cage and the complexes with the 3R, 3S enantiomers are presented in Table S5 of the ESI.† Most of them depend only weakly on complexation and guest chirality. As the lowest excitation energy of CHFClBr is placed in the UV region outside normal experimental observation ranges, we do not discuss the excited states of the guest molecule.

The data in the table reveal that the vertical excitation energy of the first excited state is significantly shifted upon complexation by about 0.05 eV, and for the second and third states the shift amounts to more than 0.02 eV. On the other hand, all intensities are largely independent of the complexation. There are also no noticeable differences in the vertical excitation energies and oscillator strengths for the diastereomeric complexes with the R and S guests. Thus, whereas UV-vis spectra could provide information on the formation of the complex of C₈₂ with the CHFClBr guest, they cannot be used to detect and study chiral recognition of the guest enantiomers by the fullerene cage.

4. Conclusions

Quantum chemical calculations (using density-functional theory and symmetry-adapted perturbation theory) of the chiral recognition of complexes involving the CHFClBr enantiomers by the most stable C₈₂-3 isomer reveal that the guests are too large for the fullerene cage and that they undergo considerable squeezing (shortening of bond lengths and distortions of bond angles) upon complex formation. However, despite the considerable steric strain, the guests are stabilized inside the host cavity by electrostatic interactions. The complexation results in considerable changes in the IR, VCD, NMR and UV-vis spectra, but the significant effect of chiral recognition between the guests was observed only by ¹⁹F signals in the NMR spectrum and by the sign reversal of the ν_CH vibrational band of S-CHFClBr in the VCD spectrum.^101–104

What are the prospects for the experimental verification of these predictions? Both C₈₂-3 enantiomers, probably as a mixture, and the CHFClBr separated into enantiomers³⁷ are known. It would be feasible to obtain the complexes studied here by using a ‘molecular surgery’ approach applied successfully in the case of H₂@C₆₀¹⁰⁶ and a few other fullerene complexes. To avoid tedious separation of the fullerene C₈₂-3 enantiomers, one could insert the S guest enantiomer into both enantiomers of the fullerene cage. By measuring the VCD spectra of R- and S-CHFClBr@C₈₂-3, it should be possible to experimentally verify the results of our calculations. To check the structural predictions, the separation of the C₈₂-3 enantiomers and crystallization of the complexes will be necessary.

Acknowledgements

This research was supported by The Research Council of Norway [grant no. 179568/V30] and a European Research Council starting grant [grant no. 279619]. Computer time was provided by the Norwegian Supercomputing Program NOTUR [grant no. NN4654K] and by PL-Grid Infrastructure.

References

1. L. Echegoyen and L. E. Echegoyen, Acc. Chem. Res., 1998, 31, 593–601.
2. J. E. Grose, E. S. Tam, C. Timm, M. Scheloske, B. Ulgut, J. J. Parks, H. D. Abruna, W. Harneit and D. C. Ralph, Nat. Mater., 2008, 7, 884–889.
3. E. Xenogiannopoulou, S. Couris, E. Koudoumas, N. Tagmatarchis, T. Inoue and H. Shinohara, Chem. Phys. Lett., 2004, 394, 14–18.
4. P. Norman, Y. Luo, D. Jonsson and H. Ĺgren, J. Chem. Phys., 1997, 106, 8788,  DOI:8710.1063/8781.473961.
5. M. S. Dresselhaus, G. Dresselhaus and P. C. Eklund, Science of Fullerenes and Carbon Nanotubes: Their Properties and Applications, Elsevier, Oxford, 1995.
6. Y. Yasutake, Z. J. Shi, T. Okazaki, H. Shinohara and Y. Majima, Nano Lett., 2005, 5, 1057–1060.
7. G. Gu, H. Huang, S. Yang, P. Yu, J. Fu, G. K. Wong, X. Wan, J. Dong and Y. Du, Chem. Phys. Lett., 1998, 289, 167–173.
8. M. S. Dresselhaus, G. Dresselhaus and P. C. Eklund, Science of Fullerenes and Carbon Nanotubes: Their Properties and Applications, Elsevier, Oxford, 1995, pp. 670–673.
9. Strained Hydrocarbons. Beyond the van't Hoff and Le Bel hypothesis, ed. H. Dodziuk, Wiley-VCH, Weinheim, 2009.
10. J. F. Stoddart, Angew. Chem., Int. Ed. Engl., 1991, 30, 70–71.
11. R. D. Bolskar, Nanomedicine, 2008, 3, 201–213.
12. R. Bakry, R. M. Vallant, M. Najam-ul-Haq, M. Rainer, Z. Szabo, C. W. Huck and G. K. Bonn, Int. J. Nanomed., 2007, 2, 639–649.
13. V. J. Morris, A. R. Kirby and A. P. Gunning, Atomic Force Microscopy for Biologists, World Scientific, 2009, p. 14.
14. C. Y. Yu, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, art. 012318.
15. M. S. Garelli and F. V. Kusmartsev, Eur. Phys. J. B, 2005, 48, 199–206.
16. M. Gong, T. A. Shastry, Y. Xie, M. Bernardi, D. Jasion, K. A. Luck, T. J. Marks, S. Ren and M. C. Hersam, Nano Lett., 2014, 14, 5308–5314.
17. H. Dodziuk, J. Nanosci. Nanotechnol., 2007, 7, 1102–1110.
18. M. Ge, U. Nagel, D. Hüvonen, T. Rõõm, S. Mamone, M. H. Levitt, M. Carravetta, Y. Murata, K. K. Komatsu, J. Y.-C. Chen and N. J. Turro, J. Chem. Phys., 2011, 134, 054507.
19. G. Min, U. Nagel, D. Hüvonen, T. Rőőm, S. Mamone, M. H. Levitt, M. Carravetta, Y. Murata, K. Komatsu, J. Y.-C. Chen and N. J. Turro, J. Chem. Phys., 2011, 134, art. 054507.
20. S. Mamone, J. Y.-C. Chen, R. Bhattacharyya, M. H. Levitt, R. G. Lawler, A. J. Horsewill, T. Rõõm, Z. Bačić and N. J. Turro, Coord. Chem. Rev., 2011, 255, 938–948.
21. S. Mamone, M. Concistre, E. Carignani, B. Meier, A. Krachmalnicoff, O. G. Johannesen, X. Lei, Y. Li, M. Denning, M. Carravetta, K. Goh, A. J. Horsewill, R. J. Whitby and M. H. Levitt, J. Chem. Phys., 2014, 140, 194306.
22. K. Kurotobi and Y. Murata, Science, 2011, 333(6042), 613–616.
23. E. H. T. Olthof, A. van der Avoird and P. E. S. Wormer, J. Chem. Phys., 1996, 104, 832–847.
24. D. J. Cram, M. E. Tanner and R. Thomas, Angew. Chem., Int. Ed., 1991, 30, 1024–1027.
25. J. L. Dye, J. Phys. IV, 1991, 1, C5-259–C5-282,  DOI:10.1051/jp4:1991531.
26. J. R. Nitschke, P. Mal, B. Breiner and K. Rissanen, Science, 2009, 324(5935), 1697–1699,  DOI:1610.1126/science.1175313.
27. P. Jakes, K.-P. Dinse, C. Meyer, W. Harneit and A. Weidinger, Phys. Chem. Chem. Phys., 2003, 5, 4080–4083.
28. H. Dodziuk, Modern Conformational Analysis. Elucidating Novel Exciting Molecular Structures, VCH Publishers, New York, 1995, pp. 119–134.
29. R. Ettl, I. Chao, F. Diederich and R. L. Whetten, Nature, 1991, 353, 149–153.
30. H. Dodziuk, G. Dolgonos and O. Lukin, Carbon, 2001, 39, 1907–1911.
31. T. Korona, M. Hesselmann and H. Dodziuk, J. Chem. Theory Comput., 2009, 5, 1585–1596.
32. T. Korona and H. Dodziuk, J. Chem. Theory Comput., 2011, 7, 1476–1483,  DOI:1410.1021/ct200111a.
33. H. Dodziuk, T. Korona, E. Lomba and C. Bores, J. Chem. Theory Comput., 2012, 8, 4546–4555.
34. H. Dodziuk, Chem. Phys. Lett., 2005, 410, 39–41.
35. M. Murata, S. Maeda, Y. Morinaka, Y. Murata and K. Komatsu, J. Am. Chem. Soc., 2008, 130, 15800–15801.
36. Z. Jiang, J. Crassous and V. Schurig, Chirality, 2005, 17, 488–493.
37. T. R. Doyle and O. Vogl, J. Am. Chem. Soc., 1989, 111, 8510–8511.
38. J. Costante, L. Hecht, P. L. Polavarapu, A. Collet and L. D. Baron, Angew. Chem., Int. Ed., 1997, 36, 885–887.
39. B. Darquie, C. Stoeffler, A. Shelnikovnikov, C. Daussy, A. Amy-Klein, C. Chardonnet, S. Zrig, L. Guy, J. Crassous, P. Soulard, P. Asselin, T. R. Huet, P. Schwerdtfeger, R. Bast and T. Saue, Chirality, 2010, 22, 870–884.
40. J. Crassous, F. Monier, J. P. Dutasta, M. Ziskind, C. Daussy, C. Grain and C. Chardonnet, ChemPhysChem, 2003, 4, 541–548,  DOI:510.1002/cphc.200200536.
41. J. Crassous and S. Hediger, J. Phys. Chem. A, 2003, 107, 10233–10240,  DOI:10.1021/jp0305685.
42. J. Canceill, L. Lacombe and A. Collet, J. Am. Chem. Soc., 1985, 107, 6993–6996.
43. A. Hirsch and M. Brettreich, Fullerenes. Chemistry and reactions, Wiley-VCH, 2005.
44. Y. Liu, C. Chen, P. Qian, X. Lu, B. Sun, X. Zhang, L. Wang, X. Gao, H. Li, Z. Chen, J. Dong, R. Ru Bai, P. E. Lobie, Q. Wu, S. Liu, H. Zhang, F. Zhao, M. S. Wicha, T. Zhu and Y. Zhao, Nat. Commun., 2015, 1, 5988.
45. J. Meng, X. Liang, X. Chen and Y. Zhao, Integr. Biol., 2013, 5, 43–47.
46. D. W. Cagle, S. J. Kennel, S. Mirzadeh, J. M. Alford and L. J. Wilson, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 5182–5187.
47. S. Yang, C. Chen, F. Fupin Liu, Y. Xie, F. Li, M. Jiao, M. Suzuki, T. Wei, S. Wang, C. Chen, X. Lu and T. Akasaka, Sci. Rep., 2013, 3 DOI:10.1038/srep01487.
48. W. Fu, L. S. Xu, H. Azurmendi, J. Ge, T. Fuhrer, T. Zuo, J. Reid, C. Shu, K. Harich and H. C. Dorn, J. Am. Chem. Soc., 2009, 131, 11762–11769,  DOI:10.1021/ja902286v.
49. T. Shimada, Y. Ohno, T. Okazaki, T. Sugai, K. Suenaga, S. Kishimoto, T. J. Mizutani, T. Inoue, R. Taniguchi, N. Fukui, H. Okubo and H. Shinohara, Physica E, 2004, 21, 1089–1092.
50. T. Shimada, Y. Ohno, K. Suenaga, T. Okazaki, S. Kishimoto, T. Mizutani, R. Taniguchi, H. Kato, B. P. Cao, T. Sugai and H. Shinohara, Jpn. J. Appl. Phys., Part 1, 2005, 44, 469–472.
51. T. Shimada, T. Okazaki, R. Taniguchi, T. Sugai, H. Shinohara, K. Suenaga, Y. Ohno, S. Mizuno, S. Kishimoto and T. J. Mizutani, Appl. Phys. Lett., 2002, 81, 4067–4069.
52. Y. Nakayama, S. Fujiki, Y. Hirado, H. Shiozawa, H. Ishii, T. Miyahara, Y. Maniwa, T. Kodama, Y. Achiba, H. Kataura, Y. Kubozono, M. Nakatake and T. Saitoh, Phys. Status Solidi B, 2008, 245, 2025–2028.
53. A. A. Taherpour, Chem. Phys. Lett., 2009, 483, 233–240.
54. P. W. Fowler and D. E. Manolopoulos, An Atlas of Fullerenes, Clarendon Press, Oxford, 1995.
55. K. Kikuchi, N. Nakahara, T. Wakabayashi, S. Suzuki, H. Shiromaru, Y. Miyake, K. Saito, I. Ikemoto, M. Kainosho and Y. Achiba, Nature, 1992, 357, 142.
56. M. Zalibera, A. A. Popov, M. Kalbac, P. Rapta and L. Dunsch, Chem. – Eur. J., 2008, 14, 9960–9967.
57. G. Sun and M. Kertesz, J. Phys. Chem. A, 2001, 105, 5468–5472.
58. A. Marcelli, W. Xu, L. Liu, C. Wang, W. Chu and Z. Wu, J. Nanophotonics, 2009, 3, 031975.
59. L. Feng, T. Wakahara, T. Tsuchiya, Y. Maeda, Y. Lian, T. Akasaka, N. Mizorogi, K. Kobayashi, S. Nagase and K. M. Kadish, Chem. Phys. Lett., 2005, 405, 274–277.
60. A. R. Khamatgalimov and V. I. Kovalenko, J. Phys. Chem. A, 2011, 115, 12315–12320.
61. H. Gao, W. H. Zhu, C. M. Tang, F. F. Geng, C. D. Yao, Y. L. Xu and K. M. Deng, Acta Phys. Sin., 2010, 59, 1707–1711.
62. B. Gao, L. Liu, C. Wang, Z. Wu and Y. Luo, J. Chem. Phys., 2007, 127, 164314.
63. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
64. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
65. R. Yamakado, K. Mikami, K. Takagi, I. Azumaya, S. Sugimoto, S.-I. Matsuoka, M. Suzuki, K. Katagiri, M. Uchiyama and A. Muranaka, Chem. – Eur. J., 2013, 19, 11853–11857.
66. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
67. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
68. S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102.
69. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
70. N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, Can. J. Chem., 1992, 70, 560–571.
71. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930.
72. A. Hesselmann, G. Jansen and M. Schütz, J. Chem. Phys., 2005, 122, art. 054306.
73. R. Podeszwa and K. Szalewicz, Chem. Phys. Lett., 2005, 412, 488–493.
74. M. Grüning, O. V. Gritsenko, S. J. A. van Gisergen and E. J. Baerends, J. Chem. Phys., 2001, 114, 652–660.
75. D. M. P. Holland, A. W. Potts, L. Karlsson, I. L. Novak, I. L. Zaytseva, A. B. Trofimov, E. V. Gromov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 135101.
76. M. Jeziorska, B. Jeziorski and J. Cizek, Int. J. Quantum Chem., 1987, 32, 149–164.
77. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Phys. Chem., 1997, 106, 9639–9646.
78. A. Anoop, W. Thiel and F. Neese, J. Chem. Theory Comput., 2010, 6, 3137–3144.
79. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
80. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schuetz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Koeppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflueger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, Molpro, version 2012.1, a package of ab initio programs, Cardiff, UK, 2012.
81. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
82. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
83. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224.
84. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
85. E. V. Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516.
86. E. V. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
87. E. J. Baerends, J. Autschbach, A. Berces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, L. Deng, R. M. Dickson, D. E. Ellis, M. van Faassen, L. Fischer, T. H. Fan, C. Fonseca Guerra, S. J. A. van Gisbergen, J. A. Groeneveld, O. V. Gritsenko, M. Gruning, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, G. Jensen, G. van Kessel, F. Kootstra, E. van Lenthe, D. A. McCormack, A. Michalak, J. Neugebauer, V. P. Osinga, S. Patchkovskii, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, P. Ros, P. R. T. Schipper, G. Schreckenbach, J. G. Snijders, M. Sola, M. Swart, D. Swerhone, G. teVelde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. van Wezenbeek, G. Wiesenekker, S. Wolff, T. Woo, A. Yakovlev and T. Ziegler, http://www.scm.com/, Vrije Universiteit: Amsterdam, The Netherlands, 2014.
88. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228.
89. E. V. Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
90. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
91. T. Kupka, M. Stachów, M. Nieradka and L. Stobiński, Magn. Reson. Chem., 2011, 49, 549–557.
92. T. Kupka, M. Stachów, E. Chełmecka, K. Pasterny and L. Stobiński, Synth. Met., 2012, 162, 573–583.
93. T. Kupka, M. Stachów, E. Chełmecka, K. Pasterny, M. Stobińska and L. Stobiński, J. Chem. Theory Comput., 2013, 9, 4275–4286.
94. R. T. Sanderson, J. Am. Chem. Soc., 1983, 105, 2259–2261.
95. L. Pauling, J. Am. Chem. Soc., 1932, 54, 3570–3582.
96. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
97. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
98. R. F. W. Bader, Atoms in Molecules – A Quantum Theory, Oxford University Press, Oxford, 1990.
99. P. Hobza, H. L. Selzle and H. W. Schlag, J. Phys. Chem., 1996, 100, 18790–18794.
100. M. Hesselmann and T. Korona, J. Chem. Phys., 2014, 141, 094107.
101. P. J. Stephens, F. J. Devlin and J. R. Cheeseman, VCD Spectroscopy for Organic Chemists, CRC Press, Boca Raton, 2012.
102. T. A. Keiderling, in Circular Dichroism: Principles and Applications, ed. N. Berova, K. Nakanishi and R. W. Woody, Wiley-VCH, New York, 2nd edn, 2000, pp. 621–666.
103. P. J. Stephens, F. J. Devlin and J.-J. PAN, Chirality, 2008, 20, 643–663.
104. B. Ranjbar and P. Gill, Chem. Biol. Drug Des., 2009, 74, 101–120,  DOI:10.1111/j.1747-0285.2009.00847.x.
105. J. Crassous and S. Hediger, J. Phys. Chem. A, 2003, 107, 10233–10240.
106. K. Komatsu, M. Murata and Y. Murata, in XIX International Winterschool on Electronic Properties of Novel Materials, ed. H. Kuzmany, Kirchberg, Tirol, 2005.

---

Footnote

† Electronic supplementary information (ESI) available: Excitation energies, changes in free energies, charges, IR and NMR results as well as the optimized geometries of the molecules studied. See DOI: 10.1039/c6cp05030a

---