Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mobility and association of ions in aqueous solutions: the case of imidazolium based ionic liquids†
Marija
Bešter-Rogač
*a,
Marina V.
Fedotova
*b,
Sergey E.
Kruchinin
b and
Marco
Klähn
*c
aFaculty of Chemistry and Chemical Technology, University of Ljubljana, Slovenia. E-mail: marija.bester@fkkt.uni-lj.si
bG.A. Krestov Institute of Solution Chemistry of the RAS, Ivanovo, Russia. E-mail: hebrus@mail.ru
cInstitute of Chemical and Engineering Sciences, Agency for Science, Technology and Research, Singapore. E-mail: marco.klaehn@gmail.com
First published on 22nd September 2016
Abstract
The mobility and the mechanism of ion pairing of 1,1 electrolytes in aqueous solutions were investigated systematically on nine imidazolium based ionic liquids (ILs) from 1-methylimidazolium chloride, [MIM][Cl], to 1-dodecyl-3-methylimidazolium chloride, [1,3-DoMIM][Cl], with two isomers 1,2-dimethylimidazolium chloride, [1,2-MMIM][Cl], and 1,3-dimethylimidazolium chloride, [1,3-MMIM][Cl]. Molecular dynamics (MD) simulations, statistical mechanics calculations in the framework of the integral equation theory using one-dimensional (1D-) and three-dimensional (3D-) reference interaction site model (RISM) approaches as well as conductivity measurements were applied. From experiment and MD simulations it was found that the mobility/diffusion coefficients of cations in the limit of infinite dilution decrease with an increasing length of the cation alkyl chain, but not linearly. The aggregation tendency of cations with long alkyl chains at higher IL concentrations impedes their diffusivity. Binding free energies of imidazolium cations with the chloride anion estimated by RISM calculations, MD simulations and experiments reveal that the association of investigated ILs as model 1,1 electrolytes in water solutions is weak but evidently dependent on the molecular structure (alkyl chain length), which also strongly affects the mobility of cations.
1. Introduction
Salt solutions are ubiquitous, and solvated ions greatly influence many processes, such as protein folding and conformational changes of nucleic acids, permeability, conductance, and electrostatic potential of cell membranes, micellization of surfactants and (in water) hydrophobic effects (also Hofmeister effects), and behaviour of enzymes, or have some other properties (e.g. acid–base properties) that influence the activity of biomolecules. Charged species also affect the mechanism and kinetics of chemical reactions consequently the mechanism of ion-exchange, the sol–gel transition, and many other phenomena. Thus, solvated ions were, not surprisingly, the subject of many experimental and theoretical studies. Recently, a systematic investigation of the interactions between oppositely charged ions in aqueous solutions of simple alkali halide salts has been carried out, based on conductance experiments and Monte Carlo simulations.1It has been found that ion pairs with a large difference in hydration free energy of cations and anions (large difference in size) have a relatively low association constant compared to those which exhibit similar hydration free energies and tend to associate in water. The microscopic structure was obtained by Monte Carlo simulations, using a simple two-dimensional water model. It has been shown that in all cases, the relative water density between the two ions increases, compared to the relative water density around two separate ions. In the case of two small ions, the two are associated due to stronger electrostatic interactions (in agreement with Collins' “law of matching water affinities”), while in the case of two large ions, we attribute ion pairing to entropic reasons. On the other hand, in the case of two ions with very different water affinities, the small ion would be strongly hydrated and not release its water upon pairing, thereby leading to a small association constant.
In order to obtain more information about the mechanism of ion pairing in solutions, ionic liquids (ILs) can serve as an excellent model system, because they exist in diverse structures. For a long time, water was considered as an impurity in ILs. However, recent studies treat the mixtures of ILs and water as a novel class of solvents. These solvents are very attractive systems for different applications, in particular, they are used as the solvents for biopolymers2–4 and therefore the body of literature examining IL–water mixtures has been growing steadily.
Molecular dynamic (MD) simulations have been used in combination with empirical force fields to study various ILs either in the bulk phase or in mixtures with water with varying IL concentrations.5 The association of ions in water has also been investigated using MD simulations directly. In ab initio MD simulations it was observed that small 1-ethyl-3-methylimidazolium ([1,3-EMIM]+) cations and chloride anions remained associated in water throughout simulations, which was explained using hydrophobic effects.6 Ion association has also been observed in classical MD simulations, especially when hydrophobic ions are involved, as in the case of imidazolium-based cations with long alkyl chains paired with hydrophobic NTf2.7 When small hydrophilic iodide anions were used, however, ion association was observed with small dimethyl imidazolium cations but not with imidazolium cations that contained long octyl chains.8 Also the influence of the alkyl chain length of imidazolium-based cations on cation diffusion in water has been studied in a few cases. A linear decrease of diffusivity with increasing alkyl length was found.9,10 These values were obtained for large IL concentrations around 1.1–1.3 M and 0.3–0.4 M, respectively, where strong interactions among the ions determined self-diffusion. However, the experimental values of diffusion coefficients for comparison were missing.
Among various experimental techniques for investigation of the mobility and the association properties of ionic systems in solutions, the electric conductivity measurement of dilute solutions is probably one of the most accurate techniques.11,12 Some attempts have been made to apply this method also on ILs diluted in aqueous solutions.13,14 Whereas for 1-butyl-3-methylimidazolium chloride, [1,3-BMIM][Cl], at 298.15 K the value of KA is reported,13 it is claimed that 1-ethyl-3-methylimidazolium tetrafluoroborate and 1-butyl-3-methylimidazolium tetrafluoroborate exist as free ions in aqueous solutions.14 Unfortunately there are no systematic investigations on diluted ILs in aqueous solutions which can provide more insights into their transport properties.
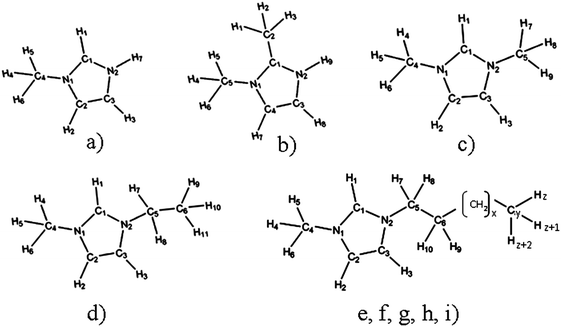
So we decided to carry out a systematic computational and experimental investigation of the influence of the ion size and its molecular structure on ion association and on ion mobility in water. Here we present the results for a series of imidazolium based chlorides with different alkyl chain lengths, from 1-methylimidazolium chloride, [MIM][Cl] to 1-dodecyl-3-methylimidazolium chloride, [1,3-DoMIM][Cl]. Among them there are also two isomers 1,2-dimethylimidazolium chloride, [1,2-MMIM][Cl] and 1,3-dimethylimidazolium chloride [1,3-MMIM][Cl]. The structures of all investigated systems are presented in Fig. 1.
In this work, the experimental conductivity data will be analyzed by Barthel's low-concentration chemical model (lcCM) to obtain the association constants, KA (T), and limiting molar conductivities at infinite dilution, Λ∞(T).15Λ∞(T) will be split into the ionic contributions with the help of known values of limiting conductivity of chloride ions, λ∞(T, Cl−), enabling us to determine the diffusion coefficients D∞(T, Cl−). These diffusion coefficients will then be compared with values derived from MD simulations. In these simulations, the diffusivity of imidazolium cations will be derived in aqueous solution and close to the limit of infinite ion dilution to enable a straightforward comparison with D∞.
To explain the obtained results of KA on a microscopic scale, we will apply statistical mechanics calculations in the framework of the integral equation theory using one-dimensional (1D-) and three-dimensional (3D-) reference interaction site model (RISM) approaches. The RISM integral equation theory is actively and successfully employed for the study of different liquids16–21 (and references therein) including ILs.22–24 Using the aforementioned approaches, one can obtain detailed information about atom–atom and molecular–atom interactions, including interactions among ions. Due to the latter it is thus possible to investigate ion association in the systems of interest. For our purpose the free energy of ion pairing will be estimated based on the RISM potential of mean force (PMF).25–35 The PMF is a suitable property to study possible ion-binding, because the probability and the stability of ion pairs can be derived from it by estimating the depth of the corresponding PMF minima.
2. Methods
2.1. Molecular dynamics simulations
Imidazolium cations and chloride anions were described with the force field developed by Lopez et al.36–38 However, partial charge on the atoms was adjusted to an aqueous environment. These charges were derived as described in Section 2.2 and are identical with those shown in Fig. B1–B9 in part B of the ESI.† Water was represented using the TIP5P model.39MD simulations were performed in the isothermal–isobaric ensemble (NPT) using GROMACS 4.5.5.40 Hydrogen was treated explicitly, while the lengths of covalent bonds that involved hydrogen were constrained using the LINC algorithm.41 Full period boundary conditions were used. The integration step size was 2 fs. The solution was simulated at 298 K using a velocity rescaling thermostat42 and a coupling constant of 0.1 ps. The target pressure of 1 atm was regulated using a Berendsen barostat43 with a coupling constant of 1 ps and a compressibility of 4.5 × 10−5 bar−1. For long range electrostatic interactions beyond 1.5 nm the fast particle-mesh Ewald method with dispersion corrections was used.44,45 Lennard-Jones interactions were taken into account up to atom pair distances of 1.2 nm. The translation of the center-of-mass of the system was removed.
Six different systems were simulated that contained one cation [MIM]+, [1,3-EMIM]+, [1,3-BMIM]+, [1,3-HMIM]+, [1,3-OMIM]+, [1,3-DeMIM]+ or [1,3-DoMIM]+, respectively. These cations were solvated with 2050 water molecules, which correspond to an ion concentration of 0.0266 M. One chloride anion was added to ensure charge neutrality. After a minimization of the potential energy to remove initial close contacts between atoms, the systems were equilibrated for 1 ns. Subsequently, the systems were simulated for 50 ns for data analysis. The diffusion coefficients were derived from the resulting trajectories using the Einstein relation that connects the mean square displacement of a cation center-of-mass position, rcom, with its diffusion coefficient, D:
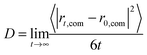 | (1) |
In Fig. A1 in part A of the ESI† the mean square displacements of the center-of-mass of cations as a function of time interval, derived from MD simulations, are presented. Diffusion coefficients for the different cations were derived as slopes of these curves.
To examine the effect of cation aggregation on the diffusion coefficients, we also simulated ILs in aqueous solutions at high concentrations. In two MD simulations of 20 ns length, we solvated 90 ion pairs of [MIM][Cl] and [1,3-DoMIM][Cl] with 3500 water molecules, which resulted in IL concentrations of 1.0 M and 1.2 M, respectively. These very high concentrations are comparable to those that have been used before in ref. 9. Diffusion coefficients for the cations were derived as slopes of the curves presented in Fig. A2 in part A of the ESI.†
Binding free energies, ΔGbind, of ion pairs were calculated using the thermodynamic integration method as implemented in GROMACS. In this process, ΔGbind is calculated by deriving the solvation free energy of Cl− at the cation binding site, while the ion pair is solvated in water, and the solvation free energy of Cl− in pure water without cations. The difference of these two solvation free energies is ΔGbind of the ion pair. This energy is also equivalent to the free energy change that occurred when Cl− is gradually displaced from its cation binding site into bulk water. The solvation free energy of Cl− is calculated in MD simulations by a step-wise switching off of all Coulomb interactions of the anion with its environment in the first phase. In the second phase, all Lennard-Jones interactions are gradually switched off, thereby fully decoupling the anion from the rest of the system. The coupling strength of Cl− to its environment is described by the coupling parameter λ as shown in eqn (2):
| E(λ) = (1 − λ)E1 + λE2 | (2) |
The parameter λ is increased in steps from 0 to 1, so that the total energy, E(λ), gradually changes from E1, the energy that contains all interactions of Cl− with its environment, to E2, where Cl− is fully decoupled. In our case λ was increased with an increment of Δλ = 0.1 from 0 to 1 for Coulomb and Lennard-Jones interactions, respectively. For each λ-value, a MD simulation of 2 ns length was carried out (resulting in a total simulation length of 44 ns per system), in which after each 100 fs the derivative of the system enthalpy with respect to λ, ∂H/∂λ, was written out. The results from the first 0.5 ns were discarded to account for equilibration. In the next step, values of ∂H/∂λ were averaged over each respective trajectory. These average 〈∂H/∂λ〉 values are plotted as a function of λ in Fig. A3 and A4 in part A in the ESI.† A numerical integration of these curves over λ yielded ΔGbind. In Lennard-Jones decoupling simulations where λ is close to zero, i.e. where Cl− is almost fully decoupled from the system, it is necessary to use a soft-core potential. This additional potential avoids close contacts between atoms that would lead to singularities when the energy potentials are evaluated. For the soft-core potential we used an α-parameter of 0.5, a distance parameter of 0.3 nm and a λ exponential of 1. The functional form of the soft-core potential and further details of the simulation procedure are given in the literature.46 We chose for Cl− binding sites at the cation that were found to be energetically most favorable according to results from 3D-RISM calculations. These 3D-RISM results were also in line with previously published work as discussed in the results part. To avoid diffusion of Cl− away from the cation binding site during free energy simulations, it is necessary to restrain the distance between Cl− and the cation hydrogen that according to 3D-RISM coordinates directly with Cl−. This distance restraint is particularly important taking into account that ion pair association was found to be very weak, thereby facilitating dissociation. The H–Cl distance was restrained with a harmonic potential with its minimum at the optimal distance and a force constant of 5000 kJ nm−2 mol−1. The optimal H–Cl distances were found by minimizing the potential energy of the system. Otherwise, the same simulation parameters were used as described in the previous paragraph. Statistical errors were calculated using the block averaging method for each value of 〈∂H/∂λ〉 and error propagation was used to derive the error of ΔGbind, subsequently.
2.2. RISM calculations
The foundations of the 1D- and 3D-RISM theories were described in detail elsewhere16,20,47,48 including our recent publications,29–31,49–51 therefore it may suffice here to give only a brief outline of the aspects relevant to our study.Wαβ(r) = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gαβ(r) gαβ(r) | (3) |
Wuu(r) = − kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) guu(r). guu(r). | (4) |
An important point is that the accuracy of both the 1D- and 3D-RISM PMFs depends significantly on the closure approximation used. It was established53 that the most reasonable results are obtained using the Kovalenko–Hirata closure.54 Correspondingly, we used 1D-55 and 3D-28 versions of this closure in our calculations. As in this study, first of all, we were interested in the possibility of contact ion pairing (see below), and therefore we limited our discussion to the behavior of the PMF at its first minimum.
In the framework of the RISM calculations, the systems under study were considered as a mixture of water molecules and ILs with the common form of the interaction potential represented by the long-range electrostatic (Coulomb) and short-range Lennard-Jones (LJ) terms. The corresponding LJ parameters were taken from the Optimized Potentials for Liquid Simulations (OPLS) force field.56 For water the modified version of the SPC/E model (MSPC/E) was used.57 The parameters of the optimized (bond lengths and angles) structures of the IL cations under study were adopted by the DFT (Density Functional Theory) method at the B3LYP/6-311++G** level in combination with a polarizable continuum model (PCM) for the water solvent58–61 as implemented in the ab initio code GAUSSIAN 09.62 The optimized geometries are presented in the ESI† in the form of atom coordinates (Tables in part B). The partial charges of IL atoms in water were derived from the electrostatic potential induced by the structurally optimized cations (ESP charges) using the CHELPG scheme.63 Charges on chemically equivalent atoms were averaged. The charges are shown in Fig. B1–B9 in part B of the ESI.†
The RISM calculations were carried out using the rism1d and rism3d.snglpnt codes from the AmberTools package (version 14).64 The numerical solution of the 1D- and 3D-RISM integral equations was obtained using the MDIIS (Modified Direct Inversion in the Iterative Subspace) iterative scheme.65 The 1D-RISM equations were solved on a 1D grid of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 points with a spacing of 2.5 × 10−3 nm and 10 MDIIS vectors. A residual tolerance of 10−6 was chosen. The 3D-RISM equations were solved on a three-dimensional grid of 256 × 270 × 250 points for [MIM][Cl] and [1,3-MMIM][Cl], 270 × 270 × 250 points for [1,2-MMIM][Cl] and [1,3-EMIM][Cl], 270 × 280 × 250 points for [1,3-BMIM][Cl], 280 × 288 × 252 points for [1,3-HMIM][Cl], 288 × 288 × 250 points for [1,3-OMIM][Cl], 294 × 300 × 250 points for [1,3-DeMIM][Cl] and 300 × 320 × 250 points for [1,3-DoDMIM][Cl] with 4 MDIIS vectors and a spacing of 0.025 nm in a parallelepiped cell. These parameters correspond to a cell of size (6.38 × 6.75 × 6.25) nm3 for [MIM][Cl] and [1,3-MMIM][Cl], (6.75 × 6.75 × 6.25) nm3 for [1,2-MMIM][Cl] and [1,3-EMIM][Cl], (6.75 × 7.00 × 6.25) nm3 for [1,3-BMIM][Cl], (7.00 × 7.20 × 6.30) nm3 for [1,3-HMIM][Cl], (7.20 × 7.20 × 6.25) nm3 for [1,3-OMIM][Cl], (7.35 × 7.50 × 6.25) nm3 for [1,3-DeMIM][Cl], and (7.50 × 8.00 × 7.25) nm3 for [1,3-DoDMIM][Cl]. The residual tolerance of 10−6 was also chosen for both 1D- and 3D-RISM calculations. All above mentioned parameters are large enough to accommodate the complex together with sufficient solvation space around it so that the obtained results are without significant numerical errors. All calculations were performed for ambient conditions and the same concentrations of ILs(aq) as in the conductivity experiments.
384 points with a spacing of 2.5 × 10−3 nm and 10 MDIIS vectors. A residual tolerance of 10−6 was chosen. The 3D-RISM equations were solved on a three-dimensional grid of 256 × 270 × 250 points for [MIM][Cl] and [1,3-MMIM][Cl], 270 × 270 × 250 points for [1,2-MMIM][Cl] and [1,3-EMIM][Cl], 270 × 280 × 250 points for [1,3-BMIM][Cl], 280 × 288 × 252 points for [1,3-HMIM][Cl], 288 × 288 × 250 points for [1,3-OMIM][Cl], 294 × 300 × 250 points for [1,3-DeMIM][Cl] and 300 × 320 × 250 points for [1,3-DoDMIM][Cl] with 4 MDIIS vectors and a spacing of 0.025 nm in a parallelepiped cell. These parameters correspond to a cell of size (6.38 × 6.75 × 6.25) nm3 for [MIM][Cl] and [1,3-MMIM][Cl], (6.75 × 6.75 × 6.25) nm3 for [1,2-MMIM][Cl] and [1,3-EMIM][Cl], (6.75 × 7.00 × 6.25) nm3 for [1,3-BMIM][Cl], (7.00 × 7.20 × 6.30) nm3 for [1,3-HMIM][Cl], (7.20 × 7.20 × 6.25) nm3 for [1,3-OMIM][Cl], (7.35 × 7.50 × 6.25) nm3 for [1,3-DeMIM][Cl], and (7.50 × 8.00 × 7.25) nm3 for [1,3-DoDMIM][Cl]. The residual tolerance of 10−6 was also chosen for both 1D- and 3D-RISM calculations. All above mentioned parameters are large enough to accommodate the complex together with sufficient solvation space around it so that the obtained results are without significant numerical errors. All calculations were performed for ambient conditions and the same concentrations of ILs(aq) as in the conductivity experiments.
2.3. Conductivity measurements and data analysis
Stock solutions were prepared by mass from the pure compounds and demineralized distilled water. Demineralized water was distilled two times in a quartz bidestillation apparatus (Destamat Bi 18E, Heraeus). The final product with the specific conductivity <6 × 10−7 S cm−1 was distilled into a flask permitting storage under an atmosphere of nitrogen permitting storage and transfer of water into the measuring cell under an atmosphere of nitrogen. The concentration of the stock solution was checked by titration with a standard solution of AgNO3 potentiometric indication.
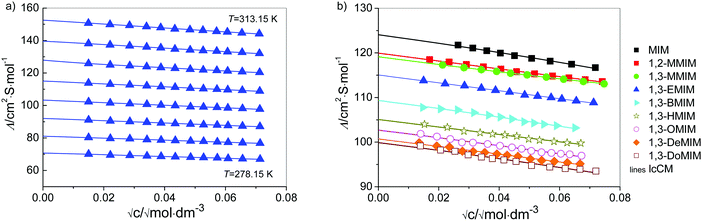
The molar concentrations c were determined from the masses and the corresponding solution densities, d, of stock solutions and the last solutions in the cell. They were determined at 298.15 K using the method of Kratky et al.69 using a Paar densimeter (DMA 5000) combined with a precision thermostat. A linear change of d with increasing salt content for diluted solutions was assumed, i.e. d(T) = d0(T) + bm, where d0(T) is the density of water (Table C1 in part C of the ESI†), m is the molality, and the b-coefficients are assumed as independent of temperature. They are given in Table C2 in part C of the ESI† together with molar conductivities, Λ(c), of all investigated systems. Molar conductivities are given as a function of electrolyte molality, m, which is related to the corresponding (temperature-dependent) molar concentration, c, via c = m·d/(1 + M2·m), where M2 is the molar mass of the solute (given also in Table C2 in part C of the ESI†) and d is the density of solution. The estimated uncertainty of d is within 0.005 kg m−3. The results for Λ(c) are shown in Fig. 2a for [1,3-EMIM][Cl] in water, whereas Fig. 2b compares the data for all investigated solutes at 298.15 K. Considering the sources of error (calibration, measurements, impurities), the values for Λ(c) are believed to be certain within 0.3%.
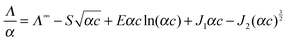 | (5) |
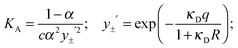 | (6) |
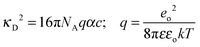 | (7) |
The coefficients of eqn (5) are explained in ref. 15. The parameters S and E are estimated with the help of the solvent parameters. The coefficients J1 and J2 additionally depend on the distance parameter R, which represents the distance up to which oppositely charged ions are counted as non-conducting ion pairs, and hence is the upper limit of ion-pair association represented by the upper limit of the association constant KA and the distance parameter of the mean activity coefficient y±′ (eqn (6) and (7)).
Analysis of the conductivity data was carried out by setting the coefficients S, E, J1 and J2 of eqn (5) to their calculated values15 using the properties of water, d(T),70ε(T),71η(T)72 (Table C1 in part C of the ESI†) and the distance parameter R. The lower limit a of the association integral is the distance of closest approach of the cation and the anion (contact distance), a = a+ + a. It was calculated from the ionic radii of the chloride anion (a− = 0.181 nm)15 and the same effective cation radius, a+ = 0.325 nm for all investigated ILs. For the latter it was assumed that the anion mainly interacts with the acidic hydrogen at the C2 position of the imidazolium ring (for 1,3-ILs). Thus, the chosen a+ corresponds to the molecular dimension of the imidazolium ring along the C2–H axis obtained from semiempirical MOPAC calculations and used also in our previous work on [1,3-BMIM][Cl] in water.13
From extensive investigations on electrolyte solutions in different solvents it has been found15 that the upper limit of association is most realistically defined as R = a+ + a_ + n·s, where s is the length of an orientated solvent molecule (located between the cation and the anion) and n is an integer. A value of s = dOH = 0.28 nm for water was taken into account. Assuming that only contact (CIP) and solvent-shared (SIP) ion pairs were likely to form, a value of n = 1 was used and R(J2) was fixed to 0.786 nm.
Then two-parameter fits were used to obtain the limiting values of molar conductivity, Λ∞, and the association constant, KA, by non-linear least squares iterations. All results are summarized in Table C3 in part C of the ESI.†
Here it has to be stressed that the experimental quantification of weak association is not a trivial task. According to Marcus and Hefter11 even the conductivity measurements, as one of the most established techniques, yield only a rough estimation for the association constant, KA ≤ 10, what is the case in our work. However, in our previous work we have shown that this method is applicable at least for an excellent comparison of the associating behavior in diverse weak associating systems.1,73,74 From Table C3 in the ESI† (part C) it can be seen that the same trend in KA was found at all temperatures.
3. Results and discussion
3.1. Ion mobility
Using a literature value for λ∞−(Cl−)75 (Table C1 in part C of the ESI,†λ∞(Cl−, 298.15 K) = 76.35 S cm2 mol−1), the limiting molar conductivity can be split into separate ionic contributions, λ∞i, where limiting ionic conductivities were estimated for all cations. Consequently, the diffusion coefficients D∞i were calculated by using the relation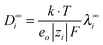 | (8) |
Diffusion coefficients at infinite dilution are the characteristic properties of ionic transport, which are not affected by ionic interactions. Thus, for Cl− at 298.15 K, a value of 20.35 × 10−10 m2 s−1 can be estimated. For all investigated cations, values at 298.15 K are gathered in Table 1 (together with values of Λ∞ and λ∞+ at 298.15 K for all investigated solutes) and presented in Fig. 3, as a function of the number of C atoms in the alkyl side chain, together with values that were obtained from MD simulations that were carried out at the same temperature of 298 K.
| Cation | n c | Λ ∞ | λ ∞+ | D ∞+,calc | D ∞+,exp |
|---|---|---|---|---|---|
| a Units: Λ∞, λ∞+, S cm2 mol−1; D∞+,calc, D∞+,exp, 10−10 m2 s−1. b Ref. 13. | |||||
| [MIM]+ | 0 | 124.06 ± 0.10 | 47.71 ± 0.05 | 12.8 ± 0.6 | 12.72 ± 0.05 |
| [1,2-MMIM]+ | 1 | 119.94 ± 0.05 | 43.59 ± 0.03 | — | 11.62 ± 0.03 |
| [1,3-MMIM]+ | 1 | 119.13 ± 0.01 | 42.78 ± 0.01 | — | 11.40 ± 0.01 |
| [1,3-EMIM]+ | 2 | 115.05 ± 0.05 | 38.70 ± 0.03 | 11.5 ± 0.3 | 10.31 ± 0.03 |
| [1,3-BMIM]+ | 4 |
109.34 ± 0.09
108.64b |
32.99 ± 0.05 | 9.2 ± 0.1 | 8.79 ± 0.05 |
| [1,3-HMIM]+ | 6 | 105.07 ± 0.10 | 28.72 ± 0.05 | 8.3 ± 0.8 | 7.65 ± 0.05 |
| [1,3-OMIM]+ | 8 | 102.71 ± 0.09 | 26.36 ± 0.05 | 7.5 ± 0.2 | 7.03 ± 0.05 |
| [1,3-DeMIM]+ | 10 | 100.73 ± 0.09 | 24.38 ± 0.05 | 5.8 ± 0.1 | 6.50 ± 0.05 |
| [1,3-DoMIM]+ | 12 | 99.90 ± 0.14 | 23.55 ± 0.07 | 6.3 ± 0.4 | 6.28 ± 0.07 |
| Cl− | — | — | — | — | 20.35 |
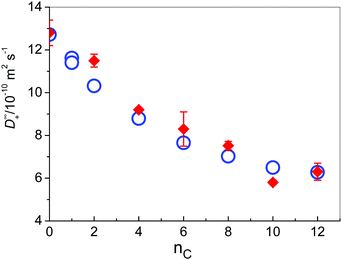 | ||
Fig. 3 Diffusion coefficients of IL cations in water at 298.15 K as a function of the number of carbon atoms in the side chain; ( ) experiment; ( ) experiment; ( ) MD simulations. ) MD simulations. | ||
As expected, the mobility of cations decreases with the increasing length of the alkyl chain (Table 1 and Fig. 3), but not linearly with its number of C atoms as it has been obtained in previous MD simulations of imidazolium-based cations in aqueous solution as reported by Bhargava and Klein.9 In these previous simulations high ion concentrations above 1 M were used in contrast to the very low ion concentration (c = 0.0266 M) and the lack of inter-ionic interactions in our case. For the medium sized cations [1,3-BMIM]+ and [1,3-HMIM]+ we observe a good agreement between calculated values in the present work and values reported in ref. 9 (about 9 × 10−10 m2 s−1 and 7 × 10−10 m2 s−1, respectively). In the case of small [1,3-EMIM]+ cations the previously reported value was substantially larger (15 × 10−10 m2 s−1) and for larger [1,3-OMIM]+ a slower diffusion (2 × 10−10 m2 s−1) was predicted. These deviations are expected due to the presence of strong inter-ionic interactions that are found at high ion concentrations. For instance, it is well known that cations with long alkyl chains tend to aggregate to form structures similar to micelles.76 Even more, Goodchild and coworkers have found out that in water solutions of 1-alkyl-3-methylimidazolium bromides there are no immediately apparent aggregates in the systems with nc = 2 and nc = 4,77 but already at [1,3-HMIM][Br] small oblate aggregate forms were detected by SANS, increasing in size with increasing concentration. These bulky aggregates effectively lower the diffusivity of the involved cations.
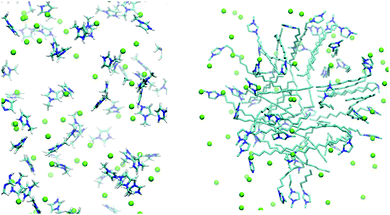
This assumption was confirmed by the results of MD simulations at high concentrations. We observed that within less than 1 ns [1,3-DoMIM]+ cations formed micelles that remained stable throughout the rest of the simulations as expected. In contrast, [MIM]+ cations remained dispersed in water and did not show any signs of aggregation. The cation distribution in water is visualized for these two cases in Fig. 4. Diffusion coefficients of 10.4 and 1.1 × 10−10 m2 s−1 were derived for [MIM]+ and [1,3-DoMIM]+, which can be compared to 12.8 and 6.3 × 10−10 m2 s−1, respectively, close to the limit of infinite IL dilution. The drastic reduction of [1,3-DoMIM]+ diffusivity is a result of the cation aggregation. [1,3-DoMIM]+ cations diffuse as members of these micelle aggregates, which move much slower through the solvent than single cations because of the large aggregate sizes.
3.2. Ion association
As can be seen in Tables 2a and C3 (part C of the ESI†), KA values are small (∼2.5 ≤ KA ≤ ∼6) but distinctly higher than those obtained using the same model recently used for alkali metal halides in water.1| Cation | n c | (a) | (b) | (c) | (d) | (e) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp | 1D-RISM PMF X–Cl− | 1D-RISM PMF Hi–Cl− | 3D-RISM PMF | ΔGexpbindd | ΔGMDbind | |||||||||
| K A | Interacting cation atom X | Interacting cation atom | Cation's atom closest to the anion | |||||||||||
| H1 | H2 | H3 | H7 | H8 | H9 | |||||||||
| a Units: PMF, ΔGexpbind, ΔGMDbind; kcal mol−1. b Estimated errors are given in Table C3 in part C in the ESI. c Ref. 13. d Errors are denoted with error bars in Fig. 7. | ||||||||||||||
| [MIM]+ | 0 | 4.9 |
−0.84
−0.87 |
C1
N2 |
−0.82 | −0.71 | −0.81 | −0.70 | −1.44 | H7 | −0.94 | −2.7 ± 0.2 | ||
| [1,2-MMIM]+ | 1 | 2.5 | −0.78 | N2 | −0.68 | −0.69 | −0.62 | −1.51 | H9 | −0.54 | ||||
| [1,3-MMIM]+ | 1 | 1.6 | −0.65 | C1 | −0.70 | −0.69 | −0.69 | −1.46 | H1 | −0.28 | ||||
| [1,3-EMIM]+ | 2 | 3.1 | −0.52 | C1 | −0.55 | −0.68 | −0.69 | −1.38 | H1 | −0.67 | ||||
| [1,3-BMIM]+ | 4 |
5.2
6.4c |
−0.53 | C1 | −0.54 | −0.70 | −0.70 | −1.39 | H1 | −0.98 | −0.8 ± 0.2 | |||
| [1,3-HMIM]+ | 6 | 2.6 | −0.52 | C1 | −0.54 | −0.69 | −0.69 | −1.40 | H1 | −0.57 | −0.3 ± 0.1 | |||
| [1,3-OMIM]+ | 8 | 3.8 | −0.51 | C1 | −0.53 | −0.69 | −0.69 | −1.39 | H1 | −0.79 | ||||
| [1,3-DeMIM]+ | 10 | 3.5 | −0.51 | C1 | −0.53 | −0.69 | −0.69 | −1.39 | H1 | −0.74 | ||||
| [1,3-DoMIM]+ | 12 | 4.9 | −0.51 | C1 | −0.52 | −0.69 | −0.68 | −1.39 | H1 | −0.94 | −0.9 ± 0.1 | |||
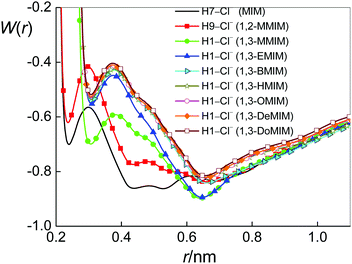
Before considering the RISM results to explain the experimental results for KA, we should give some information on features of ion-pairing in imidazolium-based ILs. The positive charge of their cations is located at the imidazolium ring78 (see also Fig. B1–B9 in part B of the ESI†). Therefore, it is not a surprise that the interactions of anions with the non-polar cation alkyl chains are very weak.9 At the same time, however, the anions are found to be present in the vicinity of the five-membered ring, both in pure ILs (see, for instance, ref. 79–83) and in their mixtures with water.80,84–86 Obviously, this location of the anion relative to the cation is a result of the strong electrostatic interaction mediated by the ring. Moreover, similar to the fact that the polar heads of pure imidazolium-based ILs are known to form H-bonded ion pairs (see, for instance, ref. 79–83), it was found for their aqueous mixtures that the anions are also interacting with cations via hydrogen bonds mediated by ring hydrogen atoms.6,84–86 Thus, we encounter C–H⋯Cl interactions with imidazolium ring protons acting as hydrogen-bond donors to the anion. Note that for [MIM][Cl] and [1,2-MMIM][Cl] one may also consider N–H⋯Cl interactions. More precisely, because of steric hindrances, only N2–H7⋯Cl for [MIM][Cl] and N2–H9⋯Cl for [1,2-MMIM][Cl] could occur (Fig. 1). Thus, ion pairing is expected for species that can bind through specific intermolecular interactions such as hydrogen bonding. Based on this information, we give the results of 1D-RISM PMF calculations for the above-named atoms (Table 2b and c). Fig. 5 presents the 1D-RISM PMF for Hi–Cl as an example.
As it can be seen from the 1D-RISM PMF values (Tables 2b and c), the hydrogen-bonded interactions between the anion and cations mediated by ring hydrogen atoms are weak. This result is in agreement with NMR/IR/Raman spectroscopy data80,87 and MD simulations.9,82,85 It is also noteworthy that the obtained Hi–Cl PMF values are rather similar. This fact suggests that the probabilities to form cation–anion pairs with the different available ring hydrogens are similar. However, earlier studies that used different methods85,86,88 have shown that the H-bonding affinity with the anion, including Cl−, is highest for the acidic hydrogen (the H atom bonded to the C atom located between the two N atoms of the ring), compared to the other two ring hydrogens, i.e. it could be that the C1–H1⋯Cl bond for our systems, with the exception of [1,2-MMIM]+ having a structure different from other ILs (Fig. 1).
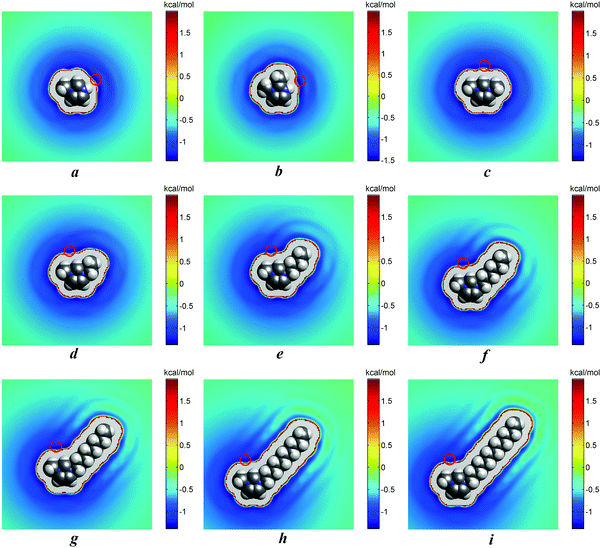
The analysis of the results of 3D-RISM calculations (Table 2d) has indicated that chloride ions prefer to interact with cations via hydrogen H7 (N2–H7⋯Cl) in [MIM][Cl] aqueous solutions, via hydrogen H9 (N2–H9⋯Cl) in [1,2-MMIM][Cl] aqueous solutions, and via atom H1 (C1–H1⋯Cl) in all other IL aqueous solutions. The energetically most favourable position of the anion relative to the cations is shown in Fig. 6a–i. These results are also consistent with the charge distributions that were used for our IL models (see the Figures in part B of the ESI†). Thus, the valid values of 1D-RISM PMFs are for the above-named atoms of cations (Table 2b and c in bold) and should be chosen for the discussion.
As to the deeper minima of 1D-RISM PMFs (H2/H3–Cl−) in comparison with (H1–Cl−) for ILs ranging from ethyl to dodecyl (Table 2c), that, probably, they are overvalued due to the influence of additional charges of the alkyl chain atoms at the transition from [1,3-MMIM][Cl] to [1,3-EMIM][Cl] and to the next ILs in the set (Fig. B3–B9 in part B of the ESI†).
Thus, we have found the same type of cation–anion hydrogen-bonded interaction (Cl–H1⋯Anion) for ILs ranging from dimethyl to dodecyl as it was shown in the literature previously.85,86,88 Moreover, for the systems under study, the additional confirmation of our results follows from MD simulations of [1,3-EMIM][Cl](aq)6,89 and [1,3-OMIM][Cl](aq).89 The data of NIR spectroscopy demonstrate a similar pairing of chloride anions with 1-alkyl-3-methylimidazolium cations ([1,3-AMIM]+).86 One can also see from Table 2 that the increase of alkyl chain length affects the interaction between hydrogen atoms and the chloride anion only slightly.
According to the results from the 3D-RISM, we found for [MIM]+ and [1,2-MMIM]+ a different energetically most favorable anion position relative to the cation compared to the other IL solutions. Chloride appears to interact most favorably in these systems with H7/H9 ([MIM]+/[1,2-MMIM]+). This is not surprising, considering the charge distributions shown in Fig. B1 and B2 of the ESI.† The largest positive charges can be found on H7/H9, which resulted in stronger attractive electrostatic interactions with the anion.
Table 2b and c reveal that the cation–anion interaction strength, indeed, depends on the particular structure of the ions contained in the ILs. Whereas the order in KA for [MIM][Cl] > [1,2-MMIM][Cl] > [1,3-MMIM][Cl] could be explained by the change in 1D-RISM PMFs this is not the case for the other investigated systems.
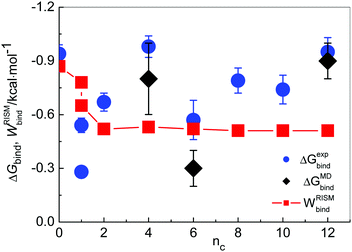
For four different imidazolium cations, namely for [MIM]+, [1,3-BMIM]+, [1,3-HMIM]+ and [1,3-DoMIM]+, the binding free energies with Cl−, ΔGMDbind, were also obtained from MD simulations, using thermodynamic integration as specified in Section 2.1. From measured values of KA binding free energies were calculated using the relation ΔGexpbind = −RT·ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KA. The values of ΔGMDbind and ΔGexpbind are presented in Table 2e.
KA. The values of ΔGMDbind and ΔGexpbind are presented in Table 2e.
In the case of MIM+, ΔGMDbind seems to be overestimated, whereas for the other three cases with alkyl chains longer than n > 0, the results from MD simulations agree with experimental values and deviations are within the statistical uncertainty. The somewhat overestimated binding in the case of [MIM][Cl] could be a result of a neglected transfer of charge from Cl− to [MIM]+ in the MD model. Such a charge transfer is to be expected considering the tighter ion pairing of Cl− to the small cation, compared to other larger cations with more delocalized charge. Compared to the RISM, binding free energies derived using MD show a larger variation with the alkyl chain length, similar to what we observed in the experiment. The basically constant binding free energy (PMF) found in the RISM for chain lengths longer than or equal to n = 2 is likely a result of the fixed geometry of the cation that does not consider the flexibility of the cation alkyl chain. Overall, MD simulations confirm that the strength of ion association varies indeed with the cation alkyl chain length and that these variations are nonlinear and more generally that imidazolium–Cl association is very weak and that it depends on the specific imidazolium cation structure.
In Fig. 7 ΔGexpbind and ΔGMDbind (without the value for [MIM][Cl]) are compared with the minimal values of 1D-RISM-PMFs, calculated between chloride and those cation hydrogen atoms that were selected as described above, WRISMbind. The trend of WRISMbind values from the 1D-RISM suggests that the interaction between the anion and the cation is slightly decreasing with increasing alkyl chain length (nc > 2). This can be rationalized with the fact that the cation charge becomes more delocalized with increasing cation size, thereby somewhat weakening the interaction strength with the anion. Our result is also confirmed by recent MD simulations,89 where [1,3-MMIM]+ was found to associate more strongly with Cl− than [1,3-OMIM]+.
Here it has to be stressed that the model of ion association applied in the data analysis is assuming only equilibrium between (neutral) ion pairs and free ions (Section 2.3) in diluted solutions (lcCM). For investigated ILs this assumption seems to be valid for systems with a shorter alkyl chain, where the association behavior can also be confirmed well by 1D- and 3D-RISM calculations. However, the results from MD simulation are in reasonable agreement with those from the experiment.
As it was already mentioned in Section 3.1, at longer chains the additional interactions, resulting in bulky aggregates, became inevitable.77 Despite the fact that experiments were carried out in diluted solutions (<0.005 mol dm−3) they may affect the possible ion equilibrium in the solutions and in this case the applied lcCM model would not be valid. Moreover, the investigated ILs should be regarded as typical 1,1-electrolytes, and with increasing length of the side alkyl chain hydrophobic interactions also become important and may lead to (additional) cation–cation interactions which are not taken into account in the here applied model.
4. Conclusion
The ion mobility and association of dilute solutions of nine imidazolium based ILs, from 1-methylimidazolium chloride, [MIM][Cl] to 1-dodecyl-3-methylimidazolium chloride, [1,3-DoMIM][Cl], with two isomers 1,2-dimethylimidazolium chloride, [1,2-MMIM][Cl], and 1,3-dimethylimidazolium chloride, [1,2-MMIM][Cl] in water, were systematically studied using MD simulations, statistical mechanics calculations in the framework of the integral equation theory with one-dimensional (1D-) and three-dimensional (3D-) reference interaction site model (RISM) approaches as well as conductivity measurements.From MD simulation, the diffusion coefficients close to infinite dilution, D∞+,calc, were calculated and compared with the experimental values D∞+,exp. The measured values were obtained from the cationic contributions, λ∞+, to the molar conductivity at infinite dilution, Λ∞, and were estimated by applying the low concentration Chemical Model (lcCM) to experimental conductivity data. Experimental and calculated values from MD simulations were found to be in very good agreement, thereby confirming the conductivity measurements.
As expected, it was found that the mobility of cations is decreasing with increasing length of its alkyl chain, but not linearly as it has been reported previously.9 That seemingly linear decrease could be explained by the aggregation of cations with long alkyl chains and thus slower diffusivity, when larger cation concentrations, i.e. stronger inter-ionic interactions, are present.
The results of RISM calculations have shown a weak ion pairing between the anions and cations. It was found that their interactions are hydrogen-bonded and mediated by ring hydrogen atoms. From minimal values of 1D-RISM PMFs for atom pairs N2–Cl− ([MIM][Cl] and [1,2-MMIM][Cl]) or C1–Cl− (all other ILs) it was concluded that the ion association weakens first with the increasing length of the alkyl chain up to two C atoms but that beyond this length this association should not be affected any further. This assumption was partially confirmed by the values of association constants, KA, yielded also from experimental conductivity data by lcCM. Generally, estimated KA values are slightly higher than those obtained for 1,1-electrolytes in water, but the values for [1,3-BMIM][Cl] show distinctly a strong deviation with a value of KA = ∼5.2 at 298.15 K being still in reasonable agreement with a reported value of 6.4.13 This fact led to the assumption that there must be a difference in cation–anion interactions depending on the particular structure of the cations in the ILs, which may also affect the ion pairing process.
The most favorable anion position at cations was predicted by the 3D-RISM calculations. In particular, for the case of 1,3-ILs the chloride ions prefer to interact with cations via the acidic hydrogen of the IL ring. However, 3D-RISM data do not predict any strong influence of the alkyl chain length on the ion-pairing for nc ≥ 4.
Overall, we demonstrated that studied ILs serve as an excellent model system for investigating the influence of the ion structure on the mobility and ion pairing by combining MD simulations and RISM calculations with experiments, even in aqueous solutions, where the interionic interactions are weak.
Acknowledgements
The financial support by the Slovenian Research Agency through Grant No. P1-0201 and the Bilateral project SLO-Ru (2014–2015) is gratefully acknowledged. This work was partially supported by COST Action CM1206. Access to the A*STAR Computational Resource Centre in Singapore, where the MD simulations were performed, is greatly appreciated. M. B.-R. wishes to express her sincere thanks to Prof. Dr J. Mavri for his kind support of this work.References
- J. Gujt, M. Bešter-Rogač and B. Hribar-Lee, J. Mol. Liq., 2014, 190, 34–41 CrossRef CAS PubMed.
- Q. Yang, H. Xing, B. Su, K. Yu, Z. Bao, Y. Yang and Q. Ren, Chem. Eng. J., 2012, 181–182, 334–342 CrossRef CAS.
- N. D. Khupse and A. Kumar, J. Phys. Chem. A, 2011, 115, 10211–10217 CrossRef CAS PubMed.
- V. V. Chaban and V. O. Prezhdo, J. Phys. Chem. Lett., 2013, 4, 1423–1431 CrossRef CAS PubMed.
- S. Feng and G. A. Voth, Fluid Phase Equilib., 2010, 294, 148–156 CrossRef CAS.
- C. Spickermann, J. Thar, S. B. C. Lehmann, S. Zahn, J. Hunger, R. Buchner, P. A. Hunt, T. Welton and B. Kirchner B, J. Chem. Phys., 2008, 129, 104505 CrossRef CAS PubMed.
- P. Yee, J. K. Shah and E. J. Maginn, J. Phys. Chem. B, 2013, 117, 12556–12566 CrossRef CAS PubMed.
- H. V. R Annapureddy and L. X. Dang, J. Phys. Chem. B, 2013, 117, 8555–8560 CrossRef PubMed.
- B. L. Bhargava and M. L. Klein, Soft Matter, 2009, 5, 3475–3480 RSC.
- S. Palchowdhury and B. L. Bhargava, J. Phys. Chem. B, 2014, 118, 6241–6249 CrossRef CAS PubMed.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- G. Hefter, Pure Appl. Chem., 2006, 78, 1571–1586 CrossRef CAS.
- M. Bešter-Rogač, A. Stoppa, J. Hunger, G. Hefter and R. Buchner, Phys. Chem. Chem. Phys., 2011, 13, 17588–17598 RSC.
- A. Boruń, C. Fernandez and A. Bald, Int. J. Electrochem. Sci., 2015, 10, 2120–2129 Search PubMed.
- J. M. G. Barthel, H. Krienke and W. Kunz, Physical Chemistry of Electrolyte Solutions: Modern Aspects, Springer, New York, 1998 Search PubMed.
- Molecular Theory of Solvation, ed. F. Hirata, Kluwer Academic Publishers, Dordrecht, 2003 Search PubMed.
- S. A. Shah, Y. L. Chen, S. Ramakrishnan, K. S. Schweizer and C. F. Zukoski, J. Phys.: Condens. Matter, 2003, 15, 4751–4778 CrossRef CAS.
- A. Ben-Naim, Molecular Theory of Solutions, University Press, Oxford, 2006 Search PubMed.
- L. Sarkisov and P. R. Van Tassel, J. Phys.: Condens. Matter, 2008, 20, 333101 CrossRef.
- M. V. Fedotova and M. F. Holovko, in Theoretical and Experimental Methods of Solution Chemistry (Monograph in Russian), Prospect, Moscow, 2011, pp. 68–152 Search PubMed.
- T. Luchko, I. S. Joung and D. A. Case, in Innovations in Biomolecular Modeling and Simulations, ed. T. Schlick, Royal Society of Chemistry, London, 2012, pp. 51–86 Search PubMed.
- S. Bruzzone, M. Malvaldia and C. A. Chiappe, Phys. Chem. Chem. Phys., 2007, 9, 5576–5581 RSC.
- M. Malvaldi, S. Bruzzone, C. Chiappe, S. Gusarov and A. Kovalenko, J. Phys. Chem. B, 2009, 113, 3536–3542 CrossRef CAS PubMed.
- H. Nakano, J. Noguchi, T. Mochida and H. Sato, J. Phys. Chem. A, 2015, 119, 5181–5188 CrossRef CAS PubMed.
- B. M. Pettitt and P. J. Rossky, J. Chem. Phys., 1986, 84, 5836–5844 CrossRef CAS.
- S. W. W. Chen and P. J. Rossky, J. Phys. Chem., 1993, 97, 6078–6082 CrossRef CAS.
- K. Koga, X. C. Zeng and H. Tanaka, Fluid Phase Equilib., 1998, 144, 377–385 CrossRef CAS.
- A. Kovalenko and F. Hirata, J. Phys. Chem. B, 1999, 103, 7942–7957 CrossRef CAS.
- M. V. Fedotova and S. E. Kruchinin, J. Mol. Liq., 2012, 169, 1–7 CrossRef CAS.
- M. V. Fedotova and S. E. Kruchinin, J. Mol. Liq., 2013, 179, 27–33 CrossRef CAS.
- M. V. Fedotova and S. E. Kruchinin, Biophys. Chem., 2014, 190–191, 25–31 CrossRef CAS PubMed.
- M. V. Fedotova and O. A. Dmitrieva, Amino Acids, 2015, 47, 1015–1023 CrossRef CAS PubMed.
- M. V. Fedotova and O. A. Dmitrieva, New J. Chem., 2015, 39, 8594–8601 RSC.
- I. Terekhova, E. Chibunova, R. Kumeev, S. Kruchinin, M. Fedotova, M. Kozbiał, M. Wszelaka-Rylik and P. Gierycz, Chem. Eng. Sci., 2015, 122, 97–103 CrossRef CAS.
- A. Eiberweiser, A. Nazet, S. E. Kruchinin, M. V. Fedotova and R. Buchner, J. Phys. Chem. B, 2015, 119, 15203–15211 CrossRef CAS PubMed.
- J. N. C Lopes, A. A. H. Padua and K. Shimizu, J. Phys. Chem. B, 2008, 112, 5039–5046 CrossRef PubMed.
- C. A. N de Castro, E. Langa, A. L. Morais, M. L. S. M. Lopes, M. J. V. Lourenco, F. J. V. Santos, M. S. C. S Santos, J. N. C. Lopes, H. I. M. Veiga and M. Macatrao, et al. , Fluid Phase Equilib., 2010, 294, 157–179 CrossRef.
- K. Shimizu, D. Almantariotis, M. F. Costa Gomes, A. A. Padua and J. N. Canongia Lopes, J. Phys. Chem. B, 2010, 114, 3592–3600 CrossRef CAS PubMed.
- M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922 CrossRef CAS.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C Berendsen, J. P. M. Postma, W. F. v. Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- A. Seduraman, P. Wu and M. Klähn, J. Phys. Chem. B, 2011, 116, 296–304 CrossRef PubMed.
- D. Chandler and H. C. Andersen, J. Chem. Phys., 1972, 57, 1930–1937 CrossRef CAS.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, New York, 2006 Search PubMed.
- M. V. Fedotova and S. E. Kruchinin, J. Mol. Liq., 2013, 186, 90–97 CrossRef CAS.
- M. V. Fedotova and S. E. Kruchinin, J. Mol. Liq., 2011, 164, 201–206 CrossRef CAS.
- G. N. Chuev, M. Valiev and M. V. Fedotova, J. Chem. Theory Comput., 2012, 8, 1246–1254 CrossRef CAS PubMed.
- H. Hirata, P. J. Rossky and B. M. Pettitt, J. Chem. Phys., 1983, 78, 4133–4144 CrossRef.
- A. Kovalenko and F. Hirata, J. Chem. Phys., 2000, 112, 10403–10417 CrossRef CAS.
- A. Kovalenko and F. Hirata, J. Chem. Phys., 2000, 113, 2793–2805 CrossRef CAS.
- A. Kovalenko and F. Hirata, J. Chem. Phys., 1999, 110, 10095–10112 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- L. Lue and D. Blankschtein, J. Phys. Chem., 1992, 92, 8582–8594 CrossRef.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- R. Cammi and J. Tomasi, J. Comput. Chem., 1995, 16, 1449–1458 CrossRef CAS.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS.
- C. Amovilli, V. Barone, R. Cammi, E. Cancès, M. Cossi, B. Mennucci, C. S. Pomelli and J. Tomasi, in Advances in Quantum Chemistry, ed. L. Per-Olov, Academic Press, New York, 1998, pp. 227–261 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalman, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota,R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz and J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, T. E. Cheatham, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitber, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, Amber 14, University of California, San Francisco, 2014 Search PubMed.
- A. Kovalenko, S. Ten-no and F. Hirata, J. Comput. Chem., 1999, 20, 928–936 CrossRef CAS.
- J. Barthel, R. Wachter and H.-J. Gores, in Modern Aspects of Electrochemistry, ed. B. E. Conway and J. O. M. Bockris, Plenum Press, New York, 1979, pp. 1–79 Search PubMed.
- J. Barthel, F. Feuerlein, R. Neueder and R. Wachter, J. Solution Chem., 1980, 9, 209–219 CrossRef CAS.
- M. Bešter-Rogač and D. Habe, Acta Chim. Slov., 2006, 53, 391–395 Search PubMed.
- O. Kratky, H. Leopold and H. N. Stabinger, Z. Angew. Phys., 1969, 27, 273–277 CAS.
- E. F. G. Herington, Pure Appl. Chem., 1976, 48, 1–9 CrossRef.
- B. B. Owen, R. C. Miller, C. E. Milner and H. L. Cogan, J. Phys. Chem., 1961, 65, 2065–2070 CrossRef CAS.
- L. Korson, W. Drost-Hansen and F. J. Millero, J. Phys. Chem., 1969, 73, 34–39 CrossRef CAS.
- D. Rudan-Tasic, T. Župec, C. Klofutar and M. Bešter-Rogač, J. Solution Chem., 2005, 34, 631–644 CrossRef CAS.
- M. Bešter-Rogač, C. Klofutar and D. Rudan-Tasic, J. Mol. Liq., 2019, 156, 82–88 CrossRef.
- H. S. Harned and B. B. Owen, The Physical Chemistry of Electrolytic Solution, Reinhold, New York, 1958 Search PubMed.
- K. R. Ramya, P. Kumar, A. Kumar and A. Venkatnathan, J. Phys. Chem. B, 2014, 118, 8839–8847 CrossRef CAS PubMed.
- I. Goodchild, L. Collier, S. L. Millar, I. Prokeš, J. C. D. Lord, C. P. Butts, J. Bowers, J. R. P. Webster and R. K. Heenan, J. Colloid Interface Sci., 2007, 307, 455–468 CrossRef CAS PubMed.
- J. N. Canongia, J. Deschamps and A. A. H Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
- J. Ross and J. Xiao, Chem. – Eur. J., 2003, 9, 4900–4906 CrossRef CAS PubMed.
- A. Mele, C. D. Tran and S. H. De Paoli Lacerda, Angew. Chem., 2003, 115, 4500–4502 CrossRef.
- C. Hardacre, J. D. Holbrey, S. E. J. McMath, D. T. Bowron and A. K. Soper, J. Chem. Phys., 2003, 118, 273–278 CrossRef CAS.
- B. L. Bhargava and S. Balasubramanian, Chem. Phys. Lett., 2006, 417, 486–491 CrossRef CAS.
- T. Köddermann, C. Wertz, A. Heintz and R. Ludwig, ChemPhysChem, 2006, 7, 1944–1949 CrossRef PubMed.
- B. L. Bhargava and M. L. Klein, J. Phys. Chem. A, 2009, 113, 1898–1904 CrossRef CAS PubMed.
- M. Moreno, F. Castiglione, A. Mele, C. Pasqui and G. Raos, J. Phys. Chem. B, 2008, 112, 7826–7836 CrossRef CAS PubMed.
- B. Wu B, Y. Liu, Y. Zhang and H. Wang, Chem. – Eur. J., 2009, 15, 6889–6893 CrossRef PubMed.
- B. Fazio, A. Triolo and G. Di Marco, J. Raman Spectrosc., 2008, 39, 233–237 CrossRef CAS.
- T. Takamuku, Y. Kyoshoin, T. Shimomura, S. Kittaka and T. Yamaguchi, J. Phys. Chem. B, 2009, 113, 10817–10824 CrossRef CAS PubMed.
- H. V. R. Annapureddy and L. X. Dang, J. Phys. Chem. B, 2013, 117, 8555–8560 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp05010g |
| This journal is © the Owner Societies 2016 |