Adsorption and diffusion of Li with S on pristine and defected graphene

Abstract

Li–S batteries are the promising high energy density alternative to current rechargeable battery technologies, particularly since it has been shown that the use of graphene, nanotubes and other nanostructured carbons in the cathode can improve the cyclability. We explore the microscopic interactions between Li_nS and graphene and diffusion of Li ions through pristine and defected graphene in the presence of S using first-principles methods. The introduction of Li weakens the interaction of atomic S with graphene, increasing the height of adsorbed S and leading to the formation of Li_nS clusters. These Li_nS clusters are adsorbed accompanied by charge transfer to the graphene. We find that double vacancies in the graphene are sufficient to allow Li ions to pass through the graphene plane. This is impeded in the presence of S due to the binding of Li to Li_nS clusters, but still can happen for larger clusters. The electronic properties confirm the excellent conductivity of pristine and defected graphene cathodes in contact with Li_nS clusters.

---

Introduction

Energy storage in the form of rechargeable batteries is central to many modern technologies. However, current Li-ion batteries have insufficient capacities to meet the demands of key markets.^1–7 The currently used transition metal oxide based cathodes have theoretical specific capacities of ∼300 mA h g⁻¹, which is very limiting, for example in vehicle electrification.^7–9 Recently, Li–S batteries have attracted much more attention due to the large specific capacity (1673 mA h g⁻¹) of sulfur as the cathode. Based on the reaction S₈ + 16Li⁺ + 16e⁻ ↔ 8Li₂S with an average working voltage at around 2.1 V (V vs. Li/Li⁺), Li–S batteries with a lithium anode can offer very high theoretical energy densities (gravimetric energy density of ∼2600 W h kg⁻¹ and volumetric energy density of 2500 W h L⁻¹).^10–18 In addition, sulfur is sufficient in the earth, cheap and environmentally friendly.^5,19,20 However, the shortcomings also are obvious, including the low electrical conductivity of sulfur S₈ (5 × 10⁻³⁰ S cm⁻¹ at 25 °C), solution phase reduction of long chain polysulfide to short-chain polysulfide, and the large volume (∼76%) and morphology changes of sulfur electrodes during the discharge–charge process.^21–27 Short-chain polysulfides, such as Li₂S_4–8, are easily dissolved in the electrolyte solution, and this results in the mass loss of active sulfur.²⁸ These shortcomings limit the cycle life leading to a series of issues including the capacity fade, low Coulombic efficiency during cycling, lithium metal corrosion, and dendrite formation.^13,16 The significant challenges to develop these batteries remain, particularly because of the need to contain sulfur in the cathode due to the large volume changes upon charging and discharging and the need to obtain conduction due to the insulating nature of S.

In order to overcome these obstacles, various approaches have been proposed to raise the actual capacity and the cycle stability of the sulfur cathode. In order to prevent the dissolution of lithium polysulfide, a big tide in the research is the confining of sulfur in nano-carbons.^14,20,28,29 Commonly, a composite cathode consisting of sulfur in various carbon matrices, such as meso-/micro-porous carbon, graphene or graphene oxide, carbon nanotubes, carbon fibers, hollow carbon microspheres, is used.^30–32 It is generally understood that the nano-structured carbon performs two functions: (1) its sorption properties provide the close contact between the sulfur and a conductive network and (2) it encapsulates or otherwise impedes the diffusion of polysulfides into the electrolyte.³³ However, the microscopic mechanisms, which will be important for optimizing the electrode structures, are poorly understood at present. Interestingly, there are recent reports that graphene-based sulfur cathodes may be used in Li–S batteries and the graphene-encapsulation layers can substantially improve the cycling life.^{4,13,15,18,31,34–38} The binding between lithium polysulfide and doped graphene (such as the B and N co-doping) has been reported theoretically.³⁹ In addition, to provide a practical cathode material, this gives us a model system for understanding the detailed microscopic mechanisms operative in nano-carbon-sulfur cathodes.

Here we focus on the interaction between Li_nS clusters and graphene and the diffusion of Li through graphene in the presence of S. Specifically we analyze the adsorption of Li including the formation of Li_nS clusters on pristine and vacancy-defected graphene. Then the desorption of S from graphene and at the edge of double-vacancy both by itself and in clusters with Li is explored. We find that Li greatly assists the desorption of S via the formation of Li_nS clusters, the same process works against the diffusion of Li through the graphene plane. However, this inhibition is only present for the small size of clusters, and Li from larger size Li_nS can readily diffuse through divacancy pores in graphene. The results can be understood in terms of the incremental binding of Li to Li_nS clusters and the charge transfer between Li, S, Li_nS clusters and graphene. Additionally, we present the analysis of electronic structures, which confirms the conductivity of the carbon system in the presence of Li and S.

Computational methods

Our calculations have been carried out based on density functional theory employing the projector augmented wave potentials as implemented in the VASP code.^40–42 We used the generalized gradient approximation (GGA) with the parameterization of Perdew–Burke–Ernzerhof (PBE)⁴³ and added van der Waals (vdW) corrections for the adsorption on the surface. The k-point sampling of the Brillouin zone and the plane-wave basis sets were chosen to obtain the total energy convergence at the 1 meV per atom level. This corresponds to a kinetic energy cutoff of 450 eV for the plane wave expansion. We did the spin-polarized calculations to include the moments on isolated Li atoms and defective graphene. The effect of the dispersion interaction is included by the empirical correction scheme of Grimme (DFT+D/PBE).⁴⁴ This approach has been successful in describing graphene-based structures.^45,46

The lattice constant of graphene is calculated to be 2.468 Å, which is basically identical to that from previous work,⁴⁷ and is a little larger than the experimental value of 2.46 Å. For graphene with a double-vacancy, the change of lattice parameters in a 4 × 4 cell is found to be small and can be ignored. To treat the adsorption of Li and S, we used a supercell method, specifically a 4 × 4 supercell with a vacuum layer of 18 Å. The Brillouin zone was sampled with the Γ-centered 12 × 12 × 1 grid of k-points. We note that the adatom–graphene system lacks inversion symmetry and therefore requires the use of a large vacuum to reduce the spurious effects due to the dipole interactions,⁴⁸ which is the reason for the large vacuum layer in our calculations. The in-plane supercell lattice constant is 9.87 Å, which is also the distance between the neighboring adatoms (or clusters).

Results and discussion

Adsorption of Li with S on pristine and double-vacancy graphene

We start with the analysis for the S₂ molecule. We obtain an S–S bond length of 1.90 Å, which is similar to the experimental value of 1.889 Å.^49,50 With the consideration of the different configurations of S₂ and S₈ adsorbed on graphene (see Fig. S1, S2, Tables S1 and S2 of ESI†), it is found the adsorption energy of poly-sulfur on pristine graphene is small. For example, with the consideration of the vdW effect, the adsorption energies of S₈ and S₂ on graphene are −0.088 eV per S-atom and −0.094 eV per S-atom, respectively. The interaction between poly-sulfur and graphene is mainly by the dispersion force. With the increase of the atom number in poly-sulfur, the interaction between poly-sulfur, such as S₈, and graphene becomes stronger. On the other hand, the interaction between single-atom S and graphene is considerable due to charge transfer. The most stable site on pristine graphene among the possible sites, such as hollow, bridge and top sites, is the bridge site between two carbon atoms (in Fig. 1A) with an adsorption energy of −0.995 eV per S-atom (see Fig. S3 and Table S3 of ESI†).

Fig. 1 Schematic representation of possible configurations of Li adsorption on S-absorbed graphene (A), S-adsorbed double-vacancy graphene (B). Note the numbers in the figures represent the number and corresponding possible locations of Li atoms.

With double-vacancy on graphene by which it is expected that Li can diffuse from one side of graphene to the other side, the interaction between poly-sulfur and defected graphene isn't strengthened obviously, for example, the adsorption energies of S₈ and S₂ are −0.092 eV per S-atom and −0.091 eV per S-atom (see Fig. S4, S5, Tables S4 and S5 of ESI†). The localized states near the Fermi level introduced by double-vacancy can't enhance the interaction between poly-sulfur and graphene obviously. While the interaction between single-atom S and defected graphene becomes much stronger due to the formation of a chemical bond. The most stable one on double-vacancy graphene is the edge of the vacancy with a 5-ring (in Fig. 1B) with an adsorption energy of −4.22 eV per S-atom. This is based on the results for the different possible adsorption sites (see Fig. S6 and Table S6 of ESI†).

For graphene as the encapsulation layer, it is expected to prevent the dissolution of lithium polysulfide into electrolytes, while Li-ions can easily diffuse from the one side of the encapsulation layer (with lithium polysulfide) to the other side (into the electrolytes). It is well known that the chain of polysulfide will become shorter upon reaction with Li (from S₈ to Li₂S). Therefore, the Li_nS cluster will be possible stay near the surface of graphene, since the interaction between polysulfide and graphene is weaker. We next consider Li with S on pristine and double-vacancy graphene.

Possible adsorption configurations were investigated by relaxing the adatom Li around the S atom on S-adsorbed graphene with the consideration of symmetry (see Fig. S7–S10 and Tables S7–S10 of ESI†).⁵¹ With these results, the possible adsorption sites of Li_n (n = 1, 2, 3 and 4) around S adsorbed on graphene were investigated, as depicted in Fig. 1A and B. Taking Li_nS as a molecular cluster adsorbed on graphene, the adsorption energy can be defined by the formula

E_ad = E_ad-g − E_g − E_ad, (1)

where E_ad-g, E_g and E_ad are the total energies of the system of Li_nS–graphene, isolated graphene and isolated adsorbate Li_nS. This energy quantifies the interaction between graphene and adsorbate Li_nS. Turning to the Li, the energy of Li_n adsorption per atom (cohesive energy) can be obtained as

ΔE_c = (E_ad-g − E_g-S − nE_Li)/n (2)

where E_ad-g, E_g-S and E_Li are the total energies of the system of Li_nS–graphene, isolated S-adsorbed graphene and isolated Li atoms. This energy shows the influence of Li on the adsorption of S on graphene. The geometric structure and adsorption energy were obtained after all the atoms in the models were fully relaxed. Furthermore, the lattice parameters were additionally relaxed with double-vacancy in order to account for distortions that could occur. In this case, the in-plane supercell lattice constant is reduced to about 9.67 Å.

The results of calculations are listed in Table 1. It is found that the adsorption energy of Li_nS clusters gradually increases as the number of Li atoms increases. By comparing the distance between graphene and S (d_S–C) in S–graphene (Table S3 of ESI†) and LiS–graphene (Table 1), the height of the S atom is increased due to the adsorption of Li on graphene. Li results in the weakening of bonds between S and graphene. By the value of d_Li–C, d_S–C, and θ_C–S–C, graphene prefers Li atoms to S atoms. The value of d_S–Li (about 2.2 Å) in Li_nS clusters implies the direct interaction between Li and S. Therefore, Li–S clusters are formed on graphene. Based on the cohesive energy (Table 1) defined in formula (2), the interaction between Li and S–graphene is stronger than the binding between Li atoms in bulk Li where the binding energy is about 1.61 eV per Li.

Table 1 Average distance between S and Li (d_S–Li), average distance between Li and near-neighbor C (d_Li–C), distance between S and the nearest-neighbor C (d_S–C), angle between S and the near-neighbor C (θ_C–S–C), adsorption energy (E_ad) and cohesive energy (ΔE_c) for the adsorption of Li_nS cluster on pristine graphene and double-vacancy graphene

	N	d S–Li	d Li–C	d S–C	θ C–S–C	E ad (eV)	ΔEc (eV)
Graphene	1	2.23	2.37	3.67	21.6	−0.813	−3.136
	2	2.20	2.35	3.51	23.4	−1.086	−3.326
	3	2.20	2.35	3.57	23.1	−2.800	−3.340
	4	2.32	2.30	3.47	23.8	−4.289	−3.065
Graphene-dv	1	2.56	2.10	1.75	94.0	−3.212	−2.307
	2	2.17	2.30	2.94	34.5	−1.501	−1.919
	3	2.21	2.37	3.67	26.4	−3.622	−2.538
	4	2.33	2.31	3.47	27.1	−6.100	−2.710

---

For the defected graphene, the interaction between S and the edge of double vacancy is very strong. Single Li atoms don't raise S atoms adsorbed on double-vacancy graphene. The distance between S and graphene is about 1.75 Å, as shown in Fig. S9 and Table S9 of ESI.† Interestingly, on the other hand, as few as two Li atoms can result in the lifting of S on double-vacancy graphene in Table 1. With the introduction of the second Li, a Li₂S cluster is formed with the breaking of S–C bonds. Therefore, the adsorption energy of Li₂S is significantly lower than that of LiS on double-vacancy graphene.

Dynamics of S-desorption under the influence of adsorbed Li and diffusion of Li with S-adsorption on double-vacancy graphene

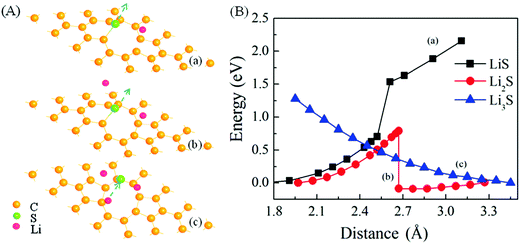
One use of graphene in the cathode is as an encapsulation layer to enhance the electronic conduction of the sulfur cathode while preventing the dissolution of polysulfide into the electrolyte. There are important issues about the dynamical processes of S-desorption and Li-diffusion through the graphene plane. As above, Li atoms can make the adsorption of single-S on pristine graphene unstable. As shown in Fig. 2B, there is a dynamical barrier of approximately 0.34 eV in the desorption process. Interestingly, with the introduction of two Li atoms, the barrier in the process is zero (Fig. 2). This means that Li_nS clusters will be formed easily when Li ions diffuse from the electrolyte into the cathode upon the discharge of the battery, in the case of pristine graphene as an encapsulation layer.

Fig. 2 Schematic representations of the dynamical process of S-desorption on graphene with the single-Li adsorption (a, LiS cluster) and double Li ion adsorption (b, Li₂S) (A), and the potential–energy curves of S-desorption in both cases (B). Note that the direction of S diffusion is perpendicular to the graphene sheet and the zero of energy is cited at the position where S is far way from the graphene plane.

For defected graphene, such as double-vacancy containing graphene, the binding of S at the edge of the defect is stronger. As shown in Fig. 3, when a single Li is introduced, the adsorption of S at the edge of vacancy is still stable. With the introduction of two Li atoms, the adsorption of S becomes unstable. However, there is a dynamical barrier of about 0.80 eV for the S-desorption and formation of Li₂S. With three Li atoms, the process of desorption has no dynamical barrier and Li₃S clusters are then readily formed.

Fig. 3 Schematic representations of the dynamical process of S-desorption at the edge of double-vacancy graphene with single Li adsorption (a, LiS), double Li ion adsorption (b, Li₂S) and triple Li ion adsorption (c, Li₃S) (A) and the potential–energy curves of S-desorption in three cases (B). Note that the direction of S diffusion is perpendicular to the graphene sheet. For LiS and Li₂S, the zero points of energies are cited at the positions where S is trapped at the edge of double-vacancy with the adsorption of single-Li and double Li. For LiS₃, the zero of energy is cited at the position where S is far way from the graphene plane.

The diffusion of Li from Li_nS by going through the graphene encapsulation layer is important. Prior work⁵² shows that Li cannot diffuse in the direction perpendicular to the graphene sheet for pristine graphene or/and graphene with single vacancies. The smallest pore through which Li can pass through graphene is the double-vacancy. Here the diffusion of Li in the Li_nS cluster through the graphene plane with double-vacancies is analyzed in Fig. 4. Two models, specifically Li₂S and Li₃S, were treated using the nudged elastic band method and the diffusion barriers along the pathway were obtained. For Li₂S, the barrier is very high – approximately 14.5 eV if the lattice sites near the pathway are not relaxed in the diffusion of one of the Li ions in Li₂S and 3.5 eV with relaxation. This implies that it will not be easy for Li to go through the graphene plane in the case of Li₂S. Interestingly, in the case of Li₃S, the barriers for Li through the double-vacancy are lower – approximately 12.7 eV and 2.6 eV without and with the relaxation of the lattice sites near vacancy, respectively. This relatively small barrier compared with that in the case of Li₂S can be possibly ascribed to the weakening of S–graphene interaction by the formation of Li₂S clusters. In the case of Li₂S, the diffusion of Li results in LiS near double-vacancy. As shown in Fig. 3, there is a strong interaction between S and the edge of vacancy for LiS near double-vacancy. This may be the main reason that there is a relatively large barrier for the diffusion of Li in the Li₂S near graphene plane. Compared to the diffusion barrier (about 0.54 eV) without the effect of S in the previous work,⁵² the higher barrier (2.6 eV) is due to the attraction of Li₂S to the diffusing Li, as illustrated in the inset of Fig. 4. The energy will presumably decrease by following the increase of the Li number in the Li_nS cluster. On the other side, the effect of poly-sulfur (such as S₈ and S₂) on the diffusion of Li is relatively weak, since the interaction between poly-sulfur and graphene is weak, as discussed above. These results imply that the diffusion of Li through the double-vacancy is relatively facile, though there is an energy barrier in the presence of sulfur.

Fig. 4 Schematic representations of the diffusion of Li through the graphene plane by double-vacancy in the case of Li₂S and Li₃S (A), and potential–energy curves of S diffusion in the direction perpendicular to the graphene plane for both cases (B). Note that there is a large barrier in the process of Li diffusion if the lattice sites near the diffusion path are not relaxed and potential–energy curves of the case of Li₃S with the relaxation of lattice sites near the diffusion path is shown with a small energy scale in the inset of (B).

It is also possible that Li-ions diffuse along the plane of graphene and then go through the graphene encapsulation layer by the large pore openings freely. Here the effect of S-adsorption on the diffusion of Li around the double-vacancy is analyzed. As shown in Fig. 5, the diffusion of Li-ions near double-vacancy under the interaction of S, LiS and LiS₂ is simulated. For the case of LiS, S is coupled strongly to the edge of double-vacancy with the formation of chemical bonds, and the interaction between Li and S is weak. Therefore, the diffusion of Li-ions near double-vacancy with the effect of S is similar to that of Li-ions near single-vacancy,⁵² and there is a barrier of about 0.52 eV due to the trapping of double-vacancy with S. For Li₂S, Li makes the interaction between S and the edge weak, while the interaction between the diffused Li and S is increased and the barrier of Li diffusion becomes 0.68 eV due to the trapping effect of S. For Li₃S, the effect of the trapping of S becomes stronger and a deep well with a barrier of 1.71 eV is formed. In addition, from the H₁ to H₂ site, an obvious barrier of about 0.18 eV is found, compared with that of LiS and Li₂S. From the above analysis, the diffusion of Li in the graphene plane is easier than that by passing through the double-vacancy.

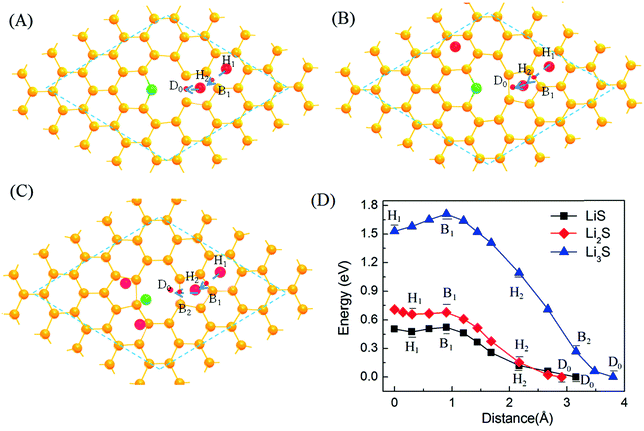Fig. 5 Schematic representations of the paths (A, B, and C) and potential–energy curves (D) of Li diffusion on double-vacancy graphene for LiS, LiS₂ and LiS₃.

Electronic properties of pristine and double-vacancy graphene with Li_nS clusters

To analyze the nature of interaction between the Li_nS cluster and graphene, we compute the distribution of charge in real place. In Fig. 6, the charge redistribution is analyzed based on the following formula:

ΔCH(r) = CH_Li–S-g(r) − CH_Li–S(r) − CH_g(r) (3)

where CH_Li–S-g(r), CH_Li–S(r) and CH_g(r) are the real-space electronic charge distributions of the Li_nS cluster adsorbed on graphene (pristine or with double-vacancy), the isolated Li_nS cluster and isolated graphene, respectively. For pristine graphene with the absorption of Li₂S and Li₃S in Fig. 6A and B, the charge is transferred from Li_nS to the graphene plane. The charge is mostly distributed in the region under the cluster as may be anticipated. This is characteristic of the typical ionic bond. The charge from Li_nS enters graphene and occupies the bands associated with graphene. The attractive Coulomb interaction provides the binding of the cluster to graphene. With the increase of Li-ions, even the charge is transferred to the region on graphene, which is away from the cluster of Li_nS (Fig. 6B). The same case appears in double-vacancy graphene in Fig. 6C.

Fig. 6 The side and top views of charge redistributions by calculating charge density difference in real space for pristine graphene with the Li₂S cluster (A) and cluster Li₃S (B), and double-vacancy graphene with the Li₃S cluster (C). The isovalue for rendering the isosurface is 1.4 × 10⁻³ e Å⁻³. Note that magenta and red correspond to charge accumulation and charge depletion, respectively.

In graphene, the bands near the Fermi level are formed from the p_z orbitals by following sp² hybridization. The valence and conduction bands intersect at the Fermi level with linear dispersion. When S is adsorbed, S–C bonds form, which results in local breaking of sp² hybridization. Due to the local symmetry breaking of potential, the band gap at K point is opened (see Fig. S11 of ESI†). The coupling between S_p and C_p_z results in a bonding state at about −1.1 eV and an antibonding state at about 1.0 eV.

When Li is introduced, the Li_nS cluster can form and the interaction between graphene and Li_nS is mainly associated with charge transfer, as above. From the band structures in Fig. 7A and B, it is found clearly that the Fermi level is shifted up into the conduction band of graphene with spin-polarization of localized states from the Li_nS cluster (in Fig. 8A) for the cases of LiS and Li₂S. Upon increasing the number of Li atoms, more electrons transfer into the conduction band of graphene. Interestingly, for the Li₃S cluster (in Fig. 7C), spin-polarization disappears, and the Fermi level is shifted up to about 1 eV above the Dirac point with the localized states from the Li₃S cluster near −1.5 eV (in Fig. 8A).

Fig. 7 Spin-polarized band structures of LiS-adsorbed graphene (A), Li₂S-adsorbed graphene (B), Li₃S-adsorbed graphene (C), two-vacancy graphene (D), two-vacancy graphene with adsorption of the Li₃S cluster (E), two-vacancy graphene with one S adsorbed at the edge of vacancy and one Li adsorbed near the vacancy (LiS) (F). Note that red and black correspond to spin-up bands and spin-down bands, respectively.

Fig. 8 The density of states (DOS) and partial density of states (PDOS) of LiS-adsorbed, Li₂S-adsorbed and Li₃S-adsorbed graphene (A), and double-vacancy graphene, two-vacancy graphene with one S adsorbed at the edge of vacancy and one Li adsorbed near the vacancy, and two-vacancy graphene with the adsorption of the Li₃S cluster (B). Note the PDOS of double-vacancy graphene in (B), C2 and C1, represent the carbon atom at the edge of double-vacancy and that away from double-vacancy. The DOS (PDOS) is the sum of spin-up and spin-down channels.

The introduction of double-vacancies results in the redistribution of local charge and leads to a gap in the valance band under the Dirac point in Fig. 7D. This gap is an artifact of the periodicity of the supercell, but nonetheless, indicates a likelihood of localization of states near in energy to the band crossing (Fig. 8B). At the double-vacancy, the interaction between S and graphene is not weakened by a single Li in the case of LiS. As seen in Fig. 8B and Fig. S12 (ESI†), it is clear that S is hybridized fully with the near-neighbor C from the partial density of states. A band gap is opened near the Dirac point because the interaction from the S atom and the Fermi level is shifted up due to the electronic doping of Li, as seen in Fig. 7F. However, the Fermi level still is lower than the Dirac point. This implies that S adsorption with one Li atom results in the p-type doping of graphene. Considering Li₃S, the formation of the Li₃S clusters breaks the S–graphene bond so that the interaction between Li₃S and graphene is just by charge transfer. The Fermi level is shifted up further relative to LiS but still is under the Dirac point, i.e. with weaker, but still p-type doping.

Conclusions

The microscopic mechanisms of interaction between Li_nS and graphene related to Li–S batteries are explored using first-principles methods. It is found that the introduction of Li on graphene results in the increase in the distance of S adsorbed on graphene and the formation of Li_nS clusters. A single Li atom can lift the S atom with an energy barrier of 0.34 eV and two Li ions can induce the desorption of S readily. For the double-vacancy defected graphene, the binding of S is stronger and at least two Li atoms are needed for the desorption of S at the edge of double-vacancy. It is found that the interaction between Li_nS clusters and graphene is strong due to charge transfer. This makes graphene a good encapsulation layer for preventing the dissolution of lithium polysulfide into electrolytes. However, the formation of Li_nS and adsorption of S at the edge of double-vacancy also limit the diffusion of Li into the electrolyte. This implies the importance of vacancy defects on graphene. It is found that the diffusion barrier is too high for Li to go through the graphene plane at a double-vacancy if S is adsorbed at the edge of double-vacancy. Interestingly, S can be desorbed at the edge with the trapping of Li ions near the vacancy. Li atoms from Li_nS can go through the graphene plane at double-vacancy with a small diffusion barrier. The analysis of electronic properties indicates that the pristine and defected graphene can have good conductivity in the process of intercalating in or/and out graphene. This is because Li_nS clusters act as dopants moving the Fermi level away from the gap position where states may be localized by defects. Understanding the interaction between lithium polysulfide and graphene and the diffusion of Li is very important since recent experimental results show that defected graphene is a good encapsulation layer for trapping Li_nS and hindering the dissolution of lithium polysulfide into the electrolyte with good electronic conductivity. The present results suggest further work clarifying the nature of defects in graphene layers in cathodes and Li_nS cluster formation in relation to atomic and electronic transport in the cathode.

Acknowledgements

The research was supported by the National Natural Science Foundation of China (Grant no. 11504123 and no. 51627805) and the National Key Research and Development Program of China (2016YFA0200401). Work at the University of Missouri was supported by the Department of Energy, BES through the MAGICS center.

References

1. P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Li-O₂ and Li–S Batteries with High Energy Storage, Nat. Mater., 2012, 11, 19–29.
2. A. Luntz, Beyond Lithium Ion Batteries, J. Phys. Chem. Lett., 2015, 6, 300–301.
3. C. M. Hayner, X. Zhao and H. H. Kung, Materials for Rechargeable Lithium-Ion Batteries, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 445–471.
4. G. Zhou, S. Pei, L. Li, D. W. Wang, S. Wang, K. Huang, L. C. Yin, F. Li and H. M. Cheng, A Graphene-Pure-Sulfur Sandwich Structure for Ultrafast, Long-Life Lithium–Sulfur Batteries, Adv. Mater., 2014, 26, 625–631.
5. H. A. Salem, G. Babu, C. V. Rao and L. M. R. Arava, Electrocatalytic Polysulfide Traps for Controlling Redox Shuttle Process of Li–S Batteries, J. Am. Chem. Soc., 2015, 137, 11542–11545.
6. M. S. Islam and C. A. J. Fisher, Lithium and Sodium Battery Cathode Materials: Computational Insights into Voltage, Diffusion and Nanostructural Properties, Chem. Soc. Rev., 2014, 43, 185–204.
7. J. B. Goodenough and K.-S. Park, The Li-Ion Rechargeable Battery: A Perspective, J. Am. Chem. Soc., 2013, 135, 1167–1176.
8. Q. Zhang, Y. Wang, Z. W. Seh, Z. Fu, R. Zhang and Y. Cui, Understanding the Anchoring Effect of Two-Dimensional Layered Materials for Lithium–Sulfur Batteries, Nano Lett., 2015, 15, 3780–3786.
9. M. S. Whittingham, Lithium Batteries and Cathode Materials, Chem. Rev., 2004, 104, 4271–4302.
10. H. Wei, J. Ma, B. Li, Y. Zuo and D. Xia, Enhanced Cycle Performance of Lithium–Sulfur Batteries Using a Separator Modified with a PVDF-C Layer, ACS Appl. Mater. Interfaces, 2014, 6, 20276–20281.
11. F. Wu, J. Qian, R. Chen, J. Lu, L. Li, H. Wu, J. Chen, T. Zhao, Y. Ye and K. Amine, An Effective Approach to Protect Lithium Anode and Improve Cycle Performance for Li–S Batteries, ACS Appl. Mater. Interfaces, 2014, 6, 15542–15549.
12. X. Ji and L. F. Nazar, Advances in Li–S Batteries, J. Mater. Chem., 2010, 20, 9821–9826.
13. J. Liu, W. Li, L. Duan, X. Li, L. Ji, Z. Geng, K. Huang, L. Lu, L. Zhou, Z. Liu, W. Chen, L. Liu, S. Feng and Y. Zhang, A Graphene-like Oxygenated Carbon Nitride Material for Improved Cycle-Life Lithium/Sulfur Batteries, Nano Lett., 2015, 15, 5137–5142.
14. X. Niu, X. Wang, D. Wang, Y. Li, Y. Zhang, Y. Zhang, T. Yang, T. Yu and J. Tu, Metal Hydroxide – a New Stabilizer for the Construction of Sulfur/Carbon Composites as High-Performance Cathode Materials for Lithium–Sulfur Batteries, J. Mater. Chem. A, 2015, 3, 17106–17112.
15. L. Sun, W. Kong, Y. Jiang, H. Wu, K. Jiang, J. Wang and S. Fan, Super-Aligned Carbon Nanotube/Graphene Hybrid Materials as a Framework for Sulfur Cathodes in High Performance Lithium Sulfur Batteries, J. Mater. Chem. A, 2015, 3, 5305–5312.
16. J. H. Kim, K. Fu, J. Choi, K. Kil, J. Kim, X. Han, L. Hu and U. Paik, Encapsulation of S/SWNT with PANI Web for Enhanced Rate and Cycle Performance in Lithium Sulfur Batteries, Sci. Rep., 2015, 5, 8946.
17. S. Wei, L. Ma, K. E. Hendrickson, Z. Tu and L. A. Archer, Metal–Sulfur Battery Cathodes Based on PAN-Sulfur Composites, J. Am. Chem. Soc., 2015, 137, 12143–12152.
18. D.-W. Wang, Q. Zeng, G. Zhou, L. Yin, F. Li, H.-M. Cheng, I. R. Gentle and G. Q. Max Lu, Carbon–Sulfur Composites for Li–S Batteries: Status and Prospects, J. Mater. Chem. A, 2013, 1, 9382–9394.
19. H. Kim, J. Lee, H. Ahn, O. Kim and M. Park, Synthesis of Three-Dimensionally Interconnected Sulfur-Rich Polymers for Cathode Materials of High-Rate Lithium–Sulfur Batteries, Nat. Commun., 2015, 6, 7278.
20. F. Wu, J. T. Lee, F. Fan, N. Nitta, H. Kim, T. Zhu and G. Yushin, A Hierarchical Particle-Shell Architecture for Long-Term Cycle Stability of Li₂S Cathodes, Adv. Mater., 2015, 27, 5579–5586.
21. H. Chen, C. Wang, W. Dong, W. Lu, Z. Du and L. Chen, Monodispersed Sulfur Nanoparticles for Lithium–Sulfur Batteries with Theoretical Performance, Nano Lett., 2015, 15, 798–802.
22. A. Manthiram, Y. Fu, S.-H. Chung, C. Zu and Y.-S. Su, Rechargeable Lithium–Sulfur Batteries, Chem. Rev., 2014, 114, 11751–11787.
23. Z. Li, Y. Jiang, L. Yuan, Z. Yi, C. Wu, Y. Liu, P. Strasser and Y. Huang, A Highly Ordered Meso@Microporous Carbon-Supported Sulfur@Smaller Sulfur Core–Shell Structured Cathode for Li–S Batteries, ACS Nano, 2014, 8, 9295–9303.
24. L. Pauling, On the Stability of the S₈ Molecule and the Structure of Fibrous Sulfur, Proc. Natl. Acad. Sci. U. S. A., 1949, 35, 495–499.
25. H. J. Bernstein and J. Powling, The Vibrational Spectra and Structure of Inorganic Molecules. II. Sulfur S₈, Sulfur Chloride S₂Cl₂, Phosphorous P₄, J. Chem. Phys., 1950, 18, 1018.
26. B. E. Warren and J. T. Burwell, The Structure of Rhombic Sulphur, J. Chem. Phys., 1935, 3, 6.
27. S. C. Abrahams, The Crystal and Molecular Structure of Orthorhombic Sulfur, Acta Crystallogr., 1955, 8, 661–671.
28. R. Xu, I. Belharouak, X. Zhang, R. Chamoun, C. Yu, Y. Ren, A. Nie, R. Shahbazian-Yassar, J. Lu, J. C. M. Li and K. Amine, Insight into Sulfur Reactions in Li–S Batteries, ACS Appl. Mater. Interfaces, 2014, 6, 21938–21945.
29. J.-J. Chen, R.-M. Yuan, J.-M. Feng, Q. Zhang, J.-X. Huang, G. Fu, M.-S. Zheng, B. Ren and Q.-F. Dong, Conductive Lewis Base Matrix to Recover the Missing Link of Li₂S₈ during the Sulfur Redox Cycle in Li–S Battery, Chem. Mater., 2015, 27, 2048–2055.
30. Q. Qu, T. Gao, H. Zheng, Y. Wang, X. Li, X. Li, J. Chen, Y. Han, J. Shao and H. Zheng, Strong Surface-Bound Sulfur in Conductive MoO₂ Matrix for Enhancing Li–S Battery Performance, Adv. Mater. Interfaces, 2015, 2, 1500048.
31. K. Ding, Y. Bu, Q. Liu, T. Li, K. Meng and Y. Wang, Ternary-Layered Nitrogen-Doped Graphene/Sulfur/Polyaniline Nanoarchitecture for the High-Performance of Lithium–Sulfur Batteries, J. Mater. Chem. A, 2015, 3, 8022–8027.
32. Z. Yuan, H.-J. Peng, J.-Q. Huang, X.-Y. Liu, D.-W. Wang, X.-B. Cheng and Q. Zhang, Hierarchical Free-Standing Carbon-Nanotube Paper Electrodes with Ultrahigh Sulfur-Loading for Lithium–Sulfur Batteries, Adv. Funct. Mater., 2014, 24, 6105–6112.
33. Z. Zhang, H.-K. Jing, S. Liu, G.-R. Li and X.-P. Gao, Encapsulating Sulfur into a Hybrid Porous Carbon/CNT Substrate as a Cathode for Lithium–Sulfur Batteries, J. Mater. Chem. A, 2015, 3, 6827–6834.
34. G. He, C. J. Hart, X. Liang, A. Garsuch and L. F. Nazar, Stable Cycling of a Scalable Graphene-Encapsulated Nanocomposite for Lithium–Sulfur Batteries, ACS Appl. Mater. Interfaces, 2014, 6, 10917–10923.
35. G. M. Yang, H. Z. Zhang, X. F. Fan and W. T. Zheng, Density Functional Theory Calculations for the Quantum Capacitance Performance of Graphene-Based Electrode Material, J. Phys. Chem. C, 2015, 119, 6464–6470.
36. H. Wang, Y. Yang, Y. Liang, J. T. Robinson, Y. Li, A. Jackson, Y. Cui and H. Dai, Graphene-Wrapped Sulfur Particles as a Rechargeable Lithium–Sulfur Battery Cathode Material with High Capacity and Cycling Stability, Nano Lett., 2011, 11(7), 2644–2647.
37. S. Lu, Y. Cheng, X. Wu and J. Liu, Significantly Improved Long-Cycle Stability in High-Rate Li–S Batteries Enabled by Coaxial Graphene Wrapping over Sulfur-Coated Carbon Nanofibers, Nano Lett., 2013, 13, 2485–2489.
38. S. Wu, R. Ge, M. Lu, R. Xu and Z. Zhang, Graphene-based Nano-materials for Lithium–Sulfur Battery and Sodium-ion Battery, Nano Energy, 2015, 15, 379–405.
39. F. Li, Y. Su and J. Zhao, Shuttle inhibition by chemical adsorption of lithium polysulfides in B and N co-doped graphene for Li–S batteries, Phys. Chem. Chem. Phys., 2016, 18, 25241–25248.
40. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864.
41. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11189.
42. G. Kresse and J. Furthmüller, Efficiency of Ab Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. S. Grimme, Semiempirical GGA-type Density Functional Constructed with a Long-range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787.
45. X. F. Fan, W. T. Zheng, V. Chihaia, Z. X. Shen and J.-L. Kuo, Interaction between Graphene and the Surface of SiO₂, J. Phys.: Condens. Matter, 2012, 24, 305004.
46. G. Mercurio, E. R. McNellis, I. Martin, S. Hagen, F. Leyssner, S. Soubatch, J. Meyer, M. Wolf, P. Tegeder, F. S. Tautz and K. Reuter, Structure and Energetics of Azobenzene on Ag(111): Benchmarking Semiempirical Dispersion Correction Approaches, Phys. Rev. Lett., 2010, 104, 036102.
47. X. Fan, W. T. Zheng, J.-L. Kuo and D. J. Singh, Adsorption of Single Li and the Formation of Small Li Clusters on Graphene for the Anode of Lithium-Ion Batteries, ACS Appl. Mater. Interfaces, 2013, 5, 7793–7797.
48. K. T. Chan, J. B. Neaton and M. L. Cohen, First-Principles Study of Metal Adatom Adsorption on Graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430.
49. B. Meyer, Solid Allotropes of Sulfur, Chem. Rev., 1964, 64, 429–451.
50. B. Meyer, Elemental Sulfur, Chem. Rev., 1976, 76, 367–388.
51. T. O. Wehling, A. I. Lichtenstein and M. I. Katsnelson, Transition-Metal Adatoms on Graphene: Influence of Local Coulomb Interactions on Chemical Bonding and Magnetic Moments, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235110.
52. X. Fan, W. T. Zheng and J.-L. Kuo, Adsorption and Diffusion of Li on Pristine and Defective Graphene, ACS Appl. Mater. Interfaces, 2012, 4, 2432–2438.

---

Footnote

† Electronic supplementary information (ESI) available: Possible configurations of S and Li_nS (n = 1, 2) on pristine graphene and double-vacancy graphene with the important parameters calculated in Fig. S1–S10 and Tables S1–S10. The band structure, DOS and PDOS of S-adsorbed graphene in Fig. S11 and DOS and PDOS of two-vacancy graphene with the adsorption of LiS in Fig. S12. See DOI: 10.1039/c6cp04984b

---