Application of the dielectric-dependent screened exchange potential approach to organic photocell materials
Received
13th July 2016
, Accepted 12th September 2016
First published on 12th September 2016
Abstract
This paper discusses the fundamental features of the dielectric-dependent screened exchange potential approach for organic molecules and photocell materials. The energy difference (gap) between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) is a key factor when designing organic photocell materials. The magnitude of this energy gap strongly depends on the ratio of the Hartree–Fock (HF) exchange term combined with hybrid density functional theory (DFT) functionals. In ordinary hybrid DFT functionals, the HF exchange term ratio is often determined empirically and a constant value is employed for all materials. Conversely, the dielectric-dependent exchange potential approach employs a system-dependent value for this parameter, which is proportional to the inverse of the dielectric constant. The organic materials examined in this paper take different dielectric constant values according to their material types and unit lengths; therefore, their HF exchange ratios are also different. This paper discusses the relationship between the energy gaps, the dielectric constants, and the HF exchange ratios in the dielectric-dependent screened exchange potential approach. For a series of acene-type compounds, it was found that the HOMO–LUMO gap decreased when their conjugation systems are extended. The dielectric-dependent screened exchange potential approach demonstrated that the values of the dielectric constants of the compounds increased; consequently, the HF exchange ratio decreased. Similar results were obtained for a series of thiophene-based donor molecules. The calculated values were compared with those obtained via experimental measurements. We found that although the theoretical calculations of the HOMO–LUMO gap usually overestimate experimental optical gaps, a better agreement between the experimental and calculated values can be obtained if we correct for the exciton binding energy.
I. Introduction
In recent years, organic electronic devices such as electroluminescent displays, transistors, and photocells have been extensively studied because of their useful properties such as light weight, thin film structures, flexibility, low manufacturing costs, and design. In order to more widely utilize organic materials in electronic devices, a deeper understanding of their electronic structure properties is required. For example, the highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gap of the donor material is an important indicator when fabricating organic photocell devices because the energy of the photon absorbed by the device is closely related to this gap.1,2 The energy of the light absorbed is roughly equivalent to the value obtained by subtracting the binding energy of an electron–hole pair (exciton) from the HOMO–LUMO energy gap. The dielectric constants of organic materials are usually smaller than those of inorganic semiconductors; therefore, the electron and the hole generated by photon absorption are strongly bound in organic materials. The LUMO energy difference (offset) between the donor and acceptor materials plays an essential role in the dissociation of such strongly bound excitons.2–9 The energy offset at the donor–acceptor junction can give excess energy to the exciton and assist the dissociation process required to generate a free electron and a hole.8,9 Several experiments have demonstrated that the energy conversion efficiency of an organic photocell device is suppressed in small offset cases. Thus, the ability to determine energy difference properties, such as the HOMO–LUMO gap, is essential in the development of organic photocell devices.
Unfortunately, it is not a simple matter to precisely predict the HOMO–LUMO gap of materials using density functional theory (DFT). For example, it is well known that local density approximation used in DFT calculations underestimates the HOMO–LUMO (band) gap as a result of the lack of nonlocal exchange interaction.10,11 Hybrid DFT methods, which possess partial nonlocal Hartree–Fock (HF) exchange terms, can reduce the bandgap underestimation, but ordinary hybrid DFT functionals sometimes fail to accurately reproduce the energy difference.12 This may be because the ratio of the HF exchange term is empirically determined in most hybrid DFT functionals. For example, in the B3LYP functional, the HF exchange ratio is empirically determined to reproduce the experimental results of molecules and atoms.13 To overcome this deficiency, we have proposed the dielectric-dependent screened exchange potential approach, in which the HF exchange term ratio can change according to the target system.14,15 In the dielectric-dependent exchange potential, the HF exchange ratio is proportional to the inverse of the dielectric constant. In contrast, an ordinary DFT functional usually employs a constant value for all materials. The dielectric-dependent approach has also been applied by other research groups and has been shown to give good descriptions of the energy gap for several systems.12,16–28 Skone et al. recently reported that their dielectric-dependent range-separated hybrid DFT functional can describe the electronic structure of molecular systems well.29 Our dielectric-dependent exchange potentials have been mainly applied to inorganic materials, although we previously demonstrated simple polymer calculations together with the Gaussian-based range-separation method.30,31 This paper discusses the dielectric-dependent exchange potential approach to organic molecules. We focus specifically on several donor materials suitable for use in organic photocell devices, because their energy gap properties are especially important for solar cells. In the next section, we briefly explain the calculation methodology for the screened exchange potential approach; calculation results are presented and discussed in Section III. In the final section, we give a summary of this paper.
II. Calculation method
In this section, we discuss several dielectric-dependent screened exchange potentials with Coulomb hole (COH) and screened exchange (SEX) interactions.32 The dielectric-dependent screened exchange potential can be derived from the dielectric function ε(q) = 1 + [(εs − 1)−1 + β(q2/qTF2)]−1.14 Here, q is the wave vector, qTF is the Thomas–Fermi wave number, and εs is the electronic part of the static dielectric constant. Bechstedt et al. reported that the value of β is independent of the target semiconductor, and in this paper we employ their suggested value of β = 1.563.33 The physical concept of the dielectric-dependent exchange approach is summarized in the following equations:34| |  | (1.1) |
| |  | (1.2) |
| |  | (1.3) |
| |  | (1.4) |
Here, ρ(r) is the electron density. The Fermi momentum kF(r) is written as 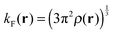 . r12 is the distance between two electrons. This paper employs the simple potential description. The precise one is found in the literature.34,35Eqn (1.3) is used to correct the behavior of the dielectric function in the large q region.33,34,36 The first term gives the local COH interaction, and the second and third terms express the nonlocal SEX contributions. The third term may be the most important, because it represents the partial fragment of the HF exchange interaction in the potential. In the dielectric-dependent screened exchange potential, the HF exchange ratio is proportional to the inverse of the dielectric constant. In semiconductors and insulators, the screening effect is not complete, and therefore the bare interaction of 1/r appears in the third term of eqn (1.1), but the interaction is modified by the inverse of the dielectric constant.14 In the limit of εs = 1, the potential of eqn (1.1) reduces to the ordinary HF exchange interaction. In a metallic system in which εs → ∞, the SEX part of the dielectric-dependent exchange potential reduces to a Thomas–Fermi-like screening interaction.36 On the other hand, the nonlocal behavior of the second term, which is described by the Yukawa-type potential, is not strong because of the large
. r12 is the distance between two electrons. This paper employs the simple potential description. The precise one is found in the literature.34,35Eqn (1.3) is used to correct the behavior of the dielectric function in the large q region.33,34,36 The first term gives the local COH interaction, and the second and third terms express the nonlocal SEX contributions. The third term may be the most important, because it represents the partial fragment of the HF exchange interaction in the potential. In the dielectric-dependent screened exchange potential, the HF exchange ratio is proportional to the inverse of the dielectric constant. In semiconductors and insulators, the screening effect is not complete, and therefore the bare interaction of 1/r appears in the third term of eqn (1.1), but the interaction is modified by the inverse of the dielectric constant.14 In the limit of εs = 1, the potential of eqn (1.1) reduces to the ordinary HF exchange interaction. In a metallic system in which εs → ∞, the SEX part of the dielectric-dependent exchange potential reduces to a Thomas–Fermi-like screening interaction.36 On the other hand, the nonlocal behavior of the second term, which is described by the Yukawa-type potential, is not strong because of the large ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) TF values for molecules. Thus, we can approximate the weak nonlocal term by the local potential based on the dielectric-dependent Slater term as follows:34,37
TF values for molecules. Thus, we can approximate the weak nonlocal term by the local potential based on the dielectric-dependent Slater term as follows:34,37| |  | (2.1) |
| |  | (2.2) |
| |  | (2.3) |
The first and second terms of eqn (2.1) are local, but the third term is nonlocal. In this paper, the Yukawa-type potential, exp(−ηr)/r, is replaced by the complementary error function erfc(2ηr/3)/r because of their similar behaviors.14,38 This paper also examines the following dielectric-dependent DFT potential to compare with eqn (1.1) and (2.1).| |  | (3) |
Here, VVWN is the Vosko–Wilk–Nusair correlation DFT potential.39 The dielectric-dependent exchange potential of eqn (3) may be more easily used in ordinary quantum chemistry, because the terms VSlater and VVWN are already prepared in many quantum chemistry program packages.
Finally, we describe the self-consistent procedure used to automatically determine the dielectric constant.21,40 In our approach, the dielectric constant is determined by the following equation.30,34,36,41
| |  | (4) |
Here, the indices
i and
a represent the occupied and virtual (unoccupied) orbitals, respectively;
Ei and
Ea are the orbital energies for occupied and virtual orbitals of
ϕi and
ϕa, respectively;
V is the volume of the target molecule; and an electron density of 0.01 a.u. is used to determine the boundary of the volume. The integral value of 〈
ϕi(
r)|exp(
iq·
r)|
ϕa(
r)〉 is calculated as described in the previous study.
35 We estimate the dielectric constant from the isotropically averaged value at the limit
q → 0. In the self-consistent dielectric constant approach, the
εs value used in
eqn (1.1), (2.1), and (3) is renewed for each self-consistent field (SCF) step. Thus, information about the virtual orbital (conduction band) is taken into account through
eqn (4) to obtain the electronic structure of the materials. We will show the calculation results based on these self-consistent dielectric-dependent screened exchange potentials in the next section.
III. Calculations and discussions
A. Acene molecules
First, we employed several acene molecules such as naphthalene, anthracene, tetracene, and pentacene to explain the fundamental behaviors of the dielectric-dependent screened exchange potential when applied to conjugated molecular systems. We consider n = 1–8, where n is the number of benzene rings, as shown in the inset of Fig. 1a. We investigated the electronic structure of these acenes based on the dielectric-dependent potentials given in eqn (1.1), (2.1), and (3). We also adopted the SVWN, B3LYP, and half-and-half (HandH) functionals for comparison purposes.13,42 These functionals are described as follows:| | | VSVWNXC = VSlater + VVWN | (5) |
| |  | (6) |
| |  | (7) |
Here, VB88 is the Becke88 (B88)-type gradient correction.43VLYP is the Lee–Yang–Parr correlation potential.44 The SVWN functional does not have any nonlocal exchange interaction, but the B3LYP and HandH methods contain 20% and 50% of the HF exchange term, respectively. We employ a dynamic-language framework for the calculations.45 The B3LYP/6-31G* method was used to obtain the optimized structures of these molecules.
 |
| | Fig. 1 (a) HOMO–LUMO gaps, (b) HOMO and LUMO energies, (c) dielectric constants, and (d) HF exchange ratios combined with DFT functionals with respect to unit lengths for acene molecules. The white triangles show the Half and Half (HandH) method, and black ones indicate the SVWN method. The black circles express the B3LYP method. The white circles represent the dielectric-dependent screened exchange potential of eqn (1.1). | |
The HOMO–LUMO gaps and the dielectric constants calculated using the 6-31G* and 6-311G* basis sets are summarized in Table 1. We can confirm that the HOMO–LUMO gap is narrowed when conjugated systems are extended. For example, in the case of naphthalene, B3LYP gave a HOMO–LUMO gap of 4.79 eV for the 6-311G* basis set. For the tetracene molecule, the HOMO–LUMO gap was reduced to 2.75 eV. When the dielectric-dependent screened exchange potential of eqn (1.1) was employed in conjunction with the 6-311G* basis set, the HOMO–LUMO gap for naphthalene was 6.16 eV and that for tetracene was 3.45 eV. From Table 1, it can be seen that the dielectric-dependent potentials of eqn (2.1) and (3) provide very similar results to eqn (1.1). Fig. 1a shows the HOMO–LUMO gaps calculated using the 6-311G* basis set as a function of the length of the conjugated system. Compared with the other methods, the SVWN method largely underestimated the HOMO–LUMO gaps because of the lack of nonlocal HF interaction. The HandH method yielded larger gaps, and the B3LYP method gave values intermediate between the SVWN and HandH methods. The dielectric-dependent approach gave similar HOMO–LUMO gaps to the HandH method for smaller unit lengths. However, at longer unit lengths, the HOMO–LUMO gaps calculated using eqn (1.1) gradually approached those obtained in the B3LYP calculations. Fig. 1b shows the HOMO and LUMO energies calculated using B3LYP, HandH, and the dielectric-dependent exchange potential approach of eqn (1.1). When the conjugated systems were extended, the HOMO (LUMO) energies gradually increased (decreased), and the HOMO–LUMO gaps narrowed. In the dielectric-dependent exchange potential approach, the HOMO and LUMO energies changed from values close to those obtained using the HandH method to values more closely corresponding to those generated by the B3LYP method. We will discuss these behaviors in the dielectric-dependent potential later from the viewpoint of the HF exchange ratio.
Table 1 Dielectric constants and HOMO–LUMO gaps [eV] for acene molecules
| |
SVWN |
B3LYP |
HandH |
Eqn (1.1)
|
Eqn (2.1)
|
Eqn (3)
|
| 6-31G* basis set |
| Benzene |
| Dielectric constant εs |
2.76 |
2.43 |
2.14 |
2.20 |
2.17 |
2.17 |
| HOMO–LUMO gap |
5.23 |
6.80 |
9.13 |
8.52 |
8.84 |
8.84 |
| Naphthalene |
| Dielectric constant εs |
3.32 |
2.82 |
2.41 |
2.51 |
2.53 |
2.53 |
| HOMO–LUMO gap |
3.46 |
4.83 |
6.87 |
6.28 |
6.16 |
6.16 |
| Anthracene |
| Dielectric constant εs |
3.84 |
3.16 |
2.63 |
2.83 |
2.85 |
2.86 |
| HOMO–LUMO gap |
2.37 |
3.59 |
5.42 |
4.62 |
4.50 |
4.50 |
| Tetracene |
| Dielectric constant εs |
4.33 |
3.46 |
2.81 |
3.12 |
3.16 |
3.16 |
| HOMO–LUMO gap |
1.67 |
2.78 |
4.44 |
3.52 |
3.41 |
3.41 |
|
|
| 6-311G* basis set |
| Benzene |
| Dielectric constant εs |
2.83 |
2.49 |
2.20 |
2.23 |
2.24 |
2.24 |
| HOMO–LUMO gap |
5.17 |
6.71 |
8.99 |
8.72 |
8.60 |
8.60 |
| Naphthalene |
| Dielectric constant εs |
3.39 |
2.89 |
2.47 |
2.58 |
2.61 |
2.61 |
| HOMO–LUMO gap |
3.43 |
4.79 |
6.80 |
6.16 |
6.02 |
6.02 |
| Anthracene |
| Dielectric constant εs |
3.91 |
3.22 |
2.69 |
2.90 |
2.94 |
2.95 |
| HOMO–LUMO gap |
2.35 |
3.56 |
5.36 |
4.54 |
4.39 |
4.40 |
| Tetracene |
| Dielectric constant εs |
4.39 |
3.53 |
2.88 |
3.20 |
3.26 |
3.26 |
| HOMO–LUMO gap |
1.65 |
2.75 |
4.39 |
3.45 |
3.32 |
3.33 |
The energy differences between occupied and virtual (unoccupied) molecular orbitals appear in the denominator of the equation, as seen in eqn (4), so we can expect an inverse relationship between the HOMO–LUMO gap and the dielectric constant. Fig. 1c shows the calculated dielectric constants as a function of the unit lengths of the acene molecules. We note that the dielectric constants are automatically determined using the self-consistent procedure in the dielectric-dependent screened exchange potentials. In contrast, the dielectric constants for the SVWN, B3LYP, and HandH methods are estimated after SCF convergence. Fig. 1c shows that small systems such as benzene and naphthalene give smaller dielectric constants. When the conjugation lengths of the acene molecules were extended, an increase in the dielectric constants was observed. For example, in the case of naphthalene, the dielectric-dependent exchange potential of eqn (1.1) yielded a value of 2.51 for the dielectric constant at the 6-31G* level, as seen in Table 1. For tetracene, this value was 3.12. Thus, we can confirm that molecular systems with larger HOMO–LUMO band gaps give smaller dielectric constants. On the other hand, the SVWN and B3LYP methods calculated larger dielectric constants than those obtained using the dielectric-dependent exchange potentials of eqn (1.1), (2.1), and (3). This means that the SVWN and B3LYP methods provide smaller HOMO–LUMO gaps than the dielectric-dependent exchange potential approach.
In the dielectric-dependent exchange potential approach, the ratio of the exact HF exchange term is determined by the inverse of the dielectric constant value. We summarize the HF exchange ratio in Fig. 1d. In the case of the dielectric-dependent exchange potentials, the HF exchange ratio decreased when the conjugation lengths were extended. For example, eqn (1.1) gives a dielectric constant of 2.20, and therefore about 45% of the HF exchange interaction is employed for benzene at the 6-31G* level. In the case of tetracene, the dielectric constant and the HF exchange ratio were 3.12 and 32%, respectively. Conversely, the B3LYP method always employs 20% of the HF exchange term, which was empirically determined by Becke to reproduce the experimental data of several atoms and molecules.13 The HF exchange ratio of the HandH functional is 50%.42Fig. 1d shows that the dielectric-dependent exchange potential approach employs a higher ratio for the partial HF exchange term at smaller unit lengths, which is closer to that of the HandH method; however, when the conjugation length is extended, the dielectric-dependent approach can adopt an HF exchange ratio similar to the B3LYP method. In the n = 8 case shown in Fig. 1d, the HF exchange ratio of eqn (1.1) was reduced to about 0.23, where the dielectric-dependent exchange approach gave similar calculation results to the B3LYP method.
In this paper, we employed acenes to simply explain basic behaviors of the dielectric-dependent approach according to the conjugation size. Here, we discuss several studies. Rangel et al. reported the G0W0 and evGW calculations for acene crystals.46 The G0W0 method depends on the DFT starting point, but the evGW method can partly compensate for the starting-point effect by using the self-consistent scheme. They reported the change in the gap properties according to the conjugation size. For example, the G0W0 and evGW method yields the fundamental gap properties of 4.0 and 4.5 eV for anthracene crystals, and 2.9 and 3.5 eV for tetracene crystals, respectively. The dielectric-dependent method gives the fundamental gap of 3.91 and 2.80 eV for anthracene and tetracene crystals, respectively.29 The dielectric-dependent approach is closely related to the GW method,12,14,34 and can give comparable results to the more expensive GW method.24 On the other hand, Stein et al. calculated the fundamental gap of acenes and Si nanocrystals based on the range-separated hybrid functional within the generalized Kohn–Sham approach.47 The range-separated hybrid DFT function possesses a system-dependent parameter. They showed that the system-dependent parameter is essential to consider the quantum size effect such as the conjugation length of acene oligomers. When the electron delocalization increases with the system size, the necessary weight of exact exchange term becomes smaller. In this paper, we also presented the change of the HF exchange term ratio in dielectric-dependent potentials according to the conjugation length. The behavior of the long-range HF exchange term discussed in this paper is similar to that of Stein's approach, although the system-dependent parameters used in two methods are different.
B. Organic photocell materials
Organic photocell devices have heterojunctions that are composed of donor and acceptor materials. For the acceptor region, fullerene derivatives such as phenyl-C61-butyric acid methyl ester are frequently employed. In the donor region, various types of molecules and polymers have been explored to improve the energy conversion efficiency of the organic photocell. In this paper, we examine the three materials depicted in Fig. 2: thieno[3,4-c]pyrrole-4,6-dione (TPD), benzo[c][1,2,5]thiadiazole (BTz), and naphtho[1,2-c:5,6-c′]bis[1,2,5]thiadiazole (NTz). Takimiya et al. have experimentally studied these materials for use as the donor components of organic photocells.48 We investigate the electronic structure of these materials using the dielectric-dependent screened exchange potentials of eqn (1.1), (2.1), and (3) and the 6-31G* and 6-311G* basis sets. We also adopt the SVWN, B3LYP, and HandH methods for comparison. The optimized structures used in our previous study were employed here.49 We summarize the calculation results for TPD, BTz, and NTz in Tables 2, 3, and 4, respectively.
 |
| | Fig. 2 Thiophene-based polymers used in this study. R is replaced with a methyl group. | |
Table 2 Dielectric constants and HOMO–LUMO gaps [eV] for TPD units
| |
SVWN |
B3LYP |
HandH |
Eqn (1.1)
|
Eqn (2.1)
|
Eqn (3)
|
| 6-31G* basis set |
| Monomer |
| Dielectric constant εs |
4.72 |
3.58 |
2.79 |
3.16 |
3.21 |
3.22 |
| HOMO–LUMO gap |
1.79 |
2.79 |
4.43 |
3.45 |
3.40 |
3.39 |
| Dimer |
| Dielectric constant εs |
5.62 |
3.98 |
2.96 |
3.58 |
3.63 |
3.64 |
| HOMO–LUMO gap |
1.38 |
2.30 |
3.84 |
2.71 |
2.68 |
2.68 |
| Trimer |
| Dielectric constant εs |
5.96 |
4.13 |
3.02 |
3.75 |
3.80 |
3.80 |
| HOMO–LUMO gap |
1.29 |
2.18 |
3.71 |
2.52 |
2.50 |
2.50 |
| Tetramer |
| Dielectric constant εs |
6.13 |
4.20 |
3.05 |
3.84 |
3.88 |
3.89 |
| HOMO–LUMO gap |
1.25 |
2.13 |
3.65 |
2.44 |
2.43 |
2.42 |
|
|
| 6-311G* |
| Monomer |
| Dielectric constant εs |
4.73 |
3.60 |
2.83 |
3.21 |
3.27 |
3.27 |
| HOMO–LUMO gap |
1.79 |
2.78 |
4.41 |
3.41 |
3.35 |
3.35 |
| Dimer |
| Dielectric constant εs |
5.61 |
4.00 |
3.00 |
3.63 |
3.68 |
3.69 |
| HOMO–LUMO gap |
1.38 |
2.29 |
3.82 |
2.68 |
2.65 |
2.65 |
| Trimer |
| Dielectric constant εs |
5.93 |
4.14 |
3.05 |
3.80 |
3.84 |
3.85 |
| HOMO–LUMO gap |
1.29 |
2.18 |
3.68 |
2.49 |
2.48 |
2.48 |
| Tetramer |
| Dielectric constant εs |
6.10 |
4.22 |
3.09 |
3.88 |
3.93 |
3.93 |
| HOMO–LUMO gap |
1.26 |
2.13 |
3.63 |
2.43 |
2.40 |
2.40 |
Table 3 Dielectric constants and HOMO–LUMO gaps [eV] for BTz units
| |
SVWN |
B3LYP |
HandH |
Eqn (1.1)
|
Eqn (2.1)
|
Eqn (3)
|
| 6-31G* basis set |
| Monomer |
| Dielectric constant εs |
5.06 |
3.69 |
2.84 |
3.27 |
3.33 |
3.33 |
| HOMO–LUMO gap |
1.36 |
2.38 |
4.02 |
2.96 |
2.93 |
2.92 |
| Dimer |
| Dielectric constant εs |
6.11 |
4.08 |
2.99 |
3.68 |
3.74 |
3.74 |
| HOMO–LUMO gap |
1.11 |
2.07 |
3.64 |
2.44 |
2.41 |
2.41 |
| Trimer |
| Dielectric constant εs |
6.52 |
4.22 |
3.05 |
3.85 |
3.90 |
3.91 |
| HOMO–LUMO gap |
1.04 |
1.97 |
3.53 |
2.28 |
2.26 |
2.25 |
| Tetramer |
| Dielectric constant εs |
6.73 |
4.29 |
3.08 |
3.93 |
3.99 |
4.00 |
| HOMO–LUMO gap |
1.00 |
1.93 |
3.49 |
2.20 |
2.19 |
2.18 |
|
|
| 6-311G* |
| Monomer |
| Dielectric constant εs |
5.07 |
3.72 |
2.88 |
3.32 |
3.39 |
3.38 |
| HOMO–LUMO gap |
1.36 |
2.38 |
4.00 |
2.93 |
2.89 |
2.88 |
| Dimer |
| Dielectric constant εs |
6.10 |
6.10 |
3.04 |
3.73 |
3.80 |
3.80 |
| HOMO–LUMO gap |
1.11 |
2.05 |
3.61 |
2.41 |
2.37 |
2.37 |
| Trimer |
| Dielectric constant εs |
6.51 |
4.25 |
3.09 |
3.89 |
3.97 |
3.96 |
| HOMO–LUMO gap |
1.04 |
1.96 |
3.50 |
2.25 |
2.22 |
2.22 |
| Tetramer |
| Dielectric constant εs |
6.71 |
4.32 |
3.12 |
3.99 |
4.06 |
4.05 |
| HOMO–LUMO gap |
1.00 |
1.92 |
3.46 |
2.18 |
2.15 |
2.15 |
Table 4 Dielectric constants and HOMO–LUMO gaps [eV] for NTz units
| |
SVWN |
B3LYP |
HandH |
Eqn (1.1)
|
Eqn (2.1)
|
Eqn (3)
|
| 6-31G* basis set |
| Monomer |
| Dielectric constant εs |
5.36 |
3.85 |
2.94 |
3.45 |
3.52 |
3.52 |
| HOMO–LUMO gap |
1.25 |
2.23 |
3.81 |
2.67 |
2.68 |
2.66 |
| Dimer |
| Dielectric constant εs |
6.27 |
4.17 |
3.06 |
3.82 |
3.86 |
3.87 |
| HOMO–LUMO gap |
1.03 |
1.94 |
3.47 |
2.23 |
2.24 |
2.23 |
| Trimer |
| Dielectric constant εs |
6.62 |
4.29 |
3.10 |
3.95 |
4.00 |
4.02 |
| HOMO–LUMO gap |
0.97 |
1.87 |
3.38 |
2.10 |
2.12 |
2.11 |
| Tetramer |
| Dielectric constant εs |
6.80 |
4.35 |
3.13 |
4.03 |
4.08 |
4.08 |
| HOMO–LUMO gap |
0.94 |
1.84 |
3.35 |
2.05 |
2.07 |
2.06 |
|
|
| 6-311G* |
| Monomer |
| Dielectric constant εs |
5.37 |
3.88 |
2.98 |
3.51 |
3.58 |
3.58 |
| HOMO–LUMO gap |
1.25 |
2.23 |
3.79 |
2.65 |
2.65 |
2.63 |
| Dimer |
| Dielectric constant εs |
6.25 |
4.20 |
3.10 |
3.86 |
3.93 |
3.93 |
| HOMO–LUMO gap |
1.03 |
1.94 |
3.45 |
2.21 |
2.22 |
2.20 |
| Trimer |
| Dielectric constant εs |
6.57 |
4.31 |
3.14 |
4.00 |
4.06 |
4.06 |
| HOMO–LUMO gap |
0.97 |
1.87 |
3.37 |
2.09 |
2.10 |
2.09 |
| Tetramer |
| Dielectric constant εs |
6.75 |
4.37 |
3.17 |
4.08 |
4.13 |
4.14 |
| HOMO–LUMO gap |
0.94 |
1.84 |
3.33 |
2.04 |
2.05 |
2.04 |
In the organic photocell materials, the HOMO–LUMO gaps decreased as their oligomer lengths were extended. Conversely, at longer conjugation (unit) lengths, those molecules gave smaller dielectric constants because of the inverse relationship between the magnitude of the HOMO–LUMO gap and the dielectric constant. For example, the HOMO–LUMO gap and the dielectric constant of the TPD monomer were 3.45 eV and 3.16, respectively, based on eqn (1.1) with the 6-31G* basis set, as seen in Table 2. Trimeric TPD exhibited a HOMO–LUMO gap and a dielectric constant of 2.52 eV and 3.75, respectively. Thus, the conjugation (unit) lengths of these materials strongly influenced both the HOMO–LUMO gaps and the dielectric constants. Conversely, at large unit lengths, the HOMO–LUMO gaps and the dielectric constants become saturated. For example, the HOMO–LUMO gaps for trimeric and tetrameric NTz were 2.09 and 2.04 eV, respectively, when eqn (1.1) was employed together with the 6-311G* basis set, as seen in Table 4. The B3LYP method and the dielectric-dependent exchange potential approach gave similar calculation results. It should be noted that, compared with both the B3LYP method and the dielectric-dependent approach, the SVWN method underestimated the HOMO–LUMO gap and overestimated the dielectric constant. This occurs as a result of the lack of nonlocal HF exchange interaction in the SVWN method. Conversely, the HandH method overestimated the gap and underestimated the dielectric constant.
We summarize the HOMO–LUMO gaps, HOMO and LUMO energies, and dielectric constants of the organic photocell materials in Fig. 3a, b, and c, respectively. In Fig. 3d, we show the inverse values of dielectric constants, which represent the HF exchange ratio for each target system. To generate these figures, we employed eqn (1.1) with the 6-311G* basis set. Fig. 3a shows that the HOMO–LUMO gaps decreased when the unit lengths were extended. The HOMO and LUMO energies changed according to the unit length, as seen in Fig. 3b, but those influences were saturated in the tetramer cases. In addition, the HOMO–LUMO gaps narrowed when the conjugation lengths were extended. Fig. 3c shows that the values of the dielectric constants increased in parallel with the increase in the conjugation (unit) lengths. However, the calculated dielectric constant values were different and depended on the type of material and the unit length. For example, the TPD monomer exhibited a dielectric constant of 3.21 in eqn (1.1) with the 6-311G* basis set. Conversely, for the NTz trimer, this value was estimated to be 4.00. Thus, organic photocell materials can take different dielectric constant values. These different dielectric constants give different HF exchange ratios in the dielectric-dependent exchange potentials, as seen in Fig. 1d.
 |
| | Fig. 3 (a) HOMO–LUMO gaps, (b) HOMO and LUMO energies, (c) dielectric constants, and (d) HF exchange ratios combined with the potential of eqn (1.1) in accordance with unit lengths for organic photocell materials. The black and white circles show calculation results for TPD and BTz materials, respectively. The black triangles represent the NTz material. | |
Next, we discuss comparisons between theoretical calculations and experiments. For organic materials, reliable experimental measurements of the HOMO–LUMO gap may be more difficult than analogous experiments on inorganic bulk materials. In the case of polymeric materials, changes in the polymer type and/or experimental conditions can lead to the formation of several different crystal structures, which may include amorphous and semi-crystalline states. This disturbance and disorder in a crystal structure causes the localization of electrons in the organic material, and may make it more difficult to accurately estimate the HOMO–LUMO gap. In addition, the dielectric constants of organic materials are usually lower than those of inorganic materials. Therefore, when a photon is absorbed by an organic photocell material, a strongly bound exciton is generated instead of a free electron and hole. Thus, the light absorption energy (optical gap) is usually lower than the HOMO–LUMO gap energy; the difference corresponds to the exciton binding energy. The HOMO–LUMO gap expresses the energy difference between a free electron and a hole. Thus, we need some correction to estimate the HOMO–LUMO gap from photon absorption experiments of organic materials. Vanossi et al. reported the correction of ΔEEC = 0.53 + 0.99ΔEopt from electrochemical and optical experimental measurements on several organic photocell materials,50 where ΔEopt is the optical bandgap and ΔEEC is the electrochemically determined bandgap property; the latter parameter is more suitable to compare with the theoretical HOMO–LUMO gap. In Table 5, we show the optical gaps measured by Takimiya et al.48 and the corrected experimental values calculated using the Vanossi method.50 Also presented are theoretical calculations using the 6-311G* basis set for the tetrameric materials. It can be easily seen that there are large differences between the optical gap and the theoretical HOMO–LUMO gap resulting from the strong exciton binding energy. Conversely, the Vanossi correction gives values closer to the theoretical calculations. For example, in the NTz case, the optical band gap was found to be 1.56 eV. The corrected experimental gap was 2.07 eV. The dielectric-dependent exchange potential of eqn (1.1) gave a HOMO–LUMO gap of 2.04 eV. The B3LYP method produced a similar calculation result of 1.84 eV, although it slightly underestimated the experimental value. Conversely, the larger HF exchange ratio employed in the HandH method meant that the HOMO–LUMO gap was overestimated to be 3.33 eV. The SVWN method yielded a HOMO–LUMO gap of 0.94 eV; this method largely underestimated the experimental values because of the lack of the HF exchange term. Thus, the DFT methods gave different values according to the HF exchange ratio combined with the DFT functional. The B3LYP method, in which a suitable HF exchange ratio was used for the TPD, BTz, and NTz materials, resulted in better predictions for the HOMO–LUMO gap. The self-consistent dielectric-dependent approach can automatically determine a suitable HF exchange ratio according to the target system. Thus, we have shown that the dielectric-dependent exchange approach can produce good agreement between theoretical and experimental results. On the other hand, it has also been demonstrated that the physical concept of the dielectric-dependent approach, where the HF exchange ratio becomes the inverse value of the dielectric constant, may be helpful in selecting an appropriate DFT functional to investigate organic photocell materials.
Table 5 Comparisons between experimental and theoretical gap energies [eV] for organic photocell materials
| |
TPD |
BTz |
NTz |
|
Optical gaps.48
The values were obtained using the Vanossi method to correct for the exciton binding energy.50
|
| ΔEopta |
1.76 |
1.65 |
1.56 |
| ΔEECb |
2.27 |
2.16 |
2.07 |
| SVWN |
1.26 |
1.00 |
0.94 |
| B3LYP |
2.13 |
1.92 |
1.84 |
| HandH |
3.63 |
3.46 |
3.33 |
|
Eqn (1.1)
|
2.43 |
2.18 |
2.04 |
|
Eqn (2.1)
|
2.40 |
2.15 |
2.05 |
|
Eqn (3)
|
2.40 |
2.15 |
2.04 |
The dielectric-dependent approach can reproduce experimental gaps well, for the fullerene molecular crystal,29 and for other molecular crystals and semiconductors.21,30 Thus, the validity of the dielectric-dependent approach for various systems has been investigated by several research groups.19,21,24,34 Conversely, it is not a simple matter to consider polymer materials, because of their “dirty” material quality. The experimental absorption energies summarized in Table 5 are for the polymer materials. This means that the data are modified by various effects, such as electrostatic and polarized interactions among polymers, deformations and amorphous structures of polymers, impurities, and so on.51 In simulation studies, it may be difficult to consider all of those. So, this paper focused on the conjugation length, because it is one of the most influential effects for the gap property. Polymer materials usually are composed of a plurality of conjugated parts. Therefore, the relationship between the conjugation size and the band gap property is an important factor to investigate actual polymers. In the NTz case, the monomer unit gave the HOMO–LUMO gap of 2.65 eV in eqn (1.1) with the 6-311G* basis set, and the trimer and tetramer units yielded 2.10 and 2.05 eV, respectively. The experimental value corrected by the Vanossi method was 2.07 eV, as shown in Table 5. For other organic photocell materials, we can observe similar behaviors. These results suggest that the trimer and tetramer units can be used to discuss more complex effects on the gap property. On the other hand, Rafaely-Abramson et al. discussed the gap renormalization of molecular crystals based on the DFT approach,20 and Neaton et al. studied the renormalization at metal-molecular interfaces based on the GW method.52 These theoretical considerations may be useful for organic photocells.
Here, we discuss the HOMO–LUMO gap and the fundamental gap.47,50 The simple evaluations of ionization energy (electron affinity) from the HOMO (LUMO) energy may lead to some errors due to orbital relaxations, electron correlations, and the derivative discontinuity.53–55 Thus, the HOMO–LUMO gap tends to underestimate the fundamental gap properties, especially in small molecular systems. The DFT-based many body perturbation theory (MBPT) may be used to correct such errors in the molecular orbital energies.56 Conversely, in the infinite limit under the periodic boundary condition, the energy difference between quasiparticles is frequently employed to estimate the fundamental gap.36 This means that the evaluation based on quasiparticle energies can give fairly acceptable results for the gap property, when molecular systems become larger and orbitals more delocalized.57 Thus, the HOMO–LUMO gap is suitable to evaluate the fundamental gap of organic photocell materials with large conjugated systems.
The fundamental gap can be estimated from the total energy difference of neutral and ionized molecules in the ΔSCF scheme. In other words, the ΔSCF approach is based on the total energy expression. Conversely, this paper focused on the quasiparticle description, because it is essential to understand the energy conversion mechanism of the organic photocell device. It should be noted that the HOMO–LUMO gap gives a good estimation for the fundamental gap in large conjugated systems. Therefore, the quasiparticle description is often employed to analyze organic photocell materials.48,58 The dielectric-dependent screened exchange potentials were originally developed to improve the quasiparticle description, and therefore this paper paid more attention to it. In addition, the description is required to develop more realistic theoretical models for organic photocells.8,9 Accurate quasiparticles can give a better starting point for advanced methods such as the MBPT calculation. The dielectric-dependent quasiparticle description will be useful to investigate organic photocell materials further.
IV. Summary
This paper focused on the fundamental behaviors of the dielectric-dependent screened exchange potential when applied to conjugated molecular systems. In particular, the HOMO–LUMO gap of the donor material of an organic photocell device was investigated, because this gap is an essential factor in the development of organic photosolar devices. When conjugation systems are extended, the HOMO–LUMO gaps decrease, but the dielectric constants increase because of the inverse relationship between these properties. In the dielectric-dependent exchange potential approach, the ratio of the exact HF exchange term combined with the potentials is determined by the inverse of the dielectric constant. Therefore, when the conjugation (unit) lengths are extended, the HF exchange ratio decreases in the dielectric-dependent approach. The molecules and materials examined in this paper take different dielectric constant values in accordance with the material types and unit lengths; thus, the HF exchange ratios are also different among the dielectric-dependent exchange potentials. We also compared our calculated results with experimental measurements. The theoretical HOMO–LUMO gap usually overestimates experimental optical gaps as a result of the strong binding energy between an electron and a hole (exciton) in organic materials; however, if we correct for the exciton binding energy, we can observe better agreement between experimental and calculated values. To develop organic photocell materials, information regarding the gap property is essential. The dielectric-dependent exchange potential approach will be useful to investigate organic photocell materials. Additional studies in this area are ongoing in our laboratory.
Acknowledgements
This work was partially supported by the FOCUS Establishing Supercomputing Center of Excellence and the JSPS KAKENHI, Grant Number 15K05403.
References
- J. L. Bredas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5003 CrossRef CAS PubMed.
- T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767 CrossRef CAS PubMed.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 335, 1340–1344 CrossRef CAS PubMed.
- G. Grancini, M. Binda, L. Criante, S. Perissinotto, M. Maiuri, D. Fazzi, A. Petrozza, H. J. Egelhaaf, D. Brida, G. Cerullo and G. Lanzani, Nat. Mater., 2013, 12, 594–595 CrossRef CAS PubMed.
- G. Grancini, M. Maiuri, D. Fazzi, A. Petrozza, H. J. Egelhaaf, D. Brida, G. Cerullo and G. Lanzani, Nat. Mater., 2013, 12, 29–33 CrossRef CAS PubMed.
- A. E. Jailaubekov, A. P. Willard, J. R. Tritsch, W. L. Chan, N. Sai, R. Gearba, L. G. Kaake, K. J. Williams, K. Leung, P. J. Rossky and X. Y. Zhu, Nat. Mater., 2013, 12, 66–73 CrossRef CAS PubMed.
- P. Peumans and S. R. Forrest, Chem. Phys. Lett., 2004, 398, 27–31 CrossRef CAS.
- T. Shimazaki and T. Nakajima, Phys. Chem. Chem. Phys., 2015, 17, 12538–12544 RSC.
- T. Shimazaki and T. Nakajima, J. Chem. Phys., 2016, 144, 234906 CrossRef PubMed.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
-
S. Louie and A. Rubio, in Handbook of Materials Modeling, ed. S. Yip, Springer Netherlands, 2005, pp. 215–240 Search PubMed.
- M. A. L. Marques, J. Vidal, M. J. T. Oliveira, L. Reining and S. Botti, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 035119 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- T. Shimazaki and Y. Asai, Chem. Phys. Lett., 2008, 466, 91 CrossRef CAS.
- T. Shimazaki and Y. Asa, J. Chem. Phys., 2010, 132, 224105 CrossRef PubMed.
- A. Alkauskas, P. Broqvist, F. Devynck and A. Pasquarello, Phys. Rev. Lett., 2008, 101, 106802 CrossRef PubMed.
- A. Alkauskas, P. Broqvist and A. Pasquarello, Phys. Status Solidi B, 2011, 248, 775–789 CrossRef CAS.
- Z. H. Wang, M. W. Zhao, X. P. Wang, Y. Xi, X. J. He, X. D. Liu and S. S. Yan, Phys. Chem. Chem. Phys., 2012, 14, 15693–15698 RSC.
- D. Koller, P. Blaha and F. Tran, J. Phys.: Condens. Matter, 2013, 25, 435503 CrossRef PubMed.
- S. Refaely-Abramson, S. Sharifzadeh, M. Jain, R. Baer, J. B. Neaton and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 081204(R) CrossRef.
- J. H. Skone, M. Govoni and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195112 CrossRef.
- J. M. Mobeck, I. Narkeviciute, T. Jaramillo and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155204 CrossRef.
- M. Gerosa, C. E. Bottani, L. Caramella, G. Onida, C. Di Valentin and G. Pacchioni, J. Chem. Phys., 2015, 143, 134702 CrossRef PubMed.
- M. Gerosa, C. E. Bottani, L. Caramella, G. Onida, C. Di Valentin and G. Pacchioni, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155201 CrossRef.
- M. Gerosa, C. Di Valentin, C. E. Bottani, G. Onida and G. Pacchioni, J. Chem. Phys., 2015, 143, 111103 CrossRef PubMed.
- A. M. Ferrari, R. Orlando and M. Rerat, J. Chem. Theory Comput., 2015, 11, 3245–3258 CrossRef CAS PubMed.
- A. P. Gaiduk, M. Govoni, R. Seidel, J. H. Skone, B. Winter and G. Galli, J. Am. Chem. Soc., 2016, 138, 6912–6915 CrossRef CAS PubMed.
- H. Seo, M. Govoni and G. Galli, Sci. Rep., 2016, 6, 20803 CrossRef CAS PubMed.
- J. H. Skone, M. Govoni and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 235106 CrossRef.
- T. Shimazaki and T. Nakajima, Chem. Phys. Lett., 2015, 634, 83–87 CrossRef CAS.
- T. Shimazaki and T. Nakajima, Chem. Phys. Lett., 2016, 647, 132–138 CrossRef CAS.
- L. Hedin, Phys. Rev., 1965, 139, A796 CrossRef.
- F. Bechstedt, R. Delsole, G. Cappellini and L. Reining, Solid State Commun., 1992, 84, 765–770 CrossRef CAS.
- T. Shimazaki and T. Nakajima, J. Chem. Phys., 2014, 141, 114109 CrossRef PubMed.
- T. Shimazaki and Y. Asai, J. Chem. Theory Comput., 2009, 5, 136 CrossRef CAS PubMed.
-
G. Grosso and G. P. Parravicini, Solid State Physics, Academic Press, Orlando, 2000 Search PubMed.
- J. E. Robinson, R. S. Knox, F. Bassani and J. R. Schrieffer, Phys. Rev. Lett., 1962, 9, 215 CrossRef.
- F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235118 CrossRef.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- T. Shimazaki and Y. Asai, J. Chem. Phys., 2009, 130, 164702 CrossRef PubMed.
- T. Shimazaki and T. Nakajima, J. Chem. Phys., 2015, 142, 074109 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
-
T. Shimazaki, M. Hashimoto and T. Maeda, Proceedings of the 3rd International Workshop on Software Engineering for High Performance Computing in Computational Science and Engineering, 2015, 9, DOI: 10.1145/2830168.2830170.
- T. Rangel, K. Berland, S. Sharifzadeh, F. Brown-Altvater, K. Lee, P. Hyldgaard, L. Kronik and J. B. Neaton, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 115206 CrossRef.
- T. Stein, H. Eisenberg, L. Kronik and R. Baer, Phys. Rev. Lett., 2010, 105, 266802 CrossRef PubMed.
- K. Takimiya, I. Osaka and M. Nakano, Chem. Mater., 2014, 26, 587–593 CrossRef CAS.
- T. Matsui, Y. Imamura, I. Osaka, K. Takimiya and T. Nakajima, J. Phys. Chem. C, 2016, 120, 8305–8314 CAS.
- D. Vanossi, L. Cigarini, A. Giaccherini, E. da Como and C. Fontanesi, Molecules, 2016, 21, 110 CrossRef PubMed.
- C. Poelking, M. Tietze, C. Elschner, S. Olthof, D. Hertel, B. Baumeier, F. Wurthner, K. Meerholz, K. Leo and D. Andrienko, Nat. Mater., 2015, 14, 434–439 CrossRef CAS PubMed.
- J. B. Neaton, M. S. Hybertsen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216405 CrossRef CAS PubMed.
-
A. Szabo and N. S. Ostlund, Modern Quantum Chemistry, McGraw-Hill, Inc., Tronto, Canada, 1989 Search PubMed.
- J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884–1887 CrossRef CAS.
- L. J. Sham and M. Schluter, Phys. Rev. Lett., 1983, 51, 1888–1891 CrossRef.
- P. Rinke, A. Qteish, J. Neugebauer, C. Freysoldt and M. Scheffler, New J. Phys., 2005, 7, 126 CrossRef.
-
C. A. Ullrich, Time-Dependent Density-Functional Theory: Concepts and Applications, Oxford University Press, Oxford, UK, 2011 Search PubMed.
- Y. F. Li, Acc. Chem. Res., 2012, 45, 723–733 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article



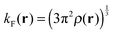 . r12 is the distance between two electrons. This paper employs the simple potential description. The precise one is found in the literature.34,35Eqn (1.3) is used to correct the behavior of the dielectric function in the large q region.33,34,36 The first term gives the local COH interaction, and the second and third terms express the nonlocal SEX contributions. The third term may be the most important, because it represents the partial fragment of the HF exchange interaction in the potential. In the dielectric-dependent screened exchange potential, the HF exchange ratio is proportional to the inverse of the dielectric constant. In semiconductors and insulators, the screening effect is not complete, and therefore the bare interaction of 1/r appears in the third term of eqn (1.1), but the interaction is modified by the inverse of the dielectric constant.14 In the limit of εs = 1, the potential of eqn (1.1) reduces to the ordinary HF exchange interaction. In a metallic system in which εs → ∞, the SEX part of the dielectric-dependent exchange potential reduces to a Thomas–Fermi-like screening interaction.36 On the other hand, the nonlocal behavior of the second term, which is described by the Yukawa-type potential, is not strong because of the large
. r12 is the distance between two electrons. This paper employs the simple potential description. The precise one is found in the literature.34,35Eqn (1.3) is used to correct the behavior of the dielectric function in the large q region.33,34,36 The first term gives the local COH interaction, and the second and third terms express the nonlocal SEX contributions. The third term may be the most important, because it represents the partial fragment of the HF exchange interaction in the potential. In the dielectric-dependent screened exchange potential, the HF exchange ratio is proportional to the inverse of the dielectric constant. In semiconductors and insulators, the screening effect is not complete, and therefore the bare interaction of 1/r appears in the third term of eqn (1.1), but the interaction is modified by the inverse of the dielectric constant.14 In the limit of εs = 1, the potential of eqn (1.1) reduces to the ordinary HF exchange interaction. In a metallic system in which εs → ∞, the SEX part of the dielectric-dependent exchange potential reduces to a Thomas–Fermi-like screening interaction.36 On the other hand, the nonlocal behavior of the second term, which is described by the Yukawa-type potential, is not strong because of the large ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) TF values for molecules. Thus, we can approximate the weak nonlocal term by the local potential based on the dielectric-dependent Slater term as follows:34,37
TF values for molecules. Thus, we can approximate the weak nonlocal term by the local potential based on the dielectric-dependent Slater term as follows:34,37









