Micro-heterogeneity versus clustering in binary mixtures of ethanol with water or alkanes

Abstract

Ethanol is a hydrogen bonding liquid. When mixed in small concentrations with water or alkanes, it forms aggregate structures reminiscent of, respectively, the direct and inverse micellar aggregates found in emulsions, albeit at much smaller sizes. At higher concentrations, micro-heterogeneous mixing with segregated domains is found. We examine how different statistical methods, namely correlation function analysis, structure factor analysis and cluster distribution analysis, can describe efficiently these morphological changes in these mixtures. In particular, we explain how the neat alcohol pre-peak of the structure factor evolves into the domain pre-peak under mixing conditions, and how this evolution differs whether the co-solvent is water or alkane. This study clearly establishes the heuristic superiority of the correlation function/structure factor analysis to study the micro-heterogeneity, since cluster distribution analysis is insensitive to domain segregation. Correlation functions detect the domains, with a clear structure factor pre-peak signature, while the cluster techniques detect the cluster hierarchy within domains. The main conclusion is that, in micro-segregated mixtures, the domain structure is a more fundamental statistical entity than the underlying cluster structures. These findings could help better understand comparatively the radiation scattering experiments, which are sensitive to domains, versus the spectroscopy-NMR experiments, which are sensitive to clusters.

---

Motivation

This work illustrates, perhaps for the first time, the profound difference between clustering and micro-segregation in complex liquids, despite the fact that clustering is at the origin of micro-segregation. This difference allows us to attribute a heuristic importance to some physical observables (structure factors) with respect to others (cluster distribution). Although our work is theoretical, our findings should impact the experimental ones, related to each of these observable-radiation scattering versus spectroscopy and NMR, as well as favour a deeper understanding of molecular association in soft-matter.

1 Introduction

In the statistical analysis of computer simulations, it is important to distinguish between various types of observables.^1,2 Some observables, such as correlation functions, have a deep meaning in statistical physics, since they can be related to many physical properties of the system through various integrals involving them.^3,4 However, correlation functions themselves are not physical observables, although some of them can be extracted through scattering experiments.⁵ Other observables can be introduced, which provide useful insight about the microscopic state of the system. Hydrogen bond and cluster counting⁶ are such examples, which can be recoupled using many experimental techniques, such as various spectroscopy techniques.⁷ Such observables often appear to be more useful than those related to statistical physics, since they provide finer details of the microscopic structure of the system. An important methodological question is whether or not the introduction of such a convenient observable can be compared to the fundamental ones. We illustrate here a case where this question can be answered precisely.

In computer simulations of neat ethanol, the hydroxyl groups are found to form H-bonded chain-like structures,⁸ which span the entire system. When mixed with alkanes, such as hexane for example, or benzene, these hydrogen bonded structures persist, since they are energetically favourable,⁹ and induce the subsequent local segregation of ethanol from the alkane molecules, at any mixing ratios.¹⁰ Consequently, in alkane environments, ethanol clusters are rather well characterised structures. In contrast, when mixed with water, ethanol can also hydrogen bond with water molecules. Since in all the classical force field representation of the interactions, the values of the partial charges of water are larger than those of the ethanol hydroxyl group, water molecules are found to generally prefer to hydrogen bond with themselves, rather than with ethanol.^11–13 This competition tends to destroy the chain-like structure of the ethanol clusters, making these rather fuzzy aggregated structures. In ethanol–alkane mixtures, the hydroxyl groups of ethanol are hidden inside the ethanol clusters,¹⁰ while in water, these groups are rather dispersed. Following these facts, one could compare the micro-segregation of ethanol in benzene with that of surfactant-in-oil type emulsions, while ethanol in water would have analogies with surfactant-in-water type emulsions.

How does these visually appealing findings translate into observables in physical-chemistry? With the help of computer simulations, we compute structural statistical quantities, such as the pair distribution functions between different atoms, as well as cluster distributions. These calculations help provide a more clear answer to the question of the nature of the cluster structure of a hydrogen bonding molecule in various types of solvents. Indeed, the structure of ethanol in alkanes is more on the cluster side of the description, while in water, these look more like concentration fluctuations. Since the words “cluster” and “concentration fluctuation” mean very different measurable physical characteristics, our analysis should help understand the relationship between microscopic molecular association and different macroscopic observables which are related to the local distribution of the molecules.

The principal argument of this paper is to show that micro-segregated domains are not reducible to the clusters of which they are made. We reach this conclusion by analyzing the differences between structure factor pre-peaks and direct cluster analysis. The latter analysis cannot provide the difference between concentration fluctuations and segregated domain structures that shows up as a pre-peak in atom–atom structure factors. As shown in our previous studies,^10,14,15 this difference is essential to understand clustering in complex mixtures. In particular, concentration fluctuations are thermodynamic observables through the Kirkwood–Buff integrals,^10,16–18 while the pre-peak in the atom–atom structure factor is a proof of micro-segregated domains.^10,14,15 Interestingly, both types of analyses are more in agreement between them when segregated domains are single clusters, such as the case of low concentration ethanol in alkanes. These differences in the methodology have a heuristic significance, which we discuss in the last section of this paper.

The remainder of this paper is organized as follows. In the next section, we recall important theoretical details, describe our simulation protocol and give details about our cluster analysis methodology. We display our findings in the Results section. Finally, we discuss these findings and present our conclusion in the last part.

2 Theoretical and computational details

Thermodynamic quantities such as energy or density do not really reflect the micro-structure of liquids. For this reason, it is preferable to compute the atom–atom radial distribution function. Such functions are defined as fluctuations of the microscopic density of atoms of type a: where r⃑_i is the position of any atom of type a. Considering this microscopic quantity as a random variable, one can compute usual statistical quantities, such as the mean density of atom a, ρ_a = 〈ρ_a(r⃑_i)〉 where the average is taken over a suitable statistical ensemble. The second moment ρ⁽²⁾_ab(|r⃑ − r⃑′|)〈ρ_a(r⃑)ρ_b(r⃑′)〉 is related to the correlation function through ρ⁽²⁾_ab(r) = ρ_aρ_bg_ab(r). The Kirkwood–Buff theory relates the integrals of the g_ab functions – the so-called Kirkwood–Buff integrals (KBI) – to the composition fluctuations 〈N_aN_b〉 − 〈N_a〉〈N_b〉, where N_a and N_b are the number of atoms of species a and b, respectively. It turns out that these integrals are simply zero wave vector k = 0 values of the corresponding structure factors S_ab(k), which are the Fourier transforms of g_ab(r). In the case of multicomponent molecular systems made of molecules instead of atoms, the integrals of the atom–atom g_ab(r) are also the KBI of this system, because of the invariance of these integrals with respect to any arbitrary center of mass of the molecules.³ This is summarised in the following expression

where

are the KBI, the integrals over the pair distribution functions g_ab(r) between atomic sites a and b belong to two related molecular species,
is the Fourier transform of the correlation functions, and the last term ε_ab is related to the thermodynamics
through the partial derivatives involving the number density ρ_a of species a, the mole fraction x_a and the chemical potential μ_b (β = 1/k_BT is the Boltzmann factor). This expression, however, does not give any indication about the nature of the clustering and domain segregation in the mixtures.

The relationship between concentration fluctuations and micro-heterogeneous clustering is not very clear, and this remains an important currently unsolved problem in the statistical description of liquids. Since the local segregation of one species with respect to the others indicates a heterogeneity in spatial distribution, it can be mistaken for a concentration fluctuation. Conversely, concentration fluctuations which occur during critical demixing are clearly not an arrested clustering of either species. Such phase separation processes are well understood both from theoretical and computational points of view,²⁰ and their approach is signalled by the growth and divergence of all the partial structure factors exactly at k = 0, according to the corresponding diverging growth of concentration fluctuations. Such growth can be unambiguously detected in computer simulations.^20,21 However, this scenario is not what occurs in micro-segregation. In a series of papers,^10,14,15,19 we have argued that micro-heterogeneous clustering is a non-zero wave vector fluctuation of the microscopic density, which arises at a specific k-vector which corresponds to the mean size of the heterogeneity and should be manifested as a pre-peak in specific atom–atom structure factors S_ab(k). This assumption was confirmed by computer simulations on a variety of systems we have studied, both aqueous and non-aqueous. However, the prediction of details of such a micro-heterogeneity pre-peak from microscopic details of the interactions between various types of molecules remains an open field of investigation.¹⁵

2.1 Simulation details

All the calculations have been conducted using the Gromacs 4.5.5 package.²² We have used N = 160 00 particles in order to have a good description of the domain structure. In our previous analysis,^11–13 we used mostly N = 2048 particles, which were sufficient to obtain many thermodynamic properties, but clearly insufficient to determine long range domain oscillations in the correlation functions. The initial configurations were all started using the very convenient PackMol code.²³ The run lengths for statistics are of a few nano-seconds, between 2 and 10, depending on systems, with a time step of 2 fs in all cases. We use ambient conditions of T = 300 K and 1 bar atmospheric pressure. A Nose–Hoover thermostat and a Stillinger–Rahman barostat are used, with a time constant of 0.1 ps. We used the SPC/E²⁴ force field for water, the TraPPe force fields for ethanol,²⁵ and the OPLS force field for alkanes.²⁶

2.2 Cluster analysis details

Cluster analysis depends crucially on the criteria defining how two particles are connected neighbours. Since in a dense liquid, two neighbouring particles can be very close, any criteria describing such a situation can be a robust descriptor. This way, one can describe clustering in a simple Lennard-Jones liquid.^27,28 However, there is a strong difference between such a simple liquid and an associated liquid, as in the case of a hydrogen bonding system, where clustering has an element of reality. We have previously studied clustering in pure alcohol and water.^29,30 We found that the cluster size distribution in neat alcohol shows a specific peak at some particular cluster size (broadly around 5–7 particles), whereas water has a cluster size distribution much like a Lennard-Jones system,^31,32 with the maximum occurring for the monomer.³³ In addition, we found that the specific clusters of the alcohols had a precise shape (chain and loop for methanol, globular clusters for tbutanol).^29,30 In contrast, water has no such characteristic clusters. Here we compute the same property, but in mixtures.

The cluster is defined as the group of particles where each particle has at least one connection with the neighboring particles. The connectivity criteria can be geometrical constraints, or for example the Hills energetic criteria where particles are considered to be connected if their attractive interaction energy is higher than their relative kinetic energy.²⁸ Here we used Stillinger distance criteria³⁴ where the cutoff distance is defined by the first minima of the particle–particle radial distribution function. This way, the interactions between bonded particles are indirectly related to their interactions through the radial distribution function. The cluster size distributions are calculated for the clustering of the like–like sites, using several different statistical approaches. We show the results for the cluster size probability functions:

where s_n is the probability for the cluster formed of n sites, s(k,n) represents the number of clusters of the size n in the configuration k. Varying the contact distance between neighbouring atoms that are part of a cluster distance around the first minima shows a relative robustness in the resulting cluster distributions.^29,30 The cutoff distances (r_c) defined in this work are 3.5 Å between the oxygens of the water molecules, 3.7 Å between the oxygens of the ethanol molecules, 4.5 Å between the methyl groups of the ethanol molecules, and 6 Å between the carbon atoms of the benzene molecules.

3 Results

Ethanol–water mixtures were previously studied using computer simulations in our group.^11–13 There is a major difference in clustering between ethanol and water. Neat ethanol contains specific clusters in the form of chains and loops, much like methanol.^29,30 In contrast, neat water does not produce any specific clusters.^29,30 The principal reason seems to be the distribution of partial charges in each molecule. The ethanol has only one hydroxyl group. Therefore, the hydrogen bonds can form chaining patterns ⋯OH–OH–OH⋯ despite thermal agitation, small chains can be relatively stable, and conserved through the sample. This is what we observe in simulations of many linear alcohols. In contrast, in water, there are two hydroxyl groups disposed in tetrahedral conformation, which allows branched OH chaining, which is more fragile to thermal agitation because of the increased topological constraints to maintain such a network over large distances. As a result, no robust clustering is observed, despite permanent tetrahedral H-bonding. Recent spectroscopic studies³⁵ suggest that linear OH clusters exist, but, in our opinion, these clusters are fragilized by permanent competition with the potential trimer of quadrumer branching. These intuitive arguments find some support in our recent study of the aqueous-DMSO mixtures,³⁶ where we found that water forms linear clusters in the presence of DMSO, and at all concentrations. In contrast, only bulky clusters of water are found in alcohols^29,30 and solvents such as acetone.^31,32

3.1 Snapshot analysis

Snapshots represent only one micro-state of the system, and it would be generally unadvised¹ to make any serious conclusions of the general behaviour of any system, based on such a single micro-state. However, in the case of micro-heterogeneous mixtures, with at least one associating species, much can be learned from a single micro-state. In fact, this single micro-state is a very good representation of all possible micro-states, since they appear to be simple permutations of the segregation patterns. This is an interesting peculiarity of micro-heterogeneous systems, pertaining to a local “symmetry” property, which deserves further scrutiny.

Fig. 1 summarizes the findings that we want to report here, namely the morphology of the aqueous-ethanol (upper figures) and alkane–ethanol mixtures (lower figures), each for 3 concentration of ethanol, namely x_Eth = 0.2 (left column), 0.5 (middle column) and 0.8 (right column). Let us first focus on the upper figures, concerning aqueous-ethanol mixtures. The left-most figure shows the loose domain structure of ethanol molecules in water (shown as semi-transparent dark blue molecules). The oxygen (red) and hydrogen (white) atoms of ethanol are put into evidence, as to better visualise the chain-like clusters. The methyl united atoms are shown as semi-transparent groups. We notice that there are many non-bonded ethanol hydroxyl groups. These groups are in fact bonded to the surrounding water molecules. As a result, despite segregation, the ethanol domains are rather fuzzy. The central figure shows the water molecules, with the ethanol molecules in semi-transparent representation, for x_Eth = 0.5 and the picture in the right shows a similar representation for x_Eth = 0.8. We can see that in both pictures, water is segregated in domains, which are also loose, although the hydrogen bonding between the hydroxyl groups is quite apparent. The general picture that emerges from these 3 snapshots is that both water and ethanol form fuzzy micro-segregated domains. The fuzziness comes from the incomplete self-hydrogen bonding of each species with its own kind. From this observation, we expect that the cluster distributions will not show any peak at some particular cluster size.

Fig. 1 Selected snapshots of aqueous-ethanol (top figures) and alkane–ethanol (lower figures) mixtures. Figures on right correspond to 20% ethanol, in the middle for 50% ethanol and on the right for 80% ethanol. See the text for details of color conventions for different molecules.

In the lower set of figures we have shown comparative clustering in 3 different alkanes. The lower left figure shows 20% ethanol in hexane, with the hexane molecules in semi-transparent representation, and the ethanol molecules shown with the same convention as in the figure just above. It is seen that the ethanol molecules are segregated from hexane. In addition, we can clearly see that the hydroxyl groups within each domain are bound in chains and loops. In fact, almost all hydroxyl groups are bound into such a shape, as will be confirmed below in cluster analysis. The middle picture shows 50% ethanol in benzene, with a representation of the molecules analogous to the previous snapshot. Once again, we see clearly the segregation in species domains, as well as chain/loop clusters of the hydroxyl groups inside the ethanol domains. The lower right picture shows 80% ethanol in pentane, and this time the ethanol molecules are shown entirely. We again observe a domain segregation by species, and geometric clusters of the hydroxyl groups. In fact, ethanol in the latter system is clustered more or less like in pure ethanol, which is not surprising, and this will be confirmed by the cluster analysis in the next section.

The study of the snapshots shows a profound difference in domain segregation between the aqueous and the alkane mixtures with ethanol, with fuzzy domains in the first and the ethanol domain underlying the precise geometrical hydroxyl cluster in the second. These differences obviously come from the fact that water offers hydrogen possibilities to the ethanol hydroxyl groups, contrary to alkanes.

3.2 Correlation function analysis

Fig. 2 shows the correlation function between the oxygen sites of ethanol, for 3 different concentrations of ethanol, while the inset shows the correlations between the oxygen sites of water. The pure liquid correlations are also shown in black. In all cases we observe the strong first peak, which witnesses the underlying hydrogen bonding between hydroxyl groups, which is at the heart of micro-segregation. However, micro-segregation is seen in the long range correlation between segregated domains, and not in the short range correlations. In all cases, correlation between the oxygens of water is more important than that between the oxygen of ethanol. We equally observe a feature we have pointed out in other aqueous mixtures:^13,31,37,38 water OO correlations tend to increase at contact with decreasing water concentrations, while solute (here ethanol) correlations at contact tend to decrease with decreasing solute concentrations. This can be seen clearly through the identical trends of the first peaks with the same color codes, while they correspond to different concentrations in terms of the concerned species (except of course for pure components shown in black). This remarkable feature is not however specific to water, and is equally seen for any associating molecule mixed with a less associating one. It indicates that the less associating species bonds less and less with itself with the increase of concentration of the more associating species, while the more associating species bond more and more with itself when its concentration decreases.

Fig. 2 Oxygen–oxygen correlation function in ethanol–water mixtures. Main panel for ethanol, the inset for water. Blue curves for 20% ethanol, green for 50% ethanol and red for 80% ethanol. The pure component is shown in black. These color conventions are preserved in all subsequent figures.

Fig. 3 show correlations between the oxygen sites of ethanol, but in alkanes. The main panel, which shows ethanol oxygen correlations, confirms the feature discussed above. Since ethanol is now the associating species, the first peak increases with decreasing ethanol content. The various alkane correlations – shown in the inset – show the opposite trend, although these correlations concern very different alkanes. These findings, common to Fig. 2 and 3 prove a universal feature in mixtures of associating liquids. We also observe in the main panel the very strong first peak, much stronger than anything in Fig. 2. It indicates the stronger hydrogen bonding of the hydroxyl groups of ethanol when in an alkane environment. This is the inverse micelle effect that we have mentioned in the Introduction, supporting the energetically favoured association of the hydroxyl sites.

Fig. 3 Site–site correlations in ethanol–alkane mixtures. Main panel: ethanol oxygen–oxygen correlation function. Inset: Methyl–methyl correlation (blue for pentane, green for benzene and red for hexane). Color convention according to ethanol mole fraction as in Fig. 2.

The contrast of short range association between hydroxyl groups of ethanol in water and ethanol in alkanes will be reconfirmed below in the cluster distribution study. However, the micro-segregated domains affect the medium and long range correlations, and this is better analysed by looking at the structure factors.

3.3 Structure factor analysis

Fig. 4 shows the structure factors for the correlations shown in Fig. 2, with the same color conventions. In addition, the oxygen–oxygen structure factors of the pure components are shown in black. As noted before,³⁹ pure water has a main peak about k ≈ 2 Å⁻¹, corresponding to the water diameter σ_W ≈ 3 Å, and a shoulder-peak at k ≈ 3 Å⁻¹ corresponding to the hydrogen bonding distance r_HB ≈ 2 Å. Pure ethanol has only one main peak at around k ≈ 2.8 Å⁻¹, which corresponds more to a hydrogen bonding distance r ≈ 2 Å, as well as a pre-peak at around k ≈ 0.8 Å⁻¹, which corresponds to the chain and ring clusters,¹³ similar to those observed in the snapshots in the previous Section 3.1. In other words, in contrast to water, ethanol is entirely structured by the hydrogen bonding, since both peaks are related to this interaction. So, these two hydrogen bonding associating liquids have a very different micro-structure, a fact that we recognized in earlier studies^29,30 to be equally shared by other alcohols such as methanol and tbutanol.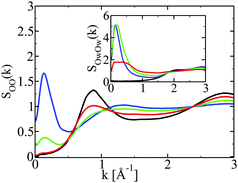

Fig. 4 Structure factors for the correlation functions shown in Fig. 2, with the same conventions. Structure factors of neat liquids shown in black. Main panel: ethanol; inset: water.

Under mixing conditions, by monitoring the behaviour of these peaks, we can account for changes in the micro-structure, with respect to the pure fluid state. The structure factors in Fig. 4 show remarkable microscopic changes.

Let us focus first on the water structure in the inset. As ethanol is added, the main peak at k ≈ 2 Å⁻¹ changes little until ethanol mole fraction 80% (red) where it nearly disappears. The Hbond peak at k ≈ 3 Å⁻¹ diminishes more clearly. From these facts, we can conclude that water is less and less hydrogen bonded when ethanol concentration increases. Fig. 4 shows another remarkable feature: an intense pre-peak growing at k ≈ 0.4–0.2 Å⁻¹, which corresponds to water domain sizes of d ≈ 12–30 Å. These numbers match roughly the domains seen in the upper snapshots shown in Fig. 2. These pre-peaks witness water–solute domain segregation under mixing. In order to see this clearly, it is necessary to use N = 16 000 particles instead of N = 2048 as we did previously.^11,13 A remarkable feature is that these pre-peaks are maximal at lower ethanol concentrations (20% and 50%) – witnessing the large water segregated domains that we observe in the snapshots, but diminish as this concentration increases (80%) as the water domains become smaller. Gathering all the peak information, we see that the small water segregated domains (at large ethanol concentrations) have less hydrogen bonded water molecules than in pure water. This picture confirms the fuzzy water cluster picture that we have found from snapshot analysis.

Turning now to the ethanol structure factor in the main panel, we see that the Hbond peak at k ≈ 2.8 Å⁻¹ diminishes very strongly with an increase of the water content, while the cluster pre-peak at k ≈ 0.8 Å⁻¹ diminishes and shifts to higher k-values. The overall picture is that of less hydrogen bonded ethanol molecules at lower concentrations, with an apparent diminution of cluster sizes. Much like water, ethanol also develops a domain pre-peak at around k ≈ 0.1 − 0.2 Å⁻¹, which corresponds to the segregated domains complementary to those of water. These domains are seen to grow, as the population of the cluster peak diminishes. This implies that smaller Hbonded clusters populate the large ethanol segregated domains, suggesting a fuzzyness of these domains. But it is also an indication that there is more to ethanol domain segregation than just ethanol self hydrogen bonding. Indeed, since ethanol molecules are less Hbonded at low concentrations, and yet they are gathered into a growing pre-peak, it means that these ethanol molecules are grouped through their interaction with water, and not by their own self Hbonding. This is a direct manifestation of the so-called hydrophobic effect,^40,41 of which we see here an interesting microscopic insight, through the hydroxyl groups of the solute, while this is usually described in terms of the hydrophobic groups of the solutes.⁴¹

Fig. 5 shows the oxygen–oxygen structure factors of ethanol in alkanes, as well as the carbon–carbon structure factors of the alkanes in the inset. Again, the pure ethanol structure factor is shown in black. We note that the ethanol Hbond peak at k ≈ 2.8 Å⁻¹ is not affected by mixing with alkanes, contrarily to what happened with water. It is a direct indication of the robustness of ethanol Hbonded clusters – as opposed to their fuzziness in water. Now, however, with the increase of the alkane concentration, we see a phenomenon different than in water. We see that it is the hydroxyl group cluster pre-peak, at k ≈ 0.8 Å⁻¹, that moves, with the addition of alkanes, into a domain pre-peak at smaller k-values k ≈ 0.1 − 0.15 Å⁻¹. This is a remarkable result, since it confirms the visual information that we gathered through the snapshots in Fig. 1: the ethanol domains are essentially made of hydroxyl group clusters, larger than those found in pure ethanol. We note that the alkane structure factors in the inset have a main peak at around k ≈ 1.4 Å⁻¹, which corresponds to the diameter of the carbon atoms in various force field models σ_C ≈ 4 Å. Despite large differences in the various alkane molecules, the structure factors look nearly the same around this value of k. We note that the increase of the domain segregation leads to an increase of these structure factors but only at k = 0. In other words, these liquids witness concentration fluctuations instead of segregated domains, unlike the ethanol molecules. This asymmetry of the solvent behaviour between water and alkanes under the same ethanol insertion is remarkable. It confirms the picture of simple and complex disorder which we previously introduced.^10,14

Fig. 5 Structure factors for the correlation functions shown in Fig. 3, with same conventions.

3.4 Cluster distributions

We turn now towards the cluster distribution. Perhaps the most important challenge in this study is to see if it can confirm the micro-heterogeneous structure of mixtures involving associating molecules.

Fig. 6 shows the cluster distribution of water oxygen atoms in aqueous-ethanol, for different concentrations of ethanol. Since these aqueous mixtures are micro-segregated, we expect to see this in the cluster distribution. We note that these curves present no specific peak i.e. the probability distribution of a cluster of smaller size is always greater than that of a larger size, which is a trivially expected behaviour for simply disordered liquids. Indeed, the first inset shows the cluster probability in a Lennard-Jones type mixture, which is strikingly similar to that of water in water–ethanol. The latter mixture is in fact a one-liquid carbon–tetrachloride (we have used the OPLS model⁴²), which is artificially treated as a mixture by the simple labelling of molecules. We considered the central carbon atom for the computer cluster distribution of this system. The second inset shows the probability distribution of clusters of the pentane carbon atom in ethanol–pentane mixtures, for different ethanol concentrations, which are again trivial cluster distributions. All these curves in Fig. 6 show an additional common property: for a given size, the cluster probability at lower concentrations is always larger than that at larger concentrations. This property is also a trivial effect of random mixing at different concentrations. From these curves in Fig. 6, we learn that there are almost no differences in these various distributions, which is very counter-intuitive, particularly after having noticed the strong micro-segregation in aqueous-ethanol mixtures in previous sections.

Fig. 6 Cluster distribution functions. Main panel, for water oxygen atoms in aqueous ethanol mixtures (color conventions according to the ethanol mole fraction as in Fig. 2). Top inset: Cluster distributions in a binary Lennard-Jones type mixture (see the text). Lower inset: Cluster distribution for the pentane central carbon atom in ethanol–pentane mixtures.

Fig. 7 shows a comparison of the cluster distribution of ethanol oxygen atoms in pentane (main panel) and water (inset), for different concentrations of ethanol, including pure ethanol (shown in black). We note that the pure ethanol cluster peak (around 6–7 oxygen atoms) in pentene increases with decreasing ethanol concentrations, which confirms the clustering trend observed through the pre-peak analysis of the structure factors in Fig. 5. The inset, however, shows only the trivial clustering, as seen in Fig. 6, despite the micro-segregation present in aqueous-ethanol. From the difference in clustering of ethanol, which we have observed in the previous sections, we see that the cluster distribution is only able to detect clusters that are not fuzzy. By extension, we could say that cluster analysis is more performing for the surfactant in oil, rather than the surfactant in water.

Fig. 7 Cluster distribution functions. Main panel, for ethanol oxygen atoms in ethanol–pentane mixtures. Inset, for ethanol oxygens in aqueous mixtures (color conventions according to the ethanol mole fraction as in Fig. 2).

Fig. 8 shows a comparison of the clustering of the methyl group in ethanol–pentane mixtures, and aqueous-ethanol (inset). Since these methyl groups are randomized in pure ethanol, we do not expect to see any specific-peak, which is indeed confirmed for pure ethanol. However, since there is strong clustering of ethanol at small concentrations in benzene, we expect to see some signs of specific clustering, which are absent in these plots: they look very similar for ethanol in benzene and in water, despite obvious differences.

Fig. 8 Cluster distribution functions for the ethanol methyl group. Main panel, for ethanol–pentane mixtures. Inset, for aqueous-ethanol mixtures (color conventions according to the ethanol mole fraction as in Fig. 2).

The obvious, and almost counter-intuitive conclusion of this section is that direct cluster calculation is not generally able to detect the micro-heterogeneous distribution of molecules. To be more precise, it detects all clusters, but there seems to be more to micro-segregation than just clustering. This is why only the correlation function analysis, and particularly the structure factor analysis, can account for micro-segregation properly. The fact that the latter observables have a sound theoretical and statistical basis is certainly in favour of these methods, as opposed to cluster detection, which is empirical and cannot be related to any quantity in statistical physics of the disordered liquids.

4 Discussion and conclusion

The principal idea behind the simple and complex disorder in liquids is the fact that all liquids, being disordered systems, are characterised by the same order parameter, namely the number density,⁴ but the description of complexity requires a new type of order parameter. Indeed, the H-bond interaction is not a Landau type order parameter since it is related to a pair interaction. Landau type order parameters are, by definition,⁴ related to external fields and corresponding 1-body functions. In that sense, it is not possible to describe the local order produced by the H-bond induced clustering through a classical Landau-type order parameter description. On the other hand, it is clear that a proper statistical description of the local order produced by the H-bonding interaction is required, if one wishes to describe complexity emerging from the hydrophobic interaction, for example. One way around this problem is to consider that specific fluctuations related to H-bonding can be conveniently averaged into the concentration fluctuations. This is the route taken by the KBI formalism,^16–18 and also field theoretical variants.^40,41 These routes can explain only the part that concentration fluctuations contribute to the complex local order produced by H-bonding. In particular, such approaches ignore the presence of a non-zero pre-peak in the structure factor. As shown here and in our previous studies,^10,14,37 this pre-peak witnesses the specificity of the clustering over concentration fluctuations.

The present study reveals a non-intuitive finding since direct cluster analysis is not able to reveal micro-segregation. This is very surprising since micro-segregation can be interpreted as a form of clustering. The only possible explanation is that cluster analysis can only detect the clusters within the domains, but cannot detect the domains themselves, when these are made of groups of disjoint clusters. This is the case of the fuzzy domains in ethanol-water, but not the case of ethanol in benzene, where the base of the domain is made of underlying ethanol OH group clusters. Both scenarios were confirmed through the analysis of snapshots and structure factors. This explanation shows that the cluster study of mixtures with a fuzzy domain structure is deceitful since it predicts distributions indistinguishable from those found in a Lennard-Jones mixture. Although this result is correct, it does not give any information on the micro-segregation of these systems.

This difference in information about the morphology of complex mixtures, as given by structure factors and cluster distribution, has a direct impact on the corresponding experiments, which are radiation scattering methods – which detect domain pre-peaks, and NMR, infrared and mass spectrometry – which detect clusters. Our study shows that these two different sets of techniques may not detect the same type of aggregation of molecules. This important point deserves further scrutiny.

The asymmetry of the prediction of the cluster structure in aqueous mixtures and alkane–alcohol mixtures can be connected to the direct and inverse micelle structure, when extrapolated to the binary emulsions, such as water–surfactant and oil–surfactant. Inverse micelles in an oil–surfactant system consist of a dense core of hydroxyl groups, which are bound by energetic restraints. In a way, such micelles are energetically simple to obtain, and do not require any intervention of the surrounding oily solvent. On the other hand, direct micelles do require the solvent (water) to cooperate in order to shy away the oily parts of the surfactant inside a micellar core. Such micelles require more coordination at the molecular level than the formers. In view of this, it is not surprising that ethanol clustering in alkanes gives a specific clustering in alkanes, as opposed to ethanol in water.

From a heuristic point of view, the fact that the correlation function formalism of liquid state theory has a sounder statistical and theoretical basis than the direct cluster distribution analysis supports the findings of the present work. It confirms that micro-segregation in complex liquid mixtures should be investigated through statistical physics of liquids.

Acknowledgements

This work has been partially supported by the Croatian Science Foundation under the project 4514 “Multi-scale description of meso-scale domain formation and destruction”. M. Požar thanks the French Embassy in Croatia for financial support through “bourse du Gouvernement Français”.

References

1. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford, 1987.
2. K. Binder and D. W. Heermann, Monte Carlo Simulation in Statistical Physics: An Introduction, Springer, Berlin, Heidelberg, 1986.
3. J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic, London, 1986.
4. P. M. Chaikin and T. C. Lubensky, Principles of condensed matter physics, Cambridge University Press, 1995.
5. H. E. Fisher, A. C. Barnes and P. S. Salmon, Neutron and X-ray diffraction studies of liquids and glasses, Rep. Prog. Phys., 2006, 69, 233–299.
6. D. C. Rappaport, Hydrogen bonds in Water, Mol. Phys., 1983, 50(5), 1151.
7. J.-H. Guo, et al. Molecular Structure in Alcohol–Water Mixtures, Phys. Rev. Lett., 2003, 91(15), 157401.
8. C. J. Benmore and Y. L. Loh, The structure of liquid ethanol: A neutron diffraction and molecular dynamics study, J. Chem. Phys., 2000, 112, 5877.
9. K. M. Murdoch, T. D. Ferris, J. C. Wright and T. C. Farrar, Infrared Spectroscopy of ethanol clusters in ethanol–hexane binary solutions, J. Chem. Phys., 2002, 116, 5717.
10. M. Požar, et al. Simple and complex disorder in binary mixtures with benzene as common solvent, Phys. Chem. Chem. Phys., 2015, 17, 9885.
11. M. Mijaković, et al. Ethanol–water mixtures: ultrasonics, Brillouin scattering and molecular dynamics, J. Mol. Liq., 2011, 164, 66.
12. A. Asenbaum, et al. Structural changes ethanol–water mixtures: Ultrasonics, Brillouin scattering and molecular dynamics studies, Vib. Spectrosc., 2012, 60, 102.
13. M. Mijaković, K. D. Polok, B. Kežić, F. Sokolić, A. Perera and L. Zoranić, A comparison of force fields for ethanol–water mixtures, Molecular Simulation, J. Mol. Sim, 2012, 42, 699.
14. A. Perera, From Solutions to Molecular Emulsions, Pure Appl. Chem., 2016, 88, 189.
15. A. Perera, in Fluctuation Theory of Solutions: Applications in Chemistry, Chemical Engineering, and Biophysics, ed. P. E. Smith, J. P. O'Connell and E. Matteoli, CRC Press Taylor and Francis, 2012ISBN 9781439899229.
16. J. G. Kirkwood and F. Buff, The Statistical Mechanical Theory of Solutions, J. Chem. Phys., 1950, 19, 774.
17. E. Matteoli and J. Lepori, Solute–solute interactions in water. II. An analysis through the Kirkwood–Buff integrals for 14 organic solutes, J. Chem. Phys., 1984, 80, 2856.
18. A. Ben-Naim, Inversion of the Kirkwood–Buff theory of solutions: Application to the water–ethanol system, J. Chem. Phys., 1977, 67, 4884.
19. A. Perera, B. Kežić, F. Sokolić and L. Zoranić, in Molecular Dynamics, ed. L. Wang, InTech, Rijeka, vol. 2, 2012.
20. K. Binder, Kinetics of Phase separation in Stochastic Non linear systems, ed. L. Arnold and E. Lefever, Springer Series in Synergetics, vol 8, 1980.
21. J. Zauschn, P. Virnau, K. Binder, J. Horbach and R. L. Vink, Statics and dynamics of colloid–polymer mixtures near their critical point of phase separation: A computer simulation study of a continuous Asakura–Oosawa model, J. Chem. Phys., 2009, 130, 064906.
22. D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: fast, flexible and free, J. Comput. Chem., 2005, 26, 1701.
23. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, Packmol: A package for building initial configurations for molecular dynamics, J. Comput. Chem., 2009, 30(13), 2157.
24. J. C. Berendsen, J. P. M. Postma, W. F. Von Gusteren and J. Hermans, in Intermolecular Forces, ed. B. Pullman Reidel, Dordrecht, 1981.
25. B. Chen, J.-J. Potoff and J. I. Siepmann, Monte Carlo calculations for alcohols and their mixtures with alkanes. Transferable potentials for phase equilibria. 5. United-atom description of primary, secondary, and tertiary alcohols, J. Phys. Chem., 2001, 105(15), 3093.
26. W. L. Jorgensen, J. D. Madura and C. J. Swenson, J. Am. Chem. Soc., 1984, 106, 6638; W. L. Jorgensen, J. Phys. Chem., 1986, 90, 1276.
27. H. Jonsson and H. C. Andersen, Icosahedral Ordering in the Lennard-Jones Crystal and Glass, Phys. Rev. Lett., 1988, 60, 2295.
28. L. A. Pugnaloni and F. Vericat, New criteria for cluster identifaction in continuum systems, J. Chem. Phys., 2002, 116, 1097.
29. A. Perera, F. Sokolic and L. Zoranic, Microstructure of neat alcohols, Phys. Rev., 2007, E75, 060502-(R).
30. L. Zoranic, F. Sokolic and A. Perera, Microstructure of neat alcohols: A Molecular Dynamics study, J. Chem. Phys., 2007, 127, 024502.
31. A. Perera and F. Sokolic, Modeling nonionic aqueous solutions: the acetone–water mixture, J. Chem. Phys., 2004, 121(22), 11272.
32. B. Kežić and A. Perera, Revisiting aqueous-acetone mixtures through the concept of molecular emulsions, J. Chem. Phys., 2012, 137, 134502.
33. A. Geiger, F. H. Stillinger and A. Rahman, Aspects of the Percolation Process for Hydrogen-Bond Networks in Water, J. Chem. Phys., 1979, 70, 4185.
34. F. H. Stillinger, Rigorous Basis of the Frenkel-Band Theory of Association Equilibrium, J. Chem. Phys., 1963, 38, 1486.
35. Ph. Wernet, et al. The structure of the first coordination shell in liquid water, Science, 2004, 104, 995.
36. A. Perera and R. Mazighi, Simple and complex forms of disorder in ionic liquids, J. Chem. Phys., 2015, 143, 154502.
37. B. Kežić and A. Perera, Aqueous tert-butanol mixtures: a molecular-emulsion, J. Chem. Phys., 2012, 137, 014501.
38. A. Perera and B. Kežić, Fluctuation and micro-heterogeneity in mixtures of complex liquids, Faraday Discuss., 2013, 167, 145.
39. A. Perera, On the microscopic structure of liquid water, Mol. Phys., 2011, 109, 2433.
40. K. Lum, D. Chandler and J. D. Weeks, Hydrophobicity at Small and Large Length Scales, J. Phys. Chem. B, 1999, 103, 4570.
41. D. Chandler, Interfaces and the driving force of hydrophobic assembly, 2005, 437, 640.
42. A. M. Duffy, D. L. Severance and W. L. Jorgensen, Solvent Effects on the Barrier to Isomerization for a Tertiary Amide from ab Initio and Monte Carlo Calculations, J. Am. Chem. Soc., 1992, 114, 7535.

---