Modelling the chemistry of Mn-doped MgO for bulk and (100) surfaces

Abstract

We have investigated the energetic properties of Mn-doped MgO bulk and (100) surfaces using a QM/MM embedding computational method, calculating the formation energy for doped systems, as well as for surface defects, and the subsequent effect on chemical reactivity. Low-concentration Mn doping is endothermic for isovalent species in the bulk but exothermic for higher oxidation states under p-type conditions, and compensated by electrons going to the Fermi level rather than cation vacancies. The highest occupied dopant Mn 3d states are positioned in the MgO band gap, about 4.2 eV below the vacuum level. Surface Mn-doping is more favourable than subsurface doping, and marginally exothermic on a (100) surface at high O₂ pressures. For both types of isovalent Mn-doped (100) surfaces, the formation energy for catalytically important oxygen defects is less than for pristine MgO, with F⁰ and F²⁺-centres favoured in n- and p-type conditions, respectively. In addition, F⁺-centres are stabilised by favourable exchange coupling between the Mn 3d states and the vacancy-localised electrons, as verified through calculation of the vertical ionisation potential. The adsorption of CO₂ on to the pristine and defective (100) surface is used as a probe of chemical reactivity, with isovalent subsurface Mn dopants mildly affecting reactivity, whereas isovalent surface-positioned Mn strongly alters the chemical interactions between the substrate and adsorbate. The differing chemical reactivity, when compared to pristine MgO, justifies further detailed investigations for more varied oxidation states and dopant species.

---

1 Introduction

Rocksalt alkali-earth oxides, such as CaO and MgO, are amongst the materials currently under investigation for adsorbing and catalysing the transformation of CO₂.^1,2 The bulk and surface structures of these oxides have been extensively studied,^3–5 owing both to the simplicity of the rocksalt geometry and also the high degree of ionicity, which gives rise to a relatively simple electronic structure.^6,7 Additionally, basic oxides such as MgO are popular as catalyst support materials but have displayed interesting reactivity when dopants or defects are included,⁸ which opens up the possibility for their use as catalysts in their own right.^3,9–12 Whilst the surface chemistry and reactivity of MgO is well studied, only recently have investigations begun to show the potential of MnO in areas such as photocatalytic water splitting and CO₂ reduction applications when alloyed with ZnO,¹³ and the (100) MnO surface has also been considered for CO₂ adsorption as part of a systematic study of transition metal monoxides.¹⁴ The doping of rocksalt alkali-earth oxides with transition metals has proven to result in novel physical and catalytic properties^15–17 and thus the catalytic reactivity of MnO, coupled with the stability of the MgO surface, makes Mn-doped MgO an appealing material when designing novel catalytic systems. Furthermore, Mn²⁺ can directly replace Mg²⁺ without significant structural distortion as the ions are roughly equivalent in size; Mn-doped MgO is therefore structurally very similar to pristine MgO but can be differing in chemical reactivity, due to the range of stable oxidation states for the Mn-dopant.^18–21

Previous studies on Mn-doped MgO, which we refer to henceforth as Mn–MgO, have focused on the enthalpies of mixing for MgO and MnO,^22–24 which are generally positive (endothermic) and small (<0.1 eV), as well as formation energies and defect properties for low concentration isovalent Mn-dopants with the aim of finding a dilute magnetic semiconductor (DMS) for use in spintronic applications.^25–31 In particular, recent work has emphasised understanding the consequences of increasing Mn concentration and the coupling between extrinsic and intrinsic defects for both bulk and discrete systems. Experimental and modelling work by Azzaza et al. has shown that increasing the Mn content in MgO decreases the band gap and Curie temperature for dopant concentrations of 5 to 40%, and magnetic interaction between isovalent Mn dopants and oxygen vacancies is postulated as influencing the stability.²⁷ Panigrahi et al. showed via computation that isovalent Mn dopants are favourably positioned at (100) surfaces, rather than in the bulk, for an MgO slab model, and that short-range anti-parallel coupling between multiple Mn dopants is favoured in the absence of intrinsic defects;³⁰ they then additionally highlighted that exchange coupling between isovalent Mn dopants and oxygen vacancies was also energetically favourable for bulk and surface models.^30,31 MgO surfaces are commonly host to significant concentrations of oxygen defects^8,32 and, in the presence of the Mn 3d dopants, strong hybridisation between the Mn 3d and O 2p bands³⁰ means that novel chemistry of the material could be driven by the interchange of electrons between the redox active manganese atom and oxygen vacancy, e.g.:

Mn⁺ + F²⁺ ⇌ Mn²⁺ + F⁺ ⇌ Mn³⁺ + F⁰ (1)

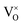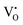The equilibrium in eqn (1) depends on both the ionisation potential and electron affinity for the F-centres and Mn⁺, Mn²⁺ and Mn³⁺ cations within the octahedrally coordinated lattice, with the lowest energy configuration taking precedence. For clarity, in Kröger–Vink notation,³³ the F⁰, F⁺ and F²⁺-centres are denoted as , and , respectively, and the equivalent equations are:In this work, we present high-level simulations of Mn–MgO, in order to elucidate the energetic and electronic properties of bulk- and surface-doped Mn–MgO. Firstly, formation energies of the Mn-doped systems are presented for a range of oxidation states and then complemented by calculations that highlight the role of electron–spin coupling between the Mn 3d states and electrons trapped at intrinsic vacancies such as surface F-centres. The strength of this spin-coupling is then used to help explain the interaction between a CO₂ adsorbate and the Mn–MgO(100) surface, both with and without F-centres.

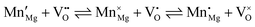2 Computational methodology

Calculations were performed using the hybrid quantum mechanical and molecular mechanical (QM/MM) embedded-cluster methodology that has previously proven to be accurate in modelling the bulk and surface chemistry of MgO.^8,34–43 Our chosen QM/MM implementation is the software environment ChemShell,^44–46 with QM and MM energy evaluations performed with the NWChem⁴⁷ and GULP^48–50 software packages, respectively, and geometry optimisation was performed using the DL-FIND software routines.⁴⁵

For the QM calculations, density functional theory (DFT) was used with the B3LYP^51–53 and B97-3⁵⁴ exchange–correlation (XC) functionals. Results obtained using B3LYP provide a direct comparison with previous work for MgO,⁴² while B97-3 provides comparison with an XC functional that was fitted to a more extensive set of molecular thermochemical data. A Def2 triple-zeta valence plus polarisation (TZVP) basis set⁵⁵ was used for all atoms except Mn, where a Stuttgart/Dresden relativistic small-core effective core potential (ECP) was used with a complementing modified basis set:⁵⁶ the most diffuse functions were removed to prevent the artificial spreading of charge density outside the QM region. Large core ECP⁵⁷ for Mg²⁺ ions were placed on cations at the border of the QM region, representing the QM/MM boundary. The redox-active Mn dopant can adopt different energetically-competitive spin configurations, particularly when neighbouring an unpaired electron on an oxygen vacancy (F⁺), and therefore the spin-states were explicitly checked. High-spin (HS) configurations were energetically favoured for defect-free systems, which preserves the unpaired Mn d⁵ configuration in Mn–MgO in agreement with previous calculations.^26,28 For pure MgO, a closed-shell configuration was always preferable. Unless otherwise stated, all calculations use these configurations.

The MM energy is calculated using a polarisable interatomic forcefield with Coulomb (E^Coul_MM), Buckingham (E^Buck_MM) and spring (E^spring_MM) terms that are defined as:⁴⁹

between two centres with indices i and j, separated by a distance of r_ij. The parameters are the charge (q, in e), the spring constants (k₂ and k₄, in eV Å⁻² and eV Å⁻⁴, respectively) and the Buckingham potential parameters A, ρ and C. The parameterisations we have used, which are presented in Table 1, are slightly modified versions of those derived by Lewis and Catlow:⁵⁸ the cut-off radius has been extended from 6 to 12 Å and the O_shell–O_shell interaction tuned in order to reproduce accurately the dielectric constants of MgO, with polarisable shells included on cations as well as anions. No additional potential terms were included to account for the interactions of the CO₂ adsorbates with the surface as the closest MM atoms were at least 5 Å away.

Table 1 Forcefield parameters for the Mn–MgO calculations. Coul. and Buck. are contractions for Coulomb and Buckingham, respectively. The parameters are the core charge (q_core, in e), the shell charge (q_shell, in e), the spring constants (k₂ and k₄, in eV Å⁻² and eV Å⁻⁴, respectively), the Buckingham potential parameters A (in eV), ρ (in Å) and C, and the cutoff for the potential (r_c) in Å

Coul. & spring	q core	q shell	k 2	k 4
Mg	0.415	1.585	361.60	0.0
Mn	−1.420	3.420	95.00	0.0
O	1.000	−3.000	54.76	0.0

---

Buck.	A	ρ	C	r c
Mgshell–Oshell	1428.5	0.2945	0.0	12.0
Mnshell–Oshell	1007.4	0.3262	0.0	12.0
Oshell–Oshell	22764.3	0.1490	23.0	12.0

---

A spherical or hemispherical QM/MM cluster was used for bulk and surface models, respectively, with a total radius of 30 Å centred on either an oxygen atom or vacancy. The central QM region contained a total of 33 atoms for the bulk and from 22 to 26 atoms for the surface (e.g.Fig. 2); this setup previously produced accurate results for MgO.⁴² The radius of the active MM region was set to 15 Å as atoms beyond this distance did not move during previous geometry optimisations.⁴² This partitioning meant that ∼1500(∼850) atoms underwent ionic relaxation in our bulk (slab) models, with atoms beyond 15 Å fixed in their lattice positions. The lattice constant was obtained for MgO using GULP and the forcefield of choice. Once cut, the surface clusters were oriented so that the x- and y-axes are in the plane of the surface, and the z-axis is perpendicular to the surface.

The total energy of the system is defined additively as:

E_Total = E_QM + E_MM + E_Jost (6)

where E_MM and E_QM are the energies of the MM and QM regions, respectively, and E_Jost is the Jost correction, necessary due to the finite size of the relaxed region of the QM/MM model when dealing with charged defects, thus incorporating long range effects through a dielectric medium term. For the bulk, E_Jost is:⁵⁹where Q denotes the total charge of any defect in the system, R is the radius of the relaxed region in a₀ (Bohr units) and ε is the dielectric constant of the material, which in this case is MgO. For a surface, E_Jost is:⁵⁹We have used the static (ε₀) and high-frequency (ε_∞) dielectric constants when calculating E_Jost for adiabatic and instantaneous processes, respectively. The MM forcefield was used to calculate ε₀(9.7033) and ε_∞(3.01584), with both values matching closely the available experimental literature for static (9.65, 9.8) and optical (2.95) dielectric constants.⁶⁰

3 Mn-doped MgO bulk

In order to test and validate our QM/MM model, we calculated the energy required to replace Mg with an Mn atom in MgO. The reaction scheme of this substitution is:

MgO(s) + Mn(ref) → Mn–MgO(s) + Mg(ref), (9)

where (ref) indicates a reference state. Thus, the formation energy, E_f(Mn–MgO), can be written as:

E_f(Mn–MgO) = E(Mn–MgO) − E(MgO) + E(Mg) − E(Mn) + qε_f, (10)

where E(Mn–MgO), E(MgO), E(Mg) and E(Mn) are the energy of the doped Mn–MgO, pristine MgO, Mg reference and Mn reference, respectively, and the charge of non-isovalent systems are accounted through the inclusion of the final qε_f term, where q is the formal charge of the defect, i.e. Mn^(2+q)+, and ε_f is the Fermi level of the system. An alternative charge compensation is provided by cationic vacancies,^61,62 which we have considered as doubly-charged Mg vacancies () formed as:Considering our Mn-doped systems, can be replaced with Mg^×_at with the corresponding holes instead localised on the extrinsic defects, with substitution of the formation energy for the Mg vacancy in the place of ε_f in eqn (10) giving:where q is again the formal charge of the Mn-dopant in MgO and a factor of appears due to the double charge on the Mg vacancy. In all cases, the energy of the Mg reference state is:

E(Mg) = E(Mg_at) + μ(Mg), (13)

where E(Mg_at) is the calculated energy of the gas-phase atom and μ(Mg) is the chemical potential of Mg, with E(Mn) calculated similarly. E(Mg_at) and E(Mn_at) were calculated as E(Mg_at²⁺) and E(Mn_at²⁺) minus the respective 1st and 2nd experimental ionisation energies for each element, as successfully applied previously for embedded-cluster calculations with modified basis sets.⁶³μ(Mg) and μ(Mn) were derived using a Born–Haber cycle and literature values for energetic processes.⁶⁴

Mg(s) and Mn(s) are the reference states at low oxygen partial pressure, p(O₂), and thus their vaporisation enthalpies of 143.38 and 279.58 kJ mol⁻¹ are used to derive μ(Mg) − μ(Mn) = 136.2 kJ mol⁻¹ (1.41 eV). In a physical sense, a positive value means the stronger bonding in the Mn(s) reactant would inhibit the reaction. In contrast, for high p(O₂) the reference states are MgO(s) and MnO(s), respectively. In this case, the formation enthalpy for MgO (−601.6 kJ mol⁻¹) and MnO (−385.2 kJ mol⁻¹) are combined with the values above to give μ(Mg) − μ(Mn) = −80.2 kJ mol⁻¹ (−0.83 eV), with the negative value indicating favourability for the MgO product over the MnO reactant.

Our results for isovalent E^bulk_f(Mn–MgO) are presented in Table 2. The formation of Mn-dopants at low and high p(O₂) are endothermic, with energies of 2.73(2.55) and 0.49(0.31) eV, respectively, for the B3LYP(B97-3) XC functional. Our high p(O₂) results match previous work by Konigstein et al. and Heath et al. for the enthalpies of mixing (ΔH_mix) of MgO and MnO: 12.5% MnO in MgO was found to be endothermic by 0.03 and 0.05–0.06 eV at the GULP and Hartree–Fock levels of theory, respectively,^22,24 in good agreement with experiment (0.02 eV).²³ We consider that ΔH_mix(MgO/MnO) is lower than for our results due to the relaxation of the bulk lattice constants in this previous work;²² an effect that is not included in our calculations. Interestingly, all of these results are contrary to the Mn-doping DFT calculations of Panigrahi et al.³⁰ where results using the generalised-gradient approximation⁶⁵ give E^bulk_f(Mn–MgO) = −0.1 eV for a 64-atom unit cell, relative to atomic reference states, and adjustment for a high p(O₂) environment gives E_f(Mn–MgO) = −0.93 eV, which is surprisingly exothermic.

Table 2 E _f(Mn–MgO), in eV, for isovalent bulk (Mn_bulk), surface (Mn_surf) and subsurface (Mn_sub) sites as calculated for environments with low (high) p(O₂) with the B3LYP and B97-3 XC functionals. For reference, E_f(Mn–MgO) for an Mn-dopant in an infinitely dilute MgO environment at high p(O₂), as calculated using the presented MM forcefields, is also given. For E_f(Mn–MgO) relative to the gas phase atoms, one can subtract μ(Mg) − μ(Mn) from these values. A HS configuration (sextuplet multiplicity) was energetically preferred for Mn–MgO in all DFT calculations

	B3LYP	B97-3	MM
Mnbulk	2.73(0.49)	2.55(0.31)	−(0.23)
Mnsub	2.67(0.43)	2.53(0.28)	−(0.23)
Mnsurf	2.16(−0.08)	2.00(−0.24)	−(−0.35)
5.354(516.566)

---

Structural analysis of the B3LYP calculation shows that the Mn–O bond length in the doped system is 2.18 Å, which is an extension of the Mg–O bond length (2.12 Å); identical extension of the metal–oxygen bond occurs when the XC is B97-3. Our results are in broad agreement with experimental lattice parameters for MgO (2.11 Å) and MnO (2.22 Å),⁶⁴ and with previous computational reports for isolated Mn dopants in MgO, which give an Mn–O bond distance of ∼2.1 Å.³⁰

Fig. 1 illustrates the formation energy for Mn dopants of differing charge states in MgO, in the range 0 ≤ q ≤ 5, within the limits of ε_f. This graph can be considered as a guide to the favoured oxidation state of an Mn-dopant in either p- or n-type conditions. The lower bound for ε_f is the valence band maximum (VBM), which we position as the negative of the vertical ionisation potential (VIP) for MgO. QM/MM allows us to calculate the VIP for MgO as 6.27(6.51) eV for the B3LYP(B97-3) XC functional using the ΔSCF technique,⁶⁶ which is a slight underestimate of experiment (7.16 eV)⁶⁷ and lower than our previous estimates using XC functionals tuned for bulk materials (PBE0: 6.89 eV; PBESol0: 6.97 eV).⁶ The upper bound for ε_f would typically be the conduction band minimum (CBM) but the band gap of MgO (7.83 eV)⁶⁸ is greater than the VIP, which means the conduction band is actually above the vacuum level. As electrons would not favour going into a CBM with a positive energy, the vacuum level (0 eV) becomes the upper bound for ε_f. Comparison of the Mulliken analysis for the bulk MgO and [MgO]⁺ models shows that the electrons are ionised from the 2p states of the central oxygen, though the remaining electron hole is delocalised over neighbouring atoms as also previously documented for MgO surfaces.³⁵ In addition to these observations, we also calculated the 1st and 2nd VIPs for Mn_bulk–MgO to be 4.27(4.38) and 5.62(5.86) eV, respectively, which means that the highest occupied Mn 3d states are positioned in the bandgap, in agreement with previous reports.^25–27 For higher order VIPs, the Mn 3d states hybridise with the O 2p states in the energy range of −8 to −11 eV to form ill-defined resonance states.

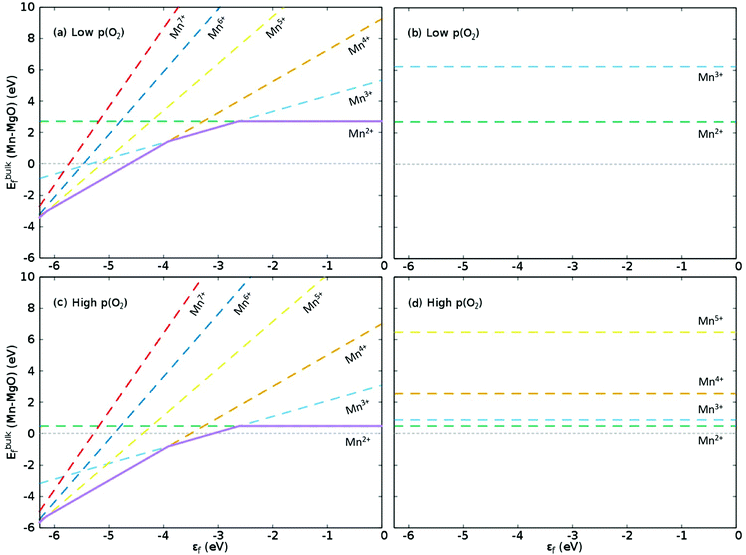Fig. 1 E _f for bulk Mn dopants in MgO when using the B3LYP XC functional at (a and b) low and (c and d) high p(O₂), with ε_f ranging from the VBM (−6.27 eV) through to vacuum level (0 eV). (a and c) Show E_f as compensated by electrons transferring to the Fermi level, ε_f, as calculated with eqn (10) whilst (b) and (d) show E_f as compensated by cation (Mg) vacancies (eqn (12)). Dashed green, aqua, gold, yellow, navy blue and red lines show E_f when the defect charge is respectively q = 0, 1, 2, 3, 4 and 5, i.e. ranging from Mn²⁺ to Mn⁷⁺ as Mn^×_Mg, , , , and , respectively. The overall preferred defect charge as a function of ε_f, which is found to be compensated by the Fermi level in all cases, is given as a solid purple line in (a) and (c).

The graphs for Fermi level-compensated Mn-dopants in (a) low and (c) high p(O₂) in Fig. 1 are clear translations of each other, with both showing that a like-for-like replacement of Mg with Mn is preferred when ε_f is close to 0 eV. Reducing ε_f results in a shift towards higher oxidation states, which may be attributed to the stability of Mn in 3+, 4+ and 5+ oxidation states; in experiment the position of ε_f would be strongly dependent on factors such as the dopant concentration. For low p(O₂), E_f for Mn⁴⁺ is exothermic below ε_f = −4.63 eV, and for high p(O₂) the formation of Mn³⁺ and Mn⁴⁺ is exothermic below ε_f = −3.10 and −3.51 eV, respectively, with formation of higher oxidation states also exothermic at lower ε_f in both cases: Mn⁵⁺ is the most favourable dopant state in both environments in the range of ε_f from −6.13 to −6.27 eV. We note from graphs (b) and (d) in Fig. 1, and Table 3, that using Mg vacancies as compensating defects results in higher formation energies than using electron compensation, though the Mn³⁺ defect is competitive with the isovalent defect at high p(O₂), differing by 0.38 eV. This observation is general to our calculations for B3LYP and B97-3, as shown in Table 3, with only the former plotted in Fig. 1 and discussed in detail here: the difference in E_f for isovalent (2+) and 3+ Mn-dopants when using the latter XC functional is also 0.38 eV.

Table 3 E _f(Mn–MgO), in eV, for bulk (Mn_bulk), surface (Mn_surf) and subsurface (Mn_sub) sites as calculated with the B3LYP(B97-3) XC functional at high p(O₂) for varying charge (q) and position of ε_f, with the latter ranging between vacuum (0 eV) and the valence band maximum (VBM). Values of q marked with ^a have been compensated by cation vacancies (eqn (12)), with all other values compensated by the use of the Fermi level (eqn (10))

	q	ε f = 0 eV		ε f = VBM
Mnbulk	0	0.49	(0.31)	0.49	(0.31)
	1	3.10	(3.11)	−3.18	(−3.40)
	2	7.01	(7.23)	−5.53	(−5.79)
	3	13.15	(13.49)	−5.67	(−6.03)
	1^a	0.87	(0.68)	0.87	(0.68)
	2^a	2.55	(2.37)	2.55	(2.37)
	3^a	6.45	(6.20)	6.45	(6.20)
Mnsub	0	0.43	(0.28)	0.43	(0.28)
	1	3.00	(3.00)	−3.15	(−3.40)
	2	7.13	(7.37)	−5.17	(−5.42)
	3	13.67	(13.95)	−4.78	(−5.23)
	1^a	0.76	(0.58)	0.76	(0.58)
	2^a	2.67	(2.50)	2.67	(2.50)
	3^a	6.98	(6.65)	6.98	(6.65)
Mnsurf	0	−0.08	(−0.24)	−0.08	(−0.24)
	1	2.54	(2.56)	−3.60	(−3.83)
	2	7.54	(7.72)	−4.76	(−5.06)
	3	14.16	(14.32)	−4.29	(−4.85)
	1^a	0.31	(0.13)	0.31	(0.13)
	2^a	3.08	(2.86)	3.08	(2.86)
	3^a	7.46	(7.03)	7.46	(7.03)

---

In general, it is noted that Mn-doping is exothermic in p-type conditions, both at low and high p(O₂). As the dopant concentration increases the material will become more n-type due to the presence of Mn-defect states in the band gap, resulting in changes to the most stable Mn oxidation state: at ε_f = −4.27(−4.38) eV, Mn⁴⁺ is thermodynamically favoured. Lower oxidation states, such as isovalent Mn²⁺, are endothermic in formation and would require n-type conditions during synthesis. Typically, n-type conditions are achieved by using low p(O₂), which results in oxygen vacancies with defect states high in the band gap, as discussed later; surface oxygen vacancies are also of interest for catalytic purposes, where the F-centres can play an important role in reactivity. Therefore, the material properties could be tuned with careful synthesis protocols.

Due to the similarity of our results thus far for the different XC functionals, only those acquired using the B3LYP XC functional will be discussed subsequently unless explicitly stated.

4 Mn-doped MgO(100) surface

4.1 Position of Mn-dopant

As illustrated in Fig. 2, two different QM/MM clusters were used for the Mn–MgO surfaces: (a) the Mn dopant positioned in the surface layer (Layer 1, L1), adjacent to the central oxygen; (b) the Mn dopant situated in the first subsurface layer (Layer 2, L2), directly beneath the central oxygen. Henceforth, these two configurations will be referred to as Mn_surf and Mn_sub, respectively. The Cartesian axes of the QM/MM cluster have been defined so that the xy-plane aligns with the surface-plane of the model; thus Mn_sub occupies the Mg lattice position (0,0,z) and Mn_surf occupies the Mg lattice position (x,0,0), with the primary oxygen lattice site (O_5c or F-centre) at (0,0,0).

Fig. 2 QM cluster illustrating the Mn-dopant in (a) surface (Mn_surf) and (b) subsurface (Mn_sub) positions. O atoms are shown in red, Mg in green and Mn in purple. Bond lengths are given in Å.

Our results, which are presented in Tables 2 and 3, show that formation of isovalent Mn-doped surface layers is exothermic at high p(O₂) when compensated using ε_f, whereas formation of subsurface dopants is very similar to bulk behaviour, being endothermic for all p(O₂). With reduction of ε_f from 0 eV towards the VBM, higher oxidation states become preferable with Mn⁴⁺ the most stable at ε_f = VBM. In contrast, cation-vacancy compensated defects remain endothermic (Table 3). Overall, Mn_surf is energetically favoured over Mn_sub (and Mn_bulk) for q = 0 and 1 as the electronic and structural flexibility of the surface minimises any strain induced by the discrepancy in radius between Mn and Mg (0.83 vs. 0.72 Å for 2+ cations, respectively).⁶⁹ In addition, at these charge states E_f(Mn_surf) < E_f(Mn_bulk), whereas E_f(Mn_sub) ≈ E_f(Mn_bulk). We note that low-spin (LS) Mn²⁺ is in fact structurally smaller (0.67 Å) than HS Mn²⁺,⁶⁹ in octahedral coordination, but a half-filled d-shell with no degenerate occupancy (HS d⁵) is energetically preferable, which also means no Jahn–Teller distortion is observed, in agreement with previous calculations.³⁰ For q > 1, it is apparent that long-distance bulk electrostatics are more important, with Mn⁵⁺ unstable with respect to Mn⁴⁺ at the surface and sub-surface, yet preferred in the bulk.

On the un-doped MgO(100) surface, the Mg–O bond lengths are 2.12 Å in the xy-plane and the z-direction (L1 to L2). These bonds extend to 2.17 and 2.23 Å, respectively, for isovalent Mn_surf and the O–Mn_surf–O bond angles are 90.0° in the xy-plane but as low as 88.5° and 87.3° in the xz- and yz-planes, respectively. The same bond angles are 91.6° for O–Mg–O, showing that the Mn dopants protrude outwards from the (100) surface whereas Mg withdraws inwards. For isovalent Mn_sub, Mn–O bond lengths are similarly extended to 2.17 Å in the xy-plane (L2–L2) and 2.22(2.19) Å in the z-direction between L1 and L2 (L2 and Layer 3, L3), which is partly due to the relaxation of the surface oxygen atom outwards from the surface.⁷ For comparison, the same bonds for Mg–O in the pure surface are 2.18 and 2.07 Å for L1–L2 and L2–L3 interactions, which shows that the subsurface bond lengths increase by >0.1 Å due to the Mn_sub-dopant. The O–Mn_sub–O bond angles within the xy-plane were maintained at 90.0°, similar to Mn_surf, whilst the elongation of the bonds in the z-direction, and upwards movement of Mn_sub, creates bond angles of up to 90.6° in the xz- and yz-planes between the L1 and L2 oxygens.

In order to place the VBM for the surface, as well as to ascertain which atoms contribute to the band edges and dopant states, we calculated the VIP and the adiabatic ionisation potential (AIP) of the pure and Mn-doped MgO(100) surfaces (Fig. 3). For the MgO surface a VIP of 6.15(6.39) eV is calculated with the B3LYP(B97-3) XC functional, which is in fair agreement with experiment (6.7 ± 0.4 eV)⁷⁰ though slightly lower than previous results from periodic DFT using XC functionals for bulk materials (6.52–6.57 eV)⁷ and QM/MM calculations with the B3LYP XC functional (6.46, ∼6.5 eV).^35,42 We attribute this difference to the incomparable XC potentials used in the previous periodic DFT,⁷ the improvements in the MM forcefield and basis sets when compared to our own prior work,⁴² and an absence of long-range corrections (E_Jost) in the work of Sushko et al.;³⁵ if we remove E_Jost from our calculations to match the latter work, the agreement between results improves with our VIP becoming 6.39(6.63) eV for the B3LYP(B97-3) XC functional. In all cases, Mulliken analysis shows that the electron removed during ionisation is taken from the surface oxygen atoms, which associates the VBM with O 2p states, in agreement with well-developed theories of metal oxide band structures.^71,72 We also calculated the AIP of MgO(100) to be 5.21(5.23) eV, for the B3LYP(B97-3) XC functional, i.e. the relaxation of the nuclei around an electronic defect lowers the energy of the system by 0.94(1.16) eV. The smaller VIP of the MgO surface when compared to bulk MgO is due to surface band bending, as we have discussed previously elsewhere.⁷

Fig. 3 Position of the surface valence band and defect states, relative to vacuum, for (a) MgO; (b) Mn_surf–MgO; and (c) Mn_sub–MgO(100) surfaces. Red, green and purple circles represent O, Mg and Mn atoms, respectively. The colour scheme of the electronic transitions matches the origin of electrons for the vertical ionisation potential (VIP): the valence band is O 2p states and Mn 3d defect states are positioned in the band gap. The energies presented are calculated with the B3LYP XC functional, and the adiabatic ionisation potential (AIP) was calculated as 5.21, 2.62 and 2.56 eV for models (a), (b) and (c), respectively.

The VIP for Mn_surf– and Mn_sub–MgO is calculated as 6.16(6.41) and 6.14(6.32) eV, respectively, when using the B3LYP(B97-3) XC functional with a septuplet multiplicity i.e. an ionised electron is removed from the O 2p orbitals, with the HS Mn d⁵ configuration preserved. Unsurprisingly, these results match the VIP for the pure MgO surface, reported above, as the O 2p states contribute to the VBM. However, changing our setup to an intermediate quintet spin-configuration, with the ionised electron removed instead from the Mn 3d states to give an Mn d⁴ electronic configuration, the VIP is 4.40(4.63) and 4.20(4.32) eV for the same dopant systems and XC functionals, respectively (Fig. 3). The smaller VIP indicates that the highest occupied Mn 3d states are 1.76–1.94 eV above the O 2p states and thus in the band gap, matching the bulk systems (Section 3); the VIP of Mn_sub–MgO is noted as being similar to the bulk, for which the VIP was calculated as 4.27(4.38) eV. Mulliken analysis further confirms that the electrons are removed from the Mn 3d and O 2p orbitals on ionisation calculated with multiplicities of 5 and 7, respectively. Full localisation of the remaining holes is not achieved with 0.55 and 0.2 e removed from the Mn and central O in each respective calculation; however the hole does fully localise on the Mn dopant after geometry relaxation of the HS configuration. The AIP for the intermediate spin-state (IS) was calculated for Mn_surf– and Mn_sub–MgO as 2.62(2.81) and 2.56(2.71) eV, respectively, using the B3LYP(B97-3) XC functional; the energetic relaxation of the nuclei, and localisation of the hole, results in significant stabilisation by 1.61–1.83 eV. In addition, higher-order 2nd and 3rd VIPs were calculated for Mn_surf– and Mn_sub–MgO: the results for Mn_sub–MgO match those of Mn_bulk with the 2nd Mn 3d state at −6.02 eV, just above the VBM, whilst the 3rd Mn 3d state is in the valence band i.e. a resonance state. For Mn_surf–MgO, the 2nd Mn 3d state is already in the valence band, showing that the surface strongly stabilises the 3d states and indicating a reason for the improved stability of the Mn-dopant at the surface.

4.2 Oxygen vacancy formation

Oxygen vacancies that contain trapped electrons on the surface of a material, i.e. surface F-centres,⁸ have previously been postulated as active sites for the conversion of CO₂ to CH₃OH on metal oxides, e.g. Cu/ZnO/Al₂O₃.^46,73–77 As discussed in Section 3, the formation of such vacancies would require careful material preparation, however their presence would be beneficial for catalytic applications. Therefore, we have calculated the formation energies of oxygen vacancies at the Mn–MgO(100) surface, as presented in Table 4. The formation energy, E_f(F^q+), was calculated relative to the energy of the Mn-doped surface, E(Mn–MgO), and half an oxygen dimer, :As in eqn (10), ε_f is a variable that can vary between an upper limit of vacuum (0 eV) and a lower limit of the VBM, which we calculate as −6.15(−6.39) eV for the B3LYP(B97-3) XC functional (Section 4.1). We discuss only ε_f = 0 eV in the text unless otherwise stated, as this is typical for a low p(O₂) environment that would facilitate the formation of oxygen vacancies.

Table 4 E _f(F^q+) for the Mn–MgO(100) surface, as calculated with ε_f set at the vacuum (VBM) level. Both intermediate-spin (IS) and high-spin (HS) configurations were considered for q = 1 and 2; see the text for detailed justification. E_f(F^q+) for a low-spin MgO(100) surface are also presented from literature, with values updated using the B3LYP XC functionals, equivalent basis sets and a VBM of −6.46 eV.⁴² All values are in eV

q	Spin	Mnsurf		Mnsub		MgO^42
		B3LYP	B97-3	B3LYP	B97-3	B3LYP
0	IS	6.16(6.16)	5.86(5.86)	6.13(6.13)	5.85(5.85)	6.59(6.59)
1	IS	7.64(1.49)	7.49(1.10)	7.59(1.44)	7.43(1.04)	8.26(1.80)
1	HS	7.92(1.77)	7.75(1.36)	7.88(1.73)	7.71(1.32)	—
2	IS	11.65(−0.65)	12.24(−0.54)	11.09(−1.21)	11.11(−1.67)	10.87(−2.05)
2	HS	10.48(−1.82)	10.38(−2.40)	10.41(−1.89)	10.28(−2.50)	—

---

A closed-shell configuration is energetically favoured for a neutral F⁰-centre on the (100) surface, with both electrons occupying the oxygen vacancy, i.e. V^×_O, and the Mn²⁺ ion maintaining an open-shell d⁵ valence configuration. We denote this as intermediate-spin (IS), as a high-spin (HS) configuration would unpair the vacancy electrons and low-spin (LS) configuration would have the Mn d⁵ electrons paired together, both of which are energetically unfavourable. For Mn_surf– and Mn_sub–MgO, E_f(F⁰) is 6.14(5.85) ± 0.02 eV for the B3LYP(B97-3) XC functional, which is ∼0.4 eV lower than that of the pure MgO(100) surface,⁴² as shown in Fig. 4.

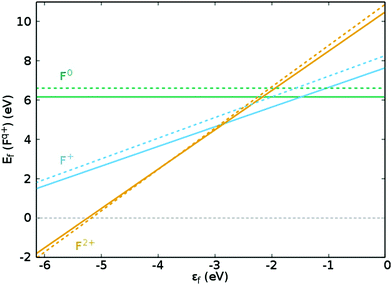Fig. 4 E _f for F^q+-centres using the B3LYP XC functional, with solid lines representing Mn_surf–MgO, with ε_f ranging from the VBM (−6.15 eV) through to vacuum level (0 eV), and dashed lines representing the same defects on a pristine MgO surface, as calculated in Table 4 from the work of Downing et al.⁴² Dashed green, blue and yellow lines show E_f when the defect charge is q = 0, 1 and 2, respectively (i.e. F⁰, F⁺ and F²⁺).

In order to explore the effect of exchange coupling between the vacancy-trapped electrons and the Mn 3d-states for an F⁺-centre, we compare a parallel and anti-parallel alignment of the V_O and Mn 3d electrons. As can be seen in Table 4, IS (anti-parallel) alignment gives E_f(F⁺) of 7.64 eV for Mn_surf, with a very similar result for Mn_sub, and E_f(F⁺) is ∼0.27 eV greater for the HS (parallel) configuration. The position of ε_f has significant effect on E_f(F⁺): when below −1.48 eV, E_f(F⁰) > E_f(F⁺) for both Mn-doped surfaces. Additionally, E_f(F⁺Mn–MgO) is at least 0.35 eV lower than E_f(F⁺MgO), indicating that an Mn-dopant facilitates formation of an F⁺-centre (Fig. 4).

Ionisation of a second electron to form an F²⁺-centre could also be from the oxygen vacancy or the Mn dopant, which could potentially lead to doubly-charged (a) or (b) defects, or alternatively (c) sharing of the holes between both extrinsic and intrinsic defects, i.e.:

We investigated the spin-configuration explicitly by controlling the system multiplicity, with the possible spin being (a) an IS quartet or (b and c) a HS sextuplet. From the energies presented in Table 4, it is clear that E_f(F²⁺) is preferred in HS, with E_f(F²⁺) = 10.48 and 10.41 eV for Mn_surf and Mn_sub, respectively. However, as (b) and (c) are indistinguishable by spin-state alone, comparison of the Mulliken spin populations is necessary, which shows that the spin-density on the Mn dopant is ∼4.7 e and ∼4.6 e for Mn_surf and Mn_sub, respectively. Thus, we can conclude that both electrons are removed from the vacancy, i.e., irrespective of Mn position or XC functional. We again note that E_f(F²⁺) for Mn–MgO is generally lower than for MgO, in the favoured HS state, though not when ε_f drops towards the VBM. Perhaps more pertinently, E_f(F⁺) > E_f(F²⁺) for Mn_surf when ε_f is lower than −2.84(−2.89) eV, and F²⁺-centre formation is exothermic when ε_f is lower than −5.21(−5.14) eV, i.e. p-type, when using the B3LYP(B97-3) XC functional (Fig. 4).

As illustrated in Fig. 5, the IS VIP for the F⁰-centre with an Mn_surf-dopant is found to be 2.62 eV whereas the HS VIP is 2.94 eV. Referring to our prior comment that HS corresponds to parallel alignment of the vacancy electrons and the Mn 3d states, we can re-affirm the larger E_f(F⁺) for a HS configuration is based on the greater stability of the highest occupied molecular orbital (HOMO) when compared to an anti-parallel (IS) configuration. The VIP of the oxygen vacancy is similar for Mn_sub: 2.51 and 2.92 eV for the IS and HS configuration, respectively. The upwards shift of the HOMO for an anti-parallel alignment, which is between 0.3 and 0.4 eV, gives a reasonable approximation to the exchange coupling energy, whereas the position of the parallel aligned V_O state at ∼−2.9 eV is only slightly lower than the −3.05 eV calculated previously for an F⁰-centre on an MgO(100) surface.⁴² The increased stability of the parallel states is in agreement with previous observations for ferromagnetic Mn–O and Mn–C coupling in doped MgO,²⁵ though higher concentrations of Mn dopants would result in strong Mn–Mn anti-parallel coupling.^26,30

Fig. 5 Intrinsic defect levels, relative to vacuum, for F-centres on the Mn_surf–MgO(100) surface. The colour scheme of the atoms is the same as Fig. 3, with an additional white circle to show an surface oxygen vacancy. The colour scheme of the electronic transitions matches the origin of electrons: the valence band is O 2p states, with the F⁰ and F⁺ defect states positioned in the band gap. F⁰_HS and F⁰_IS are used to denote parallel and anti-parallel alignment, respectively, of the oxygen vacancy electrons with the Mn 3d states. The energies presented are calculated with the B3LYP XC functional, and the adiabatic ionisation potential (AIP) was calculated as 1.48, 1.76 and 2.84 eV for the F⁰_IS, F⁰_HS and F⁺ defect states, respectively.

Using the lower energy IS F⁺-centre as our starting point, we also calculated the energy required to remove a second electron from the V_O site to form a HS F²⁺-centre. The VIP is 4.53 eV for Mn_surf with a very similar result of 4.52 eV for Mn_sub, very close to the previously calculated 2nd VIP of an MgO F-centre (4.55 eV). Coupled with Mulliken analysis, we conclude that the second electron is also ionised from the oxygen vacancy, which means that the highest Mn 3d states must be below −4.5 eV, implying that they are stabilised by the presence of the V_O when compared to the pristine surface, for which the VIP was 4.2 to 4.4 eV (Section 4.1).

5 CO₂ adsorption on Mn-doped MgO(100) surface

Within the reaction process of CO₂ to CH₃OH conversion, CO₂ is bound to a surface oxygen vacancy and undergoes hydrogenation, leading to the formation of CH₃OH and the removal of the surface defect; CO is then used to regenerate the defect sites via its transformation to CO₂, completing the catalytic cycle.⁷³ Such a reaction cycle is transferable and highly tunable via modification of the surface as we have recently shown for F-centres on MgO.^42,43 As a fundamental step in this topically relevant reaction, a number of CO₂ adsorption processes were considered here for the Mn–MgO(100) surfaces investigated in Section 4. The CO₂ adsorbate was aligned with the O–C–O axis along either the Cartesian x- or z-axes of the system, “parallel” or “perpendicular” to the surface.⁴² A third CO₂ adsorbate orientation was included for Mn_surf, with the O–C–O axis aligned along the y-axis of the model. The adsorption energy, E_ads, for the CO₂ molecule was defined as:

E_ads(CO₂) = E(CO₂–MnMgO) − E(CO₂) − E(MnMgO), (16)

where E(CO₂) and E(CO₂–MnMgO) are the energies of the gas phase CO₂ and Mn–MgO adsorbed CO₂ systems, respectively. Energetic errors from basis set superposition were not explicitly calculated; however we expect them to be similar to the quantity calculated previously for CO₂ chemisorbed on MgO (0.15–0.18 eV).⁴² An HS configuration was considered for the O_5c site and F²⁺ defects, with the F⁰ defects modelled using the lower-energy IS configuration, and both IS and HS configurations investigated for F⁺-centres. We note that the CO₂ molecule has a closed-shell (singlet) electronic configuration in the gas-phase and so electron transfer to an adsorbed CO₂ could be to either the α- or β-channels with equal probability. At this stage, we have limited our investigation to the determination of adsorbed structures and analysis of any electron transfer, with adsorption profiles and barriers reserved for future work.

5.1 O_5c site

The structures for chemisorbed CO₂ parallel to the Mn_surf–MgO(100) surface are shown in Fig. 6(a) and (b), whilst CO₂ chemisorption parallel to the Mn_sub–MgO surface is shown in Fig. 6(c). The CO₂ physisorbed perpendicular to the O_5c site is not shown as significant interactions were not seen, which was expected, based on previous results for MgO,⁴² and the data presented in the ESI† shows that the interaction is negligible. In experiment, van der Waals interactions that are absent from our calculations would, perhaps, allow the CO₂ to be physisorbed near the Mn–MgO surface.

Fig. 6 CO₂ adsorbed on the Mn–MgO(100) surface, where the CO₂ molecule is adsorbed in the xy-surface plane. In (a) and (b), the CO₂ molecule is positioned in the x- and y-axes, respectively, over an Mn_surf–MgO substrate; in (c), the CO₂ molecule is adsorbed over an Mn_sub–MgO substrate. O atoms are shown in red, Mg in green, Mn in purple and C in grey. Bond lengths are given in Å.

For the x- and y-axis aligned adsorbates, a carbonate species forms, and E_ads(CO₂) on the O_5c site ranges between −0.66 and −0.86 eV, which is similar to that observed for MgO;⁴² full results are included in the ESI.† We note for Mn_surf that stronger CO₂ adsorption is seen for y-axis alignment, compared to x-axis, which can be correlated with the longer Mn–O bond of 2.29 Å between the (100) surface and the CO₂ in the latter system. Mulliken analysis shows that there is partial withdrawal of 0.5 e from the O_5c and neighbouring Mg atoms to the adsorbate; however the Mn-dopant retains its d⁵ configuration, which hinders charge transfer.

Comparison of the different XC functionals shows consistently stronger binding when using B97-3, with the interactions around 10% stronger than for B3LYP. This result is consistent with the parameterisation of this XC functional towards thermochemical processes such as chemisorption, supporting stronger electron localisation.

5.2 F⁰-centre

For a neutral oxygen vacancy, the z-axis (vertically) aligned CO₂ dissociates to produce a defect-free surface and a CO molecule, as shown in Fig. 7(a). Table 5 shows that this process is strongly exothermic (∼−3 eV) due to the healing of the oxygen vacancy. Strong adsorption also occurs when CO₂ is aligned parallel to the surface, with E_ads(CO₂) ≈ −2 eV. The strong binding results in a bent CO₂ geometry, as seen previously for F⁰-centre on MgO;⁴² however healing of the oxygen vacancy does not occur in this particular case. Regardless of the position of the Mn dopant, the CO₂ rotates so that the central C atom is directed towards a surface Mg, rather than downwards into the vacancy as seen for undoped MgO.⁴² It is noted that, in the y-axis orientation on Mn_surf–MgO, the CO₂ is able to rotate towards either an Mn or Mg atom, however, the latter is favoured.

Fig. 7 CO₂ adsorbed on the Mn_sub–MgO(100) surface at an (a) F⁰-centre, (b) F⁺-centre and (c) F²⁺-centre. O atoms are shown in red, Mg in green, Mn in purple and C in grey. Bond lengths are given in Å.

Table 5 E _ads(CO₂) on F⁰-centres at the (100) surface. Also presented are previously calculated results for CO₂ adsorption on MgO using the B3LYP XC functional and similar basis sets.⁴² All values are given in eV

	CO2 axis	B3LYP	B97-3
Mnsurf	x	−2.00	−1.74
	y	−2.25	−1.98
	z	−3.13	−2.80
Mnsub	x	−2.24	−1.98
	z	−3.20	−2.87
Mg^42	x	−2.36	—
	z	−3.52	—

---

5.3 F⁺-centre

Due to the energetic competition between the IS and HS F⁺-centres, both were considered as adsorption sites for CO₂ (Table 6), which resulted in a range of adsorption strengths. E_ads(CO₂) is greatest for IS Mn_surf–MgO with the adsorbate aligned along the x-axis of the surface (−2.00 eV). Fig. 8(a) shows that the CO₂ has dissociated, with one O healing the surface vacancy and the remaining CO coordinated to a surface Mg. Mulliken analysis shows that the electron previously trapped at the F⁺-centre has reduced the Mn²⁺ cation to Mn⁺, which has a spin-density of 3.90 e; further calculations would be necessary to determine if an entirely LS configuration is preferable for the Mn cation. For the same system with a HS configuration, no dissociation is observed and instead the vacancy-trapped electron transfers to the CO₂, hence the smaller E_ads(CO₂). The second greatest E_ads(CO₂) is with the CO₂ aligned in the y-axis of an IS-configured surface (−1.38 eV): the CO₂ remains parallel to the surface but the C bonds directly to the Mn, with the two atoms separated by 2.14 Å compared to 2.61 Å for the HS equivalent as shown in Fig. 8(c) and (d), respectively. The spin-density is 4.08 e in the former case, which is ∼0.76 e lower than for HS (4.76 e) and again indicates that the vacancy electron has moved to the Mn.

Table 6 E _ads(CO₂) on F⁺-centre sites, with an IS (HS) electronic configuration, on Mn–MgO(100) surface. Also presented are previously calculated results for CO₂ adsorption on MgO using the B3LYP XC functional and similar basis sets.⁴² All values are given in eV

	CO2 axis	B3LYP	B97-3
Mnsurf	x	−2.00(−0.62)	−1.64(−0.48)
	y	−1.38(−0.80)	−1.06(−0.64)
	z	−0.90(−1.12)	−0.76(−0.97)
Mnsub	x	−0.64(−0.85)	−0.49(−0.69)
	z	−0.99(−1.18)	−0.85(−1.05)
Mg^42	x	−0.71	—
	z	−1.11	—

---

Fig. 8 CO₂ adsorbed on the Mn_surf–MgO(100) surface at an F⁺-centre with the adsorbate aligned (a and b) in the x-axis, (c and d) in the y-axis, and (e and f) in the z-axis. (a, c and e) Are with anti-parallel spin for the vacancy and the Mn 3d states, i.e. IS configuration, and (b), (d) and (f) are parallel spin for the vacancy and the Mn 3d states, i.e. HS configuration. O atoms are shown in red, Mg in green, Mn in purple and C in grey. Bond lengths are given in Å.

In contrast to the above, E_ads(CO₂) for z-axis aligned CO₂ on the Mn_surf is stronger for HS than IS, with no chemisorption, which indicates that exchange coupling benefits physisorption. The resulting bent CO₂ remains perpendicular to the surface for both systems [Fig. 8(e) and (f)], with the terminal O only ∼0.7 Å above the surface plane, but the difference in E_ads(CO₂) between HS and IS is 0.22 eV. Similar differences are seen for the Mn_sub systems [Fig. 7(b)], where E_ads(CO₂) for HS is consistently ∼0.2 eV greater than for IS. Mulliken analysis of the CO₂ when x-axis aligned on Mn_sub–MgO shows that the spin-density is 0.69 and 0.84 e when using IS and HS configurations, respectively, which correlates charge transfer with adsorption energy; we also note that the majority of this spin density is located on the central C atom.

5.4 F²⁺-centre

E _ads(CO₂) on HS F²⁺-centres is presented in Table 7, with similar structures observed for CO₂ adsorbed on Mn_sub– and Mn_surf–MgO [Fig. 7(c)]. Bonding is marginally exothermic for z-axis aligned CO₂, with the lack of bend in the adsorbate suggesting that no significant charge transfer occurs, which is consistent with results for undoped MgO⁴² and confirmed by Mulliken analysis. CO₂ adsorption is endothermic when the molecule is aligned with the x- or y-axis; as separation of the CO₂ and surface would be more favourable, this is a local minimum. Electron density transfers from the Mn atom to the CO₂ to form a CO₂⁻/Mn³⁺ surface complex, with greater charge transfer when the Mn interacts with a terminal O (x-axis) rather than the C atom (y-axis), which correlates with the more endothermic nature of the x-axis aligned adsorption (0.90 eV compared to 0.50 eV).

Table 7 E _ads(CO₂) on F²⁺-centres. Also presented are previously calculated results for CO₂ adsorption on MgO using the B3LYP XC functional and similar basis sets.⁴² All values are given in eV

	CO2 axis	B3LYP	B97-3
Mnsurf	x	0.90	1.14
	y	0.50	0.00
	z	−0.09	−0.11
Mnsub	x	0.24	0.52
	z	−0.12	−0.13
Mg^42	x	0.11	—
	z	0.04	—

---

6 Summary and conclusions

We have performed embedded-cluster QM/MM calculations for Mn-doped MgO, studying bulk and (100) surface systems, as well as testing the reactivity of the doped material using CO₂ adsorption as a representative catalytic process. Low concentration Mn-doping is endothermic for isovalent bulk defects, irrespective of a low or high p(O₂) reference environment, with the Mn 3d levels positioned in the band gap ∼4.2 eV below the vacuum level, however, Mn-doping is energetically favourable in higher oxidation states, especially under p-type conditions. The formation of isovalent Mn-doped (100) MgO surfaces is marginally exothermic at high p(O₂), with subsurface doping being exothermic; however higher oxidation states become more favourable in p-type conditions.

Once present, an isovalent Mn-dopant aids the formation of oxygen vacancies, i.e. F-centres, on the (100) surface: F⁺-centres particularly benefit from an exchange-coupling mechanism between the trapped electrons and the Mn 3d-states, with a parallel aligned electron 0.32 eV lower in energy than an anti-parallel aligned electron when using the B3LYP XC functional. In general, formation energies for F⁰ and F²⁺-centres indicate their prevalence in n- and p-type environments, respectively, in broad agreement with findings for undoped MgO; in future work we will extend this analysis to Mn-dopants in higher oxidation states.

When a CO₂ probe molecule is adsorbed on the pristine and defective Mn–MgO(100) surface, the interaction between substrate and adsorbate is dependent on both defect charge and adsorbate orientation. Strongest adsorption is for CO₂ over an F⁰-centre, with the CO₂ dissociating when aligned perpendicular to the surface so that the oxygen vacancy can be filled by one of the oxygen atoms from the CO₂ molecule. We also observe strong binding between F⁺-centres and CO₂ when the Mn-dopant is positioned at the surface, with interaction strengths less varied when the Mn is subsurface. In general, positioning of an Mn-dopant subsurface implicitly affects CO₂ adsorption through exchange coupling effects, whereas Mn dopants on the surface strongly influence the chemical reactivity, with distinctly different interactions compared to MgO. In general our results justify further investigation of the doping of stable alkaline-earth metal oxides with transition metal species, which we will continue in our future work with an emphasis on catalytic reactivity: it has been previously noted that high-valence dopants activate molecular adsorbates for other transition metal dopants in rocksalt oxides⁷⁸ and clearly we need to investigate this further for Mn–MgO.

Acknowledgements

The authors are grateful to David Scanlon and John Buckeridge for discussions associated with this work. AJL acknowledges the Ramsay Memorial Trust and University College London for the provision of a Ramsay Fellowship. CAD acknowledges the Molecular Modelling and Materials Science Industrial Doctorate Centre (M3S IDC) and the Science and Technology Facilities Council (STFC) for funding. AJL, TWK, PS, AAS and CRAC acknowledge funding from EPSRC grants EP/IO30662/1 and EP/K038419/1. The authors acknowledge the use of the ARCHER high-performance computing facilities, and associated support services, via our membership of the UK HPC Materials Chemistry Consortium (EP/L000202).

References

1. S. Wang, S. Yan, X. Ma and J. Gong, Energy Environ. Sci., 2011, 4, 3805–3819.
2. S. Choi, J. H. Drese and C. W. Jones, ChemSusChem, 2009, 2, 796–854.
3. H. A. Al-Abadleh and V. H. Grassian, Surf. Sci. Rep., 2003, 52, 63–161.
4. D. P. Woodruff, Chem. Rev., 2013, 113, 3863–3886.
5. C. Noguera, Physics and Chemistry at Oxide Surfaces, Cambridge University Press, 1996.
6. A. J. Logsdail, D. O. Scanlon, C. R. A. Catlow and A. A. Sokol, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155106.
7. A. J. Logsdail, D. Mora-Fonz, D. O. Scanlon, C. R. A. Catlow and A. A. Sokol, Surf. Sci., 2015, 642, 58–65.
8. G. Pacchioni, ChemPhysChem, 2003, 4, 1041–1047.
9. K. Honkala, Surf. Sci. Rep., 2014, 69, 366–388.
10. H. Hattori, Appl. Catal., A, 2001, 222, 247–259.
11. J. Goniakowski and C. Noguera, Surf. Sci., 1995, 340, 191–204.
12. G. Pacchioni and H. Freund, Chem. Rev., 2013, 113, 4035–4072.
13. D. K. Kanan and E. A. Carter, J. Phys. Chem. C, 2012, 116, 9876–9887.
14. R. Hammami, A. Dhouib, S. Fernandez and C. Minot, Catal. Today, 2008, 139, 227–233.
15. N. Nilius and H.-J. Freund, Acc. Chem. Res., 2015, 48, 1532–1539.
16. E. W. McFarland and H. Metiu, Chem. Rev., 2013, 113, 4391–4427.
17. N. Nilius, J. Phys.: Condens. Matter, 2015, 27, 303001.
18. A. Cimino and V. Indovina, J. Catal., 1974, 33, 493–496.
19. P. Koidl and K. W. Blazey, J. Phys. C: Solid State Phys., 1976, 9, L167.
20. R. Mariscal, J. Soria, M. Pena and J. Fierro, J. Catal., 1994, 147, 535–543.
21. M. Abramishvili, Z. Akhvlediani, M. Galustashvili, G. Dekanozishvili, T. Kalabegishvili, V. Kvatchadze and V. Tavkhelidze, J. Mod. Phys., 2011, 2, 6759.
22. M. Königstein, F. Cora and C. R. A. Catlow, J. Solid State Chem., 1998, 137, 261–275.
23. H. Gripenberg, S. Seetharaman and L. Staffansson, Chem. Scr., 1979, 13, 162–164.
24. K. D. Heath, W. C. Mackrodt, V. R. Saunders and M. Causà, J. Mater. Chem., 1994, 4, 825–829.
25. V. Sharma, G. Pilania and J. E. Lowther, AIP Adv., 2011, 1, 032129.
26. L.-J. Shi, Phys. Lett. A, 2010, 374, 1292–1296.
27. S. Azzaza, M. El-Hilo, S. Narayanan, J. J. Vijaya, N. Mamouni, A. Benyoussef, A. El Kenz and M. Bououdina, Mater. Chem. Phys., 2014, 143, 1500–1507.
28. S. Meskine, A. Boukortt, R. Hayn and A. Zaoui, Phys. Status Solidi B, 2014, 251, 845–849.
29. P. Wu, G. Cao, F. Tang and M. Huang, Comput. Mater. Sci., 2014, 86, 180–185.
30. P. Panigrahi, T. Hussain, C. M. Araujo and R. Ahuja, J. Phys.: Condens. Matter, 2014, 26, 265801.
31. P. Panigrahi, C. M. Araujo, T. Hussen and R. Ahuja, Sci. Technol. Adv. Mater., 2014, 15, 035008.
32. N. A. Richter, S. Sicolo, S. V. Levchenko, J. Sauer and M. Scheffler, Phys. Rev. Lett., 2013, 111, 045502.
33. F. Kröger and H. Vink, Solid State Phys., 1956, 3, 307–435.
34. E. Scorza, U. Birkenheuer and C. Pisani, J. Chem. Phys., 1997, 107, 9645–9658.
35. P. V. Sushko, A. L. Shluger and C. R. A. Catlow, Surf. Sci., 2000, 450, 153–170.
36. P. Sushko, J. Gavartin and A. Shluger, J. Phys. Chem. B, 2002, 106, 2269–2276.
37. Y. Wang, H. N. Nguyen and T. N. Truong, Chem. – Eur. J., 2006, 12, 5859–5867.
38. E. Florez, P. Fuentealba and F. Mondragon, Catal. Today, 2008, 133, 216–222.
39. C. Qin, Chem. Phys. Lett., 2008, 460, 457–460.
40. G. Pacchioni and H.-J. Freund, Chem. Rev., 2013, 113, 4035–4072.
41. K. Kwapien, J. Paier, J. Sauer, M. Geske, U. Zavyalova, R. Horn, P. Schwach, A. Trunschke and R. Schlögl, Angew. Chem., Int. Ed., 2014, 53, 8774–8778.
42. C. A. Downing, A. A. Sokol and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2014, 16, 184–195.
43. C. A. Downing, A. A. Sokol and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2014, 16, 21153–21156.
44. S. Metz, J. Kästner, A. A. Sokol, T. W. Keal and P. Sherwood, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 101–110.
45. J. Kaestner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865.
46. P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjovoll, A. Fahmi, A. Schafer and C. Lennartz, J. Mol. Struct.: THEOCHEM, 2003, 632, 1–28.
47. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. V. Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
48. J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637.
49. J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341.
50. J. Gale, Z. Kristall., 2005, 220, 552–554.
51. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
52. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
53. P. J. Stephens, F. J. Devlin, C. F. Chablowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
54. T. W. Keal and D. J. Tozer, J. Chem. Phys., 2005, 123, 121103.
55. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
56. M. Dolf, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872.
57. P. Fuentealba, L. Vonszentpaly, H. Preuss and H. Stoll, J. Phys. B: At., Mol. Opt. Phys., 1985, 18, 1287–1296.
58. G. V. Lewis and C. R. A. Catlow, J. Phys. C: Solid State Phys., 1985, 18, 1149–1161.
59. W. Jost, J. Chem. Phys., 1933, 1, 466–475.
60. A. E. Hughes and B. Henderson, Color Centers in Simple Oxides, in Point Defects in Solids: General and Ionic Crystals, ed. J. H. Crawford and L. M. Slifkin, Springer US, Boston, MA, 1972, pp. 381–490.
61. F. Stavale, X. Shao, N. Nilius, H.-J. Freund, S. Prada, L. Giordano and G. Pacchioni, J. Am. Chem. Soc., 2012, 134, 11380–11383.
62. Y. Cui, X. Shao, S. Prada, L. Giordano, G. Pacchioni, H.-J. Freund and N. Nilius, Phys. Chem. Chem. Phys., 2014, 16, 12764–12772.
63. A. Walsh, J. Buckeridge, C. R. A. Catlow, A. J. Jackson, T. W. Keal, M. Miskufova, P. Sherwood, S. A. Shevlin, M. B. Watkins, S. M. Woodley and A. A. Sokol, Chem. Mater., 2013, 25, 2924–2926.
64. D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, Florida, 84th edn, 2003.
65. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
66. R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746.
67. T. Jaouen, G. Jézéquel, G. Delhaye, B. Lépine, P. Turban and P. Schieffer, Appl. Phys. Lett., 2010, 97, 232104.
68. R. Whited, C. J. Flaten and W. C. Walker, Solid State Commun., 1973, 13, 1903–1905.
69. R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767.
70. L. N. Kantorovich, A. L. Shluger, P. V. Sushko, J. Gunster, P. Stracke, D. W. Goodman and V. Kempter, Faraday Discuss., 1999, 114, 173–194.
71. H. H. Kung, Transition metal oxides: surface chemistry and catalysis, Elsevier, 1989, vol. 45.
72. D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798–801.
73. S. A. French, A. A. Sokol, S. T. Bromley, C. R. A. Catlow, S. C. Rogers, F. King and P. Sherwood, Angew. Chem., Int. Ed., 2001, 40, 4437–4440.
74. A. Sokol, S. Bromley, S. French, C. Catlow and P. Sherwood, Int. J. Quantum Chem., 2004, 99, 695–712.
75. S. French, A. Sokol, S. Bromley, C. Catlow and P. Sherwood, Top. Catal., 2003, 24, 161–172.
76. S. Bromley, S. French, A. Sokol, C. Catlow and P. Sherwood, J. Phys. Chem. B, 2003, 107, 7045–7057.
77. C. Catlow, S. French, A. Sokol and J. Thomas, Philos. Trans. R. Soc., A, 2005, 363, 913–936.
78. Y. Cui, X. Shao, M. Baldofski, J. Sauer, N. Nilius and H.-J. Freund, Angew. Chem., Int. Ed., 2013, 52, 11385–11387.

---

Footnote

† Electronic supplementary information (ESI) available: Additional data table with CO₂ adsorption energies for pristine Mn–MgO(100) surfaces. See DOI: 10.1039/c6cp04622c

---