Mass effects in the photodissociation of homonuclear diatomic molecules in helium nanodroplets: inelastic collision and viscous flow energy exchange regimes

Abstract

The influence of the mass in the photodissociation dynamics of a homonuclear diatomic molecule (X₂), embedded in a superfluid helium nanodroplet (T = 0.37 K) of 300 atoms, has been investigated using a hybrid quantum dynamics method recently proposed by us. Several hypothetical isotopic variants of Cl₂ have been examined in order to make possible the analysis of a wide diversity of masses (m_X: 0.25m_Cl–1.50m_Cl). This is probably the first time that this problem has been considered theoretically. The photodissociation mechanism of X₂(B) is very similar to that of Cl₂(B) and the efficiency of the X₂–helium energy exchange mechanism can be so great that it leads to the full and partial (≈86%) geminate recombination for the lower masses explored (m_X = 0.25m_Cl and 0.50m_Cl, respectively). From the energy exchange perspective two dynamic regimes have been identified. The first regime occurs at the initial times of the photodissociation and corresponds to a perfectly inelastic collision (IC) between the atomic fragments (X) and some helium atoms of the solvation shell. The second regime occurs when the atomic fragments are moving through the nanodroplet, which behaves as a viscous fluid (VF). The ICVF mechanism has probably general character in the photodissociation of molecules embedded in superfluid helium nanodroplets.

---

1. Introduction

Superfluid helium nanodroplets, (⁴He)_N, have attracted lots of interest from the scientific community, not only for exploring finite-size superfluidity but also because of their characteristics as a solvent.^1,2 Their superfluidity, chemically inert character, ability to be doped with almost any chemical species, very low temperature (0.37 K) and large heat capacity make these systems ideal nanoreactors to investigate a wide variety of chemical processes.^3,4 Another main feature of helium nanodroplets is their capacity to stabilize chemical species such as ions, molecules, nanoclusters^5,6 and nanowires.^7,8 This is important from a chemical perspective and it is of great interest to understand the impurity relaxation mechanism, i.e. how the energy is released from the dopant chemical species to the liquid helium.

The first experiments on this topic were focused on the cage effect in the fragmentation of photoionized molecules^9–12 and rare-gas clusters^13–16 embedded in helium nanodroplets. The energy relaxation by helium nanodroplets has also been studied experimentally considering neutral species (photoinduced isomerization of linear and bent isomers of HCN–HF¹⁷ and photodissociation of alkyl iodides; R–I + hν → R + I).^18–20 In the former case the amount of population transfer has been found to be very different for pumping the two isomers;¹⁷ while in the second case the velocity and angular distributions of the photofragments were measured and an important cage effect, which strongly depends on the fragment mass, was observed.^18–20 Most of the experiments pointed out that the cooling by helium is not a thermal evaporative process, i.e. the mean energy per evaporated helium atom is greater than the binding energy per atom in liquid helium (≈7 K). Furthermore, the cooling efficiency was found to depend on the nanodroplet size.

Different energy relaxation mechanisms have been proposed in the experimental works to understand the different features found. Thus, e.g., in the fragmentation of rare gas clusters the detection of He₂⁺ showed that the nanodroplet released the excess energy by the ejection of this ion,¹³ rather than through an evaporative process. Besides, the breakup of the nanodroplet was postulated to explain that the mean energy released per evaporated helium atom is greater for the smaller nanodroplets.^11,12 Regarding the R–I photodissociation, the results were interpreted in terms of hard-sphere binary collisions between the fragments and the helium atoms.¹⁸ In this context it is clear that studying these kinds of processes theoretically is interesting, so as to obtain a deeper insight into the dopant species-helium energy exchange process.

In a theoretical study of the Cl₂(B) photodissociation in helium nanodroplets at T = 4 K (i.e. non-superfluid liquid helium) an important cage effect was determined,²¹ leading to a reduction of the Cl(²P_3/2) + Cl*(²P_1/2) fragment velocities compared with the gas phase result. A semiclassical path integral centroid molecular dynamics was used for liquid helium and a quantum wave packet dynamics for the impurities.

The fragmentation of rare gas clusters inside helium nanodroplets was studied theoretically employing a quantum/classical strategy for the dopant, while the liquid helium was described by a friction force (acting only for atom velocities above the Landau critical velocity).²² This method was improved using the so-called averaged zero point (AZP) method,²³ where the helium atoms are described classically but including the zero point motion coming from the definition of a wave function centered at the position of each atom.

The strong correlation found experimentally between the amount of energy released from the molecule to the nanodroplet and the mass of the photofragments in the photodissociation of alkyl iodides¹⁸ (where a similar energy excess but different masses of the fragments were examined) has encouraged us to carry out the present work. Thus, our main goal here has been to try to understand better the role played by the fragment mass in the photodissociation inside a superfluid helium nanodroplet

X₂(ground state)@(⁴He)_N + hν → [X₂(excited state)@(⁴He)_N]* (1a)

[X₂(excited state)@(⁴He)_N]* → X(²P_3/2) + X*(²P_1/2) + [(⁴He)_N′]* + (N − N′)⁴He. (1b)

Eqn (1a) shows the electronic excitation of the embedded X₂ molecule (λ ≈ 400 nm; 3.10 eV);²⁴eqn (1b) refers to the photodissociation process, the (N–N′)⁴He term of eqn (1b) only reflects the total number of evaporated He atoms, and here N has been taken to be equal to 300.

To model this situation in a comprehensive way we have analyzed the photodissociation of several hypothetical X₂ isotopic variants of the Cl₂ reference system (photodissociation induced by the B ← X electronic transition),²⁵ in order to explore in a systematic manner a fairly wide range of masses (m_X: 0.25m_Cl–1.50m_Cl). This means that both the initial ground state vibrational wave function and the potential energies involved in the dynamics have been taken as identical to those of Cl₂. Proceeding in this way we can attribute the differences found in the dynamical simulations exclusively to the mass of each specific case analyzed.

This study has been performed using a quantum hybrid approach recently proposed by us²⁵ and previously applied to investigate the dynamics of several physicochemical problems involving (⁴He)_N and atoms or molecules.^25–28 Consequently, the helium and the X₂ molecule have been described using the time dependent density functional (TDDFT) theory and standard quantum mechanics, respectively, analogously to the Cl₂(B) photodissociation.^25,26 This method provides a good compromise between the quality of the description of the doped quantum fluid and the computational feasibility of the calculations, and can also be a powerful tool for studying the mechanisms implied in the energy exchange between the helium nanodroplets and the dopant species.

This paper is organized as follows: the theoretical methods used are concisely described in Section 2, the analysis of the most important results obtained is considered in Section 3, and the summary and conclusions are reported in Section 4.

2. Theoretical method

The theoretical method used to describe the quantum dynamics of the photodissociation of a homonuclear diatomic molecule, X₂, embedded in a superfluid helium nanodroplet has been recently proposed by us.²⁵ This method has hybrid character: the helium atoms are described employing the mean field TDDFT method and the X₂ molecule is described using a standard time dependent quantum wave packet (WP). Moreover, the energy functional used in the previous reference to describe the helium is the so-called Orsay-Trento (OT) phenomenological functional (T = 0 K),²⁹ with some reasonable and commonly used approximations (the backflow term and the non-local contribution to the helium correlation energy have not been considered).^{25–28,30–32} Therefore, in this section we will only review the main features of the TDDFT/WP approach and address the interested reader to ref. 25 for further details.

Differing from ref. 25 where, as a first application of the TDDFT/WP method, the photodissociation of Cl₂ (B excited state) in (⁴He)_N was investigated analyzing the influence of the nanodroplet size on the dynamics (N: 50–500), here we have focused the attention on the effect of the atomic mass on the dynamics. To do this in a comprehensive manner we have examined several hypothetical isotopes of the Cl₂ (B ← X electronic transition) reference system, to be able to sample a wide variety of masses for the X atom (m_X: 0.25m_Cl, 0.50m_Cl, 0.75m_Cl, 1.00m_Cl and 1.50m_Cl).

To consider exclusively the effect of the mass we needed to keep constant the remaining ingredients of the system contributing to the photodissociation process. Hence, the initial (Cl₂) ground electronic state rovibrational wave function φ_Cl2(v = 0, j = 0), that in the B ← X electronic transition suddenly evolves into the Cl₂ B potential energy curve, according to the Frank–Condon principle (vertical transition; cf. Fig. 1 of ref. 25), and the potential energy curves of Cl₂(X) and Cl₂(B) have not been modified, when considering the photodissociation of the X₂ molecules containing the X “isotopes”.

The choice to maintain the initial rovibrational ground state wave function of Cl₂(X) only produces slight differences in the initial kinetic energy, due to the different masses and the resulting zero point energy (ZPE) considered for the X₂ wave function (cf.Table 1). Since this kinetic energy of the X₂ molecule in the electronic ground state is related to the uncertainty principle (vibrational motion), rather than to a purely translational kinetic energy, we do not expect this to influence in a significant way the photodissociation process on which we want to focus (the kinetic energy associated with the mean velocity of each X atom a little after the excitation into the B state is much larger than the ZPE). Of course, if we had decided to employ the rovibrational ground state wave function that really corresponds to each mass (X₂), this would have produced a wide variety of initial X₂ potential energies for the dynamics, once the Franck–Condon principle is applied in the B ← X electronic transition. The energies of the X₂ model molecules at the initial time (t = 0) of the dynamics are collected in Table 1, where it can be seen that the energy differences are in the 3.4–5.6% interval (taken as a reference the energy of X₂ for m_X = 0.25 m_Cl).

Table 1 Initial time (t = 0) energies of the X₂ diatomic molecules^a

m X (mCl unit)	〈Ekin〉 (K)	〈Etot〉 (K)	〈Etot〉 diff. (%)
a Mean values of the zero point energy motion (kinetic energy part only) and total energies. The relative differences between the mean values of Etot with respect to the mX = 0.25mCl case are also shown.
0.25	797.8	11891.9	0.0
0.50	398.7	11492.8	3.4
0.75	265.8	11359.9	4.5
1.00	199.2	11293.3	5.0
1.50	132.8	11226.5	5.6

---

A nanodroplet with 300 ⁴He atoms has been selected for this study. This nanodroplet size (radius = 17.5 Å) represents a compromise between the computational cost and dealing with a size comparable to the experiments. Besides, this nanodroplet is large enough to make possible the determination of the two operating modes for the X₂–helium energy exchange (cf. Section 3.2). If a smaller nanodroplet had been selected, e.g. the case N = 50 (and similarly for N = 100), the energy exchange would only result from the collision of the X fragment atoms with the solvation shell (cavity wall); as after this collision the fragment atoms would essentially be leaving the nanodroplet surface.

In our approach, the evolution of the nanodroplet is coupled with that of the molecule and, due to the symmetry of the problem and assuming a zero angular momentum situation,²⁵ for the molecule is only needed to deal with the relative coordinate between the two atoms, which is denoted by r. The photodissociation takes place along the molecular axis, which is placed in the z-axis, and the origin of coordinates is placed in the centre of the nanodroplet.

The two coupled Schrödinger-like non-linear equations of motion that describe the temporal evolution of the helium effective complex wave function, |Ψ_He(R_He,t)|² ≡ ρ_He(R_He,t), and the relative coordinate molecular wave function (wave packet), φ_X2(r,t), read, respectively, as:

ρ_He(R_He) and are the density and the sum of the correlation and potential energy densities of liquid ⁴He, respectively, the OT functional, that is introduced through the term, describes the superfluid helium, and the He–Cl₂(X, B) and Cl₂(X, B) potential energies have been taken from ref. 33, where the “X” symbol in the parentheses here refers to the electronic ground state of the Cl₂ molecule.

The time propagation of the wave functions has been determined by solving eqn (2a) and (2b) numerically, using discretization techniques and applying standard procedures. Besides, negative imaginary potentials (NIPs) have been added for X₂ and helium in order to avoid non-physical reflections of the wave functions at the limits of the grid.²⁵

3. Results and discussion

3.1. Photodissociation mechanism

The aim of this section is to obtain a deep insight into the influence of the atomic mass on the photodissociation dynamics inside superfluid helium nanodroplets. Thus, five different values of the atomic mass have been selected for the X₂ diatomic molecule, in order to cover a wide enough mass range keeping the investigation computationally affordable. These masses correspond to m_X = 0.25, 0.50, 0.75, 1.0 and 1.5m_Cl, i.e. expressed in terms of the atomic chlorine (³⁵Cl) mass. Furthermore, to ensure that the possible differences observed in the dynamical behavior arise exclusively from the mass effect, we have considered the same values for the other initial properties specifying the input data for the dynamics study. Among other things, this framework includes all masses using the same initial relative coordinate wave packet that corresponds to the ground state of the chlorine molecule.

The photodissociation mechanism of X₂(B) is very similar to that observed for the chlorine molecule in the B excited electronic state.^25,26 Therefore, e.g., it takes place in the picosecond timescale with an efficient energy exchange between the molecule and the nanodroplet; and the quantum interference resulting from the interaction of X₂(B) with the helium environment leads to an oscillating velocity distribution of the atomic (X) photofragments. However, the particularly large energy exchange produced for the lowest masses explored (0.25m_Cl and 0.50m_Cl) can even induce the geminate recombination of the X atoms regenerating the X₂ molecule. Thus, for m_X = 0.50m_Cl there is a recombination probability of ≈86% while for m_X = 0.25m_Cl the probability is 100%.

In the former case (m_X = 0.50m_Cl) the wave packet remains for a long time close to the nanodroplet inner surface, until the X₂–helium attractive interaction induces the re-solvation (at the surface) of a fraction of the X₂ wave packet and then it splits into two parts. The solvated fragment recombines and the remaining one leaves the nanodroplet leading to dissociation. The photodissociation process for the m = 0.25m_Cl “isotope” variant has a rather different mechanism, since the energy exchange is even more efficient than that for m_X = 0.50m_Cl and the wave packet comes back to the center of the nanodroplet before reaching the nanodroplet inner surface. The process of recombination, however, does not occur directly, as a “rebound” effect occurs due to the high excitation of the nanodroplet that produces density waves.

Some snapshots showing the time evolution of the X₂ wave packet probability density and the effective potential energy that governs its dynamics (i.e. the sum of the Cl₂(B) potential energy and the Cl₂(B)–helium interaction potential energy)²⁵ are shown in Fig. 1a for the case m_X = 0.25m_Cl, in order to visualize its unsuccessful photodissociation mechanism. Important oscillations are formed in the wave packet due to the collision with the first solvation shell, which are progressively attenuated, and the confinement provided by the surrounding helium avoids the continuous spatial spreading of the wave packet with time.

Fig. 1 Snapshots of the X₂ (m_X = 0.25m_Cl) squared modulus of the relative coordinate wave packet (blue) and the effective potential energy (black) (a); snapshots of the helium density in the xz-plane (three- (b) and two-dimensional (c) representations) at the same time values as in (a). The z-axis corresponds to the molecular photodissociation axis and in (c) the highest helium density is indicated in yellow, while the absence of helium is indicated in black.

The evolution of the helium density (xz plane) is presented in Fig. 1b and c (three- and two-dimensional representations, respectively). At the beginning of the process strong distortions are generated in the helium density, mainly in the vicinity of the z axis (photodissociation axis), and shock waves are produced due to the collision of the wave packet with the first solvation shell. Once the shock waves collide with the nanodroplet surface some helium density escapes from the nanodroplet (evaporation process). The circular like black areas observed inside the nanodroplet in the two-dimensional plots (Fig. 1c) correspond to the cavities formed around the X₂ molecule or the X atoms (depending on the time values considered) where no helium can be found.

It is worth noting that the geminate recombination is induced by the geometry, i.e. by the fact that we are dealing with nanodroplets (finite systems) rather than by the nature of the liquid. Before the lightest atoms (m_X = 0.25m_Cl) reach the inner surface of the nanodroplet, the X-helium net attractive interaction force acting on them arising from the asymmetric helium distribution around each atom (one sided forces in the vicinity of the surface) is able to stop them and change the direction of their velocities. Then, both X atoms start moving towards the center of the nanodroplet, progressively approaching each other, and, finally, the recombination takes place. However, if the velocity of the X atoms is high enough (m_X above 0.50m_Cl, approximately) the force generated by the asymmetric distribution of helium is not capable of stopping them and, consequently, they are able to leave the nanodroplet completing the photodissociation process. Indeed, it should be mentioned that if the photodissociation would take place in superfluid bulk liquid helium, there would not be a driving net force coming from the impurity-helium interaction motivating the approach of the two X atoms.

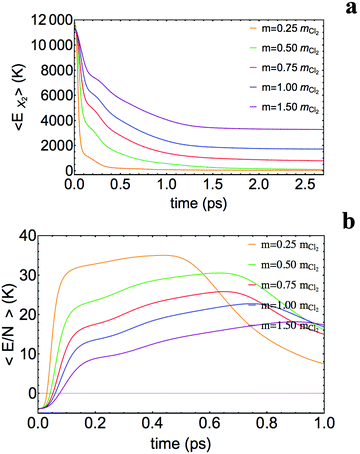
The temporal evolution of the mean value of the relative coordinate and its corresponding velocity are shown in Fig. 2 and 3, respectively. These plots end when the NIP begins to absorb the wave packet, at a large distance from the nanodroplet. The general behaviour is coincident with that observed in the case of the Cl₂ photodissociation;²⁵ but as for the X₂ molecules with the lower masses (m_X = 0.25m_Cl and 0.50m_Cl) the energy exchange is even more effective than that for Cl₂, the atomic X fragments can be stopped leading to the geminate recombination process (i.e. negative relative velocities can occur; cf. the inner panel of Fig. 3). In Fig. 2 and 3 the “rebound” effect taking place during the X + X* recombination can also be observed for the m_X = 0.25m_Cl case.

Fig. 2 Time evolution of the mean value of the relative coordinate.

Fig. 3 Time evolution of the mean value of the relative velocity. The inset shows the time evolution for the two lower masses at higher time values.

The most important general feature observed is the strong relationship that exists between the mass of the atoms and the magnitude of energy exchange between the dopant molecule and the helium: the lower the mass, the higher the energy exchange; and in the photodissociation process this may even lead to the recombination of the atomic fragments inside the nanodroplet, as we have already mentioned (for m_X = 0.25m_Cl the whole wave packet recombines, while for m_X = 0.50m_Cl only a small fraction of the wave packet (≈14%) leaves the nanodroplet). In Table 2 are given the final mean values of the (kinetic) energy and velocity of the atomic photofragments. The final mean energy increases with the atomic mass and varies from 7.0 to 29.3% of the initial total mean energy of X₂ within the m_X: 0.75m_Cl–1.50m_Cl interval.

Table 2 Mean values of the X + X* (kinetic) energy and of the atomic fragments velocity distributions at the end of the photodissociation process

m X (mCl unit)	〈Etot〉 final (K)	% of 〈Etot〉 initial	〈vX〉 final (m s^−1)
a This value only corresponds to the outgoing part of the X2 relative motion wave function.
0.25	—	—	—
0.50	—	—	242^a
0.75	790.8	7.0	493
1.00	1736.5	15.4	628
1.50	3294.2	29.3	716

---

To conclude this section, we analyze the velocity distribution of the leaving X atoms (cf.Fig. 4), which is the main observable that can be measured in the X₂ doped nanodroplet. This distribution is strongly oscillating for all the masses leading to photodissociation products, as it was already observed in the case of Cl₂ (m_X = 1.00m_Cl).^25,26 These oscillations arise from quantum interference resulting from the interaction of X₂(B) with the ⁴He environment in the early times of the photodissociation (0.00–0.20 ps; cf.ref. 26). Besides, from the velocity distribution of m_X = 0.50m_Cl it can be seen that the small lower limit value of the velocity occurs at around 50 m s⁻¹.

Fig. 4 Velocity distribution of the atomic (X) photofragments.

3.2. Energy exchange mechanism

In order to obtain deeper insights into the mechanism of the X₂–helium energy exchange, the temporal evolution of the X₂ molecule energy (kinetic + X–X potential energies) and the energy per helium atom of the nanodroplet has been plotted in Fig. 5a and b, respectively. From these figures two markedly different dynamic regimes are evident: at the very initial times, from t = 0 to around 0.10–0.15 ps (depending on the case), and the rest of the time, from around 0.10–0.15 ps to the end of the photodissociation process. From Fig. 5a and b it is clear that the fastest energy exchange is produced at the very initial times.

Fig. 5 Time evolution of the mean value of the X₂ energy (kinetic + X₂ potential energies) (a) and time evolution of the mean value of the energy per helium atom of the nanodroplet (the decrease of this magnitude results from the evaporation process) (b).

The first dynamic regime corresponds to the initial collision of the X atoms with the walls of the helium cavity (i.e. the volume found inside the nanodroplet and centered in the X₂ molecule where no He atoms are found; a cavity radius of about 4.8 Å).²⁵ It should be noted that in a very short time period after the B ← X electronic transition (from t = 0 to ≈0.01 ps) the initial potential energy of the molecule in the excited state is transformed into kinetic energy of X₂(B), due to the shape of the B potential energy curve.

The temporal evolution of the X₂–helium interaction potential energy, 〈E_int〉, is given in Fig. 6. The 〈E_int〉 value for the initial and main peak (repulsive interaction energy), which corresponds to the initial collision between the X atoms and the walls of the cavity, increases as the X mass decreases. This indicates that for the lighter masses the walls of the helium cavity and the X atoms get closer to each other than for the larger masses, due to the higher velocities reached by the lower masses, which lead to a collision of more sudden character. However, at the end of this collision the X₂–helium interaction potential energy decreases in an important way and becomes negative (of the order of a few hundreds of Kelvin; cf.Fig. 6 and Table 3), with the only exception of what happens for the lowest mass. This means that the X atoms and the surrounding liquid helium have been adapted to each other in a substantial manner. Because of this at the end of the first dynamic regime both the X atoms and the helium atoms placed in the cavity walls are moving at a rather similar velocity. Thus, the X atoms, which were initially moving very fast, push the surrounding helium atoms, which were initially at rest, until they reach an essentially coincident velocity.

Fig. 6 Time evolution of the mean value of the X₂–helium interaction potential energy.

Table 3 Frontier time between the two X₂–helium energy exchange regimes and mean values of the total energy of X₂ (kinetic + potential energies) and X₂–helium interaction energy at this time^a

m X (mCl unit)	Frontier time (ps)	〈Etot〉 frontier (K)	〈Eint〉 frontier (K)
a The initial total energy of X2 is in the range of 11 892–11 227 K (cf.Table 1).
0.25	0.078	1864	228
0.50	0.120	3900	−229
0.75	0.128	5619	−243
1.00	0.138	6545	−293
1.50	0.159	7717	−379

---

These results serve as inspiration to formulate a model to account for the initial dynamic regime. This model is based on an initial perfectly inelastic collision between an X atom of mass m_X, moving originally at the velocity v_i and an “effective” particle (helium atoms involved) of mass M originally at rest (a more detailed explanation is given after eqn (3)). At the end of this collision both species are moving together at the velocity v_f. Moreover, as the two X atoms are well separated when the collision is produced their interaction potential energy can be neglected and we can consider only their kinetic energy (E_i,f), which would be half of the kinetic energy corresponding to the reduced mass associated with the X–X relative motion. Thus, the velocities of each one of the X atoms before and after the collision (v_i,f) are given by and imposing the conservation of the total linear momentum (m_Xv_i = (m_X + M)v_f) we arrive at a rather simple relation between the atomic (X) kinetic energy ratio and the atomic mass m_X:

In this classical mechanics model E_i corresponds to the kinetic energy attained by each one of the X atoms once the initial potential energy resulting from the B ← X vertical excitation (energy taken with respect to the X + X* dissociated atoms) has been transformed into kinetic energy. This conversion from potential to kinetic energy occurs in a very short time (≈0.01 ps) and well before the collision of the X atoms with the surrounding helium atoms has taken place. Moreover, E_f corresponds to the kinetic energy of each one of the X atoms once the perfectly inelastic collision with the surrounding helium atoms has occurred, i.e. once the X atoms have reached the wall of the cavity, the radius of which (≈4.8 Å)²⁵ is about two times the equilibrium distance of Cl₂(B).²⁵ The time required for this collision to occur depends on the mass of the atoms and is in the 0.08–0.16 ps time interval (cf.Table 3).

Plotting the left side of eqn (3) as a function of m_X we obtain a remarkable good agreement with the linear behavior predicted by this equation (Fig. 7). Hence, from the energy exchange perspective, the initial step for the photodissociation of a homonuclear diatomic molecule inside a helium nanodroplet can be rationalized in terms of a perfectly inelastic collision of the X atoms with the cavity wall. From the analysis of the data represented in Fig. 7 we determine a value of M equal to 10.1 amu; which means that in the early step of the photodissociation process each X atom collides and pushes on average a little more than two He atoms.

Fig. 7 Dependence of the expression as a function of the atomic mass (m_X), for the first dynamic regime (perfectly inelastic collision) of the photodissociation process.

In order to discern whether the perfectly inelastic collision involved in this part of the process arises from the presence of snowball structures in the initial helium configuration, we have carried out an analogous calculation, but using a hypothetic initial helium density without snowballs, and the same pattern has been found. Therefore, the reproduction of the theoretical results on the basis of a perfectly inelastic collision results from the induction of movement in helium as a result of the collision and not from the collision with a rigid snowball structure. Furthermore, it is worth noting that the nanodroplet induced geminate recombination of X + X* to lead to X₂(B) for the lower masses is mainly caused by the first part of the photodissociation process, because the X₂–helium energy exchange is particularly large.

The second dynamic regime for the energy exchange refers to the situation in which the atoms are travelling through the nanodroplet at velocities higher than the Landau critical velocity. In the previous investigation on the Cl₂ photodissociation,²⁵ from the 〈v_r〉 vs. 〈r〉 representation, we pointed out that a viscous fluid model could be applied in this context, but without analyzing it in quantitative terms.

Here, the exploration of different masses (m_X) allowed us to examine this question in a detailed way, reinforcing the previous qualitative arguments²⁵ by comparison of the friction parameters (b) obtained in the different simulations. A velocity of each X atom proportional to the friction force, , leads to a linear relationship between the velocity (v) and the distance travelled by the X atom (z):

The dependence of 〈v_r〉 versus 〈r〉 for the second regime of the energy exchange presents a rather linear shape in all the cases (Fig. 8). Defining v(z) ≡ 〈v_r〉/2 and z ≡ 〈r〉/2 similar values of the friction parameter b have been found for all the masses (Table 4). The resulting mean value is b = 0.37 atomic units. This value is about five times the friction coefficient obtained experimentally from the mobility of Na⁺ in superfluid bulk liquid helium at T = 1.42 K (b = 0.078 au).³⁴ Moreover, in a theoretical study of the fragmentation of Ne₃⁺ in helium nanodroplets, where the helium environment was modelled by a friction force, from the comparison with the experimental data a lower (0.025 au) and a upper (1.5 au) limit were proposed for the friction coefficient of Ne⁺.²²

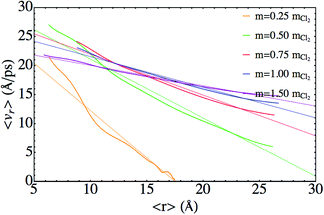Fig. 8 Dependence of 〈v_r〉 as a function of 〈r〉, for the second dynamic regime (viscous flow) of the photodissociation process.

Table 4 Friction coefficients

m X (mCl unit)	b (au)
0.25	0.32
0.50	0.40
0.75	0.41
1.00	0.41
1.50	0.39

---

In addition, we have recently published a dynamics investigation on the capture of a Ne atom by a helium nanodroplet using the same theoretical framework employed here.²⁷ When the mean value of the velocity is represented versus the mean value of position we also found a linear dependence for the Ne atom velocities above the Landau critical velocity. From the plots in Fig. 4 of ref. 13 a value of b equal to 0.38 au is obtained, which is very close to the values obtained from the present photodissociation study.

It is worth noting here that, for the lower mass considered (m_X = 0.25m_Cl), in the recombination process the X atoms come back towards the nanodroplet center at rather low absolute values of the mean velocity (cf.Fig. 3). Moreover, even though at some time values the velocity of each X atom is below the Landau critical velocity (≈58 m s⁻¹ (0.58 Å ps⁻¹) in superfluid (bulk) helium^35,36 and, due to the reasonable simplifications made in the OT functional to make possible this type of study, the theoretical value is ≈90 m s^−1 31), it does not remain constant (in absolute value).

This is caused by the highly excited helium density waves which are present in the nanodroplet. When these waves collide with the atoms some energy and momentum are exchanged between them and due to this the velocity of the X atoms is not constant over time. This is in contrast to the behavior found in the capture of a Ne atom, as once the atom mean velocity is below the critical velocity it remains constant in absolute value (cf. Fig. 3 and 4 of ref. 27). The energy conditions examined in the Ne capture are much softer (〈E_kin〉 initial: 9.74–2031.7 K)²⁷ than those in the present photodissociation study and this is the main reason for the observed differences.

To conclude the present analysis we have estimated the viscosity (η) of liquid helium from the values of the friction force parameter (b) and the van der Waals radius of the X atoms (i.e. the Cl value), assuming a Stokes flow of a sphere. We have obtained a value of η = 4.41 × 10⁻⁶ Pa s from the X₂ data obtained here and η = 4.95 × 10⁻⁶ Pa s from the Ne data of ref. 27. These similar values are comparable with the experimental results for superfluid bulk liquid helium at saturated vapor pressure (e.g. η = 2.385 × 10⁻⁶, 3.028 × 10⁻⁶, 4.806 × 10⁻⁶ and 9.537 × 10⁻⁶ Pa s for T = 2.17, 1.05, 0.95 and 0.85 K, respectively).³⁷

4. Summary and conclusions

In this work we have carried out a theoretical study on the influence of the mass in the photodissociation dynamics of a homonuclear diatomic molecule (X₂) embedded in a superfluid helium nanodroplet (T = 0.37 K) of 300 atoms (cf.eqn (1)). To do this we have employed a hybrid quantum dynamics method recently proposed by us (TDDFT (helium) + time dependent WP (X₂)) and considered several hypothetical isotopes of the Cl₂ reference system (B ← X electronic transition) in order to sample a wide variety of masses (m_X: 0.25m_Cl–1.50m_Cl). To the best of our knowledge this is the first time that this problem has been investigated theoretically.

The photodissociation mechanism of X₂(B) is very similar to that of Cl₂(B). It occurs in the picosecond timescale, there is an efficient X₂–helium energy exchange and the existence of quantum interference results in an oscillating velocity distribution of the dissociating X atoms.

The efficiency of the X₂–helium energy exchange mechanism increases in a substantial way when the X atom mass (m_X) decreases. Thus, the energy exchanged from the molecule to the nanodroplet can be so large that it leads to the full and partial (≈86%) geminate recombination of the dissociating X atoms, for the lower mass values investigated here (m_X = 0.25m_Cl and m_X = 0.50m_Cl, respectively).

A detailed analysis of the photodissociation process has shown that, from the point of view of the energy exchange, it consists of two main steps. The former step occurs at the initial times of the photodissociation and can be rationalized in terms of a perfectly inelastic collision occurring between the atomic photofragments (X) and some helium atoms of the solvation shell. In the latter step the atomic photofragments are moving through the nanodroplet that behaves as a viscous fluid.

The two dynamic regimes for the energy exchange found in the present study (perfectly inelastic collision (IC) + viscous flow (VF); ICVF mechanism) are probably of general character for the photodissociation of molecules embedded in superfluid helium nanodroplets.

Acknowledgements

This work has been supported by the Spanish Ministry of Science and Innovation (project ref. CTQ2011-27857-C02-01), and we also want to acknowledge the support from the Autonomous Government of Catalonia (A. V. predoctoral fellowship and project ref. 2009SGR 17, 2014SGR 25 and XRQTC). Thanks are also given to Professor Ricardo Mayol (University of Barcelona) for helpful comments on the theoretical description of helium and reading the manuscript.

References

1. J. P. Toennies and A. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622.
2. M. Barranco, R. Guardiola, S. Hernández, R. Mayol, J. Navarro and M. Pi, J. Low Temp. Phys., 2006, 142, 1.
3. A. Slenczka and J. P. Toennies, in Low Temperature and Cold Molecules, ed. I. W. M. Smith, Imperial College Press, London, 2008, pp. 345–392.
4. S. Yang and A. M. Ellis, Chem. Soc. Rev., 2013, 42, 472.
5. J. Tiggesbäumker and F. Stienkemeier, Phys. Chem. Chem. Phys., 2007, 9, 4748.
6. S. Yang, A. M. Ellis, D. Spence, C. Feng, A. Boatwright, E. Latimer and C. Binns, Nanoscale, 2013, 5, 11545.
7. L. F. Gomez, E. Loginov and A. F. Vilesov, Phys. Rev. Lett., 2012, 108, 155302.
8. E. Latimer, D. Spence, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Nano Lett., 2014, 14, 2902.
9. A. Scheidemann, B. Schilling and J. P. Toennies, J. Phys. Chem., 1993, 97, 2128.
10. B. E. Callicoatt, D. D. Mar, V. A. Apkarian and K. C. Janda, J. Chem. Phys., 1996, 105, 7872.
11. W. K. Lewis, B. E. Applegate, J. Sztáray, B. Sztáray, T. Baer, R. J. Bemish and R. E. Miller, J. Am. Chem. Soc., 2004, 126, 11283.
12. W. K. Lewis, R. J. Bemish and R. E. Miller, J. Chem. Phys., 2005, 123, 141103.
13. B. E. Callicoatt, K. Fröde, L. F. Jung, T. Ruchti and K. C. Janda, J. Chem. Phys., 1998, 109, 10195.
14. B. E. Callicoatt, K. Fröde, T. Ruchti, L. Jung, K. C. Janda and N. Halberstadt, J. Chem. Phys., 1998, 108, 9371.
15. T. Ruchti, K. Fröde, B. E. Callicoatt, H. Ludwigs and K. C. Janda, J. Chem. Phys., 1998, 109, 10679.
16. T. Ruchti, B. E. Callicoatt and K. C. Janda, Phys. Chem. Chem. Phys., 2000, 2, 4075.
17. G. E. Douberly, J. M. Merritt and R. E. Miller, Phys. Chem. Chem. Phys., 2005, 7, 363.
18. A. Braun and M. Drabbels, J. Chem. Phys., 2007, 127, 114303.
19. A. Braun and M. Drabbels, J. Chem. Phys., 2007, 127, 114304.
20. A. Braun and M. Drabbels, J. Chem. Phys., 2007, 127, 114305.
21. T. Takayanagi and M. Shiga, Chem. Phys. Lett., 2003, 372, 90.
22. D. Bonhommeau, A. Viel and N. Halberstadt, J. Chem. Phys., 2004, 120, 11359.
23. D. Bonhommeau, M. Lewerez and N. Halberstadt, J. Chem. Phys., 2008, 128, 054302.
24. Y. Asano and S. Yabushita, J. Phys. Chem. A, 2001, 105, 9873.
25. A. Vilà, M. González and R. Mayol, J. Chem. Theory Comput., 2015, 11, 899.
26. A. Vilà, M. González and R. Mayol, Phys. Chem. Chem. Phys., 2015, 17, 32241.
27. A. Vilà, M. González and R. Mayol, Phys. Chem. Chem. Phys., 2016, 18, 2006.
28. A. Vilà, M. González and R. Mayol, Phys. Chem. Chem. Phys., 2016, 18, 2409.
29. F. Dalfovo, A. Lastri, L. Pricaupenko, S. Stringari and J. Treiner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1193.
30. D. Mateo, A. Hernando, M. Barranco, E. Loginov, M. Drabbels and M. Pi, Phys. Chem. Chem. Phys., 2013, 15, 18388.
31. N. B. Brauer, S. Smolarek, E. Loginov, D. Mateo, A. Hernando, M. Pi, M. Barranco, W. J. Bruma and M. Drabbels, Phys. Rev. Lett., 2013, 111, 153002.
32. D. Mateo, F. Gonzalez and J. Eloranta, J. Phys. Chem. A, 2015, 119, 2262.
33. J. Williams, A. Rohrbacher, J. Seong, N. Marianayagam, K. C. Janda, R. Burcl, M. M. Szczezśniak, G. Chałasiński, S. M. Cybulski and N. Halberstadt, J. Chem. Phys., 1999, 111, 997.
34. H. Günther, M. Foerste, G. zu Putlitz and T. Schumacher, Low Temp. Phys., 1996, 22, 143.
35. D. R. Tilley and J. Tilley, Condensates and Excitations. Superfluidity and Superconductivity, Institut of Physics Publishing, Bristol, 1990, pp. 41–53.
36. J. F. Annet, Superfluid Helium-4. Superconductivity, Superfluids and Condensates, Oxford University Press, Oxford, 2004, pp. 38–43.
37. R. J. Donnelly and C. F. Barenghi, J. Phys. Chem. Ref. Data, 1998, 27, 1217.

---