Stepwise collapse of highly overlapping electrical double layers

Abstract

When two charged surfaces and their accompanying electrical double layers (EDLs) approach each other in an electrolyte solution, the EDLs first begin to overlap and finally collapse under confinement. During this collapse we can observe repulsive forces and film-thickness transitions, which contain valuable information about different structural elements present at the interface. Sensing and discriminating these transitions by size and frequency of occurrence is possible via direct force measurements. Changing salt concentration or pH provide additional means to shift chemical potentials and interfacial populations, and therefore also to shift the relative stability of these structural elements. We provide new evidence that the previously observed oscillatory surface force appearing at the final stages of collapse of the EDL is initially due to layering transitions between hydrated ions, which then develop into smaller transitions between highly confined adsorbed ion states.

---

Introduction

Surface forces that arise between two surfaces with overlapping electrical double layers (EDL) can be approximately described by the DLVO theory,^1,2 which is the sum of a double-layer repulsion and the attractive van der Waals force between the surfaces. Deviations from DLVO theory are known to occur at high electrolyte concentrations and small surface separations (<5 nm), where the role of ion–ion correlations, ion-specific effects, ion hydration and molecular structure are no longer negligible.^3,4 Significant deviations were measured by direct surface-force measurements and have revealed repulsive hydration forces with decay lengths ranging from 0.1 to 1 nm,⁵ which turned out to be oscillatory forces, supposedly due to water layering, at surface separations below some 2 nm.⁶ There is another class of deviations, namely the adsorption of hydrated ions,⁷ and more recently their confinement-induced layering,^8–10 which have also been considered to be responsible for the repulsive hydration forces.

The exact structure and ordering of hydrated ions at the interface is still an active subject of investigation. Open questions include whether hydration forces cause depletion of ionic solutes in the water layer near the surface¹¹ and whether there are signs of the forced adsorption (or surface condensation) of ions or expulsion of the bound water upon application of external forces.^8,10,12,13

In addition, ion hydration modulates the adsorption energy of ions at charged interfaces.¹⁴ Namely, it has been suggested that counter-ions adsorbing on a single charged mica surface can take the following adsorption states: OS_ext (external outer sphere), when the hydrated cation is located above the surface hydration layer retaining its hydration shell, OS_ads (adsorbed outer sphere), when the hydrated cation disturbs or displaces the surface hydration layer and adsorbs to the mica, and IS (inner sphere), when the cation is partially dehydrated of its primary hydration shell and forms close bonds with the oxygen atoms within the mica surface.^15,16 Unlike hard-sphere model fluids such as OMCTS or cyclohexane, which create rather periodic oscillatory forces between hard surfaces,^4,17,18 the layering of hydrated ions is more like a layering of “soft spheres” due to the composite nature of the layering structural units and has not been experimentally explored in comparable detail. Although molecular-dynamics simulations have shown that water molecules tend to order next to single mica surfaces in the presence of hydrated K⁺ ions¹⁹ and that the overlap of hydration shells can lead to a strong repulsive hydration force,²⁰ the real confined interface seems to be more complex.

The atomically smooth model surface of choice to create strongly overlapping and confined EDLs over micrometer lateral scales is muscovite mica; it consists of a layered aluminosilicate structure with octahedral sheets of Al³⁺ sandwiched between tetrahedral sheets of Al³⁺ and Si⁴⁺. The permanent negative lattice charge of the mica results from the substitution of Si⁴⁺ by Al³⁺ in the tetrahedral layer, which is balanced in the crystal by interlayer K⁺ positioned at 1.7 Å above the outermost basal oxygen atoms. Dry cleavage of the mica along the (001) direction results in half of the interlayer K⁺ atoms remaining on one of the created surfaces in order to balance the surface charge. When in contact with an aqueous electrolyte solution, the negative mica lattice charge of 1e⁻ per 47 A² is balanced by an excess of mobile or adsorbed counter ions in the EDL.²¹

Espinosa-Marzal et al.¹⁰ measured compression isotherms (surface force vs. distance) of aqueous KNO₃ electrolyte confined between mica surfaces with an eSFA as a function of electrolyte concentration. They identified three different phenomenological regimes of KNO₃ concentration, characterized by distinct features seen in force–distance curves, film-thickness transitions, and pull-off forces. These are the “DLVO” regime below 0.3 mM, the “ordering” regime above 0.3 mM and the “solidification” regime above ≈20 mM KNO₃. Only above ≈0.3 mM does the layering of hydrated K⁺ ions occur, which leads to multiple film-thickness transitions of 4 ± 1 Å size. The final hydrated ion layer—reminiscent of the Inner Helmholtz Plane (OHP)—causes a 2.9 ± 0.3 Å transition, accompanied by a sharp decrease of pull-off force.

In the present study, we have further investigated the narrow concentration range at the crossover between the “DLVO” and the “ordering” regimes around 0.3–3 mM KNO₃, in which a discontinuous sudden decrease of the pull-off force, π, henceforth called the “π-transition”, occurs. The coincidence of the π-transition and occurrence of film-thickness transitions is remarkable. Therefore, we have studied the evolution of this π-transition in great detail and analyzed the associated film-thickness transitions (FTTs), in order to propose a detailed structural hypothesis for the underlying molecular mechanisms.

Experimental methods

The surface forces apparatus (SFA) makes use of the micro contact between two crossed cylinders.^22,23 The overlap of two EDLs can be studied within this micrometer-sized contact area. To determine the surface force, one surface is mechanically fixed and the other is attached to a compliant spring. The interaction force between the surfaces is readily determined from the deflection, Δs, of this spring as F = k × Δs, where k is the spring constant (here k = 1602 ± 55 N m⁻¹). The surface separation can be controlled with sub-nanometer precision by means of a specialized actuator. This separation between the surfaces, D, is also constantly measured using white light Multiple Beam Interferometry (MBI) by detection and analysis of the Fringes of Equal Chromatic Order (FECO). In our instrument, the statistical precision of the surface-separation measurement is ±20 pm, thanks to an automated simultaneous evaluation of multiple fringe wavelengths.^24–26 The geometrical radius of the cylinder surfaces is measured using an integrated X-Y scanning feature. As is commonly practiced, we have chosen to plot the normalized force, F/R(D), generally termed the “force curve”. The geometric normalization F/R relates to the equivalent interaction energy between flat surfaces, according to the Derjaguin approximation.²⁷ The maximum F/R-value applied in our measurements was 700 mN m⁻¹. As the contour of the mica surfaces appreciably flattens above some 10 mN m⁻¹, the F/R-values are overestimated because, in the normalization process, we choose to ignore the increase of R upon deformation. The absolute optical error of D is typically smaller than 2 nm at the applied maximum load. Possible systematic errors due to mica-layer compression can lead to negative surface distance (D) values, but this does not affect the size of the measured film-thickness transitions mainly considered here, since each of them is occurring over a particular but fixed load. Our extended surface forces apparatus (eSFA) provides previously described improvements in precision, sampling frequency and stability.²⁸

Most force–distance curves were measured during approach or loading at a constant actuator speed of 5 Å s⁻¹. For comparison with previous data we also reproduced some experiments with the reciprocating loading/unloading pattern that is commonly practiced with non-automated SFAs, e.g. to explore the different force minima of the oscillatory potential. The pull-off force, π, was determined during unloading at a constant actuator speed of 5 Å s⁻¹. The experimental data set presented here is based on a statistically relevant investigation (>50) of different mica surfaces submerged first in deionized water then in aqueous solutions of different salt concentrations at uncontrolled or selected pH-values for each given pair of surfaces.

Mica samples were prepared from Grade I Ruby Muscovite (S&J Trading, New York) by manually splitting sheets down to 2–5 μm thickness, followed by cutting into ≈1 cm² large pieces using ceramic surgical scissors. A 40 nm silver (99.99%, abcr GmbH, Germany) layer was then deposited onto one side of each mica piece at a vacuum base pressure of 1 × 10⁻⁶ mbar. The entire sample preparation and final mounting of the mica pieces in the eSFA was carried out in a very clean laminar-flow cabinet. A series of KNO₃ solutions was prepared at room temperature by dissolving the KNO₃ (99%, Sigma-Aldrich) in ultrapure water (puriss p.a., Fluka). The pH of the solutions was optionally adjusted using HNO₃ or KOH. All the solutions were also filtered through a 0.22 μm membrane prior to filling the eSFA cuvette. Samples of all solutions used were kept in sample storage and a random 10% of these samples were cross-checked using ion chromatography to verify salt concentrations and the stability of the pH. The mean absolute error in concentration was thus ±0.016 mM in the narrow concentration range around 1 mM considered here.

The fluid cell of the eSFA is in the form of a glass cuvette (volume = 22.4 ml). After being filled with the electrolyte solution, the instrument was allowed to equilibrate, while the instrumental drift was continuously monitored, without actuator action, at a safe surface separation of around D ≈ 1 μm. Equilibrium was deemed to be achieved when the instrumental drift rate of surface separation was ≤5 Å min⁻¹. At the beginning of each experiment, the two mica surfaces were approached at a constant actuator velocity of 5 Å s⁻¹ and allowed to snap into adhesive contact in air, as well as in water, where we also calibrated the optical zero; i.e. we determined the mica thickness and interference fringes order via white light interferometry. It was observed and verified that the actuator motion was linear at distances outside the range of expected surface forces, i.e. >0.5 μm, i.e. the optically measured speed of approach of the surfaces was checked to be linear and equal to the set actuator speed. The occurrence of a snapping into solid adhesive mica–mica contact in pure water was taken as a test that the surface contact was free of micro- or nano-contamination. The optical zero, which defines D = 0, was set at the adhesive yet externally unloaded mica–mica contact in water, relative to which all the surface separations, D, are reported here. While this method standardizes mica compression effects due to equivalent contact loading by the mica–mica adhesion in the contact, it may still include additional small systematic errors, e.g. due to a tightly bound hydration layer remaining on the mica surfaces in contact. Such errors affecting the absolute measurement of film thickness at the (sub)nanometer level were thus maintained as constant as possible throughout the experimental series. All data shown here are raw data, i.e. without cosmetic shifting of the D-axis, and may therefore also include negative values in cases of significant mica compression at higher loads. The experimental series were completed using both sequences of increasing and decreasing electrolyte concentrations to assess interfacial structural history effects or progressive contamination, which may affect the results. The temperature of all measurements was controlled to be 22.0(2) °C. The concentration of the solutions within the cuvette remained constant during the force measurements as confirmed by ion chromatography on selected control samples, both before and at the end of the experiment.

Results

The π-transition is the key characteristic feature that marks the crossover from the low-concentration “DLVO regime” to the medium-concentration “ordering regime”, as previously defined by Espinosa-Marzal et al.¹⁰Fig. 1 shows a compilation of previously measured data points together with some measured in this study. By specifically focusing on the narrow concentration range 0.1–10 mM KNO₃ at a pH of ≈5.7, we wanted to gain more detailed insights into the molecular structure of the confined EDLs.

Fig. 1 The π-transition, measured as abrupt decrease of pull-off force upon surface separation in KNO₃ solution at the concentration C_π ≈ 1 mM (shifting with pH as we shall see). The presented measurements were made without rigorous pH control at pH ≈ 5.7, i.e. under a solution that was at equilibrium with air. Two independent data sets are included here that were measured with two completely different eSFA apparatus designs. There is excellent quantitative overlap of the two data sets. The initial pull-off forces measured in deionized water are included along the left axis (0.001 mM KNO₃) as a reference.

In agreement with earlier results, the measured pull-off force initially decreases gradually with [K⁺] concentration, followed by a prominent discontinuous reduction of the pull-off force near 1 mM at uncontrolled pH ≈ 5.7. The magnitude of this π-transition (see arrow) is in the order of 20 mN m⁻¹ (equivalent to 3.18 mJ m⁻² according to the Derjaguin approximation). The abrupt nature of this π-transition suggests a sudden change of molecular structure at the buried interface, which reduces the adhesion energy. The hypothesis of an instability mechanism involving hydrated-ion layering was previously suggested based on the observation of a concurrent small film-thickness transition (FTT) during the mechanical loading of the contact.¹⁰ To this end we measured the size of FTTs at high resolution and carefully analyzed the data with statistical tools. The goal was to find and discern prominent characteristic sizes, which can provide additional information about structural elements present.

Indeed, if a large number of molecules throughout a load-bearing confined film collectively undergo a concerted structural transition, this is detected by the instrument as a discontinuous, often rapid, FTT. The observed size of such a film-thickness transition cannot be directly assigned to the size of a structural element like a particular molecule or complex at the interface, because it rather represents the difference between two molecular arrangements. In terms of mechanics, a FTT occurs if the second derivative of the effective surface interaction potential exceeds the spring constant of the force measuring spring, i.e. stiffness of the apparatus. It is important to note that not all FTTs are necessarily due to structural forces. For example, at a surface separation of some 1–4 nm, which is typically before any hydrated-ion layering is detected, the gradient of the attractive van der Waals interaction between the surfaces counteracts the EDL repulsion until the total gradient becomes attractive and exceeds the spring constant of the apparatus; a first mechanical instability occurs, which causes the surfaces to accelerate and jump closer, often to a small yet positive distance. We refer to this well-known initial mechanical instability as the vdW-jump (vdW = van der Waals). Its magnitude should not be analyzed and interpreted together with structural FTTs, since a vdW-jump also occurs in vacuum and its size contains no information about structural elements.

In practice, it is straightforward to identify the initial vdW jump; it is distinct from any subsequent FTTs due to its distance of occurrence and its size, which is often >1 nm as seen in Fig. 2(a) and (b). In this context we note that the size of the van der Waals jump decreases with increasing pH while maintaining the ionic strength constant, as seen in Fig. 2(b). Since the Debye length is not changing with pH if ionic strength is kept constant, this is thus an effect of surface potential. The surface potential is more negative at higher pH, which strengthens repulsive EDL forces at small distances and therefore brings the point of critical gradient (i.e. equal to the spring constant) to smaller distances.

Fig. 2 (a) Typical force–distance curve measured during loading, illustrating the vdW-jump followed by one FTT at a concentration of 0.7 mM KNO₃; the dotted line at D > 4 nm is a fit using the DLVO theory and assumes constant surface charge, with resulting surface potential −130 mV. (b) Magnitude of different film-thickness transitions and their dependence on pH at a total K⁺ concentration kept constant at 0.1 mM; the magnitude of the vdW-jump decreases with pH; for the FTT analysis in this paper the first vdW jump is systematically filtered out.

For the determination of EDL physical quantities, the surface forces measured at distances before the vdW-jump can be fitted to the DLVO equation using the expression developed by Chan et al. for the electrostatic repulsion at low electrolyte concentration under boundary conditions of constant surface charge.²⁹ This is a numerical solution of the non-linear Poisson–Boltzmann equation. The fitting parameters include surface potential and salt concentration. The calculated Hamaker constant is 1.9 × 10⁻²⁰ J. We note however that this fitting procedure is inadequate to determine the very small concentration differences (±0.1 mM) used in this experiment, the reason being the accuracy in force measurements (±10 μN m⁻¹). Thus, for a true concentration on the order of 0.1 mM, the fitting procedure would lead to errors as high as 0.5 mM (i.e. 500% rel. error) as estimated from attempts to fit many measured force curves.

It was previously reported that multiple FTTs start to occur coincidently at the concentration where the π-transition is observed.¹⁰ Using the finer resolution of salt concentrations used in the present data we shall verify this and attempt to establish the causalities and structural elements involved in this π-transition. Fig. 3 shows how the π-transition as well as the relevant concentration thresholds shift with pH. These thresholds shall be referred to as C_π, the concentration at which the π-transition occurs, C_L, the concentration above which FTT's are first observed, and, C_ML, the concentration above which multiple (more than one) FTTs are observed. The main characteristics of the π-transition are a sudden decrease in pull-off force, which is seen at all pH values, albeit less clearly at pH = 3.3. The insets show histograms of the pull-off forces measured over the displayed range of concentrations and they reveal a notable value gap, indicated by arrows. It is also evident from Fig. 3 that the values C_π, C_L and C_ML are altogether shifted to higher concentrations for lower pH. Remarkably, C_π and C_ML remain grouped together over this rather wide range of pH, which suggests a profounder link between the π-transition and (multiple) hydrated ion layering. We also observe how, at low pH, hydronium plays the role of an antagonist that delays and weakens both the π-transition as well as multiple layering; see also Fig. 5d for a schematic illustration of hydronium at the interface. We note that FTTs are only observed above a threshold bulk KNO₃ concentration, C_L, of 0.05 mM (pH 9.7), 0.3 mM (pH 5.7), 0.4 mM (pH 4.0) and 0.7 mM (pH 3.3). We also note that the values of C_L have intrinsic uncertainty, subject to the limited number of solution concentrations probed. One can recognize a general trend to higher threshold concentrations, C_L, with decreasing pH. A similar or even stronger trend can be observed for the multiple-layering threshold, C_ML, of 0.05 mM (pH 9.7), 0.6 mM (pH 5.7), 20 mM (pH 4.0) and 25 mM (pH 3.3).

Fig. 3 The π-transition measured over a wide range of pH. The pull-off forces are measured after loaded contact of mica surfaces in KNO₃ solutions; an increasing hydronium concentration (lower pH) tends to shift the concentration thresholds of the π-transition, C_π, and the occurrence of multiple layering, C_ML, to higher salt concentrations. At pH = 3.3, the π-transition has virtually ceased to exist. The bar near the bottom illustrates the effective uncertainty of C_π. Gray bands are added to guide the eye. Inset: Histogram of pull-off forces at a given pH value illustrating the data gap (arrow) resulting from the discontinuous character of the π-transition.

Fig. 4 shows an analysis of a large number of FTTs that were detected under various conditions. The evolution of the FTT size with concentration is displayed as histograms presenting their frequency of occurrence over the concentration range. Fig. 4 emphasizes the final FTTs, since this final FTT establishes the final interfacial structure—defining the pull-off force and hence is accountable for the π-transition.

Fig. 4 (a, c, e and g) Sizes of measured final FTTs as a function of electrolyte concentration obtained each on at least five different pairs of mica surfaces; note that the vdW jump-in was dismissed for this analysis. The gray bands are added to guide the eye. Graphs (b, d, f, and h) display FTT size distributions in the form of normalized histograms showing the size distribution of non-final (light blue) and final (black) FTTs at (b) pH = 9.7; (d) pH ≈ 5.7; (f) pH = 4.0; (h) pH = 3.3; the superposed light blue and black colors appear as dark blue. For normalization, the frequency of occurrence in the histograms was divided by the number of experiments done at each concentration to represent a measure for probability of occurrence. Between the thresholds C_L and C_ML the single FTT is counted as the final FTT. At pH ≈ 5.7, the pH of the solution was not actively controlled. The positions of the peaks (uni- and bimodal Gauss fitted) for the FTT are given numerically in the upper right corner. At lower pH we observe a single dominant peak around 3 Å whereas the data at higher pH contains two or more different structural elements. Two noticeably distinct FTT sizes are present at the high pH = 9.7 where the interface is largely depleted of hydronium and predominately populated by K⁺ ions. The displayed concentration range was extended for the data sets at lower pH as required by the shift of the π-transition to higher concentrations.

Fig. 5 Schematic illustration of different ion-hydration structures discussed here; black dots represent K⁺ ions and the graded halo (blue) sketches hydration water; (a) traditional model³⁴ of adsorbed ions that bind water at the surface, which are hypothesized to cause (oscillatory) hydration forces; this hydration force increases with concentration until full surface coverage by adsorbed hydrated ions is achieved (b) hydrated-ion layering with “soft-sphere” characteristics¹⁰ and a FTT magnitude ≥4 Å. (c) Different adsorbed ion states on a single mica surface according to Lee et al.³⁶ Translation into transition magnitudes between the outer-sphere states (OS) and inner-sphere state (IS) are Δ = 2.15 Å and Δ = 3.49 Å, respectively, pretending similar adsorbed states under confinement. The inner adsorbed state (IS) would correspond to the least polar configuration. (d) At low pH the interface structure is ruled by hydronium, which predominantly neutralizes surface charge; hydrated potassium layering is weak and the π-transitions vanish. (e) Schematic representation of the surface interaction potential as found at concentrations around the π-transition. Two or three hydrated ion layering maxima are followed by at least one maximum of highly confined adsorbed state; the last minimum determines the measured pull-off force.

The size of the final FTTs is displayed in Fig. 4(a), (c), (e) and (g) for different pH values, across the concentration range of the π-transition. There is a general trend showing an initially broader or bimodal distribution, which eventually converges towards the previously reported¹⁰ final FTT size around 3 Å at higher concentrations (indicated by gray bands).

For the following discussion it is important to realize how the final FTTs are different from non-final FTTs above C_ML. From the histograms in Fig. 4(b), (d), (f) and (h), one can readily see that the final FTTs are of small size (3 Å) at low pH, while at neutral and basic pH, these final FFTs reveal much more structural diversity. At (uncontrolled) pH 5.7 and pH 9.7, the distribution is clearly multi-modal and thus exhibits at least two characteristic transition sizes. In contrast, the histograms of the non-final FTTs (above C_ML) in Fig. 4(b), (d), (f) and (h) (blue bars) show a distinctively different statistical distribution than the final FTTs (grey bars). The overall trend is that the characteristic size of the non-final FTTs is 0.5–1.5 Å higher than that of the final FTT. We are aware, of course, that the classification “final” FTT remains somewhat arbitrary because it refers to the last experimentally observed FTT, before reversing the actuator direction at a chosen maximal spring load of 700 mN m⁻¹; one could never exclude occurrence of additional FTTs possibly occurring at even higher loads. To justify the term “final”, the maximum spring load was chosen to be at least five times higher than the maximum load usually applied in such loading experiments.³⁰

Discussion

The adhesive energy of a dry mica–mica contact is known to be stronger than expected from van der Waals interactions alone, and thus the polar component is substantial.³¹ Indeed, mica is cleaved along its basal plane during sample preparation; this is the crystal plane that consists of a charged layer of potassium cations compensating for the crystal lattice charge. Solvation dissociation of these ions is responsible for the negative charging of mica in aqueous solutions.

In deionized water, the pull-off force between two basal cleaved mica surfaces is reduced by roughly an order of magnitude compared to that of a comparable dry contact.³² While an important part of the reduction has been attributed to the high dielectric constant of water and/or the exchange of the interlayer K⁺ by H₃O⁺;³³ adhesion has also been hypothesized to be reduced by counter-ion hydration forces³⁴ and experimentally shown to depend on the relative crystallographic mismatch between the mica surfaces in a narrow angular range Δθ ± 1° near perfect crystallographic alignment.³⁵ While this angular dependence was reported to be relevant in similar salt solutions to those used here (i.e. 1.2 mM KCl), all experiments presented here were obtained with two surfaces aligned at around 90 ± 5° relative to each other, in order to minimize optical birefringence effects, i.e. we are not expecting to see such mica alignment effects. For reference, we always measured the pull-off force in deionized water with each set of mica surfaces and found a consistent average value of π = 90 ± 20 mN m⁻¹, which is well in agreement with above literature values.

Finally, what determines the pull-off force of our loaded interface after collapse of the EDL is predominantly a mixture of contributions from (i) remaining surface modulations due to molecular ordering, which involves the separation, (ii) local polar interactions and (iii) entropic modulations due to molecular ordering; the latter involves ions and water molecules alike. Essentially, the pull-off force is an integral yet sensitive indicator for changes of the molecular arrangement at the interface.⁴

The competition between [K⁺] and [H₃O⁺] at the interface is particularly relevant to our discussion about the origin of the π-transition.³⁷ The mere fact that the π-transition occurs with increasing [K⁺] concentration, yet is retarded and weakened at lower pH (i.e. higher [H₃O⁺]), suggests that K⁺ is indeed the ion species that enables the π-transition. These observations suggest that the number of K⁺ ions at the collapsed interface must abruptly increase at C_π. The attempt to relate C_π to the contact value of K⁺ is conversely not meaningful (see ESI†) because the underlying model does not account for confinement-induced structural or molecular ordering effects that start to dominate the thin film behavior at such small surface separations, i.e. <3–5 nm. Furthermore, the predicted K⁺ surface-population equilibria are predicted to change in a continuous manner with bulk concentration and therefore cannot provide an explanation for the abrupt nature of the observed π-transition. The conclusion is that any comparison with existing EDL theory is inherently insufficient since the collapsed EDL no longer is an EDL.

It is interesting to note that K⁺ and H₃O⁺ ions are known to have distinctive properties, not only regarding the affinity to the mica surface, but perhaps more importantly, regarding the associated water structure.³⁶ For single mica surfaces, recent XRR studies have shown that K⁺ adsorbs discernably as 63% inner-sphere (IS) complexes and the rest as outer-sphere (OS) complexes. The hydronium ion is rather different; at pH 2.5, where hydronium largely predominates at the mica surface, the electron density appears fairly diffuse, indicating the absence of well-defined hydration layers.^14,36 In bulk water, the hydronium ion does not have a hydration shell structure as such but rather a water complexing or delocalized clustering effect,^38–40 corresponding to a picture of a diffuse water cushion covering the surface. Furthermore, Monte Carlo simulations^41,42 also support this view and show that K⁺ adsorbs discernably in IS and OS states at 2.15 Å and ∼5 Å, respectively, above the (001) mica surface, while H₃O⁺ smears out over a distance range of 1–3 Å away from the surface in the form of polygonal water islands. Thus, the different hydration structures adopted by K⁺ and H₃O⁺ ion species lead to considerably pH-dependent hydration structures at the interface. It is to be remembered that these are all studies on single surfaces, and hence, they are expected to be modified or amplified under conditions of strong nanoconfinement between two surfaces. Both types of ions may be mutually affected by the presence of the other.

Though the effect of bulk pH on the hydration structure of metal ions has not been studied in detail, XRR studies on single mica surfaces have shown that the pH can definitely influence how Sr²⁺ binds to the mica interface, namely as an IS or OS variant.⁴³

In addition, it has been conjectured by others that the rigid hydration shells of metal ions, such as K⁺, could be responsible for the “load-bearing capacity” of the electrolyte⁹ between mica surfaces. Meanwhile, it has been calculated that a stress on the order of 1000 MPa would be required to expel the final hydration water between mica surfaces.⁴⁴ In comparison, the maximum force we apply is 700 mN m⁻¹ (i.e. a maximum Hertzian contact pressure of 16.7 MPa), which would probably be insufficient to push out this very last bound hydration water layer.

The abrupt nature of the π-transition is particularly clear from the gap of π-values found in the histograms of Fig. 3 (insets). It suggests that an instability mechanism, which presumably depends on the number of K⁺ ions during collapse of the interface, is causing the phenomenon. The final FTT and the associated mechanical instability must be key to understanding the sudden change in pull-off force.

A picture, which is historically used to describe the interaction between two hydrated mica surfaces in salt solution, invokes multiple water layers at the interface.⁶ Two years before the oscillatory nature of these forces was resolved by Israelachvili, Pashley recognized that exponentially repulsive hydration forces, seen at surface separations below some 2–3 nm, are related to hydrated counter-ions adsorbed onto the mica surface.^34,37 The situation is schematically illustrated in Fig. 5a. It was also noted by Pashley that these repulsive hydration forces suddenly appear around a concentration of 0.3 mM of KCl at pH ≈ 5.7. We note that his finding coincides perfectly with the C_L value found for KNO₃ in this work. Both historic interpretations seem to be guided by the available data with the limited instrumental resolution at that time.

An interpretation of our results within these traditional models is however not satisfactory: according to the traditional model by Pashley, hydronium ions substitute K⁺ counter-ions at the interface during the van der Waals jump-in (i.e. collapse), at initially low salt concentration. At the concentration C_L, this substitution would come to an end and extra repulsive hydration forces due to trapped hydrated potassium ions would appear that could explain the reduction of pull-off force; if measured at high resolution, a maximum of only one FTT per surface is expected to be observed—the model is thus in fundamental contradiction with the observation of multiple (>2) FTTs.

In contrast to Israelachvili's data, our statistical analysis of step sizes clearly shows that FTTs are structurally diversified, and, for example, the non-final transitions are significantly larger than expected from the initially proposed ≈2.5 Å water layering. The interpretation suggested by Israelachvili does not clarify the role of ions and the physical mechanisms leading to the multiple, apparently periodic oscillations. We conclude that, while traditional interpretations provided by Pashley or Israelachvili were able to provide a working hypothesis for the historical data, these models cannot account for the existence of a π-transition nor the structural richness presented here.

We now consider the hydrated-ion-layering model proposed by Espinosa-Marzal et al.¹⁰ (Fig. 5b). At the concentrations used in the present study, hydrated K⁺ ions can be seen as quasi spherical particles with associated mobility in water. It is known both experimentally and theoretically that spherical molecules, vesicles or colloids in solution near a flat surface tend to produce layering effects¹⁸ due to the geometrical constraint imposed by the surface. Oscillatory layering forces superposed on a repulsive force arise because the (multi-) layered system as a whole resists reordering with an energetic (mainly entropic) barrier, which can be overcome by external loading. It is interesting to note that layering displays a quantized yet overall exponentially increasing repulsive force during stepwise drainage—a feature also assigned to the “hydration” forces measured early on, using the conventional SFA.³⁴ Every time when the layering energy is overcome by external work, i.e. when the second derivative of potential equals the apparatus compliance, a typical FTT is observed with step size resembling some 0.8–1σ, σ being the layering particle diameter. The number of layers at the interface changes abruptly from N to N − 1. Layering transitions thus represent a mechanical instability mechanism that can be observed in the form of FTTs. While the layering phenomenon is maximally prominent in a neat liquid of spherical molecules, the magnitude of the force modulation is now a function of concentration for dissolved spherical particles.^45,46 In agreement with theory, Richetti et al. observed in a system with dissolved monodisperse spherical micelles in the SFA that an increasing micellar volume fraction in the solution resulted in more and stronger oscillations in the force profile due to the layering.⁴⁷ A similar trend was observed for mixtures of water and a protic ionic liquid by Horn and Israelachvili.⁴⁸ To maintain overall charge neutrality layering of hydrated ions must involve hydrated co-ions of similar particle size.

The experimental results can be described with this model as follows: the stability of a first occurring layer of hydrated ions at the interface gradually increases with hydrated-ion concentration. A layer may be present undetected before any FTT is measured as long as the van der Waals attraction wins over the layering force. The force associated with the layering transition grows further with hydrated-ion concentration. As the concentration of K⁺ ions reaches C_L in the bulk, layering forces start to dominate over the van der Waals attraction and additional external load is required to destabilize this first layer—one single FTT at the size of the hydrated ion layer (>3.5 Å) is observed. The appearance of this first FTT in the data is rather sudden because it is based on a mechanical instability condition (the repulsive part of the layering-force gradient being stronger than the attractive vdW force gradient). Nevertheless, the interfacial structure and pull-off force do not change as of yet at C_L because the layered ions are still collectively expelled from the contact during the final collapse (i.e. collective squeeze out). It seems sensible that hydronium ions (i.e. protons) still compensate for surface charge during and after collective expulsion of hydrated ions at this stage. Some adsorbed K⁺ ions neutralize the contact to the extent of the gradual and slow decrease in the pull-off force before the instability, similarly to the model originally proposed by Pashley. The situation changes suddenly at a slightly higher concentration C_π; namely when the layering force grows to the next threshold strength, that is the force to collectively collapse the entire layer of hydrated ions into a highly confined or surface-condensed state (Fig. 3(b) and (c) in ref. 10). It is important to note that the resulting single FTT (later to become the final FTT) is consequently not a layering transition per se, but a transition between confined adsorbed states of the ions, which involves a change of water structure such as a suggested partial dehydration (Fig. 5e). Existence of an additional adsorbed “condensed-ion state” was previously also proposed by Raviv et al.¹² to explain an experimentally revealed change of EDL forces after mica–mica contact. An estimation of the “condensed” state release barrier of 33kT and associated lifetime of 11 minutes was given by these authors. More recently, Lee et al. have obtained more detailed evidence for the existence of different equilibrium adsorbed states of K⁺ on single mica surfaces using an independent X-ray scattering method.³⁶ For K⁺ ions at a single mica surface (in the absence of mechanical loading) at pH ≈ 5.7 three different states with characteristic surface offset were described, as shown in Fig. 5c.

In summary, above a concentration C_ML one can therefore observe and distinguish up to three different types of film-thickness transitions: (i) van der Waals jump, (ii) hydrated-ion layering and (iii) transitions into or between different confined adsorbed states (Fig. 5e). The existence of different adsorbed ion states in combination with a forced transition between them is key to the correct interpretation of the π-transition, because it provides the structural factor needed to explain the observed sudden reduction in pull-off force by a change of polarity at the interface.

Although we have no extra information concerning the detailed structure of the collapsed interface in contact we can expect that both effective charge and the dipole moments generated by counter-ions adsorbed at the negatively charged surface will be reduced, the closer the counter-ion is adsorbed to the center of charge. An adsorbed state similar to the IS-state is expected to best fulfill this criterion and therefore effectively reduce the polar component of the mica–mica adhesion, which will reduce the measured pull-off force.

It is also worth noting that both the hydrated-ion layering as well as the existence of different adsorbed states extends the classical DLVO theory with physically new features. The previously suggested upper validity bound of the “DLVO” regime at C_π is thus physically justified.¹⁰

Comparing the sizes of the observed FTTs we can surmise that the film-thickness transitions recorded preceding the final FTT are layering FTTs due to successive squeezing out/reordering of hydrated ion layers; until a highly confined layer of hydrated ions (predominantly K⁺) is left.

Although we note a coincidence between the surface separation differences of adsorbed states as reported at pH ≈ 5.7³⁶ (ΔOS_ads → IS = 1.34 Å, ΔOS_ext → OS_ads = 2.15 Å, ΔOS_ext → IS = 3.49 Å) and the histogram peaks of Fig. 4(d) at pH ≈ 5.7, we cannot make a more detailed statement about the role of such adsorbed states under high confinement from direct force measurements alone.

Since the interplay of hydrated-ion layering and transitions between different adsorbed potassium states should account for the existence of the π-transition, it should disappear with the weakening of layering at lower pH. This seems to be the case, as can be seen in Fig. 3(d), where at pH = 3.3 the π-transition has mostly disappeared.

Until now, we have presented and analyzed recent FTT data measured with the eSFA. Typically, these are measured in an automated fashion under constant external loading rate and the actuator is reversed only at the final load. This is not the most commonly used procedure in traditional SFA measurements. The bulk of data measured with overlapping double layers was obtained in the conventional surface forces apparatus by manually controlling the actuator speed and direction. In order to relate the different procedures and data sets, we reproduced the repeated progressive loading–unloading patterns used traditionally. For example, Israelachvili and Pashley⁶ manually reversed the actuator direction after detection of each individual FTT in KCl solutions. Different loading–unloading curves are thus sequentially recorded at progressively increasing loads before the final load is reached and all results are superimposed into a single force curve as illustrated in Fig. 5e. We have used our automated eSFA in manual actuation mode to reproduce this scenario while the surface separation was continuously measured with FSC at a fixed rate around 1 Hz. These experiments were again done without pH control to be comparable to the historic data. While existence of an overall connected oscillatory potential is suggested in the former literature, the raw data from different loading–unloading curves, measured here with the eSFA at higher resolution, cannot be readily overlapped and connected to form a consistent oscillatory potential (Fig. 6(a)). We think this mismatch is a systematic error imposed by the compression/decompression of mica at different loads. The compression effect of mica scales with mica thickness, and, at higher loads can even lead to apparently negative distances measured relative to the uncompressed mica thickness (i.e. optical zero). For the sake of simplicity, we will not correct for this systematic error here and cease to connect the individual curves to a master curve.

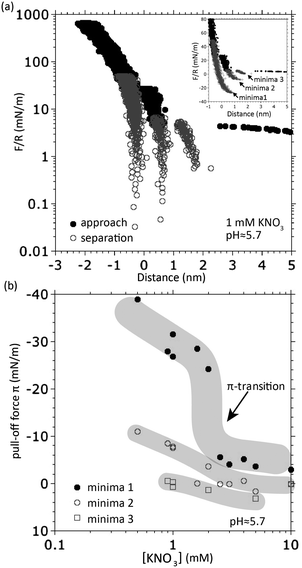Fig. 6 (a) Oscillatory forces measured with two mica surfaces in 1 mM KNO₃ at uncontrolled pH ≈ 5.7. The forces measured during isothermal compression (filled black dots) and separation (open grey dots) from several cycles are plotted together. Inset: The forces plotted on a linear scale zoomed in to the maximum force at which FTTs were observed. (b) Pull-off forces for individual minima of the (oscillatory) surface potential as a function of concentration showing that the final FTT (minima 1) is the only one that shows the discontinuous π-transition. We note that the π-transition of minima 1 occurs at roughly twice the concentration compared to Fig. 1; we think this is due to small variations in the uncontrolled pH, which we showed in Fig. 3 to strongly affect C_π.

Now, we can determine an individual pull-off force for each of the measured and numerated minima and compare these for different salt concentrations as shown in Fig. 6(b). Note how the graph of the innermost “minima 1” (after the final FTT) reveals the π-transition while the two other minima follow their own trends without such discontinuous transition. This finding clearly justifies our hypothesis that (i) the final FTT is responsible for the π-transition and (ii) the final FTT is physically different from the preceding FTTs (hydrated ion layering).

Conclusions

The narrow concentration regime near the π-transition is particularly well suited to reveal and study different structural elements during the collapse of EDLs. This work confirms that the π-transition, marked by a sharp drop in pull-off force, coincides with the onset of hydrated ion layering. We propose a model that invokes the collaborative interplay of hydrated-ion layering forces and different confined adsorbed-ion states, to explain the sudden change of interfacial adhesion after EDL collapse at the π-transition. We also show how the π-transition shifts to higher bulk [K⁺] concentration with decreasing pH, due to progressive substitution of hydrated K⁺ ions by differently structured hydronium ions.

These results demonstrate how the interface structure following collapse of overlapping EDLs can be critically determined by a subtle balance between different structural forces, and how these can combine, leading to inherent instabilities.

Compared to the historical understanding of surface hydration, we can thus draw a more precise and complete picture. Namely, the (oscillatory) hydration force is not due to some periodic layering of water at surfaces but to multiple layering of hydrated ions, which become transitions between different confined adsorbed ion states during the final step of the EDL collapse.

Acknowledgements

We acknowledge G. Cossu, T. Bartos and M. Elsener for technical support. The IC control measurements were performed by K. Kehl and E. Michel at EMPA, St. Gallen and this work was financially supported by the Swiss National Science Foundation.

References

1. B. Derjaguin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633–662.
2. E. J. W. Verwey and J. Overbeek, Theory of the Stability of Lyophobic Colloids, Dover Publications, Amsterdam, 1948.
3. L. Boinovich, Curr. Opin. Colloid Interface Sci., 2010, 15, 297–302.
4. J. N. Israelachvili, Intermolecular and Surface Forces, 3rd edn, 2011, pp. 1–674.
5. R. M. Pashley, Adv. Colloid Interface Sci., 1982, 16, 57–62.
6. J. N. Israelachvili and R. M. Pashley, Nature, 1983, 306, 249–250.
7. P. Claesson, R. G. Horn and R. M. Pashley, J. Colloid Interface Sci., 1984, 100, 250–263.
8. T. Baimpos, B. R. Shrestha, S. Raman and M. Valtiner, Langmuir, 2014, 30, 4322–4332.
9. Y. S. Leng, Langmuir, 2012, 28, 5339–5349.
10. R. M. Espinosa-Marzal, T. Drobek, T. Balmer and M. P. Heuberger, Phys. Chem. Chem. Phys., 2012, 14, 6085–6093.
11. V. A. Parsegian and T. Zemb, Curr. Opin. Colloid Interface Sci., 2011, 16, 618–624.
12. U. Raviv, P. Laurat and J. Klein, J. Chem. Phys., 2002, 116, 5167–5172.
13. Q. Y. Tan, G. T. Zhao, Y. H. Qiu, Y. J. Kan, Z. H. Ni and Y. F. Chen, Langmuir, 2014, 30, 10845–10854.
14. S. S. Lee, P. Fenter, K. L. Nagy and N. C. Sturchio, Geochim. Cosmochim. Acta, 2013, 123, 416–426.
15. S. S. Lee, P. Fenter, C. Park, N. C. Sturchio and K. L. Nagy, Langmuir, 2010, 26, 16647–16651.
16. G. Sposito, Chimia, 1989, 43, 169–176.
17. R. G. Horn and J. N. Israelachvili, Chem. Phys. Lett., 1980, 71, 192–194.
18. R. G. Horn and J. N. Israelachvili, J. Chem. Phys., 1981, 75, 1400–1411.
19. H. Sakuma and K. Kawamura, Geochim. Cosmochim. Acta, 2009, 73, 4100–4110.
20. Y. S. Leng, Y. J. Lei and P. T. Cummings, Modell. Simul. Mater. Sci. Eng., 2010, 18, 034007.
21. M. L. Schlegel, K. L. Nagy, P. Fenter, L. Cheng, N. C. Sturchio and S. D. Jacobsen, Geochim. Cosmochim. Acta, 2006, 70, 3549–3565.
22. J. N. Israelachvili and D. Tabor, Proc. R. Soc. London, Ser. A, 1972, 331, 19–38.
23. D. Tabor and R. H. S. Winterton, Proc. R. Soc. London, Ser. A, 1969, 312, 435–450.
24. M. Heuberger, Rev. Sci. Instrum., 2001, 72, 1700–1707.
25. M. Heuberger, J. Vanicek and M. Zach, Rev. Sci. Instrum., 2001, 72, 3556–3560.
26. M. Zach, J. Vanicek and M. Heuberger, Rev. Sci. Instrum., 2003, 74, 260–266.
27. B. Derjaguin, Kolloid Z., 1934, 69, 155–164.
28. M. Heuberger, M. Zach and N. D. Spencer, Rev. Sci. Instrum., 2000, 71, 4502–4508.
29. D. Y. C. Chan, R. M. Pashley and L. R. White, J. Colloid Interface Sci., 1980, 77, 283–285.
30. S. Perkin, R. Goldberg, L. Chai, N. Kampf and J. Klein, Faraday Discuss., 2009, 141, 399–413.
31. H. K. Christenson and N. H. Thomson, Surf. Sci. Rep., 2016, 71, 367–390.
32. H. K. Christenson, J. Phys. Chem., 1993, 97, 12034–12041.
33. G. L. Gaines and D. Tabor, Nature, 1956, 178, 1304–1305.
34. R. M. Pashley, J. Colloid Interface Sci., 1981, 80, 153–162.
35. P. M. Mcguiggan and J. N. Israelachvili, J. Mater. Res., 1990, 5, 2232–2243.
36. S. S. Lee, P. Fenter, K. L. Nagy and N. C. Sturchio, Langmuir, 2012, 28, 8637–8650.
37. R. M. Pashley, J. Colloid Interface Sci., 1981, 83, 531–546.
38. P. Intharathep, A. Tongraar and K. Sagarik, J. Comput. Chem., 2006, 27, 1723–1732.
39. M. Tuckerman, K. Laasonen, M. Sprik and M. Parrinello, J. Chem. Phys., 1995, 103, 150–161.
40. T. S. Zwier, Science, 2004, 304, 1119–1120.
41. A. Meleshyn, J. Phys. Chem. C, 2008, 112, 20018–20026.
42. A. Meleshyn, J. Phys. Chem. C, 2008, 112, 14495–14500.
43. C. Park, P. A. Fenter, N. C. Sturchio and K. L. Nagy, Langmuir, 2008, 24, 13993–14004.
44. H. Sakuma, J. Geophys. Res.: Solid Earth, 2013, 118, 6066–6075.
45. P. A. Kralchevsky, K. D. Danov and S. E. Anachkov, Curr. Opin. Colloid Interface Sci., 2015, 20, 11–18.
46. P. Attard, J. Chem. Phys., 1989, 91, 3083–3089.
47. P. Richetti and P. Kékicheff, Phys. Rev. Lett., 1992, 68, 1951–1954.
48. R. G. Horn, D. F. Evans and B. W. Ninham, J. Phys. Chem., 1988, 92, 3531–3537.

---

Footnote

† Electronic supplementary information (ESI) available: Discussion of contact value of the K⁺ ion. See DOI: 10.1039/c6cp04222h

---