Hot electron and hole dynamics in thiol-capped CdSe quantum dots revealed by 2D electronic spectroscopy

Abstract

Colloidal quantum dots (QDs) have attracted interest as materials for opto-electronic applications, wherein their efficient energy use requires the understanding of carrier relaxation. In QDs capped by bifunctional thiols, used to attach the QDs to a surface, the relaxation is complicated by carrier traps. Using 2D spectroscopy at 77 K, we follow excitations in thiol-capped CdSe QDs with state specificity and high time resolution. We unambiguously identify the lowest state as an optically allowed hole trap, and identify an electron trap with excited-state absorption. The presence of traps changes the initial dynamics entirely by offering a different relaxation channel. 2D electronic spectroscopy enables us to pinpoint correlations between states and to easily separate relaxation from different starting states. We observe the direct rapid trapping of 1S_3/2, 2S_3/2, and 1S_1/2 holes, and several competing electron relaxation processes from the 1P_e state.

---

1 Introduction

Colloidal semiconductor nanocrystals with quantum confinement, so-called quantum dots (QDs), have attracted interest as materials for applications in displays, lighting, catalysis and potentially highly efficient solar cells.^1–8 In contrast to bulk semiconductors, QDs have quasi-quantized, atomic-like energy levels and a size-dependent band gap.⁹ In all the applications listed above, the relaxation of carriers represents an important process, where part of the initial energy is lost as heat. Several strategies to avoid such losses have been proposed, such as multiple exciton generation or hot electron transfer.^10,11 The quantum confinement has been argued to enhance these effects.^10,12–16 In this context, understanding the details of the energy relaxation in QDs is the key for converting as much energy of the excited e–h pair as possible.¹⁷

Most earlier studies of the electronic decay pathways have focused on as-synthesized QDs capped by oleic acid with very few surface traps, showing stepwise relaxation to the nearest lower-lying state.¹⁸ For many applications, however, QDs need bifunctional capping agents such as thiols, enabling attachment of the QDs to the surfaces of other nanostructures.^6,19 The new capping agent introduces surface traps for both electrons and holes, both due to the identity of the capping agent and the exchange process,²⁰ which leads to the additional complexity of the level structure and carrier dynamics.²¹ While it is possible to synthesize CdSe QDs with bifunctional capping agents directly,²² this would not solve the problem completely and characterization of the traps is necessary. Trapping from the band-edge state in PbSe has been studied by multidimensional spectroscopy,^23,24 but the character of the trap states is still a matter of active investigation.²⁵

In this article, we address the question of energy relaxation in QDs with bifunctional capping agents by using 2D electronic spectroscopy. 2D electronic spectroscopy (2DES) has in recent years shown its utility when it comes to showing correlations and connectivity between different energy levels, as well as achieving high time and energy resolution in QDs and other systems.^26–31 The correlations can be tracked by the ability of 2DES to create spectral maps (see Fig. 1 for example) resolving both excitation energy (x-axis) and detection energy (y-axis). The x-axis of a 2D spectrum is created by two-pulse time-domain interferometric excitation with Fourier transform over the delay (the coherence time) between the pulses, while the y-axis shows the spectral resolution of the signal after a probe pulse, detected by spectral interferometry. To a certain extent, the x-axis is analogous to the pump energy in pump–probe spectroscopy, while the y-axis corresponds to the detection energy. The delay between the first two pulses and the third one corresponds to the time delay in pump–probe, here called the population time.

Fig. 1 2D spectra at early and late population times with energy levels and important features marked, laser and absorption spectra. Middle panel: Total real 2D spectrum of 7.1 nm CdSe QDs in methanol/ethanol glass at 77 K, at a population time of 5 fs. Even at this early time, the nonresonant response of the glass is minor (ESI†). The diagonal line marks where ℏω₁ = ℏω₃; the horizontal and vertical lines mark the energy levels (see Fig. 2). Bottom panel: The same, at 10 ps. The solid horizontal line marks where a cut was taken for state analysis. Note the rescaling by a factor 2. For letter labels, see the text. Side and top panels: Sample absorbance (red line) and spectrum of the laser employed in the 2D experiment (blue line) in arbitrary units.

In conventional transient absorption spectroscopy, the Fourier transform forces a compromise between temporal and spectral resolution. 2D spectroscopy avoids this limitation due to the two excitation pulses, enabling simultaneous high time and energy resolution. In the 2D spectrum, inhomogeneous broadening only affects the diagonal direction, and cross-peaks (off-diagonal) show correlations between different states. Furthermore, the high resolution of our setup makes it possible to measure large QDs with closely spaced states, letting us cover more states than previous experiments.

The ability of 2D spectroscopy to reveal correlations between states is to a great extent limited by the homogeneous linewidth of the states. If the sample is cooled, spectral bands are narrower due to reduced phonon-related broadening.³² In this article, we carry out low-temperature (77 K) measurements, enabling us to observe a structure in the 2D spectra that would be smeared out at room temperature.

By combining 2D spectroscopy with cooling the QD sample, we were able to identify states present in the QDs, as well as signals originating from trapping processes. This enables us to reveal the interplay between carrier trapping and relaxation in the QDs.

2 Experimental

The studied CdSe QDs were synthesized as described previously.^33,34 Briefly, CdO with oleic acid as a capping agent is heated to 340 °C, then Se with trioctylphosphine as a capping agent is injected, all in octadecene solution, and QDs are grown for 2 min before rapid cooling, purification and transfer to hexane solution. Finally, the capping agent is exchanged for 3-mercaptopropionic acid and the solvent for ethanol. The diameter was determined to be 7.1 nm (ESI†).³⁵

The measurements were performed with the QDs in a solvent glass. The QDs were redispersed in a 1 : 1 mixture of methanol and ethanol,³⁶ and cooled to 77 K in a cryostat (Optistat DN2, Oxford Instruments). Some cracking of the solvent glass occurred, but it was possible to position the beam path away from the cracks. The absorbance was below 0.4 at the first absorption peak (635 nm) in a 0.5 mm cuvette measured at room temperature, and the average number of excitations per QD was 0.12 (ESI†).

We used a previously described 2D spectroscopy setup.³⁷ 1030 nm pulses are generated in a Yb:KGW laser at 10 kHz, and feed a nonlinear optical parametric amplifier (Light Conversion), the output of which is then compressed to 9.2 fs long pulses (FWHM) centered at 600 nm. Pulses are delayed using a delay stage (for population time) and glass wedges (for coherence time) and sent through the sample, with the signal beam being detected via heterodyning with a low-intensity pulse in a phase-matching direction. The energy per pulse at the sample is 1 nJ and the diameter of the spot is 100 μm. The interferogram is recorded using a CCD coupled to a spectrometer. 2D spectra were obtained using a broad range of coherence times (−141 fs to 360 fs with 1.5 fs steps) for 85 population times up to 20 ps, with increasing timesteps at longer times (ESI†).

3 Results and discussion

The total real 2D spectra show well separated diagonal and cross-peaks (see Fig. 1). This enables us to identify the peaks associated with different energy levels and follow the population dynamics between the levels. The dominating feature is the elongated diagonal bleach signal (positive by convention) marked A at 16 200 cm⁻¹ arising from the lowest QD exciton state. It is accompanied by a red-shifted excited-state absorption, which can be ascribed to a biexcitonic shift. Owing to the lifting of inhomogeneous broadening, 2D spectroscopy reveals more details about the shift compared to regular pump–probe measurements.

Other prominent features are the diagonal peak B of the second exciton state and the cross-peaks C between the first and second exciton states, showing a strong correlation of these transitions. One can also identify negative peaks D that are a result of the excited-state absorption which is stronger than the bleach in this region. Such spectral features are the result of complex multibody interactions giving rise to biexcitonic shifts.

Finally, for ℏω₃ energies below 16 000 cm⁻¹, a broad positive feature E arises for later population times. Above 17 000 cm⁻¹ but below the diagonal, a broad negative feature F appears. We will later show that these features can be ascribed to QDs with trapped holes and electrons, respectively.

In order to identify all states in the studied energy range, we have carried out an analysis of the long-lived 2D signal. After a population time of 10 ps, all excited QDs will be in the lowest excited state,¹⁸ and by cutting through the total amplitude 2D spectrum at the ℏω₃ of the lowest state (16 200 cm⁻¹), we can identify the energies of the states which were initially excited (see Fig. 2). This is done by fitting the cut to a sum of Gaussians. Before the fitting, the raw cut is divided by the laser spectrum, as the signal scales with laser intensity along the ω₁ axis.³⁸ The main peak (at 16 200 cm⁻¹) is fitted to a sum of two Gaussians. The fit is consistent with absorption spectra at 77 K and room temperature (the details are given in the ESI†).

Fig. 2 To identify the electronic states of the QDs, we fit a slice of the 2D spectrum along with absorption spectra. All panels show fits of data (black squares) as a sum (gray line) of Gaussians (colored lines, average energies marked by vertical dashed lines) corresponding to specific states. Values were normalized to the maximum. Top panel: 2D total signal amplitude along a cut at ℏω₃ = 16 200 cm⁻¹ and T = 10 ps, divided by the laser spectrum. Middle panel: Absorption spectrum at 77 K, smoothed and with a linear background subtracted. Bottom panel: As the middle panel, but at room temperature. The spectrum is shifted by 610 cm⁻¹ to lower energies compared to that at 77 K, and the x-axis is shifted correspondingly to align the peaks. For peak positions, see Fig. 4.

Apart from a low-energy weakly absorbing state, which can be assigned to the trap-related signal as we will show later, all peaks are in good agreement with the energies given by Norris and Bawendi (ESI†)³⁹ after taking the temperature shift from 10 K to 77 K into account.^40,41 We can therefore identify the peaks using their description. In order, they are 1S_3/2–1S_e, 2S_3/2–1S_e, 1S_1/2–1S_e, 1P_3/2–1P_e and 2S_1/2–1S_e. For convenience, we label them as |X₁〉, |X₂〉, |X₃〉, |X₄〉, and |X₅〉. |X₅〉 is at the edge of the 2D spectra and will not be considered further. We point out that all exciton states but one contain the 1S_e electron state.

The weak absorption band, 600 cm⁻¹ below the first main peak (on the ω₁ axis), is not part of the effective mass model. We consider it to arise from a trap, justified by how relaxation appears in the measured 2D spectra (see Fig. 1): the lowest band (on the ω₃ axis) forms a horizontal feature (labeled E in Fig. 1), i.e. the resulting energy of the carriers after relaxation (along the ℏω₃ axis) is independent of the excitation energy (ℏω₁) which is characteristic of traps. This is quite unlike the exciton–exciton cross-peaks (e.g. the C peaks) in the 2D spectra, where the ℏω₃ and ℏω₁ energies are clearly correlated (due to inhomogeneous broadening and the size–energy relationships of the energy levels³⁹). The slope of the laser spectrum shifts the E band upwards compared to the position expected from the analysis of the cut and absorption spectra. The absence of correlation between the lowest state and the energies of the excitonic states also rules out an assignment to trions, as it has been reported previously that the trion energy is correlated with the exciton state energies.⁴² As thiol groups are known to cause hole traps,^43,44 we assign this band to a trapped hole combined with the 1S_e core electron, and label it as |R₁〉. We summarize the initial states in Fig. 3.

Fig. 3 Transitions that correspond to the signals in the 2D spectra (arrows) and corresponding exciton labels. The R₂ state consists of the electron and hole trap states, but the corresponding signal is excited-state absorption from the electron trap. Trap states are marked with dashed lines. The energy of the electron trap state is not known.

With the energy state picture established, we turn to the dynamics. If one disregards signals arising due to coherent dynamics, which show up as oscillatory signals in this system, the total real 2D signal for a chosen ℏω₁ and ℏω₃ value can be seen as analogous to the pump–probe signal with ℏω₁ excitation energy and ℏω₃ probe energy, with population time representing the pump–probe delay. Vertical slices through the 2D spectra therefore correspond to excitation wavelength-resolved transient absorption.‡ The signals are a sum of several different contributions, such as bleach, excited-state absorption and stimulated emission. The bleach is due to electrons or holes already residing in the final state, thus blocking a transition. The 1S_e state is only twofold degenerate and thus causes strong bleach, but the 1P_e state and the hole states have higher degeneracy and therefore the corresponding bleach is much weaker. The bleach contribution from the hole states is also diminished because they are so close together that they overlap partially.

By knowing the energy of each electronic state, we can track the population dynamics at the particular ℏω₁ energies and observe carrier relaxation or trapping with state resolution. If the set of 2D spectra is viewed along the population time axis, the population dynamics can be followed as excitons relax from state to state. We select a number of ℏω₁ values where one initial exciton state should be dominant and slice the 2D spectra at these values, following the development of the ℏω₃ spectrum as a function of population time (see Fig. 4). We choose the excitation energies ℏω₃ in such a way that they correspond to the peak positions in Fig. 2, except for the |R₁〉 and |X₃〉 states where we pick a lower energy to avoid the otherwise overwhelming signal from the |X₁〉 or |X₄〉 state, respectively. The large width of the |X₃〉 and |X₄〉 bands means that the corresponding excitation energies will necessarily lead to contributions from both initial populations. Still, the decay from |X₃〉 dominates in panel 4 and the decay from |X₄〉 in panel 5.

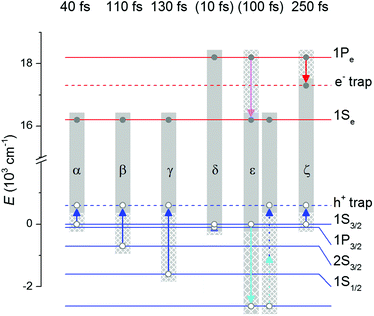
Fig. 4 In order to study the population dynamics of specific electronic states, we follow the development of the total real 2D signal as a function of population time and ℏω₃, at a number of fixed excitation energies ℏω₁ where one electronic state should be dominant (not necessarily the state energy). Each panel can be thought of as a slice along a vertical (constant ℏω₁) line through a stack of 2D spectra spaced along a logarithmic time axis. Note that the color schemes of the panels are normalized differently. The gray horizontal lines mark the actual energies of the states according to the fit described in Fig. 2, with the exception of the e–h trap state, the energy of which is unknown (see the text). The blue horizontal lines mark the diagonals in the 2D spectra. The letters are the peak labels from Fig. 1. At right, a summary of the kinetic scheme derived from the slices (see the text) and the identity of the states (according to Norris and Bawendi). Dark blue: hole trapping; dark red: electron and hole trapping; light red: electron and hole (Auger) relaxation. Not all intermediate steps are shown for electron and hole decays, indicated by the dashed line.

A detailed description of each panel is given in the ESI.† In brief, panels 1–4 show decay directly from the initial (diagonal) states (e.g. the A and B peaks in Fig. 1) to the trap state (the E peak), remarkably without passing through the intermediate states as can be seen from the constant cross-peaks (the C peaks). Trapping occurs on a 50–100 fs timescale, outcompeting hole relaxation which has been shown to have time constants on the order of ∼10 ps.⁴⁵

2D spectroscopy also allows us to monitor a slower process leading to the disappearance of the negative signal below the diagonal in panel 2 (the negative signal below the A peak in Fig. 1). This can be understood as a process analogous to heterogeneous line shape dynamics in the 2D spectra of chlorosomes,⁴⁶i.e. as relaxation and equilibration between closely spaced states. Such additional levels within a band appear both in descriptions based on density functional theory¹⁷ and when the effective mass model is extended by including crystal anisotropy.⁴⁷ Additionally, phonons contribute to the level structure.⁴⁷

Panel 5 presents a more complicated picture, due to the larger numbers of decay pathways theoretically possible from higher energies. |X₄〉 is also the first state where the electron is in the 1P_e state rather than the 1S_e state, which means that we need to consider both hole and electron relaxation processes in addition to trapping.

The diagonal peak for the |X₄〉 state disappears within 20 fs (ESI†). For the 1P_3/2 hole, two pathways are possible: the hole could either relax to the 1S_3/2 state (a process with time constant ∼10 fs¹⁸), from whence it would be trapped, or it could be trapped directly. It seems likely that trapping from 1P_3/2 should have a time constant similar to the other hole trapping processes, meaning that relaxation to 1S_3/2 should outcompete direct trapping, but the present data do not allow us to clearly distinguish the two scenarios. These hole relaxation processes would occur on the same timescale as the electron decay, giving rise to a number of possible electron–hole state combinations. Their short lifetime and the number of combinations make the spectroscopic identification difficult.

For the 1P_e electron in the |X₄〉 state, three decay pathways can be imagined. One is Auger relaxation to the 1S_e state, which takes place on a timescale of 150–250 fs.¹⁸ Auger relaxation involves energy transfer to the hole, which ends up in a high-energy state such as 2S_1/2, and can occur if the hole is not yet trapped. If the hole is trapped, relaxation to the 1S_e state is still possible, but takes place via a much slower process (a few picoseconds) mediated by surface states.^17,18 Additionally, trapping of the electron might be possible.

Getting back to what we observe in the current measurements, in a broad region around ℏω₃ = 17 300 cm⁻¹, a strong negative band grows in, i.e. an excited-state absorption signal (the F peak in Fig. 1). Even though it is very strong at high ℏω₁, it is negligible at low ℏω₁. This means that it should come from a state that is only accessible from high-energy excitons. Two such possible states could be a second hole trap or an electron trap. If it is a hole trap, the signal should be growing after Auger relaxation has brought the holes to otherwise unpopulated high-energy hole states but before hole trapping inhibits Auger relaxation. Considering that the band grows in as a single exponential with a lifetime of 200–300 fs (ESI†), this explanation appears unlikely, and electron trapping from the 1P_e state is instead suggested as the cause. The data cannot reveal the origin of the electron trap; however, clearly the trapping cannot occur for energies close to the band gap, which is also consistent with previous observations.²¹ P states are on average further from the QD center than S states, so the 1P_e state should be expected to have a better spatial overlap with a trap state on the surface of the QD.

Considering the timescales, Auger relaxation can still be expected to make a minor contribution to the electron relaxation, in competition with the trapping processes. The decay pathway followed by the hole after Auger relaxation would be hard to distinguish from the hole relaxation from the |X₃〉 state. The electron would cause a growing bleach in the 16 200 cm⁻¹ band, again overlapping with signals from the |X₃〉 decay pathway. Finally, a simple calculation can show that the bleach signal (induced by electrons) normalized by the number of e–h pairs is much lower for the |X₄〉 state compared to the |X₁〉 state. This implies that only a minor part of the electrons excited via |X₄〉 reaches the 1S_e level. If no electron trapping would occur, this band would be much stronger, further supporting the existence of the trap.

One could imagine that the negative band is in fact constant, but hidden by positive signals at early times. However, excited-state absorption signals can only come from populations, so this scenario would require excitons to remain in the |X₄〉 (or possibly |X₃〉) state without decaying over the experimental timescale, which is clearly contradicted by earlier experiments.¹⁸

Putting this information together, we see that the endpoint of the main |X₄〉 decay pathway on a 10 ps timescale is a state where both the electron and the hole are trapped. We call this state |R₂〉. Several paths to this state are possible depending on the order of trapping of the carriers and whether |X₄〉 relaxes to 1S_3/2–1P_e initially. A minor pathway leads via Auger relaxation to the |R₁〉 state.

We summarize the initial and final states of all decays in Fig. 3 and show the decay pathways in Fig. 5. 2DES shows that almost all carriers end up trapped – in agreement with the low fluorescence quantum yield (below 10%) of thiol-capped QDs. This contrasts with the relaxation processes in OA-capped QDs.¹⁸ In natively MPA-capped QDs with an intermediate density of traps,²² one would expect a more pronounced competition between the two types of pathways.

Fig. 5 Relaxation (magenta for electrons and cyan for holes) and trapping (red and blue) pathways (arrows). At the top are the obtained or estimated (in parentheses) time constants of the processes. α, β, and γ are the trapping pathways of |X₁〉, |X₂〉, and |X₃〉, respectively. δ, ε, and ζ are the pathways from the |X₄〉 state, assuming that the |1P_3/2〉 hole relaxes to |1S_3/2〉 as the first step (δ). From there, either ε or ζ is followed. ε consists of several substeps: first Auger relaxation, with the hole going into an unspecified state, followed by hole relaxation and trapping from this state, which was not studied in detail in our work. The first step of ε is prevented by either electron trapping from |1P_e〉 or hole trapping from |1S_3/2〉 which occurs in parallel rather than simultaneously and together forms pathway ζ. If the δ step does not occur, ε and ζ will have the hole in |1P_3/2〉 instead of |1S_3/2〉. The light grey rectangles mark the excitons before (solid and densely patterned) and after (solid and sparsely patterned) each step.

4 Conclusion

In conclusion, using 2D electronic spectroscopy, we directly observed state-resolved energy relaxation in thiol-capped functionalized CdSe QDs. We exploit the benefits of using very short pulses (FWHM 10 fs) and low-temperature measurements decreasing the overlap between states due to homogeneous broadening. This allows us to track down relaxation pathways, state-by-state, even for times well below 100 fs. In some cases, namely 1S_3/2, 2S_3/2, and 1S_1/2 holes, and 1P_e electrons, we observe direct rapid trapping of carriers without proceeding through any lower electronic state of the QD. Thus, we see that the presence of traps entirely changes the relaxation dynamics in the QDs by offering a different relaxation channel. Furthermore, we can unambiguously identify the lowest state as a trap, which would not be possible without 2DES.

Acknowledgements

This work was financed by the Swedish Research Council (VR), the Knut and Alice Wallenberg Foundation, the Swedish Energy Agency, and NPRP grant # NPRP7-227-1-034 from the Qatar National Research Fund. We acknowledge collaboration within NanoLund. We thank Erling Thyrhaug for advice regarding solvent glasses and David Paleček for fruitful discussions.

References

1. K. Bourzac, Nature, 2013, 493, 283.
2. H. Kisch, Angew. Chem., Int. Ed., 2013, 52, 812–847.
3. M. B. Wilker, K. J. Schnitzenbaumer and G. Dukovic, Isr. J. Chem., 2012, 52, 1002–1015.
4. A. Alivisatos, J. Phys. Chem., 1996, 100, 13226–13239.
5. P. V. Kamat, J. Phys. Chem. C, 2008, 18737–18753.
6. P. V. Kamat, J. Phys. Chem. Lett., 2013, 4, 908–918.
7. M. Nirmal, D. J. Norris, M. Kuno, M. G. Bawendi, A. Efros and M. Rosen, Phys. Rev. Lett., 1995, 75, 3728–3731.
8. K. Zheng, K. Karki, K. Žídek and T. Pullerits, Nano Res., 2015, 8, 2125–2142.
9. D. J. Norris, in Nanocrystal Quantum Dots, ed. V. I. Klimov, CRC Press, 2nd edn, 2010, ch. 2, pp. 63–96.
10. K. Žídek, M. Abdellah, K. Zheng and T. Pullerits, Sci. Rep., 2014, 4, 7244.
11. K. J. Karki, J. R. Widom, J. Seibt, I. Moody, M. C. Lonergan, T. Pullerits and A. H. Marcus, Nat. Commun., 2014, 5, 5869.
12. R. D. Schaller and V. I. Klimov, Phys. Rev. Lett., 2004, 92, 186601.
13. R. J. Ellingson, M. C. Beard, J. C. Johnson, P. Yu, O. I. Micic, A. J. Nozik, A. Shabaev and A. L. Efros, Nano Lett., 2005, 5, 865–871.
14. M. T. Trinh, L. Polak, J. M. Schins, A. J. Houtepen, R. Vaxenburg, G. I. Maikov, G. Grinbom, A. G. Midgett, J. M. Luther, M. C. Beard, A. J. Nozik, M. Bonn, E. Lifshitz and L. D. A. Siebbeles, Nano Lett., 2011, 11, 1623–1629.
15. K. J. Karki, F. Ma, K. Zheng, K. Zidek, A. Mousa, M. A. Abdellah, M. Messing, L. R. Wallenberg, A. Yartsev and T. Pullerits, Sci. Rep., 2013, 3, 2287.
16. K. Tvrdy, P. A. Frantsuzov and P. V. Kamat, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 29–34.
17. S. Kilina, K. A. Velizhanin, S. Ivanov, O. V. Prezhdo and S. Tretiak, ACS Nano, 2012, 6, 6515–6524.
18. R. R. Cooney, S. L. Sewall, E. A. Dias, D. M. Sagar, K. E. H. Anderson and P. Kambhampati, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245311.
19. I. Robel, V. Subramanian, M. Kuno and P. V. Kamat, J. Am. Chem. Soc., 2006, 128, 2385–2393.
20. B. Omogo, J. F. Aldana and C. D. Heyes, J. Phys. Chem. C, 2013, 117, 2317–2327.
21. M. Abdellah, K. J. Karki, N. Lenngren, K. Zheng, T. Pascher, A. Yartsev and T. Pullerits, J. Phys. Chem. C, 2014, 118, 21682–21686.
22. M. N. Kalasad, M. K. Rabinal and B. G. Mulimani, Langmuir, 2009, 25, 12729–12735.
23. S. B. Block, L. A. Yurs, A. V. Pakoulev, R. S. Selinsky, S. Jin and J. C. Wright, J. Phys. Chem. Lett., 2012, 3, 2707–2712.
24. D. D. Kohler, S. B. Block, S. Kain, A. V. Pakoulev and J. C. Wright, J. Phys. Chem. C, 2014, 118, 5020–5031.
25. P. Kambhampati, Chem. Phys., 2015, 446, 92–107.
26. D. B. Turner, Y. Hassan and G. D. Scholes, Nano Lett., 2012, 12, 880–886.
27. E. Harel, S. M. Rupich, R. D. Schaller, D. V. Talapin and G. S. Engel, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075412.
28. G. B. Griffin, S. Ithurria, D. S. Dolzhnikov, A. Linkin, D. V. Talapin and G. S. Engel, J. Chem. Phys., 2013, 138, 014705.
29. J. R. Caram, H. Zheng, P. D. Dahlberg, B. S. Rolczynski, G. B. Griffin, D. S. Dolzhnikov, D. V. Talapin and G. S. Engel, J. Chem. Phys., 2014, 140, 084701.
30. Y. Kobayashi, C.-H. Chuang, C. Burda and G. D. Scholes, J. Phys. Chem. C, 2014, 118, 16255–16263.
31. E. Cassette, R. D. Pensack, B. Mahler and G. D. Scholes, Nat. Commun., 2015, 6, 6086.
32. T. Pullerits, F. van Mourik, R. Monshouwer, R. Visschers and R. van Grondelle, J. Lumin., 1994, 58, 168–171.
33. C. R. Bullen and P. Mulvaney, Nano Lett., 2004, 4, 2303–2307.
34. K. Zheng, K. Žídek, M. Abdellah, N. Zhu, P. Chábera, N. Lenngren, Q. Chi and T. Pullerits, J. Am. Chem. Soc., 2014, 136, 6259–6268.
35. W. Yu, L. Qu, W. Guo and X. Peng, Chem. Mater., 2003, 15, 2854–2860.
36. S. L. Murov, Handbook of Photochemistry, Marcel Dekker, 1973, ch. 9-4, p. 91.
37. R. Augulis and D. Zigmantas, Opt. Express, 2011, 19, 13126–13133.
38. A. Nemeth, F. Milota, T. Mančal, V. Lukeš, H. F. Kauffmann and J. Sperling, Chem. Phys. Lett., 2008, 459, 94–99.
39. D. Norris and M. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 16338–16346.
40. Y. Varshni, Physica, 1967, 34, 149–154.
41. A. Joshi, K. Y. Narsingi, M. O. Manasreh, E. A. Davis and B. D. Weaver, Appl. Phys. Lett., 2006, 89, 131907.
42. M. J. Fernée, B. N. Littleton and H. Rubinsztein-Dunlop, ACS Nano, 2009, 3, 3762–3768.
43. A. L. Rogach, A. Kornowski, M. Gao, A. Eychmüller and H. Weller, J. Phys. Chem. B, 1999, 103, 3065–3069.
44. K. Zheng, K. Žídek, M. Abdellah, W. Zhang, P. Chábera, N. Lenngren, A. Yartsev and T. Pullerits, J. Phys. Chem. C, 2014, 118, 18462–18471.
45. C. Liu, J. J. Peterson and T. D. Krauss, J. Phys. Chem. Lett., 2014, 5, 3032–3036.
46. J. Dostál, T. Mančal, R. Augulis, F. Vácha, J. Pšenčík and D. Zigmantas, J. Am. Chem. Soc., 2012, 134, 11611–11617.
47. A. L. Efros, in Nanocrystal Quantum Dots, ed. V. I. Klimov, CRC Press, 2nd edn, 2010, ch. 3, pp. 97–132.

---

Footnotes

† Electronic supplementary information (ESI) available: Sample characterization, average number of excitons per QD (〈N〉), 2D experiments, energy levels, and population dynamics. See DOI: 10.1039/c6cp04190f

‡ This analogy has to be taken with care since in pump–probe, high spectral resolution in ℏω₁ leads to low time resolution in T – a limitation which is avoided in 2D spectroscopy. To achieve the same ℏω₁ resolution here using pump–probe spectroscopy, the T pulses would need to be 300 fs long.

---