Open Access Article
Open Access ArticlePicosecond to nanosecond dynamics provide a source of conformational entropy for protein folding
Andreas M.
Stadler
 *a,
Franz
Demmel
b,
Jacques
Ollivier
c and
Tilo
Seydel
c
*a,
Franz
Demmel
b,
Jacques
Ollivier
c and
Tilo
Seydel
c
aJülich Centre for Neutron Science JCNS and Institute for Complex Systems ICS, Forschungszentrum Jülich GmbH, 52425 Jülich, Germany. E-mail: a.stadler@fz-juelich.de
bISIS Facility, Rutherford Appleton Laboratory, Didcot OX11 0QX, UK
cInstitut Laue-Langevin, 71 Avenue des Martyrs, CS 20156, 38042 Grenoble Cedex 9, France
First published on 11th July 2016
Abstract
Myoglobin can be trapped in fully folded structures, partially folded molten globules, and unfolded states under stable equilibrium conditions. Here, we report an experimental study on the conformational dynamics of different folded conformational states of apo- and holomyoglobin in solution. Global protein diffusion and internal molecular motions were probed by neutron time-of-flight and neutron backscattering spectroscopy on the picosecond and nanosecond time scales. Global protein diffusion was found to depend on the α-helical content of the protein suggesting that charges on the macromolecule increase the short-time diffusion of protein. With regard to the molten globules, a gel-like phase due to protein entanglement and interactions with neighbouring macromolecules was visible due to a reduction of the global diffusion coefficients on the nanosecond time scale. Diffusion coefficients, residence and relaxation times of internal protein dynamics and root mean square displacements of localised internal motions were determined for the investigated structural states. The difference in conformational entropy ΔSconf of the protein between the unfolded and the partially or fully folded conformations was extracted from the measured root mean square displacements. Using thermodynamic parameters from the literature and the experimentally determined ΔSconf values we could identify the entropic contribution of the hydration shell ΔShydr of the different folded states. Our results point out the relevance of conformational entropy of the protein and the hydration shell for stability and folding of myoglobin.
1. Introduction
Protein folding is a fundamental process in molecular biology. The protein folding transition occurs from the fully unfolded peptide chain via metastable and partially folded intermediates towards the stable and native folded structure at the end of the folding collapse.1 In the nucleation-condensation model of protein folding the cooperative formation of secondary and tertiary structures is a key aspect,2 while in the diffusion–collision model the diffusion of micro-domains and their collision have central importance for protein folding kinetics.3 This illustrates that motions in proteins are highly relevant for protein folding. From a thermodynamic point of view, it is the difference in the free energy ΔG between the unfolded state and the folded state (ΔG = ΔGunfolded − ΔGfolded = ΔH − TΔS) that drives the folding transition along the folding pathway. Weak van der Waals forces, hydrogen bonds, and, to a smaller extent, screened electrostatic interactions contribute to the enthalpic stabilization ΔH in proteins,4 whereas the entropic term TΔS contains contributions both from the protein ΔSconf and from the hydration shell ΔShydr. Internal protein dynamics contribute importantly to the conformational entropy ΔSconf of the macromolecule as well as to the sampling of different conformations during the folding process.Localized fast diffusive motions of amino-acid side-chains provide a source of conformational entropy ΔSconf of the macromolecule.5 The conformational entropy content of the amino-acid side-chains depends on the degree of folding and on the compactness of the local environment.6 Therefore, amino-acid side-chain dynamics are relevant for the entropic stabilization of the unfolded states as compared to the folded native protein conformation. Motions in proteins are known to span a wide time range from the femtosecond of fast bond vibrations to the millisecond of slow and large domain motions.7 Protein side-chain dynamics, however, take place mostly on the pico- to nanosecond time scale.8 Internal localized protein dynamics are not limited to fast side-chain motions, but extend into the nanosecond time scale for slow motions of the protein backbone or loops,7 or of flexible and disordered regions.9 Apart from internal dynamics, proteins in solution also undergo global protein diffusion. Global diffusion depends strongly on the size and shape of the protein as well as on interactions with the environment. In dilute solution, protein–protein interactions are negligible, but are relevant for macromolecular diffusion at higher concentrations.
Myoglobin (Mb) serves as a model system in the field of biophysics10 as it is comparatively small, which allows us to obtain an understanding of the underlying physical principles governing its dynamical behaviour, and it is still sufficiently complex to show typical protein behaviour. In the following context, the heme-bound protein is termed holo-Mb. Apomyoglobin (apo-Mb) – myoglobin without the heme group – is less stable than holo-Mb and can be trapped in different folded, partially folded molten globules (MGs) and unfolded states under equilibrium conditions depending on the solvent conditions chosen.11–13 The structural and dynamic properties of the different equilibrium folding states of apo-Mb have been studied by NMR spectroscopy,14–17 SAXS18,19 and also by FRET.20 In our recent work, we have investigated the fast internal dynamics of apo- and holo-Mb on the time scale of a few picoseconds using neutron spectroscopy.21 However, further information concerning the internal dynamics of different folded states on the slower picosecond to nanosecond time scale and the properties of global protein diffusion as a function of the degree of folding is still missing.
Quasielastic incoherent neutron spectroscopy (QENS) is a well-suited technique to measure the average dynamics of biological macromolecules on the picosecond to the nanosecond time scale.22 QENS measurements of protein solutions performed on neutron spectrometers with high-energy resolution allow us to determine internal protein dynamics and global protein diffusion simultaneously. Mostly, proton dynamics are observed by QENS due to the large incoherent scattering cross section of 1H compared to all other chemical elements. As protons are uniformly distributed in proteins, QENS probes average protein dynamics. On the accessible time scale of QENS, protons act as reporters for the dynamics of chemical groups to which they are bound covalently.
In this article, we report on a comparative experimental study on the dynamics of different folded structural states of holo- and apo-Mb as a function of temperature that extends our previous investigation on the fast picosecond dynamics.21 We used high-resolution neutron time-of-flight and backscattering spectroscopy to focus on slower picosecond to nanosecond dynamics. The samples have been measured in the solution state to allow for solvent induced effects and to enable reversible thermodynamic properties. Global protein diffusion and internal macromolecular dynamics could be separated from the recorded QENS spectra. Detailed insight into the properties of the internal dynamics of different folded states of the protein was obtained from the recorded data.
2. Material and methods
2.1 Sample preparation
Mb from equine skeletal muscle was obtained commercially (product number M0630, Sigma Aldrich). Apo-protein was obtained by using the butanone method as described in the previous work.21 To remove exchangeable protons, the dry protein powders were dissolved in D2O (99.9% atom D, Sigma Aldrich), incubated for one day and lyophilized afterwards. The D2O exchanged protein powders were then dissolved in different D2O buffers ((i and ii) 20 mM NaH2PO4/Na2HPO4 at pD 4 and 6; (iii) 10 mM DCl at pD 2; (iv) 10 mM DCl, 20 mM NaTCA at pD 2; (v) 10 mM DCl, 100 mM NaCl at pD 2) at a concentration of approximately 5 mg mL−1 and dialyzed against the corresponding D2O buffer in excess volume (Slide-A-Lyzer dialysis devices, 3500 MWCO, Thermo Scientific, Rockford, IL). The protein solutions were concentrated to the concentrations used for neutron scattering experiments (Vivaspin 3000 MWCO concentration units, Sartorius, Goettingen, Germany). The pD of the filtered D2O buffer was measured to verify whether the correct pD value has been achieved in the concentrated protein solution. The pD was calculated by adding 0.4 to the value measured on a normally calibrated pH meter.23 Deuterated DCl and NaOD (99 atom%, Sigma-Aldrich) were used for pD adjustment of the D2O buffers.The protein concentration was measured using UV/vis absorption spectroscopy (Nano-Drop 2000c, Thermo Scientific). The concentration of the apo-Mb solutions was determined using the calculated extinction coefficient E1% = 8.25 at 280 nm from the amino acid sequence using the ExPASy web server.24 Mb was found to be in the oxygenated state, and the concentration was determined using extinction coefficients of 13.9 and 14.4 mM−1 cm−1 at 542 and 579 nm, respectively, and a molecular mass of 18.8 kDa as reported by Antonini and Brunori.25
2.2 QENS experiments
The neutron scattering experiments were performed on the disc chopper neutron time-of-flight spectrometer IN526 at the Institut Laue–Langevin (ILL) in Grenoble, France, on the neutron backscattering spectrometer IRIS27 at the ISIS spallation source at the Rutherford Appleton Laboratory in Oxfordshire, UK, and on the high-resolution neutron backscattering spectrometer IN16 at the ILL.26 On IN5, the incident wavelength was set at 10 Å and a chopper speed of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm combined with a chopper ratio of 5/6 was used, which yielded an energy resolution of approximately 12 μeV (full-width half-maximum FWHM). Data recorded on IN5 were analysed in the scattering vector range between 0.29 and 1.10 Å−1 and in the energy transfer range between −2 and 0.5 meV. The IRIS spectrometer is characterized by an energy resolution of 18 μeV (FWHM). Data recorded on IRIS were analysed between 0.5 and 1.49 Å−1 and between −0.5 and 0.5 meV. The energy resolution of the neutron backscattering spectrometer IN16 is 0.9 μeV (FWHM). IN16 data were analysed between 0.19 and 0.88 Å−1 and between −14.1 and 14.1 μeV. Resolution functions were measured using a 1 mm thick vanadium slab. The individual spectra of the neutron detectors were grouped and energy channels were binned for better statistics for all instruments. Measured intensities were corrected for energy-dependent neutron detector efficiency, normalized to vanadium, and transformed into energy transfer and scattering vector space. The measured intensities of the samples were divided by the calculated sample transmissions. Multiple scattering corrections were not performed, as the transmissions of all samples were above or close to 0.9. All samples were mounted in flat Al cells with 1 mm thickness and were oriented at 135° with respect to the incident beam. The sample holders were sealed with In wire against vacuum. All protein samples and buffer solutions received around 4 h neutron beam time on IN5, 8 h on IRIS and 24 h on IN16 per temperature point.
000 rpm combined with a chopper ratio of 5/6 was used, which yielded an energy resolution of approximately 12 μeV (full-width half-maximum FWHM). Data recorded on IN5 were analysed in the scattering vector range between 0.29 and 1.10 Å−1 and in the energy transfer range between −2 and 0.5 meV. The IRIS spectrometer is characterized by an energy resolution of 18 μeV (FWHM). Data recorded on IRIS were analysed between 0.5 and 1.49 Å−1 and between −0.5 and 0.5 meV. The energy resolution of the neutron backscattering spectrometer IN16 is 0.9 μeV (FWHM). IN16 data were analysed between 0.19 and 0.88 Å−1 and between −14.1 and 14.1 μeV. Resolution functions were measured using a 1 mm thick vanadium slab. The individual spectra of the neutron detectors were grouped and energy channels were binned for better statistics for all instruments. Measured intensities were corrected for energy-dependent neutron detector efficiency, normalized to vanadium, and transformed into energy transfer and scattering vector space. The measured intensities of the samples were divided by the calculated sample transmissions. Multiple scattering corrections were not performed, as the transmissions of all samples were above or close to 0.9. All samples were mounted in flat Al cells with 1 mm thickness and were oriented at 135° with respect to the incident beam. The sample holders were sealed with In wire against vacuum. All protein samples and buffer solutions received around 4 h neutron beam time on IN5, 8 h on IRIS and 24 h on IN16 per temperature point.
For the QENS spectra of the protein solutions measured on IN5 and IRIS the D2O buffers make a notable contribution. Therefore, the measured spectra of the D2O buffers were subtracted from the spectra of the protein solutions according to
| S(q,ω) = S(q,ω)protein solution − (1 − ϕ)·S(q,ω)buffer, | (1) |
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ·c is the volume fraction of the protein with the partial specific volume
·c is the volume fraction of the protein with the partial specific volume ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) of the protein and the measured protein concentration c. The partial specific volume of proteins is typically in the range between 0.70 and 0.75 mL g−1,28 with an experimentally determined average value of 0.73 mL g−1.29 The measured value of Mb is
of the protein and the measured protein concentration c. The partial specific volume of proteins is typically in the range between 0.70 and 0.75 mL g−1,28 with an experimentally determined average value of 0.73 mL g−1.29 The measured value of Mb is ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) = 0.74 mL g−1,30 which is close to the reported experimental average value. For the subtraction of the D2O buffers we used the reported value of Mb, but the resulting protein spectra are not modified within the error bars when the average value is taken instead.
= 0.74 mL g−1,30 which is close to the reported experimental average value. For the subtraction of the D2O buffers we used the reported value of Mb, but the resulting protein spectra are not modified within the error bars when the average value is taken instead.
With regard to the data measured on IN16, the contribution of the empty Al sample holder was subtracted from the protein solutions as the D2O buffers appear only as a flat background in the limited energy transfer window. The D2O contribution was accounted for during data analysis with a linear background.
2.3 QENS data analysis
A description of the QENS technique can be found in the book by Bée.31 The application of QENS for the study of biomolecular dynamics is described in the book by Fitter, Gutberlet and Katsaras.22The QENS spectra of internal protein dynamics can be described by a model independent approach according to22
| SI(q,ω) = A0(q) × δ(ω) + [1 − A0(q)] × LI(q,ω), | (2) |
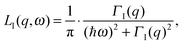 | (3) |
Within the accessible time- and length scale of neutron backscattering and time-of-flight spectrometers, the combination of translational and rotational diffusion of proteins in solution can be described effectively using one Lorentzian32–36
 | (4) |
The theoretical scattering function for proteins in solution is the convolution of eqn (2) and (4) yielding
| S(q,ω) = {A0(q) × LG(q,ω) + [1 − A0(q)] × LG+I(q,ω)}, | (5) |
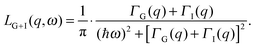 | (6) |
| Smeas(q,ω) = [exp(−〈xvib2〉q2) × S(q,ω) + B(ω)] ⊗ Sres(q,ω). | (7) |
3. Results and discussion
3.1 QENS experiments with protein solutions
A compilation of the different samples investigated by QENS in this study is given in Table 1. The α-helical content of the samples in heavy water buffer was measured by circular dichroism and has been reported before.21 Depending on the solvent composition, unfolded, partially folded MGs, or folded conformations can be stabilized under equilibrium conditions. On the high-resolution instrument IN16, all the listed conformational states were measured at concentrations of 5–6% (w/v) at a uniform temperature of 289.2 K. The high-energy resolution ΔE = 0.9 μeV of IN16 allows probing slow dynamics on a time-scale up to approximately Δt = 1 ns (Δt = ℏ/ΔE). On IRIS and IN5, temperature-dependent QENS experiments have been performed on the acid denatured state of apo-Mb, a MG state and a folded conformation, either the fully folded apo-Mb or the heme-bound holo-Mb. The energy resolutions of IRIS and IN5 are 18 and 12 μeV corresponding to the slowest observable motions up to approximately Δt = 40 and 60 ps, respectively. Higher protein concentrations have been measured on IRIS (6–8%) to reduce the required neutron beam time per sample, while on IN5 lower protein concentrations (3–5%) could be used due to the higher incident neutron flux and the large detector of the instrument. We would like to mention that the protein solutions of partially folded apo-Mb in the MG states had a gel-like viscosity at 5% or above. The MGs remained completely liquid at a concentration of 3%.| α-Helical content (%) | State | Solvent composition | c (IN16) (mg mL−1) | c (IRIS) (mg mL−1) | c (IN5) (mg mL−1) |
|---|---|---|---|---|---|
| 6 | U | apo-Mb pD 2 | 62 | 65 | 41 |
| 22 | MG | apo-Mb pD 2, 0.1 M NaCl | 54 | 84 | — |
| 43 | MG | apo-Mb pD 4 | 54 | — | 32 |
| 54 | F | apo-Mb pD 6 | 50 | — | 48 |
| 66 | F | holo-Mb pD 6 | 56 | 56 |
A selection of representative QENS spectra of unfolded, partially folded MGs and folded conformations of apo- and holo-Mb that have been measured on the instrument IN16 are given in Fig. 1. In Fig. 2, exemplary QENS spectra of unfolded acid denatured apo-Mb measured on IRIS and IN5 at small and large scattering vectors are shown. The QENS spectra of the protein solutions after buffer subtraction were analysed according to eqn (7) containing one narrow Lorentz function for global protein diffusion and one broad Lorentzian to account for the combination of global diffusion and internal diffusive motions in the protein. The used theoretical model provides a good description of the measured QENS data of all investigated samples measured on all the spectrometers used. In the following sections, we present and discuss the results obtained by using this simplified standard model32,33 (and references therein). We begin with the section concerning global protein diffusion.
3.2 Global protein diffusion
The line-widths Γ1 of the narrow Lorentzian contain the relevant information about global protein diffusion. The dependence of Γ1(q) as a function of the scattering vector q of acid denatured unfolded apo-Mb at pD 2 (6% α-helical content) measured on all the neutron spectrometers used, is shown in Fig. 3, as an illustrative case. The line-widths of all measured samples show the expected behaviour of Γ1(q) = Deff·q2 with the effective diffusion coefficient Deff that describes the combination of translational and rotational protein diffusion. Each spectrum was fitted independently and no Deff·q2 behaviour was imposed for the fit. This further corroborates the robustness of the results. It has been shown that on the time-length window of neutron time-of-flight and backscattering spectroscopy, rotational diffusion yields Deff values that are about 30% larger than pure translational centre-of-mass diffusion.32–36 The shape of the QENS spectra due to the combination of rotational and translational diffusion remains Lorentzian with a linear increase of Γ1(q) versus q2.32–36 The line-widths measured on IRIS and IN5 at the lowest temperatures deviate from the linear behaviour for q2 → 0. The explanation for this behaviour is the comparatively large energy resolution of IRIS and IN5, which does not allow resolving very narrow line-widths in the range of only a few μeV accurately.The effective diffusion coefficients measured on IRIS and IN5 as a function of temperature are shown in Fig. 4(A) for the different folded conformations. In the investigated small temperature range, we find a linear increase of the diffusion coefficients with temperature as expected for a Stokes–Einstein temperature dependence. This also means that the proteins do not significantly change the effective volume they occupy in this regime. However, the Deff of apo-Mb at pD 6 (54% α-helical content) deviate from linearity at 310 and 320 K. An explanation for this behaviour is the onset of protein aggregation or oligomerisation at higher temperatures, which reduces global protein diffusion. All samples were prepared in our lab in Jülich a few days before the neutron scattering experiments, and the apo-Mb sample (at pD 6) was measured on the last day of the experiment. The aging process might have contributed to the aggregation tendency at higher temperatures. It is already evident from Fig. 4(A) that there is a systematic decrease in Deff with the proteins being more folded for data recorded on both spectrometers. To allow for a quantitative and facilitated comparison of the results obtained from the spectrometers used, the Deff values determined on IRIS and IN5 were linearly interpolated to 289.2 K and are plotted in Fig. 4(B) together with the Deff determined on IN16 at 289.2 K.
In the following section, we focus our discussion on the properties of the global effective diffusion coefficients at 289.2 K as shown in Fig. 4(B). Due to the lower protein concentrations of acid denatured apo-Mb at pD 2 (c = 3%) and of the MG state at pD 4 (c = 4%) measured on IN5, the diffusion coefficients determined are larger than the values of the other samples investigated on IRIS and IN5, and remain at a similar level irrespective of the degree of α-helical content. The reason here is that hydrodynamic interactions slow down global protein diffusion at higher protein concentration.37 In the long-time limit of global protein diffusion observed by dynamic light scattering, unfolded and MG states of apo-Mb are characterized by slower protein diffusion due to the larger structural expansion as compared to the native folded states.21 On the other hand, the short-time limit of global protein diffusion probed on IRIS and IN5 follows an inverse behaviour for proteins at higher concentration (c ≥ 5%): a reduced diffusivity with the increasing degree of α-helical content. A physical explanation for this behaviour would be that repulsive interactions between charged proteins at pD 2 and 4 at high concentrations increase protein diffusion in the short-time limit. Indeed, charged colloidal spheres diffuse slightly faster than non-charged spheres at the volume fractions explored here.37 At lower protein concentration (c = 3–4%) charge interactions seem to play a minor role.
With regard to the Deff measured on IN16, we obtain reduced absolute values as compared to the IRIS and IN5 results. Global protein diffusion of acid denatured apo-Mb is slightly faster than the folded conformations, which is in agreement with the observations described above. We find the Deff value of holo-Mb measured on IRIS being a factor of 1.64 larger than the corresponding IN16 result. After rescaling, the Deff values of acid denatured and folded apo-Mb determined on the low-resolution spectrometers coincide with the IN16 results (see the dotted line in Fig. 4(B)). The explanation here is that the slow internal process in the protein (vide infra) interferes with the narrow Lorentzian in the QENS spectra measured on the lower-resolution instruments, which cannot discriminate both processes accurately due to the lower energy resolution. As a result, larger effective diffusion coefficients are obtained on IRIS and IN5.
A further remarkable observation is that the diffusivity of the MG states measured on the high-resolution spectrometer is strongly reduced as compared to the other protein solutions. We would like to remind that the samples of the MG states had gel-like properties. Previously, it was observed by high-resolution neutron spectroscopy of concentrated protein solutions around the denaturing temperature that protein denaturation results in the formation of an entangled gel-like network with significantly reduced global protein diffusion as compared to the native folded state.38 With regard to the MG states the reduced Deff values also seem to be the signature for the onset of protein entanglement of the partially folded proteins on the nanosecond time scale. Although the acid denatured state is even fully unfolded, the higher charge of the protein increases protein repulsion, which appears to prevent protein entanglement and the reduction of global protein diffusion. With regard to the MG state with 22% α-helical content we find a significant discrepancy between the scaled IRIS and IN16 data. That observation indicates that on the faster picosecond time scale probed on IRIS the initial step of global protein diffusion is not sensitive to protein entanglement, while on the slow nanosecond time scale as observed on IN16 the individual proteins sense the presence of the neighbouring macromolecules, which reduces global protein diffusion.
3.3 Internal protein diffusive motions
The properties of internal diffusive protein motions can be deduced from the broad Lorentzian of the QENS spectra. The q-dependence of the line-widths Γ2 provides information on the relaxation times, jump-diffusion coefficients and residence times of internal protein dynamics on the investigated time-scales. Representative line-widths related to internal protein dynamics of MG states of apo-Mb recorded on different neutron spectrometers are shown in Fig. 5.Line-widths Γ2 extracted from measurements on the high-resolution spectrometer IN16 – see Fig. 5(A) for the case of the MG state of apo-Mb at pD 2 stabilized by 0.1 M NaCl – were found to be independent of the scattering vector q indicative of a localised dynamic process. Fig. 5(A) depicts the unbiased fit results, without imposing any q-dependence. The IN16 QENS spectra were consequently described by a global fitting approach using a q-independent line-width Γ2. The corresponding relaxation times τ = ℏ/Γ2 as a function of the α-helical content of the protein are given in Fig. 6(A). We find a relaxation time of τ = 200 ps for all samples being independent of the secondary structure content of the protein. The observed slow dynamic process could be, for example, attributed to the reorientational motions of buried groups in the protein or the slow rotational motions of side-chains. The slow relaxation time of apo-and holo-Mb determined is similar to the previous results on the dynamics of alcohol dehydrogenase (τ = 160 ps),39 the LOV photoreceptor protein SB1 in the dark- and light-adapted states (τ = 170 and 150 ps, respectively),40 but appears to be larger than that of the structurally related haemoglobin in red blood cells (τ = 121 ps),33 or also of the membrane protein bacteriorhodopsin (τ = 120 ps).41
 | ||
| Fig. 6 Information on internal diffusive protein dynamics as deduced from the line-shape analysis of the QENS broadening. (A) Average relaxation times as a function of the α-helical content determined on IN16 at a temperature of 289.2 K. The dotted line indicates an average value of 200 ps. (B) Diffusion coefficients and (C) residence times of apo-Mb measured on IRIS (empty symbols) and IN5 (filled symbols). The α-helical content of the native folded (F), partially folded molten globule (MG), and unfolded (U) states is given in the legend. The dotted lines in (B) and (C) are literature values of D2O solvent.44 The dashed line in (B) are diffusion coefficients of H2O solvent.43 | ||
The Γ2 recorded on IRIS and IN5 of the apo-Mb states showed a q-dependent behaviour and could be described analytically by a jump-diffusion mechanism. Fits were done in the q2-range of 0.21–1.12 Å−2 for IN5 data and 0.56–2.23 Å−2 for IRIS data according to
 | (8) |
The observed type of motions on the picosecond time-scale has been attributed to rotational and librational motions of amino acid side-chains along the C–C bonds.45 More recently, we have attributed the observed dynamics to the jumps of amino-acid side-chains mostly located on the surface of the protein.39,46 We find no significant variations of the jump-diffusion coefficients of apo-Mb between the different folded states. The diffusivity of internal protein motions on the picosecond time-scale agrees well with the values of H2O bulk solvent. The diffusion coefficients of D2O buffer, which was used as solvent for the neutron scattering experiments, are significantly lower than those of internal protein dynamics. This is also consistent with the results found for other proteins (see e.g. ref. 47 and references therein). This demonstrates that internal diffusive motions in proteins on the picosecond time-scale are governed by H-bonding and depend weakly on the secondary structure content. However, significant variations are observed concerning the residence times of internal protein dynamics. The τ0 of all protein samples are clearly larger than the values of bulk solvent. At low temperatures, the residence times of the folded apo-Mb seems to be increased as compared to the MGs and the unfolded states. The observation indicates that a larger secondary structure content and a higher local compactness of the structure confine an amino-acid residue in its location, and increases the time the side-chain spends in its initial position. This behaviour is also visible in the measured root mean square displacements (RMSDs) (vide infra).
Activation energies Ea were determined from the temperature dependence of the jump-diffusion coefficients and residence times by using the Arrhenius equation. The Ea values determined are summarized in Table 2.
| Spectrometer | Sample | α-Helical content (%) | E a from D (kJ mol−1) | E a from τ0 (kJ mol−1) |
|---|---|---|---|---|
| a Determined over whole temperature range. b Limited temperature range 283–303 K. | ||||
| IN5 | apo-Mb pD 6 | 54 | 12.3 ± 0.4 | 17.2 ± 0.8 |
| apo-Mb pD 4 | 43 | 11.7 ± 0.2 | 23.2 ± 0.6 | |
| apo-Mb pD 2 | 6 | 13.6 ± 0.3 | 18.3 ± 0.7 | |
| IRIS | apo-Mb pD 2 0.1 M NaCl | 22 | 12.5 ± 0.8 | 10.6 ± 1.0a (17.6 ± 3.9b) |
| apo-Mb pD 2 | 6 | 12.5 ± 1.4 | 10.1 ± 1.6a (16.4 ± 5.6b) | |
Within the statistical errors the activation energy extracted from the jump-diffusion coefficients is similar for all the investigated structural states (mean value of 12.5 ± 0.7 kJ mol−1) measured on both neutron spectrometers. The τ0 at the two highest temperatures determined on IRIS might be overestimated, which changes the activation energies to smaller values. We find larger deviations of the Ea determined from the residence times of the different samples: using the data of IN5 an average value of 19.6 ± 3.2 kJ mol−1 is obtained, while for the proteins measured on IRIS we find an average value of 10.4 ± 0.4 kJ mol−1 in the whole temperature range (17.0 ± 0.8 kJ mol−1 in the restricted temperature range of 283–303 K). The determined values are well in the range of activation energies of internal protein dynamics in haemoglobin (9.5 kJ mol−1 from jump-diffusion coefficients at 100 μeV instrumental resolution)46 and free and inhibited acetylcholinesterase (9.4 and 14.5 kJ mol−1 from MSDs at 50 μeV resolution)48 or heat denatured bovine serum albumin (12 and 18 kJ mol−1 from the residence times of side-chain and backbone dynamics, respectively, at 3.5 μeV resolution).47
3.4 Localized internal protein dynamics
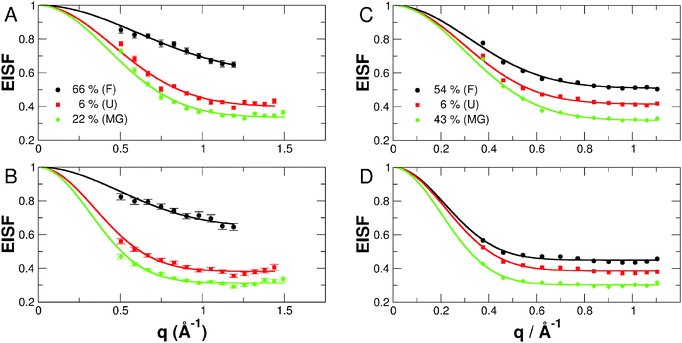
Information about the amplitude of internal protein dynamics was obtained from the EISF. The measured EISF could be described analytically according to49| A0(q) = e−〈x2〉q2(1 − p) + p, | (9) |
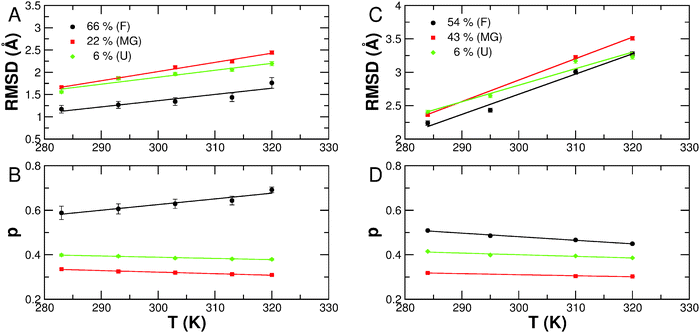
Due to lower counting statistics, the EISF could not be determined accurately from data measured on the high-resolution spectrometer IN16. The obtained RMSD  and the fractions of immobile H-atoms p are plotted in Fig. 8. It is important to stress that the RMSD and p values depend on the energy resolution of the neutron spectrometer. Therefore, a quantitative comparison is strictly only applicable for data sets recorded on neutron spectrometers with the same resolution. The RMSDs extracted from measurements on IN5 are found to be larger than those obtained on IRIS, which is expected, as the energy resolutions of both instruments are different (12 vs. 18 μeV FWHM). On IN5, lower protein concentrations have been measured compared to IRIS, which might point out that molecular fluctuations are suppressed at the investigated concentrations on IRIS. The strong increase in the RMSD going from IRIS to IN5 is nevertheless unexpected as no significant molecular crowding interactions are expected for all the measured protein concentrations, which might influence internal molecular dynamics.
and the fractions of immobile H-atoms p are plotted in Fig. 8. It is important to stress that the RMSD and p values depend on the energy resolution of the neutron spectrometer. Therefore, a quantitative comparison is strictly only applicable for data sets recorded on neutron spectrometers with the same resolution. The RMSDs extracted from measurements on IN5 are found to be larger than those obtained on IRIS, which is expected, as the energy resolutions of both instruments are different (12 vs. 18 μeV FWHM). On IN5, lower protein concentrations have been measured compared to IRIS, which might point out that molecular fluctuations are suppressed at the investigated concentrations on IRIS. The strong increase in the RMSD going from IRIS to IN5 is nevertheless unexpected as no significant molecular crowding interactions are expected for all the measured protein concentrations, which might influence internal molecular dynamics.
The folded apo- and holo-Mb conformations are found to be significantly less flexible than the partially and unfolded conformations, which is in agreement with the previous results on the fast dynamics on the time scale of a few picoseconds.21A priori, one would assume that the fully unfolded states of apo-Mb at pD 2 would be more flexible than the partially folded states of apo-Mb at pD 4 and at pD 2 with 0.1 M NaCl. The experimental data obtained from both experiments show that this is not the case on the accessible time scales of IRIS and IN5, with the MGs states having nearly similar or even higher flexibility than the acid denatured state. The slope of RMSD vs. temperature is also flatter for the acid denatured state than the MG states being indicative of stronger internal forces in the fully unfolded protein. An explanation could be that repulsive interactions of charged amino-acid residues in the acid denatured state restrict molecular motions to smaller amplitudes and also lead to stronger internal forces. Less charged residues at pD 4 or a smaller screening length due to the 0.1 M NaCl content would therefore result in larger amplitudes of motions and a softer structure, albeit the secondary structure content is larger in the MGs than in the acid denatured state.
The fraction of immobile H-atoms p is attributed to slow moving residues that are located in the hydrophobic core of the protein being shielded from the solvent,21,39 and we find general features of the measured samples being independent of the energy resolution of the instruments. For all the investigated conformations of apo-Mb, we find a decrease of p with temperature, which is expected, as higher temperature enhances internal protein dynamics. With regard to holo-Mb, p increases with temperature, which might be related to the fact that the EISF could be determined only in a smaller scattering vector range than for the apo-Mb samples, and the extracted p-values for holo-Mb are slightly too large at higher temperatures. Therefore, we discuss only the p-values averaged over all temperatures. The folded conformations of holo- and apo-Mb are characterised by the largest p-values. We find average values of p = 0.63 for holo-Mb and p = 0.48 for apo-Mb at pD 6. For the acid denatured state, quasi-identical values of p = 0.39 and 0.40 are determined from IRIS and IN5 data, respectively. This observation is in agreement with the molecular picture that the removal of the heme-group allows water molecules to enter into the heme-pocket,50 thus increasing the solvent accessible surface area of the protein. Denaturation of the protein destabilises the hydrophobic core of the folded protein and allows solvent molecules to interact with the otherwise shielded hydrophobic residues. On the other hand, the MG states are characterised by smaller fractions of immobile H-atoms than the unfolded state. The average values are nearly identical for both MG states with p = 0.32 for apo-Mb at pD 2 with 0.1 M NaCl and p = 0.31 for apo-Mb at pD 4. Although the MGs of apo-Mb were found to have a larger secondary structure content and a higher compactness than the acid denatured state,21 the experimental data concerning their dynamic properties show that they are highly dynamic objects as also observed before for pressure induced MG states of acetylcholinesterase.51 The measured fractions of immobile H-atoms point out that solvent molecules can penetrate into the hydrophobic core of the MG states facilitating fast dynamics on the picosecond time-scale.
3.5 Conformational entropy of the protein and of the hydration layer
The knowledge of RMSDs allows the determination of the difference in conformational entropy ΔSconf between two protein conformations. In this study, we consider the acid denatured state of apo-Mb at pD 2 as a reference of the unfolded state of apo-Mb. The difference in conformational entropy ΔSconf is then given as52,53 | (10) |
The experimentally determined ΔSconf(T) profiles of the partially and fully folded conformations of apo- and holo-Mb are plotted in Fig. 9(A) as a function of temperature. In general, larger ΔSconf values are found for more folded conformations. The difference in conformational entropy is close to or below zero for the MG states, which is an obvious result as the RMSDs of the acid denatured state are found to be similar or larger than the corresponding values of the MGs. A remarkable result is the parabolic shape of the ΔSconf(T) profiles most clearly visible for the native holo- and apo-Mb states at pD 6. The parabolic profile is reminiscent of the parabolic shape of the thermodynamic free energy difference ΔG(T) = ΔH − TΔS between the unfolded and folded states of proteins, where ΔH is the enthalpic component and ΔS is the contribution due to entropy. The maxima of ΔSconf(T) are shifted to lower temperatures from holo-Mb via apo-Mb at pD 6 to the MG states, which is also the case for the thermodynamic ΔG(T) profiles.21 It is important to note here that ΔG, ΔH and ΔS are thermodynamic quantities that contain the contributions of both the protein and the hydration layer, e.g. ΔSconf and ΔShydr for the entropic contributions. The entropy difference ΔS(T) can be calculated as a function of temperature using the Gibbs–Helmholtz equation
 | (11) |
 | ||
| Fig. 9 (A) Difference in conformational entropy ΔSconf between the acid denatured state of apo-Mb and the protein in the investigated partially folded and folded states as obtained from eqn (10). The α-helical content of the native folded (F), partially folded molten globule (MG), and unfolded (U) states is given in the legend (empty symbols IRIS, filled symbols IN5 data). The dotted lines are ΔS = ΔSconf + ΔShydr calculated from the thermodynamic parameters Tm, ΔCp and ΔH. (B) Difference in conformational entropy ΔShydr = ΔS − ΔSconf related to water molecules of the hydration shell and protein motions that are out of the time window of the neutron spectrometers. The solid lines in (A) and (B) are polynomial fits of second order and serve as a guide to the eye. | ||
Thermodynamic parameters were taken from the literature (Tm: 81, 61, 60 °C; ΔH: 615, 222, 63.3 kJ mol−1 K−1; ΔCp: 11.9, 6.5, 0.82 kJ mol−1 for holo- and apo-Mb at pH 6 and apo-Mb at pH 2 0.1 M NaCl, respectively), see ref. 21 and references therein. The values of apo-Mb at pH 4 are not known. The ΔS(T) curves of folded holo- and apo-Mb (66% and 54% α-helical content) and of the MG state stabilised by 0.1 M NaCl (22% α-helical content) are plotted in Fig. 9(A) in comparison to ΔSconf(T). The quantities ΔS and ΔSconf are different as ΔSconf is derived from the extent of protein fluctuations without the contribution of the hydration shell. The entropy difference between the unfolded and the folded states that is related to the contribution of water molecules in the hydration layer of the protein can be determined by
| ΔShydr(T) = ΔS(T) − ΔSconf(T). | (12) |
4. Conclusions
Protein dynamics is of great importance for protein folding, as the polypeptide chain needs to explore the accessible conformational space during the folding transition. In this manuscript, we present an investigation on the global and internal dynamics of Mb with respect to the secondary structure content of the protein by neutron spectroscopy. The degree of folding is found to have a significant impact on global and internal protein dynamics. An increase in the charge of the macromolecule accelerates global protein short-time diffusion, while a gel-like phase of the MGs at the investigated protein concentrations reduces the overall diffusion on the slow nanosecond time scale. The fully folded protein conformations are found to be significantly less flexible with a higher fraction of immobile H atoms than the partially and unfolded conformations. The experimental data concerning the internal motions of the MGs demonstrate that they are highly dynamic objects. With regard to internal diffusive protein motions, we find no significant variations of the jump-diffusion coefficients or relaxation times between the different folded states.The most relevant thermodynamic quantity concerning protein folding that can be determined from the neutron scattering experiments is the difference in conformational entropy ΔSconf between two specific structural states. Only few methods are able to determine ΔSconf experimentally. NMR, for example, allows determining residue resolved information on the picosecond to nanosecond time scale in terms of the order parameter, which is related to an entropy contribution. Neutron scattering, on the other hand, is a direct method that probes average protein dynamics on the time scale accessible by a neutron spectrometer. As all dynamic processes contribute to ΔSconf, the average information provided by neutron scattering is actually not a drawback.
In our article, we determined ΔSconf between the acid denatured state, which is considered as a reference for the fully unfolded state, and the partially and fully folded conformations as a function of temperature. We find parabolically shaped profiles ΔSconf(T) mostly visible for the folded conformations reminiscent of the shape of the thermodynamic free energy difference ΔG(T). A further important question is, on which time scale the strongest contribution of conformational motions to ΔSconf is occurring. In a previous study investigating protein dynamics on the fast time scale of a few picoseconds we found a linear correlation between ΔSconf and the secondary structure content,21 whereas in the present study we find the ΔSconf of the MG states of apo-Mb being similar or below that of the acid denatured states. A general conclusion, therefore, is that the strongest contribution of localised molecular motions detectable by neutron scattering to ΔSconf comes from protein fluctuations acting on the fast picosecond time scale.
Thermodynamic experiments allow the determination of ΔS, which contains both the contribution of the protein (ΔSconf) and that of the hydration shell (ΔShydr). Using thermodynamic parameters from the literature and the experimentally determined ΔSconf values as input we could determine the ΔShydr of different folded states of the protein. While the hydration layer of the MG state is found to be slightly more ordered than that of the acid denatured unfolded state, mobile and disordered water molecules in the hydration layer of the folded states make a significant contribution to the entropic stabilisation of the folded structures. At higher temperatures, the hydration layer around the folded states becomes less mobile and more ordered than in the unfolded state, which provides a source for the entropic stabilisation of the unfolded state and facilitates protein unfolding.
Acknowledgements
The experiments at the ISIS Pulsed Neutron and Muon Source were supported by a beam time allocation from the Science and Technology Facilities Council. We acknowledge the Institut Laue-Langevin for provision of the neutron beam time.References
- J. D. Bryngelson, J. N. Onuchic, N. D. Socci and P. G. Wolynes, Proteins, 1995, 21, 167–195 CrossRef CAS PubMed.
- V. Daggett and A. R. Fersht, Trends Biochem. Sci., 2003, 28, 18–25 CrossRef CAS PubMed.
- M. Karplus and D. L. Weaver, Protein Sci., 1994, 3, 650–668 CrossRef CAS PubMed.
- C. N. Pace, J. M. Scholtz and G. R. Grimsley, FEBS Lett., 2014, 588, 2177–2184 CrossRef PubMed.
- A. J. Doig and M. J. E. Sternberg, Protein Sci., 1995, 4, 2247–2251 CrossRef CAS PubMed.
- J. Zhang and J. S. Liu, PLoS Comput. Biol., 2006, 2, e168 Search PubMed.
- K. Henzler-Wildman and D. Kern, Nature, 2007, 450, 964–972 CrossRef CAS PubMed.
- R. B. Best, J. Clarke and M. Karplus, J. Mol. Biol., 2005, 349, 185–203 CrossRef CAS PubMed.
- A. M. Stadler, L. Stingaciu, A. Radulescu, O. Holderer, M. Monkenbusch, R. Biehl and D. Richter, J. Am. Chem. Soc., 2014, 136, 6987–6994 CrossRef CAS PubMed.
- H. Frauenfelder, B. H. McMahon and P. W. Fenimore, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8615–8617 CrossRef CAS PubMed.
- H. J. Dyson and P. E. Wright, Chem. Rev., 2004, 104, 3607–3622 CrossRef CAS PubMed.
- H. J. Dyson and P. E. Wright, Nat. Struct. Biol., 1998, 5, 499–503 CrossRef CAS PubMed.
- D. Eliezer, J. Yao, H. J. Dyson and P. E. Wright, Nat. Struct. Biol., 1998, 18, 148–155 CrossRef.
- D. Eliezer and P. E. Wright, J. Mol. Biol., 1996, 263, 531–538 CrossRef CAS PubMed.
- F. Hughson, P. Wright and R. Baldwin, Science, 1990, 249, 1544–1548 CAS.
- D. Eliezer, J. Chung, H. J. Dyson and P. E. Wright, Biochemistry, 2000, 39, 2894–2901 CrossRef CAS PubMed.
- J. Yao, J. Chung, D. Eliezer, P. E. Wright and H. J. Dyson, Biochemistry, 2001, 40, 3561–3571 CrossRef CAS PubMed.
- M. Kataoka, I. Nishii, T. Fujisawa, T. Ueki, F. Tokunaga and Y. Goto, J. Mol. Biol., 1995, 249, 215–228 CrossRef CAS PubMed.
- O. Tcherkasskaya and V. N. Uversky, Proteins, 2001, 44, 244–254 CrossRef CAS PubMed.
- P. C. Aoto, C. Nishimura, H. J. Dyson and P. E. Wright, Biochemistry, 2014, 53, 3767–3780 CrossRef CAS PubMed.
- A. M. Stadler, M. M. Koza and J. Fitter, J. Phys. Chem. B, 2015, 119, 72–82 CrossRef CAS PubMed.
- Neutron Scattering in Biology – Techniques and Applications, ed. J. Fitter, T. Gutberlet and J. Katsaras, Springer Berlin Heidelberg New York, Berlin Heidelberig, 2006 Search PubMed.
- A. K. Covington, M. Paabo, R. A. Robinson and R. G. Bates, Anal. Chem., 1968, 40, 700–706 CrossRef CAS.
- E. Gasteiger, C. Hoogland, A. Gattiker, S. Duvaud, M. R. Wilkins, R. D. Appel and A. Bairoch, in The Proteomics Protocols Handbook, Humana Press, 2005, pp. 571–607 Search PubMed.
- E. Antonini and M. Brunori, Hemoglobin and myoglobin in their reactions with ligands, North-Holland Pub. Co, Amsterdam, 1971 Search PubMed.
- http://www.ill.eu/instruments-support/instruments-groups/yellowbook/ .
- C. J. Carlile and M. A. Adams, Phys. B, 1992, 182, 431–440 CrossRef CAS.
- Y. Harpaz, M. Gerstein and C. Chothia, Structure, 1994, 2, 641–649 CrossRef CAS PubMed.
- L. R. Murphy, N. Matubayasi, V. A. Payne and R. M. Levy, Folding Des., 1998, 3, 105–118 CrossRef CAS PubMed.
- S. J. Edelstein and H. K. Schachman, J. Biol. Chem., 1967, 242, 306–311 CAS.
- M. Bée, Quasielastic neutron scattering: principles and applications in solid state chemistry, biology, and materials science, Adam Hilger, Bristol and Philadelphia, 1988 Search PubMed.
- F. Roosen-Runge, M. Hennig, F. Zhang, R. M. J. Jacobs, M. Sztucki, H. Schober, T. Seydel and F. Schreiber, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11815–11820 CrossRef CAS PubMed.
- A. M. Stadler, L. van Eijck, F. Demmel and G. Artmann, J. R. Soc., Interface, 2011, 8, 590–600 CrossRef CAS PubMed.
- J. Pérez, J. M. Zanotti and D. Durand, Biophys. J., 1999, 77, 454–469 CrossRef.
- A. M. Gaspar, M.-S. Appavou, S. Busch, T. Unruh and W. Doster, Eur. Biophys. J., 2008, 37, 573–582 CrossRef CAS PubMed.
- A. M. Stadler, I. Digel, G. M. Artmann, J. P. Embs, G. Zaccai and G. Büldt, Biophys. J., 2008, 95, 5449–5461 CrossRef CAS PubMed.
- A. J. Banchio and G. Nägele, J. Chem. Phys., 2008, 128, 104903 CrossRef PubMed.
- M. Hennig, F. Roosen-Runge, F. Zhang, S. Zorn, M. W. A. Skoda, R. M. J. Jacobs, T. Seydel and F. Schreiber, Soft Matter, 2012, 8, 1628 RSC.
- M. Monkenbusch, A. Stadler, R. Biehl, J. Ollivier, M. Zamponi and D. Richter, J. Chem. Phys., 2015, 143, 075101 CrossRef CAS PubMed.
- A. M. Stadler, E. Knieps-Grünhagen, M. Bocola, W. Lohstroh, M. Zamponi and U. Krauss, Biophys. J., 2016, 110, 1064–1074 CrossRef CAS PubMed.
- J. Fitter, R. E. Lechner and N. A. Dencher, Biophys. J., 1997, 73, 2126–2137 CrossRef CAS PubMed.
- F. Volino and A. J. Dianoux, Mol. Phys., 2006, 41, 271–279 CrossRef.
- A. M. Stadler, J. P. Embs, I. Digel, G. M. Artmann, T. Unruh, G. Büldt and G. Zaccai, J. Am. Chem. Soc., 2008, 130, 16852–16853 CrossRef PubMed.
- Y. Edura and N. Morishima, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 545, 309–318 CrossRef CAS.
- J. M. Zanotti, M. C. Bellissent-Funel and J. Parello, Biophys. J., 1999, 76, 2390–2411 CrossRef CAS PubMed.
- A. M. Stadler, C. J. Garvey, J. P. Embs, M. Koza, T. Unruh, G. Artmann and G. Zaccai, Biochim. Biophys. Acta, 2014, 1840, 2989–2999 CrossRef CAS PubMed.
- M. Grimaldo, F. Roosen-Runge, M. Hennig, F. Zanini, F. Zhang, N. Jalarvo, M. Zamponi, F. Schreiber and T. Seydel, Phys. Chem. Chem. Phys., 2015, 17, 4645–4655 RSC.
- M. Trapp, M. Trovaslet, F. Nachon, M. M. Koza, L. van Eijck, F. Hill, M. Weik, P. Masson, M. Tehei and J. Peters, J. Phys. Chem. B, 2012, 116, 14744–14753 CrossRef CAS PubMed.
- F. Volino, J.-C. Perrin and S. Lyonnard, J. Phys. Chem. B, 2006, 110, 11217–11223 CrossRef CAS PubMed.
- A. M. Stadler, E. Pellegrini, M. Johnson, J. Fitter and G. Zaccai, Biophys. J., 2012, 102, 351–359 CrossRef CAS PubMed.
- J. Marion, M. Trovaslet, N. Martinez, P. Masson, R. Schweins, F. Nachon, M. Trapp and J. Peters, Phys. Chem. Chem. Phys., 2015, 17, 3157–3163 RSC.
- J. Fitter, Biophys. J., 2003, 84, 3924–3930 CrossRef CAS PubMed.
- V. Receveur, P. Calmettes, J. C. Smith, M. Desmadril, G. Coddens and D. Durand, Proteins, 1997, 28, 380–387 CrossRef CAS.
- P. Ball, Chem. Rev., 2008, 108, 74–108 CrossRef CAS PubMed.
- F. X. Gallat, A. Laganowsky, K. Wood, F. Gabel, L. van Eijck, J. Wuttke, M. Moulin, M. Hartlein, D. Eisenberg, J. P. Colletier, G. Zaccai and M. Weik, Biophys. J., 2012, 103, 129–136 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |