First-principles analysis on role of spinel (111) phase boundaries in Li_4+3xTi₅O₁₂ Li-ion battery anodes

Abstract

The practical anode material Li_4+3xTi₅O₁₂ is known to undergo a two-phase separation into Li₇Ti₅O₁₂ and Li₄Ti₅O₁₂ during charging/discharging. This phase-separated Li_4+3xTi₅O₁₂ exhibits electron conduction, although individual phases are expected to be insulators. To elucidate the role played by spinel (111) phase boundaries on these physical properties, first principles calculations were carried out using the GGA+U method. Two-phase Li₇Ti₅O₁₂/Li₄Ti₅O₁₂ models are found to exhibit metallic characteristics near their phase boundaries. These boundaries provide conduction paths not only for electrons, but also for Li ions. Judging from the formation energy of Li vacancies/interstitials, the phase boundaries preferentially uptake or release Li via in-plane conduction and then continuously shift in a direction perpendicular to the phase boundary planes. The continuous phase boundary shift leads to a constant electrode potential. A three-dimensional network of cubic {111} planes may contribute to smooth electrochemical reactions.

---

1. Introduction

Energy storage systems are an indispensable factor for realizing a truly sustainable society, and this has seen spinel-type Li_4+3xTi₅O₁₂ attract considerable attention for its potential application as an anode material in Li-ion battery systems.^1–4 One advantage offered by this material is its capability to absorb and desorb Li with almost no change in volume, which leads to good cyclic performance. Its constant electrode potential also helps to provide a stable open circuit voltage (OCV). Electron and ion conduction can also be achieved without the need for a conductive additive. All of these physical properties occur within the rigid Ti–O framework of a spinel-type structure.

Clear phase boundaries between Li₄Ti₅O₁₂ and Li₇Ti₅O₁₂ have been observed in spinel-type Li_4+3xTi₅O₁₂ during electro-chemical reaction,^5,6 but the role played by its phase boundaries in Li diffusion and electronic conduction is not yet fully understood. What is known is that transition metal oxides of Li_4+3xTi₅O₁₂ are categorized as strongly correlated electron systems, and the characteristic features of their electrons have been identified through real space observations.⁵ Localized electrons acting on specific Ti sites as Ti³⁺ have been observed in Li₇Ti₅O₁₂, and these are presumed to act as a Mott insulator. The behaviour of electrons in Li₄Ti₅O₁₂ is also known to provide an intrinsic insulator, and yet electron conduction occurs in this material Li_4+3xTi₅O₁₂. This discrepancy between practical experience and scientific interpretation cannot be described by their bulk properties alone, which suggests that further investigation is needed to understand the fundamental properties of the phase boundaries.

This study investigates how the conduction of electrons is possible in Li_4+3xTi₅O₁₂ using a two-phase coexistence model: Li₇Ti₅O₁₂/Li₄Ti₅O₁₂. This is aimed at identifying how the bands align and where metallization is most likely to occur, with a particular focus on the role played by phase boundaries. The movement of the phase boundary, and the effect this has on the constant electrode potential, are discussed in relation to Li vacancies and the interstitial formation energy. To ensure a proper description of the strongly correlated electron system, the GGA+U method was used.⁷

2. Method and crystal structures

2.1. Methodologies

First principles calculations were carried out using the Vienna ab initio package,^8,9 wherein the projector-augmented wave (PAW) potentials were taken and exchange–correlation was treated using a Perdew–Burke–Ernzerhof gradient-corrected functional.^10–12 To ensure accurate total energies and band structure calculations for the Ti 3d electrons, aspherical contributions to the gradient corrections inside the PAW spheres were taken into account.¹³ The wave functions were expanded into plane waves using a 500 eV cutoff, and the Brillouin zone integrations were sampled by a 1 × 3 × 3 mesh. The geometries were optimized by a conjugate gradient algorithm¹⁴ until all forces became less than 0.01 eV Å⁻¹. The rotationally invariant GGA+U calculations were treated in the Hubbard U potential form introduced by Dudarev et al.⁷ The U_eff values have been reported to be 4.5–5.0 eV for Ti 3d states.^5,15,16 We have used a U_eff value of 5.0 eV and found that this U_eff value reproduces the localized states of Ti-3d in Li₇Ti₅O₁₂. The spin-polarization effect was taken into account. Since spin-flips in the same charge ordering give almost the same total energy in this system, the initial spin configuration of Li_4+3xTi₅O₁₂ was assumed to be ferromagnetic. Throughout the calculation, no symmetrical restriction was imposed. The formation energy was evaluated using the total energy of Li in a body centred cubic (BCC) structure with an optimized lattice parameter of a = 3.51 Å.

2.2. Crystal structure

In principle, Li_4+3xTi₅O₁₂ contains a large amount of spare room for adsorbing Li, with a spinel-type crystal structure that is categorized in the Fd3̄m space group (No. 227).¹⁷ In this study, Li_4+3xTi₅O₁₂ is hereafter distinguished by its Li content as Li(4 + 3x); e.g., Li7 represents Li₇Ti₅O₁₂. In this symmetry, the Li occupancy sites are 8a in Li4 and 16c in Li7. The surrounding polyhedron is composed of oxygen as the first nearest neighbour, but while this is a tetrahedron in Li4, it is an octahedron in Li7. The average bond length between Li–O is also longer by 8% when Li is at 16c than at 8a. In order to obtain the most favourable atomic configuration, every possible option in a 3 × 1 × 1 primitive spinel cell was explored. In addition to the 8a and 16c Li sites, the 16d sites were occupied by Ti and Li to investigate the most stable cation arrangement in the unit cell. The optimum arrangement found is used for our phase boundary model.

Using the features of the spinel structure, namely its three-dimensional space channels along 〈110〉 directions that coincide with Li ion migration, a two-phase coexistence model was constructed, as shown in Fig. 1. As primitive lattice vectors of face centred cubic (FCC) structures are composed of 〈110〉 vectors, two 〈110〉 vectors were used to define a {111} plane that has been observed experimentally as one of the phase boundary planes.^6,7 Along the spinel 〈111〉 directions is an alternating sequence of coarse and fine TiO₆ octahedra, which have a stacking sequence of AB AB in the calculated unit cell. Taking these facts into consideration, a stoichiometric Li7/Li4 two-phase structure was modelled that has periodic (111) phase boundary planes. This consists of two Li7 and two Li4 unit cell, with two asymmetric phase boundary planes at their edges. Since the difference in optimized cell volume between Li7 and Li4 is less than 1%, the cell parameters were fixed to the average of the two throughout the calculations. The lattice constant of the spinel structure was 8.41 Å, which is consistently within 1% of experimental data.^1,3 As illustrated in Fig. 1, the Ti atoms were labelled from 1 to 12, with those between 1 and 6 belonging to the Li7 side, while the others belong to the Li4 side.

Fig. 1 Structure of optimized stoichiometric two-phase Li₇Ti₅O₁₂/Li₄Ti₅O₁₂ model with two (111) interface planes as its phase boundaries drawn by VESTA.¹⁸ Dotted lines show the phase boundaries. In Ti–O framework Li occupancy sites are different from 8a in Li₄Ti₅O₁₂ to 16c in Li₇Ti₅O₁₂. TiO₆ octahedra have a stacking sequence of ABAB… along spinel 〈111〉 directions in the cell.

3. Results and discussion

3.1. Two-phase coexistence and formation energy

The origin of the constant electrode potential of this material is attributed to reactions that occur under equilibrium conditions in which two phases coexist.¹ Though various Li compositions can be achieved in the Li_4+3xTi₅O₁₂ system by altering the ratio of the two phases, these reactions require constant energy for the movement of phase boundaries, which determines the constant chemical potential of Li. Thus, it is this energy that determines the electrode potential of the material.

For two phases to coexist in Li_4+3xTi₅O₁₂, the free energy of the system must have two local minima. Since the Li content varies in the Ti–O framework, the energy of the system as a function of Li content is presumed to have local minima at around x = 0 (Li4) and 1 (Li7), as it is here that the system has a common energy gradient.¹⁹ The total energy of various configurations of Li_4+3xTi₅O₁₂ (x = 1/3, 2/3) calculated from the solid solution model was compared with values obtained from a simple mixture model of Li4 and Li7. The difference in total energy between the two was defined as the formation energy, ΔE_f, as per the following:

ΔE_f = E_tot[Li_4+3xTi₅O₁₂] − {(1 − x)E_tot[Li₄Ti₅O₁₂] + xE_tot[Li₇Ti₅O₁₂]} (1)

Here, E_tot[A] denotes the total energy of system A. These values are plotted in Fig. 2, in which we can see that all are positive. The formation energies therefore support the notion that two phases coexist.

Fig. 2 Formation energy of Li_4+3xTi₅O₁₂ per formula unit as a function of Li content.

3.2. Interface energy

In practical applications, Li_4+3xTi₅O₁₂ materials are used as particles with finite sizes. If a particle in solid solution undergoes two-phase separation, then it gains energy through its phase separation from the solid solution (the formation energy described above), but loses energy due to the formation of a boundary between the two separated phases (the interface energy). Whether a particle with a finite size undergoes phase separation is determined by whether the formation energy, which is proportional to the volume of the particle, is greater than the interface energy that is determined by the area of the phase boundary. This means that small particles may not undergo phase separation, and that smaller interface energy reduces the particle size needed for separation to occur. The interface energy, ΔE_inter, is defined by the difference in total energy between the stoichiometric two-phase coexistence model and the sum of the bulk Li4 and Li7 per unit area:

2SΔE_inter = E_tot[Li₄Ti₅O₁₂/Li₇Ti₅O₁₂] − {E_tot[Li₄Ti₅O₁₂] + E_tot[Li₇Ti₅O₁₂]}

where S is the area of the interface. Note that the energy is divided by two because the model contains two boundaries in periodic condition. The interface energy of the (111) phase boundary that exists between Li4 and Li7 is calculated to be 0.01 eV Å⁻². Compared with the formation energy of two-phase separation, the calculated interface energy is small enough for even a nanosized Li_4+3xTi₅O₁₂ particle to contain a (111) phase boundary inside it.

3.3. Electronic structures of bulks

Individual Li4 and Li7 phases have an insulating type of electronic structure in their density of state (DOS), as seen in Fig. 3. The structure of Li4 is somewhat similar to that of titanium dioxide,²⁰ in that the highest occupied molecular orbital is mainly composed of oxygen (p orbital), while the lowest unoccupied molecular orbitals is composed of titanium (d orbital). This makes the electronic structures of bulk Li4 an intrinsic insulator type.

Fig. 3 DOS of (a) Li₄Ti₅O₁₂ and (b) Li₇Ti₅O₁₂. Vertical line shows Fermi levels (E_F).

In Li7, electrons donated by excess Li atoms to Ti atoms occupy localized states on Ti³⁺, where they induce Jahn–Teller distortion of the local Ti³⁺O₆ octahedra.²¹ This characteristic is well reproduced by the +U method. The localized states emerge only by introducing the +U term, and so we have categorized Li₇Ti₅O₁₂ as a Mott insulator. Electronic repulsion between oxygen p orbitals and localized Ti d orbitals causes elongation of the Ti³⁺–O ligand bond along two of the three axes in D_4h symmetry, which splits the degenerated d states.²² The volume of the Ti³⁺O₆ octahedra is subsequently increased by about 10% when compared to Ti⁴⁺O₆. A lower Hubbard band (LHB) representing localized b_2g states appears in the band gap and becomes the valence band (VB) top, while the upper Hubbard band raises the conduction band (CB) bottom. In this way, the electronic structures of Li7 come to show insulator type.

3.4. Electronic structures of spinel (111) phase boundaries

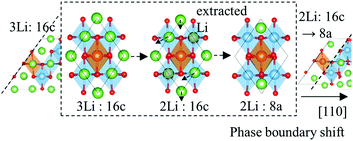
Unlike the insulating electronic structures of Li4 and Li7, the two-phase coexistence model has a metallic character, as evidenced by a DOS that exists at the Fermi level (E_F) in Fig. 4(b). The charge density around E_F (that is, in the energy range from E_F − 0.4 eV to E_F) is illustrated in Fig. 4(a). It is sown that the electron carriers emerge near the phase boundaries, which are coming from the partially-occupied shallow Ti-3d states near the boundaries as described later.

Fig. 4 (a) Charge density around E_F and (b) total DOS for a stoichiometric two-phase coexistence model (Li₄Ti₅O₁₂/Li₇Ti₅O₁₂). In (a) the contour surface of charge density of 0.018 Å⁻³ is plotted and the dotted lines show the phase boundaries and in (b) the energy is referred to E_F and the red circle denotes the energy range for calculation of the charge density around E_F. Conductive electrons are distributed near the (111) phase boundaries.

In a two-phase system, reactions occur when phase boundaries move. Thus, in order to confirm whether carriers appear wherever a boundary is located, the electronic structure was studied with varying phase boundary edges. As described earlier, the TiO₆ octahedra in this system have a basic stacking sequence of AB AB in the unit cell, which means that in this model different phase boundaries can be prepared by extracting one Li atom from a 16c site on the Li7 side boundaries. As these will always have a DOS at the E_F, this approach ensures that the boundaries are metallic.

Continuous extraction of Li atoms from the phase boundary provides the same effect as boundary shifts along the spinel [110] direction. The model therefore produces alternate symmetric and asymmetric boundaries with each Li atom extraction from the Li7 side of the boundary plane, which results in layer-by-layer movement of the (111) phase boundary. The extraction or insertion of Li atoms preferentially occurs at the phase boundaries, which is a phenomenon that is described in more detail later. The charge density around the E_F with various phase boundary edges is shown in Fig. 5 for the same energy range used in Fig. 4. The bottom to the top extraction of Li atoms from the boundary edge of the Li7 side is depicted in Fig. 5, in which it is evident that electrons near the phase boundaries follow the boundary shift. Carriers continue to exist near the (111) phase boundaries, and so Li ions and electrons gain a conduction path along the system boundaries rather than having to cross them.

Fig. 5 Phase boundary shifts induced by Li extractions from Li₇Ti₅O₁₂ side phase boundaries. Charge density around E_F is illustrated in the same energy range and the same contour surface in Fig. 4. Li atoms are extracted one by one from the (d) bottom to the (a) top. Li vacancy formation energy is listed on the side in the unit of eV.

Although both Li7 and Li4 are insulators, Fig. 4 and 5 show that the Li7/Li4 phase boundaries have a metallic character. Moreover, while the volume of Ti³⁺O₆ octahedra is enlarged by ∼10% compared to Ti⁴⁺O₆, TiO₆ at the boundaries is enlarged by 5% at most. This makes the magnitude of the Ti-d band splitting smaller than that of Ti³⁺, and so it is the shallow 3d levels at the phase boundaries that are responsible for the metallic nature of the boundaries.

3.5. Local density of states

Fig. 6 shows the local DOS of Ti up-spin. In this, the Ti sites of Li7 (labelled 1 to 6 in Fig. 1) are presumed to be Ti³⁺, whereas those from 7 to 12 in Li4 are believed to be Ti⁴⁺. In both cases, no states are considered to be at the E_F based on the calculations of pristine Li7 and Li4. However, Ti-6, Ti-7 and Ti-12 located near the boundaries do have finite states at the E_F, which come from the partially-occupied shallow Ti-3d states. Then, it is clear that carriers exist near the phase boundaries.

Fig. 6 Local DOS of up-spin electrons for the Ti atoms labelled from 1 to 12 in Fig. 1 in stoichiometric Li₇Ti₅O₁₂/Li₄Ti₅O₁₂ two-phase coexistence model with asymmetric phase boundary planes. Dotted lines show the location of phase boundaries. The energy is referred to E_F.

Since the stoichiometric Li7/Li4 two-phase coexistence model has asymmetric phase boundary planes, examination of the local DOS in various structures with different phase boundaries edges was used to confirm the emergence of carriers near the phase boundaries. A model structure was obtained from the stoichiometric model structure by extracting one Li atom from a 16c site on the Li7 side of the boundary. Once again, DOS exist at the E_F near the boundaries, but the stacking sequence along the spinel 〈111〉 direction in the unit cell means that this model has symmetric phase boundaries edges. Importantly, this shows that carriers exist near the phase boundaries regardless of the boundary edge type.

3.6. Li vacancy interstitial formation energy

The extraction of Li from the Li7 side of the (111) phase boundaries produces the same effect as phase boundary shift. As illustrated in Fig. 7, even when there are three 16c Li atoms at the boundary, when one is extracted the other Li atoms transfer to 8a sites. This rearrangement of Li atoms forms a new phase boundary.

Fig. 7 Schematic showing the rearrangement of Li at spinel {111} phase boundaries.

The extraction/insertion of Li at phase boundaries seems to replicate the same procedure as a phase boundary shift. Thus, in order to make clear the role played by phase boundaries, the formation energies of Li vacancies and interstitials (ΔE_V/ΔE_I) were estimated as follows:

ΔE_V = [E_tot(V_Li) + E(Li_bcc)] − E_tot

ΔE_I = E_tot(I_Li) − [E(Li_bcc)] + E_tot

Here E_tot and E_tot(V_Li)/E_tot(I_Li) are the total energies of the phase boundary systems before and after introducing a Li vacancy/interstitial, and E(Li_bcc) is the energy of Li metal per atom in a bcc structure. Since the values of the sites in the inner region of Li7 and Li4 are almost the same as those of equivalent sites in the respective pristine bulks, the inner regions can be considered to retain the properties of bulks. A comparison was made of the Li vacancy/interstitial formation energies at the boundaries and in the inner (bulk) region when Li is extracted/inserted and these are tabulated in Table 1.

Table 1 Li vacancy/interstitial formation energies for Li7/Li4 phase boundaries and their respective bulk phases (eV)

	ΔEV	ΔEI
Li7/Li4 (phase boundaries)	1.2–1.5	−1.5 to −1.2
Li4 (bulk)	5.3–5.5	−1.0 to −0.3
Li7 (bulk)	1.7–2.0	−0.1 to 0.0

---

When Li is extracted from a phase boundary, less energy is required than when it is removed from the inner (bulk) region. Conversely, when Li is inserted into the boundaries, the system gains more energy than in the inner (bulk) region. These results indicate that Li extraction/insertion preferentially occurs at the phase boundaries, which in the case of a spinel {111} boundary plane, includes two spinel 〈110〉 Li diffusion directions. Thus, during the lithiation/delithiation of Li_4+xTi₅O₁₂, Li ions are expected to be extracted/inserted through in-plane diffusion without crossing the boundary.

The Li vacancy/interstitial formation energy at the boundaries ranges from 1.2 to 1.5 eV, which is reasonably consistent with the average Li vacancy formation energy of 1.35 eV in Li_4+xTi₅O₁₂ when it changes from Li7 to Li4, as estimated from the difference between the total energy of Li7 and the sum of Li4 and Li metal. The Li vacancy/interstitial formation energy per electron, on the other hand, is interpreted as representing the electrode potential or the maximum OCV against Li metal.²³ The evaluated narrow energy range of 1.2 to 1.5 V is also in good agreement with the experimental data for Li_4+xTi₅O₁₂.^1–3 During lithiation/delithiation of Li_4+3xTi₅O₁₂, it is believed that Li ions and electrons are extracted from, or inserted into, (111) phase boundaries via conduction in the boundary planes, and that these reactions continuously shift the boundaries in a direction perpendicular to the planes, as shown in Fig. 8. These continuous phase boundary movements, in turn, lead to a constant electrode potential, which is one of the advantages of the Li_4+xTi₅O₁₂ anodes.

Fig. 8 Schematic diagram of the role played by spinel {111} phase boundary. The phase boundary provides a conduction path for electrons and Li ions. The boundaries preferentially uptake or release Li via in-plane conduction (along the white arrow) and then continuously shift in a direction perpendicular to the boundary planes (along the black arrow).

4. Summary

Formation energies obtained through first-principles analysis using the GGA+U method have revealed that Li_4+xTi₅O₁₂ undergo phase separation into Li₇Ti₅O₁₂ and Li₄Ti₅O₁₂. A Li₇Ti₅O₁₂/Li₄Ti₅O₁₂ two-phase coexistence model with spinel (111) phase boundaries confirmed a metallic character exists near the phase boundaries. Moreover, the interface energy of this plane is so small that even nano-sized Li_4+xTi₅O₁₂ particles can contain a (111) phase boundary. In view of the Li vacancy/interstitial formation energies, Li ions are expected to be extracted from or inserted into (111) phase boundaries via in-plane conduction, and these reactions produce continuous phase boundary shifts perpendicular to the plane. Since the spinel {111} planes form a three-dimensional network, the (111) phase boundaries provide conduction pathways for both electrons and Li ions. These linked networks may contribute to the stable open circuit voltage and smooth electrochemical reaction of this material.

Acknowledgements

This work has been supported by Global Research Center for Environment and Energy based on Nanomaterials Science (GREEN) and JST ALCA project. The computation in this study was performed using the numerical materials simulators at NIMS and ISSP.

References

1. K. M. Colbow, J. R. Dahn and R. R. Haering, J. Power Sources, 1989, 26, 397.
2. E. Ferg, R. J. Gummow, A. de Kock and M. M. Thackeray, J. Electrochem. Soc., 1994, 142, L147.
3. T. Ohzuku, A. Ueda and N. Yamamoto, J. Electrochem. Soc., 1995, 142, 1431.
4. S. Scharner, W. Weppner and P. Schmind-Beurmann, J. Electrochem. Soc., 1999, 146, 857.
5. X. Lu, L. Zhao, X. He, R. Xiao, L. Gu, Y.-S. Hu, H. Li, Z. Wang, X. Duan, L. Chen, J. Maier and Y. Ikuhara, Adv. Mater., 2012, 24, 3233.
6. M. Kitta, T. Akita, S. Tanaka and M. Kohyama, J. Power Sources, 2014, 257, 120.
7. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
8. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
9. G. Kresse and J. Furhmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
10. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
11. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
12. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
13. http://https://www.vasp.at .
14. W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes, Cambridge University Press, 2007.
15. S. Tanaka, M. Kitta, T. Tamura, T. Akita, Y. Maeda and M. Kohyama, J. Phys. D: Appl. Phys., 2012, 45, 494004.
16. H. Unal, E. Mete and S. Ellianluoglu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115407.
17. T. Hahn, International Tables for Crystallography A, Springer, 5th edn, 2006.
18. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 658.
19. J. E. Hillard, Phase Transformations, American Society for Metal, 1968.
20. D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798.
21. H. A. Jahn and E. Teller, Proc. R. Soc. London, Ser. A, 1937, 161, 220.
22. K. C. Molloy, Group Theory for Chemists, Woodhead Publishing Limited, 2010.
23. F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121.

---