Open Access Article
Open Access ArticleUltrafast electron injection into photo-excited organic molecules†
Dean
Cvetko
*abc,
Guido
Fratesi
 *d,
Gregor
Kladnik
ab,
Albano
Cossaro
*d,
Gregor
Kladnik
ab,
Albano
Cossaro
 b,
Gian Paolo
Brivio
e,
Latha
Venkataraman
*fg and
Alberto
Morgante
bh
b,
Gian Paolo
Brivio
e,
Latha
Venkataraman
*fg and
Alberto
Morgante
bh
aFaculty of Mathematics and Physics, University of Ljubljana, Slovenia. E-mail: dean.cvetko@fmf.uni-lj.si
bCNR-IOM, Laboratorio TASC, Basovizza, Trieste, Italy
cJ. Stefan Institute, Ljubljana, Slovenia
dETSF and Dipartimento di Fisica, Università degli Studi di Milano, Italy. E-mail: guido.fratesi@unimi.it
eDipartimento di Scienza dei Materiali, Università di Milano-Bicocca, Italy
fDepartment of Applied Physics, Columbia University, New York, NY, USA. E-mail: lv2117@columbia.edu
gDepartment of Chemistry, Columbia University, New York, NY, USA
hDipartimento di Fisica, Università di Trieste, Italy
First published on 14th July 2016
Abstract
Charge transfer rates at metal/organic interfaces affect the efficiencies of devices for organic based electronics and photovoltaics. A quantitative study of electron transfer rates, which take place on the femtosecond timescale, is often difficult, especially since in most systems the molecular adsorption geometry is unknown. Here, we use X-ray resonant photoemission spectroscopy to measure ultrafast charge transfer rates across pyridine/Au(111) interfaces while also controlling the molecular orientation on the metal. We demonstrate that a bi-directional charge transfer across the molecule/metal interface is enabled upon creation of a core-exciton on the molecule with a rate that has a strong dependence on the molecular adsorption angle. Through density functional theory calculations, we show that the alignment of molecular levels relative to the metal Fermi level is dramatically altered when a core-hole is created on the molecule, allowing the lowest unoccupied molecular orbital to fall partially below the metal Fermi level. We also calculate charge transfer rates as a function of molecular adsorption geometry and find a trend that agrees with the experiment. These findings thus give insight into the charge transfer dynamics of a photo-excited molecule on a metal surface.
1 Introduction
The performance of organic-based electronic devices relies on efficient charge transport across hybrid interfaces where electronically different materials couple; such interfaces often represent a bottleneck in the overall performance of organic electronic and photovoltaic devices.1 Charge transfer (CT) across interfaces is most easily studied using small aromatic molecules that can form ordered molecular films on a variety of substrates. Often, such systems exhibit rather uniform coupling schemes to metal electrodes as well as to other molecules, thereby minimizing structural disorder, which is a major limiting factor in the device performance.2,3 Such ordered prototypical systems open up the possibility to experimentally address charge transport phenomena on the molecular level using X-ray based spectroscopy techniques.4–7Here we focus our study on films of pyridine molecules (PYR, C5H5N, inset, Fig. 1B) formed on Au(111) surfaces with adsorption geometries that can be experimentally varied by adjusting the molecular coverage.8 Our motivation for using this archetypical π-conjugated aromatic system is its ability to bind to Au surfaces through the formation of a weak Au–N donor–acceptor bond, with geometry-dependent coupling, that has previously been shown to assist in charge transport through single-molecule conductance experiments.9 In this work, we use near edge X-ray absorption fine structure (NEXAFS), X-ray resonant photoemission (RPES) and apply core-hole-clock (CHC) analysis4 to study electron transfer between empty molecular orbitals and the Au continuum of states in the core-excited systems. The CHC method has been used previously to determine ultrafast electron transfer times from organic molecules to underlying surfaces,6,10–15 between aromatic molecules with π–π coupling16 and also between molecules interacting through hydrogen bonding17 as well as between donor and acceptor organic molecules.18,19
Here, we present evidence for new core-hole decay channels present in the PYR-on-Au(111) system that reflect efficient injection of electrons from the Au substrate to PYR molecules on the femtosecond timescale, at a rate that depends on the orientation of the molecule on the Au substrate. We extend the standard CHC analysis to quantify the dynamics of electron injection to the molecule and find a strong dependence on the adsorption angle. The rate of electron injection from Au to the molecule increases as the molecular π system becomes flatter, enabling a greater overlap with the Au substrate, in agreement with single-molecule transport measurements.9 Through density functional theory (DFT) calculations, we demonstrate that the core-excited lowest unoccupied molecular orbital (LUMO*) of the molecule lies partially below the Fermi level explaining the origin of the additional core–hole decay channels observed here. We also demonstrate that the coupling of the LUMO* to the Au continuum states varies with the PYR adsorption angle in agreement with the experimentally observed trends.
2 Results and discussion
We first present results from near-edge X-ray absorption fine-structure spectroscopy (NEXAFS) for PYR films on Au(111) and use them to determine the orientation of the molecule relative to the surface.8 We show, in Fig. 1A and B, NEXAFS spectra measured across the C K-edge over an energy range of 283–301 eV for a multilayer film and a monolayer film created by flash-heating a multilayer film to −55 °C (see Fig. S1, ESI,† for additional details on film preparation and characterization through XPS). The main double-peak at 285 eV corresponds to a photon absorption excitation from a C1s core level to the lowest unoccupied molecular orbital (LUMO). The double-peak feature results from different C1s initial states as presented in the ESI† with the help of DFT based calculations for an isolated molecule. The calculated NEXAFS spectra confirm that the LUMO can be excited from both C and N sites. The LUMO of PYR has π*-character with its nodal plane coinciding with the molecular aromatic ring.9We exploit the polarization dependence of the NEXAFS spectra, which are subject to dipole selection rules, to determine the molecular orientation on the surface.8 Specifically, the C1s → LUMO transition is forbidden for light polarized in the plane of aromatic rings. We therefore determine the average angle for PYR on Au(111) by comparing the intensity of this transition with an incident electric field perpendicular (p-pol) and parallel (s-pol) to the surface. For a multilayer film the intensity of the π* excitation is independent of the electric field polarization, as can be expected for a randomly oriented molecular film.8 In contrast, the monolayer PYR film displays a strong linear dichroism with a higher intensity peak observed in p-pol compared to s-pol. For this film, the average molecular tilt angle (θ) from the surface, determined following previously published methods8 (see the ESI†), is 32° ± 3°.
In Fig. 1C, we show a series of p-pol NEXAFS spectra collected while annealing a multilayer PYR film over a temperature range from −106 °C to −25 °C. The relative intensity of the C1s → LUMO peak increases gradually with increasing temperature indicating that the molecular orientation gets flatter upon annealing. The molecular adsorption angles obtained through heating a multilayer film range from ∼25° to ∼65°.
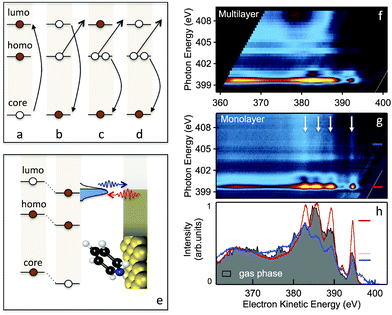
We now turn to measurements of charge transfer dynamics at the PYR/Au interface by using the RPES technique and CHC analysis. As applied here, a core N1s electron is excited to an unoccupied molecular orbital (Fig. 2a) leaving a core-hole on the molecule. This excited state decays via three different scenarios.
In the first, known as the participator decay (Fig. 2b), the electron excited to the LUMO* de-excites in the core-hole decay with emission of an Auger electron. This leaves a single hole in one of the filled molecular orbitals and the LUMO empty. In the RPES spectrum these channels are found energetically degenerate with the respective direct photoemission from the filled molecular orbitals, i.e. HOMO−n; n = 0, 1, 2, 3, etc., but with resonantly enhanced intensity. The second, known as spectator Auger decay (Fig. 2c), involves filling the core-hole with an electron from an occupied orbital, accompanied by electron emission from another occupied orbital; this leaves the system with two holes and an additional (spectator) electron in the LUMO. Finally, when the molecule is electronically coupled to the substrate, the excited LUMO* electron can escape to the substrate, quenching both the participator and spectator decay channels and the core-hole decays via a normal Auger process (Fig. 2d). By comparing the participator decay intensity in the monolayer and multilayer systems and knowing the core-hole lifetime (5 fs for N1s and 6 fs for C1s)20 we can determine the charge transfer times from the molecule to the substrate. However, another core-hole decay scenario arises if the LUMO* is lying below the Fermi level upon a core-hole creation (Fig. 2e). In this case, the LUMO* may get filled via electron transfer from the substrate. Thus, the characteristic spectral lines due to the decay of the LUMO* electron are observed regardless of the incident light energy;21,22 hereafter we term this process super-participator decay.
We measure the RPES spectra, which are comprised of XPS measurements taken at a series of incident photon energies across the N K-edge of the PYR multilayer and 5 different monolayer films having PYR oriented with an angle ranging from 32° to 56°. The experimental details are given in the ESI.† Briefly, XPS spectra over a 50 eV kinetic energy range were measured with photon energy (hν) tuned across the N K-edge in steps of 0.1 eV (from 395 eV to 415 eV) and all spectra are presented as two-dimensional maps of intensity plotted against photon energy and electron kinetic energy. Fig. 2f and g show RPES maps for a multilayer film and a monolayer film with molecules oriented at 32°. We see strong resonances in the RPES maps at hν = 399.5 eV, corresponding to an excited state decay following a N1s → LUMO* transition. These correspond to electron emission through the participator decay channel involving different occupied molecular orbitals at electron kinetic energies between 375 and 395 eV. Thus the photoemission spectrum on resonance (hν = 399.5 eV) resembles that of a direct valence band photoemission (see ESI,† Fig. S2) but with an enhanced intensity that depends on the spatial overlap of the occupied orbital and the LUMO with the N1s core orbital.6
We then analyze data of the PYR monolayer with an average molecular angle of 32° relative to the Au surface. The monolayer RPES map (Fig. 2g) reveals additional features, marked by white arrows, not present in the multilayer map (Fig. 2f). These start at participator peaks in the spectrum at hν = 399.5 eV, and are visible even beyond excitations to the free electron continuum above ∼405 eV. These features are most clearly visible in the line scans shown in Fig. 2h, where we compare data at hν = 399.5 eV and at hν = 405 eV with a valence band spectrum acquired for the molecule in the gas phase. The clear peaks seen in the line scan taken at 405 eV (beyond the ionization edge) indicate that there are additional features that occur at constant kinetic energy. We attribute these features to the super-participator process (Fig. 2e). Once a N1s core-hole is created in PYR, the energy level alignment of all orbitals relative to the metal Fermi level is altered. The LUMO* drops at least partially below the Fermi level and may get occupied with charge from the metal as long as it is electronically well-coupled to the substrate. Thus for all incident photon energies required to create a N1s core-hole (hν ≥ 399.5 eV), if an ultrafast charge injection into the LUMO* occurs within the core-hole life-time, the core-hole can decay through the super-participator channel.
Qualitatively we note that the intensity ratio of the super-participator to participator peak is large and indicative of a fast electron injection into the molecule due to a significant fraction of the LUMO* lying below the Fermi level. To quantify the charge injection rate based on the data presented in Fig. 2, we measure the participator intensity, Ip, at the LUMO* excitation (hν = 399.5 eV) and the super-participator intensity above the ionization edge, Isp (hν = 405 eV) for PYR on Au(111) and compare them with the participator intensity at the LUMO* excitation in the gas phase, I0p. Details of the extended CHC analysis that use these peak intensities to determine charge transfer rates are given in the ESI.† For the PYR/Au system shown in Fig. 2 with a tilt angle of 32°, we measure Isp/Ip = 0.7 ± 0.05 and Ip/I0p = 0.95 ± 0.05. This latter ratio already takes into account the angular dependence of the matrix element for the oriented molecules on the surface as cos(θ)/cos(θm), where θm = 54.7° is used for the average over molecular orientations in the gas phase. This gives the fractional occupation of the LUMO* below Fermi x ∼ 1, and for the electron injection time τ = τch(1 − Isp/Ip)/(Isp/Ip) = 3.2 ± 0.5 fs, where τch = 5 fs is used for the N1s core-hole lifetime.20
We now repeat the RPES measurements and CHC analysis for four films with different molecular tilt angles ranging from 32° to 56°. The results are summarized in Fig. 3. We find that the charge injection time increases from ∼3.2 fs to ∼30 fs with increasing tilt angle of the PYR molecules. In all cases we determine the fractional occupation of the LUMO* to be close to unity (x = 0.9 ± 0.1), indicating that LUMO* is filled by nearly one electron at all tilt angles of the adsorbed molecule. We also find a consistent trend of the Auger peak position above the ionization edge, passing from mostly “spectator shifted” to almost exclusively “normal Auger” for increasing tilt angles, in agreement with the observed trend in the charge injection times (details are shown in the ESI†). These observations imply that the spatial overlap of LUMO* with the Au continuum of states is responsible for the strong angular dependence of the charge injection dynamics. We also find that ultrafast transfer of electrons from the Au occurs on both carbon and nitrogen sites of the core-excited molecule, and for both excitation sites flat lying adsorption geometries strongly enhance the rate of charge injection into the molecule.
In order to understand the effect of molecular adsorption geometry on the orbital level alignment in the presence of a core-hole and the influence of charge transfer across the organometallic interface, we turn to DFT calculations. For this work, we investigate five different molecular tilt angles: θ = 0°, 30°, 45°, 60°, and 90°, and show in Fig. 4a the computed density of states (projected on the LUMO of PYR) as a function of θ, both for the ground state (blue bullets) and the N1s ionization (LUMO*, red triangles). To compare computational results with the experiment, we focus on the LUMO* case, with an added valence electron as eventually attracted from the substrate to screen the perturbation.23–27 This corresponds to a fully relaxed electronic configuration after the molecule is ionized. The attractive potential introduced by the core hole lowers the energy of the molecular orbitals with respect to the ground state. The LUMO*, in particular, shows a significant fraction going below the Fermi level (see red triangles in Fig. 4a) and hence being filled by electrons from the substrate, in agreement with the experimental observations, while the ground state LUMO is always well above the Fermi level (blue bullets). The resonant transfer times for the LUMO and LUMO* are calculated from their Lorentzian width Γ, obtained for θ = 45°, Γ = 95 meV and Γ = 167 meV, i.e., τ = 7 fs and τ = 4 fs, for the ground state and core-excited state, respectively. The difference between these values reflects the altered shape of the orbital as well as the interfacial energy-level alignment upon excitation. Although the computed value is smaller than the experimental one, the agreement is remarkable given the simplicity of the theoretical model.
We now consider the effect of the molecular adsorption angle on this charge transfer time. At variance with the moderate dependence found for the ground state LUMO, the energy alignment of the LUMO* is almost independent of θ so that electron transfer from the surface is expected at all angles considered. The π symmetry of the orbital, which is depicted in the inset of Fig. 4a, is essential in determining the overlap with the substrate states and hence the dependence of τ on the angle. We observe a monotonous increase in the transfer time with θ (by a factor 3 when passing from θ = 30° to 60°), as shown in Fig. 4b, both for the values computed in the ground state and upon excitation, in agreement with the experimentally observed trend.
The electron transfer from the substrate to the ionized molecule can be visualized by evaluating the modification of the valence charge upon excitation, Δρ = ρexc − ρgs. That is reported in Fig. 4c for θ = 45° and shows an increase of electron density in the molecular region: Mulliken population analysis28 performed in the ground and excited states show that about 0.89 e are transfered to the molecule. A similar result was obtained at the other angles, with increased charge transfer from 0.83 e to 0.93 e when passing from θ = 0° to 90°. These values are in excellent agreement with the experimental ones (0.9 ± 0.05). The remaining charge, 0.11 e for θ = 45°, can be attributed to the Au atoms in the surface layer while the bottom layers are practically unaffected (we recall that ρexc includes the added electron as provided by the metal). The electron displacement Δρ can be further decomposed into a molecular contribution Δρ(g), as it would result for the ionization of free molecules in the gas phase (without the possibility of electron transfer), and a substrate contribution Δρ′ for electron transfer and screening also accounting for the additional valence electron: Δρ = Δρ(g) + Δρ′. These quantities are shown in Fig. 4c, d and e, respectively. While Δρ(g) shows in Fig. 4d a contraction of the molecular charge towards the N atom, the substrate contribution Δρ′ in Fig. 4e highlights the filling of the LUMO* state by surface electrons. We stress that these findings follow from the specific structure of Δρ of the PYR/Au system and may not occur generally for organic molecules adsorbed on metals. For example, a similar alignment of LUMO* to the Fermi level was computed for pyridine on graphene,27 but complete filling of LUMO* for pentacene/Al(001) has been evaluated and observed.24,26
3 Conclusions
We explored the dynamics of charge transfer in a series of PYR/Au(111) layers with different adsorption angles, and found that the LUMO* of the core excited molecules falls partially below the Au Fermi level, opening a gateway for ultrafast injection of electrons from the gold substrate to the molecule. Importantly, we have extended the standard CHC analysis of the RPES spectra to determine this charge transfer rate and have shown that it depends on the orientation of the molecule to the metal surface; the flatter molecules have a significantly faster charge transfer. Through DFT calculations, we have shown that the core-excited PYR/Au has a LUMO* that lies partially below the Fermi level, with an excellent agreement between computed occupation values and best-fit results from the measurements. We have also demonstrated that the broadening of this orbital due to its electronic coupling to the Au continuum of states enables an ultrafast charge transfer from the Au to the molecule within the core-hole lifetime. We have further calculated the angular dependence of the charge injection rate and find a trend consistent with the experiment of faster dynamics for flatter lying molecules. These findings have a direct consequence on understanding the mechanism of charge transfer at molecular junctions for hetero-organic photovoltaics, where the alignment of donor and acceptor orbitals in the presence of a valence exciton dictates the efficiency of exciton dissociation, charge separation, and consequently device performance.4 Methods
Condensed phase and gas phase measurements have been performed at the ALOISA and ANCHOR beamlines of the Elettra Synchrotron in Trieste, Italy.29 The Au(111) substrate was prepared by cycles of Ar+ ion sputtering and temperature annealing. Pyridine molecules were vacuum deposited on the Au substrate through a leak valve operated in ∼10−7 mbar pressure range. The PYR multilayer was grown with the sample held below 200 K, whereas monolayer phases with variable adsorption geometry were produced by temperature annealing of multilayer films up to T ∼ 250 K. NEXAFS at the nitrogen (carbon) K-edge was performed by collecting the emission of secondary electrons as a partial absorption yield with the high pass filter set to 370 eV (250 eV). All NEXAFS spectra were measured with linear photon polarization in s-pol geometry (electric field vector![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) parallel to the surface plane), p-pol geometry (
parallel to the surface plane), p-pol geometry (![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) along the surface normal) or at a magic angle (angle between
along the surface normal) or at a magic angle (angle between ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) and the surface normal, 54.7°). Photoemission experiments were performed using an electron analyzer positioned along the photon polarization
and the surface normal, 54.7°). Photoemission experiments were performed using an electron analyzer positioned along the photon polarization ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) . Photon energies of hν = 650, 500, and 130 eV were used for core-level and valence band spectra, with an overall energy resolution of ∼100 meV. RPES at the N (C) K-edge was conducted by taking a series of XPS scans with photon energy between 395 and 425 eV (280–310 eV) in steps of 0.1–0.2 eV. For each photon energy, the XPS spectrum covering ∼60 eV kinetic energy (Ek) range was measured to construct a two-dimensional like RPES map I(hν,Ek). The non-resonant spectra were measured in the pre-edge region with a photon energy of 395 eV (283 eV), and were subtracted from each XPS spectrum in the RPES maps I(hν,Ek). Participator intensity was evaluated after normalization to the integrated Auger, from the integrated intensities of the upper valence peaks (e.g. HOMO in the 0–8 eV binding energy range). Super-participator intensity was evaluated from the XPS spectra with photon energy above the ionization edge, hν > 405 eV (hν > 292 eV) as integrated intensity in the fixed kinetic energy range (∼380 eV), containing the electron emission from the HOMO. More details about the spectra acquisition conditions, the preparation of the sample, and the implementation of the CHC method are given in the ESI.†
. Photon energies of hν = 650, 500, and 130 eV were used for core-level and valence band spectra, with an overall energy resolution of ∼100 meV. RPES at the N (C) K-edge was conducted by taking a series of XPS scans with photon energy between 395 and 425 eV (280–310 eV) in steps of 0.1–0.2 eV. For each photon energy, the XPS spectrum covering ∼60 eV kinetic energy (Ek) range was measured to construct a two-dimensional like RPES map I(hν,Ek). The non-resonant spectra were measured in the pre-edge region with a photon energy of 395 eV (283 eV), and were subtracted from each XPS spectrum in the RPES maps I(hν,Ek). Participator intensity was evaluated after normalization to the integrated Auger, from the integrated intensities of the upper valence peaks (e.g. HOMO in the 0–8 eV binding energy range). Super-participator intensity was evaluated from the XPS spectra with photon energy above the ionization edge, hν > 405 eV (hν > 292 eV) as integrated intensity in the fixed kinetic energy range (∼380 eV), containing the electron emission from the HOMO. More details about the spectra acquisition conditions, the preparation of the sample, and the implementation of the CHC method are given in the ESI.†
We use the SIESTA/TranSIESTA simulation packages30,31 with the Perdew, Burke, and Ernzerhof (PBE) exchange–correlation functional.32 To obtain a detailed analysis of the coupling between the PYR molecule and the substrate, especially to deal with the lineshapes of the resonant orbitals, it is most convenient to consider a continuum of Au states. We adopt a description derived from electron transport31 where a semi-infinite substrate is taken into account by a Green's function approach.33,34 For computational convenience we replicate the system and model two facing semi-infinite Au substrates, each having a PYR molecular layer. Facing molecules are separated by at least 20 Å to prevent any interaction between the two sides (see Fig. 5). Periodic boundary conditions in the lateral directions are taken within a 4 × 4 Au surface unit cell (coverage fixed to 1/16).
 | ||
| Fig. 5 Structural setup for computing the electronic structure of PYR adsorbed on semi-infinite Au(111). The inset shows the dependence of the N–Au distance d on the angle θ as determined in ref. 35. | ||
In describing the angle-dependent properties, we adopt the molecular adsorption geometry on the Au(111) surface from the work of Mollenhauer et al.,35 with the PYR N atom on the a-top site on the Au surface and an Au–N distance that depends on the molecular tilt angle. Such a dependence was determined by structural optimizations within DFT corrected for van der Waals interactions, and is summarized in the inset of Fig. 5. To describe the case of a molecule excited by X-ray radiation, we promote a N1s electron from the core to a valence state. The core-hole is included in the pseudopotential that accounts for the interaction of valence electrons with a core-excited N1s* ion. The resonant electron/hole injection time τ from the LUMO is then determined as τ = ℏ/Γ36,37 from the Lorentzian full width at half-maximum (FWHM) Γ in the density of states projected onto the LUMO:
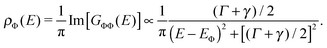 | (1) |
Acknowledgements
The authors greatly acknowledge fruitful discussions with A. Batra and O. Adak. We acknowledge support from the MIUR of Italy through PRIN projects (no. 20104XET32 and 20105ZZTSE), ANCHOR project of the FIRB 2010 call (ref. RBFR10FQBL), and MAE project (US14GR12). Part of this research was also funded through Progetto Premiale 2012 ABNANOTECH. Computational resources are made available in part by CINECA (application codes HP10C0TP0R and HP10CESYLM). D. C. and G. K. acknowledge support from the Slovenian Research Agency (Project no. P1-0112 and Z1-6726). L. V. thanks the Packard Foundation for support.References
- S. R. Forrest, Nature, 2004, 428, 911–918 CrossRef CAS PubMed.
- F. Schreiber, Prog. Surf. Sci., 2000, 65, 151–257 CrossRef CAS.
- J. V. Barth, Annu. Rev. Phys. Chem., 2007, 58, 375–407 CrossRef CAS PubMed.
- P. A. Brühwiler, O. Karis and N. Mårtensson, Rev. Mod. Phys., 2002, 74, 703–740 CrossRef.
- D. Menzel, Chem. Soc. Rev., 2008, 37, 2212–2223 RSC.
- P. Vilmercati, D. Cvetko, A. Cossaro and A. Morgante, Surf. Sci., 2009, 603, 1542–1556 CrossRef CAS.
- L. Cao, X.-Y. Gao, A. T. S. Wee and D.-C. Qi, Adv. Mater., 2014, 26, 7880–7888 CrossRef CAS PubMed.
- J. Stöhr, NEXAFS Spectroscopy, Springer, Berlin, Heidelberg, 1992, vol. 25 Search PubMed.
- S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Nat. Nanotechnol., 2009, 4, 230–234 CrossRef CAS PubMed.
- L. Cao, Y.-Z. Wang, T.-X. Chen, W.-H. Zhang, X.-J. Yu, K. Ibrahim, J.-O. Wang, H.-J. Qian, F.-Q. Xu, D.-C. Qi and A. T. S. Wee, J. Chem. Phys., 2011, 135, 174701 CrossRef PubMed.
- L. Cao, Y. Wang, J.-q. Zhong, Y.-Y. Han, W. Zhang, X. Yu, F. Xu, D. Qi and A. T. S. Wee, J. Phys. Chem. C, 2014, 118, 4160–4166 CAS.
- G. Kladnik, D. Cvetko, A. Batra, M. DellâĂŹngela, A. Cossaro, M. Kamenetska, L. Venkataraman and A. Morgante, J. Phys. Chem. C, 2013, 117, 16477–16482 CAS.
- J. Schnadt, P. A. Brühwiler, L. Patthey, J. N. O'Shea, S. Södergren, M. Odelius, R. Ahuja, O. Karis, M. Bässler, P. Persson, H. Siegbahn, S. Lunell and N. Mårtensson, Nature, 2002, 418, 620–623 CrossRef CAS PubMed.
- F. Blobner, P. B. Coto, F. Allegretti, M. Bockstedte, O. Rubio-Pons, H. Wang, D. L. Allara, M. Zharnikov, M. Thoss and P. Feulner, J. Phys. Chem. Lett., 2012, 3, 436–440 CrossRef CAS PubMed.
- O. Adak, G. Kladnik, G. Bavdek, A. Cossaro, A. Morgante, D. Cvetko and L. Venkataraman, Nano Lett., 2015, 15, 8316–8321 CrossRef CAS PubMed.
- A. Batra, G. Kladnik, H. Vázquez, J. S. Meisner, L. Floreano, C. Nuckolls, D. Cvetko, A. Morgante and L. Venkataraman, Nat. Commun., 2012, 3, 1086 CrossRef PubMed.
- G. Kladnik, M. Puppin, M. Coreno, M. de Simone, L. Floreano, A. Verdini, A. Morgante, D. Cvetko and A. Cossaro, Nano Lett., 2016, 16, 1955–1959 CrossRef CAS PubMed.
- P. Vilmercati, C. Castellarin-Cudia, R. Gebauer, P. Ghosh, S. Lizzit, L. Petaccia, C. Cepek, R. Larciprete, A. Verdini, L. Floreano, A. Morgante and A. Goldoni, J. Am. Chem. Soc., 2009, 131, 644–652 CrossRef CAS PubMed.
- T. Schiros, G. Kladnik, D. Prezzi, A. Ferretti, G. Olivieri, A. Cossaro, L. Floreano, A. Verdini, C. Schenck, M. Cox, A. a. Gorodetsky, K. Plunkett, D. Delongchamp, C. Nuckolls, A. Morgante, D. Cvetko and I. Kymissis, Adv. Energy Mater., 2013, 3, 894–902 CrossRef CAS.
- M. Coville and T. D. Thomas, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 6053–6056 CrossRef CAS.
- A. J. Britton, A. Rienzo, J. N. O'Shea and K. Schulte, J. Chem. Phys., 2010, 133, 094705 CrossRef PubMed.
- C. Sauer, M. Wießner, A. Schöll, F. Reinert, M. WieBner, A. Schöll and F. Reinert, Mater. Sci., 2013, 17, 1–5 Search PubMed.
- S. García-Gil, A. García and P. Ordejón, Eur. Phys. J. B, 2012, 85, 239 CrossRef.
- A. Baby, G. Fratesi, S. R. Vaidya, L. L. Patera, C. Africh, L. Floreano and G. P. Brivio, J. Phys. Chem. C, 2015, 119, 3624–3633 CAS.
- T. Susi, D. J. Mowbray, M. P. Ljungberg and P. Ayala, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 081401 CrossRef.
- A. Baby, H. Lin, G. P. Brivio, L. Floreano and G. Fratesi, Beilstein J. Nanotechnol., 2015, 6, 2242–2251 CrossRef CAS PubMed.
- A. Ravikumar, A. Baby, H. Lin, G. P. Brivio and G. Fratesi, Sci. Rep., 2016, 6, 24603 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- L. Floreano, G. Naletto, D. Cvetko, R. Gotter, M. Malvezzi, L. Marassi, A. Morgante, A. Santaniello, A. Verdini, F. Tommasini and G. Tondello, Rev. Sci. Instrum., 1999, 70, 3855 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garca, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor, K. Stokbro and P. Ordejo, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 1–17 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Sánchez-Portal, D. Menzel and P. M. Echenique, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 235406 CrossRef.
- G. Fratesi, C. Motta, M. I. Trioni, G. P. Brivio and D. Sánchez-Portal, J. Phys. Chem. C, 2014, 118, 8775–8782 CAS.
- D. Mollenhauer, N. Gaston, E. Voloshina and B. Paulus, J. Phys. Chem. C, 2013, 117, 4470–4479 CAS.
- S. Datta, Quantum Transport – Atom to Transistor, Cambridge University Press, 2005 Search PubMed.
- A. Nitzan, Chemical Dynamics in Condensed Phases: Relaxation, Transfer and Reactions in Condensed Molecular Systems, Oxford University Press, 2006 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04099c |
| This journal is © the Owner Societies 2016 |