Origin of the catalytic activity of face-centered-cubic ruthenium nanoparticles determined from an atomic-scale structure

Abstract

The 3-dimensional (3D) atomic-scale structure of newly discovered face-centered cubic (fcc) and conventional hexagonal close packed (hcp) type ruthenium (Ru) nanoparticles (NPs) of 2.2 to 5.4 nm diameter were studied using X-ray pair distribution function (PDF) analysis and reverse Monte Carlo (RMC) modeling. Atomic PDF based high-energy X-ray diffraction measurements show highly diffuse X-ray diffraction patterns for fcc- and hcp-type Ru NPs. We here report the atomic-scale structure of Ru NPs in terms of the total structure factor and Fourier-transformed PDF. It is found that the respective NPs have substantial structural disorder over short- to medium-range order atomic distances from the PDF analysis. The first-nearest-neighbor peak analyses show a significant size dependence for the fcc-type Ru NPs demonstrating the increase in the peak height due to an increase in the number density as a function of particle size. The bond angle and coordination number (CN) distribution for the RMC-simulated fcc- and hcp-type Ru NP models indicated inherited structural features from their bulk counterparts. The CN analysis of the whole NP and surface of each RMC model of Ru NPs show the low activation energy packing sites on the fcc-type Ru NP surface atoms. Finally, our newly defined order parameters for RMC simulated Ru NP models suggested that the enhancement of the CO oxidation activity of fcc-type NPs was due to a decrease in the close packing ordering that resulted from the increased NP size. These structural findings could be positively supported for synthesized low-cost and high performance nano-sized catalysts and have potential application in fuel-cell systems and organic synthesis.

---

Introduction

Catalysts play a major role in the technological development of conversion processes for natural gas, coal and biomass.¹ It is well known that catalysts accelerate chemical reactions, where chemical bonds are dissociated or recombined, and interactions between the catalyst and the reactant lower the reaction energy barrier. However, because the catalyst does not alter the thermodynamics of the reaction, the overall change in free energy remains unchanged.² In heterogeneous catalysis, the reactants and the catalyst are present in different phases. The structure of the reactive sites on the catalyst surface strongly influences the observed catalytic behavior, because of the intimate contact between the surface metal atoms with neighboring metal atoms. Therefore, the coordination number (CN) of the metal atoms strongly influences the catalytic activity.³ Because catalytic reactions occur at the surface, nanosized metal catalysts are typically used in catalysis to improve the catalytic efficiency, by increasing the surface-to-volume ratio.⁴ The use of transition-metal NPs in catalysis is important because they mimic metal surface activation and catalysis on the nanoscale, and thus provide superior heterogeneous catalysis efficiency in terms of activity, selectivity and lifetime.^5,6 Metallic ruthenium (Ru) adopts an hcp structure at all temperatures and has attracted much attention recently as a catalyst for CO oxidation, because of its high catalytic activity.^7,8 CO oxidation catalysts are in demand for the removal of CO from car exhaust and for the prevention of CO poisoning in fuel-cell systems. Recently, the structural identification of Ru NPs and the size dependency of their catalytic activity have been reported, and novel fcc-type Ru NPs^8,9 were more efficient than conventional hcp-type Ru NPs larger than 3 nm.¹⁰ The catalytic properties of NPs are strongly dependent on their structure and the size of Ru NPs must be determined more precisely to improve our understanding of the behavior of transition-metal NPs in heterogeneous catalysis. The 3-dimensional (3D) atomic structures of crystalline materials have been determined by crystallography and diffraction techniques such as single crystal X-ray structure analysis and powder X-ray diffraction.¹¹ However, such techniques are not suitable for NPs that are much smaller than the X-ray spatial coherence length.¹² Recently high-energy X-ray pair distribution function (PDF) analysis revealed the 3D atomic arrangement of small metal NPs, which deviates significantly from their corresponding bulk crystalline structures.^13,14 Furthermore reverse Monte Carlo (RMC)^15–17 modeling based on high-energy X-ray diffraction data has suggested that the atomic-scale structure of such NPs exhibits distinct structural disorder.¹⁸ We used the RMC_POT program¹⁹ to model isolated and finite-sized spherical NPs without using periodic boundary conditions in the simulations. We herein report the results of PDF analysis and RMC modeling based on high-energy XRD data of novel fcc-type and conventional hcp-type Ru NPs, which ranged from 2.2 to 5.4 nm in size. The short- and intermediate-range structures of the Ru NPs were investigated in terms of the coordination number and bond angle distributions. Furthermore, the surface structures of the NPs were discussed to elucidate their CO oxidation activity.

Experimental

Uniformly sized fcc and hcp Ru nanoparticles (2.2–5.4 nm) were prepared by chemical reduction methods using Ru(acac)₃ and RuCl₃·nH₂O, respectively, with the metal precursors and poly(N-vinyl-2-pyrrolidone) (PVP) as the stabilizing agent. Ethylene glycol (EG) or triethylene glycol (TEG) was employed as the solvent and reducing agent for the synthesis. Phase control was achieved by varying both the metal precursor and the solvent, and size control was achieved by adjusting the concentrations of the reagents and the PVP stabilizer used for the synthesis. In a typical synthesis of fcc Ru NPs with a diameter of 2.4 nm, Ru(acac)₃ (2.1 mmol) and PVP (10 mmol of monomer units) were dissolved in TEG (500 mL) at room temperature. The solution was then heated to 200 °C and maintained at this temperature for 3 h. After the reaction was complete, the prepared NPs were separated by centrifugation.¹⁰ The size of the prepared samples was determined from transmission electron microscopy (TEM) images, which were obtained using a Hitachi HT7700 transmission electron microscope operated at 100 kV. The mean diameter and distributions were estimated by averaging over 200 particles. The average particle sizes of the Ru NPs were 2.2, 3.5, 3.9, and 5.0 nm for the hcp structure and 2.4, 3.5, 3.9, and 5.4 nm for the fcc structure.

X-ray diffraction measurements were performed using a two-axis diffractometer installed at the BL04B2 beamline²⁰ of the third-generation synchrotron radiation facility SPring-8, Hyogo, Japan. The incident X-ray beam was 61.46 keV, with a wavelength of 0.02017 nm; it was generated using an Si(111) monochromator. The synthesized Ru NPs were loaded into a capillary column and measured at room temperature. Fine powders of bulk 99.9% Ru and PVP were used as the reference materials. The XRD data were corrected for background, polarization and absorption and were then normalized to the structure factor and Fourier transformed using the SPring-8 BL04B2 analysis software. RMC simulations^15,16 were performed on Ru NPs of different structures and different sizes. For example, an RMC run was carried out on 4857 Ru atoms in a spherical configuration closely resembling that of a spherical hcp-type Ru NP approximately 5 nm in diameter. A number density of 0.0742095 Å⁻³ corresponding to 12.45 g cm⁻³ was used. A randomly generated spherical configuration of Ru was used as the starting point of the RMC simulation. The simulations were guided by the experimental structure factor and were stopped when the RMC computed and experimental data agreed very well over the entire range of wave vectors (i.e., from 0.2 to 2.5 nm⁻¹). The simulation was carried out using a new version of the RMC_POT software¹⁹ furnished in the case of nonperiodic boundary conditions. The average coordination constraint enforcing 12 first neighbors between 0.21 and 0.35 nm was applied to take into account the close-packed nature of the Ru metal structures.

Results and discussion

High-energy synchrotron X-ray diffraction

To understand the physical properties of the Ru NP catalysts, detailed and reliable information in the atomic and intermediate range is required. Such structural information is obtained from high-energy synchrotron X-ray diffraction data, the total structure factor S(Q), and the PDF g(r) which is obtained by the Fourier transform of the S(Q). Here Q is a wave vector defined as (4π/λ)sin(θ) with θ being half the scattering angle.^9,13 The experimental XRD patterns of nanosized hcp- and fcc-type Ru particles are shown in Fig. S1 in the ESI† together with that of bulk Ru and poly(N-vinyl-2-pyrrolidone) (PVP) as a reference. In contrast, the XRD patterns of hcp-type bulk Ru were described in terms of a periodic lattice with space group P6₃/mmc, using lattice parameters a = 0.27042 nm and c = 0.42816 nm (ICSD #52261).²¹ However, the concept of Miller indices is not practically applicable for NPs. This is because their infinite 3D lattice periodicity and Bragg-peak based crystallography is broken at the nanoscale. We observed Bragg peaks at 2.85, 3.22, 4.62 and 5.44 Å⁻¹ for fcc-type Ru NPs (see Fig. S1 in the ESI†) corresponding to the (111), (200), (220), and (311) planes of the fcc structure Ru phase (ICSD #41515).^10,22 The peak at 3.22 Å⁻¹ for 2.4 nm fcc-type Ru NPs is not clear. It is interesting to note that the peak at 2.89 Å⁻¹ is obviously asymmetric in its (111) plane for 2.4 nm fcc-type Ru NPs, but the reflections from the (200) plane is very weak and rather diffuse. Furthermore, the two peaks at 0.82 and 1.40 Å⁻¹ were attributed to PVP, which are commonly observed in the XRD patterns of Ru NPs protected by the PVP stabilizer.

As shown in Fig. S1 (ESI†) the diffraction peaks of Ru NPs are highly diffuse and hence it is very difficult to analyze them using conventional crystallographic methods such as the Rietveld analysis.⁹ By contrast, the atomic-scale structure of non-crystalline systems can be described in terms of the total structure factor S(Q) and Fourier-transformed PDF g(r). S(Q) is related to the coherent part, I^coh(Q), of the diffraction data:

where c_i and f_i are the atomic concentration and X-ray atomic scattering factor, respectively, for the atomic species of type i.¹³S(Q) in a wide Q range enables a higher resolution to be obtained in the real-space information g(r) using:where ρ is the local atomic number density and r is the radial distance.

Fig. 1(b) and (d) shows the experimental g(r) data for fcc-type Ru NPs and hcp-type Ru NPs of different sizes with the assignment of fcc- (Fig. 1(a)) and hcp-type (Fig. 1(c)) ideal Ru bulk, respectively. All Ru NP PDFs exhibit significant oscillations up to approximately 1 nm, which indicates that the Ru NPs exhibit only short- to intermediate-range ordering. However, we cannot access long-range atomic distance due to limitations of the Q-resolution (ΔQ/Q = 0.1%) with a photon flux of 9.2 × 10¹⁰ (photons per second per mm² at 100 mA) in the present high energy X-ray diffraction measurements.²⁴

Fig. 1 Fourier-transformed PDF g(r) with (a) bond-length assignment of the ideal fcc Ru phase (from ICSD #41515),²³ (b) experimental g(r) function of fcc-type Ru NPs, (c) bond-length assignment of the ideal hcp Ru phase (from ICSD #52261),²¹ and (d) g(r) function of hcp-type Ru NPs.

All these Ru NP PDF peaks are broader than those of the bulk Ru, which strongly indicates that the structures of the NPs were disordered.^9,25 In addition, the PDF data implied that the positions of each coordination shell (indicated by dashed lines in Fig. 1(b) and (d)) are distorted with the size and structure of the Ru NPs. As shown in Fig. 1(b), the first nearest neighbor peaks are shifted to low-r direction with respect to the ideal fcc Ru bulk phase (2.71 Å) by approximately 0.014 and 0.018 Å for 2.4 and 5.4 nm fcc-type Ru NPs, respectively. In general, the first nearest neighbor peak of the Ru–Ru atomic pair of the conventional hcp-type Ru NPs is approximately 2.67 Å for all NP sizes.^9,25 The peak shift in the higher coordination shell (above the second coordination shell) is slightly increased to the higher-r direction with decreasing NP size of the fcc- and hcp-type Ru NPs (see Fig. 1(b) and (d)). The fifth coordination shell of the fcc-type Ru NPs clearly shows that the peak shift for the 2.4 and 5.4 nm fcc-type Ru NPs is approximately 0.053 and 0.018 Å. Several missing peaks were observed in the g(r) data for hcp-type Ru NPs. However, as shown in Fig. S2 in the ESI,† the experimental g(r) data of the bulk Ru were very close to the ideal hcp Ru phase with considerably low statistical errors at around 3.0 and 3.4 Å.

The first nearest neighbor peak analysis

The first g(r) peak positions and widths of fcc- and hcp-type Ru NPs were evaluated via Gaussian peak fitting (see Fig. 2(a) and (b)). As can be seen in Fig. S3(a) in the ESI,† the Ru–Ru bond-lengths are slightly elongated as the nanoparticle size decreases for both fcc- and hcp-type Ru NPs. Fig. 2(c) shows the widths of the first g(r) peaks for the fcc- and hcp-type Ru NPs, as a function of the NP diameter. We observed a clear peak broadening for 2.4 nm fcc-type Ru NPs compared with larger fcc-type Ru NPs (see Fig. 2(c)). This effect is attributed to the increases of width of Ru–Ru bond-length distribution in the smallest fcc-type Ru NPs. Meanwhile, the first-nearest-neighbor (1NN) peak height for the hcp NPs increased with increasing NP size, as a result of the higher number density of NPs with diameters above 3.5 nm (Fig. S3(b) in the ESI†). In contrast, the fcc structure NPs showed an opposite tendency (see Fig. S3(b) in the ESI†), compared with the hcp structure. This tendency originated from the higher relative thermal vibration of fcc-type Ru NPs, reported in the previous study by Song et al. (2016).²² However, we observed the lowest g_1NN(r) peak height at an NP size of 3.5 nm for both structures. This result suggested that the enhanced catalytic activity for CO oxidation of the fcc-type Ru NPs might have arisen from a low sample density (∼11.77 g cm⁻³) compared with hcp-type Ru NPs (∼12.15 g cm⁻³) above 3 nm in size.¹⁰ Interestingly, the shortest interatomic distances were slightly shorter than the ideal bulk counterparts of the fcc-type Ru NPs (see Fig. 1(a) and (b)). As can be seen in Fig. 2(b) and (c), the 1NN peaks for the hcp-type NPs remained comparably sharp for smaller NPs, as reported for CdSe NPs elsewhere.²⁶ The increases in the Ru–Ru bond length (see Fig. S3(a) in the ESI†) and peak-width broadening (see Fig. 2(c)) with decreasing NP size for the fcc-type NPs resulted from the structural disorder and near-neighbor atomic vibration, respectively.²⁵

Fig. 2 Widths for the first g(r) peaks: (a) for the fcc-type Ru NPs (circle) fitted with Gaussian (solid line), (b) for the hcp-type Ru NPs (circle) fitted with Gaussian (solid line), and (c) peak widths for the fcc-type Ru NPs (red solid line) and the hcp-type Ru NPs (blue dashed line).

The low-r components at around 2.0 Å in the g(r) profiles are assigned to Ru–O and/or Ru–N atomic correlations; in addition, N and O atoms originate from the PVP stabilizer used as a capping agent. The PDFs for the PVP-capped 5 nm hcp-type Ru NPs and 5.4 nm fcc-type Ru NPs, however, do not exhibit any peaks at approximately 2 Å. This result indicates that the use of PVP capping agents did not result in the formation of a substantial number of atomic correlations at the NP surface. Thus, we were able to analyze the atomic-scale structure of the fcc- and hcp-type Ru NPs by employing the RMC modeling technique.

The reverse Monte Carlo (RMC) modeling

Three-dimensional RMC models were constructed to obtain structural information, including the atomic pair distribution, coordination number, and bond angle distribution, for all Ru NP samples. The RMC simulation of the hcp-type bulk Ru was performed using the RMCPOW²⁷ software. The RMC simulated and experimental structure factor I(Q) data agreed very well, as shown in Fig. S4 in the ESI.† The hcp-type NPs shown in Fig. S5 (ESI†) are in better fit. This is to be expected since the RMC configuration models feature an hcp-type structure that is intrinsic to the hcp-type Ru bulk counterpart. We see from Fig. S6 (ESI†) that the RMC fit and experimental data agreed well for the smallest fcc-types Ru NPs. We observed somewhat misfits for 3.5, 3.9 and 5.4 nm fcc-type NPs. That is, the new fcc-type of local atomic ordering in the respective Ru NPs is not completely captured by the present RMC simulation techniques. In contrast, we obtained satisfactory RMC configuration models for our hcp- and fcc-type NPs but not perfect. The RMC simulated and experimental structure factor data sets for the fcc- and hcp-type Ru NPs are shown in Fig. 3(a) and (b), respectively. The RMC generated 3D atomic configuration model of fcc and hcp-type NPs clearly shows the ABCABC and ABABAB stacking in the cluster near the center of nanoparticles, respectively. The substantial broadening of the first PDF peak for small Ru NPs should be consistent with the fact that they have a high ratio of stacking faults.²⁸

Fig. 3 Experimental and RMC-generated X-ray total structure factor S(Q) profiles for the (a) fcc-type Ru NPs and (b) hcp-type Ru NPs at room temperature. The black solid circles represent the experimental total structure factor S(Q) profiles. The RMC-generated total structure factor S(Q) profiles are shown as red solid lines.

As shown in Fig. 4, the bond-angle distributions have been evaluated from the atomic configurations obtained by the RMC procedure. Fig. 4(b) and (d) shows the bond angle distributions for the fcc- and hcp-type Ru NPs, respectively, together with those for bulk crystals (Fig. 4(a) and (c)). We observed very broad peaks in the bond angle distribution for both fcc and hcp-type Ru NPs compared with the bulk counterparts. This suggested a distinct disorder in the atomic-scale structure of the Ru NPs. The bond angle distribution for the fcc-type ideal Ru phase (ICSD #41515)²³ exhibited peaks at 60, 90, and 120°, as shown in Fig. 4(a). For the fcc-type Ru NPs, the bond angle distribution showed a sharp peak at approximately 58° and very broad peaks at approximately 87 and 114°. We observed a relatively narrower peak pattern for 2.4 nm size fcc-type Ru NPs rather than for other larger Ru NPs in the same structure (see Fig. 4(b)). As shown in Fig. 4(c), the bond angle distribution for the ideal hcp structure exhibited peaks at 60, 90, 108, 120, and 146°.⁹ However, the hcp-type Ru NPs showed only one prominent peak at approximately 58°, and two further broad peaks at approximately 87 and 114°, similar to the results observed for the fcc-type Ru NPs. The bond angle distribution for the hcp-type NPs did not show a clear size dependence in contrast to the fcc-type NPs.

Fig. 4 Ru–Ru–Ru bond-angle distributions of the (a) ideal fcc-type Ru phase (from ICSD #41515), (b) fcc-type Ru NPs, (c) hcp-type bulk Ru phase (from ICSD #52261), and (d) hcp-type Ru NPs.

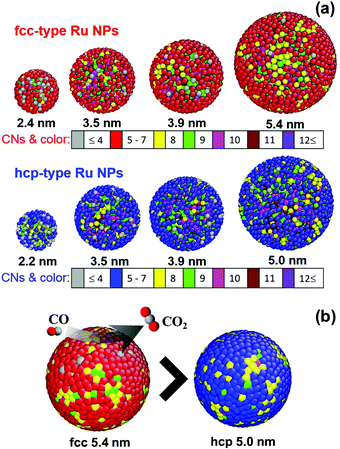
We shall now discuss the CN for describing the atomic arrangement in the Ru NPs. Note that the first main PDF peak for the bulk Ru reflected the presence of 12 first atomic neighbors. Here, we introduce two different CNs for the Ru NPs: one is the whole-CN, which is obtained by counting the number of atoms in the nth coordination shell of a NP and the other is the surface-CN which is obtained by counting the number of atoms in the nth coordination shell inside the NP surface shell with a thickness of 0.53 nm (2 atomic layers) from the most distant surface atom. The whole-CN and surface-CN in the first coordination-shell were evaluated by counting the number of Ru atoms in the spherical shell with a radius between 0.23 and 0.32 nm around each central atom. The CNs in the second shell were obtained by counting the number of Ru atoms in the spherical shell with a radius between 0.33 and 0.41 nm. Fig. 5(a) shows the three-dimensional RMC produced configurations of fcc- and hcp-type Ru NPs with different whole-CNs in highlighted colors. It was found that atoms with whole-CNs smaller than 4 were more dominant in fcc-type 2.4 nm and hcp-type 2.2 nm, with 5.96% and 12.8% of the total number of atoms, respectively. The percentages of whole-CNs of atoms were estimated from the coordination number statistics obtained using the RMC configuration models of the Ru NPs (Table S1 in the ESI†). Moreover, the whole-CNs of many of the surface atoms fell within the range of 5 to 7, as shown in Fig. 5(a) (red color atoms for fcc-type Ru NPs and blue color atoms for hcp-type Ru NPs). Among the Ru NPs, the smallest hcp-type NP, with a diameter 2.2 nm, had the most populous whole-CN, with a lowest number of 5, and 17.15% out of a total of 414 atoms. Other NPs showed that the most populous whole-CNs were 9 or 10.

Fig. 5 Three-dimensional atomic configurations of Ru NPs and the CO conversion site on the NP surfaces: (a) three-dimensional view of the RMC generated fcc-type (top) and hcp-type (bottom) Ru NP models with different coordination numbers in highlighted colors and (b) CO (C and O represented in gray and red, respectively) conversion sites on the Ru fcc 5.4 nm and hcp 5.0 nm NPs.

Although the surfaces of the NPs were highly disordered, various well-defined surface topologies were expected at different weights. As in previous reports, the hcp-type NP model contained five types of potential sites related to corner sites (CN = 6), square-planar sites (CN = 8), close-packed (CN = 9), B₅ (Step-edge) sites (CN = 10), and sawtooth sites (CN = 11).^25,29 Notably, the notation P_CN was introduced for the probability of Ru atoms at the different activation sites with CN determined from the RMC configuration models of Ru NPs. The 5.4 nm fcc-type Ru NP model showed a higher probability for the existence of B₅ sites of P₁₀ = 29.3% and sawtooth sites of P₁₁ = 21.2% compared with the 5.0 nm hcp-type Ru NP model, with the corresponding probabilities P₁₀ = 27.3% and P₁₁ = 19.6%. Furthermore, the 5.0 nm hcp-type Ru NP model exhibited a higher probability of containing close-packed (P₉ = 18.9%) and square-planar (P₈ = 10.0%) sites, compared with the whole-CN probabilities of close-packed (P₉ = 16.5%) and square-planar (P₈ = 8.3%) sites for the 5.4 nm fcc-type Ru NPs. Fig. S7 in the ESI† presents a summary of the percentages of atoms of different sites for the fcc and hcp-type Ru NPs as a function of the NP diameter. In both structures, smaller NPs showed a higher number of corner sites with whole-CN = 6 or 7; these values decreased with increasing NP diameter.²⁹ However, the previous density functional theory calculations for hcp-type Ru NP³⁰ and fcc-type Au NP³¹ surfaces indicated that the CO oxidation reaction required a lower activation energy at less-packed B₅ and sawtooth sites, in comparison with close-packed surfaces. The observed high catalytic reaction rate of CO oxidation (see Fig. S11 in the ESI†) of 5.4 nm size fcc-type NPs is consistent with higher P₁₀₊₁₁ = 50.5% and lower P₈₊₉ = 24.7% total probabilities of different sites compared to 5.0 nm hcp-type Ru NPs with P₁₀₊₁₁ = 46.9% and P₈₊₉ = 28.9% values. Herein, the total probabilities of different activation sites are given by P_CN1+CN2 = P_CN1 + P_CN2. According to the latter results, the newly discovered fcc-type Ru NPs were more reactive than the conventional hcp-type Ru NPs, as graphically depicted by the surface atoms with different coordination numbers in highlighted colors as shown in Fig. 5(b). In contrast, the smallest hcp-type Ru NPs showed a highly disordered atomic structure, and the lowest whole-CNs, with few closed-packed sites. The results of this whole-CN analysis are consistent with the previously reported CO conversion catalytic activity of fcc- and hcp-type Ru NPs.¹⁰

The rate of CO oxidation is a function of the local geometry of the NP surface structure.³² We performed further analysis of the surface-CN distribution using RMC models. As shown in Fig. S8 in the ESI,† we observed that the percentage of surface atom numbers for both fcc- and hcp-type Ru NP models increased sharply with decreasing NP diameter.³³ The high surface-to-volume ratio of the Ru NPs also improved the catalytic efficiency in the chemical reaction. The average whole-CNs and surface-CNs for the Ru NPs are summarized in Table 1. The average first shell whole-CNs and surface-CNs increased significantly with increases in the fcc- and hcp-type NP size. Fig. 6(a) and (b) shows the average whole-CN and surface-CN of the first coordination shell for the atom in the whole NP and the surface, respectively. The average surface-CN in the first coordination shell for the 2.4 nm fcc-Ru NPs was 5.71 ± 0.16, significantly higher than that of the 2.2 nm hcp-Ru NPs (5.22 ± 0.21). Conversely, the average first shell surface-CN value (6.52 ± 0.18) for the 5.4 nm fcc-type Ru NPs was smaller than that for the 5.0 nm hcp-type Ru NPs (6.57 ± 0.18). This trend in the average surface-CN was observed for particle diameters larger than 3.5 nm. In contrast, the average first-shell whole-CNs for both the fcc- and hcp-type Ru NPs were converged as particle diameter increased (Fig. 6(a)). Fig. S9(a) and (b) in the ESI† shows the average whole-CNs and surface-CNs of the second coordination shell of the Ru NPs, respectively. The average whole-CNs in the second coordination shell of the fcc- and hcp-type Ru NPs also increased with increasing particle size. However, the average whole-CNs in the second coordination shell for the fcc-type NPs were lower than those for the hcp-type NPs. Interestingly, the second shell average surface-CNs for the hcp-type NPs were stable; in particular, they increased slightly with increasing NP diameter for the fcc-type NPs. The surface atoms of the fcc-type Ru NPs showed lower surface-CNs in the second coordination shell, compared with those of the hcp-type Ru NPs. In particular, the observed high catalytic activity of fcc-type Ru NPs (see Fig. S11 in the ESI†) is consistent with higher P₁₀₊₁₁ and lower P₈₊₉ probabilities of different sites with CNs determined using RMC models, rather than the average first and second CN analysis (see Fig. 6 and Fig. S9 in the ESI†). The surfaces of these RMC-simulated models deviated significantly from the ideal hcp and fcc structures, even for the largest 5.0 nm hcp- and 5.4 nm fcc-type Ru NPs. In this NP diameter range, we observed that for all of the Ru NP structures, the surface atoms were highly disordered compared with the inner atoms.

Table 1 Average whole-CNs and surface-CNs of the first and second coordination shells obtained using RMC models of Ru NPs

Type	Ru NP	Whole-CNavg		Surface-CNavg
	diameter (nm)	First shell	Second shell	First shell	Second shell
fcc	2.4 ± 0.5	7.78 ± 0.38	4.85 ± 0.13	5.71 ± 0.16	2.88 ± 0.18
	3.5 ± 0.7	8.51 ± 0.37	5.60 ± 0.05	6.11 ± 0.20	3.40 ± 0.07
	3.9 ± 0.8	8.79 ± 0.21	5.79 ± 0.05	6.31 ± 0.17	3.46 ± 0.06
	5.4 ± 1.1	9.42 ± 0.14	6.02 ± 0.04	6.52 ± 0.18	3.54 ± 0.06
hcp	2.2 ± 0.5	6.92 ± 0.29	5.39 ± 0.16	5.22 ± 0.21	3.48 ± 0.05
	3.5 ± 0.6	8.36 ± 0.34	5.86 ± 0.06	6.05 ± 0.17	3.69 ± 0.09
	3.9 ± 0.6	8.70 ± 0.22	6.00 ± 0.05	6.32 ± 0.17	3.74 ± 0.05
	5.0 ± 0.7	9.28 ± 0.17	5.98 ± 0.05	6.57 ± 0.18	3.53 ± 0.09

---

Fig. 6 Average whole-CN and surface-CN analysis of the first coordination shell of fcc- and hcp-type Ru NP RMC models: (a) average whole-CN of the first coordination shell of fcc- and hcp-type Ru NP spheres, (b) average surface-CN of the first coordination shell of fcc- and hcp-type Ru NP surfaces.

Order parameter

To obtain a structural parameter that could be used to estimate the influence of the atomic disorder resulting from particle size and the structure type on the PDF and the bond angles of the fcc- and hcp-type Ru NPs RMC models, let us propose a factor S_type obtained from the peak width (W^X_cos(θ)) and the peak center (C^X_cos(θ)) of the bond angle main peak at cos(θ) (∼0.5) and the peak width (W^X_r) and peak center (C^X_r) of the 1NN peak at bond distance r (∼2.69 Å) (Fig. S10 in the ESI†) for X in the form of Ru NPs or bulk in fcc and hcp phases using the following formula:

Fig. 7 shows the behavior of the calculated order parameter S_fcc and S_hcp for the RMC models of, respectively, fcc-type and hcp-type Ru NPs, as a function of the particle diameter. Upon comparing fcc-type Ru NPs with hcp-type Ru NPs, we observed that the structural parameter for the fcc-type NPs decreased in value with increasing NP diameter. Conversely, the order parameter for the hcp-type Ru NPs was larger than that for fcc-type NPs of diameter larger than 3 nm, which confirmed that the catalytic activity (such as CO oxidation) was reduced as a result of the dense, close packing atomic arrangement of the larger hcp-type NPs. Interestingly, the new fcc-type Ru NPs showed diminished close packing in larger NPs, especially on surfaces with lower CNs, suggesting that NPs with highly enhanced catalytic activity could be used for future environmentally friendly, scientific and technological applications.

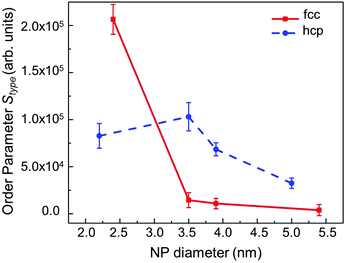Fig. 7 NP-diameter dependence of the order parameters S_fcc and S_hcp, defined for the RMC models of fcc- (red solid line) and hcp-type (blue dashed line) Ru NPs, respectively.

Conclusions

This work described the atomic structure of newly synthesized fcc-type Ru NPs and conventional hcp-type Ru NPs using high-energy XRD, atomic PDF analysis, and RMC modeling of spherical NPs without applying periodic boundary conditions. RMC models of fcc-type Ru NPs of 2.4, 3.5, 3.9 and 5.4 nm in diameter and hcp-type Ru NPs of 2.2, 3.5, 3.9 and 5.0 nm in diameter were compared, to obtain a complete view of the atomic-scale structures and to explain the enhancement of the catalytic activity. The corresponding diffuse nature of the XRD patterns was considered in terms of the total structure factor. The pair distribution functions and RMC models indicate that all of the Ru NPs were arranged with short- to medium-range order atomic distances.

The following four principal findings were obtained from the analysis of RMC simulated NP models. (1) The fcc- and hcp-type Ru NPs possess some of the close-packed structural features of their Ru bulk counterparts. (2) The Ru NPs were disordered at short- to intermediate-range atomic distances, but unable to access particle–particle (intra-domain) correlations over long-range orders. (3) Through the bond-angle and CN analysis of the RMC model for Ru NPs, we found that the fcc-type NPs dominate low activation energy packing sites particularly on the surface. (4) Our defined order parameter clearly described the effects of changes in the structure and size of the fcc- and hcp-type Ru NPs, and it was suggested that the enhancement of CO oxidation activity of fcc-type NPs resulted from the decrease in the close packed ordering with increasing NP size.

Using the PDFs, bond angles, and coordination number analysis of the RMC-simulated Ru NP models, we demonstrated a critical difference between the newly synthesized PVP-capped fcc-type Ru NPs and conventional hcp-type Ru NPs; this difference is consistent with their relative catalytic activities as a function of particle size. The combined method of high-energy diffraction and RMC modeling that we have used here is a promising tool for elucidating the details of atomic-scale structures of many other NPs.

Acknowledgements

We are grateful to O. Gereben for the useful discussions. This work was supported by ACCEL, Japan Science and Technology Agency (JST). The high-energy XRD measurements were carried out at SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) under Proposal No. 2013B1207, 2014A1321, 2014B1210 and 2015B1245. This work was also partly supported by the Ministry of Education, Culture, Sports, Science and Technology of Japan (OS: 15K04616).

References

1. J. R. Ross, Chapter 1 – Heterogeneous Catalysis – Chemistry in Two Dimensions, Elsevier, Amsterdam, 2012, pp. 1–15.
2. J. Hu, F. Yu and Y. Lu, Catalysts, 2012, 2, 303–326.
3. Z. M. Michalska and D. E. Webster, Platinum Met. Rev., 1974, 18, 65–73.
4. D. Astruc, Transition-metal Nanoparticles in Catalysis: From Historical Background to the State-of-the Art, Wiley-VCH Verlag GmbH & Co. KGaA, 2008, pp. 1–48.
5. M. Zahmakıran and S. Özkar, Nanoscale, 2011, 3, 3462–3481.
6. M. Zahmakıran and S. Özkar, Top. Catal., 2013, 56, 1171–1183.
7. Y. H. Kim, S.-D. Yim and E. D. Park, Catal. Today, 2012, 185, 143–150.
8. S. H. Joo, J. Y. Park, J. R. Renzas, D. R. Butcher, W. Huang and G. A. Somorjai, Nano Lett., 2010, 10, 2709–2713.
9. N. Bedford, C. Dablemont, G. Viau, P. Chupas and V. Petkov, J. Phys. Chem. C, 2007, 111, 18214–18219.
10. K. Kusada, H. Kobayashi, T. Yamamoto, S. Matsumura, S. Naoya, K. Sato, K. Nagaoka, Y. Kubota and H. Kitagawa, J. Am. Chem. Soc., 2013, 135, 5493–5496.
11. A. Le Bail, I. Madsen, L. M. D. Cranswick, J. K. Cockcroft, P. Norby, A. D. Zuev, A. Fitch, J. Rodriguez-Carvajal, C. Giacovazzo, R. B. Von Dreele, P. Scardi, N. C. Popa, R. Allmann, L. A. Solovyov, B. Hinrichsen, U. Schwarz, A. Altomare, A. Moliterni, R. Caliandro, R. Rizzi, N. V. Y. Scarlett and M. Jansen, Powder Diffr., The Royal Society of Chemistry, Cambridge, 2008, pp. 1–19.
12. A. M. M. Abeykoon, H. Hu, L. Wu, Y. Zhu and S. J. L. Billinge, J. Appl. Crystallogr., 2015, 48, 244–251.
13. V. Petkov, Mater. Today, 2008, 11, 28–38.
14. V. Petkov, N. Bedford, M. R. Knecht, M. G. Weir, R. M. Crooks, W. Tang, G. Henkelman and A. Frenkel, J. Phys. Chem. C, 2008, 112, 8907–8911.
15. R. L. McGreevy and L. Pusztai, Mol. Simul., 1988, 1, 359–367.
16. R. McGreevy, Nucl. Instrum. Methods Phys. Res., Sect. A, 1995, 354, 1–16.
17. L. S. R. Kumara, K. Ohara, Y. Kawakita, P. Jóvári, M. Hidaka, N. Eon Sung, B. Beuneu and S. Takeda, EPJ Web Conf., 2011, 15, 02007.
18. O. Gereben and V. Petkov, J. Phys.: Condens. Matter, 2013, 25, 454211.
19. O. Gereben and L. Pusztai, J. Comput. Chem., 2012, 33, 2285–2291.
20. S. Kohara, M. Itou, K. Suzuya, Y. Inamura, Y. Sakurai, Y. Ohishi and M. Takata, J. Phys.: Condens. Matter, 2007, 19, 506101.
21. J. Paschoal, H. Kleykamp and F. Thümmler, J. Less-Common Met., 1984, 98, 279–284.
22. C. Song, O. Sakata, L. S. R. Kumara, S. Kohara, A. Yang, K. Kusada, H. Kobayashi and H. Kitagawa, Sci. Rep., 2016, 6, 31400.
23. J. Häglund, A. Fernández Guillermet, G. Grimvall and M. Körling, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 11685–11691.
24. T. Egami and S. J. L. Billinge, Underneath the Bragg Peaks Structural Analysis of Complex Materials, Elsevier, Amsterdam, 2nd edn, 2012, pp. 87–90.
25. X.-Y. Quek, I. A. W. Filot, R. Pestman, R. A. van Santen, V. Petkov and E. J. M. Hensen, Chem. Commun., 2014, 50, 6005–6008.
26. A. S. Masadeh, E. S. Božin, C. L. Farrow, G. Paglia, P. Juhas, S. J. L. Billinge, A. Karkamkar and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115413.
27. A. Mellergård and R. L. McGreevy, Acta Crystallogr., Sect. A: Found. Crystallogr., 1999, 55, 783–789.
28. X. Yang, A. S. Masadeh, J. R. McBride, E. S. Božin, S. J. Rosenthal and S. J. L. Billinge, Phys. Chem. Chem. Phys., 2013, 15, 8480–8486.
29. M. Sarwar, C. Cooper, L. Briquet, A. Ukpong, C. Perry and G. Jones, Johnson Matthey Technol. Rev., 2015, 59, 257–283.
30. R. A. V. Santen, Acc. Chem. Res., 2009, 42, 57–66.
31. T. Proffen and S. J. L. Billinge, J. Appl. Crystallogr., 1999, 32, 572–575.
32. H. Falsig, B. Hvolbæk, I. S. Kristensen, T. Jiang, T. Bligaard, C. H. Christensen and J. K. Nørskov, Angew. Chem., Int. Ed., 2008, 47, 4835–4839.
33. B. Rogers, J. Adams and S. Pennathur, Nanotechnology: Understanding Small Systems, CRC Press, Taylor & Francis Group, Boca Raton, 2014, pp. 103–106.

---

Footnote

† Electronic supplementary information (ESI) available: High-energy XRD patterns of Ru bulk, Ru fcc- and hcp-type NPs, and PVP samples, PDF data analysis, RMC fitting data and results, percentage of surface atom number, g(r) of RMC simulated NP models, and the catalytic activity of Ru NPs (Fig. S1–S11 and Table S1). See DOI: 10.1039/c6cp04088h

---