Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Capacity-limiting mechanisms in Li/O2 batteries
Jing
Liu
a,
Saeed
Khaleghi Rahimian
b and
Charles W.
Monroe
*c
aThe Dow Chemical Company, Midland, Michigan, USA
bUniversity of Michigan, Chemical Engineering, Ann Arbor, Michigan, USA
cUniversity of Oxford, Department of Engineering Science, Parks Road, Oxford, England, UK. E-mail: charles.monroe@eng.ox.ac.uk
First published on 4th July 2016
Abstract
A continuum model of an aprotic lithium/oxygen battery is validated against experimental first-discharge data and used to examine how the apparent cell capacity is affected by macroscopic multicomponent mass transfer, interfacial kinetics, and electronic conduction or tunneling through the discharge product. The model accounts for the three-phase nature of the positive electrode in detail, including an explicit discharge-product layer whose properties and volume distribution generally depend on the local discharge depth. Several hypothetical positive-electrode reaction mechanisms involving different product morphologies and electron-transfer sites are explored within the theoretical framework. To match experimental discharge-voltage vs. capacity and capacity vs. discharge-current trends qualitatively, the discharge-product layer must be assumed to have electronic resistivity several orders of magnitude lower than typical insulators, supporting the notion that the presence of lithium peroxide does not wholly prevent electrons from reaching dissolved reactants. The discharge product also appears to allow charge transport over length scales longer than electron tunneling permits. ‘Sudden death’ of voltage in lithium/oxygen cells is explained by macroscopic oxygen-diffusion limitations in the positive electrode at high rates, and by pore clogging associated with discharge-product formation at low rates.
The extremely high theoretical energy density associated with the reaction between metallic lithium and molecular oxygen suggests that rechargeable lithium/oxygen (Li/O2) batteries could compete with combustion-based automotive propulsion systems.1 This observation has bolstered significant research interest2–16 as the demand for electric and hybrid-electric vehicles grows. A non-aqueous (aprotic) rechargeable Li/O2 battery was first demonstrated by Abraham and Jiang.17 The desired basic chemistry of the aprotic Li/O2 cell is now well accepted, and is based on the half-reactions
| Li ⇌ Li+ + e− | (1) |
| 2Li+ + O2 + 2e− ⇌ Li2O2 | (2) |
Several barriers must be overcome before Li/O2 technology can be put to practical use.18,33–35,37–40 One problem is the ‘sudden death’ of the cell voltage during the discharge process, which occurs far below the theoretical maximum capacity and has been observed by many research groups.17,41–48 Numerous experimental investigations have been performed to shed light on the sudden-death phenomenon. Scholars divide primarily into two camps: one group suggests that the insulating nature of the lithium peroxide (Li2O2) layer deposited during discharge bars electron transport after its dimensions reach a certain threshold, limiting capacity by constraining the discharge-product layer's thickness;10–12,27,49–51 the other group contends that the low permeability of dissolved oxygen limits capacity by restricting mass-transport rates, which lowers the utilization of the positive electrode's available pore volume.20,26,52–55
A main challenge confronted when modeling Li/O2 cells is that the deposition of insoluble discharge products on pore walls causes microstructural changes within the positive electrode as discharge progresses. In principle, discharge-product growth may shrink (or even block) the electrode's pores, displace liquid electrolyte, and alter the surface area available for charge transfer;52,56 the discharge-product layer itself may incur resistances to material transport and charge exchange (by conduction or tunneling mechanisms).10–12
Neidhardt et al. recently extended porous-electrode theory, providing a macrohomogeneous approach to the modeling of spatial domains comprising more than two phases.57 Within this general framework, it is possible to formulate a model in which morphology changes in porous electrodes are associated with the formation of insoluble discharge products. The present paper implements that formalism to describe the porous positive electrode of a Li/O2 cell, accounting for three distinct phases within it, and allowing for possible charge-exchange processes at electrolyte/solid interfaces or discharge-product/electrolyte interfaces. This model design provides sufficient flexibility to investigate several of the discharge-product growth mechanisms hypothesized in the literature.52,56,58
Simulations are performed to probe how three hypothetical peroxide-formation mechanisms affect the voltage response during Li/O2-cell discharge. In one case, heterogeneous kinetics is assumed to occur at the substrate/electrolyte interface: peroxide growth is controlled by reactant diffusion through a discharge-product layer with a porous morphology. In two other cases, heterogeneous kinetics is assumed to occur at the discharge-product/electrolyte interface, so that the electronic resistance of the discharge-product phase participates in its growth. Both compact and porous discharge-product morphologies are considered in the latter two scenarios.
First-discharge experiments59 in the superficial current-density range of 0.1 to 1.0 mA cm−2 are found to agree with simulations that assume oxygen transport to be rate limiting. Here ‘agree’ is meant in the sense that when the model is parameterized with property values from literature, it predicts discharge-voltage curves that qualitatively match experimental data, as well as quantitatively matching the dependence of cell capacity on discharge rate. For simulations to exhibit the sudden-death behavior seen in experiments, the electrical resistivity of the discharge product must be orders of magnitude lower than a typical bulk insulator. For cells with porous positive electrodes, electron tunnelling through a compact discharge product causes predictions of the cell capacity to be far lower than capacities observed in experiments.
Model development
Cell geometry and ambient conditions
An aprotic Li/O2 cell is typically constructed as a planar device, comprising a metallic lithium negative electrode, an inert separator permeated by a non-aqueous liquid electrolyte, and a porous, electronically conductive, electrolyte-saturated positive electrode that is exposed to ambient oxygen gas. Table 1 presents the full set of model equations used to describe the discharge of such a one-dimensional Li/O2 cell.The model resolves the distributions of material and potential in detail throughout the liquid-saturated-separator and positive-electrode domains, which are taken to have finite thicknesses of Lsep and L+, respectively. The negative electrode is assumed to be a plane metallic surface normal to the position coordinate x, located at x = 0. Transport processes in the gas phase are not considered explicitly: the liquid surface at the outer surface of the positive electrode (x = Lsep + L+) is taken to be in equilibrium with the adjacent O2 gas, which is stagnant and at constant ambient pressure p. This pressure does not appear directly in the model, but presumably affects the saturated oxygen concentration in the liquid,  . (The experiments modeled here used pure O2 gas at a gauge pressure of 1 bar.) The cell's absolute temperature T is also taken to be uniform and constant.
. (The experiments modeled here used pure O2 gas at a gauge pressure of 1 bar.) The cell's absolute temperature T is also taken to be uniform and constant.
Initial and boundary conditions
At the outset of every simulation, the electrolyte and dissolved O2 are taken to be uniformly distributed throughout the liquid, with O2 at its saturated concentration; it is further assumed that no discharge product is present. These conditions correspond to an experiment in which an undischarged cell is initially brought to equilibrium at open circuit under a constant O2 pressure.The model was used to simulate the cell response during galvanostatic discharge at total applied current density iT (positive iT is a discharge current, and flows in the direction of increasing x). At the negative-electrode/separator interface (x = 0), all the current enters the liquid, manifesting as an ionic current density iliq; the liquid-phase species fluxes are proportional to iliq through the stoichiometry of interfacial half-reaction (1). At the opposing current collector (x = Lsep + L+), all the current leaves through the porous-solid phase. The concentration of O2 in the liquid is saturated at the liquid/gas boundary throughout the discharge process.
As discharge proceeds, electrolyte can be forced to flow out of the cell by two phenomena: the occlusion of pores by discharge product16 and reaction-induced convection.60 The convective efflux of liquid constituents due to discharge-product displacement and solute-volume effects is associated with a nonzero volume-average solution velocity v□ at the positive-electrode/gas interface, whose value is determined by the material balances. In the present analysis the expelled liquid is taken to remain outside the outer boundary of the simulation (i.e., outside the positive current collector) as discharge progresses. The possible presence of a thin liquid layer is assumed not to affect the O2 saturation of the liquid at the boundary.
Liquid and solid phases
The physical description of the liquid phase – both within the separator and in the electrolyte that occupies free volume in the porous electrode – is presented in a general form that allows an arbitrary number n of ionic or molecular constituents to be included if necessary.Simulations were performed for comparison to the experiments of Griffith et al.,59 who employed a four-species electrolyte (n = 4), comprising a single solvent (dimethoxyethane, or DME), dissolved O2, Li+, and bis-(trifluoromethanesulfonyl)imide (TFSI−) anions. Standard material balances account for all these liquid-phase species in both the separator and positive-electrode domains. Contemporary air-battery research efforts typically employ separators comprising an inert matrix such as Celgard54,61–65 or glass fiber,28,66–68 which is also porous and permeated by liquid electrolyte. The material balances include the volume fraction available for liquid, which generally differs between the separator (εsep) and the positive electrode (ε). (Glass-fiber separators were used to gather the experimental data modeled here.)
Previous efforts to simulate Li/O2 batteries26,52,57 have mostly adopted the transport equations developed by Doyle, Fuller, and Newman – based on the concentrated-solution theory for binary electrolytes69,70 – and appended a separate flux law for oxygen. The framework used here extends those approaches by allowing for drag interactions between dissolved O2 and ions, which could in principle cause electro-osmosis of oxygen and cross-diffusion (i.e., oxygen flux induced by salt gradients). At present, these phenomena are neglected for simplicity, but their effects may be significant in some metal/O2 systems and will be illustrated in a later communication.
Multicomponent transport in the liquid is taken to follow Onsager–Stefan–Maxwell constitutive laws, which establish how the electrochemical-potential gradient of species k, ∂μk/∂x, relates to the differences between its molar flux, Nk, and the fluxes of every other species j. This relationship involves diffusional drag coefficients, which depend on effective Stefan–Maxwell diffusivities ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) effkj, as well as local composition, temperature, and the universal gas constant R. To account for dispersion induced by pore networks in the simplest possible way, all the liquid-phase diffusivities are corrected using the Bruggeman correlation71,72
effkj, as well as local composition, temperature, and the universal gas constant R. To account for dispersion induced by pore networks in the simplest possible way, all the liquid-phase diffusivities are corrected using the Bruggeman correlation71,72
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) effkj = ε1.5 effkj = ε1.5![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) kj, kj, | (3) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) kj is the Stefan–Maxwell diffusivity that quantifies interactions between species k and j in the bulk liquid.
kj is the Stefan–Maxwell diffusivity that quantifies interactions between species k and j in the bulk liquid.
Molecular diffusion and charge migration are distinguished by incorporating thermodynamic constitutive laws that cast μk in terms of species particle fractions yk (whose gradients drive diffusion) and a liquid-phase quasi-electrostatic potential Φliq (whose gradient drives migration). Activity coefficients λk – which in principle can vary with composition – were included to allow for solution nonideality, but were found to impact results minimally when reasonable values73 were used. Data presented here were computed under the ideal-electrolyte assumption that λk = 1 for every species.
A unique aspect of the model presented in Table 1 is that it accounts rigorously for the changes in liquid volume that accompany concentration polarization during the discharge process. A proper volume balance is insured by augmenting the standard equations from concentrated-solution theory72,74–78 with a local volume-explicit equation of state. This state equation locally enforces the known dependence of total molar solution concentration cT on composition through species partial molar volumes ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) k. Note that this consideration of solute-volume effects provides rigor, but also restricts the model to one-dimensional applications; for simulations of higher-dimensional geometries a momentum balance must be appended to the equation system to ensure model closure.60
k. Note that this consideration of solute-volume effects provides rigor, but also restricts the model to one-dimensional applications; for simulations of higher-dimensional geometries a momentum balance must be appended to the equation system to ensure model closure.60
Three (i.e., n − 1) flux laws are written to describe transport of solvent, dissolved O2, and Li+. A fourth transport law, governing the electrochemical potential of TFSI−, is omitted from Table 1; it depends on the others through the Gibbs–Duhem equation and kinematic considerations. Use of a particle-fraction composition basis ensures that when the ideal-solution approximation is applied to the other species, TFSI− will also have an activity coefficient of 1.
Faraday's law for charge flux is adopted to express the liquid-phase current density in terms of molar fluxes and species equivalent charges zk. As is typical when simulation volume elements are large compared to the Debye length, a local electroneutrality relation is used in place of Poisson's equation throughout the liquid phase.
To describe electron transport through the conductive-solid phase in the positive-electrode domain, a charge-continuity equation is included, following the porous-electrode theory.69,70,72,78 Charge flux through the solid is described by Ohm's law, which relates the electronic current density in the solid, isol, to the spatial variation of solid-phase potential, Φsol. The charge balance contains a generation term proportional to the reaction-current density in, associated with local electron transfer via interfacial half-reactions at reactive surfaces within the porous electrode. (Anodic reaction currents are positive.) Since in parameterizes a heterogeneous process, it is naturally expressed per unit of surface area available for electron exchange; in balance equations, multiplication by a surface-to-volume ratio aV converts in to a rate of anodic charge transfer per unit porous-electrode volume. An equation is also included to define the local volumetric extent of discharge q, whose rate of change with respect to time is −inaV.
The species balances in the electrode-permeating-liquid phase include generation terms that are complementary to the generation term in the solid-phase charge balance. These account for how the electron-exchange events at interfaces within the positive electrode drive the consumption or production of liquid constituents. Again following typical practice from porous-electrode theory, these terms are taken to be proportional to the local value of inaV through stoichiometric coefficients sk and the number of electrons involved in the half-reaction, ne−, as well as Faraday's constant F. Note that this general structure provides some flexibility in the treatment of reaction mechanisms involving multiple species (or intermediates), although the present simulations are based on reactions (1) and (2).
In addition to the use of the Onsager–Stefan–Maxwell transport theory and the incorporation of a local volumetric equation of state for the liquid, two other features suggested by Neidhardt et al.57 differentiate the present model from most multiphysics air-battery models. First, the porosity of the positive electrode available to liquid, ε, is allowed to vary locally within it. Second, the surface-to-volume ratio aV available for charge exchange between the liquid and discharge-product phase may vary. Different hypotheses about product morphology and the discharge pathway for half-reaction (2) can be explored by choosing different dependences of ε and aV on q.
Cell potential
During discharge, a Li/O2 cell expends free energy on a number of internal processes. Consider a path that initially crosses the negative-electrode/separator interface at x = 0, proceeds through the liquid phase to some point within the positive electrode x = r at which in is nonzero, crosses the discharge-product phase and the discharge-product/solid interface at that location, and then proceeds through the solid matrix to the positive-electrode current collector at x = Lsep + L+. Along this path there are five distinct sources of potential loss: surface overpotential associated with half-reaction (1) at the negative electrode, η−s; voltage associated with liquid-phase transport, ΔVliq; surface overpotential at the positive electrode, η+s; ohmic potential drop associated with the areal resistance![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) dp of the discharge-product layer; and ohmic loss in the solid phase, ΔVsol. The total cell potential, V, is written as
dp of the discharge-product layer; and ohmic loss in the solid phase, ΔVsol. The total cell potential, V, is written as | (4) |
All of the overpotentials and ohmic drops in eqn (4) represent potential losses during a discharge process. The terms in eqn (4) describing positive-electrode overpotential and ohmic loss through the discharge-product layer are both negative; the negative-electrode overpotential and solid-phase voltage drop are positive. The term describing the liquid-phase voltage drop includes both ohmic drop (always a loss) and diffusion potential, whose sign may vary according to the distributions of species concentrations. Assuming that a reference electrode reversible only to lithium cations is used to establish the liquid-phase potential, the liquid-phase voltage drop can be expressed as
 | (5) |
Electron-transfer kinetics
The exchange-current density for the negative-electrode half reaction, i0−, is relatively large. Therefore the surface overpotential η−s was computed under the assumption that half-reaction (1) is elementary, following a linear kinetic law with respect to overpotential.At the positive electrode, half-reaction (2) is taken to be elementary and to follow Butler–Volmer kinetics, with the species activities involved in prefactors of the anodic and cathodic terms:
 | (6) |
 is the exchange-current density; β is the symmetry factor; and sLi+ = −2, sO2 = −1, sLi2O2 = 1, and ne− = 2 are stoichiometric coefficients in reaction (2). A superscript ‘ref’ represents a property measured in the standard reference state (i.e., the equilibrium composition at which
is the exchange-current density; β is the symmetry factor; and sLi+ = −2, sO2 = −1, sLi2O2 = 1, and ne− = 2 are stoichiometric coefficients in reaction (2). A superscript ‘ref’ represents a property measured in the standard reference state (i.e., the equilibrium composition at which  and U⊖ are measured). Since Li2O2 forms a separate solid phase, its activity aLi2O2 is unity whenever Li2O2 is present. The term is left in eqn (6) to emphasize that the Li2O2-particle structure or surface energy may contribute to differences in the activity of the discharge phase that forms – a consideration potentially useful for future efforts to account for the current dependence of Li2O2 morphology.
and U⊖ are measured). Since Li2O2 forms a separate solid phase, its activity aLi2O2 is unity whenever Li2O2 is present. The term is left in eqn (6) to emphasize that the Li2O2-particle structure or surface energy may contribute to differences in the activity of the discharge phase that forms – a consideration potentially useful for future efforts to account for the current dependence of Li2O2 morphology.
Material properties
Table 2 lists the baseline properties from literature that were used for simulations, alongside their sources.8,52,73,79–82 Mechanical characteristics of cell materials, such as the separator and electrode thicknesses and porosities, are chosen to match the apparatus recently described by Griffith et al.59| Prop. | Value | Ref. | Prop. | Value | Ref. |
|---|---|---|---|---|---|
| Electrolyte | Positive electrode kinetics | ||||
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 0+ 0+ |
4.96 × 10−10 m2 s−1 | 8 |

|
100 nA m−2 | 52 |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 0− 0− |
6.57 × 10−10 m2 s−1 | 8 | β | 0.5 | 52 |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 0O2 0O2 |
7.30 × 10−10 m2 s−1 | 8 |
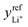
|
0.088 | 52 |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) +− +− |
2.89 × 10−10 m2 s−1 | 73 |

|
1.85 × 10−4 | 52 |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) +O2 +O2 |
∞ | a Li2O2 | 1.0 | ||
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) −O2 −O2 |
∞ | Negative electrode kinetics | |||

|
2.1 mM | 19 | i 0− | 6.17 A m−2 | 79 |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) 0
0
|
104.3 cm3 mol−1 | 81 | Discharge-product layer | ||
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) +
+
|
12.0 cm3 mol−1 | 8 and 82 |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) Li2O2
Li2O2
|
19.9 cm3 mol−1 | 81 |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) −
−
|
9.0 cm3 mol−1 | 8 and 82 | Porous carbon | ||
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) O2
O2
|
0 cm3 mol−1 | L + | 235 μm | — | |
| Separator | a V0 | 4.7 μm−1 | — | ||
| L sep | 650 μm | — | ε 0 | 0.8 | — |
| ε sep | 0.5 | — | σ C | 1 S mm−1 | 80 |
Stefan–Maxwell coefficients describing ion/ion and ion/solvent interactions were calculated from the diffusivity, transference number, and ionic conductivity of the binary LiTFSI/DME system, using the conversion formulas provided by Newman and Thomas-Alyea.72 In the calculations, dissolved O2 was taken to interact only with solvent, i.e., 1/![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) +O2 = 1/
+O2 = 1/![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) −O2 = 0 s m−2, and to occupy no partial molar volume. These assumptions may be reasonable since the saturated oxygen concentration is so low; as mentioned earlier, the neglect of ion/oxygen interactions is consistent with prior models.16,26,58,83 Reference activities of all liquid species are calculated on the basis of a 1 M LiTFSI solution saturated with oxygen.
−O2 = 0 s m−2, and to occupy no partial molar volume. These assumptions may be reasonable since the saturated oxygen concentration is so low; as mentioned earlier, the neglect of ion/oxygen interactions is consistent with prior models.16,26,58,83 Reference activities of all liquid species are calculated on the basis of a 1 M LiTFSI solution saturated with oxygen.
Exchange-current densities at both the negative and positive electrodes are commensurate with reported values.6,49,79 The symmetry factor for the positive half-reaction was taken to be 0.5.
Reaction mechanisms
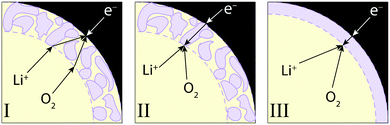
The model was used to investigate three discharge mechanisms, depicted schematically in Fig. 1. Reaction (2) was assumed to be elementary in all cases; the mechanisms describe different discharge-product morphologies and various sites for electron exchange.In every mechanism, the discharge-product layer is taken to shrink the positive-electrode porosity available to liquid through
 | (7) |
 | (8) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) Li2O2, can be corrected in the model by a factor accounting for its porosity, εdp. In general, εdp could depend on the local discharge rate and discharge history. It will be important in the future to develop microscopic models that predict this dependence; here, discharge-product porosity is treated as a constant.
Li2O2, can be corrected in the model by a factor accounting for its porosity, εdp. In general, εdp could depend on the local discharge rate and discharge history. It will be important in the future to develop microscopic models that predict this dependence; here, discharge-product porosity is treated as a constant.
Mechanism I
| aV(ε) = aV0, | (9) |
| η+s = Φsol − Φliq − U⊖, | (10) |
Mechanism II
 | (11) |
The kinetic overpotential in mechanism II is reduced by an electronic resistance of the discharge-product layer, according to
η+s = Φsol − Φliq − U⊖ − in![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) dp. dp. | (12) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) dp also varies with the pore geometry. Again assuming that the discharge-product layer is a cylindrical annulus, and that charge transport occurs in the radial direction, the areal resistance would be expected to vary as
dp also varies with the pore geometry. Again assuming that the discharge-product layer is a cylindrical annulus, and that charge transport occurs in the radial direction, the areal resistance would be expected to vary as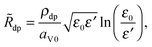 | (13) |
Mechanism III
Viswanathan et al. investigated charge transport through dense Li2O2 with a metal–insulator–metal (MIM) model, and reported the resistivity of the layer as a function of its thickness. The resistivity rises exponentially with the thickness d; an empirical expression
 | (14) |
Maximum capacity
Given any of the three mechanisms, there is a maximum concentration of discharge product, , that a volume element of the porous positive electrode can hold. In mechanisms I and II,
, that a volume element of the porous positive electrode can hold. In mechanisms I and II,  is determined by the native pore volume and the discharge product's compactness. If discharge-product porosity is constant throughout the discharge history, as has been assumed here, then
is determined by the native pore volume and the discharge product's compactness. If discharge-product porosity is constant throughout the discharge history, as has been assumed here, then | (15) |
In mechanism III, 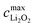 is restricted by the largest thickness of the discharge-product layer that electrons can cross, dmax. For a compact discharge-product with annular geometry,
is restricted by the largest thickness of the discharge-product layer that electrons can cross, dmax. For a compact discharge-product with annular geometry,
 | (16) |
Results and discussion
Validation
The model was validated by comparison to the experimental first-discharge curves produced by Griffith et al., which were gathered at four rates ranging from 0.1 to 1.0 mA cm−2.59Fig. 2 illustrates simulation results using mechanism I alongside the experimental discharge curves.Discharge-product-layer porosity, εdp, was the only fitting parameter used to match the experimental data. A value of εdp = 0.87 was found to provide the best fit. The range of this parameter was confirmed to be between 0.5 and 0.9 by counting Li2O2 particles on SEM images of fully discharged electrodes provided by Griffith.59
The simulations successfully reproduce the initial relaxation of voltage, as well as the typical voltage-plateau and sudden-death features observed in experiments.17,41–48 As well as agreeing qualitatively with the experimental curves, the simulation data quantitatively match the cell capacities at various discharge rates well, supporting possible validity of mechanism I.
Discharge curves produced at four different rates from all three mechanisms are compared in Fig. 3. For fair comparison of the mechanisms, the parameters in Table 2 were adopted as the baseline; εdp was taken to equal 0.87 in cases where the discharge product was not assumed to be compact.
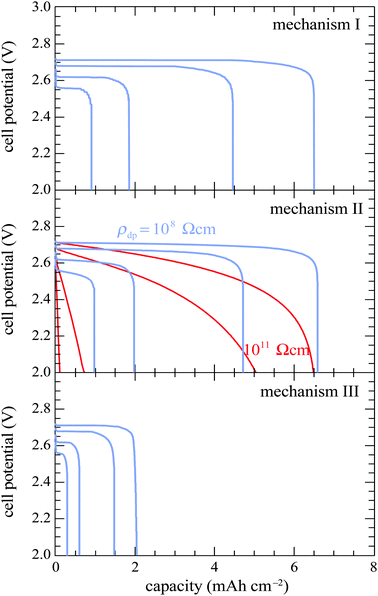 | ||
| Fig. 3 Discharge curves generated with all three mechanisms at rates of 0.1, 0.2, 0.5 and 1.0 mA cm−2. Two discharge-product-layer resistivities are shown for simulations with mechanism II. | ||
For mechanism II, Fig. 3 shows simulations with two different discharge-product-layer resistivities. A resistivity of 108 Ω cm (at the border of the insulator regime and semiconductor regime) or lower yields discharge curves similar to those produced assuming mechanism I, matching experimental cell capacity and reproducing the sudden-death feature. With higher resistivities, the qualitative appearances of the simulated discharge curves differ significantly from the experimental results. Ohmic potential loss across the discharge-product layer rises rapidly as the product layer thickens, eliminating the voltage plateau, spreading out the sudden-death feature, and lowering the total cell capacity. These results show that if mechanism II predominates, then the effective electronic resistance of the discharge-product layer must be many orders of magnitude lower than would be expected for bulk Li2O2.
Under mechanism III, discharge curves retain the plateau and sudden-death features, but the cell capacities are far lower than those observed experimentally. Electron tunneling through the Li2O2 layer manifests as a very low product resistivity when the discharge layer is thin (less than about 6 nm12), which grows exponentially as the layer thickens. Since both theory and experiments with planar electrodes have confirmed the kinetic parameters for the ‘tunneling mechanism’,12 the inability to match experimental cell capacities suggests that tunneling does not control the capacity in porous-electrode systems of the type studied by Griffith et al.59
Overpotential
Higher exchange-current density and larger available reaction area both lead to faster kinetics, and consequently lower overpotential. Increasing or aV raises the discharge-voltage plateau, which raises the energy capacity to some degree, but does not improve coulomb capacity.
or aV raises the discharge-voltage plateau, which raises the energy capacity to some degree, but does not improve coulomb capacity.
Fig. 4 breaks down the five sources of potential loss in Li/O2 cells as functions of depth of discharge (DOD) for the three hypothesized mechanisms, at a relatively low discharge rate of 0.1 mA cm−2. The losses attributed to each source were obtained by spatially averaging the appropriate terms in eqn (4) across the ‘reaction zone’ – i.e., the domain where in ≠ 0.
For every mechanism, potential losses due to negative-electrode kinetics, liquid-phase transport, and solid-phase charge conduction together contribute less than 2% of the total overpotential; this contribution always decreases as discharge progresses. Positive-electrode kinetic overpotential is one dominant source of potential loss, and ohmic drop across the discharge-product layer is another if the resistivity of the layer is high (or becomes high, in the case of the tunnelling mechanism).
For mechanism II, the contribution of product-phase ohmic drop rises relatively steadily throughout the discharge process; this steady rise reduces the cell potential dramatically when resistivity is large, eliminating the voltage plateau. Thus electron transport through the discharge-product layer is not a likely capacity-limiting factor in Li/O2 cells that exhibit a voltage plateau on discharge. It could be that electrons can propagate across the surfaces of the Li2O2 particles within the deposition layer, as suggested by Radin et al.89 In the case where there is surface conduction of electrons, the apparent resistivity of the layer would be relatively low, and mechanism II could be a reasonable description of the peroxide growth process.
It has also been suggested that the positive-electrode reaction involves an intermediate (such as superoxide) that forms electrochemically at the solid-backbone surface and diffuses through the liquid to form Li2O2 chemically at some distance from the electron-exchange site.24 In this case, the solid surface would always be accessible if the discharge phase were liquid-permeable; there would be no need for electron conduction through the discharge product and mechanism I would provide a reasonable physical description. Since the present simulations suggest that this scenario is very likely, an extended model will be developed in the future to probe the voltage response when the reaction mechanism involves liquid-phase intermediate species.
Capacity-limiting factors
Lu et al. recorded the first-discharge curves of independent Li/O2 cells at a series of rates;8 Adams et al. reported the overall discharge capacity as a function of current density for Li/O2 cells, and observed a sudden drop in capacity as discharge rate increased;90 Griffith et al. put the capacity vs. rate data on a log–log scale, and reported a Peukert's slope of about 1.6.59 To rationalize these observations and summarize the data, all three experimental data sets are collected on Fig. 5. Each set qualitatively shows three key features: a plateau at low rates, a transition region (shoulder), and a power-law decay at high rates. The red curve on Fig. 5 shows simulation data using parameters from Table 2 and assuming mechanism I with εdp = 0.87, consistent with the model validated against Griffith et al.'s experimental conditions. The simulation falls within the bounds established by the experimental data at all rates.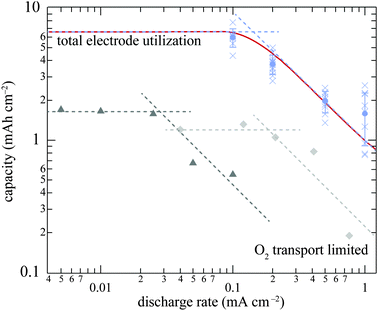 | ||
| Fig. 5 Cell capacity as a function of discharge rate. Circles: experimental data from Griffith et al.;59 triangles, data from Adams et al.;90 diamonds, data from Lu et al.8 The red curve is generated by simulations assuming mechanism I and Griffith's experimental conditions. For each data set, two dashed lines indicate expected low- and high-rate dependences of capacity. | ||
Using different cell properties in the simulation moves the location of the shoulder on the log-capacity vs. log-rate curve, but never changes its general shape. For example, decreasing oxygen solubility or diffusivity in the liquid phase moves the shoulder to lower rate; decreasing positive electrode thickness pushes the shoulder to higher rate and lower capacity.
These observations suggest that two distinct mechanisms determine the cell capacity in the limits of low and high rate, as indicated by the two dashed lines associated with each data set on Fig. 5. At low rates, the O2 consumption rate is slow enough for the active species to penetrate through the entire positive electrode, and the whole electrode is utilized. Thus eqn (15) determines the cell capacity, which is relatively constant in the low-rate regime. At higher rates, the O2 flux required by the current is so high that diffusion cannot deliver enough O2 to locations that are relatively far away from the O2 source. Thus O2 is entirely consumed near the outer surface of the positive electrode, limiting the cell capacity. In the high-rate regime, electrode utilization is not complete and capacity falls as the current rises.
To illustrate the different behaviors in different regimes of current, Fig. 6 presents the distributions of porosity, reaction rate, and O2 concentration at six discharge depths under mechanism I. At the low discharge rate of 0.05 mA cm−2, O2 transport is sufficiently facile that O2 is available throughout the positive electrode; thus the reaction zone (the domain where O2 is present and there is also free porosity, so in ≠ 0) spans the entire electrode. Note that the reaction distribution is skewed toward the gas side of the porous electrode, so the discharge product forms faster there. At about 80% DOD, the maximum occupancy of the discharge product is achieved at the electrode/oxygen interface, and the reaction zone begins to shrink. Since the discharge product is not compact, the growing ‘full zone’ (the domain with no free electrode porosity) still permits oxygen diffusion into the electrode interior. The discharge rate is sufficiently low that O2 diffusion across the full zone does not limit capacity. Eventually, the full zone grows to span the entire electrode, and the cell ‘dies’. In this situation, the electrode is completely utilized at sudden death – at least to the extent that the discharge-product porosity allows.
At a higher current of 0.5 mA cm−2, the O2 transport rate is too slow to match its consumption rate by the electrode reaction. Even before 30% DOD, O2 only penetrates about three quarters of the way into the electrode, leaving a ‘starved zone’ (where O2 is unavailable) on the separator side of the electrode in which the cell reaction cannot occur. As a full zone begins to form, the total rate of reaction throughout the reaction zone has to rise; this forces a higher flux of O2, causing the reaction zone to shrink and the starved zone to grow. Eventually, the reaction zone vanishes and the cell dies. In this situation, the electrode is only partially utilized at sudden death.
Capacity vs. rate
It is worth noting that in the high-rate limit, simulated capacity appears to fall in perfect inverse proportion to the applied current. To understand the power-law slopes of −1 apparent in Fig. 5, one can use the fact that the maximum flux of oxygen through the full zone should match the applied current at sudden death, and that the capacity in this state should scale as the thickness of the full zone. This yields a scaling law that connects the cell capacity to the discharge rate, | (17) |
 is an average diffusivity of oxygen through the pore-filling liquid. (Since local porosity varies during the discharge process, this average diffusivity differs somewhat from the diffusivity used in simulations.) Eqn (17) suggests that the cell capacity is inversely proportional to the discharge rate, and explains the slope of −1 at high rates on the log-capacity vs. log-rate plot. Deviations from −1 can arise from variation of the effective oxygen diffusivity with position and time as discharge progresses; thus the average quantity in eqn (17) is expected to vary somewhat with discharge rate.
is an average diffusivity of oxygen through the pore-filling liquid. (Since local porosity varies during the discharge process, this average diffusivity differs somewhat from the diffusivity used in simulations.) Eqn (17) suggests that the cell capacity is inversely proportional to the discharge rate, and explains the slope of −1 at high rates on the log-capacity vs. log-rate plot. Deviations from −1 can arise from variation of the effective oxygen diffusivity with position and time as discharge progresses; thus the average quantity in eqn (17) is expected to vary somewhat with discharge rate.
Although the agreement between simulations and experiments falls within experimental error, it is worth noting that the simulated capacity in Fig. 5 appears to be increasingly lower than the experimental values given by Griffith et al.59 as rate increases. This probably owes to rate dependence of the morphology of the Li2O2 layer,3,4,6,42 which is neglected in the present model. SEM images from the literature8,59,87,90 show that various sizes of Li2O2 particles form when different discharge currents are applied; in the model these would reflect different values of discharge-product-layer porosity εdp. At low rates, Li2O2 particles are disk-like, and εdp is relatively high; at high rates, the particles are smaller and more compact, making εdp lower. Combining eqn (14) with scaling law 17, one can conclude that that lower εdp should yield higher cell capacity, as shown by the comparison between the simulation and the experimental data in Fig. 5.
Conclusion
Three discharge mechanisms were studied within a continuum-scale three-phase model, which was used to simulate the first discharges of Li/O2 cells. Simulated discharge curves were compared to experimental data to validate the mechanisms.Although reaction rate constants and pore surface-to-volume ratios were found to affect overall cell voltage, they had minimal impact on cell capacity. Simulations where peroxide formation was assumed to occur by electron transport through a resistive discharge-product phase did not exhibit a voltage plateau during discharge. Simulations in which electron tunnelling through the discharge product was assumed to control the deposition process significantly underpredicted the capacities observed in experiments with porous electrodes. It was concluded that ohmic potential drop across the discharge-product layer does not make a substantial contribution to the overpotential, which is instead dominated by positive-electrode kinetics. Experimental data are consistent with mechanisms in which liquid-phase species diffuse through the discharge product to reach reaction sites at the surface of the conductive substrate, or where electron transport occurs through the discharge-product phase. In the latter situation, the electric resistivity must be in the semiconductor range – far lower than bulk lithium peroxide.
The simulations predicted a dependence of cell capacity on discharge rate that is consistent with experimental observations of cells with porous electrodes. This relationship is easily visualized on a log–log scale: the maximum capacity allowed by the electrode pore structure is achieved at low rate; the capacity is limited by O2 diffusion at high rate, leading to a power-law decrease with current. Using different cell properties in the simulation moves the transition between these limiting behaviors without varying the general shape of the log-capacity vs. log-rate curve. Distributions of O2 concentration, the electrode reaction, and free porosity within the positive electrode at different discharge depths confirm the hypotheses about capacity limitations.
In closing, it is important to emphasize that the model presented here assumes that the Li/O2 cell in question contains an electrolyte composed only of a single nonreactive solvent, a simple lithium salt, and dissolved molecular oxygen; it further assumes that pure lithium peroxide forms directly from liquid-phase lithium cations and oxygen via an elementary half-reaction. Although these assumptions have proved sufficient to describe the voltage response during first discharge, and also allowed simple conclusions to be drawn about discharge processes, experiments have suggested that the reaction pathway by which discharge-product formation occurs may involve a variety of intermediates and comprise several elementary steps. Side reactions may also affect rechargeability and cycle life, which is one reason the study here focussed on first discharge.
Many possible modifications could be made to the present model to shed light on various aspects of cell performance. One main advantage of the general framework presented above is that the equation system in Table 1 can easily be augmented to include more liquid-phase species, as well as accounting for more complicated multi-step reaction mechanisms. A first logical extension would be to include dissolved superoxide ions or LiO2 in the liquid phase, and to modify the kinetic laws to account for a superoxide-mediated reaction pathway. Such pathways have been verified to occur in Li/O2 systems,91 and may be relevant to several other metal/oxygen battery chemistries.92 Understanding the electrochemically formed intermediates involved in the cell reaction may also provide insight into the asymmetry of voltage signatures when Li/O2 cells recharge. It is known that lithium carbonate can form from the electrolyte's solvent or from materials that make up the solid positive electrode, and that the behavior of carbonate material may be critical to cell performance during repeated discharge/charge cycling.93 Recent literature has suggested that trace water or lithium-hydroxide formation may dramatically affect both discharge capacity and rechargeability,35 and that the presence of dopants may affect electron transport through the discharge product.94,95 Extensions that account for reaction intermediates, dissolved water, hydroxide ions, and carbonate formation may all be fruitful.
Acknowledgements
This work was supported by Robert Bosch LLC through the Bosch Energy Research Network, grant no. 19.04.US11, and by the U.S. National Science Foundation, grant no. CBET-1336387.References
- J. Heywood, Internal Combustion Engine Fundamentals, McGraw-Hill Science/Engineering/Math, 1988 Search PubMed.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J. M. Tarascon, Nat. Mater., 2012, 11, 19–29 CrossRef CAS PubMed.
- B. M. Gallant, R. R. Mitchell, D. G. Kwabi, J. Zhou, L. Zuin, C. V. Thompson and Y. Shao-Horn, J. Phys. Chem. C, 2012, 116, 20800–20805 CAS.
- B. M. Gallant, D. G. Kwabi, R. R. Mitchell, J. Zhou, C. V. Thompson and Y. Shao-Horn, Energy Environ. Sci., 2013, 6, 2518–2528 CAS.
- B. Horstmann, T. Danner and W. G. Bessler, Energy Environ. Sci., 2013, 6, 1299–1314 CAS.
- B. Horstmann, B. Gallant, R. Mitchell, W. G. Bessler, Y. Shao-Horn and M. Z. Bazant, J. Phys. Chem. Lett., 2013, 4, 4217–4222 CrossRef CAS PubMed.
- J. S. Hummelshøj, A. C. Luntz and J. K. Nørskov, J. Chem. Phys., 2013, 138, 034703 CrossRef PubMed.
- Y.-C. Lu, D. G. Kwabi, K. P. C. Yao, J. R. Harding, J. Zhou, L. Zuin and Y. Shao-Horn, Energy Environ. Sci., 2011, 4, 2999–3007 CAS.
- Y.-C. Lu and Y. Shao-Horn, J. Phys. Chem. Lett., 2013, 4, 93–99 CrossRef CAS PubMed.
- A. C. Luntz, V. Viswanathan, J. Voss, J. B. Varley, J. K. Nørskov, R. Scheffler and A. Speidel, J. Phys. Chem. Lett., 2013, 4, 3494–3499 CrossRef CAS.
- J. B. Varley, V. Viswanathan, J. K. Norskov and A. C. Luntz, Energy Environ. Sci., 2014, 7, 720–727 CAS.
- V. Viswanathan, K. S. Thygesen, J. S. Hummelshøj, J. K. Nørskov, G. Girishkumar, B. D. McCloskey and A. C. Luntz, J. Chem. Phys., 2011, 135, 214704 CrossRef CAS PubMed.
- V. Viswanathan, J. K. Nørskov, A. Speidel, R. Scheffler, S. Gowda and A. C. Luntz, J. Phys. Chem. Lett., 2013, 4, 556–560 CrossRef CAS PubMed.
- Y. Wang and H. Zhou, Chem. Commun., 2010, 46, 6305–6307 RSC.
- K.-H. Xue, E. McTurk, L. Johnson, P. G. Bruce and A. A. Franco, J. Electrochem. Soc., 2015, 162, A614–A621 CrossRef CAS.
- K. Yoo, S. Banerjee and P. Dutta, J. Power Sources, 2014, 258, 340–350 CrossRef CAS.
- K. M. Abraham and Z. Jiang, J. Electrochem. Soc., 1996, 143, 1–5 CrossRef CAS.
- J. Christensen, P. Albertus, R. S. Sanchez-Carrera, T. Lohmann, B. Kozinsky, R. Liedtke, J. Ahmed and A. Kojic, J. Electrochem. Soc., 2011, 159, R1–R30 CrossRef.
- C. O. Laoire, S. Mukerjee, K. M. Abraham, E. J. Plichta and M. A. Hendrickson, J. Phys. Chem. C, 2010, 114, 9178–9186 CAS.
- J. Read, J. Electrochem. Soc., 2002, 149, A1190–A1195 CrossRef CAS.
- J. Read, K. Mutolo, M. Ervin, W. Behl, J. Wolfenstine, A. Driedger and D. Foster, J. Electrochem. Soc., 2003, 150, A1351–A1356 CrossRef CAS.
- T. Ogasawara, A. Débart, M. Holzapfel, P. Novák and P. G. Bruce, J. Am. Chem. Soc., 2006, 128, 1390–1393 CrossRef CAS PubMed.
- S. D. Beattie, D. M. Manolescu and S. L. Blair, J. Electrochem. Soc., 2009, 156, A44–A47 CrossRef CAS.
- C. O. Laoire, S. Mukerjee, K. M. Abraham, E. J. Plichta and M. A. Hendrickson, J. Phys. Chem. C, 2009, 113, 20127–20134 CAS.
- X.-h. Yang, P. He and Y.-y. Xia, Electrochem. Commun., 2009, 11, 1127–1130 CrossRef CAS.
- P. Andrei, J. P. Zheng, M. Hendrickson and E. J. Plichta, J. Electrochem. Soc., 2010, 157, A1287–A1295 CrossRef CAS.
- J. S. Hummelshøj, J. Blomqvist, S. Datta, T. Vegge, J. Rossmeisl, K. S. Thygesen, A. C. Luntz, K. W. Jacobsen and J. K. Nørskov, J. Chem. Phys., 2010, 132, 0711011 CrossRef PubMed.
- S. A. Freunberger, Y. Chen, Z. Peng, J. M. Griffin, L. J. Hardwick, F. Bardé, P. Novák and P. G. Bruce, J. Am. Chem. Soc., 2011, 133, 8040–8047 CrossRef CAS PubMed.
- Y. Chen, S. A. Freunberger, Z. Peng, F. Bardé and P. G. Bruce, J. Am. Chem. Soc., 2012, 134, 7952–7957 CrossRef CAS PubMed.
- B. D. McCloskey, R. Scheffler, A. Speidel, G. Girishkumar and A. C. Luntz, J. Phys. Chem. C, 2012, 116, 23897–23905 CAS.
- Z. Peng, S. A. Freunberger, Y. Chen and P. G. Bruce, Science, 2012, 337, 563–566 CrossRef CAS PubMed.
- T. Zhang and H. Zhou, Nat. Commun., 2013, 4, 1817–1823 CrossRef PubMed.
- D. S. Kim and Y. J. Park, J. Alloys Compd., 2014, 591, 164–169 CrossRef CAS.
- Z. Y. Guo, X. L. Dong, S. Y. Yuan, Y. G. Wang and Y. Y. Xia, J. Power Sources, 2014, 264, 1–7 CrossRef CAS.
- T. Liu, M. Leskes, W. J. Yu, A. J. Moore, L. N. Zhou, P. M. Bayley, G. Kim and C. P. Grey, Science, 2015, 350, 530–533 CrossRef CAS PubMed.
- J. W. Wang, Y. L. Zhang, L. M. Guo, E. K. Wang and Z. Q. Peng, Angew. Chem., Int. Ed., 2016, 55, 5201–5205 CrossRef CAS PubMed.
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- P. G. Bruce, Solid State Ionics, 2008, 179, 752–760 CrossRef CAS.
- J. M. Tarascon, Philos. Trans. R. Soc., A, 2010, 368, 3227–3241 CrossRef PubMed.
- A. Kraytsberg and Y. Ein-Eli, J. Power Sources, 2011, 196, 886–893 CrossRef CAS.
- I. Kowalczk, J. Read and M. Salomon, Pure Appl. Chem., 2007, 79, 851–860 CrossRef CAS.
- Y.-C. Lu, B. M. Gallant, D. G. Kwabi, J. R. Harding, R. R. Mitchell, M. S. Whittingham and Y. Shao-Horn, Energy Environ. Sci., 2013, 6, 750–768 CAS.
- B. D. McCloskey, D. S. Bethune, R. M. Shelby, G. Girishkumar and A. C. Luntz, J. Phys. Chem. Lett., 2011, 2, 1161–1166 CrossRef CAS PubMed.
- M. M. O. Thotiyl, S. A. Freunberger, Z. Peng and P. G. Bruce, J. Am. Chem. Soc., 2013, 135, 494–500 CrossRef PubMed.
- M. M. O. Thotiyl, S. A. Freunberger, Z. Q. Peng, Y. H. Chen, Z. Liu and P. G. Bruce, Nat. Mater., 2013, 12, 1049–1055 Search PubMed.
- H. Wang, K. Xie, L. Wang and Y. Han, RSC Adv., 2013, 3, 8236–8241 RSC.
- J. Xiao, W. Xu, D. Wang and J.-G. Zhang, J. Electrochem. Soc., 2010, 157, A294–A297 CrossRef CAS.
- G. Q. Zhang, J. P. Zheng, R. Liang, C. Zhang, B. Wang, M. Hendrickson and E. J. Plichta, J. Electrochem. Soc., 2010, 157, A953–A956 CrossRef CAS.
- J. M. Garcia-Lastra, J. D. Bass and K. S. Thygesen, J. Chem. Phys., 2011, 135, 121101 CrossRef CAS PubMed.
- N. Imanishi, A. C. Luntz and P. G. Bruce, The Lithium Air Battery: Fundamentals, Springer, 2014 Search PubMed.
- C. Ó. Laoire, S. Mukerjee, E. J. Plichta, M. A. Hendrickson and K. M. Abraham, J. Electrochem. Soc., 2011, 158, A302–A308 CrossRef CAS.
- P. Albertus, G. Girishkumar, B. McCloskey, R. S. Sánchez-Carrera, B. Kozinsky, J. Christensen and A. C. Luntz, J. Electrochem. Soc., 2011, 158, A343–A351 CrossRef CAS.
- J. Read, J. Electrochem. Soc., 2006, 153, A96–A100 CrossRef CAS.
- S. S. Zhang, D. Foster and J. Read, J. Power Sources, 2010, 195, 1235–1240 CrossRef CAS.
- S. S. Zhang, K. Xu and J. Read, J. Power Sources, 2011, 196, 3906–3910 CrossRef CAS.
- V. Y. Nimon, S. J. Visco, L. C. De Jonghe, Y. M. Volfkovich and D. A. Bograchev, ECS Electrochem. Lett., 2013, 2, A33–A35 CrossRef CAS.
- J. P. Neidhardt, D. N. Fronczek, T. Jahnke, T. Danner, B. Horstmann and W. G. Bessler, J. Electrochem. Soc., 2012, 159, A1528–A1542 CrossRef CAS.
- C. Y. Jung, T. S. Zhao and L. An, J. Power Sources, 2014, 273, 440–447 CrossRef.
- L. D. Griffith, A. E. S. Sleightholme, J. Mansfield, D. J. Siegel and C. W. Monroe, ACS Appl. Mater. Interfaces, 2015, 7, 7670–7678 CAS.
- J. Liu and C. W. Monroe, Electrochim. Acta, 2014, 135, 447–460 CrossRef CAS.
- L. Li, X. Zhao and A. Manthiram, Electrochem. Commun., 2012, 14, 78–81 CrossRef CAS.
- Y.-C. Lu, H. A. Gasteiger, E. Crumlin, R. McGuire and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, A1016–A1025 CrossRef CAS.
- A. K. Thapa, K. Saimen and T. Ishihara, Electrochem. Solid-State Lett., 2010, 13, A165–A167 CrossRef CAS.
- J.-G. Zhang, D. Wang, W. Xu, J. Xiao and R. E. Williford, J. Power Sources, 2010, 195, 4332–4337 CrossRef CAS.
- X. Zhang, L. Hua, E. Yang, Z. An, J. Chen, X. Chen, X. Chao, J. Yu, M. Wu and X. Miao, Int. J. Electrochem. Sci., 2012, 7, 10562–10569 CAS.
- S. Dong, X. Chen, S. Wang, L. Gu, L. Zhang, X. Wang, X. Zhou, Z. Liu, P. Han, Y. Duan, H. Xu, J. Yao, C. Zhang, K. Zhang, G. Cui and L. Chen, ChemSusChem, 2012, 5, 1712–1715 CrossRef CAS PubMed.
- T. T. Truong, Y. Liu, Y. Ren, L. Trahey and Y. Sun, ACS Nano, 2012, 6, 8067–8077 CrossRef CAS PubMed.
- D. Wang, J. Xiao, W. Xu and J.-G. Zhang, J. Electrochem. Soc., 2010, 157, A760–A764 CrossRef CAS.
- M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533 CrossRef CAS.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 1–10 CrossRef CAS.
- D. A. G. Bruggeman, Ann. Phys., 1935, 416, 636–664 CrossRef.
- J. Newman and K. E. Thomas-Alyea, Electrochemical Systems, Wiley-Interscience, 2004 Search PubMed.
- A. Nyman, M. Behm and G. Lindbergh, Electrochim. Acta, 2008, 53, 6356–6365 CrossRef CAS.
- J. Newman, D. Bennion and C. W. Tobias, Ber. Bunsen-Ges., 1965, 69, 608–612 CrossRef CAS.
- J. Newman, Ind. Eng. Chem. Fundam., 1966, 5, 525–529 CAS.
- J. Newman and C. W. Tobias, Adv. Electrochem. Electrochem. Eng., 1967, 5, 87–135 CAS.
- J. Newman and T. W. Chapman, AIChE J., 1973, 19, 343–348 CrossRef CAS.
- J. Newman and W. Tiedemann, AIChE J., 1975, 21, 25–41 CrossRef CAS.
- C. W. Monroe, Dendrite Initiation and Growth in Lithium/Polymer Systems, PhD dissertation, University of California, Berkeley, 2004 Search PubMed.
- N. Deprez and D. S. McLachlan, J. Phys. D: Appl. Phys., 1988, 21, 101–107 CrossRef CAS.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, LLC, 2013 Search PubMed.
- D. Brouillette, G. Perron and J. E. Desnoyers, J. Solution Chem., 1998, 27, 151–182 CrossRef CAS.
- P. Andrei, J. P. Zheng, M. Hendrickson and E. J. Plichta, J. Electrochem. Soc., 2012, 159, A770–A780 CrossRef CAS.
- R. Black, S. H. Oh, J.-H. Lee, T. Yim, B. Adams and L. F. Nazar, J. Am. Chem. Soc., 2012, 134, 2902–2905 CrossRef CAS PubMed.
- D. Xu, Z.-l. Wang, J.-j. Xu, L.-l. Zhang and X.-b. Zhang, Chem. Commun., 2012, 48, 6948–6950 RSC.
- D. Xu, Z.-l. Wang, J.-j. Xu, L.-l. Zhang, L.-m. Wang and X.-b. Zhang, Chem. Commun., 2012, 48, 11674–11676 RSC.
- X.-h. Yang and Y.-y. Xia, J. Solid State Electrochem., 2010, 14, 109–114 CrossRef CAS.
- U. Sahapatsombut, H. Cheng and K. Scott, J. Power Sources, 2013, 227, 243–253 CrossRef CAS.
- M. D. Radin and D. J. Siegel, Energy Environ. Sci., 2013, 6, 2370–2379 CAS.
- B. D. Adams, C. Radtke, R. Black, M. L. Trudeau, K. Zaghib and L. F. Nazar, Energy Environ. Sci., 2013, 6, 1772–1778 CAS.
- L. Johnson, C. M. Li, Z. Liu, Y. H. Chen, S. A. Freunberger, P. C. Ashok, B. B. Praveen, K. Dholakia, J. M. Tarascon and P. G. Bruce, Nat. Chem., 2014, 6, 1091–1099 CrossRef CAS PubMed.
- G. Vardar, E. G. Nelson, J. G. Smith, J. Naruse, H. Hiramatsu, B. M. Bartlett, A. E. S. Sleightholme, D. J. Siegel and C. W. Monroe, Chem. Mater., 2015, 27, 7564–7568 CrossRef CAS.
- A. C. Luntz and B. D. McCloskey, Chem. Rev., 2014, 114, 11721–11750 CrossRef CAS PubMed.
- R. Black, J. H. Lee, B. Adams, C. A. Mims and L. F. Nazar, Angew. Chem., Int. Ed., 2013, 52, 392–396 CrossRef CAS PubMed.
- M. D. Radin, C. W. Monroe and D. J. Siegel, Chem. Mater., 2015, 27, 839–847 CrossRef CAS.
| This journal is © the Owner Societies 2016 |