 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermal effect on the morphology and performance of organic photovoltaics†
Eisuke
Kawashima
 ab,
Mikiya
Fujii
ab and
Koichi
Yamashita
*ab
ab,
Mikiya
Fujii
ab and
Koichi
Yamashita
*ab
aDepartment of Chemical System Engineering, Graduate School of Engineering, The University of Tokyo, Tokyo 113-8656, Japan. E-mail: yamasita@chemsys.t.u-tokyo.ac.jp
bCREST, Japan Science and Technology Agency (JST), Tokyo 113-8656, Japan
First published on 1st September 2016
Abstract
The morphology of organic photovoltaics (OPVs) is a significant factor in improving performance, and establishing a method for controlling morphology is necessary. In this study, we propose a device-size simulation model, combining reptation and the dynamic Monte Carlo (DMC) algorithm, to investigate the relationship between the manufacturing process, morphology, and OPV performance. The reptation reproduces morphologies under thermal annealing, and DMC showed morphology-dependence of performance: not only short-circuit current density but also open-circuit voltage had optimal interfacial areas due to competition between exciton dissociation and charge collection. Besides, we performed transient absorption spectroscopy of various BHJ morphologies under realistic conditions, which revealed prompt and delayed dynamics of charge generation—the majority of the charges were from excitons that were generated on interfaces and dissociated within a few picoseconds, and the others from excitons that migrated to interfaces and dissociated on the order of sub-nanoseconds.
1 Introduction
Organic photovoltaics (OPVs) are promising devices for ubiquitous electricity generation which replace traditional silicon solar cells because of their light weight, flexibility, roll-to-roll printability,1,2 and short energy payback time.3 However, the power conversion efficiencies (PCEs) of the OPVs are still low (11% at the highest4) and hence optimization schemes are required. The active layers of OPVs are composed of organic donor and acceptor semiconductors: π-conjugated polymers are frequently used as the donor materials, e.g., poly(3-hexylthiophene) (P3HT), while small molecules such as fullerene derivatives are used as acceptor materials, e.g., [6,6]-phenyl-C61-butyric acid methyl ester (PC61BM). P3HT:PC61BM is one of the most studied pairs of semiconductors for OPVs, the chemical structures of which are shown in Fig. 1.The morphology of OPVs—the degree of phase separation, miscibility, and crystallinity of the organic materials—is considered as one of the significant factors for the PCE improvement of OPVs because it strongly affects the efficiencies of exciton dissociation and charge collection described above. In the case of OPVs with a smaller interfacial area and a larger domain, charge carriers are collected efficiently because of transport pathways without bottlenecks, while few excitons dissociate before geminate recombination.5,6 Bulk heterojunction (BHJ) morphology is a breakthrough in OPV development because of its large interfacial area and bicontinuous charge transport pathways.7 Morphologies are determined not only by the chemical properties of materials—interaction or solubility—but also by fabrication processes. There have been various experimental studies that investigate how to control morphology to improve the PCE: thermal or solvent annealing,8–11 and control of the drying conditions.12,13 For instance, it is known that the annealing temperature has an optimum value for efficiency.8,9 Transient absorption spectroscopy was also performed to track the efficiency and dynamics of excitons and charge carriers, and influences of morphologies were examined.14
Meanwhile, various theoretical studies on OPVs have been presented to obtain a detailed understanding of the mechanism of photocurrent generation.15 Quantum chemical calculations estimate properties such as energy levels and distributions of molecular orbitals, absorbance,16–19 and rate of an elementary process.20 However, such molecular-level investigations alone are not sufficient to provide guiding principles for OPV optimization because photocurrent generation is a complicated macroscopic process. Therefore, several theoretical approaches have been presented to investigate morphologies and efficiencies, which are briefly reviewed in the remainder of this section.
To analyze morphologies, molecular dynamics (MD) calculations are performed, which reveal the molecular packing21 and molecular orientation of polymers (edge-on and face-on configurations).22 Although MD simulations can reveal all morphological properties for OPVs in principle, the computational cost of a device-size system is extremely high even if coarse-grained MD techniques are applied. Another approach is simulations using the Cahn–Hilliard equation, which has been established in soft matter physics. This method requires low computational cost and is applicable to device-size simulation.23–28 However, it cannot determine the orientation of polymers because the Cahn–Hilliard equation is a differential equation of concentration of chemical components. Based on the above, we adopt a coarse-grained model called reptation, which has been established to describe polymer melts and solutions.29,30 Frost et al. applied reptation to OPVs and revealed that the fraction of polymers would influence quantum efficiency through morphologies.31 Reptation also involves low computational cost, but additionally can reveal morphological properties like orientation and miscibility of polymers, and thermal influences on them.31 Therefore this method is suitable for studying OPVs, especially the influence of thermal annealing on them.
Several approaches to investigate the PCEs of OPVs have been presented. The simplest one is the equivalent-circuit model, which assumes a solar cell as a circuit of current sources, parallel diodes, and series and parallel resistors.32,33 Device simulators known as Scharfetter–Gummel models simultaneously solve coupled equations of electric field and carrier dynamics in the OPVs—the Poisson equation, equation of continuity, and drift-diffusion equation.34–36 The last ones are the dynamic Monte Carlo (DMC) algorithm with the first reaction method (FRM) and kinetic Monte Carlo (KMC), which stochastically simulate the dynamics of elementary processes according to the rate. There have been studies which examine morphology-dependence of performance—current density and efficiencies of elementary processes such as internal quantum efficiency (IQE)—and dynamics of excitons and charge carriers.27,28,37–46 We adopt DMC because it can treat morphologies explicitly and track carrier dynamics in the morphologies.
In this work, we present a combined model of reptation and DMC, which enables the investigation of the relationship between thermal annealing, morphologies, and OPV performances. Morphologies were generated under various conditions by use of reptation, in which current density–voltage (J–V) characteristics were simulated and performance parameters such as short-circuit current density (JSC), open-circuit voltage (VOC), and PCE were investigated. We showed the existence of optimal annealing conditions for the PCE because of a trade-off between exciton dissociation and charge recombination.
2 Methodology
In this article, we present a model of OPVs by combining the two simulation techniques. Morphologies and OPV characteristics were simulated by reptation and DMC, respectively. Various parameters used in these techniques were set to model OPVs of indium tin oxide (ITO)/P3HT:PC61BM/aluminum, and the simulations were performed at a device scale with a system size of 1503 nm3 to perform realistic analyses. The simulation details of reptation and DMC are described below.2.1 Reptation
Reptation, which was introduced by de Gennes29 and refined by Doi and Edwards,30 is a coarsening model of entangled polymer systems, such as melts or concentrated solutions. The polymer is enclosed in a space called a “tube” and can move easily along the tube, but not perpendicularly to it like a slithering snake.In this work, polymers were modeled as self-avoiding chains of a certain number of segments connected by bonds, and the excluded volume effect was considered. The system was composed of 1503 sites, each of which was occupied by either a polymer segment or a small molecule, and the lattice constant was set to 1 nm. Periodic boundary conditions were applied for the x, y, and z directions.
The reptation was simulated stochastically with the Metropolis Monte Carlo (MMC) algorithm.31 The scheme is shown in Fig. 2. In each MMC step, an end of a polymer tries to move to one of the nearest neighboring empty lattices at random, followed by the rest of the polymer. The acceptance probability p is determined by the temperature (T) and energy change (ΔE) due to the trial reptation. The total energy of the system, E, is given by the sum of interactions between the nearest neighboring sites according to the materials occupying them, while ΔE is calculated by the interaction change of only the two sites, where the polymer enters and exits, because the other segments of the polymer are unchanged.
 | ||
| Fig. 2 Schematic representation of reptation in a two-dimensional system: (a) before and (b) after the reptation of a polymer. Each site is occupied by either a polymer segment or a small molecule, which are represented by closed and open circles, respectively, and the polymer segments are connected by bonds represented by lines. Calculation of ΔE (eqn (3)) requires only the coordination number of polymers and small molecules of the lattices where the polymer enters and exits (the shaded squares). | ||
Let np and nm be the coordination numbers of polymer segments and small molecules for a site, respectively, and εpp, εpm, and εmm be polymer–polymer, polymer–small molecule, and small molecule–small molecule interactions, respectively. Interaction between polymer segments connected by a bond was assumed to be constant and ignored in the calculation of the energy because the length of the polymers was fixed in the simulation. The ΔE due to reptation is calculated as:
| ΔE = ΔEen − ΔEex, | (1) |
| ΔEen/ex = (nen/expεpp + nen/exmεpm) − (nen/expεpm + nen/exmεmm). | (2) |
| ΔE = (nenp − nexp)Δε | (3) |
The simulation scheme is as follows: (i) configure polymers randomly in the system (Fig. 5(a)). (ii) Randomly and independently choose a polymer end and direction to reptate that are possible—rechoose them if the pointed site is already occupied by another polymer. (iii) Calculate the energy difference ΔE of reptation. (iv) Accept the reptation with probability p calculated as
| p = min{1,exp(−βΔE)} | (4) |
| = min{1,exp(−(nenp − nexp)βΔε)}, | (5) |
To investigate the dependence of morphologies on annealing temperature and other conditions, reptation was simulated for various βΔε, number of polymer segments nseg, and volumetric ratios. The number of polymer segments, nseg, was set to 25, 50, 75, and 100, and the volume fraction of polymers to 33% or 50%; the number of polymers was adjusted to achieve those volume fractions in the simulation volume of 1503 nm3. The dimensionless parameter βΔε was set to nonpositive values to simulate mutually attractive or noninteracting polymers or infinite temperature.
2.2 Dynamic Monte Carlo
In DMC simulations with the FRM, waiting times of all possible events, calculated from their rate, are stored in a queue; the event holding the minimum waiting time is executed in each DMC step.37,47 This work considers three particles, i.e., excitons, holes, and electrons, which are allowed single occupancy of a site. A donor site would be occupied by an exciton or a hole, while an acceptor site by an electron. The simulation scheme is summarized as follows: (i) initialize the system: the first events under photo and dark conditions are exciton generation and charge (hole or electron) injection, respectively. (ii) Insert waiting times of all possible events associated with the particles into the queue; waiting time τ of each process is calculated as
 | (6) |
The next subsection explains the details of the stochastic modeling of elementary processes.
| Parameter | Value |
|---|---|
| Lattice constant a | 3 nm |
| Cutoff distance Rcut | 15 nm |
| Temperature T | 300 K |
| Relative permittivity εr | 3.5 |
| HOMO of the donor | −5.0 eV |
| LUMO of the acceptor | −3.7 eV |
| Work function of the cathode | 4.1 eV |
| Work function of the anode | 4.6 eV |
| Exciton generation rate Wgenex | 8 × 10−8 ps−1 nm−2 |
| Exciton lifetime τlife | 330 ps48 |
| Exciton dissociation rate Wdisex | 0.15 ps−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
| Absorption coefficient α | 3 × 104 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 49 |
| Förster radius R0 | 3 nm |
| Reorganization energy λ | 0.11 eV20 |
| Gaussian width of DOS σ | 0.062 eV39 |
| Hole mobility μh | 0.1 cm2 V−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
| Electron mobility μe | 0.025 cm2 V−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51 51 |
| Charge recombination rate Wrecch | 1.93 ns−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
2.2.2.1 Excitons. Excitons are bound electron–hole pairs generated by an absorbed photon and have no charge.
(i) In this work AM 1.5 irradiation (power of 100 W cm−2) was assumed and the exciton generation rate Wgenex was set to 8 × 10−10 ps−1 nm−2, which yields a current density of 12.8 mA cm−2 when the internal quantum efficiency (IQE) reaches 100%. To save computational resources we insert an event of exciton generation into the queue at a time, without considering where to generate an exciton; at execution of exciton generation an unoccupied donor site is randomly chosen. The probability p is weighted by depth according to the Lambert–Beer law,
| p(z) ∝ exp(−α(ztop − z)), | (7) |
(ii) Once generated, an exciton will hop to a nearby donor site; in this simulation, hopping to all possible sites is considered and the rate Whopex is calculated by the Förster energy-transfer theory,52
 | (8) |
 | (9) |
(iii) When an exciton reaches the interface, it is able to dissociate into a hole and an electron. In the simulation all possible donor–acceptor nearest neighboring pairs were considered, and after exciton dissociation a hole was created on the donor site that the dissociated exciton occupied, and an electron on the acceptor site across the interface. The exciton dissociation rate, Wdisex, was set to 0.15 ps−1, which was estimated by quantum chemical calculations.20
(iv) Otherwise, an exciton decayed to the ground state and geminate recombination occurs. The exciton recombination rate is the reciprocal of the exciton lifetime: Wrecex = 1/τlife.
2.2.2.2. Holes and electrons. Holes and electrons have charge and hence their transport is affected by the difference of site energy, ΔE, before and after the event. The site energy is a summation of the following three factors:
1. On-site energies of charge carriers (holes/electrons), which are a summation of the orbital energy (HOMO of the acceptor/LUMO of the donor) and Gaussian disorder of density of states (DOS) caused by residual solvents and structural disorder. The HOMO of the acceptor, LUMO of the donor, and Gaussian width σ were set to −5.0 eV, −3.7 eV, and 0.062 eV,39 respectively.
2. The Coulomb interaction, U, with other charge carriers and image charges, including that of itself. The Coulomb interaction of carrier i is calculated as
 | (10) |
 | (11) |
3. The electrostatic built-in potential, Vbuilt, which is induced by the applied voltage V and the difference in the work functions of the electrodes (ΔW = 0.5 V):
 | (12) |
(v) A charge carrier was created in the active layer by either exciton dissociation or injection from the electrode; a hole (an electron) is injected from the anode (cathode) to one of the donor (acceptor) sites at the surface. These injected carriers contribute to the dark current, which is enhanced by the applied voltage, V. The charge injection rate Winjh/e is calculated by the Miller–Abraham equation53 as
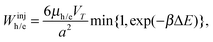 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 and 0.025 cm2 V−1 s−1,51 respectively. The prefactor is derived from the Einstein relationship.37,54
50 and 0.025 cm2 V−1 s−1,51 respectively. The prefactor is derived from the Einstein relationship.37,54
In calculations of the energy difference ΔE, the Gaussian disorder of an electrode was not considered. In addition to the above three factors, ΔE included the charge injection barrier of +0.4 eV, which is derived from the difference between the LUMO of the acceptor (−3.7 eV) and the Fermi level of the cathode (−4.1 eV). Although an injected carrier could be collected from the electrode, it was forced to hop at once before extraction if possible.
(vi) Holes and electrons inside the active layer are allowed to hop to one of the nearest neighboring donor and acceptor sites, respectively. The charge hopping rate Whoph/e is calculated using the Marcus formula as
 | (14) |
(vii) When a charge carrier reaches the electrode surface, it is able to be collected and then the current flows. The charge collection rate is also calculated by the Marcus formula (eqn (14)), but the negative of the charge injection barrier is considered for ΔE. Collection of holes from the cathode and electrons from the anode contribute to the photocurrent.
(viii) Leakage of charge carriers, i.e., extraction of holes/electrons from the anode/cathode, is simulated in the same way as above, but it contributes to the dark current.
(ix) Charge recombinations are considered when a hole and an electron are located on adjacent sites. The rate Wrecch was set to 1.93 ns−1.20
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) collh (electrons at the cathode nnet
collh (electrons at the cathode nnet![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) colle) is the number of collected holes ncollh (electrons ncolle) reduced by those of injected holes ninjh (electrons ninje) and leaked electrons nleake (holes nleakh):
colle) is the number of collected holes ncollh (electrons ncolle) reduced by those of injected holes ninjh (electrons ninje) and leaked electrons nleake (holes nleakh):nnet![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) collh/e = ncollh/e − ninjh/e − nleake/h, collh/e = ncollh/e − ninjh/e − nleake/h, | (15) |
 | (16) |
 | (17) |
The net current density J is calculated as the number of net collected charges divided by the incident area (1502 nm2) and simulation time. The J–V curves were obtained by repeating the calculation of current density under each applied voltage. Open-circuit voltage VOC, PCE, and fill factor (FF) were obtained by linear interpolation of the J–V curve.
Notably, this study also analyzed transient absorption spectroscopy. In the simulation, a certain number of excitons were created at the start under the conditions that no charge injection, leak, nor collection and no applied voltage were imposed. The initial number of excitons was set to 100 and 1000: the latter corresponds to a density of 3 × 1017 cm−3, which is consistent with the experimental value;14 the former was for comparison, and note that we can simulate dilute conditions that experimental observation is difficult. There have been studies that discuss the dynamics of carriers—the effect of mobility on charge separation,45 and the kinetic model of charge separation and recombination.46 In this work we examined the dependence of transient absorption spectroscopy on BHJ morphology in consideration of annealing temperature and analyzed space-time dynamics.
Five simulation runs were performed independently for each condition—0.5 ms and 10 ns for a simulation of current density and transient absorption spectroscopy, respectively—and the results were averaged.
3 Results and discussion
3.1 Reptation
The generated morphologies with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio and 75 polymer segments are shown in Fig. 5, whose phase separation is consistent with an experimental report55 and theoretical studies using the Cahn–Hilliard equation.23–28 See Fig. S1 and S2 in the ESI† for the other morphologies—those of different volume ratios and number of segments. Generally, the domain size grew as βΔε increased. The temperature increased under the negative constant Δε, while the polymers dispersed when the temperature was too high. These morphologies are characterized numerically: interfacial area per volume and mean distribution of domain size, shown in Fig. 6(a) and (b). Here, the domain size is defined as the length of continuous donor/acceptor domains along x, y, or z. Both characteristics depended strongly on βΔε but only slightly on the polymer length. The interfacial area and domain size indicate the minimum and maximum values, respectively, around βΔε = −1 because of the degree of diffusion. At low temperature (βΔε = −4.0, shown in Fig. 5(i)), the polymers are hindered in diffusing and trapped in a local minimum because of the attractive interaction. As the temperature rises, the polymer can diffuse and relax, therefore donor domains are formed; however, free diffusion breaks the domains when the temperature is too high. The polymer length also affects diffusion and therefore shows a similar dependence. See Section S1.2 in the ESI† for the results of a polymer/small molecule volumetric ratio of 1
1 volume ratio and 75 polymer segments are shown in Fig. 5, whose phase separation is consistent with an experimental report55 and theoretical studies using the Cahn–Hilliard equation.23–28 See Fig. S1 and S2 in the ESI† for the other morphologies—those of different volume ratios and number of segments. Generally, the domain size grew as βΔε increased. The temperature increased under the negative constant Δε, while the polymers dispersed when the temperature was too high. These morphologies are characterized numerically: interfacial area per volume and mean distribution of domain size, shown in Fig. 6(a) and (b). Here, the domain size is defined as the length of continuous donor/acceptor domains along x, y, or z. Both characteristics depended strongly on βΔε but only slightly on the polymer length. The interfacial area and domain size indicate the minimum and maximum values, respectively, around βΔε = −1 because of the degree of diffusion. At low temperature (βΔε = −4.0, shown in Fig. 5(i)), the polymers are hindered in diffusing and trapped in a local minimum because of the attractive interaction. As the temperature rises, the polymer can diffuse and relax, therefore donor domains are formed; however, free diffusion breaks the domains when the temperature is too high. The polymer length also affects diffusion and therefore shows a similar dependence. See Section S1.2 in the ESI† for the results of a polymer/small molecule volumetric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The interfacial area and domain size were smaller and their dependence on βΔε became milder than those of a 1
2. The interfacial area and domain size were smaller and their dependence on βΔε became milder than those of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, due to the lower polymer fraction and weaker entanglement effects.
1 ratio, due to the lower polymer fraction and weaker entanglement effects.
The domain-size distributions of the polymers and small molecules are shown in Fig. 6(c) and (d), respectively. Essentially, the distributions of the domain size for both polymers and small molecules exhibit exponential decay and there is no significant difference between polymers and small molecules. However, the morphology of βΔε = −0.5 has significantly different characters: the domains of small molecules in that morphology are larger than those of polymers, and exhibit exceptionally oscillating properties. This was because polymer aggregation precluded acceptors and formed large acceptor domains but polymer domains were broken due to diffusion.
The results in this subsection propose that the morphologies of OPVs strongly depend on the temperature by using the physical modeling of blends of polymers and small molecules.
3.2 Dynamic Monte Carlo
For BHJ morphologies, we chose those with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volumetric ratio and 75-segment polymers, nseg = 75, to investigate wide ranges of interfacial area and domain size (see Fig. 5 and 6). It is expected that other morphology groups—different nseg and/or volumetric fraction—show a similar but milder temperature dependence. For example, morphologies with a 1
1 volumetric ratio and 75-segment polymers, nseg = 75, to investigate wide ranges of interfacial area and domain size (see Fig. 5 and 6). It is expected that other morphology groups—different nseg and/or volumetric fraction—show a similar but milder temperature dependence. For example, morphologies with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 volume ratio have smaller donor domains, which probably enhances the exciton dissociation efficiency, but lower donor fraction yields fewer excitons and thus their effect on current density is likely canceled.
2 volume ratio have smaller donor domains, which probably enhances the exciton dissociation efficiency, but lower donor fraction yields fewer excitons and thus their effect on current density is likely canceled.
| Morphology | Interfacial area/nm−1 | |
|---|---|---|
| BHJ | Initial | 0.418 |
| βΔε = −4.0 | 0.357 | |
| −3.0 | 0.325 | |
| −2.0 | 0.267 | |
| −1.0 | 0.153 | |
| −0.5 | 0.077 | |
| 0.0 | 0.482 | |
| Stripe | 75 nm | 0.013 |
| 15 nm | 0.067 | |
| Checker | 75 nm × 75 nm | 0.027 |
| 15 nm × 75 nm | 0.080 | |
| 15 nm × 15 nm | 0.133 |
Efficiencies of exciton dissociation and charge collection, and the IQE under short-circuit conditions are shown in Fig. 8(e), (f), and (g), respectively. Their sample standard deviations were smaller than 0.02. In the morphologies with large interfacial areas, the exciton dissociation is enhanced, but the charge collection is discouraged by a longer transport path. Therefore, the IQE exhibits a maximum value because of the trade-off. These tendencies are consistent with previous studies.27,37,39,40,44
In addition, we theoretically demonstrated that the open-circuit voltage VOC and the logarithm of the IQE have a linear correlation (Fig. 8(h)), which has been reported by an experimental work.18 The extrapolated VOC to 100% IQE is a little less than 0.5 V, which equals the difference of electrode work functions. Therefore, we revealed that improving the IQE enhances not only JSC but also VOC.
The dependencies of performance parameters of BHJ morphologies on βΔε, corresponding to finite temperature, are shown in Fig. 9. The morphologies generated under higher βΔε tend to give higher JSC and FF with lower VOC. It is shown that βΔε had an optimal value for the PCE—the morphology with βΔε of −2 showed the highest PCE of 1.4%. Remarkably, we revealed that morphology only, without parameter change, determines open-circuit voltage. These effects of thermal annealing are consistent with some experimental results.56,57
 | ||
| Fig. 10 Simulated charge (a) generation and (b) recombination dynamics of initial structure and morphologies with various βΔε. | ||
The space–time dynamics of charge generation—diffusion length and lifetime of the dissociated excitons—is shown in Fig. 11; see Fig. S7 (ESI†) for the results of other BHJ morphologies. Note that the lifetime of excitons equals the simulation time. The simulation revealed prompt and delayed dynamics of the charge generation: the majority of the charges (40–95%, varying for morphologies) were from excitons that were generated on interfaces and promptly (within a few picoseconds) dissociated, corresponding to the sudden increase as shown in Fig. 10; the others were from excitons that migrated to interfaces and dissociated later (up to several hundred nanoseconds), corresponding to the slow increase. The tendency depends on the morphologies because in the case of morphologies of lower temperature, those have higher interfacial area and smaller domains, excitons are more likely generated on a site on an interface and otherwise could reach interfaces easily, resulting in prompt increase of carriers; morphologies of higher temperature show fewer prompt and more delayed exciton dissociation, therefore the number of charges takes the maximum value at a few 100 ps.
4 Concluding remarks
We revealed a relationship between the annealing temperature, which is one of the controllable parameters in the manufacturing process, and the performance of OPVs via morphologies of donor and acceptor domains in the active layers. To this end, we proposed a model that combines reptation and DMC. The reptation and DMC were performed to investigate the physical mechanism of formation of the morphologies and the electrochemical profile of photo- and dark currents, and transient absorption spectroscopy, respectively. Then, the reptation with a 1 nm-lattice showed temperature dependencies of morphology. The interfacial area exhibited a minimum value related to the annealing temperature because of the trade-off between thermal diffusion and attractive interaction. The DMC simulations, in which the generated BHJ morphologies were coarsened to a 3 nm-lattice, revealed morphology dependencies of the photo- and dark currents, and OPV performance: short-circuit current density JSC, open-circuit voltage VOC, and PCE exhibit maximum values related to the interfacial area because of the trade-off between exciton dissociation and charge collection. This work theoretically demonstrated the linear correlation between open-circuit voltage VOC and the logarithm of IQE, which agrees with experiment. Besides, we performed transient absorption spectroscopy of various BHJ morphologies, which revealed two different dynamics of charge generation—prompt (a few picoseconds) generation from excitons that were generated on interfaces and delayed (order of sub-nanoseconds) generation from excitons which migrated to interfaces; the former is dominant but its ratio depends on the domain size of morphologies.Coarsening of lattices in the DMC simulations implicitly assumes that electron–hole separation immediately reaches 3 nm, which likely leads to overestimation of the charge separation efficiency and thus shall be verified in future. It is, actually, numerically observed that charge recombination is suppressed in the case of the coarsened morphologies. A mechanism, for example the charge hopping rate increases locally on an interface due to factors like a hot process,58 is necessary to compensate it. The assumption and mechanism require further study, which is beyond the scope of this work.
Acknowledgements
This work was supported by JSPS KAKENHI Grant No. 24750012, CREST JST. We are grateful to Dr A. Ikeda for valuable discussions about polymer dynamics. We appreciate suggestive and stimulating discussions with Buyoung Jung's on DMC algorithm. Theoretical calculations in this study were performed using facilities at the Supercomputer Center in Institute for Solid State Physics (ISSP) of the University of Tokyo and at Research Center for Computational Science in the Institute for Molecular Science (IMS) in Okazaki, Japan.References
- R. Søndergaard, M. Hösel, D. Angmo, T. T. Larsen-Olsen and F. C. Krebs, Mater. Today, 2012, 15, 36–49 CrossRef.
- F. C. Krebs, J. Fyenbo, D. M. Tanenbaum, S. A. Gevorgyan, R. Andriessen, B. van Remoortere, Y. Galagan and M. Jorgensen, Energy Environ. Sci., 2011, 4, 4116–4123 CAS.
- N. Espinosa, R. Garcia-Valverde and F. C. Krebs, Energy Environ. Sci., 2011, 4, 1547–1557 CAS.
- M. A. Green, K. Emery, Y. Hishikawa, W. Warta and E. D. Dunlop, Prog. Photovoltaics, 2015, 23, 805–812 Search PubMed.
- F. Liu, Y. Gu, J. W. Jung, W. H. Jo and T. P. Russell, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 1018–1044 CrossRef CAS.
- J. A. Bjorgaard and M. E. Kose, RSC Adv., 2015, 5, 8432–8445 RSC.
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791 CAS.
- A. J. Pearson, T. Wang, R. A. L. Jones, D. G. Lidzey, P. A. Staniec, P. E. Hopkinson and A. M. Donald, Macromolecules, 2012, 45, 1499–1508 CrossRef CAS.
- S. S. van Bavel, M. Bärenklau, G. de With, H. Hoppe and J. Loos, Adv. Funct. Mater., 2010, 20, 1458–1463 CrossRef CAS.
- N. D. Treat, C. G. Shuttle, M. F. Toney, C. J. Hawker and M. L. Chabinyc, J. Mater. Chem., 2011, 21, 15224–15231 RSC.
- H.-C. Liao, C.-S. Tsao, Y.-C. Huang, M.-H. Jao, K.-Y. Tien, C.-M. Chuang, C.-Y. Chen, C.-J. Su, U.-S. Jeng, Y.-F. Chen and W.-F. Su, RSC Adv., 2014, 4, 6246–6253 RSC.
- A. H. Rice, R. Giridharagopal, S. X. Zheng, F. S. Ohuchi, D. S. Ginger and C. K. Luscombe, ACS Nano, 2011, 5, 3132–3140 CrossRef CAS PubMed.
- J. J. van Franeker, D. Westhoff, M. Turbiez, M. M. Wienk, V. Schmidt and R. A. J. Janssen, Adv. Funct. Mater., 2015, 25, 855–863 CrossRef CAS.
- D. Mori, H. Benten, H. Ohkita and S. Ito, Adv. Energy Mater., 2015, 5, 1500304 CrossRef.
- T. Shimazaki and T. Nakajima, Phys. Chem. Chem. Phys., 2015, 17, 12538–12544 RSC.
- M. Fujii and K. Yamashita, Chem. Phys. Lett., 2011, 514, 146–150 CrossRef CAS.
- K. Nishimra, M. Fujii, R. Jono and K. Yamashita, J. Phys. Chem. C, 2015, 119, 26258–26265 CAS.
- M. Fujii, W. Shin, T. Yasuda and K. Yamashita, Phys. Chem. Chem. Phys., 2016, 18, 9514–9523 RSC.
- S. Koda, M. Fujii, S. Hatamiya and K. Yamashita, Theor. Chem. Acc., 2016, 135, 1–10 CrossRef CAS.
- T. Liu and A. Troisi, J. Phys. Chem. C, 2011, 115, 2406–2415 CAS.
- F. Frigerio, M. Casalegno, C. Carbonera, T. Nicolini, S. V. Meille and G. Raos, J. Mater. Chem., 2012, 22, 5434–5443 RSC.
- S. Obata and Y. Shimoi, Phys. Chem. Chem. Phys., 2013, 15, 9265–9270 RSC.
- B. P. Lyons, N. Clarke and C. Groves, J. Phys. Chem. C, 2011, 115, 22572–22577 CAS.
- O. Wodo and B. Ganapathysubramanian, Comput. Mater. Sci., 2012, 55, 113–126 CrossRef CAS.
- A. Pershin, S. Donets and S. A. Baeurle, J. Chem. Phys., 2012, 136, 194102 CrossRef PubMed.
- J. Xue, T. Hou and Y. Li, Appl. Phys. Lett., 2012, 100, 053307 CrossRef.
- B. P. Lyons, N. Clarke and C. Groves, Energy Environ. Sci., 2012, 5, 7657–7663 CAS.
- M. L. Jones, R. Dyer, N. Clarke and C. Groves, Phys. Chem. Chem. Phys., 2014, 16, 20310–20320 RSC.
- P. G. de Gennes, J. Chem. Phys., 1971, 55, 572–579 CrossRef.
- M. Doi and S. F. Edwards, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1789–1801 RSC.
- J. M. Frost, F. Cheynis, S. M. Tuladhar and J. Nelson, Nano Lett., 2006, 6, 1674–1681 CrossRef CAS PubMed.
- K. X. Steirer, P. F. Ndione, N. E. Widjonarko, M. T. Lloyd, J. Meyer, E. L. Ratcliff, A. Kahn, N. R. Armstrong, C. J. Curtis, D. S. Ginley, J. J. Berry and D. C. Olson, Adv. Energy Mater., 2011, 1, 813–820 CrossRef CAS.
- K. Ishaque, Z. Salam, S. Mekhilef and A. Shamsudin, Appl. Energy, 2012, 99, 297–308 CrossRef.
- L. J. A. Koster, E. C. P. Smits, V. D. Mihailetchi and P. W. M. Blom, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085205 CrossRef.
- D. Scharfetter and H. Gummel, IEEE Trans. Electron Devices, 1969, 16, 64–77 CrossRef.
- H. Gummel, IEEE Trans. Electron Devices, 1964, 11, 455–465 CrossRef.
- P. K. Watkins, A. B. Walker and G. L. B. Verschoor, Nano Lett., 2005, 5, 1814–1818 CrossRef CAS PubMed.
- A. B. Walker, Proc. IEEE, 2009, 97, 1587–1596 CrossRef CAS.
- L. Meng, Y. Shang, Q. Li, Y. Li, X. Zhan, Z. Shuai, R. G. E. Kimber and A. B. Walker, J. Phys. Chem. B, 2010, 114, 36–41 CrossRef CAS PubMed.
- R. G. E. Kimber, A. B. Walker, G. E. Schroder-Turk and D. J. Cleaver, Phys. Chem. Chem. Phys., 2010, 12, 844–851 RSC.
- K. Feron, C. J. Fell, L. J. Rozanski, B. B. Gong, N. Nicolaidis, W. J. Belcher, X. Zhou, E. Sesa, B. V. King and P. C. Dastoor, Appl. Phys. Lett., 2012, 101, 193306 CrossRef.
- A. G. Gagorik, J. W. Mohin, T. Kowalewski and G. R. Hutchison, J. Phys. Chem. Lett., 2013, 4, 36–42 CrossRef CAS PubMed.
- C. Groves, Energy Environ. Sci., 2013, 6, 3202–3217 CAS.
- B. Jung, K. Kim, J. Kim, S. Kim, E. Kim and W. Kim, Sol. Energy Mater. Sol. Cells, 2014, 120(Part B), 675–684 CrossRef CAS.
- C. Groves, R. A. Marsh and N. C. Greenham, J. Chem. Phys., 2008, 129, 114903 CrossRef CAS PubMed.
- M. L. Jones, B. Chakrabarti and C. Groves, J. Phys. Chem. C, 2014, 118, 85–91 CAS.
- D. T. Gillespie, J. Comput. Phys., 1976, 22, 403–434 CrossRef CAS.
- J. Guo, H. Ohkita, H. Benten and S. Ito, J. Am. Chem. Soc., 2009, 131, 16869–16880 CrossRef CAS PubMed.
- W. C. Tsoi, S. J. Spencer, L. Yang, A. M. Ballantyne, P. G. Nicholson, A. Turnbull, A. G. Shard, C. E. Murphy, D. D. C. Bradley, J. Nelson and J.-S. Kim, Macromolecules, 2011, 44, 2944–2952 CrossRef CAS.
- H. Sirringhaus, P. J. Brown, R. H. Friend, M. M. Nielsen, K. Bechgaard, B. M. W. Langeveld-Voss, A. J. H. Spiering, R. A. J. Janssen, E. W. Meijer, P. Herwig and D. M. de Leeuw, Nature, 1999, 401, 685–688 CrossRef CAS.
- M. Chikamatsu, S. Nagamatsu, Y. Yoshida, K. Saito, K. Yase and K. Kikuchi, Appl. Phys. Lett., 2005, 87, 203504 CrossRef.
- T. Förster, Ann. Phys., 1948, 437, 55–75 CrossRef.
- A. Miller and E. Abrahams, Phys. Rev., 1960, 120, 745–755 CrossRef CAS.
- R. A. Marsh, C. Groves and N. C. Greenham, J. Appl. Phys., 2007, 101, 083509 CrossRef.
- M.-C. Shih, B.-C. Huang, C.-C. Lin, S.-S. Li, H.-A. Chen, Y.-P. Chiu and C.-W. Chen, Nano Lett., 2013, 13, 2387–2392 CrossRef CAS PubMed.
- G. Kalita, M. Masahiro, W. Koichi and M. Umeno, Solid-State Electron., 2010, 54, 447–451 CrossRef CAS.
- W. C. Tsoi, D. T. James, J. S. Kim, P. G. Nicholson, C. E. Murphy, D. D. C. Bradley, J. Nelson and J.-S. Kim, J. Am. Chem. Soc., 2011, 133, 9834–9843 CrossRef CAS PubMed.
- S. M. Falke, C. A. Rozzi, D. Brida, M. Maiuri, M. Amato, E. Sommer, A. De Sio, A. Rubio, G. Cerullo, E. Molinari and C. Lienau, Science, 2014, 344, 1001–1005 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04019e |
| This journal is © the Owner Societies 2016 |









