Electrostatically enhanced F⋯F interactions through hydrogen bonding, halogen bonding and metal coordination: an ab initio study

Abstract

In this manuscript the ability of hydrogen and halogen bonding interactions, as well as metal coordination to enhance F⋯F interactions involving fluorine substituted aromatic rings has been studied at the RI-MP2/def2-TZVPD level of theory. We have used 4-fluoropyridine, 4-fluorobenzonitrile, 3-(4-fluorophenyl)propiolonitrile and their respective meta derivatives as aromatic compounds. In addition, we have used HF and IF as hydrogen and halogen bond donors, respectively, and Ag(I) as the coordination metal. Furthermore, we have also used HF as an electron rich fluorine donor entity, thus establishing F⋯F interactions with the above mentioned aromatic systems. Moreover, a CSD (Cambridge Structural Database) search has been carried out and some interesting examples have been found, highlighting the impact of F⋯F interactions involving aromatic fluorine atoms in solid state chemistry. Finally, cooperativity effects between F⋯F interactions and both hydrogen and halogen bonding interactions have been analyzed and compared. We have also used Bader's theory of “atoms in molecules” to further describe the cooperative effects.

---

Introduction

Supramolecular chemists rely on in depth comprehension of noncovalent forces, which are pillars of modern chemistry. A proper understanding and intelligent utilization of them is essential to achieve progress in fields such as supramolecular chemistry,¹ molecular recognition² and materials science.³ One of the best known supramolecular forces that is ubiquitous in many chemical and biological environments is hydrogen bonding.⁴ A similar noncovalent force that shares strength and directionality features with hydrogen bonding is the halogen bonding interaction.⁵ A halogen bond (R–X⋯Y–Z, X = halogen, Z = electron rich atom, Z = any atom) occurs when “there is evidence of a net attractive interaction between an electrophilic region associated with a halogen atom in a molecular entity and a nucleophilic region in another, or the same, molecular entity”.⁶ Related to this, the ability of halogen atoms to interact with Lewis bases has been known for some time.⁷ For instance, the ability of iodo- and bromoperfluorocarbons to form noncovalent interactions with neutral and charged electron donors was reported by Resnati and co-workers, who remarked on the ability of haloperfluoroalkanes to participate as halogen-bond donor moieties in crystal engineering, unveiling the promising potential of halogen bonding interactions in supramolecular chemistry.^8–16 Consequently, a series of studies using the Cambridge Structural Database (CSD) have been carried out in order to shed light on the impact of this interaction in crystal structures.¹⁷ The interest among the scientific community has expanded exponentially due to the recognition of its importance in biological systems and the design of new materials; leading to a plethora of theoretical and experimental studies devoted to this topic.^18–20

Related to this, fluorine–fluorine interactions have been considered as contentious noncovalent forces in the past, conversely to the heavier halogens, which are well-known to establish X⋯X interactions, showing a dual behaviour (both electron and donor acceptors).²¹

Owing to its low polarizability,²² which provokes the attractive dispersion contribution to be rather low, F⋯F interactions were skeptically considered as a stabilization source in solid state chemistry. However, there are a significant number of studies in the literature of C–F⋯F–C interactions that have been characterized both experimentally and theoretically as important contributors in energetic stabilization.^23–27 Related to this, the exhaustive research on F⋯F interactions carried out by the group of Varadwaj and coworkers is also remarkable.²⁸ They studied the possibility of establishing attractive intermolecular interactions between aromatic fluorine atoms in perfluorobenzene and several electron donor moieties. The energetic stability of the complexes studied was slightly favourable, and the authors concluded that, analogous to C–H⋯H–C interactions,²⁹ in addition to the dispersion contribution the main stabilization force is attributed to the polarization term that is proportional to the atomic polarizabilities. Conversely, the electrostatic component is usually not attractive in regular F⋯F interactions due to the absence of a σ-hole in the fluorine atom. Herein, we study the possibility to electrostatically strengthen F⋯F interaction by using cooperative noncovalent forces.

In this study, our purpose is to investigate the ability of hydrogen and halogen bonding interactions, as well as metal coordination, to enhance F⋯F interactions involving aromatic fluorine atoms. In order to achieve that goal, we have used a series of fluoropyridine derivatives, attaching the fluorine atom in meta and para positions of the ring (Fig. 1). In addition, we have progressively increased the distance between the nitrogen and fluorine atoms in order to account for long range enhancing effects. We have used HF and IF as hydrogen and halogen bond donors, respectively, and Ag(I) as a transition metal coordinating atom (see Fig. 2 and 3). Furthermore, we have also used HF as an electron donor entity, thus establishing F⋯F interactions with the above mentioned aromatic moieties. Finally, cooperativity effects between the F⋯F interactions and either hydrogen or halogen bonding interactions have been analysed and compared. Moreover, a CSD (Cambridge Structural Database) search has been carried out and some interesting examples have been found, highlighting the impact of F⋯F interactions involving aromatic fluorine atoms in solid state chemistry. Finally, we have also used Bader's theory of “atoms in molecules” to further describe and rationalize the cooperative effects observed in the assemblies.

Fig. 1 Compounds 1–6 used in this study.

Fig. 2 Binary (7–24) and ternary complexes (25–36) used in this study.

Fig. 3 Ag compounds (37–42) and their F⋯F complexes (43–48) with HF.

Theoretical methods

The energies of all complexes included in this study were computed at the RI-MP2/def2-TZVPD level of theory by means of the program TURBOMOLE version 7.0.³⁰ The optimization of the molecular geometries has been performed imposing the C_s and C_2v symmetry point groups unless otherwise noted. The interaction energies were calculated with correction for the basis set superposition error (BSSE) by using the Boys–Bernardi counterpoise technique.³¹ The MEP (Molecular Electrostatic Potential) calculations have been performed at the MP2/def2-TZVP level by means of the Gaussian09 calculation package.³² Frequency calculations have been performed at the RI-MP2/def2TZVPD level of theory. The Bader's “Atoms in molecules” theory has been used to study the interactions discussed herein by means of the AIMall calculation package.³³ The calculations for wavefunction analyses were carried out at the MP2/def2-TZVP level of theory. In the ternary complexes where F⋯F and other interactions coexist, we have studied cooperativity effects by computing the cooperativity energy E_coop using eqn (1).

E_coop = ΔE_BSSE(ABC) − ΔE_BSSE(AB) − ΔE_BSSE(AC) − ΔE_BSSE(BC) (1)

where the ΔE_BSSE(AB) and ΔE_BSSE(AC) terms correspond to the interaction energies (BSSE-corrected) of the optimized F⋯F (AB) and σB (AC) (σB notation is used to define the hydrogen/halogen bonding interaction involving the nitrogen atom of the pyridine/CN moiety) dimeric complexes, respectively. The ΔE_BSSE(ABC) is the interaction energy of the optimized ternary complex (formed by the combination of F⋯F and σB interactions). The ΔE_BSSE(BC) term is the interaction of the HF molecule with the XF (X = H, I) molecule that interacts with the nitrogen atom in the geometry that they have in the F⋯F–σB ternary complexes (in the absence of the aromatic portion). For instance in ternary complex 25 (see Fig. 2) the E_coop = ΔE_BSSE(25) − ΔE_BSSE(7) − ΔE_BSSE(13) − ΔE_BSSE(BC). The latter term corresponds to the interaction between both HF molecules as they stand in complex 25. This expression has been successfully used in the study of cooperativity effects in a variety of systems in which two different interactions coexist, including π systems as simultaneous hydride and hydrogen-bond acceptors and the simultaneous interaction of an anion with a variety of noncovalent and covalent interactions.^34,35

Finally, we have explored the Cambridge Structural Database³⁶ in order to find evidence of F⋯F interactions in systems involving aromatic rings. For the CSD search we have restricted the C–F⋯F angle to the range between 170 and 180 degrees. Moreover, only those structures with “no ions”, “no errors”, “no powder” and “no disorder” were considered.

Results and discussion

MEPS study

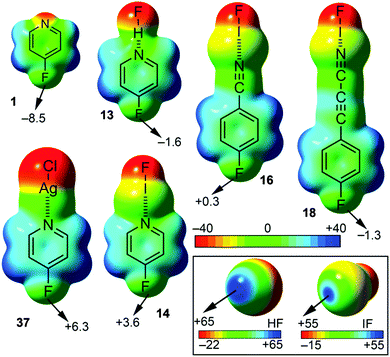
As a preliminary study, we have computed the molecular electrostatic potential (MEP) of compounds 1 to 6, 13 to 24 and 37 to 42 (see Table 1) to investigate the existence of a σ-hole in the F atom. Moreover, the MEP surface plots of some representative examples are shown in Fig. 4 and the MEP values are gathered in Table 1. From the inspection of the results several points arise. First, for compounds 1 to 6 a negative potential value ranging from −10 to −5 kcal mol⁻¹ is found on the fluorine atom along the extension of the C–F bond, thus expecting non attractive interactions with electron rich entities. Second, for complexes 13 to 24 a different behaviour is observed depending on which interaction establishes the nitrogen atom of the aromatic moiety. For hydrogen bonding complexes (13, 15, 17, 19, 21 and 23) a negative potential value is also obtained for the fluorine atom along the C–F bond, ranging from −4 to −2 kcal mol⁻¹. However, the MEP values are less negative than those obtained for compounds 1 to 6, thus expecting more attractive (or less repulsive) interaction with electron rich molecules. On the other hand, for halogen bonding complexes (14, 16, 18, 20, 22 and 24) two different tendencies are observed. First, in the para substituted complexes (14, 16 and 18) positive MEP values at the outermost part of the fluorine atom are obtained (compounds 14 and 16), ranging from 0 to +4 kcal mol⁻¹. Thus, for these compounds a σ-hole on the F atom is generated and attractive interaction with electron donor moieties is expected. For complex 18 the σ-hole on the fluorine atom was not formed due to the presence of the CC triple bond that attenuates the effect of the halogen bond. Second, in the meta substituted complexes (20, 22 and 24) only 20 showed a positive MEP value over the fluorine atom. Finally, for Ag(I) compounds (37 to 42) a positive potential region located at the outermost region of the fluorine atom appeared, thus being electrostatically favoured the interaction with an electron rich entity. It is also worth noting that both IF and HF present a positive potential region located at the outermost region of the iodine and hydrogen atoms, respectively, thus highlighting their strong electron acceptor characteristics. Therefore the H-bonding and halogen bonding complexes are expected to be very favourable.

Table 1 MEP (molecular electrostatic potential) values for compounds 1 to 6, 13 to 24 and 37 to 42 at the MP2/def2TZVP level of theory, energy values are in kcal mol⁻¹

Compound	V s max	V s fluorine^a
a Value measured at the extension of the C–F bond.
1	+23	−8.52
2	+28	−5.77
3	+28	−5.65
4	+25	−9.41
5	+28	−6.27
6	+27	−6.26
13	+31	−1.57
14	+38	+3.57
15	+33	−1.63
16	+38	+0.32
17	+30	−2.63
18	+38	−1.25
19	+31	−3.01
20	+38	+1.88
21	+31	−2.70
22	+33	−0.50
23	+32	−3.32
24	+32	−1.87
37	+41	+6.27
38	+38	+3.76
39	+36	+1.45
40	+41	+4.51
41	+38	+2.95
42	+35	+0.75

---

Fig. 4 MEP (molecular electrostatic potential) surfaces of some representative compounds.

Finally, for all three interactions (hydrogen bonding, halogen bonding and metal coordination), the MEP values become more negative on going from pyridine complexes (13, 14, 19, 20, 37 and 40) to their respective propiolonitrile analogues (17, 18, 23, 24, 39 and 42), due to the higher basicity of the former. In addition, the values obtained for the para substituted systems are more positive than the ones obtained for the meta substituted complexes, stressing the importance of resonance effects. Finally, a general trend with respect to the ability to generate a σ-hole on the fluorine atom can be establish, that is, hydrogen bonding < halogen bonding < Ag(I) coordination.

It is worth mentioning the relevance of these findings, since the formation of an N⋯I halogen bond in p-fluorocyanobenzene is able to provoke the formation of a σ-hole in the fluorine atom, thus inverting its electrostatic potential.

Energetic study

Binary complexes. The interaction energies and equilibrium distances obtained for complexes 7 to 24 (see Fig. 2) studied herein are summarized in Table 2. From the inspection of the results, several interesting conclusions can be extracted. First, for complexes 7 to 12 the binding energy values obtained are almost negligible due to the establishment of F⋯F interactions involving two negative fluorine atoms, thus the interaction is basically dominated by dispersion and polarization terms that compensate the electrostatic repulsion. Second, the binding energies involving para substituted compounds (complexes 7 to 9) are less repulsive than those obtained for the meta substituted compounds (complexes 10 to 12). The results obtained are in agreement with the MEP analysis shown above, where negative electrostatic potential values were obtained over the fluorine atom for compounds 1 to 6 (see Table 1). These results are similar to the ones obtained by Varadwaj and coworkers, remarking the subtle nature of the F⋯F interactions. Finally, for complexes 13 to 24 large and negative interaction energy values were obtained, ranging between −20 and −7 kcal mol⁻¹, thus indicating strong binding upon complexation. Furthermore, halogen bonding complexes exhibited larger binding energy values than their corresponding hydrogen bonding analogues, due to its stronger electron acceptor characteristics.

Table 2 Interaction energies with the BSSE correction (E_BSSE, kcal mol⁻¹), equilibrium distances (R, Å), charge density at the bond CP (10² × ρ, a.u.) and number of imaginary frequencies (N_imag) at the RI-MP2/def2-TZVPD level of theory for complexes 7–24

Complex	ΔEBSSE	R	10^2·ρ	N imag
7 (1 + FH)	0.19	3.028	0.27	0
8 (2 + FH)	0.08	2.996	0.29	0
9 (3 + FH)	0.08	3.001	0.29	0
10 (4 + FH)	0.21	3.127	0.21	0
11 (5 + FH)	0.09	2.984	0.30	0
12 (6 + FH)	0.09	2.995	0.30	0
13 (1 + HF)	−11.80	1.659	5.50	0
14 (1 + IF)	−19.57	2.364	6.04	0
15 (2 + HF)	−8.33	1.805	3.31	0
16 (2 + IF)	−11.42	2.482	4.07	0
17 (3 + HF)	−7.73	1.825	3.12	0
18 (3 + IF)	−10.85	2.482	4.04	0
19 (4 + HF)	−11.46	1.667	5.39	0
20 (4 + IF)	−19.15	2.366	6.01	0
21 (5 + HF)	−8.15	1.810	3.26	0
22 (5 + IF)	−11.18	2.487	4.02	0
23 (6 + HF)	−7.62	1.828	3.09	0
24 (6 + IF)	−10.70	2.485	4.01	0

---

As it can be observed in Table 2, there is a progressive weakening in the interaction energy values obtained when the distance between the nitrogen and the fluorine atoms is enlarged (see for instance complexes 14, 16 and 18), in agreement with the MEP analysis discussed above. Finally, the para and meta substituted compounds exhibit similar binding energy values, thus indicating that the resonance effect is not crucial for the global stabilization of the complexes studied herein.

Ternary complexes. The geometric and energetic features computed for ternary complexes 25 to 36 (see Fig. 2) are summarized in Table 3. Interestingly, the equilibrium distances R_e of the F⋯F interactions in F⋯F–σB complexes are shorter than in binary complexes 7 to 12. This result indicates that the presence of the N⋯X interactions (either hydrogen or halogen bonding) strengthens the F⋯F interactions. In addition, the equilibrium distances of the σ-bonding interaction R_σB are also shorter in ternary F⋯F–σB complexes compared to binary complexes 13 to 24, thus, the presence of the F⋯F interactions also strengthens the σ-bonding interaction. As expected, this mutual reinforcement varies depending on the kind of σ-interaction considered. In general, the shortening of the F⋯F interactions (0.008 ≤ ΔR_e ≤ 0.211 Å) is more significant than the shortening of the σ-interactions (0.002 ≤ ΔR_σB ≤ 0.006 Å), which likely indicates that the F⋯F interactions are more reinforced than the σ-interaction. This issue will be further discussed in the AIM analysis (see below). Moreover, with respect to the R_σB values, the greater shortening corresponds to the halogen bonding interaction (N⋯I). Table 3 also lists the computed values of cooperativity energies E_coop (see eqn (1)), which are intended to provide an estimation of the “extra” energetic stabilization or destabilization obtained in the ternary complexes as a consequence of the coexistence of both interactions. From the E_coop values listed in Table 3, several interesting points arise. First, the values of E_coop are negative in all complexes, thus indicating a positive synergy between the interactions (mutual reinforcement), in agreement with the shortening of the equilibrium distances (see ΔR values of Table 3). Second, in absolute terms, the E_coop values are more significant in halogen bonded complexes (26, 28, 30, 32, 34 and 36), contributing 4–10% of the total interaction energy. This result points out that the interaction of the IF molecule with the lone pair of the nitrogen atom by means of the σ-hole of the iodine atom enhances the F⋯F interactions established with the FH moiety to a major extent. It is also remarkable that the E_coop values are more negative in para substituted complexes than in their meta substituted analogues, thus the mutual reinforcement of both F⋯F interactions and either hydrogen or halogen bonding is higher in the former. We have also analyzed whether there is a correlation between the cooperativiy values (E_coop) and the total interaction energy ΔE_BSSE in complexes 25 to 36; and we have found a strong correlation (r = 0.951), indicating that the cooperativiy energy is related to the total interaction energy of the ternary complexes.

Table 3 Interaction energies and cooperativity energies with the BSSE correction (ΔE_BSSE and E_coop, respectively, in kcal mol⁻¹), equilibrium distances (R_e and R_σB, Å) and their variation (ΔR_e and ΔR_σB, in Å) at the RI-MP2/def2TZVPD level of theory for ternary complexes 25 to 36

Cmpd	ΔEBSSE	E coop	R e	R σB	ΔRe	ΔRσB
R e is the F⋯F equilibrium distance and RσB is the distance of N⋯X interactions.
25	−11.91	−1.10	2.957	1.654	0.071	0.005
26	−19.91	−1.66	2.913	2.359	0.115	0.005
27	−8.43	−0.29	2.962	1.800	0.034	0.005
28	−11.59	−0.57	2.947	2.476	0.049	0.006
29	−7.77	−0.24	2.978	1.822	0.023	0.003
30	−10.95	−0.50	2.970	2.479	0.031	0.003
31	−11.53	−1.00	2.972	1.661	0.155	0.006
32	−19.47	−1.59	2.916	2.360	0.211	0.006
33	−8.25	−0.29	2.957	1.806	0.027	0.004
34	−11.35	−0.56	2.941	2.481	0.043	0.006
35	−7.66	−0.24	2.987	1.826	0.008	0.002
36	−10.78	−0.48	2.960	2.481	0.035	0.004

---

As suggested by one referee, we have further analysed the reinforcement of the F⋯F interactions in the ternary complexes by comparing the binding energies of the bimolecular complexes to those of the termolecular complexes (denoted as ΔΔE in Table 4), computing the energy of the termolecular considering that the H/X-bonded complex has been previously formed (denoted as ΔE_(AB⋯C) in Table 4). This methodology has been successfully used in the analysis of cooperativity effects in F⋯O and I⋯N halogen bonding complexes.³⁷ The F⋯F interactions (ΔE_(A⋯B) values) in the bimolecular complexes are in all cases positive ranging from 0.08 kcal mol⁻¹ to 0.21 kcal mol⁻¹. In contrast the F⋯F interactions (ΔE_(AB⋯C) values) in the termolecular complexes are in all cases negative ranging from −0.36 kcal mol⁻¹ to −0.05 kcal mol⁻¹. Therefore the F⋯F interactions enhance in the termolecular complexes changing from unfavourable (ΔE_(A⋯B) values) in the bimolecular complexes to favourable in the termolecular ones (ΔE_(AB⋯C) values). For example, the F⋯F halogen–halogen interaction energy is 0.19 kcal mol⁻¹ in the bimolecular complex 7 (1⋯FH) and becomes −0.36 kcal mol⁻¹ in the termolecular complex 27 (IF⋯1⋯FH) with an increase of 0.55 kcal mol⁻¹ (ΔΔE = −0.55 kcal mol⁻¹). In general, the F⋯F interaction energy is more enhanced in those termolecular complexes where the aromatic moiety participates in F–I⋯N halogen bonding interactions than in those involving H-bonding F–H⋯N interactions, in agreement with the cooperativity energies listed in Table 3.

Table 4 F⋯F halogen-bonded interaction energies (in kcal mol⁻¹) in the bimolecular and termolecular complexes, along with its enhancement ΔΔE

Complex	ΔE(A⋯B)	ΔE(AB⋯C)	ΔΔE
ΔΔE = ΔE(AB⋯C) – ΔE(A⋯B); ΔE(AB⋯C) = EABC − EAB − EC; ΔE(A⋯B) = EAB − EA − EB.
25 (HF⋯1⋯FH)	0.19 (1⋯FH)	−0.11 (13⋯FH)	−0.30
26 (IF⋯1⋯FH)	0.19 (1⋯FH)	−0.36 (14⋯FH)	−0.55
27 (HF⋯2⋯FH)	0.08 (2⋯FH)	−0.10 (15⋯FH)	−0.18
28 (IF⋯2⋯FH)	0.08 (2⋯FH)	−0.18 (16⋯FH)	−0.26
29 (HF⋯3⋯FH)	0.08 (3⋯FH)	−0.05 (17⋯FH)	−0.13
30 (IF⋯3⋯FH)	0.08 (3⋯FH)	−0.11 (18⋯FH)	−0.19
31 (HF⋯4⋯FH)	0.21 (4⋯FH)	−0.08 (19⋯FH)	−0.29
32 (IF⋯4⋯FH)	0.21 (4⋯FH)	−0.34 (20⋯FH)	−0.55
33 (HF⋯5⋯FH)	0.09 (5⋯FH)	−0.10 (21⋯FH)	−0.19
34 (IF⋯5⋯FH)	0.09 (5⋯FH)	−0.19 (22⋯FH)	−0.28
35 (HF⋯6⋯FH)	0.09 (6⋯FH)	−0.05 (23⋯FH)	−0.14
36 (IF⋯6⋯FH)	0.09 (6⋯FH)	−0.15 (24⋯FH)	−0.24

---

AIM analysis

We have performed AIM analysis of all compounds studied in this work. It is well established that the charge density ρ at the critical points (CPs) that emerge upon complexation gives helpful information regarding the strength of the noncovalent interactions involved in the complexes. Indeed, they have been successfully used as a measure of the bond order in a variety of noncovalent interactions including anion–π, hydrogen bonding and halogen-bonding interactions. Therefore, the variation in the ρ value at CPs in ternary systems with respect to the isolated F⋯F and σB complexes can be used to analyse the mutual influence of both interactions. In Fig. 5, the F⋯F–σB complex 32 presents a ρ value of 6.12 × 10⁻² a.u. at the bond CP that characterizes the halogen bonding interaction, which is greater than the value computed at the bond CP of complex 14 (6.04 × 10⁻² a.u.). This result confirms that the halogen bond in 32 is reinforced with respect to complex 14. The same behaviour is observed for the values of ρ at the bond CP that characterizes the F⋯F interactions. Variation of the value from 0.27 × 10⁻² a.u. for complex 7 to 0.36 × 10⁻² a.u. for complex 32 also indicates a reinforcement of the F⋯F interactions. For the rest of the complexes of the study, similar conclusions can be extracted (see Table 5). In all F⋯F–σB complexes, the Δρ values are positive, thus indicating a reinforcement of both interactions, in agreement with the energetic and geometric results (vide supra). The variation of the ρ values at the bond CPs [Δρ_BCP(F⋯F) and Δρ_BCP(σB) values] can be used as a degree of strengthening of the interaction. For instance, the variation of the ρ value at the bond CP that characterized the F⋯F interactions in complex 32 is greater than in complex 31, as expected, considering the strong electron acceptor characteristics of the IF molecule.

Fig. 5 Distribution of critical points in some F⋯F, σB and F⋯F–σB complexes (bond CPs in red, ring CPs in yellow). The values of 10²·ρ for bond CPs are shown in red. The bond paths connecting the bond CPs are also represented.

Table 5 Values of the charge density (10²·ρ, a.u.) at bond CPs (ρ_BCP) and its variation (Δρ) and number of imaginary frequencies (N_imag) at the MP2/def2-TZVP level of theory for complexes 25 to 36

Complex	ρ BCP(F⋯F)	ρ BCP(σB)	ΔρBCP(F⋯F)	ΔρBCP(σB)	N imag
25	0.32	5.58	0.05	0.08	0
26	0.36	6.12	0.09	0.08	1
27	0.32	3.34	0.03	0.03	0
28	0.33	4.12	0.04	0.05	2
29	0.31	3.14	0.02	0.02	0
30	0.31	4.07	0.02	0.03	2
31	0.31	5.47	0.10	0.08	0
32	0.37	6.09	0.16	0.08	0
33	0.33	3.30	0.03	0.04	0
34	0.34	4.08	0.04	0.06	1
35	0.30	3.11	0.00	0.02	0
36	0.32	4.05	0.02	0.04	1

---

Effect of the metal coordination

It is well known that aromatic heterocyclic compounds are widely used as ligands in coordination chemistry.³⁸ Therefore, we have analysed the influence of the N–metal coordination on the binding energy values involving the compounds used in this study (see Fig. 3). We have used AgCl as the metal coordination moiety. The energetic results are gathered in Table 6. As it can be observed, the binding energy values are favourable, ranging between −0.5 and −0.1 kcal mol⁻¹. When compared to the related uncoordinated complexes (7 to 12, see ΔΔE values in Table 5) it can be observed a clear reinforcement of the F⋯F interaction, which ranges from 0.3 to 1.1 kcal mol⁻¹.

Table 6 Interaction energies with the BSSE correction (ΔE_BSSE, in kcal mol⁻¹), equilibrium distances (R in Å), charge density at the bond CP^a (ρ, a.u.) at the RI-MP2/def2TZVPD level of theory for binary complexes 43 to 48

Complex	ΔEBSSE	ΔΔE^b	R	10^2·ρ
a The charge density values at the bond CP gathered (10^2·ρ) have been calculated at the MP2/def2-TZVP level of theory. b ΔΔE, see footnote of Table 4.
43	−0.48	−0.67	2.890	0.38
44	−0.33	−0.41	2.924	0.35
45	−0.22	−0.30	2.952	0.33
46	−0.46	−0.67	2.890	0.38
47	−0.27	−0.36	2.802	0.21
48	−0.13	−0.22	2.802	0.21

---

These results are in agreement with the MEP analysis shown above, which anticipated a stronger binding for the Ag(I)–complexes. In addition, the F⋯F distances obtained are shorter than the ones obtained for the uncoordinated complexes, in agreement with the energetic and geometric results. Moreover, the values of the density at the bond CP are larger than the ones obtained for their uncoordinated analogues. Finally, it is worth mentioning that the interaction energies of all F⋯F complexes are energetically favourable, including complex 48 (HF⋯FC₆H₅–CC–CN⋯AgCl) where the Ag metal center is located distant from the F atom. Thus this is an interesting long range synergetic effect of the metal coordination on the F⋯F interactions.

CSD examples

We have examined the Cambridge Structural Database (CSD) in order to find experimental evidence that supports the calculations discussed above. We have found 497 hits exhibiting F⋯F contacts at distances that are less than the sum of their van der Waals radii. Three selected examples are shown in Fig. 6 including the CSD codes. First, in IPUSOC³⁹ F⋯F interactions are established between an aromatic fluorine atom of the organic ligand and a pentafluorobenzonitrile molecule. Although the crystal packing is governed by an intricate combination of noncovalent interactions, F⋯F contacts are numerous, thus highlighting their importance in the solid state architecture. Second, in JUBKIA⁴⁰ F⋯F interactions are established between two aromatic moieties (see Fig. 6) influencing the crystal packing. Finally, in DOMJOG⁴¹ the F⋯F interactions established between a CF₃ group and an aromatic fluorine atom create a linear disposition where the discrete units of the crystal interact with each other. These examples highlight the importance of F⋯F in solid state chemistry, especially, in the chemistry of benzene derivatives.

Fig. 6 Partial view of some X-ray structures retrieved from the CSD. The CSD codes are indicated.

Conclusions

The results reported in this manuscript stress the importance of the mutual effects between noncovalent forces involving F⋯F interactions and hydrogen bonding, halogen bonding and metal coordination, which can lead to an electrostatic enhancement of F⋯F interactions and chiefly, to remarkable cooperativity effects. These effects are even more noticeable in systems where the nitrogen atom is forming part of the π-system of the ring. We have estimated the cooperativity effects energetically (E_coop values), obtaining results that are in agreement with the geometric features of the complexes and the AIM analysis. Finally, in order to find experimental evidence that supports the calculations discussed above we have performed a search in the CSD (Cambridge Structural Database), and we have found 497 hits that exhibit F⋯F contacts, highlighting the impact of this interaction in solid state chemistry, particularly in fluorobenzene derivatives.

Acknowledgements

We thank the MINECO of Spain (projects CTQ2014-57393-C2-1-P and CONSOLIDER INGENIO 2010 CSD2010-00065, FEDER funds). We thank the CTI (UIB) for computational facilities.

References

1. H. J. Schneider, Angew. Chem., Int. Ed., 2009, 48, 3924.
2. C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525.
3. W. J. Vickaryous, R. Herges and D. W. Jonhson, Angew. Chem., Int. Ed., 2004, 43, 5831.
4. S. J. Grabowski, Chem. Rev., 2011, 111, 2597.
5. P. Metrangolo and G. Resnati, Chem. – Eur. J., 2001, 7, 2511.
6. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711.
7. P. Metrangolo and G. Resnati, Cryst. Growth Des., 2012, 12, 5835.
8. P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386.
9. P. Metrangolo, G. Resnati, T. Pilati and S. Biella, Halogen Bonding: Fundamentals and Applications, Springer, Berlin, 2008.
10. P. Metrangolo and G. Resnati, Chem. – Eur. J., 2001, 7, 2511.
11. P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114.
12. R. Bertani, P. Metrangolo, A. Moiana, E. Perez, T. Pilati, G. Resnati, I. Rico-Lattes and A. Sassi, Adv. Mater., 2002, 14, 1197.
13. H. L. Nguyen, P. N. Horton, M. B. Hursthouse, A. C. Legon and D. W. Bruce, J. Am. Chem. Soc., 2003, 126, 16.
14. C. Praesang, H. L. Nguyen, P. N. Horton, A. C. Whitwood and D. W. Bruce, Chem. Commun., 2008, 6164.
15. C. Präsang, A. C. Whitwood and D. W. Bruce, Cryst. Growth Des., 2009, 9, 5319.
16. L. C. Roper, C. Prasang, V. N. Kozhevnikov, A. C. Whitwood, P. B. Karadakov and D. W. Bruce, Cryst. Growth Des., 2010, 10, 3710.
17. P. Murrayrust and W. D. S. Motherwell, J. Am. Chem. Soc., 1979, 101, 4374.
18. P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386.
19. P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278.
20. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178.
21. M. Capdevila-Cortada and J. J. Novoa, CrystEngComm, 2015, 17, 3354.
22. K. Reichenbächer, H. I. Süss and J. Hulliger, Chem. Soc. Rev., 2005, 34, 22.
23. I. Alkorta and J. Elguero, Struct. Chem., 2004, 15, 117.
24. R. J. Baker, P. E. Colavita, D. M. Murphy, J. A. Platts and J. D. Wallis, J. Phys. Chem. A, 2012, 116, 1435.
25. S. R. Halper and S. M. Cohen, Inorg. Chem., 2005, 44, 4139.
26. M. Barceló-Oliver, C. Estarellas, A. García-Raso, A. Terrón, A. Frontera, D. Quinonero, I. Mata, E. Molins and P. M. Deyà, CrystEngComm, 2010, 12, 3758.
27. V. A. Karnoukhova, I. V. Fedyanin and K. A. Lyssenko, Struct. Chem., 2016, 27, 17; O. Brea, O. Mó, M. Yañez, I. Alkorta and J. Elguero, Chem. – Eur. J., 2015, 21, 1.
28. A. Varadwai, P. R. Varadwaj and B.-Y. Jin, RSC Adv., 2016, 6, 19098.
29. J. Echeverría, G. Alullón, D. Danovich, S. Shaik and S. Alvarez, Nat. Chem., 2011, 3, 323.
30. R. Ahlrichs, M. Bär, M. Hacer, H. Horn and C. Kömel, Chem. Phys. Lett., 1989, 162, 165.
31. S. B. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2009.
33. T. A. Keith, AIMAll (Version 13.05.06), TK Gristmill Software, Overland Park KS, USA, 2013.
34. I. Alkorta, F. Blanco, P. M. Deyà, J. Elguero, C. Estarellas, A. Frontera and D. Quiñonero, Theor. Chem. Acc., 2010, 126, 1.
35. A. Bauzá, D. Quiñonero, P. M. Deyà and A. Frontera, Theor. Chem. Acc., 2012, 131, 1219.
36. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., 2016, B72, 171.
37. (a) W. Li, Y. Zeng, X. Zhang, S. Zheng and L. Meng, Phys. Chem. Chem. Phys., 2014, 16, 19282–19289; (b) N. Han, Y. Zeng, C. Sun, X. Li, Z. Sun and L. Meng, J. Phys. Chem. A, 2014, 118, 7058–7065.
38. A. Frontera, Coord. Chem. Rev., 2013, 257, 1716.
39. R. R. Fernandes, J. Lasri, M. F. C. G. da Silva, A. M. F. Palavra, J. A. L. da Silva, J. J. R. F. da Silva and A. J. L. Pombeiro, Adv. Syn. Cat., 2011, 353, 1153.
40. D. Britton, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1992, 48, 2040.
41. J. R. Wolstenhulme, A. Cavell, M. Gredičak, R. W. Driver and M. D. Smith, Chem. Commun., 2014, 50, 13585.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of the optimized complexes. See DOI: 10.1039/c6cp03862j

---