Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
True ferroelectric switching in thin films of trialkylbenzene-1,3,5-tricarboxamide (BTA)†
A. V.
Gorbunov
a,
T.
Putzeys
b,
I.
Urbanavičiūtė
c,
R. A. J.
Janssen
a,
M.
Wübbenhorst
b,
R. P.
Sijbesma
 d and
M.
Kemerink
*ac
d and
M.
Kemerink
*ac
aDepartment of Applied Physics, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands
bDepartment of Physics and Astronomy, Laboratory for Soft Matter and Biophysics, KU Leuven, Celestijnenlaan 200D, B-3001 Heverlee, Belgium
cComplex Materials and Devices, Department of Physics, Chemistry and Biology (IFM), Linköping University, 58183 Linköping, Sweden. E-mail: martijn.kemerink@liu.se
dLaboratory of Macromolecular and Organic Chemistry, Eindhoven University of Technology, P. O. Box 513, 5600 MB Eindhoven, The Netherlands
First published on 3rd August 2016
Abstract
We have investigated the ferroelectric polarization switching properties of trialkylbenzene-1,3,5-tricarboxamide (BTA), which is a model system for a large class of novel organic ferroelectric materials. In the solid state BTAs form a liquid crystalline columnar hexagonal phase that provides long range order that was previously shown to give rise to hysteretic dipolar switching. In this work the nature of the polar switching process is investigated by a combination of dielectric relaxation spectroscopy, depth-resolved pyroelectric response measurements, and classical frequency- and time-dependent electrical switching. We show that BTAs, when brought in a homeotropically aligned hexagonal liquid crystalline phase, are truly ferroelectric. Analysis of the transient switching behavior suggests that the ferroelectric switching is limited by a highly dispersive nucleation process, giving rise to a wide distribution of switching times.
1. Introduction
In recent years there has been a significant interest in organic molecular materials that show hysteretic dipolar switching behavior.1–9 Even though true ferroelectricity was not always demonstrated, we shall refer to these behaviors as ‘ferroelectric’ – in fact demonstrating true ferroelectricity for a model compound is a major topic of this work, as will be discussed in detail below. Compared to inorganic ferroelectrics both the interest in and the technological relevance of organic ferroelectrics is still modest, possibly with the exception of the polymeric ferroelectric polyvinylidene difluoride (PVDF) and its copolymers with trifluoroethylene (TrFE).10,11 Apart from historic reasons, the often modest characteristic values for the remnant polarization Pr and the coercive field Ec of organic ferroelectrics may partially explain the low interest. In addition, lacking knowledge about basic properties makes it hard to judge the potential scientific and technological relevance of organic molecular ferroelectrics. However, compared to inorganic ferroelectrics, organic materials offer a number of significant key advantages such as the absence of costly, difficult epitaxial growth and the absence of toxic and/or rare elements. In addition, organic molecular ferroelectrics possess great mechanical flexibility, they allow for easy solution-based processing on various substrates and, importantly, they provide nearly infinite freedom to tune the material properties through chemical modification. Furthermore, materials that are similar to those studied in this manuscript have recently been suggested to show interesting photovoltaic properties.12,13The design freedom offered by organic chemistry is reflected by the different moieties that are responsible for the dipolar response in reported organic molecular ferroelectrics. A major class of organic ferroelectrics is based on molecular dipoles introduced by amide groups.4–6,8 Apart from introducing a molecular dipole of ∼3 D per amide group that can be field-reversible,5,6,8 the amide groups also contribute to the molecular stacking and the associated long-range order through the formation of hydrogen bonds.4,14,15 In previous work we demonstrated the dipolar switching of an amide-based model compound, trialkylbenzene-benzene-1,3,5-tricarboxamide (BTA, see inset to Fig. 1(d) for chemical structure).5,6 Although hysteresis and saturation in the polarization vs. field (P–E) loops were observed, the poor polarization retention, in the order of seconds to minutes, at the temperatures needed for dipolar switching, casted doubt on the true polarized nature of the materials' ground state.6
Here, we present a detailed study of the ferroelectric properties of thin-film capacitors with the BTA model compound as an active layer. We show that BTAs, when brought in a homeotropically aligned hexagonal liquid crystalline phase, are truly ferroelectric. To this end, we combine dielectric relaxation spectroscopy (DRS), depth-resolved pyroelectric probing (LIMM), and quasi-static and transient polarization switching experiments and study two BTA compounds with different alkyl chain lengths (BTA-C10 and BTA-C18). The switching properties of the compounds seem largely dominated by disorder.
2. Results and discussion
In this study we employed devices in which the BTA compounds were sandwiched between gold or indium tin oxide (ITO) electrodes. The details of the device fabrication can be found in the Experimental section. After deposition from solution both BTA-C10 and BTA-C18 form achiral stacks that are stabilized by N–H–O hydrogen bonding between successive amide groups and π-stacking of the conjugated benzene core.5 After deposition by spin coating, the individual BTA stacks form bundles that lie in the plane of the metal electrode. This is demonstrated in Fig. 1, which presents topography and phase images obtained by tapping mode atomic force microscopy (TM-AFM), showing the in-plane aligned bundles after spin coating on Au/glass substrates.After deposition of the Au top contact the BTA stacks are homeotropically aligned with the surface normal, i.e. out-of-plane, by the application of an electric field. Both the alignment and the subsequent investigation of the ferroelectric properties are performed at elevated temperatures where the materials are in a columnar hexagonally packed liquid crystalline (Colhex) phase.6 Fig. S1 (ESI†) shows the differential scanning calorimetry (DSC) traces of both compounds, indicating that the Colhex phase of BTA-C10 and BTA-C18 lies between 12–200 °C and 69–190 °C, respectively. Homeotropic out-of-plane alignment was checked by polarization optical microscopic (POM) as shown in Fig. S2 (ESI†). It should be stressed that no macroscopic polarization could be measured on non-aligned thin film devices, indicating that an out-of-plane macrodipole can only be formed along the stacking axis of the material. Supramolecular organization is essential for the dipolar response.
2.1 Establishing ferroelectric behavior
Fig. 2 shows the saturated polarization vs. field (P–E) curves of BTA-C10 and BTA-C18 as measured quasi-statically by the double wave method (DWM) that is described in detail in ref. 16 and 17; see also the Experimental section. Both materials show well-developed saturation behavior, with Pr = 44 mC m−2 and Ec = 30 V μm−1 for BTA-C10 and Pr = 25 mC m−2 and Ec = 20 V μm−1 for BTA-C18. Compared to our previous work, ref. 5 and 6, the shape of the curves is substantially closer to ideal and the values for the remnant polarization are a factor ∼1.5 (BTA-C18) to ∼2.5 (BTA-C10) higher. The coercive field values are essentially unchanged. We attribute the differences to improved alignment procedures and a further development of the DWM. Non-saturated inner loops for both materials can be found in Fig. S6 of the ESI.†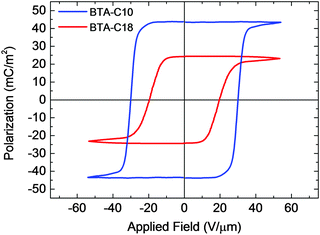 | ||
| Fig. 2 Ferroelectric polarization versus applied field for BTA-C10 (blue) and BTA-C18 (red) under quasi-static conditions (1 Hz, 100 °C). | ||
The difference in Pr between BTA-C10 and BTA-C18 can largely be attributed to the larger number of amide dipoles per unit area in the former. The lattice constant of the hexagonal columnar LC phase is 2.00 nm and 2.55 nm, respectively.6 Assuming a constant dipole moment per amide group leads to a geometric difference in dipole density of (2.55/2.00)2 ≈ 1.62, which is close to the Pr-ratio of 44/25 ≈ 1.76.
The measured values of Pr allow us to make an updated estimate for the molecular dipole μ of a single BTA unit.6 This yields μ = 16 D for BTA-C10 and μ = 15 D for BTA-C18. These numbers are on the higher end of the range of theoretical estimates for isolated stacks of BTAs that yield μ = 6–14 D.14,18–20
 | ||
| Fig. 3 (a) Dielectric permittivity ε′(f,T) for BTA-C18 measured upon cooling from 250 °C to 25 °C. The orange circle marks the pre-transitional region characterized by Curie–Weiss behavior. (b) Evolution of the dielectric loss ε′′(f) for BTA-C18 while passing the paraelectric to ferroelectric phase transition upon cooling (same experiment as shown in (a)). The temperature independent, high-frequency peak around 5 MHz is an artefact originating from the RC time constant of the ITO sample cell. (c) Temperature dependence ε′(T) at f = 220 kHz for two samples of BTA-C18. Sample (1) displays a broadened phase transition compared to (2). (d) Same data plotted in Curie–Weiss representation according to eqn (1). | ||
Well above TI→Colhex, a single relaxation process located around f = 10 kHz dominates the relaxation spectrum, which was assigned to the structural α-relaxation of the isotropic melt, see ref. 6. By approaching the phase transition, a second, faster relaxation mode (III) emerges that coexists with the α-process and gains intensity upon further cooling.
When passing TI→Colhex and entering the hexagonal columnar phase, the relaxation pattern changes drastically, see Fig. 3(b). As expected, the α-relaxation, being due to columnar macro-dipole fluctuations in randomly oriented, short columns that are present in the isotropic phase,21 almost vanishes and is basically replaced by the slower R-relaxation according to the labeling by Fitié et al.6 Ideally, the α-process should be gone in a perfect ferroelectric order. The residual intensity in the ferroelectric hexagonal columnar phase is thus indicative for the existence of short (disordered) stacks, probably near interfaces.
The slow R-process is attributed to macro-dipole fluctuations of the long columnar macro-dipoles.21 The same macro-dipoles are the molecular origin for the ferroelectric depolarization. Its intensity is however not directly linked to the polarization itself. Instead, since R-relaxation is the manifestation of spontaneous fluctuations of macro-dipoles within the columnar hexagonal order, its intensity should be a measure for the number of active columnar defects (up/down), a quantity that is related to the temporal stability of the remnant polarization – in ref. 6 R-relaxation could indeed be directly linked to the polarization loss.
Interestingly, the third relaxation (III) also disappears upon the phase transition, a behavior that classifies process (III) as a transient phenomenon that solely occurs just above TI→Colhex. We hypothesize that this fast relaxation is related to pre-transitional effects in the isotropic phase and is likely caused by individual disks, dimers or other, weakly correlated entities, the concentration of which is highest just before entering the ferroelectric phase (upon cooling). In terms of a ferroelectric/paraelectric phase transition, these appear to give rise to the typical temperature dependence of the dielectric susceptibility χ = ε − 1 according to the Curie–Weiss-law
| χ = C/(T − TC), | (1) |
Revealing Curie–Weiss behavior for BTA-C18 (or BTA-C10) would make for very strong evidence towards unambiguously confirming paraelectric and ferroelectric behavior for the BTAs. Revisiting Fig. 3(a) and inspecting the marked high-frequency region just above TI→Colhex shows a progressive rise of the permittivity towards the phase transition, strongly suggesting Curie–Weiss characteristics. To investigate this behavior more quantitatively, we have plotted the temperature dependence of the permittivity ε′(T) at f = 220 kHz in Fig. 3(c) for two samples of BTA-C18 with different alignment history. Though both curves reveal the phase transition as a peak in ε′(T), a particular broadening for sample (1) is discernible as compared to the better (AC at 3 VRMS instead of DC, at slightly higher T) aligned sample (2). The differences between the two samples show the critical importance of morphology, where the desired out-of-plane alignment is promoted by the field annealing described in the Experimental section.
By replotting the data in the form 1/χ(T) we can check for the validity of the Curie–Weiss behavior. The result for both samples of BTA-C18 is given in Fig. 3(d) and clearly reveals a linear trend confirming true paraelectric behavior in the high-temperature phase. Extrapolation of 1/χ(T) to zero yields the Curie-temperatures of both samples, which are generally somewhat lower than TI→Colhex; here the difference amounts to 15 K for sample (2) and 25 K for the poorly aligned sample (1). These numbers are in excellent agreement with the findings in ref. 21, where strong hydrogen bonding in large, aligned columnar aggregates was found to change to weak (but finite) hydrogen bonding in small, isotropic aggregates some 15 °C below TI→Colhex as probed by DSC.
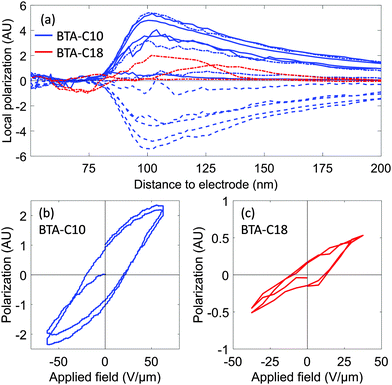
The first ∼80 nm of the BTA-C10 profiles appears to be an inactive or “dead” layer, yielding a nearly non-detectable polarization switching, see panel (a) of Fig. 4. Also for BTA-C18 a dead layer is observed, but its thickness is hard to determine. The presence of dead layers can be attributed to two effects. Due to the spin coating of the thin film, the columnar bundles at the electrode interface are oriented in-plane, i.e. parallel to the electrodes. It is assumed that dipolar switching occurs in the axial orientation of the columns, hence these first layers of flat columns do not contribute to any dipolar switching. A second effect is a screening of the external field, somehow related to the Debye-screening length due to (real or virtual) free charge concentrations near the electrodes, similar to the dead layer found in thin film P(VDF–TrFE).25 The screening of the external field in the first ∼80 nanometers implies the molecules do not experience the field required for macroscopic polarization.
At a distance further than 110 nm from the electrode, the local polarization appears to decrease. This artefact is inherent to LIMM deconvolution techniques on thin (<1000 nm) organic films. As the thermal diffusion depth increases (i.e. when the thermal waves can reach deeper into the film), the spatial resolution decreases. In addition, in thin films, the effusivity of the substrate will play a major role in the thermal amplitude at greater depths, reducing the thermal amplitude, resulting in a lower observed local polarization. Correction for this effect requires accurate knowledge of the thermal parameters of the sample, which is beyond the scope of the present work.
From the LIMM measurements on BTA-C10 and BTA-C18, it appears that the local polarization and susceptibility are inversely proportional to the size of the residual group (C10 or C18). BTA-C10 has a larger susceptibility and a higher coercive field compared to BTA-C18. While the residual group is necessary to enable dipolar switching, an increase in size seems to diminish its amplitude, as the associated molecular relaxation hinders the switching or screens the ferroelectric entities from the external field.
The hysteresis curves obtained via pyroelectric means differ in shape from those using the DWM technique in Fig. 2. This can be in part explained by the difference in external field frequency. The double wave method alternates the sign of the field at a rate around once per second, the pyroelectric setup only changes the sign every 2 hours: to increase the signal-to-noise ratio, several integration, correlation and averaging techniques are used. The longer timescale may invoke structural changes not visible in the DWM experiment and, more importantly, will allow polarization decay at lower fields. These effects introduce a linear slope in the P–E hysteresis curve, which is not present at higher switching frequencies, cf.Fig. 2.
2.2 Kinetic properties
Having established the true ferroelectric nature of the dipolar switching we shall now address its kinetic properties. To this end we performed step response measurements, in which the transient current response to a polarization-reversing voltage step is measured, as shown in Fig. 5(a and b). As expected for a ferroelectric material,26,27 the current transient shifts to shorter times with increasing field. | ||
| Fig. 5 Transient switching current after stepping the electric field at t = 0 measured on (a) BTA-C10 and (b) BTA-C18 at 100 °C. The dashed arrow indicates the peak shift with increasing electric field strength from 19.5 V μm−1 to 50 V μm−1 (BTA-C10) and 19.5 V μm−1 to 70.5 V μm−1 (BTA-C18). The integrated transient switching current, representing the time-dependence of the actual switched part at 1, 0.7, 0.6 and 0.5 of the maximal probed electric field (50 V μm−1 and 70.5 V μm−1 for BTA-C10 and BTA-C18, respectively) is given in panels (c) for BTA-C10 and (d) for BTA-C18. Thin black lines are fits to the data using KAI (eqn (2), dotted line) and NLS (eqn (4)) with log-normal (eqn (3), solid line) and log-Lorentzian (dashed line) distribution of the switching times. | ||
The switching current is proportional to d(ΔP(t))/dt, with ΔP(t) the time-dependent change in polarization. In the classical Kolmogorov–Avrami–Ishibashi (KAI) theory that accounts for space-filling domain growth after nucleation, ΔP(t) is given by28,29
 | (2) |
In ref. 32 a Lorentzian distribution of logarithmic switching times was suggested for similar experiments performed on polycrystalline Pb(Zr,Ti)O3 films. For the present experiments, we found this distribution to be inadequate, as shown by the dashed lines. However, we noticed that a simple, phenomenological lognormal distribution of switching times (eqn (3)), integrated into the NLS model (eqn (4)) gives for both materials and all fields an accurate description of the region around and beyond the maximum of the current distribution, as shown by the thin solid lines in Fig. 5(c and d). It is noticeable that the experimental polarization curves saturate at different values (used for fitting), which most likely is caused by the disorder in the active layer, which is also expressed as the broadening of the P–E loops. Apparently, due to a distribution in (local) coercive fields we cannot achieve the full switching at lower fields.17 In eqn (3)w is the width of the distribution and τ is its central value.
 | (3) |
 | (4) |
In general, lognormal distributions result from processes that depend exponentially on a (normally distributed) random variable. Such processes are abundant and include thermal activation over and tunneling through a random barrier, which may be of particular relevance for the specific case of a disordered ferroelectric.
The above analysis suggests a situation where at short times the switching is limited by a KAI-like process of nucleation and subsequent growth. At longer times, including those where most of the switching occurs, the dispersion in characteristic switching times dominates the transient. Next the process that governs this dispersive region will be further investigated.
Fig. 6 shows the position of the current maxima in Fig. 5 as a measure of the switching speed vs. the reciprocal applied field. At all temperatures, we find that the classical Merz law for nucleation-limited switching,26,27
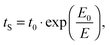 | (5) |
 | (6) |
 | ||
| Fig. 6 (a and b) Step response switching time from Fig. 5vs. electrical field for BTA-C10 (a) and BTA-C18 (b) plotted at different temperatures at double logarithmic scale. Black dash-dotted curves are fits to the Merz nucleation model (eqn (5), t0 ∼ 10−12 s), the solid lines are fits to the hybrid model eqn (6). (c) Switching time vs. reciprocal temperature at an applied field of 33 V μm−1. The solid lines correspond to activation energies of 0.57 eV = 55 kJ mol−1 (BTA-C10) and 0.58 eV = 56 kJ mol−1 (BTA-C18). | ||
It has been proposed that eqn (6) with n = 2 can be due to a switching process that is rate-limited by Fowler–Nordheim charge injection.35 In view of the presence of a ‘dead’ interfacial layer of dielectric nature in our devices (Fig. 4), it is in principle not implausible that a tunneling charge injection mechanism is relevant to these experiments. However, the mechanism proposed in ref. 35 gives rise to a continuously decaying current transient, as expected for a switching current that is determined by essentially a contact resistance. This is in stark contrast to the peaked shape observed in Fig. 6. Alternatively, assuming that a Fowler–Nordheim-type injection current limits the onset of the switching process, e.g. because the applied field initially drops over one or two interfacial layers, could possibly explain the observed peaked current transients that follow the field dependence of eqn (6). We will come back to (and rule out) this scenario in the discussion of Fig. 7 below.
 | ||
| Fig. 7 Polarization versus applied field measured in quasi-static mode on Au/BTA-C10/Au (a) and Au/BTA-C18/Au (b) capacitors at different frequencies, taken at 100 °C. (c) Corresponding coercive field versus switching frequency for BTA-C10 (blue circles and squares) and BTA-C18 (red pentagons and triangles). Open and closed symbols are taken in quasi-static and dynamic mode, respectively. The hysteresis loops corresponding to the dynamic mode are given in the ESI,† Fig. S7. The dashed lines are fits to the Ishibashi–Orihara power law (eqn (7)), the solid lines are fits to the Du–Chen model (eqn (8)). | ||
Similar behavior as in Fig. 6 has been observed for the polymeric ferroelectric PVDF by Ishii et al.,38,39 who interpreted their results in the frameworks laid out by Hayashi36 and Fatuzzo.37 Hayashi has shown that at high fields the size of the critical 2D nucleus can become smaller than the lattice constant of the system, giving rise to a transition to 1D nucleation and a nucleation rate that depends on the field as a power law.36 For the parameters investigated in ref. 36 an exponent n ≈ 1.54 is found, with the notion that n depends on the critical size of the 1D nucleus and the domain boundary energies. In view of the quasi-1D columnar morphology of the aligned BTA thin films, a field-induced transition to 1D nucleation seems intuitively plausible.
Fatuzzo rationalizes a transition from a purely exponential field dependence of the switching time (eqn (5)) to the shape eqn (6) with n = 4/3 in terms of a transition from nucleation limited to apparent sideways domain wall motion to true sideways domain wall motion.37 As was acknowledged by Fatuzzo, it is difficult to justify the assumption of apparent to true sideways domain growth. For the present case a cooperative effect may be expected for the switching of neighboring columns, but this might as well lead to apparent as to real sideways growth of domains. We finally notice that the predicted exponent differs significantly from the best fit to our data, making this model less favored.
Summarizing the discussion above, the data in Fig. 6 alone do not allow a clear conclusion regarding the physical process(es) limiting the switching kinetics. Turning to the activation energies extracted from the data in Fig. 6(c), 55 kJ mol−1 for BTA-C10 and 56 kJ mol−1 for BTA-C18, we notice that these numbers are a factor 2–3 lower than was previously found for the polarization-reversing R-relaxation.6 R-relaxation being a collective reversal of the amide bonds in a ferroelectric domain containing several BTA units as discussed above. This notion is consistent with the switching mechanisms discussed in the context of the data in Fig. 5 and 6 that all imply that bulk polarization reversal is not rate-limiting for polarization reversal driven by an electric field exceeding the coercive field.
In the DWM one measures either the negative or – in our case – the positive part of the hysteresis loop. In Fig. 7, the negative part has been added by a simple mirroring as no significant difference with negative switching has been observed. The bump that is visible in the P(E) plot of the Fig. 7(a) only appears at high frequencies due to the interaction between preparation and measurement signals and the increasing influence of the displacement part resulting from the inertia of the ferroelectric processes.
In Fig. 7 we investigate the frequency dependence of the (apparent) coercive field for both BTA-C10 and BTA-C18. As is common for ferroelectric materials Ec shifts to higher values with increasing frequency f due to slower switching domains starting to lag behind the driving signal. In the KAI framework, such shifts are commonly interpreted using the Ishibashi–Orihara (KAI) power law,
| Ec ∝ fd/α | (7) |
Interestingly, assuming a Fowler–Nordheim tunneling-limited onset of the switching process as discussed at Fig. 6 above, leads to a switching rate and hence a characteristic frequency that is proportional to the injected current f ∝ jFN ∝ E2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E0/E) with E0 a parameter with dimension V m−1 that depends on the injection barrier. Fitting this to the data in Fig. 7 leads to a functional shape that is indistinguishable from the KAI model eqn (7) (not shown). Hence, a rate-limiting Fowler–Nordheim process is not consistent with the experimental data.
exp(−E0/E) with E0 a parameter with dimension V m−1 that depends on the injection barrier. Fitting this to the data in Fig. 7 leads to a functional shape that is indistinguishable from the KAI model eqn (7) (not shown). Hence, a rate-limiting Fowler–Nordheim process is not consistent with the experimental data.
Alternatively, the Du–Chen model assumes switching is limited by the nucleation process which in turn is described as the random, thermally driven formation of a nucleus exceeding the critical size.42–44 This gives rise to an apparent coercive field that depends on the frequency as
 | (8) |
 a parameter that depends on the domain wall energy γ, the binding energy between structural defects and the wall γB, the polarization change due to passing of the domain wall P and that here will be used as empirical fitting parameter. Furthermore, f0 is the limiting domain switching frequency, kB the Boltzmann constant and T the absolute temperature. Applying this model to the data in Fig. 7(c) (thin solid lines) gives an excellent match over the full frequency range. Fitting parameters for BTA-C10 are f0 = 12 kHz for both quasi-static and dynamic modes. For BTA-C18 we find f0 = 2 kHz. In combination with the interpretation of Fig. 5 and 6 above a consistent physical picture arises by assuming that the switching kinetics are dominated by a nucleation process with a roughly log-normal distribution of waiting times. At higher fields these nuclei are most likely quasi-1D.
a parameter that depends on the domain wall energy γ, the binding energy between structural defects and the wall γB, the polarization change due to passing of the domain wall P and that here will be used as empirical fitting parameter. Furthermore, f0 is the limiting domain switching frequency, kB the Boltzmann constant and T the absolute temperature. Applying this model to the data in Fig. 7(c) (thin solid lines) gives an excellent match over the full frequency range. Fitting parameters for BTA-C10 are f0 = 12 kHz for both quasi-static and dynamic modes. For BTA-C18 we find f0 = 2 kHz. In combination with the interpretation of Fig. 5 and 6 above a consistent physical picture arises by assuming that the switching kinetics are dominated by a nucleation process with a roughly log-normal distribution of waiting times. At higher fields these nuclei are most likely quasi-1D.
3. Conclusions
The dipolar properties of trialkylbenzene-1,3,5-tricarboxamides (BTA) were investigated by a combination of techniques. True ferroelectric behavior was demonstrated using dielectric relaxation spectroscopy, in which a ferroelectric–paraelectric phase transition at the Curie temperature was observed, with strict Curie–Weiss behavior at the paraelectric side. Depth-resolved pyroelectric measurements revealed a thin non-pyroelectric interfacial layer, separating the contacts from the switching ferroelectric bulk. The kinetic switching behavior of BTA-bases metal–insulator–metal diodes indicates that the switching kinetics are dominated by domain nucleation with a highly dispersive log-normal distribution of switching times. At higher fields these nuclei are most likely quasi-1D, consistent with the 1D columnar morphology of aligned BTA films. Jointly, these results univocally show that BTAs are true ferroelectrics, albeit of a disordered type.4. Experimental section
Thin film metal–insulator–metal (MIM) capacitor devices were prepared as follows. Bottom contacts from gold (70 nm) were deposited by thermal evaporation under vacuum conditions (∼3 × 10−7 Torr) through a shadow mask on chemically cleaned glass substrates. Prior to Au deposition 5 nm Cr was deposited to promote adhesion. The liquid crystalline BTA-C10 and BTA-C18 materials were spin-coated at 500 rpm from solutions of 40 mg dry BTA-C10 and 35 mg dry BTA-C18 dissolved by 1 ml of chloroform. Obtained thin films were annealed at 70–80 °C for 10–15 min for complete solvent evaporation. Afterwards, top contacts from gold (70 nm) were evaporated through a 90°-rotated shadow mask as described above, giving rise to a cross-bar diode at the intersection of the contacts with a device area between 0.25 and 0.5 mm2. Typical film thicknesses were 600–700 nm for BTA-C10 and 350–400 nm for BTA-C18, as measured by a Dektak XT profilometer.Homeotropic (perpendicular) alignment of columnar liquid crystalline BTAs in LC cells and thin-film capacitor devices was achieved by an external electric field above the coercive field. For MIM capacitors alignment was performed at elevated temperatures of 100–110 °C; for LC cells 150–170 °C was used. The electrical alignment consisted of 30–60 minutes application of a 0.5 Hz triangular wave with an external field amplitude ≈30 V μm−1. The positive and negative parts of the triangular wave had equal amplitude but durations that differed by a factor 2. This alignment technique is more robust in the sense of avoiding device short-circuiting than application of DC field for a shorter time. After achieving the homeotropically aligned state devices were cooled down to the desired temperatures for ferroelectric switching measurements.
Homeotropically aligned thin-film capacitor devices were electrically characterized in the dark inside a Janis probe station. Alignment and switching signal waveforms were applied by an Agilent 33120a arbitrary waveform generator and amplified by a Falco WMA-300 or TReK Model PZD350A high voltage amplifier. The actual circuit current was measured by a Keithley 6485 picoammeter, visualized and saved via an Agilent DSO7104A oscilloscope. In dynamic mode, displacement–field (D–E) hysteresis loops were obtained via direct integration of the measured positive and negative current responses under a triangular periodic switching signal. Quasi-static measurements were performed using the double-wave method (DWM) in which polarization-field (P–E) hysteresis loops were obtained by integration of the pure switching-current which was calculated as the difference between the full switching and background responses. The DWM is described in detail in ref. 16 and 17. For the step-response switching experiments a similar background current subtraction scheme as in the DWM was used.
Dielectric relaxation spectra ε*(ω) = ε′(ω) − iε′′(ω) were obtained using a high precision dielectric analyser (ALPHA analyser, Novocontrol Technologies) in the frequency range of 0.1 Hz to 107 Hz in combination with a Novocontrol Quatro temperature system providing control of the sample temperature with high stability of 0.05 K. BTA-filled Linkam ITO-cells were used as samples in a parallel plate geometry. After measurement, the high frequency parasitic cell peak was partially corrected using a lumped circuit approach.
Local polarization depth profiles were obtained with a state-of-the-art LIMM setup (Laser Intensity Modulation Method). In its most basic form, the LIMM setup consists of a frequency generator (Tektronix AFG3021), which modulates the power of a laser diode (658 nm, 10 mW, Lisa Laser, HL25/M2) onto a thin sheet of sample material onto which electrodes are vacuum deposited, i.e. a MIM device is measured. These electrodes are connected to a high bandwidth current amplifier (Femto Messtechnik, HCA-5M-500K) and a Lock-in amplifier (SR 844) to isolate the pyroelectric current and correlate it to its real and imaginary part. An external bias field is applied by connecting the voltage output of a Keithley 237 Source-Measure unit to the sample electrodes with a Tektronix 2220 Voltage Probe. A 100 nF ceramic capacitor was used to block the DC contribution from the bias field to the current amplifier. The whole setup is automated via a MatLab script.
Surface topographies of spin-coated BTA films after annealing were measured by atomic force microscopy (AFM) using a Veeco MultiMode in tapping-mode at room temperature. Measurements have been done using Si AFM cantilevers (Nanosensors PPP, spring constant k ≈ 42 N m−1, apex radius <10 nm).
Acknowledgements
The work of A. V. G. was supported by the NWO Nano program. I. U. acknowledges funding by Vetenskapsrådet.References
- K. Kishikawa, S. Nakahara, Y. Nishikawa, S. Kohmoto and M. Yamamoto, J. Am. Chem. Soc., 2005, 127, 2565 CrossRef CAS PubMed.
- S. Horiuchi and Y. Tokura, Nat. Mater., 2008, 7, 357 CrossRef CAS PubMed.
- S. Horiuchi, Y. Tokunaga, G. Giovannetti, S. Picozzi, H. Itoh, R. Shimano, R. Kumai and Y. Tokura, Nature, 2010, 463, 789 CrossRef CAS PubMed.
- D. Miyajima, F. Araoka, H. Takezoe, J. Kim, K. Kato, M. Takata and T. Aida, Science, 2012, 336, 209 CrossRef CAS PubMed.
- C. F. C. Fitié, W. S. C. Roelofs, M. Kemerink and R. P. Sijbesma, J. Am. Chem. Soc., 2010, 132, 6892 CrossRef PubMed.
- C. F. C. Fitié, W. S. C. Roelofs, P. C. M. M. Magusin, M. Wübbenhorst, M. Kemerink and R. P. Sijbesma, J. Phys. Chem. B, 2012, 116, 3928 CrossRef PubMed.
- A. S. Tayi, A. K. Shveyd, A. C.-H. Sue, J. M. Szarko, B. S. Rolczynski, D. Cao, T. J. Kennedy, A. A. Sarjeant, C. L. Stern, W. F. Paxton, W. Wu, S. K. Dey, A. C. Fahrenbach, J. R. Guest, H. Mohseni, L. X. Chen, K. L. Wang, J. F. Stoddart and S. I. Stupp, Nature, 2012, 488, 485 CrossRef CAS PubMed.
- H. Anetai, Y. Wada, T. Takeda, N. Hoshino, S. Yamamoto, M. Mitsuishi, T. Takenobu and T. Akutagawa, J. Phys. Chem. Lett., 2015, 6, 1813 CrossRef CAS PubMed.
- J. Guilleme, E. Cavero, T. Sierra, J. Ortega, C. L. Folcia, J. Etxebarria, T. Torres and D. González-Rodríguez, Adv. Mater., 2015, 27, 4280 CrossRef CAS PubMed.
- M. Li, H. J. Wondergem, M.-J. Spijkman, K. Asadi, I. Katsouras, P. W. M. Blom and D. M. de Leeuw, Nat. Mater., 2013, 12, 433 CrossRef CAS PubMed.
- I. Katsouras, K. Asadi, M. Li, T. B. van Driel, K. S. Kjær, D. Zhao, T. Lenz, Y. Gu, P. W. M. Blom, D. Damjanovic, M. M. Nielsen and D. M. de Leeuw, Nat. Mater., 2016, 15, 78 CrossRef CAS PubMed.
- A. L. Sobolewski, Phys. Chem. Chem. Phys., 2015, 17, 20580 RSC.
- M. Wawrzyniak-Adamczewska and M. Wierzbowska, J. Phys. Chem. C, 2016, 120, 7748 CAS.
- A. Rochefort, É. Bayard and S. Hadj-Messaoud, Adv. Mater., 2007, 19, 1992 CrossRef CAS.
- A. S. Tayi, A. Kaeser, M. Matsumoto, T. Aida and S. I. Stupp, Nat. Chem., 2015, 7, 281 CrossRef CAS PubMed.
- M. Fukunaga and Y. Noda, J. Phys. Soc. Jpn., 2008, 77, 64706 CrossRef.
- V. Khikhlovskyi, A. V. Gorbunov, A. J. J. M. van Breemen, R. A. J. Janssen, G. H. Gelinck and M. Kemerink, Org. Electron., 2013, 14, 3399 CrossRef CAS.
- T. Shikata, Y. Kuruma, A. Sakamoto and K. Hanabusa, J. Phys. Chem. B, 2008, 112, 16393 CrossRef CAS PubMed.
- P. J. M. Stals, J. C. Everts, R. de Bruijn, I. A. W. Filot, M. M. J. Smulders, R. Martín-Rapún, E. A. Pidko, T. F. A. de Greef, A. R. A. Palmans and E. W. Meijer, Chem. – Eur. J., 2010, 16, 810 CrossRef CAS PubMed.
- R. Q. Albuquerque, A. Timme, R. Kress, J. Senker and H.-W. Schmidt, Chem. – Eur. J., 2013, 19, 1647 CrossRef CAS PubMed.
- A. Timme, R. Kress, R. Q. Albuquerque and H.-W. Schmidt, Chem. – Eur. J., 2012, 18, 8329 CrossRef CAS PubMed.
- M. Wübbenhorst and J. van Turnhout, J. Non-Cryst. Solids, 2002, 305, 40 CrossRef.
- M. Serwadczak, M. Wübbenhorst and S. Kucharski, J. Non-Cryst. Solids, 2007, 353, 4303 CrossRef CAS.
- S. B. Lang and D. K. Das-Gupta, J. Appl. Phys., 1986, 59, 2151 CrossRef CAS.
- T. Putzeys and M. Wübbenhorst, Phys. Chem. Chem. Phys., 2015, 17, 7767 RSC.
- W. J. Merz, Phys. Rev., 1954, 95, 690 CrossRef CAS.
- W. J. Merz, J. Appl. Phys., 1956, 27, 938 CrossRef CAS.
- H. Orihara, S. Hashimoto and Y. Ishibashi, J. Phys. Soc. Jpn., 1994, 63, 1031 CrossRef CAS.
- Y. Ishibashi and H. Orihara, Integr. Ferroelectr., 1995, 9, 57 CrossRef.
- X. J. Lou, J. Phys.: Condens. Matter, 2009, 21, 12207 CrossRef CAS PubMed.
- O. Lohse, M. Grossmann, U. Boettger, D. Bolten and R. Waser, J. Appl. Phys., 2001, 89, 2332 CrossRef CAS.
- J. Y. Jo, H. S. Han, J.-G. Yoon, T. K. Song, S.-H. Kim and T. W. Noh, Phys. Rev. Lett., 2007, 99, 267602 CrossRef CAS PubMed.
- Y. A. Genenko, S. Zhukov, S. V. Yampolskii, J. Schütrumpf, R. Dittmer, W. Jo, H. Kungl, M. J. Hoffmann and H. von Seggern, Adv. Funct. Mater., 2012, 22, 2058 CrossRef CAS.
- A. K. Tagantsev, I. Stolichnov, N. Setter, J. S. Cross and M. Tsukada, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 214109 CrossRef.
- A.-Q. Jiang, H. J. Lee, C. S. Hwang and T.-A. Tang, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 24119 CrossRef.
- M. Hayashi, J. Phys. Soc. Jpn., 1972, 33, 616 CrossRef.
- E. Fatuzzo, Phys. Rev., 1962, 127, 1999 CrossRef CAS.
- H. Ishii, T. Nakajima, Y. Takahashi and T. Furukawa, Appl. Phys. Express, 2011, 4, 31501 CrossRef.
- H. Ishii, T. Nakajima, T. Furukawa and S. Okamura, Jpn. J. Appl. Phys., 2013, 52, 41603 CrossRef.
- S. Hashimoto, H. Orihara and Y. Ishibashi, J. Phys. Soc. Jpn., 1994, 63, 1601 CrossRef CAS.
- J. F. Scott, Integr. Ferroelectr., 1996, 12, 71 CrossRef CAS.
- X. Du, I.-W. Chen, Symposium U – Ferroelectric Thin Film VI, MRS Online Proceedings Library Archive, 1997, vol. 493.
- Takaakitsurumi, S.-M. Num, Y.-B. Kil and S. Wada, Ferroelectrics, 2001, 259, 43 CrossRef.
- S.-M. Nam, Y.-B. Kil, S. Wada and T. Tsurumi, Jpn. J. Appl. Phys., 2003, 42, L1519 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp03835b |
| This journal is © the Owner Societies 2016 |