 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A comparative study of AumRhn (4 ≤ m + n ≤ 6) clusters in the gas phase versus those deposited on (100) MgO†
Fernando
Buendía
a,
Jorge A.
Vargas
a,
Marcela R.
Beltrán
*a,
Jack B. A.
Davis
b and
Roy L.
Johnston
b
aInstituto de Investigaciones en Materiales, Universidad Nacional Autónoma de México, Circ. ext. s/n Apdo. Postal 70-360, C.P. 04510, México D.F., Mexico. E-mail: mbeltran@unam.mx; Fax: +52 (55)56161251; Tel: +52 (55)56224624
bSchool of Chemistry, University of Birmingham, Birmingham, West Midlands B15 2TT, UK
First published on 13th July 2016
Abstract
A comparative theoretical study has been performed of the gas phase and deposited AumRhn (4 ≤ m + n ≤ 6) clusters. The combined use of a genetic algorithm and Density Functional Theory (DFT) calculations allows us to explore the potential energy surface and, therefore, find efficiently and automatically the global minimum configuration for each composition. Our results show interesting effects on the geometries of the clusters on deposition. This occurs because the rhodium atoms (electronically) prefer to be in contact with the MgO surface, sometimes promoting planar clusters to become three-dimensional when deposited, and three-dimensional clusters in the gas phase to become two-dimensional. Together with the change in geometries, the magnetic moment is reduced from the gas phase, as the electrons rearrange themselves when the cluster interacts with the substrate.
1 Introduction
Subnanometric alloy clusters are currently attracting attention from both experimental and theoretical communities due to their interesting structural and electronic properties.1 Gold clusters have been widely studied over a large size range;2–4 the relativistic effects on their electrons impart several special properties such as 2-dimensional structures of clusters with up to 8–13 atoms (depending on their charge),5–7 and some of the so-called magic numbered clusters are amorphous.8,9 Gold clusters have been known to possess catalytic activity,10–12 which has recently been tuned by doping them with other transition metals, enhancing their performance.13–15 On the other hand, rhodium clusters have been found to possess large magnetic moments at the subnanometric scale.16–21 This interesting behaviour is partly due to the special electronic configuration of rhodium (5s1 4d8) with its s-orbital not completely filled up. In this sense, the combination of two metals with different electronic configurations allows more tunability of properties. For example, it is well known that small gold clusters present an odd–even behaviour towards O2 adsorption,22–25 which was not observed for binary gold rhodium clusters in an earlier study.26In the present work we study binary gold rhodium clusters. Despite the fact that there have been very few studies,27,28 this alloy is found to possess very exciting properties. The presence of high magnetic moments and a very high reactivity has been recently reported,26,29 in comparison to pure gold clusters.30–33 From both experimental and theoretical points of view, there are advantages of studying gas-phase clusters, because of their interesting properties such as size selectivity, ionic species, and adsorption. The interplay between the electronic and geometric structures can be clearly established. In fact, gas phase experiments have already had a marked impact on the understanding of cluster structures.2–9 The deposition of clusters on a surface is, nonetheless, an important advancement in the development of future technologies based on more stable subnanoscale devices.
This study is based on the fact that many experimental and theoretical studies of small particles show important changes in both their electronic as well as their geometric structures once they are deposited.34–40 In this work, we use the well-studied and electronically stable MgO(100) surface.41–48 Its stability offers the opportunity to study the effects of the cluster geometries once deposited on the surface. Keeping the system as small as possible is very important for reducing computing time, but it is also relevant to the increased interest in catalysis by small size-selected clusters.49 The introduction of a surface increases the computational complexity of the optimization process, due to the increase in the number of atoms involved.
Additionally, when the gas-phase minima are deposited on the surface and then locally minimized (on the surface) the lowest energy surface-supported clusters are not necessarily found because of the presence of energy barriers to cluster rearrangement. Here, we use the Birmingham Parallel Genetic Algorithm (BPGA) which combined with the Vienna ab initio Simulation Package (VASP) can accurately predict the structure of clusters in the gas phase.50–53 The method can also be applied to finding the true lowest energy geometries for surface-supported clusters, optimised by the genetic algorithm in presence of the surface.52,54
In the next section, we briefly discuss the details of both the DFT and the BPGA methods used in this work. In Section 3, we present and discuss a comparative study between the structural, electronic and magnetic properties for AumRhn (4 ≤ m + n ≤ 6) clusters in the gas phase versus supported (where the global minimum search is performed over the MgO surface). Finally, we present our conclusions.
2 Methodology
This study has been performed by combining two powerful methodologies: the Birmingham Parallel Genetic Algorithm (BPGA)55–57 method and a DFT code. The DFT calculations were performed using the Vienna ab initio simulation Package VASP58–61 by means of the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) exchange and correlation functional,62 using Projected Augmented Wave (PAW) pseudopotentials.63 The plane wave energy cut-off has been taken at 400 eV for an adequate convergence. Methfessel–Paxton smearing, with a sigma value of 0.01 eV, was implemented to improve the SCF convergence of metallic systems.64 Gamma point calculations were performed. The use of this methodology has given good results in the same systems when compared to photoelectron spectroscopy data in an earlier publication.29Within the BPGA, the application of crossover and mutation operators to the given geometries and their local relaxation is managed by independently working subprocesses synchronized with a global database (pool). The initial population is generated through the minimization (with VASP) of random structures. Subsequently, the crossover and mutation operations begin. For the crossover, a pair of clusters are taken from the pool through “roulette-wheel” selection.57 Offspring are then produced through single-point, weighted crossover, carried out according to the Deaven and Ho cut and splice method.65 For the mutation, there are two possibilities, one is moving 20% of the cluster atoms, and the other (possible only in bimetallic clusters) is swapping two atoms of different elements generating a homotop. In our case, 90% of the new candidates were obtained via crossover, while 10% were determined by applying the move mutation operator to an older structure from the pool.
The BPGA can work in two modes to find the global minimum structure: in the gas phase or by taking into account the interaction with a surface. We used both for this comparative study. It is important to differentiate between the two methods to simulate the clusters on a surface. This can be done by placing onto the surface the lowest-energy clusters previously obtained in the gas phase and allowing the combined system to relax. What BPGA does, however, is to globally optimise the cluster directly on the surface, which predicts the most stable cluster (of given size and composition) that can be grown on the substrate or the result of allowing a gas phase deposited cluster to anneal on the surface. This yields structural transformations of the deposited cluster, otherwise not found using the first method mentioned above. This has been corroborated in an initial stage of this study.
The initial random pool in the gas phase consists of 10 configurations, while for the supported clusters the pool has 15 initial configurations. The calculations have been performed within a cubic supercell leaving at least 10 Å of space between periodically repeated clusters to avoid cluster–cluster interactions. In the second part, the clusters have been placed 1.5 Å above a 6 × 6 × 2 slab of an ideal MgO(100) surface leaving 14.7 Å of vacuum between slabs in the z-direction. We consider only two MgO layers after comparing both the total energies and the geometrical reconfigurations varying the number of layers and observing small differences (<2%) which are not important for the purpose of this study.
The binding energies have been calculated from the following expression,
 | (1) |
The energies, Eads, of the surface-supported global minima were calculated as follows,
| Eads = Eslab+AumRhn − (Eslab + EAumRhn), | (2) |
3 Results
The putative ground state structures for AuN−nRhn (N = 4–6) clusters are shown in Fig. 1, 2, and 3 for N = 4, 5 and 6 respectively. In these figures (a) shows the gas-phase minima, while side and top views of optimised supported clusters on the MgO(100) surface are shown in (b) and (c), respectively.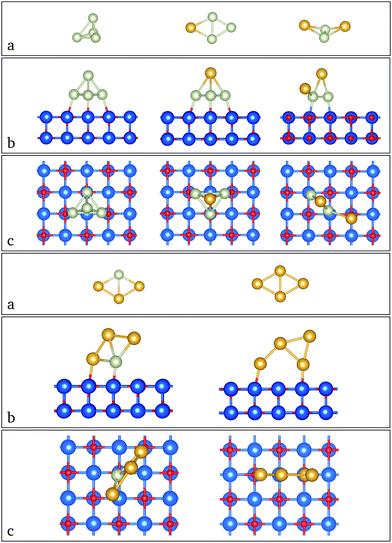 | ||
| Fig. 1 Geometry structures for (a) gas phase atomic neutral Au4−nRhn (n = 0–4) clusters and their corresponding side (b) and top (c) views when supported on MgO. | ||
 | ||
| Fig. 2 Geometry structures for (a) gas-phase atomic neutral Au5−nRhn (n = 0–5) clusters and their corresponding side (b) and top (c) views when supported on MgO. | ||
 | ||
| Fig. 3 Geometry structures for (a) gas-phase atomic neutral Au6−nRhn (n = 0–6) clusters and their corresponding side (b) and top (c) views when supported on MgO. | ||
For the 4-atom systems, we obtained a consistent decrease of the magnetic moment, both with the number of gold atoms and also in the presence of the surface. The binding energies increase with the number of rhodium atoms, due to the greater strength of Rh–Rh binding as evidenced by the higher cohesive energy of bulk Rh (5.75 eV per atom) compared to Au (3.81 eV per atom).66 The most stable cluster geometries on the substrate are often different from those optimised in the gas phase, because there is a tendency to increase the number of Rh atoms in contact with the surface as Rh–O interactions are stronger than Au–O. The clusters tend to change in geometry as they land on the surface depending on the availability of rhodium atoms to bind to the surface.
Minimal structural changes are observed for Rh4 between the gas phase (1a) and supported (1b) clusters, with only small differences in the bond lengths. The adsorption energy is −2.16 eV (Fig. 4a) and the magnetic moment of the cluster is quenched (see Fig. 5a). AuRh3 has a planar rhombic structure in the gas phase that turns into a tetrahedral structure when it is supported. Three rhodium atoms bond to the surface, giving rise to the highest adsorption energy (−2.69 eV) of all the supported 4-atom clusters. Its magnetic moment is also reduced by 2 μB when compared with the gas phase. The most drastic geometrical changes and a decrease of 2 μB in its magnetic moment happen for Au2Rh2. This phenomenon is due to the stronger interaction of the surface with rhodium rather than with gold atoms. Au3Rh has the same structure whether in the gas phase or supported, similar to what happens to pure Rh4, and has the lowest adsorption energy (−1.75 eV), but the multiplicity remains the same for the gas phase and the supported cluster. Finally Au4 has a 2D rhombohedral structure and one Au–Au bond breaks in order for stronger bonds to be made with the superficial (or uppermost) oxygen atoms, yielding an adsorption energy of −1.90 eV. The two systems (gas phase and supported) are both singlets.
 | ||
| Fig. 4 Adsorption energies on eV for (a) Au4−nRhn (n = 0–4), (b) Au5−nRhn (n = 0–5) and (c) Au6−nRhn (n = 0–6) clusters. | ||
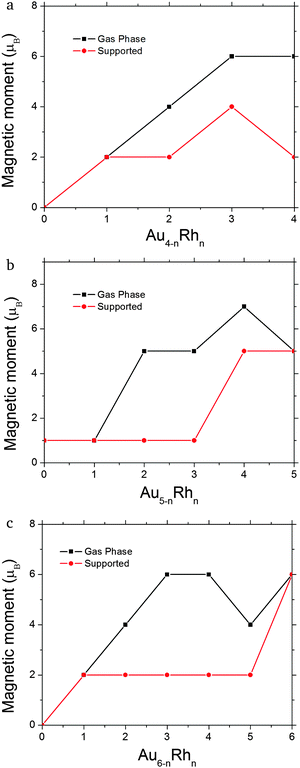 | ||
| Fig. 5 Total cluster magnetic moment (μB) for (a) Au4−nRhn (n = 0–4), (b) Au5−nRhn (n = 0–5) and (c) Au6−nRhn (n = 0–6) clusters. | ||
As a reference, we have considered the global minima in the gas phase and then relaxed them on the MgO surface. The geometries show little change, other than small changes in bond lengths. However, the magnetic moments are greatly affected by the interaction with the surface, diminishing in all cases in a similar way as in the clusters generated on the surface by means of the BPGA. The differences in energy between the surface deposited and BPGA surface optimised structures are the largest for AuRh3 (0.41 eV) and Au2Rh2 (0.33 eV), which also display the largest structural differences to the gas phase structures.
In the 5-atom systems, there are many differences between the geometrical structures of the gas phase and supported clusters. In the gas phase, the clusters are three dimensional (3D) apart from Au4Rh, which is planar. But when they are supported, the lowest energy configuration is 2D, with the exception of Rh5, which retains the 3D gas phase structure. Incidentally this cluster has the highest adsorption energy to the surface (−3.38 eV, see Fig. 4b). It also maintains its high multiplicity (M = 5). The ground state of AuRh4 exhibits structural changes when optimised on the surface; it transforms from an edge-bridged tetrahedron to an edge-bridged square (Au forms the bridge). Its adsorption energy is the lowest for these alloys; this may be due to the geometric transformation (see Fig. 4b). The magnetic moment of the gas-phase minimum is reduced from 7 to 5 μB when it is supported. Au2Rh3 and Au3Rh2 also present conformational changes when supported. The gas-phase clusters have 3D structures with a magnetic moment of 5 μB, for both clusters. However, the lowest minima for the supported clusters are W-like 2D structures, standing on their edge perpendicular to the surface. Their magnetic moment is the lowest (1 μB) of all the 5-atom clusters. The observed tendency for the planar structures standing perpendicular to the MgO surface is due to the “metal-on-top” effect, commonly known for Au clusters.52 Au4Rh and Au5 are very similar, both in their geometrical and electronic structures in the gas phase. They have 2D structures and only have one unpaired electron. Their adsorption energies are −2.11 and −1.52 eV, respectively (see Fig. 4b). Again if we only deposit the gas-phase minima on the MgO(100) surface, they do not undergo any significant geometry change, though their magnetic moment decreases.
In the 6-atom systems, we observe a very interesting behaviour both in the gas phase and when supported. Their geometry is dominated by the number of gold atoms, being 2D for high gold concentrations. The transition to 3D occurs at Au2Rh4 in the gas phase and at Au3Rh3 when supported on MgO. Their adsorption energies decrease with the number of gold atoms (see Fig. 4c). The magnetic moment for the mixed clusters generated on the surface is constant (2 μB see Fig. 5c).
The ground state structures for Rh6, both in the gas phase and when deposited, are trigonal prisms, they also have 6 unpaired electrons (see Fig. 5c), and the adsorption energy (−3.40 eV), corresponding to adsorption via one of the square faces of the trigonal prism, is the highest among all the systems studied here. The AuRh5 cluster has the same structure in the gas phase and when supported, with 4 and 2 unpaired electrons, respectively, and an adsorption energy of −2.86 eV. Au2Rh4 is slightly changed when supported, with an adsorption energy of −2.51 eV. In this case a Rh–Rh bond is broken when supported to allow two rhodium atoms to form strong bonds with the substrate and to stabilise the structure via the metal-on-top effect. The magnetic moment is significantly quenched relative to the free cluster (from 6 to 2 μB as can be seen in Fig. 5c).
Au3Rh3 is unique in the sense that its structure changes from planar in the gas phase to a 3D structure when deposited. This is possibly due to the huge interaction between the oxygen anions in the surface and the rhodium atoms. This cluster has the lowest adsorption energy of all the 6-atom systems with a value of −1.96 eV (as can be seen in Fig. 4c), and its multiplicity changes from a septet in the gas phase to a triplet for the supported cluster. In the gas phase, Au4Rh2 has a triangular structure with the rhodium atoms in central positions and has a multiplicity of five. The ground state of the supported cluster has a similar structure and lies perpendicular to the surface; the rhodium atoms change their position to the basis of the triangle to be in contact with the surface (see Fig. 3b; due to a combination of the metal-on-top effect and the stronger Rh–O bonding), and the arrangement of the rhodium atoms is different (i.e. a different homotop is selected), with 2 Rh atoms lying along the lower edge of the triangle, enabling 2 strong Rh–O bonds to be formed. A similar rearrangement has been observed for Au2Ir4/MgO,52 and the magnetic moment decreases from 4 to 2 μB. The adsorption energy in this case is −2.06 eV (see Fig. 4c).
Finally, Au5Rh and Au6 have the same triangular structure. In the case of Au5Rh the Rh atom occupies the centre of the triangular edge which is bonded to the MgO surface (see Fig. 3b) and they have low magnetic moments both in the gas phase and when supported; see Fig. 5c. The adsorption energies of Au5Rh and Au6 are −1.97 eV and −1.59 eV, respectively. Again these clusters sit perpendicular to the surface to reduce the total energy due to the metal-on-top effect.
As for the smaller clusters, depositing gas phase minima on the MgO(100) surface leads to only minor structural changes and on average these structures are 0.23 eV higher in energy than the surface-optimised clusters generated by BPGA.
4 Discussion
From our results we observe that there is a general trend for the gas-phase structures to be planar when gold concentration is predominant (larger than 50%). When they are supported on the MgO surface, the geometries are the result of the rhodium atoms creating bonds with the oxygen anions of the surface. This results in important structural transformations from 2D to 3D structures and vice versa (e.g. Au3Rh3 and Au3Rh2). Gold atoms do not bond to the surface when there are enough rhodium atoms to do so. Another characteristic is that the 2D deposited structures lie perpendicular to the MgO surface, due to the metal-on-top effect which has been extensively discussed in the previous work.34,54 On the other hand, introducing rhodium atoms into gold clusters increases the magnetic moments in the gas phase. When the clusters are deposited the magnetic moments are consistently decreased. This is due to a symmetry breaking between the gas phase versus the deposited clusters. Upon deposition, the geometry transformation leads to lower-symmetry geometries and therefore the degeneracy of electronic states is broken, creating different spin–orbital populations. This can be clearly seen for example in systems like Au4Rh2 and Au3Rh3 where the geometries are very different between the gas phase and the deposited clusters and explains why the magnetic moment is quenched upon deposition for some cases. For Rh6, Au5Rh, Rh5 and Au3Rh the magnetic moment is preserved since they do not have apparent geometry transformations after they are deposited (see Fig. 1–3). The magnitude of the adsorption energy of a cluster on the MgO surface is similar to the binding energy per atom of the gas-phase cluster and it steadily increases with rhodium concentration except for those clusters which undergo a drastic geometry transformation (AuRh4 and Au3R3), which correspond to the peaks observed in Fig. 4. All the binding and adsorption energies are reported in Table S1 in the ESI.†If we compare the clusters optimised on the surface by BPGA with those where the gas-phase minima are deposited onto the surface and locally minimized, we observe that the deposited clusters are less stable (i.e. the combined cluster + substrate energy is higher) than those which are optimised on the surface. The geometries, and also the spin multiplicities of these deposited gas phase clusters, differ from the substrate-optimised clusters discussed here.
5 Conclusions
The introduction of the interaction with the surface in the BPGA cycles proved to be of crucial importance for finding structural changes for supported structures which would be very difficult to guess otherwise. In some cases there should be substantial energy barriers for those changes and this can be the objective of a future work.We can foresee very important applications for clusters exhibiting the so-called metal-on-top effect. This could be very useful for catalytic purposes as their exposed superficial area is maximized. Another interesting result to emphasize is the fact that some pure or doped rhodium clusters may keep their magnetic moments if they do not suffer a drastic structural transformation upon deposition making them very useful for future magnetic applications.
Acknowledgements
M. R. B. and F. B. Z. acknowledge support from PAPIIT IN100515, UNAM project, and from DGSCA UNAM. The calculations were performed using the supercomputer Miztli at the supercomputer center in UNAM. We acknowledge the use of the facilities of the IIM (Instituto de Investigaciones en Materiales). F. B. Z. acknowledges support from CONACYT (financial support No. 379750). J. V. T. acknowledges a postdoctoral grant from DGAPA UNAM. J. B. A. D. and R. L. J. acknowledge the Engineering and Physical Sciences Research Council, U.K. (EPSRC), for funding under Critical Mass Grant EP/J010804/1 “TOUCAN: Towards an Understanding of Catalysis on Nanoalloy”. Calculations were performed via membership of the U.K.'s HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202); this work made use of the facilities of ARCHER, the U.K.'s national high performance computing service, which is funded by the Office of Science and Technology through EPSRC's High End Computing Programme.References
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
- P. Gruene, B. Butschke, J. Lyon, D. M. Rayner and A. Fielicke, Z. Phys. Chem., 2014, 228, 337–350 CrossRef CAS.
- P. Gruene, D. M. Rayner, B. Redlich, A. F. G. Van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Science, 2008, 321, 674–676 CrossRef CAS PubMed.
- L. M. Ghiringhelli, P. Gruene, J. T. Lyon, D. M. Rayner, G. Meijer, A. Fielicke and M. Scheffler, New J. Phys., 2013, 15, 083003 CrossRef.
- C. Jackschath, I. Rabin and W. Schulze, Ber. Bunsen-Ges., 1992, 96, 1200–1204 CrossRef CAS.
- D. Schooss, P. Weis, O. Hampe and M. M. Kappes, Philos. Trans. R. Soc., A, 2010, 368, 1211–1243 CrossRef CAS PubMed.
- L.-M. Wang and L.-S. Wang, Nanoscale, 2012, 4, 4038–4053 RSC.
- I. L. Garzón, K. Michaelian, M. R. Beltrán, A. Posada-Amarillas, P. Ordejón, E. Artacho, D. Sánchez-Portal and J. M. Soler, Phys. Rev. Lett., 1998, 81, 1600–1603 CrossRef.
- G. Bravo-Pérez, I. Garzón and O. Novaro, THEOCHEM, 1999, 493, 225–231 CrossRef.
- M. Haruta, Catal. Today, 1997, 36, 153–166 CrossRef CAS.
- W. T. Wallace, R. B. Wyrwas, R. L. Whetten, R. Mitrić and V. Bonačić-Koutecký, J. Am. Chem. Soc., 2003, 125, 8408–8414 CrossRef CAS PubMed.
- W. T. Wallace and R. L. Whetten, J. Am. Chem. Soc., 2002, 124, 7499–7505 CrossRef CAS PubMed.
- A. M. Joshi, M. H. Tucker, W. N. Delgass and K. T. Thomson, J. Chem. Phys., 2006, 125, 194707 CrossRef PubMed.
- M. Neumaier, F. Weigend, O. Hampe and M. M. Kappes, J. Chem. Phys., 2006, 125, 104308 CrossRef PubMed.
- P. V. Nhat, T. B. Tai and M. T. Nguyen, J. Chem. Phys., 2012, 137, 164312 CrossRef PubMed.
- M. R. Beltrán, F. Buendía Zamudio, V. Chauhan, P. Sen, H. Wang, Y. J. Ko and K. Bowen, Eur. Phys. J. D, 2013, 67, 1–8 CrossRef.
- B. V. Reddy, S. N. Khanna and B. I. Dunlap, Phys. Rev. Lett., 1993, 70, 3323–3326 CrossRef CAS PubMed.
- B. V. Reddy, S. K. Nayak, S. N. Khanna, B. K. Rao and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 5214–5222 CrossRef CAS.
- Y.-C. Bae, H. Osanai, V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 195413 CrossRef.
- M. Eichelbaum, K. Rademann, A. Hoell, D. M. Tatchev, W. Weigel, R. Stößer and G. Pacchioni, Nanotechnology, 2008, 19, 135701 CrossRef PubMed.
- F. Aguilera-Granja, J. L. Rodríguez-López, K. Michaelian, E. O. Berlanga-Ramírez and A. Vega, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 224410 CrossRef.
- B. Salisbury, W. Wallace and R. Whetten, Chem. Phys., 2000, 262, 131–141 CrossRef CAS.
- B. Yoon, H. Häkkinen and U. Landman, J. Phys. Chem. A, 2003, 107, 4066–4071 CrossRef CAS.
- Y. D. Kim, M. Fischer and G. Ganteför, Chem. Phys. Lett., 2003, 377, 170–176 CrossRef CAS.
- W. Huang, H.-J. Zhai and L.-S. Wang, J. Am. Chem. Soc., 2010, 132, 4344–4351 CrossRef CAS PubMed.
- F. Buendía and R. M. Beltrán, Eur. Phys. J. D, 2016, 70, 73 CrossRef.
- J.-X. Yang, C. F. Wei and J. J. Guo, Phys. B, 2010, 405, 4892–4896 CrossRef CAS.
- S. García, L. Zhang, G. W. Piburn, G. Henkelman and S. M. Humphrey, ACS Nano, 2014, 8, 11512–11521 CrossRef PubMed.
- F. Buendía, M. R. Beltrán, X. Zhang, G. Liu, A. Buytendyk and K. Bowen, Phys. Chem. Chem. Phys., 2015, 17, 28219–28227 RSC.
- H. Häkkinen and U. Landman, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R2287–R2290 CrossRef.
- C. Bürgel, N. M. Reilly, G. E. Johnson, R. Mitrić, M. L. Kimble, J. A. W. Castleman and V. Bonačić-Koutecký, J. Am. Chem. Soc., 2008, 130, 1694–1698 CrossRef PubMed.
- G. E. Johnson, R. Mitrić, V. Bonačić-Koutecký and A. C. Castleman Jr., Chem. Phys. Lett., 2009, 475, 1–9 CrossRef CAS.
- F. Wang, D. Zhang, X. Xu and Y. Ding, J. Phys. Chem. C, 2009, 113, 18032–18039 CAS.
- R. Ferrando and A. Fortunelli, J. Phys.: Condens. Matter, 2009, 21, 264001 CrossRef PubMed.
- L. Xu, G. Henkelman, C. T. Campbell and H. Jónsson, Surf. Sci., 2006, 600, 1351–1362 CrossRef CAS.
- G. Barcaro, A. Fortunelli, F. Nita and R. Ferrando, Phys. Rev. Lett., 2005, 95, 246103 CrossRef CAS PubMed.
- G. Barcaro and A. Fortunelli, New J. Phys., 2007, 9, 22 CrossRef.
- V. Musolino, A. Selloni and R. Car, Phys. Rev. Lett., 1999, 83, 3242–3245 CrossRef CAS.
- L. B. Vilhelmsen and B. Hammer, Phys. Rev. Lett., 2012, 108, 126101 CrossRef PubMed.
- R. Ferrando, G. Barcaro and A. Fortunelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 045418 CrossRef.
- A. V. Matveev, K. M. Neyman, I. V. Yudanov and N. Rösch, Surf. Sci., 1999, 426, 123–139 CrossRef CAS.
- I. Yudanov, G. Pacchioni, K. Neyman and N. Rösch, J. Phys. Chem. B, 1997, 101, 2786–2792 CrossRef CAS.
- A. Bogicevic and D. R. Jennison, Surf. Sci., 1999, 437, L741–L747 CrossRef CAS.
- V. A. Nasluzov, V. V. Rivanenkov, A. B. Gordienko, K. M. Neyman, U. Birkenheuer and N. Rösch, J. Chem. Phys., 2001, 115, 8157–8171 CrossRef CAS.
- L. Giordano, C. D. Valentin, G. Pacchioni and J. Goniakowski, Chem. Phys., 2005, 309, 41–47 CrossRef CAS.
- L. Giordano and G. Pacchioni, Surf. Sci., 2005, 575, 197–209 CrossRef CAS.
- L. O. Paz-Borbón, G. Barcaro, A. Fortunelli and S. V. Levchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155409 CrossRef.
- V. Musolino, A. Dal Corso and A. Selloni, Phys. Rev. Lett., 1999, 83, 2761–2764 CrossRef CAS.
- G. Kwon, G. A. Ferguson, C. J. Heard, E. C. Tyo, C. Yin, J. DeBartolo, S. Seifert, R. E. Winans, A. J. Kropf, J. Greeley, R. L. Johnston, L. A. Curtiss, M. J. Pellin and S. Vajda, ACS Nano, 2013, 7, 5808–5817 CrossRef CAS PubMed.
- S. Heiles, A. J. Logsdail, R. Schafer and R. L. Johnston, Nanoscale, 2012, 4, 1109–1115 RSC.
- J. B. A. Davis, S. L. Horswell and R. L. Johnston, J. Phys. Chem. A, 2014, 118, 208–214 CrossRef CAS PubMed.
- J. B. A. Davis, S. L. Horswell and R. L. Johnston, J. Phys. Chem. C, 2016, 120, 3759–3765 CAS.
- J. B. A. Davis, A. Shayeghi, S. L. Horswell and R. L. Johnston, Nanoscale, 2015, 7, 14032–14038 RSC.
- C. J. Heard, S. Heiles, S. Vajda and R. L. Johnston, Nanoscale, 2014, 6, 11777–11788 RSC.
- http://https://bitbucket.org/JBADavis/bpga/ .
- A. Shayeghi, D. Gotz, J. B. A. Davis, R. Schafer and R. L. Johnston, Phys. Chem. Chem. Phys., 2015, 17, 2104–2112 RSC.
- R. L. Johnston, Dalton Trans., 2003, 4193–4207 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmaller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS.
- D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291 CrossRef CAS PubMed.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, 7th edn, 1996 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp03735f |
| This journal is © the Owner Societies 2016 |
