A DFT study on dihydropyrazine annulated linear polyacenes: aromaticity, stability and HOMO–LUMO energy modulation

Abstract

Linear polyacenes (LPAs) beyond pentacene are highly unstable and their application potential in the optoelectronics field is very limited. On the basis of theoretical studies at the M06L/6-311++G(d,p) level of DFT, we show that annulating dihydropyrazine units to LPA cores can yield large LPA mimics. This strategy enhances the aromaticity of the LPA core and also provides a way to modulate the HOMO–LUMO energy gap by choosing an appropriate LPA core and extending dihydropyrazine annulation. The study is conducted for LPA mimics containing up to six dihydropyrazine units annulated to benzene (pB₁–pB₆), naphthalene (pN₁–pN₆), anthracene (pA₁–pA₆) and tetracene (pT₁–pT₆) cores. The longest of them pT₆ contains 34 linearly connected six-membered rings. The dehydrogenation energy (E_dh) of the N-heterocycles of the LPA mimics showed endothermic character and indicated their higher stability than dehydrogenated N-heteroacenes. The total E_dh (ΣE_dh) is proportional to the increase in the number of heterocycles and the increase in the size of the LPA core. The aromaticity of individual rings of all the LPA mimics is assessed on the basis of the harmonic oscillator model of aromaticity (HOMA) and nucleus independent chemical shift (NICS) parameters. Both parameters showed strong linear correlation with ΣE_dh, confirming the geometric, magnetic and energetic criteria of aromaticity. The electronic features of the LPA mimics assessed by analysing molecular electrostatic potential topography and molecular orbitals have shown that the LPA cores retain the reactivity of the parent LPA. Furthermore, significant mixing of the N-lone pairs of the heterocycle with carbon π-orbitals improves aromaticity and decreases the HOMO–LUMO energy gap.

---

Introduction

Linear polyacenes (LPAs), aromatic hydrocarbons composed of linearly fused benzene rings,¹ possess attractive optical and electronic properties suitable for nanotechnology applications, organic electronics,² lithium ion batteries,³ ferromagnetic materials,⁴etc. The optoelectronic application potential of these molecules is linked to their ability to tune the HOMO–LUMO gap with the increase in the oligomer size,^5,6 strong solid state two dimensional interactions in the electronic level,⁵ and charge mobility.^5,7,8 Among the LPAs, pentacene is widely studied due to its optical and semiconducting properties suitable for applications in the area of organic field effect transistors. Though LPA systems longer than pentacene such as heptacene, octacene and nonacene have been synthesized on a polymer matrix by photogeneration, the application potential of their p-type semiconducting properties is very limited due to chemical instability.^9–11 According to Clar's theory, a LPA system is inherently more reactive with the increase in its length due to the phenomenon of aromatic dilution.^12,13

Clar's rule of aromatic sextets is a very powerful tool to describe the properties of sp²-carbon bonded systems like polycyclic aromatic hydrocarbons (PAH).¹⁴ Clar proposed that in the case of PAH, the one showing the greatest number of localized sextets and the minimum number of localized double bonds is the most aromatic and most stable.^15,16 For instance, in the isomeric 4-ring systems given in Scheme 1, the aromaticity follows the order tetracene < benzophenanthrene ≈ chrysene < triphenylene. In the LPA topology of tetracene, one can draw only one sextet of π-electrons in Clar's formula (Scheme 1) whereas more than one sextet is possible for all other topologies.¹⁷ With the increase in the length of LPAs, the aromatic character decreases as only one sextet can be delocalized for the whole system, which leads to significant double bond localization in the molecule and higher reactivity (Scheme 2). The arrow emanating from the sextet ring in Scheme 2 suggests aromatic dilution. Bultinck et al. derived the atoms-in-molecule based six centre index (SCI-AIM) to study the electron delocalization in a linear polyacene series and showed that aromaticity decreases on going from outer to inner rings.¹⁸ Aromaticity is currently described as a multidimensional phenomenon, related to the structural, electronic, magnetic and energetic properties of molecules.^19–26 A large volume of literature exists in the case of linear polyacenes dedicated to the understanding of magnetic properties and aromaticity.^27–30

Scheme 1 Clar's sextet formula for isomeric 4-ring systems, from left tetracene, benzophenanthrene, chrysene, and triphenylene.

Scheme 2 Clar's notation to show the aromatic dilution in linear polyacenes.

Since LPAs larger than pentacene are chemically highly unstable, one practical way to introduce more fused hexagonal rings in the chain is by designing suitable LPA mimics. This could be done by doping heteroatoms into the LPA framework.^2,31 The nitrogen atom, isoelectronic with C–H, is an immediate choice to integrate into the acene skeleton as this could retain the π-conjugation features of the molecule.³² Synthetic strategies utilizing condensation reactions,^33,34 coupling reactions,^35–38 Diel's Alder reactions,³⁹ and oxidative coupling reactions have been utilized for the synthesis of N-heteroacenes.^40–46 Large N-heteroacenes have been known since the beginning of the 20th century^47,48 and are still being intensively researched.^32,49–56 Many diazapentacene derivatives have been successfully utilized as electronic materials in thin film transistors.^51,57–62

Herein we propose that by fusing LPA moieties with two N–H units, large LPA mimics can be designed which could show substantial improvement in the aromatic character of the LPA core. The incorporation of the N–H units proposes the utilization of N-lone pairs to enhance the π-electron conjugation as well as the net electron content within a hexagon in the molecule. This design strategy improves the aromatic sextet distribution in the LPA mimics and suggests the formation of stable oligomeric and even polymeric long chain mimics of LPAs. In such systems, the N-heterocyclic connection between two LPA moieties is fulfilled by a 1,4-dihydropyrazine unit. Even though the existence of 1,4-dihydropyrazine derivatives was known, the successful synthesis of a carboxylic acid ester derivative was performed in the year 1969 only.⁶³ The structure of these alleged 1,4-dihydropyrazines came into the scene a year after that.⁶⁴ The photophysical properties of N,N-dimethyl derivatives of the above mentioned pyrazines were also widely studied.⁶⁵ The successful synthesis of the non-substituted system took one more year for completion.⁶⁶ Attempts for an easy and economical synthesis of such systems are continuing.^67–70 Linear extensions of dihydropyrazine moieties connected through benzene groups are known and among them three benzene groups interconnected by two dihydropyrazine groups are termed tetraazapentacenes.^71,72 Halogen substituted tetraazapentacenes have been successfully synthesized,⁷² but not the unsubstituted ones. 6,13-Dihydrodibenzo[b,i]phenazine is successfully synthesised which can be used as a pentacene substitute having superior qualities.⁵⁷

Computational method

All the molecules have been optimized using the M06L/6-311++G(d,p) level of density functional theory (DFT) as implemented in the Gaussian09 suite of programs.^73–75 All the optimized structures are confirmed as energy minima by vibrational frequency calculation. The wavefunction generated using M06L/6-311++G(d,p) is used for molecular electrostatic potential (MESP) calculations. For all the molecules, the aromaticity of each ring is quantified by computing the nucleus independent chemical shift (NICS)⁷⁶ at the ring center (NICS(0)). Also NICS at 1 Å above the ring center (NICS(1)) and the z-component of NICS at 1 Å above the ring center (NICS(1)_zz) are calculated. The harmonic oscillator model of the aromaticity (HOMA) index is calculated for all the systems using the procedure of Krygowski et al.⁷⁷ The selection of the M06L functional (meta-GGA local functional with 0% Hartree–Fock (HF) exchange) is based on a previous benchmark study which showed that this method can yield a reliable geometry and interaction energy close to the CCSD(T) level accuracy for a variety of non-covalent dimers.⁷⁸ Furthermore, recent studies conducted using this method on a variety of systems have provided reliable results in agreement with high accuracy ab initio methods and dispersion-corrected DFT methods.^79–81 In order to further substantiate the use of this method to study the present set of molecules, we have done calculations using two more Minnesota functionals, viz. M06/6-311++G(d,p) (hybrid meta-GGA method with 27% HF exchange) and M06-2X/6-311++G(d,p) (hybrid meta-GGA method with 54% HF exchange) for a representative series of molecules.

Results and discussion

Design strategy

The molecular design strategy is based on improving Clar's sextet distribution in the LPA mimics. Benzene has the perfect aromatic sextet and its six π-electrons are delocalized over six CC bonds meaning that the number of π-electrons per CC bond (n_π) is 1. In all PAH systems, n_π is always less than 1 and for LPA series, this value decreases with the increase in the length. For instance, for naphthalene, anthracene, tetracene, and pentacene, n_π is 0.91, 0.88, 0.86 and 0.85, respectively. By fusing two LPA moieties through two –NH– units, a higher LPA mimic can be designed. Every fusion point will represent a 1,4-dihydropyrazine unit. In the LPA mimic, the formal π-electron count of every N-heterocycle is 8, which does not follow Hückel's rule, and hence, is antiaromatic. However, as the n_π electron count of the LPA decreases, electron flow from the electron rich N-heterocycle to the hydrocarbon core is expected which could stabilize the system. We use a notation that uses two letters and one number to represent each of the designed systems. The first letter in the notation is p which represents the 1,4-dihydropyrazine-type character of the N-heterocycle while the second letter B, N, A or T represents the core unit made up of benzene, naphthalene, anthracene or tetracene moieties, respectively. Furthermore, the numbers 1, 2, 3, 4, 5 and 6 represent the number of 1,4-dihydropyrazine-type N-heterocycles in the molecule. For a system having ‘n’ dihydropyrazine moieties, there will be ‘n + 1’ benzene, naphthalene, anthracene or tetracene units present. For example, pB₁ made up of one 1,4-dihydropyrazine-type heterocycle and two benzene cores is the dihydrophenazine molecule (Fig. 1). Similarly pN₂ represents an LPA mimic made up of three naphthalene cores and two 1,4-dihydropyrazine-type N-heterocycles. The dihydropyrazine systems selected for this study are pB₁–pB₆, pN₁–pN₆, pA₁–pA₆ and pT₁–pT₆ (ESI†).

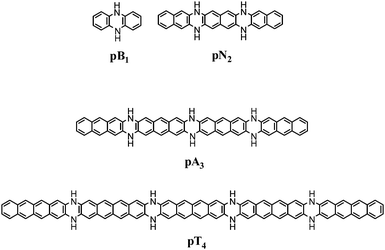Fig. 1 Representative structures of the molecules under study containing 1,4-dihydropyrazine-type N-heterocycles.

In Table 1, the n_π value of all the LPA mimics is depicted along with the n_π value of the LPA. It is very clear that annulation of an LPA with N-heterocycles improves the net electron content of the LPA mimic. This effect is dominant in the pB series as all molecules retain an n_π value of 1 for all benzene cores. In the pN, pA and pT series, n_π is always higher than the LPA core and it increases with the increase in the length of the molecule. Hence, an increase in aromatic character is expected with the increase in the net electron content of the system. The molecules in the pB series show a zigzag structure with respect to the orientation of the six-membered rings as shown in Fig. 2 while all other systems exhibit a planar structure. In the pB series, pyramidalisation to the NH group occurs in every ring and leads to the zigzag structure. This phenomenon can be attributed to the fact that benzene cores in the pB series possess a full sextet of electrons and thus are reluctant to accept lone pair electron density from N. Thus, N-centers adopt a pyramidal configuration to avoid destabilization from inherent Hückel antiaromaticity within the N-heterocycle.

Table 1 The ratio of the number of π electrons to the total number of bonds (n_π) in LPAs and LPA-based heterocycles. B, N, A and T represent benzene, naphthalene, anthracene and tetracene, respectively

System	n π	System	n π	System	n π	System	n π
B	1.000	N	0.909	A	0.875	T	0.857
pB1	1.000	pN1	0.923	pA1	0.889	pT1	0.870
pB2	1.000	pN2	0.927	pA2	0.893	pT2	0.873
pB3	1.000	pN3	0.929	pA3	0.895	pT3	0.875
pB4	1.000	pN4	0.930	pA4	0.896	pT4	0.876
pB5	1.000	pN5	0.930	pA5	0.897	pT5	0.877
pB6	1.000	pN6	0.931	pA6	0.897	pT6	0.877

---

Fig. 2 Representative set of molecules to distinguish zigzag pB and planar all other series.

Dehydrogenation energy

In a recent review on the topic of large heterocyclic acenes, Bunz described that hydrogenation of 1 to 2 is exothermic by 49.5 kcal mol⁻¹ and thermodynamically favourable while hydrogenation of 2 to 3 is endothermic by 2.5 kcal mol⁻¹ (Fig. 3).⁸² In the present study, 3 is pB₂. Bunz also correlated the synthesis of terminal substituted 2 with its thermodynamic stability. However our theoretical calculations using the method used by Bunz (B3LYP/6-31G**) suggest that hydrogenation of 1 to 2 and 2 to 3 is exothermic by 42.5 and 16.3 kcal mol⁻¹, respectively. It indicates an error in the previous calculation. Furthermore, at the M06L/6-311++G(d,p) level too, both hydrogenation reactions are found to be exothermic and the hydrogenation energy values are in agreement with the B3LYP method (hydrogenation of 1 to 2 and 2 to 3 are exothermic by −40.02 and −10.38 kcal mol⁻¹, respectively). In order to assess the thermodynamic stability of the systems (pB₁–pB₆, pN₁–pN₆, pA₁–pA₆ and pT₁–pT₆), the energy change associated with dehydrogenation of N-centers is calculated.

Fig. 3 Calculated heats of hydrogenation for the reduction of 1 to 2 and 2 to 3. Values in regular font are for the M06L/6-311++G(d,p) level and those in italics are for the B3LYP/6-31G** level.

The dehydrogenation energy (E_dh) corresponding to the N-heterocycles of all the set of molecules is given in Table 2 at the M06L/6-311++G(d,p) level. The notation N1, N2, etc. is used to indicate the number of N-heterocycles dehydrogenated in the molecule, starting from one terminal to the other. All the reactions are endothermic suggesting that the hydrogen-rich states are more stable than the dehydrogenated states. This is very clear from the total E_dh given in Table 2. The increase in the total E_dh (ΣE_dh) is proportional to the increase in the number of heterocycles and the increase in the size of the PAH moiety. In pB₁, pN₁, pA₁ and pT₁ systems, E_dh values are 23.8, 38.8, 46.3, and 50.3 kcal mol⁻¹, respectively. These numbers show a strong linear correlation with the n_π values of benzene, naphthalene, anthracene and tetracene (ESI†). This correlation suggests that lone pair donation from nitrogen to the π-system increases with a decrease in the n_π value and that enhances the overall π-bonding strength and aromaticity of the system. As a result, the dehydrogenation reaction becomes increasingly more difficult for larger acene mimics. For instance, E_dh corresponding to the dehydrogenation of all the N-heterocycles, viz. two in pB₂, pN₂, pA₂ and pT₂, three in pB₃, pN₃, pA₃ and pT₃, four in pB₄, pN₄, pA₄ and pT₄, five in pB₅, pN₅, pA₅ and pT₅ and six in pB₆, pN₆, pA₆ and pT₆ gradually increases, proportional to the decrease in n_π of the system (in all cases, n_πversus E_dh correlations show a correlation coefficient in the range 0.997–0.999).

Table 2 Dehydrogenation energy E_dh (kcal mol⁻¹) of the N-heterocycles of LPA mimics

	N1	N2	N3	N4	N5	N6	ΣEdh
pB1	23.8						23.8
pB2	40.0	12.2					52.2
pB3	45.6	25.8	11.3				82.7
pB4	47.9	30.4	24.0	11.2			113.5
pB5	48.8	32.7	27.2	24.6	11.1		144.4
pB6	49.5	34.1	30.2	27.4	18.7	15.6	175.5
pN1	38.8						38.8
pN2	48.0	32.9					80.9
pN3	47.4	41.8	31.9				121.1
pN4	39.3	44.0	40.3	31.6			155.2
pN5	34.3	44.6	24.7	57.6	31.7		192.9
pN6	31.3	45.0	43.3	41.8	39.6	31.4	232.4
pA1	46.3						46.3
pA2	51.6	43.1					94.7
pA3	38.7	48.2	42.6				129.5
pA4	32.9	49.2	47.6	42.7			172.4
pA5	49.1	43.3	35.7	47.4	42.3		217.8
pA6	18.5	49.6	48.8	49.7	45.9	42.3	254.8
pT1	50.3						50.3
pT2	41.0	48.2					89.2
pT3	45.51	39.8	47.9				153
pT4	44.2	32.5	51.0	47.9			175.6
pT5	15.9	51.8	51.4	50.9	47.7		217.7
pT6	33.6	49.6	47.5	32.0	50.9	47.7	261.3

---

Bond length equalization and aromatic character

Geometry-based indices have been used for quantifying aromaticity especially in the case of planar systems.^77,83 The bond length based index of aromaticity, HOMA developed by Krygowski et al. is one of the most prominent indices among this category and is used to compare the aromaticity of a variety of organic molecules.⁷⁷ For a perfect aromatic system, HOMA is 1 and a value close to zero indicates non-aromatic character.

Aromatic molecules tend to show bond length equalization and a HOMA value close to 1. The CC bond length of benzene (1.391 Å at M06L/6-311++G(d,p) level) is considered to be the most optimum for an aromatic hydrocarbon. In the present study, the notation Nring1, Nring2, etc. is used to indicate the most peripheral rings to the interior symmetrically distinguishable N-heterocycles. Similarly, the notation Cring1, Cring2, etc. is used to indicate the most peripheral rings to the interior carbon rings. The HOMA indices calculated for all the molecules are depicted in Tables 3–6. In the pB series, the HOMA of every benzene unit is 0.98 or 0.99, showing the perfect aromatic nature of the individual benzene rings. Furthermore, the N-heterocycle has a HOMA in the range 0.65–0.69 which indicates substantial aromatic character as only a 30–35% reduction in aromaticity is observed compared to the HOMA of 1.00 for one of the most aromatic N-heterocycles, pyridine. In the pN series, among the carbon rings, the terminal ring is the most aromatic with its HOMA being 0.85–0.86 whereas the ring adjacent to it is the least aromatic (HOMA 0.76–0.77). In pN₃–PN₅, both rings of the interior naphthalene units show nearly the same aromatic character (HOMA 0.80–0.82) and the N-heterocycles show slightly higher values (0.68–0.71) than the pB series. In the case of pA₁, the HOMA of Cring1, Cring2, and Cring3 is 0.72, 0.74 and 0.65, respectively. This pattern and magnitude of HOMA is retained in pA₂–pA₅. Furthermore, HOMA 0.68–0.75 is observed for the carbon rings of all other anthracene moieties whereas a slightly lower HOMA 0.65–0.68 is observed for all dihydropyrazine rings. In the case of the pT series, all the terminal tetracene moieties show nearly identical HOMA patterns with terminal, second, third and fourth carbon rings showing values of 0.64–0.65, 0.67–0.68, 0.64–0.65, and 0.58, respectively. The inner tetracene moieties show HOMA values in the range 0.61–0.67 whereas the aromatic character of N-heterocycles is in the range 0.62–0.64, the lowest compared to all other systems. The HOMA of benzene (1.00), naphthalene (0.77), anthracene (0.62 for Cring1, 0.70 for Cring2), and tetracene (0.53 for Cring1, 0.60 for Cring2) is almost fully retained or even enhanced in all the respective carbon rings in the LPA-based N-heterocyclic systems. The sum of the HOMA values of all the rings can be considered as a measure of the global aromaticity of the molecules. This quantity referred to as ΣHOMA is also depicted in Tables 3–6. The ΣHOMA of all the different series of compounds show strong linear correlations with the corresponding total dehydrogenation energy ΣE_dh (Fig. 4). These correlations strongly suggest that E_dh values are intimately connected with the aromatization energy of the molecule. According to Clar, the LPA systems show ‘aromatic dilution’ with the increase in the length of the molecule. This phenomenon is clearly visible in the correlation plots shown in Fig. 4 in terms of the decrease in slope as we move from pB to pN to pA to pT series of molecules.

Table 3 HOMA index of symmetrically distinguishable rings in the pB series of LPA mimics

	pB1	pB2	pB3	pB4	pB5	pB6
Cring1	0.98	0.98	0.98	0.98	0.98	0.98
Nring1	0.69	0.68	0.68	0.67	0.67	0.67
Cring2		0.99	0.99	0.99	0.99	0.99
Nring2			0.66	0.67	0.66	0.65
Cring3				0.99	0.99	0.99
Nring3					0.66	0.66
Cring4						0.99
ΣHOMA	1.67	2.65	3.31	4.3	4.95	5.93

---

Table 4 HOMA index of symmetrically distinguishable rings in the pN series of LPA mimics

	pN1	pN2	pN3	pN4	pN5	pN6
Cring1	0.85	0.85	0.85	0.85	0.86	0.86
Cring2	0.77	0.76	0.76	0.77	0.77	0.77
Nring1	0.69	0.69	0.69	0.70	0.70	0.70
Cring3		0.80	0.81	0.82	0.82	0.82
Cring4			0.80	0.81	0.81	0.81
Nring2			0.70	0.68	0.71	0.71
Cring5				0.81	0.82	0.82
Cring6					0.81	0.81
Nring3					0.71	0.71
Cring7						0.81
ΣHOMA	2.31	3.1	4.61	5.44	7.01	7.82

---

Table 5 HOMA index of symmetrically distinguishable rings in the pA series of LPA mimics

	pA1	pA2	pA3	pA4	pA5	pA6
Cring1	0.72	0.73	0.72	0.72	0.72	0.72
Cring2	0.74	0.74	0.74	0.74	0.74	0.74
Cring3	0.65	0.65	0.65	0.65	0.65	0.65
Nring1	0.65	0.65	0.65	0.65	0.65	0.65
Cring4		0.69	0.69	0.69	0.69	0.69
Cring5		0.75	0.75	0.75	0.75	0.75
Cring6			0.68	0.68	0.68	0.68
Nring2			0.66	0.66	0.66	0.66
Cring7				0.69	0.69	0.69
Cring8				0.75	0.75	0.75
Cring9					0.68	0.68
Nring3					0.66	0.66
Cring10						0.68
Cring11						0.75
ΣHOMA	2.76	4.21	5.54	6.98	8.32	9.75

---

Table 6 HOMA index of symmetrically distinguishable rings in the pT series of LPA mimics

	pT1	pT2	pT3	pT4	pT5	pT6
Cring1	0.64	0.64	0.65	0.65	0.65	0.65
Cring2	0.68	0.68	0.67	0.67	0.67	0.68
Cring3	0.65	0.65	0.65	0.65	0.64	0.65
Cring4	0.58	0.58	0.58	0.58	0.58	0.58
Nring1	0.62	0.62	0.64	0.62	0.63	0.64
Cring5		0.61	0.61	0.61	0.61	0.61
Cring6		0.67	0.67	0.67	0.67	0.67
Cring7			0.66	0.67	0.67	0.67
Cring8			0.61	0.61	0.61	0.61
Nring2			0.63	0.63	0.63	0.63
Cring9				0.61	0.61	0.61
Cring10				0.67	0.67	0.67
Cring11					0.67	0.67
Cring12					0.61	0.61
Nring3					0.63	0.63
Cring13						0.61
Cring14						0.67
ΣHOMA	3.17	4.45	6.37	7.64	9.55	10.86

---

Fig. 4 Correlation between the HOMA index and dehydrogenation energy.

Nucleus independent chemical shift and aromatic character

Magnetic criteria for aromaticity are popularly described in terms of the NICS index as portrayed by Schleyer and co-workers.⁷⁶ We have analyzed three NICS indices, viz. the NICS at the center of each six-membered ring (NICS(0)), at 1 Å above every ring center (NICS(1)) and also the z-component of the NICS at 1 Å above the ring center (NICS_zz(1)). Among these indices, NICS_zz(1) is considered to be more reliable than others and for all the discussions, this quantity is used in the text and others are provided in the ESI.† In fact, the relative ordering of the magnitude of all three indices is very similar and so the conclusions drawn from any of them are the same.

The NICS_zz(1) values of benzene, naphthalene, Cring1 of anthracene and Cring1 of tetracene are −17.30, −28.65, −26.32 and −23.95, respectively and those of Cring2 of anthracene and Cring2 of tetracene are −34.11 and −33.85, respectively. These values may give a false impression that benzene is the least aromatic and the most aromatic is Cring2 of anthracene or tetracene. The discrepancies in the NICS, its size-, shape- and distance dependencies as well as more sophisticated approaches to the NICS treatment of aromaticity have been elaborated in the past.⁸⁴ We do not attempt to directly compare the NICS of PAH molecules and LPA mimics because this index varies with respect to the number of heteroatoms, size and symmetry of the molecules. Since the NICS works best for comparing the aromaticity of a similar set of molecules, we will focus on the relative ordering of the NICS along the symmetrically distinguishable rings, starting from one at the terminal to the last in the middle.

Table 7 NICS_zz(1) values of symmetrically distinguishable rings in the pB series of LPA mimics

	pB1	pB2	pB3	pB4	pB5	pB6
Cring1	−15.56	−17.94	−18.03	−18.69	−19.22	−19.98
Nring1	18.49	16.10	16.26	16.51	16.51	16.69
Cring2		−7.02	−7.32	−7.08	−6.70	−6.45
Nring2			13.65	13.83	14.00	14.02
Cring3				−8.68	−8.63	−8.83
Nring3					13.60	13.66
Cring4						−8.71

---

In all the pB, pN, pA, and pT series of molecules, the Crings show significantly negative NICS_zz(1) indicating aromatic character whereas all the Nrings show positive NICS_zz(1) indicating antiaromaticity (Tables 7–10). In the pB series, the negative character of NICS_zz(1) increases gradually for Cring1 and reaches the most negative −19.98 for pB₆. The inner Crings show significantly lower negative NICS_zz(1) (−6.45 to −8.83) than the terminal ones whereas compared to the terminal Nrings (18.49 to 16.51), the inner Nrings appear to be less antiaromatic (13.60 to 14.02). The positive NICS_zz(1) values of Nrings can be correlated with a π-electron count of 8 for the N-heterocycle. Like the pB series, NICS_zz(1) of pN, pA and pT series too indicates a significant decrease in aromaticity for LPA moieties from the terminal to the inner region. Moreover, compared to NICS_zz(1) in the range 18.21 to 19.34 observed for N-heterocycles of the pN series, NICS_zz(1) for the pA series shows a decrease by 3.37 to 3.65 units while that of pT series shows a decrease by 5.45 to 5.54 units (Tables 9 and 10).

Table 8 NICS_zz(1) values of symmetrically distinguishable rings in the pN series of LPA mimics

	pN1	pN2	pN3	pN4	pN5	pN6
Cring1	−22.65	−22.39	−22.46	−22.17	−22.12	−21.86
Cring2	−14.48	−14.53	−14.10	−14.11	−14.19	−14.18
Nring1	19.18	19.14	19.24	19.20	19.30	19.34
Cring3		−9.95	−9.80	−9.64	−9.35	−9.13
Cring4			−10.40	−10.57	−10.57	−10.82
Nring2			18.27	18.21	18.47	18.51
Cring5				−10.35	−10.06	−9.86
Cring6					−10.30	−10.45
Nring3					18.70	18.70
Cring7						−10.10

---

Table 9 NICS_zz(1) values of symmetrically distinguishable rings in the pA series

	pA1	pA2	pA3	pA4	pA5	pA6
Cring1	−23.70	−23.09	−22.94	−22.78	−22.49	−22.47
Cring2	−26.77	−26.36	−25.93	−25.68	−25.49	−25.38
Cring3	−14.68	−14.82	−15.32	−15.68	−16.02	−16.41
Nring1	14.84	15.11	15.19	15.25	15.29	15.13
Cring4		−12.51	−11.79	−11.45	−11.02	−10.64
Cring5		−21.31	−21.25	−21.21	−21.15	−21.26
Cring6			−12.82	−13.04	−13.32	−13.74
Nring2			15.52	15.56	15.64	15.69
Cring7				−12.36	−11.93	−11.60
Cring8				−21.11	−20.97	−21.01
Cring9					−12.56	−13.00
Nring3					15.63	15.60
Cring10						−12.21
Cring11

---

Table 10 NICS_zz(1) values of symmetrically distinguishable rings in the pT series of LPA mimics

	pT1	pT2	pT3	pT4	pT5	pT6
Cring1	−22.49	−21.79	−21.17	−20.67	−20.39	−19.52
Cring2	−30.10	−29.59	−29.34	−29.05	−28.72	−28.46
Cring3	−27.96	−27.78	−27.91	−28.17	−28.57	−28.57
Cring4	−14.61	−14.64	−14.90	−15.34	−15.41	−16.00
Nring1	13.75	13.45	13.09	12.89	12.76	12.45
Cring5		−13.18	−12.67	−12.03	−12.08	−11.27
Cring6		−24.82	−24.71	−24.54	−24.48	−24.71
Cring7			−24.58	−24.63	−24.74	−24.70
Cring8			−13.31	−13.59	−13.79	−14.38
Nring2			13.69	13.67	13.60	13.77
Cring9				−12.81	−12.38	−11.98
Cring10				−24.45	−24.31	−24.32
Cring11					−24.44	−24.48
Cring12					−13.03	−13.44
Nring3					13.73	13.80
Cring13						−12.55
Cring14						−24.26

---

A linear correlation between the total negative NICS_zz(1) value (ΣNICS_zz(1)) that represents the aromatic character of the Crings and the total dehydrogenation energy ΣE_dh exists for the pB, pN, pA and pT series of molecules (Fig. 5). The magnitude of the slope of the correlation line is the highest for the pB series and it decreases along the pN, pA and pT series indicating aromatic dilution. This correlation as well as the correlation observed between ΣHOMA and ΣE_dh in Fig. 4 clearly brings out the multidimensional character of aromaticity, viz. the underlying magnetic, structural and energetic features. Previously, Solà et al.⁸⁵ noted that the NICS method has well-known problems in dealing with some condensed benzenoid structures^27,86–90 while in the case of Clar's systems analyzed here, both HOMA and NICS_zz(1) performed considerably well.⁸⁵ Solà et al. also suggested that aromaticity indices based on electron delocalization concepts may perform better than both geometry and magnetic based indices of aromaticity in dealing with condensed benzenoid molecules.⁸⁵

Fig. 5 Correlation between the ΣNICS_zz(1) index for the pB, pN, pA, and pT series of molecules and the dehydrogenation energy.

Molecular electrostatic potential and electron delocalization

Fig. 6 depicts the MESP features of benzene, naphthalene, anthracene and tetracene. The π-electron cloud of the molecules is seen in the MESP isosurface lobes and the most negative valued MESP (V_min) is useful for comparing the relative electron rich character of the π-regions in different molecules. V_min is the most negative for benzene (−15.06 kcal mol⁻¹) and along the LPA series, it gradually decreases with the increase in the n_π value. The MESP features of the LPA mimics pB₆, pN₆, pA₆ and pT₆ are depicted in Fig. 7 as representative cases. For the rest of the systems, MESP features show close similarity to the representative cases and are presented in the ESI.† The V_min observed on the LPA unit of every system is depicted in Table 11 along with the sum of all V_min values referred to as ΣV_min. In the pB series, the N-heterocycles show V_min for the N-lone pair region in the range −25.73 to −34.51 kcal mol⁻¹, wherein the innermost N-heterocycle shows the most negative character while the outermost one shows the least negative character. However, compared to V_min of dihydropyrazine (−46.25 kcal mol⁻¹), the N-lone pairs of the heterocycles are significantly less negative. This indicates minor delocalization of the N-lone pairs in the LPA mimics which is not surprising considering the pyramidal nature of the N-centers. In the pN series, V_min observed for the N-heterocycles is in the range −3.14 to −8.78 kcal mol⁻¹ while the pA and pT series do not show V_min for N-heterocycles. This indicates that the N-lone pair is strongly delocalized with the LPA units in the pN, pA and pT series of molecules and the planar configuration of N-centers substantiates this statement. The V_min data in Table 11 clearly show that as the size of the LPA mimic increases, the negative character of V_min on the outer most LPA unit increases gradually. This pattern is almost repeated in the interior LPA units as well. The enhancement in the negative character of V_min with the increase in the size of the molecule suggests the increasing participation of N-lone pairs in π-electron delocalization. This also means that the aromaticity of the molecule increases with the increase in the length of the molecule. In fact, the ΣV_min quantity emerges as a good indicator of electron delocalization in the molecule and shows a strong linear correlation with the total dehydrogenation energy ΣE_dh for different series of molecules (Fig. 8). The magnitude of the slope of the correlation plot is the highest for the pT series and it decreases along the pA, pN and pB series. This indicates that N-lone pair donation to enhance the aromaticity of hydrocarbon portions is the highest for the pT series and the lowest for the pB series. The MESP isosurface features also indicate that each of the LPA unit in the LPA mimic almost retains the MESP features of the parent hydrocarbon. This may suggest that the reactivity of an LPA unit in an LPA mimic could match the reactivity of the parent hydrocarbon irrespective of the length of the molecule. Hence, the stability of the LPA mimic could largely depend on the stability of the parent hydrocarbon. In fact, considering the enhancement in the total aromaticity of the LPA mimic due to the utilization of N-lone pairs in π-conjugation, the overall stability of the system could be predicted to be higher than the parent hydrocarbon. Thus, the MESP features strongly suggest the existence of stable LPA mimics containing N-heterocycles.

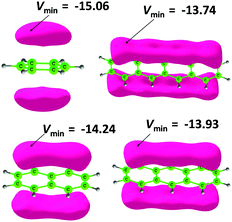Fig. 6 Plots of the MESP isosurface (−9.0 kcal mol⁻¹) for benzene, naphthalene, anthracene and tetracene along with the MESP minimum in kcal mol⁻¹.

Fig. 7 Plots of the MESP isosurface (−9.0 kcal mol⁻¹) for benzene, naphthalene, anthracene and tetracene along with the MESP minimum in kcal mol⁻¹.

Table 11 MESP minimum (kcal mol⁻¹) observed on the LPA units for the pB, pN, pA, and pT series of molecules

System	V min on the LPA unit from left to right							ΣVmin
	1	2	3	4	5	6	7
pB1	−19.0	−19.0						−38.1
pB2	−20.4	−15.4	−20.4					−56.1
pB3	−20.8	−16.6	−16.6	−20.8				−74.8
pB4	−21.1	−17.1	−17.5	−17.1	−21.1			−93.9
pB5	−21.3	−17.3	−18.0	−18.0	−17.3	−21.3		−113.2
pB6	−21.4	−17.4	−18.3	−18.5	−18.3	−17.4	−21.4	−132.4
pN1	−18.3	−18.3						−36.6
pN2	−20.1	−14.4	−20.1					−54.6
pN3	−20.8	−15.7	−15.7	−20.8				−73.1
pN4	−21.2	−16.5	−16.9	−16.5	−21.2			−92.1
pN5	−21.4	−16.8	−17.4	−17.4	−16.8	−21.4		−111.2
pN6	−21.5	−17.0	−17.8	−18.0	−17.8	−17.0	−21.5	−130.4
pA1	−17.4	−17.4						−34.9
pA2	−18.6	−15.8	−18.6					−53.1
pA3	−19.2	−16.9	−16.9	−19.2				−72.2
pA4	−19.3	−17.4	−17.9	−17.4	−19.3			−91.3
pA5	−19.6	−17.7	−18.4	−18.4	−17.7	−19.6		−111.3
pA6	−19.5	−17.6	−18.4	−18.7	−18.4	−17.6	−19.5	−129.6
pT1	−16.6	−16.6						−33.1
pT2	−17.4	−15.3	−17.4					−50.1
pT3	−17.7	−16.3	−16.3	−17.7				−67.9
pT4	−18.0	−16.6	−17.0	−16.6	−18.0			−86.0
pT5	−18.0	−16.8	−17.4	−17.4	−16.8	−18.0		−104.4
pT6	−18.0	−16.9	−17.6	−17.7	−17.6	−16.9	−18.0	−122.7

---

Fig. 8 Correlation between the ΣV_min index for the pB, pN, pA, and pT series of molecules and the dehydrogenation energy.

Frontier molecular orbitals

In the case of benzene, naphthalene, anthracene, and tetracene, the HOMO energy (ε1), LUMO energy (ε2), and the HOMO–LUMO energy gap (Δε) given as ordered triples (ε1, ε2, Δε) in eV is (−6.44, −0.95, 5.49), (−5.56, −1.88, 3.68), (−5.04, −2.49, 2.55) and (−4.69, −2.89, 1.80), respectively. A steady decrease in the Δε with respect to the size of the acene is evident and suggests that large LPA systems are attractive for HOMO–LUMO energy modulation for photonic applications and the limiting factor is the unstable character of the higher derivatives. Compared to LPA, all the corresponding LPA mimics show significantly higher ε1 and slightly higher ε2 (Table 12). For instance, in the case of LPA mimics composed of anthracene moieties, viz. pA₁–pA₆, ε1 is in the range −4.55 to −3.99 eV which is higher than ε1 of anthracene (−5.04 eV) while their ε2 falls in a narrow range −2.44 to −2.34 eV which is close to ε1 −2.49 eV observed for anthracene. The HOMO and LUMO pictures given for the representative cases pA₂ and pT₂ (Fig. 9) show that the HOMO is formed by the delocalization of N-lone pairs in the B_1g symmetric π-orbital for the former and the A_u symmetric π-orbital for the latter (see the ESI† for the HOMO and the LUMO of other molecules) whereas the LUMO localized on the LPA core shows features very similar to the B_3u symmetric LUMO of anthracene and the B_1g symmetric LUMO of tetracene (under D_2h molecular symmetry). In fact, in every molecule, two sets of π-MOs are observed, viz. one characteristic of the LPA moiety, localized exclusively on them and devoid of any contributions from the N-lone pairs and the other consisting of the contributions of N-lone pairs. The delocalization of N-lone pairs in the HOMO is observed for all the LPA mimics and the energy of the HOMO is influenced by the number of N-centers in the molecule whereas LUMO energy is independent of the N-centers. Since only the HOMO energy showed a significant increase with respect to the length of the LPA mimic, a steady decrease in the HOMO–LUMO energy gap with the increase in the size of the molecule is observed in all the systems. In fact, on going from pB₁ to pT₆, HOMO–LUMO energy modulation can be achieved from 3.21 eV to 1.22 eV, which suggests that excellent band gap tuning using dihydropyrazine annulated linear polyacenes can be achieved for solar cell applications.

Table 12 HOMO (ε1), LUMO (ε2) and HOMO–LUMO energy gap (Δε) for the pB, pN, pA, and pT series of molecules. All values in eV. B, N, A and T are benzene, naphthalene, anthracene, and tetracene, respectively

System	ε1	ε2	Δε	System	ε1	ε2	Δε
B	−6.44	−0.95	5.49	A	−5.04	−2.49	2.55
pB1	−4.15	−0.94	3.21	pA1	−4.55	−2.44	2.11
pB2	−3.61	−0.93	2.69	pA2	−4.34	−2.40	1.93
pB3	−3.40	−0.91	2.50	pA3	−4.17	−2.38	1.80
pB4	−3.28	−0.89	2.39	pA4	−4.08	−2.36	1.73
pB5	−3.21	−0.88	2.33	pA5	−4.02	−2.35	1.68
pB6	−3.17	−0.87	2.30	pA6	−3.99	−2.34	1.65
N	−5.56	−1.88	3.68	T	−4.69	−2.89	1.80
pN1	−4.43	−1.81	2.62	pT1	−4.32	−2.84	1.47
pN2	−3.96	−1.77	2.19	pT2	−4.16	−2.81	1.35
pN3	−3.75	−1.74	2.01	pT3	−4.08	−2.79	1.29
pN4	−3.62	−1.71	1.92	pT4	−4.03	−2.77	1.26
pN5	−3.55	−1.69	1.86	pT5	−4.00	−2.76	1.24
pN6	−3.49	−1.67	1.82	pT6	−3.98	−2.75	1.22

---

Fig. 9 HOMO and LUMO orbitals of pA₂ and pT₂.

The computed values of NICS indices, HOMA, MESP V_min, HOMO–LUMO gap and E_dh values at M06 and M06-2X levels are presented in the ESI† for a representative case, the pN series of molecules. The trends in all these quantities at these two levels are found to be nearly identical to the M06L results. Furthermore, the linear correlations that we discussed in this study, viz. ΣHOMA versus ΣE_dh, ΣNICS_zz(1) versus ΣE_dh and ΣV_minversus ΣE_dh, are all found to be true for both these methods.

Conclusions

Density functional theory calculations at the M06L/6-311++G(d,p) level have been carried out on 24 dihydropyrazine annulated linear polyacene systems to study their aromaticity and HOMO–LUMO energy gap. The LPA mimics composed of benzene units (pB₁–pB₆) are non-planar while those composed of naphthalene (pN₁–pN₆), anthracene (pA₁–pA₆) and tetracene (pT₁–pT₆) units are planar. In the pB series, mixing of N-lone pairs with the π-system of the benzene core is ineffective due to the core retaining six-π electron delocalization while the decrease in the net π-electron content of the higher acene cores promotes strong delocalization of N-lone pairs with the π-electrons of carbons rings, leading to planar structures. All the molecules showed strong multidimensional character of aromaticity such as energetic stabilization, bond length equalization, and magnetic properties. The dehydrogenation energy (E_dh) computed for each of the N-heterocycles of an LPA mimic provided a simple and effective way to assess the thermodynamic stability of the molecule due to aromaticity. Aromatic stabilization is enhanced in larger LPA mimics due to enhancement in the involvement of N-lone pairs in π-electron conjugation. This has been verified by the analysis of molecular electrostatic potential (MESP) features as this property showed improvements in the electron rich character of the core hydrocarbon units at the expense of N-lone pairs. Molecular orbital (MO) features also showed the mixing of N-lone pair orbitals with the π-systems of the hydrocarbon core. This mixing led to significant modification of the HOMO of the LPA unit and an increase in its energy, while the LUMO retained properties and energy close to those of the LPA unit. In other words, dihydropyrazine annulations led to a decrease in the HOMO–LUMO energy gap. Overall, MESP and MO features indicated that the reactivity of the hydrocarbon portion of the LPA mimics should be similar to that of the parent LPA unit. In fact, considering the enhancement in the aromatic character of the LPA unit, the reactivity of the LPA mimic can be predicted to be weaker than the parent LPA system.

The dihydropyrazine systems pB₁^67,91 and pN₁⁵⁷ are known in the literature while higher analogues or higher acene based systems are yet to be synthesised. As mentioned before, the benzene core could be unattractive for making planar structures while for higher acenes such as tetracene, even one annulation of the N-heterocycle can yield a planar, aromatic structure with nine rings. We hope that the theoretical predictions provided in this work may inspire synthetic chemists to explore the rich possibilities of higher LPA mimics, including the derivatization of the N-centres for improving solubility requirements.

Acknowledgements

This research work was supported by CSIR, India through the project CSC0129 and R. R. is thankful to UGC, India for providing a research fellowship. The generous computational time provided by CSIR-4PI, Bengaluru is gratefully acknowledged.

References

1. R. Firouzi and M. Zahedi, THEOCHEM, 2008, 862, 7.
2. J. E. Anthony, Chem. Rev., 2006, 106, 5028.
3. T. Yamabe, S. Yata and S. Wang, Synth. Met., 2003, 137, 949.
4. T. Strassner, A. Weitz, J. Rose, F. Wudl and K. N. Houk, Chem. Phys. Lett., 2000, 321, 459.
5. J. E. Anthony, Angew. Chem., Int. Ed., 2008, 47, 452.
6. G. Brocks, J. van den Brink and A. F. Morpurgo, Phys. Rev. Lett., 2004, 93, 146405.
7. W.-Q. Deng and W. A. Goddard, J. Phys. Chem. A, 2004, 108, 8614.
8. Y. C. Cheng, R. J. Silbey, D. A. da Silva Filho, J. P. Calbert, J. Cornil and J. L. Brédas, J. Chem. Phys., 2003, 118, 3764.
9. D. Biermann and W. Schmidt, J. Am. Chem. Soc., 1980, 102, 3163.
10. C. Tönshoff and H. F. Bettinger, Angew. Chem., Int. Ed., 2010, 49, 4125.
11. R. Mondal, B. K. Shah and D. C. Neckers, J. Am. Chem. Soc., 2006, 128, 9612.
12. E. Clar, Polycyclic hydrocarbons, Academic Press, London, 1964, vol. 1 & 2.
13. E. Clar, The aromatic sextet, J. Wiley, London, New York, 1972.
14. M. Solà, Front. Chem., 2013, 1, 22,  DOI:10.3389/fchem.2013.00022.
15. M. Randić, Chem. Rev., 2003, 103, 3449.
16. K. P. Vijayalakshmi and C. H. Suresh, New J. Chem., 2010, 34, 2132.
17. S. R. Gadre and R. N. Shirsat, Electrostatics of Atoms and Molecules, Univesities Press, Hyderabad, 2000.
18. P. Bultinck, M. Rafat, R. Ponec, B. Van Gheluwe, R. Carbó-Dorca and P. Popelier, J. Phys. Chem. A, 2006, 110, 7642.
19. A. R. Katritzky, K. Jug and D. C. Oniciu, Chem. Rev., 2001, 101, 1421.
20. F. Feixas, E. Matito, J. Poater and M. Solà, Chem. Soc. Rev., 2015, 44, 6434.
21. S. K. Pandey, D. Manogaran, S. Manogaran and H. F. Schaefer, J. Phys. Chem. A, 2016, 120, 2894.
22. K. Jug and A. M. Köster, J. Phys. Org. Chem., 1991, 4, 163.
23. A. R. Katritzky, P. Barczynski, G. Musumarra, D. Pisano and M. Szafran, J. Am. Chem. Soc., 1989, 111, 7.
24. M. K. Cyrañski, T. M. Krygowski, A. R. Katritzky and P. v. R. Schleyer, J. Org. Chem., 2002, 67, 1333.
25. M. Alonso and B. Herradón, Chem. – Eur. J., 2007, 13, 3913.
26. A. Stanger, Chem. Commun., 2009, 1939.
27. P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217.
28. S. Motomura, M. Nakano, H. Fukui, K. Yoneda, T. Kubo, R. Carion and B. Champagne, Phys. Chem. Chem. Phys., 2011, 13, 20575.
29. M. Kaipio, M. Patzschke, H. Fliegl, F. Pichierri and D. Sundholm, J. Phys. Chem. A, 2012, 116, 10257.
30. G. Monaco and R. Zanasi, J. Phys. Chem. A, 2014, 118, 1673.
31. P. O. Dral, M. Kivala and T. Clark, J. Org. Chem., 2013, 78, 1894.
32. M. Winkler and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 1805.
33. A. L. Appleton, S. M. Brombosz, S. Barlow, J. S. Sears, J.-L. Bredas, S. R. Marder and U. H. F. Bunz, Nat. Commun., 2010, 1, 91.
34. Q. Miao, Synlett, 2012, 326.
35. O. Tverskoy, F. Rominger, A. Peters, H.-J. Himmel and U. H. F. Bunz, Angew. Chem., Int. Ed., 2011, 50, 3557.
36. J. U. Engelhart, B. D. Lindner, O. Tverskoy, F. Rominger and U. H. F. Bunz, Org. Lett., 2012, 14, 1008.
37. B. D. Lindner, J. U. Engelhart, M. Märken, O. Tverskoy, A. L. Appleton, F. Rominger, K. I. Hardcastle, M. Enders and U. H. F. Bunz, Chem. – Eur. J., 2012, 18, 4627.
38. U. H. F. Bunz and J. U. Engelhart, Chem. – Eur. J., 2016, 22, 4680.
39. C.-L. Song, C.-B. Ma, F. Yang, W.-J. Zeng, H.-L. Zhang and X. Gong, Org. Lett., 2011, 15, 2880.
40. K. Goto, R. Yamaguchi, S. Hiroto, H. Ueno, T. Kawai and H. Shinokubo, Angew. Chem., Int. Ed., 2012, 51, 10333.
41. K. Seth, S. Raha Roy and A. K. Chakraborti, Chem. Commun., 2016, 52, 922.
42. J. K. Laha, K. S. S. Tummalapalli and A. Gupta, Org. Lett., 2014, 16, 4392.
43. Z. Wróbel, K. Stachowska and A. Kwast, Eur. J. Org. Chem., 2014, 7721.
44. L. Yu, X. Zhou, D. Wu and H. Xiang, J. Organomet. Chem., 2012, 705, 75.
45. F. Wudl, P. A. Koutentis, A. Weitz, B. Ma, T. Strassner, K. N. Houk and S. I. Khan, Pure Appl. Chem., 1999, 71, 295.
46. M. Altarawneh and B. Z. Dlugogorski, Environ. Sci. Technol., 2015, 49, 2215.
47. O. Hinsberg, Liebigs Ann., 1901, 319, 257.
48. G. R. Clemo and H. McIlwain, J. Chem. Soc., 1934, 1991.
49. U. H. F. Bunz, Chem. – Eur. J., 2009, 15, 6780.
50. H. Alvaro Galué, O. Pirali and J. Oomens, Astron. Astrophys., 2010, 517, A15.
51. Q. Miao, T.-Q. Nguyen, T. Someya, G. B. Blanchet and C. Nuckolls, J. Am. Chem. Soc., 2003, 125, 10284.
52. Q. Miao, Adv. Mater., 2014, 26, 5541.
53. K. E. Maly, Cryst. Growth Des., 2011, 11, 5628.
54. Y. Ma, Y. Sun, Y. Liu, J. Gao, S. Chen, X. Sun, W. Qiu, G. Yu, G. Cui, W. Hu and D. Zhu, J. Mater. Chem., 2005, 15, 4894.
55. C. An, X. Guo and M. Baumgarten, Cryst. Growth Des., 2015, 15, 5240.
56. A. H. Endres, M. Schaffroth, F. Paulus, H. Reiss, H. Wadepohl, F. Rominger, R. Krämer and U. H. F. Bunz, J. Am. Chem. Soc., 2016, 138, 1792.
57. Q. Tang, D. Zhang, S. Wang, N. Ke, J. Xu, J. C. Yu and Q. Miao, Chem. Mater., 2009, 21, 1400.
58. S.-Z. Weng, P. Shukla, M.-Y. Kuo, Y.-C. Chang, H.-S. Sheu, I. Chao and Y.-T. Tao, ACS Appl. Mater. Interfaces, 2009, 1, 2071.
59. M. M. Islam, S. Pola and Y.-T. Tao, Chem. Commun., 2011, 47, 6356.
60. X. Wang and K.-C. Lau, J. Phys. Chem. C, 2012, 116, 22749.
61. C. Li, W. Jiang, X. Zhu and Z. Wang, Asian J. Org. Chem., 2014, 3, 114.
62. M. Karim and Y. Jahng, Molecules, 2016, 21, 407.
63. G. Westphal, Z. Phys. Chem., 1969, 9, 339.
64. S.-J. Chen and F. W. Fowler, J. Org. Chem., 1970, 35, 3987.
65. G. B. Schuster, S. P. Schmidt and B. G. Dixon, J. Phys. Chem., 1980, 84, 1841.
66. F. W. Fowler and S.-J. Chen, J. Org. Chem., 1971, 36, 4025.
67. K. V. Subba Rao, B. Srinivas, A. R. Prasad and M. Subrahmanyam, Chem. Commun., 2000, 1533.
68. K. Oshima, T. Ohmura and M. Suginome, Chem. Commun., 2012, 48, 8571.
69. R. R. Schmidt, M. Dimmler and P. Hemmerich, Ber., 1976, 109, 2395.
70. M. Märken, B. D. Lindner, A. L. Appleton, F. Rominger and U. H. F. Bunz, Pure Appl. Chem., 2014, 86, 483.
71. H. Choi, X. Yang, G. W. Mitchell, C. P. Collier, F. Wudl and J. R. Heath, J. Phys. Chem. B, 2002, 106, 1833.
72. J. U. Engelhart, F. Paulus, M. Schaffroth, V. Vasilenko, O. Tverskoy, F. Rominger and U. H. F. Bunz, J. Org. Chem., 2016, 81, 1198.
73. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
74. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157.
75. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, USA, 2009.
76. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317.
77. J. Kruszewski and T. M. Krygowski, Tetrahedron Lett., 1972, 13, 3839.
78. K. Remya and C. H. Suresh, J. Comput. Chem., 2013, 34, 1341.
79. K. Remya and C. H. Suresh, Phys. Chem. Chem. Phys., 2015, 17, 27035.
80. K. Remya and C. H. Suresh, RSC Adv., 2016, 6, 44261.
81. T. D. Della and C. H. Suresh, Phys. Chem. Chem. Phys., 2016, 18, 14588.
82. U. H. F. Bunz, Acc. Chem. Res., 2015, 48, 1676.
83. T. M. Krygowski, H. Szatylowicz, O. A. Stasyuk, J. Dominikowska and M. Palusiak, Chem. Rev., 2014, 114, 6383.
84. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842.
85. F. Feixas, E. Matito, J. Poater and M. Solà, J. Comput. Chem., 2008, 29, 1543.
86. G. Portella, J. Poater, J. M. Bofill, P. Alemany and M. Solà, J. Org. Chem., 2005, 70, 2509.
87. G. Portella, J. Poater, J. M. Bofill, P. Alemany and M. Solà, J. Org. Chem., 2005, 70, 4560.
88. J. Poater, M. Solà, R. G. Viglione and R. Zanasi, J. Org. Chem., 2004, 69, 7537.
89. J. Poater, J. M. Bofill, P. Alemany and M. Solà, J. Org. Chem., 2006, 71, 1700.
90. S. Osuna, J. Poater, J. M. Bofill, P. Alemany and M. Solà, Chem. Phys. Lett., 2006, 428, 191.
91. M. G. Voronkov, É. N. Deryagina and É. N. Sukhomazova, Chem. Heterocycl. Compd., 1977, 13, 217.

---

Footnote

† Electronic supplementary information (ESI) available: Optimised geometries, correlation plots, HOMO–LUMO and MESP figures, SCF energy and NICS values etc. See DOI: 10.1039/c6cp03723b

---