Aromatic embedding wins over classical hydrogen bonding – a multi-spectroscopic approach for the diphenyl ether–methanol complex

Abstract

Dispersion interactions are omnipresent in intermolecular interactions, but their respective contributions are difficult to predict. Aromatic ethers offer competing docking sites for alcohols: the ether oxygen as a well known hydrogen bond acceptor, but also the aromatic π system. The interaction with two aromatic moieties in diphenyl ether can tip the balance towards π binding. We use a multi-spectroscopic approach to study the molecular recognition, the structure and internal dynamics of the diphenyl ether–methanol complex, employing infrared, infrared-ultraviolet and microwave spectroscopy. We find that the conformer with the hydroxy group of the alcohol binding to one aromatic π cloud and being coordinated by an aromatic C–H bond of the other phenyl group is preferred. Depending on the expansion conditions in the supersonic jet, we observe a second conformer, which exhibits a hydrogen bond to the ether oxygen and is higher in energy.

---

1 Introduction

The interplay between different intermolecular forces drives (bio)molecular aggregation and recognition.^1–4 Although significant theoretical and experimental progress has been made, non-covalent molecular recognition is still not well understood on a quantitative level.⁵ Exactly how the various individual non-covalent interactions reinforce or compete with each other in complex systems is of fundamental and practical importance. The elucidation of a hierarchy of the dominant interactions governing molecular recognition would help synthetic chemists to shape molecules in order to customize the interaction forces. The role that conformational flexibility plays in the recognition process is another challenging topic. Further insight into these points will help to predict and design the outcome of molecular recognition events, and a quantitative description of dispersion interaction is one of the key steps towards this goal.

Aromatic rings provide powerful dispersion centers due to their polarizable delocalized π electron systems and their flatness, which allows for short intermolecular contacts. Therefore, they can act as hydrogen bond acceptors for alcohols like methanol,⁶ although oxygen atoms such as in ethers are commonly expected to be more attractive hydrogen bond docking sites due to their polar nature.^7,8

Many complexes involving methanol have been studied by molecular spectroscopy.^9–16 Recently, the complex of methanol with an aromatic ether, namely the anisole–methanol complex, was characterized. It was shown to prefer an OH–O hydrogen bond in supersonic coexpansions of the two binding partners, with less than 10% detected in the form of the competing OH–π structure.¹⁷ This was somewhat surprising, because the π system in anisole is relatively electron rich due to conjugation of oxygen electron density. For the same reason, the ether oxygen is less nucleophilic than in aliphatic cases. Indeed, many standard quantum chemical methods predict the two binding sites in anisole to be more or less equivalent, within 1 kJ mol⁻¹ or less.¹⁷ Replacement of the methyl group in anisole by another phenyl ring could make the π face more attractive and more cavity-like, because the phenyl rings are twisted out of the COC plane due to Pauli repulsion. Therefore, diphenyl ether (DPE), which is the subject of the present study, has the potential to tip the methanol OH–O preference found in anisole over into an OH–π propensity.

DPE is a structurally very flexible molecule. The two phenyl rings are connected via single bonds to the ether oxygen and thus can perform large-amplitude motions. DPE also serves as a model for solvent effects on the catalytic hydrogenolysis of lignin, an important challenge in biorefining wood.¹⁸ Different alcohols perform very differently, with fluorination and branching having strong influences. Therefore, a microscopic understanding of the docking preferences of alcohols to DPE may eventually be beneficial for solvent design in catalysis.

DPE in the gas phase was spectroscopically investigated previously using resonance-enhanced multi-photon ionization,^19,20 but a detailed understanding of its conformational flexibility and rich internal dynamics is still missing and will be tackled in a separate study. DPE provides a number of plausible binding sites and pathways for methanol, and it is the aim of the present study to elucidate what type of bonding is most preferred and why. The flexibility of DPE may also allow the structure to change to accommodate the binding of methanol which could be thought of as a simple model of induced fit.

We tackle this challenging task in a collaborative effort using complementary spectroscopic techniques, namely Fourier transform infrared (FTIR), mass- and isomer-selective IR/UV double and triple resonance spectroscopy (IR/R2PI and IR/IR/R2PI) and chirped-pulse Fourier transform microwave spectroscopy (CP-FTMW), all supplemented by theory.

2 Computational and experimental methods

2.1 Computational methods

On the computational side, most explorations of the potential energy hypersurface for the monomers and complexes were carried out at the B97D/TZVP level, followed by the B3LYP-D3(BJ)/def2-TZVP level. This involves a well-characterized hybrid density functional, Grimme's dispersion correction²¹ and Becke–Johnson damping in combination with a sufficiently small basis set to allow for a systematic exploration of the high-dimensional potential energy landscapes of the clusters. For selected stationary points, single point calculations at higher levels (MP2/aug-cc-pVTZ, +CCSD(T) correction with 6-311+G* basis set) were added. Unless stated otherwise, harmonic zero point energy is always included at the B3LYP-D3(BJ)/def2-TZVP level. For selected structures, geometry optimization and harmonic frequency calculations were repeated at other levels of approximation for comparison reasons. The program packages Turbomole 6.5²² and Gaussian 09²³ were used.

2.2 FTIR jet spectroscopy

FTIR jet spectra of DPE–MeOH complexes were obtained in two setups in Göttingen. A heatable 1 cm double slit nozzle (ϑ_n = 130 °C, popcorn-jet²⁴) is fed by a helium/methanol gas pulse (helium: Linde, 99.996%; methanol: Fisher Chemical, ≥99.9%) of variable concentration flowing through a heated zone (ϑ_z = 110 °C) containing DPE(Alfa Aesar 99%)-coated molecular sieve. The focused IR beam crosses the expansion zone 3 ± 2 mm after the nozzle exit perpendicular to both the slit and the expansion direction, and its attenuation is detected by an InSb detector. By synchronizing the intense gas pulses to the interferometer scans and by expanding into a 4 m³ vacuum buffer, relatively high molecular densities can be realized without accumulating too much background pressure. The latter is further reduced by Roots pumps during a waiting time of 60 s, before a background spectrum is recorded and the next gas pulse is applied. The relative abundance of monomers, dimers, and oligomers is roughly controllable by ϑ_n and ϑ_z, but it is difficult to distinguish rigorously between mixed dimers and trimers.

The second setup involves an upscaled room temperature variant involving a 60 cm slit nozzle (filet-jet²⁵) and 23 m³ of vacuum buffer. Due to the low volatility of DPE (about 30 μbar at the nozzle temperature, consistent with a standard boiling point of 258 °C²⁶ and vaporization enthalpy of 65 kJ mol^−1 26) only clusters containing one ether unit are expected along with the monomeric species, whereas depending on the methanol concentration one or two methanol units can be incorporated. Details about the two setups, which use Bruker IFS/66v FTIR spectrometers, can be found elsewhere.^24,25

2.3 Combined IR/UV spectroscopy

The experimental setup in Kaiserslautern is described elsewhere,^27,28 thus only a brief description is given here. The experiments were carried out in a molecular beam apparatus consisting of a pulsed valve (General Valve Iota One, 500 μm orifice) for skimmed jet expansion and a differentially pumped time-of-flight mass spectrometer. The DPE sample was purchased from Fluka (≥99.9%) and used without further purification. Methanol (Uvasol®, Merck) was supplied via a cooled reservoir and coexpanded in helium (at 2.6 bar) with DPE (at room temperature).

In order to obtain mass and isomer-selective IR and UV spectra, one-color R2PI (Resonant 2 Photon ionization) spectroscopy as well as the IR/R2PI^6,27,29–31 and the IR/IR/R2PI technique^32–34 are chosen. The often used R2PI and IR/R2PI techniques are described in the ESI.† The IR/R2PI method is isomer selective as long as an UV transition does not result from more than one isomer. In case of overlapping UV resonances of more than one isomer in the R2PI spectrum, the respective IR/R2PI spectra are not isomer-selective. To retain isomer-selectivity the IR/IR/R2PI technique can be applied. Using this method, the vibrational excitation of one isomer with a frequency-fixed IR burn laser affects (i.e., reduces the intensities of) all IR transitions belonging to the same isomer in the IR/R2PI spectrum, which is subsequently recorded.

For the one-color R2PI, the IR/R2PI^6,27,29–31 and the IR/IR/R2PI technique^32–34 up to three tunable laser systems are necessary: one UV and two independent IR laser systems. The UV laser radiation is generated by a frequency-doubled dye laser (Sirah, Cobra Stretch). The IR light in the region of 3050–3750 cm⁻¹ is generated in a LiNbO₃ crystal by difference frequency mixing (DFM) of the fundamental (1064 nm) of a seeded Nd:YAG laser (Spectra-Physics, PRO-230) and the output of a dye laser (Sirah, Precision Scan) being pumped by the second harmonic (532 nm) of the same Nd:YAG laser. The obtained IR radiation is amplified in a second LiNbO₃ crystal by an optical parametric amplification (OPA) process using the output of the DFM process and again the fundamental of the Nd:YAG laser. The IR light in the region of 3300–3750 cm⁻¹ was generated with a recently modified laser system: In a first conversion stage IR light in the region of 5650–6100 cm⁻¹ is generated via DFM in a LiNbO₃ crystal using the fundamental (1064 nm) of a Nd:YAG laser (Innolas, Spitlight 1000) and the output of a dye laser (Sirah, Precision Scan) being pumped by the second harmonic (532 nm) of the same Nd:YAG laser. In a second conversion stage an OPA process via two KTiOAsO₄ crystals generates amplified DFM radiation and IR light in the region of 3300–3750 cm⁻¹ using the DFM output radiation and again the fundamental of the Nd:YAG laser.

In order to record the IR spectra, the scanning IR laser was fired 50 ns prior to the UV laser whereas for the IR/IR/R2PI measurements the additionally required frequency-fixed IR burn laser was fired 100 ns prior to the UV laser.

2.4 CP-FTMW spectroscopy

The details of the broadband microwave technique^35,36 and the COMPACT instrument in Hamburg have been described elsewhere.³⁷ Both DPE (stated purity ≥ 99%) and methanol (stated purity ≥ 99.8%) were purchased from Sigma-Aldrich and used without further purification. The molecules were seeded into a supersonic expansion using a pulse nozzle (Parker General Valve, Series 9) equipped with a heatable reservoir. In this arrangement, the sample of DPE was placed in this small sample reservoir in front of the solenoid, very close to the valve orifice and heated to 85 °C. The methanol sample was placed in a reservoir on a separate section of tubing outside of the vacuum chamber. To compensate for its high vapour pressure only a small amount of the neon carrier gas (2 bar backing pressure) was diverted to flow over the methanol.

For each supersonic expansion, the ensemble of molecules was polarized with a series of eight microwave chirps of 4 μs duration spanning 2 → 8 GHz. The chirps were generated with an arbitrary waveform generator (AWG), amplified to 300 W with a travelling wave tube amplifier, and transmitted into the vacuum chamber with a horn antenna. Following each excitation, 40 μs of the free induction decay (FID) of the macroscopic ensemble of polarized molecules were recorded, yielding a frequency resolution of 25 kHz. A total of 3.3 million FIDs were coadded and Fourier transformed with a Kaiser window function to give the broadband rotational spectrum in the frequency domain.

The initial assignment of the broadband rotational spectrum of the DPE–MeOH complex was performed using the PGOPHER software package³⁸ using Watson's S-reduced asymmetric rotor Hamiltonian. A further, detailed analysis of the observed tunneling splitting arising from internal rotation of the methanol methyl group (see discussion in Section 3.4) was performed using the XIAM program.³⁹ XIAM is a least squares fitting program specifically designed for the fitting of internal rotors by employing the combined axis method of Woods^40,41 to account for internal rotation through a potential barrier.

3 Results

3.1 Minimum structures of mixed dimers

Although the B3LYP-D3(BJ)/def2-TZVP level has a slight bias of about 0.5 kJ mol⁻¹ relative to an aug-cc-pVTZ basis set towards OH–π contacts (which is similar to the case of anisole¹⁷) it was used to explore the intermolecular interactions between methanol and DPE. It is scalable to structure optimizations of larger clusters and still sufficiently accurate in its structural predictions to allow for meaningful higher level single point energy corrections. At this level, DPE has chiral (C₂, twist, Fig. 1b) minimum structures with twisted phenyl rings. These are connected by low-lying C_s-symmetric (skew, Fig. 1c) structures with orthogonal phenyl rings for facile interconversion between the enantiomers (cf.Fig. 1a). During each of these geared motions through a C_s structure, the face of one phenyl ring is flipped such that an attached molecule can move from the inner or cleft side of the ether to the outer or tip side and back. This promises a low-barrier pathway for alcohol donors from the exposed ether oxygen to the inner cleft, where they can interact with both rings. The corresponding torsional motion in the free DPE unit is depicted in Fig. 1a. The barrier between two enantiomeric twist forms is predicted to be around 1.0 kJ mol⁻¹ (see also ref. 19, 20 and 42–44).

Fig. 1 (a) The relaxed scan of the torsional energy surface of DPE calculated at the B3LYP-D3(BJ)/def2-TZVP level (the dashed white line marks the 0.9 kJ mol⁻¹ contour). Deep troughs for geared rotation of the two phenyl groups are separated by ridges in which ortho hydrogens come into close contact. On the right (b–d), selected, optimized structures of DPE are given. Only the twist structure is a minimum on the potential energy surface.

Starting from the twist form, an extensive exploration of methanol docking events was carried out and resulted in a total of five mixed dimer structures within an energy window of about 5 kJ mol⁻¹ (see Fig. 2). Two of them engage the ether oxygen via an OH–O hydrogen bond. The more stable structure (OH–O, Fig. 2a) involves a more bent hydrogen bond due to secondary interactions of the methyl group with an outer π face and a weak aromatic CH–O hydrogen bond (to the O of methanol) from the ortho position of the other ring. A structure with a somewhat more linear hydrogen bond is found (OH–O′, Fig. 2b) 1.4 kJ mol⁻¹ higher in energy, whereas the secondary interactions are less pronounced. We shall disregard this structure in the following discussion, as it is likely to interconvert rather easily to OH–O under the conditions of a supersonic jet expansion. The other three structures locate the methanol unit on the inner or cleft side of DPE. One of them involves a rather pure OH–π interaction without further contacts of the hydroxy oxygen (OH–πp, Fig. 2e). It forces DPE into a skew-like conformation, is the least stable of the five structures and will not be discussed further. We also note in this context that OH–π starting structures coordinating the outer π clouds easily convert into one of the more stable structures.

Fig. 2 Structures of the most stable DPE–MeOH dimers at the B3LYP-D3(BJ)/def2-TZVP level with relative zero-point-corrected energies in kJ mol⁻¹ in parentheses.

The other two stable OH–π structures compete for the global minimum because they combine an inner OH–π contact to one of the phenyl groups with an aromatic ortho CH–O contact from the other phenyl ring. They essentially differ in the arrangement of the methyl group towards the tip (OH–π, Fig. 2c) or away from the tip (OH–π′, Fig. 2d), with the former being predicted slightly more stable than the latter. This extra stability amounts to less than 0.5 kJ mol⁻¹ and should thus not be overinterpreted, whereas the gap to the OH–O structures is more than 1 kJ mol⁻¹. While the primed structures OH–O′ and OH–π′ are unlikely to be stabilized under most supersonic jet conditions, the energy difference between the corresponding lower energy OH–O and OH–π structures is very relevant for this work. The values obtained at our standard level (1.8 kJ mol⁻¹ with and 0.9 kJ mol⁻¹ without zero point energy correction) as well as with the aug-cc-pVTZ basis set (1.4 and 0.6 kJ mol⁻¹) do not change substantially in energy calculations at higher level (e.g. to 2.4 and 1.5 kJ mol⁻¹ at MP2/aug-cc-pVTZ level with CCSD(T) corrections at 6-311+G* level), cf. Table S2 (ESI†). As in the case of anisole,¹⁷ MP2 calculations distort the picture in favor of π coordination and should also be used cautiously for geometry optimization. For example, a consistent MP2/aug-cc-pVTZ optimization yields an OH–O energy penalty of 2.6 kJ mol⁻¹ relative to OH–π instead of ≈1 kJ mol⁻¹ before zero point energy correction. Note that according to B3LYP/def2-TZVP calculations without including the Grimme D3 dispersion corrections the OH–O isomer is the most stable structure, whereas the OH–π isomer is 1.6 kJ mol⁻¹ less stable (including zero-point correction).

The key spectroscopic parameters obtained from harmonic frequency calculations performed on the five lowest energy conformers are shown in Table 1. Infrared spectroscopy should be able to resolve the differences between the OH vibrational frequencies of most conformers, with the notable exception of the only small difference between OH–π and OH–π′, predicted to be less than 2 cm⁻¹. Likewise the ground state rotational constants are diagnostic for each conformer with the possible exception of the OH–π and OH–π′ conformers. Here, differentiation in the microwave spectrum relies on the differences in dipole-moment components, which lead to differences in the observed transition types, i.e., mainly a-type for the OH–π conformer and mainly c-type for the OH–π′ conformer, as discussed in Section 3.4.

Table 1 Calculated spectroscopic parameters (rotational constants A_e, B_e, and C_e; components of the dipole moment μ_i; harmonic vibration wavenumber [small nu, Greek, tilde]) and IR intensities for the lowest energy conformers of DPE–MeOH, performed at the B3LYP-D3(BJ)/def2-TZVP level. The relative energies ΔE₀ are zero-point corrected. Comparison of the OH–O and OH–O′ structures shows that the OH–O hydrogen bond in the more stable structure is a compromise – the OH group has a reduced downshift and IR intensity because of competing secondary dispersion interactions of the methyl group with DPE. The corresponding structures are shown in Fig. 2

Conformer	A e/MHz	B e/MHz	C e/MHz	|μa|/|μb|/|μc|/D	[small nu, Greek, tilde] OH/cm^−1	IR int./km mol^−1	ΔE0/kJ mol^−1
(c) OH–π	1022.2	381.7	329.2	0.8/0.5/0.2	3773	113	0
(d) OH–π′	1004.3	398.3	330.1	0.6/0.2/1.9	3772	116	0.4
(a) OH–O	858.9	413.4	318.8	0.2/2.7/1.3	3741	205	1.8
(b) OH–O′	745.2	416.1	292.1	0.5/2.6/1.3	3731	344	3.2
(e) OH–πp	1035.3	364.5	314.4	2.1/1.7/0.2	3777	126	5.1

---

Thus, theory predicts a dominating OH–π structure, possibly accompanied by a related OH–π′ structure with inverted methyl group position. Whether or not an OH–O structure is observable depends on the extent of conformational cooling and thus on the actual barrier along the path from the cleft to the tip of the DPE unit. This barrier will certainly be higher than in DPE itself, because the secondary ortho CH–O contacts hinder the geared torsion.

For the calculation of a reaction pathway, different relaxed scans over selected internal coordinates were considered. The lowest path we found (see Fig. S1, ESI,† potentially still an upper bound) involves a switch between enantiomeric twist structures of DPE along the torsional coordinate of the non-π-coordinated phenyl group, leading to the OH–π′ structure over a barrier of 2.6 kJ mol⁻¹. It is followed by a π-to-O coordination switch enforced by shortening the OH⋯O distance, over a barrier of about 3.0 kJ mol⁻¹. In this second step, the methanol moves from the cleft to the outside of the DPE molecule. In total, a barrier of only 3.3 kJ mol⁻¹ has to be overcome (2.4 kJ mol⁻¹ in the reverse direction; here and elsewhere, variations on the order of 0.1–0.2 kJ mol⁻¹ may be attributed to the finite step size and the mix of different quantum chemistry codes). Nevertheless, it is conceivable that OH–π and OH–O conformers are stabilized simultaneously in a supersonic jet expansion, depending on the chosen expansion conditions. However, the entire complex population might also collapse into the OH–π structure under suitable conditions. This fluxionality makes the system attractive as a benchmark for quantum chemistry predictions, because it reduces metastable structure trapping at low temperatures.⁴⁵

3.2 FTIR spectra

Fig. 3 shows two FTIR jet spectra of DPE/MeOH coexpansions in helium. The lower one corresponds to a short heated nozzle expansion (popcorn-jet) with a relatively high DPE concentration and a low methanol concentration. Besides very weak methanol monomer (M₁) and dimer (M₂) features, it shows two sharp bands at 3623 and 3607 cm⁻¹. Together with the broader features at 3550 and 3485 cm⁻¹, these are due to complexes of one or two methanol molecules with one or more DPE units. To narrow down the assignment, a room temperature long nozzle expansion (filet-jet) at significantly lower methanol concentration and much lower (less than 100 ppm) DPE concentration was carried out (upper trace). It shows that the surviving 3623 cm⁻¹ transition (now at 3622 cm⁻¹ due to better vibrational cooling) must be due to the most stable mixed dimer, whereas the vanishing 3607 cm⁻¹ transition either belongs to a metastable mixed dimer or to a complex involving more than one DPE unit, or both. Assuming that the 3607 cm⁻¹ transition is due to the OH–O complex (Fig. 2a) and that the calculated IR band strengths are reliable, the upper spectrum rules out more than 20% OH–O contribution (due to the limited sensitivity of the FTIR spectrometer) and the lower spectrum rules out more than 35% OH–O contribution to the mixed dimer population. Depending on the interconversion barrier, this is reasonably consistent with a 0.5–2 kJ mol⁻¹ energy penalty.⁴⁵

Fig. 3 FTIR OH-stretching absorbance spectra of DPE–MeOH coexpansions in helium with different DPE content, nozzle temperature and path length. The lower trace involves high DPE concentration, 120 °C nozzle temperature and 1–2 cm absorption path (0.02 × 10⁻³ was added to avoid negative values). The upper trace involves a room temperature expansion at very low DPE concentration and 60 cm absorption path. M₁ and M₂ denote methanol monomer and dimer transitions, respectively. See Section 2.2. for the experimental setups.

3.3 Mass- and isomer-selective IR spectra

By variation of the methanol temperature within the reservoir it is possible to induce the formation of the mixed dimer DPE–MeOH, and no larger clusters (with more than one methanol molecule) are observed. To obtain mass-selective IR spectra of DPE–MeOH clusters using the IR/R2PI spectroscopy, knowledge on relevant UV excitation energies is a premise. 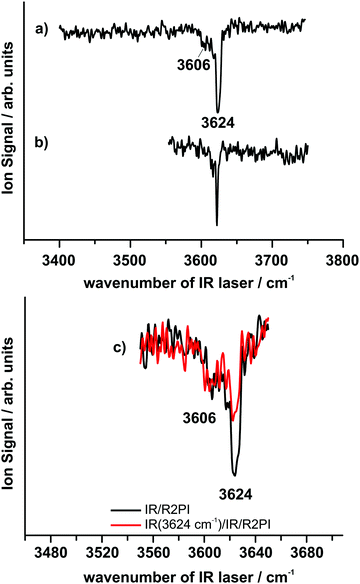Thus one-color R2PI spectra of the DPE–MeOH dimer were recorded in the range from about 35 500 to 36 300 cm⁻¹ with an electronic origin at 35 800 cm⁻¹ and further transitions at 35 869, 35 947, 36 028, 36 099 and 36 275 cm⁻¹. The IR/R2PI spectrum of the DPE–MeOH mass trace via the electronic origin is shown in Fig. 4a. This spectrum exhibits an intense transition at 3624 cm⁻¹ and a much weaker band at 3606 cm⁻¹, both corresponding to OH-stretching vibrations, in agreement with the FTIR results (Section 3.2, Fig. 3). The IR/R2PI spectra for different excitation energies of the R2PI spectrum yielded the same vibrational transitions. This result indicates that either only one isomer is observed or the electronic transitions of more than one isomer overlap. A hint on the existence of two different isomers in one IR/R2PI spectrum arises from the spectra recorded with neon as expansion gas (cf.Fig. 4b). Under these conditions only one intense transition is observed whereas the band at 3606 cm⁻¹ vanishes. Similar to the effect of better cooling described for the FTIR results the observed vibrational transition shifts from 3624 cm⁻¹ in helium to 3622 cm⁻¹ in neon.

Fig. 4 IR/R2PI spectrum of DPE–MeOH recorded via the electronic origin measured in (a) helium and (b) neon. (c) IR/IR/R2PI spectrum of DPE–MeOH (red trace) compared to a IR/R2PI spectrum (black trace), both in helium. The frequency-fixed IR burn laser was set to 3624 cm⁻¹, the UV laser was set to the electronic origin.

It can be assumed that the formation of the second isomer is suppressed by the expansion in neon, which is in line with the findings using CP-FTMW spectroscopy (discussed below in Section 3.4). This experimental finding is also in excellent agreement with the results obtained from the FTIR spectra, which indicate the dominance of one isomer under suitable expansion conditions. To clearly verify that the transitions at 3606 and 3624 cm⁻¹ indeed originate from different isomers the IR/IR/R2PI method was applied. For this purpose the IR burn laser was fixed at 3624 cm⁻¹. Fig. 4c shows the IR/IR/R2PI spectrum (red trace) in comparison to the IR/R2PI spectrum (black trace). The IR/IR/R2PI spectrum clearly shows a depletion of the transition at 3624 cm⁻¹ compared to the original IR/R2PI spectrum. In contrast the second band at 3606 cm⁻¹ is independent of the IR burn laser, proving that the two transitions must belong to different conformers.

In order to achieve an assignment of the vibrational transitions to different structures it has to be taken into account that all quantum chemical calculations predict the OH–π structure as energetically more stable. Furthermore the calculations predict that the OH–O motif has a lower harmonic OH-stretching wavenumber (about 30–40 cm⁻¹) than the OH–π motifs whereas the difference between OH–π and OH–π′ should be in an interval of less than 2 cm⁻¹ (cf.Table 1). Thus, with respect to both the spectral positions and relative intensities of the two experimentally observed vibrational transitions an assignment of the most intense transition at 3622 cm⁻¹ to the OH–π isomer can be assumed. This is in agreement with the analysis of the microwave investigations, where only the OH–π isomer was detected when using a supersonic expansion with neon (cf. Section 3.4). By using the value of 3622 cm⁻¹ for scaling the harmonic DFT-calculations (B3LYP-D3(BJ)/def2-TZVP), the obtained scaling factor of 0.9600 is very close to the commonly used factor of 0.9613 for B3LYP/TZVP calculations without dispersion corrections⁴⁶ and moreover even closer to the factor of 0.9608 which has been derived from reference systems for B3LYP-D3/TZVP.⁴⁷ Using this factor, a value of 3591 cm⁻¹ is obtained for the OH–O structure which means that its wavenumber is slightly underestimated with respect to the experimentally observed value of 3606 cm⁻¹. The experimentally observed difference of the two isomers decreases by going from the anisole–MeOH dimer (31 cm⁻¹) to the DPE–MeOH dimer (18 cm⁻¹). This trend is in agreement with the theoretical results (DFT level) predicting a decrease of the OH-stretching frequency difference both by applying the def2-TZVP and aug-cc-pVTZ basis set (for further details cf. Table S1, ESI†).

The experimental results obtained from mass selective IR/R2PI and isomer selective IR/IR/R2PI spectroscopy in combination with the theoretical descriptions give a clear indication that both the OH–π and the OH–O conformer exist in the molecular beam using helium as carrier gas. Considering the relative intensities of the OH–π and OH–O signals (see Table 1) leads to the assumption that the OH–π conformer is far more abundant, which is consistent with the predicted relative energies, the FTIR results, as well as the further experimental investigations (cf. Section 3.4).

3.4 Broadband rotational spectra

The broadband rotational spectrum obtained from the DPE/MeOH mixture with neon as carrier gas is shown in Fig. 5. The DPE and the methanol monomer as well as the methanol dimer are also observed in the spectrum. All three species were studied previously^9,19,48,49 and exhibit line splittings due to internal motions. For the DPE–MeOH complex, 120 lines (70 a-type, 50 b-type, and no c-type) could be successfully fit to Watson's S-reduced asymmetric rotor Hamiltonian using the PGOPHER software package.

Fig. 5 Broadband spectrum obtained from a DPE/MeOH coexpansion using neon as carrier gas. The top trace shows the experimental results. In the bottom trace, the simulated spectra based on fitted parameters for different species are given for the DPE monomer (red trace) and the DPE–MeOH complex (OH–π conformer, blue trace). The data also contains rotational transitions from both monomers and the methanol dimer (not indicated here).

Most of the assigned lines of the DPE–MeOH dimer spectrum show an obvious doublet splitting, the pattern of which suggests a methyl rotor type large amplitude motion. Contrary to the DPE monomer, for which we recorded a characteristic triplet splitting pattern due to the large-amplitude motion of the phenyl rings (see also Fig. 6), we observe no further splittings besides the described doublet pattern in the DPE–MeOH spectrum. This indicates that the large amplitude motion of the phenyl rings has been quenched in the cluster, in line with the increased barrier for racemization (Fig. S1, ESI†).

Fig. 6 Zoom to the broadband rotational spectrum of a DPE/MeOH coexpansion using neon as carrier gas, illustrating the characteristic triplet splitting pattern for the DPE monomer due to large-amplitude motion of the phenyl rings as well as the observed A–E splitting of the DPE–MeOH dimer, arising from the internal motion of the CH₃ group of the methanol moiety. For the DPE–MeOH dimer, the transitions corresponding to A and E symmetry are fit jointly to an effective Hamiltonian (see Table 2).

The assigned lines in the rigid rotor fit were attributed to the A-state, and the easily identifiable E-state lines due to methyl group internal rotation were subsequently assigned. These assignments were exported to the XIAM program to perform a global fit. Table 2 summarizes the experimentally determined molecular parameters together with the results obtained from a harmonic quantum-chemical calculation (harmonic B3LYP-D3(BJ)/def2-TZVP) for which also the centrifugal distortion constants were determined. The calculated rotational constants are equilibrium values, i.e., A_e, B_e, and C_e, as reported in Table 1 for the same level of theory. The differences between the calculated values reported in Tables 1 and 2 most probably arise from differences in the convergence criteria in the geometry optimization, resulting in slightly different geometries.

Table 2 Molecular parameters of the DPE–MeOH complex: results of two different fits to the experimental rotational spectrum and comparison to results from quantum-chemical calculations for the OH–π dimer (structure (c) in Fig. 2). The two fits differ in the treatment of the rotational constant of the internally rotating methyl group F (see text)

	Fit 1	Fit 2	B3LYP-D3(BJ)/def2-TZVP^c
a Ray's asymmetry parameter: b Direction cosines were fit as the polar coordinates of the methyl rotor axis with respect to the inertial axes and converted internally to the direction cosines. c Calculations performed with Gaussian09. The rotational constants are Ae, Be, Ce values.
A/MHz	997.9813(30)	997.98324(101)	1019.7
B/MHz	380.73116(85)	380.73236(28)	382.7
C/MHz	326.78987(77)	326.79163(26)	333.0
D J/kHz	0.029(4)	0.0281(12)	0.02
D JK/kHz	0.861(28)	0.8232(95)	0.37
D K/kHz	−0.234(136)	−0.169(46)	−0.05
d 1/kHz	0.008(3)	0.00157(94)	0.0005
d 2/kHz	−0.006(2)	−0.00321(54)	−0.0002
κ	−0.839	−0.839	−0.86
λ a	−0.252(2)	0.0626(8)	0.04
λ b	−0.385(17)	0.1695(73)	−0.25
λ c	0.888(18)	0.7679(78)	0.97
F 0/cm^−1	5.3	10.16(27)
V 3/cm^−1	250.74(65)	480(12)	368
A state transitions (a/b/c)	120 (70/50/0)	120 (70/50/0)
E state transitions (a/b/c)	48 (33/15/0)	48 (33/15/0)
|μa|/|μb|/|μc|			0.6/0.6/0.2
Standard deviation/kHz	36	12

---

For the XIAM fits, starting values for the angles between the methyl rotor of the methanol unit and the inertial axis were predicted from the calculated structure. The starting value for F, the rotational constant of the internally rotating methyl top, is less clear. Typical literature values for a methyl top on a rigid frame are around 5.3 cm⁻¹ (see Table 3), however, the value for methanol is 27.6 cm⁻¹ due to interactions with the large amplitude motion of the OH group. The value of F in methanol-containing complexes is dependent on the amplitude of the OH libration and thus depends on the strength of interaction between methanol with its binding partner (Table 3). As a consequence, F is determined to be somewhere between that of free methanol (27.6 cm⁻¹) and the value of just the methyl top (5.3 cm⁻¹) for molecular complexes involving methanol. A number of previous studies on methanol complexes have fixed F to 5.3 cm⁻¹ (Table 3). This has been shown to cause a large underestimation of the barrier height (V₃).⁵⁰ Indeed, when we fix F to 5.3 cm⁻¹ the fitted barrier height is 250.74(65) cm⁻¹ (‘Fit 1’ in Table 2), lower than both free methanol (373 cm⁻¹) and the predicted value from relaxed potential energy scans (368–470 cm⁻¹, depending on method/basis set).

Table 3 Barrier heights V₃ for methyl rotation in some methanol-containing complexes. The marked F values for the DPE–MeOH complex and the methanol dimer were allowed to float during the fitting procedure, while all other F values have been fixed to the values given in the table

Acceptor–MeOH	V 3/cm^−1	F/cm^−1	s	Ref.
a Reduced dimensionless barrier height s = 4V3/9F. b Allowed to float during the fitting procedures. c Referring to the hydrogen bond donor methanol.
MeOH monomer	373	27.63^b	6.00	48
DPE–MeOH	480	10.16^b	21.08	This work
DPE–MeOH	250.74	5.3	21.03	This work
MeOH dimer^c	201	5.4^b	16.53	9
Formamide–MeOH	231.01	5.26	17.53	10
Ar–MeOH	68.466	5.3	5.74	11
HCl–MeOH	74	5.3	6.21	12
SO2–MeOH	128.665	5.3	10.79	13
Trimethylamine–MeOH	174	5.30	14.59	14
CO–MeOH	183	5.76	14.12	15
Phenol–MeOH	170	5.27	15.11	16

---

To obtain more realistic values we fit F simultaneously with all the parameters. However, since the line splittings are a function of the reduced barrier height (s = 4V₃/9F), F is highly correlated to the barrier height V₃, and there are significant errors in both parameters (F = 10.16(27) cm⁻¹ and V₃ = 480(12) cm⁻¹). This fit is shown in Table 2 as ‘Fit 2’ and has a lower standard deviation compared to ‘Fit 1’ where F is fixed. The fitted value of F agrees well with the assumption that the methanol molecule is in an environment somewhere between the strongly bound case and free methanol. The higher barrier compared to that observed in the methanol monomer is an indication that the CH₃ group is involved in an intermolecular interaction with the π system, as also visible from Fig. 2. The barrier height calculated from a relaxed potential energy scan (B3LYP-D3(BJ)/def2-TZVP) is closer to that of the methanol monomer, while other levels of theory (M06-2X/cc-pVTZ and B2PLYP-D3/def2-SVP) give values (435 and 445 cm⁻¹ respectively) closer to the fitted value in Fit 2. This implies that the barrier height is highly sensitive to subtle differences in the structure and in the calculation of the long range interactions.

Comparison of the rotational constants obtained from this fit with values predicted from quantum-chemical calculations (Tables 1, 2 and Table S3, ESI†) could not unambiguously identify the geometry of the observed conformer. The calculated rotational constants for conformers OH–π and OH–π′ in Fig. 2c and d are within about 10 MHz. Often, quantum-chemical calculations show larger deviations in the absolute values of rotational constants from the experimentally determined data, but relative values, such as the differences between rotational constants (like B − C as well as the asymmetry parameter κ) are predicted more quantitatively. The experimental values are B − C = 53.94 MHz and κ = −0.839 (Table 2). For the OH–π conformer (Fig. 2c), the predicted values are B − C = 52.5 MHz (Table 1), and κ = −0.85, while for the OH–π′ conformer (Fig. 2d), values of B − C = 68 MHz, and κ = −0.80 are predicted (B3LYP-D3(BJ)/def2-TZVP level of theory, Table S3, ESI†). This gives a strong indication that indeed the lowest energy conformer, namely the OH–π conformer, is spectroscopically observed, using coexpansions with neon as carrier gas.

Unambiguous assignment could be achieved from evaluation of the observed types of rotational transitions, i.e., a-, b-, or c-type, in comparison with the calculated dipole moment components (μ_a, μ_b, and μ_c). No c-type transitions are observed for the DPE–MeOH complex (Table 2), indicating that μ_c is quite small, in agreement with the considerations above. This analysis strongly suggests the OH–π conformer, for which the predicted dipole-moment components are μ_a = 0.8 D, μ_b = 0.5 D, and μ_c = 0.2 D (B3LYP-D3(BJ)/def2-TZVP, see Table 1), resembling very well the observed ratio of rotational transitions. For the OH–π′ conformer, however, the predicted dipole-moment components are μ_a = 0.6 D, μ_b = 0.2 D, and μ_c = 1.9 D (B3LYP-D3(BJ)/def2-TZVP, see Table 1), so that we would expect to observe mainly c-type transitions.

Note that despite intense searches under varying conditions (change of carrier gas and its backing pressure, methanol concentration etc.) and while the measured microwave spectrum does contain many unaccounted lines (which can also originate from higher order clusters), we have not been able to identify any other dimer conformers. This is consistent with the IR/UV work performed using neon as a carrier gas (Section 3.3), indicating that only the lowest energy dimer is observed when neon is used. Even with helium as carrier gas, the OH–O isomer could not be observed. This might be due to the fact that FTMW spectroscopy is less sensitive than IR/R2PI spectroscopy, which relies on very sensitive ion detection while FTMW spectroscopy is based on an ensemble effect, the formation of a macroscopic dipole moment. Furthermore, we obtain higher rotational temperatures with helium than with neon or argon, thus potentially shifting the stronger part of the rotational spectrum out of our frequency range of 2–8 GHz.

4 Conclusions

The investigated dimer of diphenyl ether and methanol turns out to be very appropriate to study the close competition between hydrogen bonding to an ether oxygen atom and to an extended π system. In a cooperative effort, we performed a multi-experimental approach to analyze this system under isolated conditions in molecular beam experiments. From FTIR spectroscopy in the OH-stretching region up to two different isomers could be observed. The mass selective IR/R2PI spectroscopy clearly shows that two different isomers are observed for the dimer. This was further proven by the isomer selective IR/IR/R2PI method. According to DFT calculations the structures can be assigned to predominant OH coordination by either oxygen or a π cloud with the latter one being much more prominent. In order to verify this assignment, microwave spectroscopy has been applied leading unambiguously to the assignment of the π-bonded arrangement. Since this experiment has been performed with an expansion in neon, the collision energies in the course of the supersonic expansion are sufficient to overcome the barrier to isomerization from the oxygen-bonded to the π-bonded isomer. Consequently, only the π-bonded isomer was observed in the microwave measurements, similar to the IR/R2PI spectroscopy using the same expansion conditions.

This multi-experimental approach provides a reliable and consistent identification of the methanol docking preference in diphenyl ether. Furthermore, evidence for methyl group rotational hindrance and for the quenching of the ether torsional dynamics is collected. The findings are in full agreement with dispersion-corrected hybrid density functional predictions for the mixed dimers, and they fit qualitative expectations about secondary interactions stabilizing the primary OH–π hydrogen bond.

It will now be interesting to apply different theoretical approaches for the partitioning of the interaction energy into electrostatic, inductive and dispersion attraction as well as repulsion to learn about the key driving forces for OH–π preference over classical OH–O hydrogen bonding. An exploratory attempt using simplified SAPT theory⁵¹ is outlined in the ESI.† Although the energy sequence between OH–O and OH–π coordination is slightly inverted, the importance of electrostatics for OH–O docking and the increasing role of dispersion for OH–π docking are robustly explained. Finally, it will be essential to extend the study to larger alcohols as well as different ethers to generate a broader picture of the interplay between hydrogen bonding and dispersion in such alcohol ether systems and to exclude fortuitous matches between theory and experiment.

Acknowledgements

We greatly acknowledge financial support by the Deutsche Forschungsgemeinschaft (Ge 961/9-1, Schn 1280/4-1, Su 121/5-1) in the context of the priority program SPP 1807 on dispersion interactions. We acknowledge the use of the GWDG computer cluster. M. S. acknowledges funding by the Fonds der Chemischen Industrie via a Dozentenstipendium. This work has been supported by the excellence cluster ‘The Hamburg Centre for Ultrafast Imaging – Structure, Dynamics and Control of Matter at the Atomic Scale’ of the Deutsche Forschungsgemeinschaft. This work is part of the PhD theses of D. B., F. D., A. P., and S. Z.

References

1. M. L. Huggins, Angew. Chem., Int. Ed., 1971, 10, 147–208.
2. F. London, Z. Phys., 1930, 63, 245–279.
3. R. Eisenschitz and F. London, Z. Phys., 1930, 60, 491–527.
4. J. M. Lehn, Science, 1993, 260, 1762–1763.
5. J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296.
6. T. S. Zwier, Annu. Rev. Phys. Chem., 1996, 47, 205–241.
7. P. S. Walsh, E. G. Buchanan, J. R. Gord and T. S. Zwier, J. Chem. Phys., 2015, 142, 154303.
8. P. S. Walsh, E. G. Buchanan, J. R. Gord and T. S. Zwier, J. Chem. Phys., 2015, 142, 154304.
9. F. J. Lovas and H. Hartwig, J. Mol. Spectrosc., 1997, 185, 98–109.
10. F. J. Lovas, R. D. Suenram, G. T. Fraser, C. W. Gillies and J. Zozom, J. Chem. Phys., 1988, 88, 722.
11. X.-Q. Tan, L. H. Sun and R. L. Kuczkowski, J. Mol. Spectrosc., 1995, 171, 248–264.
12. X.-Q. Tan, I. I. Ioannou and R. L. Kuczkowski, J. Mol. Struct., 1995, 356, 105–115.
13. L. Sun, X.-Q. Tan, J. J. Oh and R. L. Kuczkowski, J. Chem. Phys., 1995, 103, 6440.
14. X.-Q. Tan, I. I. Ioannou, K. B. Foltz and R. L. Kuczkowski, J. Mol. Spectrosc., 1996, 193, 181–193.
15. F. J. Lovas, S. P. Belov, M. Y. Tretyakov, J. Ortigoso and R. D. Suenram, J. Mol. Spectrosc., 1994, 167, 191–204.
16. M. Schmitt, J. Küpper, D. Spangenberg and A. Westphal, Chem. Phys., 2000, 254, 349–361.
17. M. Heger, J. Altnöder, A. Poblotzki and M. A. Suhm, Phys. Chem. Chem. Phys., 2015, 17, 13045–13052.
18. X. Wang and R. Rinaldi, ChemSusChem, 2012, 5, 1455–1466.
19. A. C. S. Paiva, P. G. Kistemaker and T. L. Weeding, Int. J. Mass Spectrom., 2002, 221, 107–115.
20. M. Guerra, R. M. Pinto, J. P. Santos and A. C. S. Paiva, Mol. Phys., 2013, 111, 3311–3319.
21. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
22. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc.Wallingford CT, 2009.
24. J. Altnöder, S. Oswald and M. A. Suhm, J. Phys. Chem. A, 2014, 118, 3266–3279.
25. M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721.
26. D. Ambrose, J. H. Ellender, C. H. S. Sprake and R. Townsend, J. Chem. Thermodyn., 1976, 8, 165–178.
27. M. Gerhards and C. Unterberg, Phys. Chem. Chem. Phys., 2002, 4, 1760–1765.
28. C. Unterberg, A. Jansen and M. Gerhards, J. Chem. Phys., 2000, 113, 7945.
29. R. H. Page, Y. R. Shen and Y. T. Lee, J. Chem. Phys., 1988, 88, 4621.
30. C. Riehn, C. Lahmann, B. Wassermann and B. Brutschy, Chem. Phys. Lett., 1992, 197, 443–450.
31. S. Tanabe, T. Ebata, M. Fujii and N. Mikami, Chem. Phys. Lett., 1993, 215, 347–352.
32. A. Stamm, M. Weiler, A. Brächer, K. Schwing and M. Gerhards, Phys. Chem. Chem. Phys., 2014, 16, 21795–21803.
33. M. Weiler, K. Bartl and M. Gerhards, J. Chem. Phys., 2012, 136, 114202.
34. V. A. Shubert and T. S. Zwier, J. Phys. Chem. A, 2007, 111, 13283–13286.
35. G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103.
36. M. Schnell, Z. Phys. Chem., 2013, 227, 1–21.
37. D. Schmitz, V. A. Shubert, T. Betz and M. Schnell, J. Mol. Spectrosc., 2012, 280, 77–84.
38. C. M. Western, University of Bristol, http://pgopher.chm.bris.ac.uk, 2016, Version 9.1.
39. H. Hartwig and H. Dreizler, Z. Naturforsch., 1996, 51a, 923–932.
40. R. C. Woods, J. Mol. Spectrosc., 1966, 21, 4–24.
41. R. C. Woods, J. Mol. Spectrosc., 1967, 22, 49–59.
42. M. Feigel, THEOCHEM, 1996, 366, 83–88.
43. T. Straßner, Can. J. Chem., 1997, 75, 1011–1022.
44. K. Aimi, T. Fujiwara and S. Ando, J. Mol. Struct., 2002, 602–603, 405–416.
45. H. C. Gottschalk, J. Altnöder, M. Heger and M. A. Suhm, Angew. Chem., Int. Ed., 2016, 55, 1921–1924.
46. A. Stamm, K. Schwing and M. Gerhards, J. Chem. Phys., 2014, 141, 194304.
47. A. Stamm, D. Bernhard and M. Gerhards, Phys. Chem. Chem. Phys., 2016, 18, 15327–15336.
48. R. M. Lees and J. G. Baker, J. Chem. Phys., 1968, 48, 5299–5318.
49. R. M. Lees, F. J. Lovas, W. H. Kirchhoff and D. R. Johnson, J. Phys. Chem. Ref. Data, 1973, 2, 205.
50. G. T. Fraser, F. J. Lovas and R. D. Suenram, J. Mol. Spectrosc., 1994, 167, 231–235.
51. E. G. Hohenstein, R. M. Parrish, C. D. Sherrill, J. M. Turney and H. F. Schaefer, J. Chem. Phys., 2011, 135, 174107.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp03557d

---