Solvent effects on de-excitation channels in the p-coumaric acid methyl ester anion, an analogue of the photoactive yellow protein (PYP) chromophore

Abstract

In an attempt to shed light on the environmental effects on the deactivation channels of the PYP chromophore, radiative and non-radiative deactivation mechanisms of the anionic p-coumaric acid methyl ester (pCE⁻) in the gas phase and water solution are compared at the CASPT2//CASSCF/cc-pVDZ level and, when necessary, at the CASPT2//CASPT2/cc-pVDZ level. We find that the solvent produces dramatic modifications on the free energy profile of the S1 state. Two twisted structures that are minima in the gas phase could not be localized in aqueous solution. Furthermore, the relative stability of minima and conical intersections (CIs) is reverted with respect to the gas phase values, affecting the prevalent de-excitation paths. As a consequence of these changes, three competitive de-excitation channels are open in aqueous solution: the fluorescence emission from a planar minimum on S1, the trans–cis photoisomerization through a CI that involves the rotation of the vinyl double bond and the non-radiative, non-reactive, de-excitation through the CI associated with the rotation of the single bond adjacent to the phenyl group. In the gas phase, the minima are the structures with lower energy, while in solution the CI^β structure, characterized by a large charge separation, is strongly stabilized by interactions with water molecules and becomes the structure with the lowest energy on S1. These facts explain the low fluorescence signal of pCE⁻ in aqueous solution and the presence of partial trans–cis photoisomerization in this system.

---

I. Introduction

Because of the small size and structural simplicity of both the chromophore and the protein, the Photoactive Yellow Protein (PYP)^1–7 is an attractive model system for exploring the relationship between the absorption of light and the biological response.^8–11 PYP is a light sensor found in Halorhodospira halophila.¹ Its chromophore, an analogue of p-coumaric acid, in the presence of blue light, undergoes a trans–cis photoisomerization,^12–14 which initiates the negative phototaxis of the bacterium.¹⁵ It is commonly accepted that the trans–cis photoisomerization of the chromophore occurs through a conical intersection between the first excited state S1 and the ground state S0 that involves the rotation of the vinyl double bond.^16–20 This path competes with a non-radiative, non-reactive, de-excitation through an internal conversion that involves the rotation around the single bond adjacent to the phenol group. Several theoretical and experimental studies have evidenced that the de-excitation path is affected by the chemical nature^21–23 (ester or thio-ester) and the protonation state of the chromophore.^24–26 The nature of the solvent^27–34 or the environmental characteristics provided by the protein^35–53 also play an important role.

Even though a de-excitation process is intrinsically a dynamic event and hence it calls for the use of excited state dynamic simulation methods,^11,54 the description of the S1 exited state topology in terms of free energy differences between the critical points (Franck–Condon geometries, minima, conical intersections, etc.) can shed light on the factors that control the competition between different de-excitation channels. This task, however, is not easy, as the critical point geometries can be strongly dependent on the calculation level or the presence of a surrounding medium.^55–57 An adequate description of the free energy surface needs to account for both the multiconfigurational character of the excited states and the dynamic correlation contribution, with the consequent computational cost. This cost increases in solution as the calculations need to consider thermal effects and include both specific and bulk solvent interactions. It is known that the surroundings play an important role in this system.^27–34 Firstly, because chromophore–protein or chromophore–solvent interactions permit the stabilization of the negative charge hosted by the phenolic end of the chromophore and prevent autoionization^58–61 as it occurs in the gas phase. Secondly, because the surroundings modify the topology of ground and excited state surfaces.^55–57

In previous papers^62–64 we have analyzed the role played by the solvent, the protonation state and the nature of the substituent on the UV-vis absorption spectrum. It was found that the electronic spectrum substantially changes when the chromophore passes from the gas phase to aqueous solution. Furthermore, the nature of the heteroatom in the ester group modulates the solvent effects: the first two excited states become practically degenerated for oxo compounds but well separated for thio-derivatives.

In the present article, we try to extend the previous studies by describing the complete S1 free energy surface of the p-coumaric acid methyl ester, pCE⁻ (see Fig. 1), both in the gas phase and in water solution by going beyond the Franck–Condon region. This permits the comparison of the radiative and non-radiative deactivation mechanisms of the S1 excited state. The topology of this first excited state is interesting not only because it displays several minima, conical intersections (CIs), transition states (TSs), etc. but also because these structures are characterized by very different charge distributions, thus important solvent effects on their relative stabilities are expected. Furthermore, unlike thio-derivatives wherein the photoisomerization channel is deactivated in solution, in pCE⁻, several de-excitation channels are simultaneously open.³³

Fig. 1 The PYP chromophore: p-coumaric acid methyl ester.

It is interesting to know that pCE⁻ shares many features with 11-cis-retinal, the rhodopsin chromophore. They show a similar photoisomerization process, including the decrease of the photoisomerization quantum yield caused by solvation with respect to the process in the protein. Regarding the first two excited states, they are well separated in the gas phase and inside the protein whereas they become almost degenerated in water solution. Finally, as in retinal, it will be shown that for this PYP chromophore model, the number of minima on the excited state surface reduces when passing from the gas phase to aqueous solution.

The rest of the paper is organized as follows: Section II describes the methods and approximations used in the location of different structures (minima, CIs, etc.) both in the gas phase and in solution. Section III describes the topology of the S1 excited state surface in both media. Finally, Section IV displays the main conclusions.

II. Methods and computational details

Optimized geometries of pCE⁻ were obtained using the complete active self-consistent field (CASSCF)⁶⁵ method. Based on our previous experience in studying the p-coumaric acid system, the selected basis set was cc-pVDZ.⁶⁶ The active space was formed by all the combinations of 12 electrons in 11 orbitals, all of π nature. Excited state structures (Franck–Condon points, minima, and conical intersections) were calculated as the state average of the first two states (SA2), considering equal weights. The dynamic correlation energy contribution was calculated using the CASPT2 methodology^67,68 and the SA(2)-CASSCF wave function was employed as the reference wave function. The ionization potential–electron affinity (IPEA) shift used in CASPT2 calculations was 0.0. To minimize the appearance of intruder states, an additional imaginary shift of 0.1i E_h was used. Oscillator strengths were calculated using the RASSI algorithm implemented in Molcas-7.4.⁶⁵

Solvent effects were introduced using the averaged solvent electrostatic potential from the molecular dynamics data (ASEP/MD) method^69–74 developed in our laboratory. The method permits combining the quantum-mechanical description of the solute with the microscopic description of the environment. ASEP/MD is a sequential quantum mechanics/molecular mechanics (QM/MM) method implementing the mean field approximation. In this approximation, the average value of any solute property is replaced by the value calculated in the presence of an average solvent perturbation or configuration. Details of the method can be found elsewhere.^69–74

Briefly, the solvent perturbation is calculated from classical molecular dynamics (MD) simulations, using a rigid body approximation for the solute geometry and a non-polarizable force field. From the resulting simulation data, the average electrostatic potential generated by the solvent on the solute (ASEP) is obtained. This potential is introduced as a perturbation into the solute's quantum mechanical Hamiltonian, and by solving the associated Schrödinger equation, a new charge distribution and geometry for the solute are obtained, which are used in the next MD simulation. This iterative process is repeated until the electron distribution of the solute, its geometry, and the solvent structure around it become mutually equilibrated.

As for the molecular dynamics simulations, they included 1532 water molecules and one molecule of solute in a rhombic dodecahedral box. No counterion was included. Previous studies⁵⁷ in related systems have shown that because of the large dielectric screening effect of polar solvents, the effect of the counterion on the structure and the spectrum of the chromophore is minimal. All molecules had fixed intramolecular geometry. For the solute, the Lennard-Jones parameters were taken from the optimized potentials for liquid simulations all-atom (OPLS–AA) force field.^75–78 Solute atomic charges were computed from the quantum calculations through a least-squares fit to the electrostatic potential at the points where the solvent charges are located. For water molecules, the TIP4P⁷⁹ model was employed. Periodic boundary conditions were applied in all directions. Short-range electrostatic interactions were cut off at 1.3 nm and long-range interactions were calculated using the Particle-Mesh Ewald (PME) method.⁸⁰ The PME parameters are shown in Table S1 in the ESI.† Note that we are applying the PME method to a charged system. As highlighted by Hub et al.⁹⁴ this could yield to artifacts in heterogeneous systems. However, because of the quite homogeneous character of our system and the high value of the dielectric constant good performance of the PME method is expected. In fact, in a previous study⁵⁷ of a charged solute using the same force field no appreciable differences were found between the neutral (solute + counterion) and the charged (solute) description of the system. The temperature was fixed at 298 K using the Nosé–Hoover thermostat.^81,82 Each simulation was run in the NVT ensemble for 500 ps, with a time step of 1 fs, where the first 200 ps were used for equilibration and the last 300 ps for production. In solution the final results were obtained by averaging the last five ASEP/MD cycles and therefore they represent a 1.5 ns average.

As mentioned before, the geometries were optimized in the presence of the solvent perturbation. The technique followed is based on the joint use of the free-energy gradient method^83–85 (FEG) and the mean field approximation,⁸⁶ and it has been described in a previous paper.⁷⁴ This procedure has been successfully applied to the geometry optimization of ground and excited states of small and medium sized molecules in solution. All the minima were confirmed by vibrational analysis. Minimum energy conical intersection (MECI) geometries were located using a modification of Martínez's algorithm⁸⁷ implemented in ASEP/MD. The differential characteristic of Martínez's algorithm is that it does not require the calculation of the derivative coupling. In this point, it is worth introducing some considerations about the solvent regime used during the MECI optimization. Firstly, when the system is in solution, energies and gradients used in the MECI search are replaced by free energies and derivatives of the free energy, respectively. Secondly, when the system approaches the CI and in order to avoid instabilities the solvent is always equilibrated with the same electronic state independently of the CASSCF root order. Finally, solvent dynamic effects are neglected, i.e., it is assumed that the solvent is always in equilibrium with the charge distribution of the excited state, that is the CI is optimized in a subset of all the possible solvent configurations (equilibrium + non-equilibrium configurations); from this point of view, the MECI thus obtained is an upper limit to the actual value. However, as we show below, in the PYP chromophore, the two CIs involved in the non-radiative deactivation are the lowest energy points on S1; in fact, they can be located by directly minimizing the free energy of the S1 state. Consequently, in pCE⁻, the optimization procedure permits obtaining the real MECIs of this system. This equilibrium approximation has been successfully applied to the study of de-excitation paths in acrolein^55,56 and retinal.⁵⁷Ab initio simulations of the PYP chromophore performed by Boggio-Pasqua et al.¹¹ and Martínez and co-workers¹⁷ suggest that excited state deactivation does not necessarily take place at the MECI, i.e., the chromophore can return to the ground state through any point close to the CI seam and with a solvent structure that probably is “delayed” with respect to the equilibrium situation. The non-radiative deactivation mechanisms of the PYP chromophore imply a large amplitude rotation of part of the molecule that could produce the overlap between the solvent molecules and part of the chromophore. Because of this steric hindrance, a certain degree of solvent reorganization is compulsory. The static description followed in our study implies that it is not possible to obtain dynamic information such as photoisomerization yields or fluorescence decay curves. In spite of this, it has been argued⁹³ that the MECI general features are representative of the intersection space and, consequently, can be used for the mechanistic rationalization of different deactivation paths.

Once the critical points on the free energy surface have been located, (MECIs, Franck–Condon points, minima, etc.), free energy differences between them were estimated making use of a dual method, where the solute contributions are quantum-mechanically calculated but the solute–solvent interaction contributions are classically calculated. The free energy difference between two species or states, I and J, in solution, ΔG_IJ, reads:⁸⁸

ΔG_IJ = ΔE_IJ + ΔG^int_IJ + ΔV_IJ (1)

where ΔE is the internal quantum energy difference in the solute between the two species or states I and J and ΔG^int is the solute–solvent interaction free energy difference, which is calculated classically using the free energy perturbation (FEP) method.⁸⁹ The solute geometry was assumed to be rigid and a function of the perturbation parameter λ. When λ = 0, the solute geometry and charges correspond to the initial state (the chromophore ground state, for instance). When λ = 1, the charges and geometry correspond to the final state (the critical points on the chromophore excited state surface). Charges and geometries of the initial and final states are those obtained using ASEP/MD. A linear interpolation is applied for intermediate values. A value of Δλ = 0.005 was used. That means a total of 200 separate molecular dynamics simulations were carried out to determine the free-energy difference. The final value is obtained as the arithmetic mean of the backward and forward free energy values. ΔV is a term that includes the zero point energy difference and entropic contributions between the two states. This term, ΔV, can be evaluated by applying the harmonic oscillator and rigid rotor approximations to the vibrational and rotational modes of the solute in solution, and it needs the information provided by the Hessian matrix, something that makes its calculation difficult in solution systems. In a previous study⁷² it was found that the contribution of this term to the conformational equilibrium of a small dipeptide was lower than 0.1 eV. In pCE⁻ we find a similar value. Thus, in the gas phase, the contribution of this term to the free energy difference between two local minima on S1 (S1^p and S1^α, see below) is ΔV = −0.07 eV. Because of its low value and large computational cost, this component has been neglected and its value is not included in the final results. It must be noted that this ΔV term refers only to the internal nuclear degrees of freedom of the solute; free energy contributions from the solvent around the solute are appropriately accounted for in the ΔG^int term.

During the ASEP/MD cycles, Molcas-7.4⁶⁵ and Gromacs-4.5^90,91 programs were used for quantum calculations and molecular dynamics simulations, respectively.

III. Results and discussion

(a) Excited state potential energy surface in the gas phase

The topology of the first excited state surface of pCE⁻ and related molecules in the gas phase or micro-solvated has been described in detail by other authors;^11,18–20 consequently, here, we will highlight only some of its main characteristics. In the gas phase, the excited states of the anionic derivatives of p-coumaric acid are not stable and undergo auto-ionization. In spite of this, their study in vacuum remains interesting as it can help clarify the role played by the solvent in the de-excitation processes. The S1 excited state surface of the bare pCE⁻ displays three minima and one CI. These three minima are one planar (S1^p) and two twisted structures, which are the result of the rotation of the vinyl double bond (S1^β) and the torsion of the single bond adjacent to the phenyl group (S1^α). Gromov et al.^18–20 have shown that the latter structure is connected with the FC point by a non-activated path; consequently, the chromophore is unstable with respect to the α-twist. Finally, the CI is related to S1^β and it corresponds to the rotation around the same vinyl double bond, the structure denoted as CI^β. No CI associated with the rotation around the single bond α was found in this compound.

The electronic structure of the pCE⁻ ground state is the result of the equilibrium between two resonance forms, with the negative charge localized at the phenolate oxygen or carboxyl oxygen and, consequently, it displays some quinolic character. In Table 1 the most characteristic geometrical parameters for these structures are collected. The S1^p minimum exhibits dihedral and bond angles similar to the ground state minimum and hence to the FC point. However, it displays a somewhat lower quinolic character than the S0 minimum. Thus, C7–C12 and C12–C14 bond lengths increase by about 0.03 Å with respect to the FC point and, at the same time, the bond length of C14–C16 decreases.

Table 1 Selected geometrical parameters for S0, S1^p, S1^α

	S0	S1^p	S1^α	S1^β	CI^β	CI^β(b)
(O1–C2)	1.233	1.243	1.237	1.244	1.246	1.270
(C2–C3)	1.458	1.441	1.454	1.450	1.441	1.455
(C3–C5)	1.371	1.401	1.378	1.375	1.388	1.393
(C5–C7)	1.428	1.432	1.432	1.433	1.420	1.436
(C7–C8)	1.424	1.422	1.431	1.436	1.426	1.434
(C8–C10)	1.373	1.389	1.378	1.377	1.380	1.392
(C2–C10)	1.454	1.458	1.454	1.443	1.447	1.455
(C7–C12)	1.428	1.461	1.478	1.410	1.437	1.428
(C12–C14)	1.368	1.413	1.417	1.467	1.472	1.469
(C14–C16)	1.454	1.425	1.405	1.459	1.497	1.492
(C16–O17)	1.204	1.220	1.225	1.201	1.192	1.217
(C16–C18)	1.358	1.376	1.394	1.356	1.334	1.367
(O18–C19)	1.400	1.393	1.388	1.402	1.411	1.432
β (C7–C12–C14–C16)	180.0	180	180.0	93.5	72.8	79.8
α (C8–C7–C12–C14)	180.0	180	118.2	176.2	−165.3	−175.8

---

Regarding the twisted structures, S1^α shows an α-twist of around 118° without rotation around β and S1^β is characterized by a β-twist of 93° and almost no rotation around α (see Fig. 2). For the S1^α structure, the C7–C12 bond length (formally a single bond) is 1.48 Å, a value slightly larger than a typical C–C single bond. The C12–C14 bond length (formally a double bond) takes a value close to 1.42 Å. In S1^β the opposite trend is observed, the C12–C14 bond length is larger than the C7–C12 value its quinolic character being stronger than that of S1^p. Finally, the CI^β structure displays values of about 73° and 165° for the β- and α-torsion angles respectively. Note that to reach this structure, α and β rotate following a concerted mechanism. In addition, it can be said that the rotation around α helps the corresponding β twist as β does not needs to arrive to 90° in order to reach the CI.

Fig. 2 S1^α and S1^β geometries.

Fig. 3 and Table 2 display relative stabilities for all the structures located on the S1 surface, including the FC point. For the sake of simplicity, just CASPT2 energies are shown in Fig. 3, and the CASSCF values are omitted. As expected, the inclusion of the dynamic correlation decreases the transition energies. The S1^β minimum is the most stable excited state structure; it is 6.7 kcal mol⁻¹ more stable than S1^p, 5.9 kcal mol⁻¹ than S1^α and 12.2 kcal mol⁻¹ than the FC point. In turn, CI^β is 5.5 kcal mol⁻¹ above the FC point and it seems to be not accessible by direct excitation to S1. Thus, after excitation to the FC point the system could easily reach the planar minimum, as their geometries are quite similar. Once there, emission could be a possible de-excitation route. The oscillator strength calculated for S1^p is close to 1, see Table 3. In contrast, the emissions from the deepest minimum, S1^β, and from S1^α, are unlikely as they present oscillator strength close to zero. The energy gap between S1^p and the ground state is about 2.69 eV; 1.70 eV at the S1^α geometry and notably smaller for S1^β due to the proximity of CI^β.

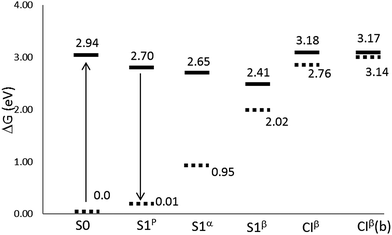Fig. 3 Relative energies (in eV) with respect to the equilibrium ground state at the CASPT2//CASSCF/cc-pVDZ level of theory in the gas phase. CI^β(b) stands for the CASPT2//CASPT2/cc-pVDZ level.

Table 2 Relative energies (in kcal mol⁻¹) for different stationary points located in the excited state surface in the gas phase at the SA2-CASSCF(12,11)-PT2/cc-pVDZ level

	pCE^−
S1^p	0
S1^α	−1.15
S1^β	−6.69
FC	+5.53
CI^β	+11.06

---

Table 3 Electronic transition energies (in eV) and oscillator strengths in the gas phase for the three S1 excited state minima of pCE⁻

	(π → π*)	Osc. str.
Planar minimum, S1^p	2.69	0.913
α-Twisted minimum, S1^α	1.70	0.000
β-Twisted minimum, S1^β	0.38	0.000

---

As mentioned before, the dynamic correlation contribution to energy was calculated by using the CASSCF optimized geometries. The same procedure was followed regarding the location of the CI^β MECI. Even though this protocol is usually useful, some inconsistencies can be found in some occasions. Thus, when the energy was recalculated at the CASPT2 level for the CASSCF CI^β MECI, the energy gap between the S1 and S0 states was 9.7 kcal mol⁻¹. This means that the CI structure located at the CASSCF level is no longer a CI at the CASPT2 level. Because of this the MECI geometry was re-optimized at the CASPT2 level. CI^β geometries calculated at SA2-CASSCF(12,11) and CASPT2(12,11) levels are shown in the last two columns of Table 1. Similarly to those found in previous studies,⁶³ the inclusion of the dynamic correlation reduces the difference between single and double bonds. It is also noticeable that a lower rotation around α is necessary to reach the CASPT2 MECI compared to the CASSCF geometry. What is more important is the effect of the inclusion of the dynamic correlation to the absolute energies. As it can be seen in Table 4, the main effect is to increase the ground state energy at the MECI geometry by about 9.5 kcal mol⁻¹, whereas the energy of the excited state is very similar in both CASSCF and CASPT2 geometries. Consequently, the relative stability of the CI^β structure with respect to the FC point is not affected.

Table 4 Absolute energies (in a.u.) and relative energies (in eV) of the CI^β structure in the gas phase for the pCE⁻ model. Geometries and energies are calculated at SA2-CASSCF(12,11)/cc-pVDZ and CASPT2(12,11)/cc-pVDZ levels of theory

	CASSCF geometry			CASPT2 geometry
	E S0 (a.u.)	E S1 (a.u.)	ΔE (eV)	E S0 (a.u.)	E S1 (a.u.)	ΔE (eV)
CASSCF	−608.5680	−608.5683	−0.01	−608.5863	−608.5695	0.46
CASPT2	−610.3182	−610.3336	−0.42	−610.3333	−610.3321	0.03

---

Finally the charge distribution for different critical points found in the gas phase is analyzed as it will be crucial to settle their relative stability in water solution. These charge distributions are collected in Table 5. For the sake of simplicity, the system has been divided into three parts: the phenolic group, the vinyl double bond and the ester part. The chromophore ground state features a large negative charge on the phenolic group; during the transition (to the FC point), part of this charge is transferred toward the rest of the molecule. Similarly, in the planar S1^p structure, most of the charge is located on the vinyl double bond. This trend increases in S1^α, where the double bond carries a charge of −0.72 e⁻. Finally, the charge distributions in S1^β and CI^β are similar to that shown by the ground state.

Table 5 Gas phase charge distribution

	S0	S1^p	S1^α	S1^β	CI^β
Phenolic group	−0.626	−0.392	−0.065	−0.671	−0.515
Vinyl double bond	−0.358	−0.474	−0.717	−0.254	−0.441
Ester group	−0.016	−0.134	−0.218	−0.075	−0.044

---

(b) Excited state free energy surface in aqueous solution

Inside the protein, the photoisomerization mechanism involves the flipping of the chromophore thioester tail, while the phenolate group of the chromophore remains unaffected, leading to the formation of the cis isomer.^14,37,92 The photoisomerization is also active in solution for some PYP chromophore derivatives, with pCE⁻ among them.³³ Transient spectroscopy studies in water solution have attributed the excited state deactivation to the rotation of the vinyl bond.^{32–34,47,51}

In polar solvents (and inside the protein) the negative charge of pCE⁻ is stabilized by solute–medium interactions and, as a consequence, the first excited states now become stable^58–61 with respect to auto-ionization. This makes the experimental study of the competition between radiative and non-radiative de-excitation paths possible. We found that the solvent causes important modifications on the free energy profile of the S1 state, compare Fig. 3 and 4. In aqueous solution the S1 excited state surface displays only one minimum: a planar structure, S1^p, with geometry similar to that obtained in the gas phase. Furthermore, there appears a new de-excitation channel through a CI that involves the rotation around the single bond adjacent to the phenyl group. We denote the corresponding MECI as CI^α. The opening of the single bond isomerization channel by the solvent in pCE⁻ is similar to what was found in pCK⁻, a molecule that has also been used as a model for the PYP chromophore and whose dynamics has been described in detail by Boggio-Pasqua et al.¹¹ and Martínez and co-workers.¹⁷ Finally, the relative stability of the minima and CIs is reversed with respect to the gas phase situation: the CI^α and CI^β structures now become more stable than the S1^p minimum and the FC point. In sum, in aqueous solution, we can distinguish three competitive de-excitation channels: fluorescence emission from S1^p, trans–cis photoisomerization through CI^β and non-radiative, non-reactive, de-excitation through CI^α.

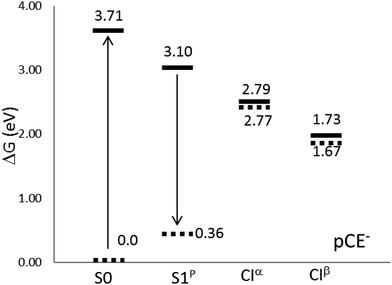Fig. 4 Relative energies (in eV) with respect to the equilibrium ground state at the CASPT2//CASSCF/cc-pVDZ level of theory in aqueous solution.

Table 6 displays some geometric parameters of the S1^p, CI^α and CI^β structures in solution. In contrast to the findings in the ground state,⁶⁴ the solvent effect on the bond lengths is in general small in the excited state structures. In S1^p the largest variations appear in the C16–O18 and O18–C19 bond lengths, the former decreasing by 0.025 Å and the latter increasing by about 0.022 Å. Surprisingly, an almost negligible effect is registered for O1–C2 and C16–O17 bonds, probably due to the scarce effect of the solvent on the charge distribution with respect to the gas phase. In CI^β, the largest variations are found in the C7–C12 and C14–C16 bonds, with a decrease of 0.043 Å and 0.056 Å, respectively, in solution. The solvent also induces some changes in the dihedral angles. In particular, for CI^β, the β- and α-angles show an increase from 72.8 until 86.5° and from −165.3° to −171.7°, respectively, when passing from the gas phase to solution. These values permit us to conclude that in aqueous solution the twist around α- and β-angles is less concerted than in the gas phase. The situation is different for the CASPT2 MECI. In this case even though β shows similar values in the gas phase and solution, a larger rotation of α is necessary in order to reach the MECI. As for the bond lengths, the solvent effect on the CASPT2 geometry is similar to that found for the CASSCF. The most evident difference is the increase of the C7–C12 bond length compared to the decrease found in CASSCF geometry. This fact is related to the bigger rotation of the α-angle found in solution CASPT2 geometry.

Table 6 Selected geometrical parameters for the S1^p, CI^β and CI^α in solution. Optimized geometries at the SA2-CASSCF(12,11)/cc-pVDZ level of theory. CI^β(b) stands for CASPT2(12,11)/cc-pVDZ optimized geometry

	S0	S1^p	CI^α	CI^β	CI^β(b)
d(O1–C2)	1.274	1.257	1.237	1.246	1.274
d(C2–C3)	1.432	1.435	1.452	1.442	1.454
d(C3–C5)	1.386	1.392	1.374	1.378	1.391
d(C5–C7)	1.415	1.432	1.425	1.430	1.435
d(C7–C8)	1.410	1.423	1.427	1.441	1.438
d(C8–C10)	1.386	1.388	1.372	1.379	1.390
d(C2–C10)	1.426	1.445	1.451	1.452	1.455
d(C7–C12)	1.453	1.458	1.474	1.394	1.448
d(C12–C14)	1.351	1.418	1.433	1.468	1.484
d(C14–C16)	1.472	1.422	1.407	1.441	1.494
d(C16–O17)	1.204	1.229	1.235	1.204	1.229
d(C16–O18)	1.321	1.351	1.359	1.334	1.327
d(O18–C19)	1.420	1.415	1.416	1.420	1.455
β(C7–C12–C14–C16)	180.0	180.0	170.9	86.5	78.9
α(C8–C7–C12–C14)	180.0	180.0	86.9	−171.7	−151.8

---

As for CI^α, the main geometrical differences with respect to CI^β are located in the middle part of the chromophore (from C7 to O18) and obviously in the value of their α- and β-twist angles. The α-twist needed to reach CI^β is similar (around 10°) to the β twist in CI^α.

Regarding the polarization of the solute charge distribution during the solvation, it can be concluded that it strongly depends on the considered structure. Thus, while in S1^p the charge distribution is very similar in the gas phase and solution, (see Tables 5 and 7), CI^β displays a very large polarization, and most of the negative charge is localized on the phenolic oxygen atom. In the same way, CI^α concentrates almost all the charges in the vinyl double bond. It is well known that polar solvents favor structures with localized charge, hence it is expected that particularly these two structures become stable in aqueous solution.

Table 7 Charge distribution in solution

	S0	S1^p	CI^β	CI^α
Phenolic group	−0.839	−0.382	−0.935	−0.024
Vinyl double bond	−0.275	−0.539	−0.089	−0.921
Ester group	0.114	−0.079	−0.024	−0.055

---

Table 8 and Fig. 4 display free-energy differences between all the structures located on the S1 surface, including the FC point. The results point out the existence of two different non-radiative de-excitation pathways in solution, which must be added to the radiative de-excitation through fluorescence emission. The S1^p minimum is 14.1 kcal mol⁻¹ below the FC point, but 7.15 and 31.55 kcal mol⁻¹ above the two MECIs. Steady-state techniques have revealed that PYP chromophore models are weakly fluorescent.^10,30 The quantum yields of fluorescence in aqueous solution have been estimated to be about 0.1%. This low value is explained by the large energy of the minimum compared to both MECIs. The calculated fluorescence band corresponds to a (π* → π) transition and it is placed at around 2.74 eV in very good agreement with the experimental value, 2.76 eV, reported by Espagne et al.³⁰ Despite the large solvent effects on the free energy profile, the solvent shift on the emission band is very low. This fact is confirmed by experiments, which found that the position of the fluorescence band does not depend on the solvent nature.³² It is well known that the solvent shift on absorption or emission bands is produced by the differential solvation of the ground and excited states. Therefore it depends on both the flux of charge during the excitation (or de-excitation) and the reaction field generated by the solvent. The low solvent shift in the emission spectrum is a consequence of the small flux of charge distribution during the transition (0.21 e⁻, about half of the flux produced during the absorption process) and the characteristics of the solvent structure around the chromophore. In S1, the solvent molecules concentrate around both moieties (phenolate and ester) of the molecule. During the emission part of the charge is translated from the ester to the phenolate moiety and the decrease of the interaction energy of the ester part (0.3 kcal mol⁻¹) is compensated by the increase in the interaction energy of the phenolate group (1.2 kcal mol⁻¹).⁶³ This is in contrast to the absorption results, where a large blue solvent shift was found. In S0, solvent molecules concentrate around the phenolic oxygen, and the concentration around the ester moiety is negligible. Consequently, when the charge moves from the phenolate to the ester moiety during the excitation there is a decrease of the interaction energy in the phenolate (44.6 kcal mol⁻¹) that is not compensated by an increase of the interaction energy of the ester moiety (21.3 kcal mol⁻¹).⁶³ Thus, the large Stokes's shift of almost 1 eV found in this system is mainly a consequence of the differences in the solvent structure around the S0 and S1 states.

Table 8 Relative free energies (in kcal/mol) in water solution and their components at the SA2-CASSCF(12,11)-PT2/cc-pVDZ level of theory

	ΔGsolute (kcal mol^−1)	ΔGint (kcal mol^−1)	ΔG (kcal mol^−1)
S1^p	0	0	0
CI^α	11.48	−18.63	−7.15 ± 0.07
CI^β	−0.62	−30.93	−31.55 ± 0.23

---

Opposite to what was found in the gas phase, the CI structures located in water solution at the CASSCF level are also CIs when the energies are recalculated at the CASPT2 level. In this case, the S0/S1 energy gaps were calculated to be 0.02 eV for CI^α and 0.06 eV for CI^β, and, consequently, it was not needed to re-optimize the MECI geometries at the CASPT2 level. In aqueous solution, the CI^β structure is 24.4 kcal mol⁻¹ lower in energy than CI^α, and contrary to what happens in the gas phase, they are clearly below the FC point and S1^p minimum. From this, it follows that both structures could be accessible from the FC point. Our results agree with the experiment. In fact, the UV-visible absorption spectrum of pCE⁻, in a basic solution of methanol under steady-state irradiation, displays an isosbestic point that has been attributed to the partial formation of the cis isomer.³³ Studies¹¹ of the dynamics of the chromophore de-excitation paths have found that the route that connects the FC point with CI^α is a non-activated path, while it is necessary to surmount a small barrier to reach CI^β. This is, probably, the reason that explains the low photoisomerization quantum yield in this system. Unfortunately, we did not succeed in the location of the corresponding TS and we cannot, for the moment, confirm this hypothesis. The calculation of TSs on excited free energy surfaces in solution by using the ASEP/MD methodology involves challenges that will be tackled in future developments.

The stability of different structures in solution, Table 8, is the result of the interplay between two components (see eqn (1)): the internal energy component (ΔG_solute) and the solvation energy (ΔG_int). Both the solvation and the internal energies favor the CI^β structure with respect to CI^α and S1^p. This is in contrast to what was found in the gas phase where the most stable structures were S1^α and S1^β, the CI^β MECI being higher in energy than the minima and even than the FC point. This happens as in solution the MECIs display a very much localized charge distribution, and as a consequence, they are strongly stabilized by the solvent becoming the most stable structures in water. This large stabilization probably now prevents the formation of S1^α and S1^β. The S1^p minimum is the only minimum that remains in solution. However, its charge is more delocalized than in the two MECIs and hence it is worse solvated. As a consequence the planar minimum is found at higher energies than the MECIs and a low quantum yield during the fluorescence emission is expected.

As it has been indicated, the charge distribution is significantly different depending on the analyzed structure (minima or MECIs). These differences result in different solvent structures around the phenolic and carbonyl groups. In Fig. 5 we gather the radial distribution functions (RDFs) of water hydrogens around O1, O17 and O18 atoms for the S0, S1^p, CI^α and CI^β structures. While in the ground state the height of the first peak is large in the O1–Hw RDF, low in the O17–Hw RDF and negligible in the O18–Hw RDF, in the S1^p excited state it turns out that there is a higher height for O17–Hw and O18–Hw RDFs and a less structured solvent around the phenolic oxygen, although the height of the first peak around O1 is still larger than that around O17 and O18. In sum, as a consequence of the flux of charge accompanying the excitation, the phenolic oxygen atom is worse solvated in the S1^p structure than in the ground state, while the opposite is found for the oxygen atoms of the ester group. The analysis of the solvent structure around CI^α and CI^β is also interesting. The CI^β charge distribution is very similar to that displayed by S0—in the two structures the charge is localized on the phenolic oxygen—and accordingly, they display very similar RDFs. In contrast, in CI^α the RDFS are very similar to that found in S1^p. Finally, Fig. 6 displays atom density maps around the S0, S1^p, CI^α and CI^β critical points. This figure permits us to easily appreciate the change in the solvent structure. When the molecule relaxes from S0 to S1^p some water molecules move from the phenyl group to the vinyl bond. CI^α concentrates most of the charge in the vinyl group and it is around this region the density of water molecules is larger. Additionally, the solvent structure around the phenolic group disappears and increases around the carbonyl group. Finally, the solvent structure around CI^β is similar to that found around S0. These facts suggest that very important solvent reorganization is necessary before the molecule reaches the CI.

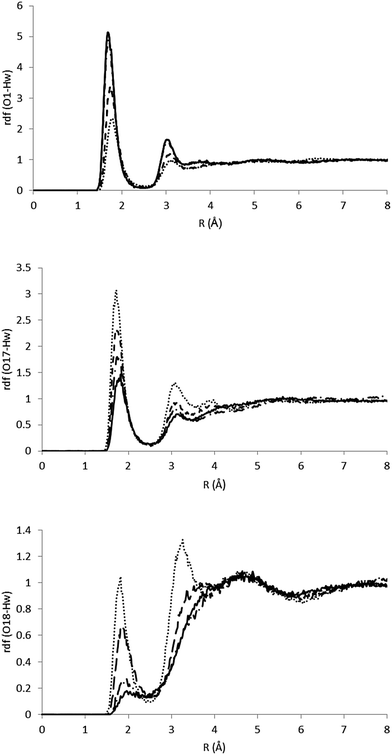Fig. 5 RDFs for the O1–Hw, O17–Hw and O18–Hw pairs. The full line indicates S0, the dashed line indicates S1^p, the dotted line indicates CI^α and the dashed-dotted line indicates CI^β.

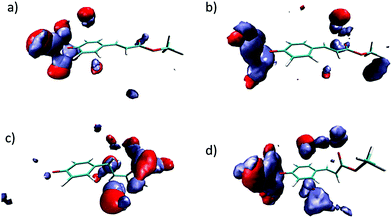Fig. 6 Three-dimensional probability distribution around S0 (a), S1^p (b), CI^α (c) and CI^β (d) in water solution. Color code: red: water oxygen atoms. Ice blue: water hydrogen atoms.

IV. Conclusions

The comparison of the excited state energy surfaces in the gas phase and solution enables one to shed light on the effect exerted by the solvent on the de-excitation channels of pCE⁻. In the gas phase the excited state of pCE⁻ is not stable as it undergoes auto-ionization; consequently, the available experimental information about the shape of the S1 excited state potential energy surface is scarce and only theoretical calculations can provide a detailed description of the energy surface. In agreement with previous studies, our calculations point to the presence of the following structures: (a) three local minima, one flat and two twisted, and (b) a CI associated with the rotation of the vinyl double bond and placed at a higher energy than the FC structure. We find that a polar solvent like water produces important modifications on the free energy profile of the S1 state. In fact, a new de-excitation channel through a CI^α that involves the rotation around the single bond adjacent to the phenyl group is opened. Furthermore, solute–water interactions stabilize the two MECI structures, which are characterized by a large charge separation. CI^β now becomes the structure with the lowest energy on S1, followed by CI^α. The presence of these CI structures destabilizes the twisted minima that are no longer stable in water solution. Only the planar minimum remains stable, but at higher energies than the CIs. Consequently, in agreement with experiment, only weak fluorescence is expected.

Acknowledgements

This work was supported by the GR15169 project of the Consejería de Economía, Comercio e Innovación of the Gobierno de Extremadura.

References

1. T. E. Meyer, Biochim. Biophys. Acta, 1985, 806, 175.
2. T. E. Meyer, E. Yakali, M. A. Cusanovich and G. Tollin, Biochem. J., 1987, 26, 418.
3. M. Baca, G. E. O. Borgstahl, M. Boissinot, P. M. Burke, D. R. Williams, K. A. Slater and E. D. Getzoff, Biochemistry, 1994, 33, 14369.
4. W. D. Hoff, P. Düx, K. Hård, B. Devreese, I. M. Nugteren-Roodzant, W. Crielaard, R. Boelens, R. Kaptein, J. van Beeuman and K. J. Hellingwerf, Biochemistry, 1994, 33, 13959.
5. A. Baltuška, I. H. M. van Stokkum, A. Kroon, R. Monshouwer, K. J. Hellingwerf and R. van Grondelle, Chem. Phys. Lett., 1997, 270, 263.
6. H. Chosrowjan, N. Mataga, N. Nakashima, Y. Imamoto and F. Tokunaga, Chem. Phys. Lett., 1997, 270, 267.
7. S. Devanathan, A. Pacheco, L. Ujj, M. A. Cusanovich, G. Tollin, S. Lin and N. Woodbury, Biophys. J., 1999, 77, 1017.
8. K. J. Hellingwerf, J. Hendriks and T. Gensch, J. Phys. Chem. A, 2003, 107, 1082.
9. M. A. Cusanovich and T. E. Meyer, Biochemistry, 2003, 42, 4759.
10. P. Changenet-Barret, A. Espagne, P. Plaza, K. J. Hellingwerf and M. M. Martin, New J. Chem., 2005, 29, 527.
11. M. Boggio-Pasqua, C. F. Burmeister, M. A. Robb and G. Groenhof, Phys. Chem. Chem. Phys., 2012, 14, 7912.
12. R. Kort, H. Vonk, X. Xu, W. D. Hoff, W. Crielaard and K. J. Hellingwerf, FEBS Lett., 1996, 382, 73.
13. E. D. Getzoff, K. N. Gutwin and U. K. Genick, Nat. Struct. Biol., 2003, 10, 663.
14. K. Heyne, O. F. Mohammed, A. Usman, J. Dreyer, E. T. J. Nibbering and M. A. Cusanovich, J. Am. Chem. Soc., 2005, 127, 18100.
15. W. W. Sprenger, W. D. Hoff, J. P. Armitage and K. J. Hellingwerf, J. Bacteriol., 1993, 175, 3096.
16. M. Boggio-Pasqua, M. A. Robb and G. Groenhof, J. Am. Chem. Soc., 2009, 131, 13580.
17. C. Ko, A. M. Virshup and T. J. Martínez, Chem. Phys. Lett., 2008, 460, 272.
18. E. V. Gromov, J. Chem. Phys., 2014, 141, 224308.
19. E. V. Gromov, I. Burghardt, J. T. Hynes, H. Köppel and L. S. Cederbaum, J. Photochem. Photobiol., A, 2007, 190, 241.
20. E. V. Gromov, I. Burghardt, H. Köppel and L. S. Cederbaum, J. Phys. Chem. A, 2011, 115, 9237.
21. E. V. Gromov, I. Burghart, H. Köppel and L. S. Cederbaum, J. Phys. Chem. A, 2005, 109, 4623.
22. P. Changenet-Barret, A. Espagne, S. Charier, J.-B. Baudin, L. Jullien, P. Plaza, K. J. Hellingwerf and M. M. Martin, Photochem. Photobiol. Sci., 2004, 3, 823.
23. P. Changenet-Barret, A. Espagne, N. Katsonis, S. Charier, J.-B. Baudin, L. Jullien, P. Plaza and M. M. Martin, Chem. Phys. Lett., 2002, 365, 285.
24. M. Vengris, D. S. Larsen, M. A. van der Horst, O. F. A. Larsen, J. Hellingwerf and R. van Grondelle, J. Phys. Chem. B, 2005, 109, 4197.
25. A. R. Kronn, W. D. Hoff, H. P. Fennema, J. Gijzen, G.-J. Koomen, J. Verhoeven, W. Crielaard and J. Hellingwerf, J. Biol. Chem., 1996, 271, 31949.
26. M. Putschögl, P. Zirak and A. Penzkofer, Chem. Phys., 2008, 343, 107.
27. D. S. Larsen, M. Vengris, I. H. M. van Stokkum, M. A. van der Horst, R. A. Cordfunke, K. J. Hellingwerf and R. van Grondelle, Chem. Phys. Lett., 2003, 369, 563.
28. D. S. Larsen, M. Vengris, I. H. M. van Stokkum, M. A. van der Horst, F. L. de Weerd, K. J. Hellingwerf and R. van Grondelle, Biophys. J., 2004, 86, 2538.
29. M. Vengris, M. A. van der Horst, G. Zgrablic, I. H. M. van Stokkum, S. Haacke, M. Chergui, K. J. Hellingwerf, R. van Grondelle and D. S. Larsen, Biophys. J., 2004, 87, 1848.
30. A. Espagne, D. H. Paik, P. Changenet-Barret, M. M. Martin and A. H. Zewail, Chem. Phys. Chem., 2006, 7, 1717.
31. A. Espagne, P. Changenet-Barret, J.-B. Baudin, P. Plaza and M. M. Martin, J. Photochem. Photobiol., A, 2007, 185, 245.
32. A. Espagne, P. Changenet-Barret, P. Plaza and M. M. Martin, J. Phys. Chem. A, 2006, 110, 3393.
33. A. Espagne, D. H. Paik, P. Changenet-Barret, P. Plaza, M. M. Martin and A. H. Zewail, Photochem. Photobiol. Sci., 2007, 6, 780.
34. Y. Wang and H. Li, J. Chem. Phys., 2010, 133, 034108.
35. P. Changenet-Barret, P. Plaza, M. M. Martín, H. Chorowjan, S. Taniguchi, N. Mataga, Y. Imamoto and M. Kataoka, Chem. Phys. Lett., 2007, 434, 320.
36. R. Nakamura, N. Hamada, K. Abe and M. Yoshizawa, J. Phys. Chem. B, 2012, 116, 14768.
37. P. A. Sigala, M. A. Tsuchida and D. Herschlag, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 9232.
38. R. Brudler, T. E. Meyer, U. K. Genick, S. Devanathan, T. T. Woo, D. P. Millar, K. Gerwert, M. A. Cusanovich, G. Tollin and E. D. Getzoff, Biochemistry, 2000, 39, 13478.
39. Z. He, C. H. Martin, R. Birge and K. F. Freed, J. Phys. Chem. A, 2000, 104, 2939.
40. G. Groenhof, M. F. Lensink, H. J. C. Berendsen, J. G. Snijders and A. E. Mark, Proteins: Struct., Funct., Genet., 2002, 48, 202.
41. A. Yamada, T. Ishikura and T. Yamato, Proteins: Struct., Funct., Bioinf., 2004, 55, 1063.
42. K. Okamoto, N. Hamada, T.-A. Okamura, N. Ueyama and H. Yamamoto, Org. Biomol. Chem., 2009, 7, 3782.
43. R. Brudler, T. E. Meyer, U. K. Genick, S. Devanathan, T. T. Woo, D. P. Millar, K. Gerwert, M. A. Cusanovich, G. Tollin and E. D. Getzoff, Biochemistry, 2000, 39, 13478.
44. A. F. Philip, R. A. Nome, G. A. Papadantonakis, N. F. Scherer and W. D. Hoff, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5821.
45. A. Yamada, T. Ishikura and T. Yamato, Proteins: Struct., Funct., Bioinf., 2004, 55, 1070.
46. K. Mihara, O. Hisatomi, Y. Imamoto, M. Kataoka and F. Tokunag, J. Biochem., 1997, 121, 876.
47. U. K. Genik, S. Devanathan, T. E. Meyer, I. L. Canestrelli, E. Williams, M. A. Cusanovich, G. Tollin and E. D. Getzoff, Biochemistry, 1997, 36, 8.
48. E. V. Gromov, I. Burghardt, H. Köppel and L. S. Cederbaum, J. Photochem. Photobiol., A, 2012, 234, 123.
49. E. V. Gromov, I. Burghardt, H. Köppel and L. S. Cederbaum, J. Am. Chem. Soc., 2007, 129, 6798.
50. G. Groenhof, L. V. Schäfer, M. Boggio-Pasqua, H. Grubmüller and M. A. Robb, J. Am. Chem. Soc., 2008, 130, 3250.
51. G. Groenhof, M. Bouxin-Cadematory, B. Hess, S. P. de Visser, H. J. C. Berendsen, M. Olivucci, A. E. Mark and M. A. Robb, J. Am. Chem. Soc., 2004, 126, 4228.
52. E. V. Gromov, I. Burghardt, H. Köppel and L. S. Cederbaum, J. Photochem. Photobiol., A, 2012, 234, 123.
53. I.-R. Lee, W. Lee and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 258.
54. A. M. Virshup, C. Punwong, T. V. Pogorelov, B. A. Lindquist, C. Ko and T. J. Martinez, J. Phys. Chem. B, 2009, 113, 3280.
55. A. Muñoz-Losa, M. E. Martín, I. Fdez. Galván and M. A. Aguilar, Chem. Phys. Lett., 2007, 443, 76.
56. A. Muñoz-Losa, I. Fdez. Galván, M. L. Sánchez, M. E. Martín and M. A. Aguilar, J. Phys. Chem. B, 2008, 112, 877.
57. A. Muñoz-Losa, M. E. Martin, I. Fdez. Galván and M. A. Aguilar, J. Chem. Theory Comput., 2013, 9, 1548.
58. D. S. Larsen, M. Vengris, I. H. M. van Stokkum, M. A. van der Horst, F. L. de Weerd, K. J. Hellingwerf and R. van Grondelle, Biophys. J., 2004, 86, 2538.
59. L. Lammich, J. Rajput and L. H. Andersen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 51916.
60. J. Zhu, L. Paparelli, M. Hospes, J. Arents, J. T. M. Kennis, I. H. M. van Stokkum, K. J. Hellinwerf and M. L. Groot, J. Phys. Chem. B, 2013, 117, 11042.
61. C. R. S. Mooney, M. A. Parkes, A. Iskra and H. H. Fielding, Angew. Chem., Int. Ed., 2015, 54, 5646.
62. F. F. García-Prieto, I. Fdez. Galván, A. Muñoz-Losa, M. A. Aguilar and M. E. Martín, J. Chem. Theory Comput., 2013, 9, 4481.
63. S. Frutos Puerto, A. Muñoz-Losa, M. E. Martín and M. A. Aguilar, Comput. Theor. Chem., 2014, 1040–1041, 287.
64. F. F. García-Prieto, M. A. Aguilar, I. Fdez. Galván, A. Muñoz-Losa, F. J. Olivares del Valle, M. L. Sánchez and M. E. Martín, J. Phys. Chem. A, 2015, 119, 5505.
65. F. Aquilante, L. de Vico, N. Ferre, G. Ghigo, P. Å. Malmquist, P. Neogrady, T. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andres, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224.
66. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
67. K. Andersson, P.-Å. Malmqvist, B. O. Ross, A. J. Sadlej and K. J. Wolinski, J. Phys. Chem., 1990, 94, 5483.
68. K. Andersson, P.-Å. Malmqvist and B. O. Ross, J. Chem. Phys., 1992, 96, 1218.
69. M. L. Sánchez, M. A. Aguilar and F. J. Olivares del Valle, J. Comput. Chem., 1997, 18, 313.
70. I. Fdez. Galván, M. L. Sánchez, M. E. Martín, F. J. Olivares del Valle and M. A. Aguilar, Comput. Phys. Commun., 2003, 155, 244.
71. M. E. Martín, M. L. Sanchez, M. A. Aguilar and F. J. Olivares del Valle, THEOCHEM, 2001, 537, 213–222.
72. G. G. Almeida, J. M. M. Cordeiro, M. E. Martín and M. A. Aguilar, J. Chem. Theory Comput., 2016, 12, 1514.
73. M. L. Sánchez, M. E. Martín, I. Fdez. Galván, F. J. Olivares del Valle and M. A. Aguilar, J. Phys. Chem. B, 2002, 106, 4813.
74. I. Fdez. Galván, M. L. Sánchez, M. E. Martín, F. J. Olivares del Valle and M. A. Aguilar, J. Chem. Phys., 2003, 118, 255.
75. W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657.
76. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225.
77. W. L. Jorgensen, J. D. Madura and C. J. Swenson, J. Am. Chem. Soc., 1984, 106, 6638.
78. W. L. Jorgensen, J. Phys. Chem., 1986, 90, 1276.
79. W. L. Jorgensen and J. D. Madura, Mol. Phys., 1985, 56, 1381.
80. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089.
81. S. Nosé, Mol. Phys., 1984, 52, 255.
82. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695.
83. N. Okuyama-Yoshida, M. Nagaoka and T. Yamabe, Int. J. Quantum Chem., 1998, 70, 95.
84. N. Okuyama-Yoshida, K. Kataoka, M. Nagaoka and T. Yamabe, J. Chem. Phys., 2000, 113, 3519.
85. H. Hirao, Y. Nagae and M. Nagaoka, Chem. Phys. Lett., 2001, 348, 350.
86. M. L. Sánchez, M. E. Martín, I. Fdez. Galván, F. J. Olivares del Valle and M. A. Aguilar, J. Phys. Chem. B, 2002, 106, 4813.
87. B. G. Levine, J. D. Coe and T. J. Martínez, J. Phys. Chem. B, 2008, 112, 405.
88. A. Muñoz-Losa, I. Fdez. Galván, M. E. Martín and M. A. Aguilar, Challenges and Advances in Computational Chemistry, 2008, vol. 6, p. 135.
89. R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420.
90. H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43.
91. E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317.
92. K. Pande, et al. , Science, 2016, 352, 725.
93. A. Migani and M. Olivucci, in Conical Intersections. Electronic structure, Dynamics & spectroscopy, ed. W. Domcke, D. R. Yarkony and H. Köppel, Advanced Series in Physical chemistry, World Scientific, Singapore, 2004, vol. 15, p. 271.
94. J. S. Hub, B. L. de Groot, H. Grubmüller and G. Groenhof, J. Chem. Theory Comput., 2014, 10, 381.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp03541h

---