 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
H3P⋯AgI: generation by laser-ablation and characterization by rotational spectroscopy and ab initio calculations†
Susanna L.
Stephens‡
a,
David P.
Tew
b,
Nicholas R.
Walker
*a and
Anthony C.
Legon
*b
aSchool of Chemistry, Newcastle University, Bedson Building, Newcastle-upon-Tyne, NE1 7RU, UK. E-mail: nick.walker@newcastle.ac.uk
bSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: a.c.legon@bristol.ac.uk
First published on 20th June 2016
Abstract
The new compound H3P⋯AgI has been synthesized in the gas phase by means of the reaction of laser-ablated silver metal with a pulse of gas consisting of a dilute mixture of ICF3 and PH3 in argon. Ground-state rotational spectra were detected and assigned for the two isotopologues H3P⋯107AgI and H3P⋯109AgI in their natural abundance by means of a chirped-pulse, Fourier-transform, microwave spectrometer. Both isotopologues exhibit rotational spectra of the symmetric-top type, analysis of which led to accurate values of the rotational constant B0, the quartic centrifugal distortion constants DJ and DJK, and the iodine nuclear quadrupole coupling constant χaa(I) = eQqaa. Ab initio calculations at the explicitly-correlated level of theory CCSD(T)(F12*)/aug-cc-pVDZ confirmed that the atoms P⋯Ag–I lie on the C3 axis in that order. The experimental rotational constants were interpreted to give the bond lengths r0(P⋯Ag) = 2.3488(20) Å and r0(Ag–I) = 2.5483(1) Å, in good agreement with the equilibrium lengths of 2.3387 Å and 2.5537 Å, respectively, obtained in the ab initio calculations. Measures of the strength of the interaction of PH3 and AgI (the dissociation energy De for the process H3P⋯AgI = H3P + AgI and the intermolecular stretching force constant FP⋯Ag) are presented and are interpreted to show that the order of binding strength is H3P⋯HI < H3P⋯ICl < H3P⋯AgI for these metal-bonded molecules and their halogen-bonded and hydrogen-bonded analogues.
1 Introduction
A programme of systematic investigations of small molecules of the type B⋯MX is being conducted, where B is a small Lewis base (e.g. N2, OC, H2O, H2S, HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, H2C
CH, H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, cyclopropane or NH3), M = Cu, Ag or Au, and X = F, Cl or I.1–19 The programme has both experimental and theoretical components. The experimental approach is to produce B⋯MX by laser ablation of the metal M in the presence of a gas pulse composed of small amounts of B and a molecular source of halogen atoms X in a large excess of argon. Following supersonic expansion of the product B⋯MX entrained in the carrier gas, its rotational spectrum is observed in isolation at a low effective temperature. Various properties of B⋯MX are available through analysis of the rotational spectrum, namely the angular geometry, the distances r(B⋯M) and r(M–X), the strength of the intermolecular bond B⋯M, and the electric charge redistribution that accompanies formation of B⋯MX. The theoretical component of the investigations involves ab initio calculations at the CCSD(T)(F12*) explicitly correlated level of theory, usually with the largest basis set affordable. These calculations have the advantage of providing accurate properties of the isolated molecule, which can be compared with the experimental results.
CH2, cyclopropane or NH3), M = Cu, Ag or Au, and X = F, Cl or I.1–19 The programme has both experimental and theoretical components. The experimental approach is to produce B⋯MX by laser ablation of the metal M in the presence of a gas pulse composed of small amounts of B and a molecular source of halogen atoms X in a large excess of argon. Following supersonic expansion of the product B⋯MX entrained in the carrier gas, its rotational spectrum is observed in isolation at a low effective temperature. Various properties of B⋯MX are available through analysis of the rotational spectrum, namely the angular geometry, the distances r(B⋯M) and r(M–X), the strength of the intermolecular bond B⋯M, and the electric charge redistribution that accompanies formation of B⋯MX. The theoretical component of the investigations involves ab initio calculations at the CCSD(T)(F12*) explicitly correlated level of theory, usually with the largest basis set affordable. These calculations have the advantage of providing accurate properties of the isolated molecule, which can be compared with the experimental results.
Several molecules H3N⋯MX, where M = Cu or Ag and X = F, Cl or I, have been detected and characterised recently in the gas phase for the first time through their rotational spectra,17–19 although H3N⋯CuCl was identified in the solid state earlier.20 Each was established to be a symmetric-top molecule, with the N⋯MX nuclei lying on the top (C3) axis, in the order indicated. To date, analogues of H3N⋯MX having phosphine instead of ammonia as the Lewis base B have not been identified experimentally, to the best of our knowledge, but several have been the subject of density functional calculations.21,22 We report here the rotational spectrum of H3P⋯Ag–I and some of its properties derived therefrom.
There is some evidence that molecules B⋯MX (M = Cu, Ag, or Au; X = F, Cl, or I)1–19 have geometries that are isomorphic with those of their hydrogen-bonded (B⋯HX, X is a halogen atom)23 and halogen-bonded (B⋯XY, XY is a dihalogen molecule)24 counterparts, but are more strongly bound and exhibit a greater electric charge rearrangement within the diatomic subunit. Our interest here is to examine the geometry and binding strength of H3P⋯Ag–I and the electric charge redistribution within Ag–I that accompanies its formation. These properties will then be compared with those of the closely related molecule H3N⋯CuI,19 with those of their hydrogen-bonded analogues H3P⋯HI25 and H3N⋯HI26 and with those of their halogen-bonded relatives, H3P⋯ICl27 and H3N⋯ICl.28
2 Experimental and theoretical methods
2.1 Detection of the rotational spectrum
A chirped-pulse Fourier-transform microwave (CP-FTMW) spectrometer fitted with a laser ablation source was used to observe rotational spectra in the frequency range 6.5 to 18.5 GHz. Detailed descriptions of the spectrometer and laser ablation source are available elsewhere.29,30 A gas sample containing ∼4.0% PH3 and ∼1.5% CF3I in argon was prepared at a total pressure of 6 bar. The sample was pulsed over the surface of a silver rod that was ablated by a suitably timed Nd:YAG laser pulse (wavelength 532 nm, pulse duration 10 ns, pulse energy 20 mJ). Subsequently, the gas pulse expanded supersonically into the vacuum chamber of the spectrometer. The rod was translated and rotated regularly at small intervals to allow each laser pulse (repetition rate of ∼1.05 Hz) to impinge on a fresh metal surface and thereby ensure shot-to-shot reproducibility.The sequence employed to record broadband microwave spectra involves repetition of two steps. The first is polarization of the sample by a microwave chirp that sweeps from 6.5 to 18.5 GHz within 1 μs and the second is recording of the subsequent free induction decay of the molecular emission over a 20 μs time period. This sequence is repeated eight times during the expansion of each gas sample pulse into the spectrometer chamber. The free induction decay (FID) of the polarization is mixed down with the signal from a 19 GHz local oscillator and then digitized by means of a 25 Gs s−1 digital oscilloscope. Each transition is observed as a single peak with full-width at half-maximum (fwhm) ≅ 150 kHz after application of a Kaiser–Bessel digital filter.
2.2 Ab initio calculations
Structure optimizations and counter-poise corrected dissociation energies were calculated using the Turbomole package31 at the CCSD(T)(F12*) level of theory,32 a coupled-cluster method with single and double excitations, explicit correlation,33 and a perturbative treatment of triple excitations.34 Only valence electrons were included in the correlation treatment. A basis set combination consisting of aug-cc-pVDZ on H and P atoms and aug-cc-pVDZ-PP on Ag and I atoms was used and will be referred to by AVDZ. ECP-10-MDF35,36 and ECP-28-MDF37 were used on Ag and I, respectively, to account for scalar relativistic effects. For the density fitting approximation used to accelerate the CCSD(T)(F12*) calculation, the respective def2-QZVPP basis sets were employed for the MP238,39 and Fock40 terms. For the complementary auxiliary basis required for the F12 treatment,41 the aug-cc-pCVDZ MP2 density fitting basis sets were used.39 Quadratic force constants were also calculated at this level of theory. For comparison, the same force constants were calculated with the GAUSSIAN 09 package42 at the MP2 level of theory. A basis set combination consisting of aug-cc-pVTZ on the H and P atoms, and aug-cc-pVTZ-PP on the Ag and I atoms was used in this case.3 Results
3.1 Determination of spectroscopic constants
The observed spectrum of H3P⋯AgI showed evidence of the presence of the two isotopologues H3P⋯107AgI and H3P⋯109AgI, each exhibiting iodine nuclear quadrupole hyperfine structure, as may be seen from consideration of Fig. 1. An iterative least-squares fit of the observed hyperfine frequencies of each isotopologue was conducted using the program PGOPHER, written and maintained by Western.43 The Hamiltonian employed was of the form | (1) |
| Spectroscopic constant | H3P⋯107AgI | H3P⋯109AgI |
|---|---|---|
| a Numbers in parentheses are one standard deviation in units of the last significant digits. b Standard deviation of the fit. c Number of hyperfine frequencies included in the fit. | ||
| B 0/MHz | 626.01307(23) | 624.76423(17) |
| D J /kHz | 0.03182(89) | 0.03238(64) |
| D JK /kHz | 4.46(14) | 4.04(10) |
| χ aa (I)/MHz | −733.83(34) | −734.54(27) |
| σ RMS /kHz | 12.0 | 9.0 |
| N | 88 | 93 |
3.2 Molecular geometry
The facts that the ground-state rotational spectrum of the detected complex of phosphine and argentous iodide is of the symmetric-top type and that the Ag atom is close to the complex centre of mass (see later) mean that the arrangement of the atoms is either H3P⋯AgI or PH3⋯AgI. The second of these is unlikely because δ+Ag–Iδ− is dipolar in the indicated sense and it is expected that the positive end of the electric dipole would interact with the P non-bonding electron pair, which lies on the C3 axis of phosphine. This expectation is confirmed by ab initio calculations at the CCSD(T)(F12*)/AVDZ level of theory, which predict that the optimised geometry of PH3⋯AgI lies higher in energy by 116 kJ mol−1 than that of the H3P⋯AgI conformer. The higher energy conformer would not be populated at the low effective temperature (∼2 K) of the supersonic expansion. The observed conformer is therefore of the general form shown in Fig. 2.The rotational constants B0 = C0 for the two isotopologues H331P⋯107Ag127I and H331P⋯109Ag127I allow only a partial determination of the lengths of the H–P, P⋯Ag and Ag–I bonds and of the angle α = ∠HPAg (between the P–H bond and the C3 axis) necessary to define the r0 geometry. The quantities of most interest are r0(P⋯Ag) and r0(Ag–I). The ab initio calculations indicate that re(P–H) decreases by 0.0114 Å when phosphine enters the complex and the angle αe decreases by 3.94°. We shall assume that the r0 geometry of phosphine (r0(P–H) = 1.420003 Å and angle α0 = 122.86° obtained by fitting the accurately known44B0 and C0 using the STRFIT program of Kisiel45) changes in the same way as does the re geometry on formation of H3P⋯Ag–I. If so, r0(P–H) = 1.4086 Å and α0 = 118.92° are appropriate to PH3 in the complex. When these values were assumed in a fit of the ground-state principal moments of inertia of H331P⋯107Ag127I and H331P⋯109Ag127I, the values r0(P⋯Ag) = 2.3488 Å and r0(Ag–I) = 2.5483 Å resulted. No errors in these quantities are generated in the fit because two constants are fitted by two parameters. However, calculations reveal the following variations: ∂r(P⋯Ag)/∂r(P−H) = 0.065, ∂r(Ag−I)/∂r(P−H) = 0.005, ∂r(P⋯Ag)/∂α = 0.002 Å deg−1. and ∂r(Ag−I)/∂α = 0.0001 Å deg−1. Thus, the length r0(Ag–I) is very insensitive to changes to the geometry of PH3 that might occur when H3P⋯AgI is formed. These partial derivatives lead, when the reasonable errors of δr0 = 0.005 Å and δα0 = 1° are assumed, to r0(P⋯Ag) = 2.3488(20) Å and r0(Ag–I) = 2.5483(1) Å. The results from the CCSD(T)(F12*)/AVDZ optimisation of H3P⋯AgI are 2.3387 Å and 2.5537 Å, respectively.
The fact that spectroscopic constants have been determined for the isotopologues H3P⋯107AgI and H3P⋯109AgI allows the coordinate aAg to be obtained by the substitution method from the expression
| aAg2 = ΔI0b/μs, | (2) |
 where M is the mass of the parent and Δm is the mass change accompanying the isotopic substitution at Ag. The result is |aAg| = 0.9017(17) Å, where the error is estimated from δa = 0.0015/|a| as recommended by Costain.46,47 The corresponding values for this coordinate implied by the determined r0 geometry and the ab initio re geometry are 0.9017 Å and 0.9056 Å, respectively.
where M is the mass of the parent and Δm is the mass change accompanying the isotopic substitution at Ag. The result is |aAg| = 0.9017(17) Å, where the error is estimated from δa = 0.0015/|a| as recommended by Costain.46,47 The corresponding values for this coordinate implied by the determined r0 geometry and the ab initio re geometry are 0.9017 Å and 0.9056 Å, respectively.
3.3 Strength of the interaction of H3P and AgI
There are two common measures of the strength of the interaction of phosphine and silver iodide in H3P⋯AgI. Both are properties of the one-dimensional potential-energy function associated with variation of the distance r(P⋯Ag) when C3v symmetry is maintained but with structural relaxation at each point (referred to as the dissociation coordinate). The first is the intermolecular stretching quadratic force constant FP⋯Ag. The second is the energy, De, required to dissociate H3P⋯AgI to give PH3 and AgI at infinite separation, with reactants and products at their equilibrium geometries. The first can be obtained from the experimental centrifugal distortion constants DJ but the second is not available from the present experiments. Both are available from the ab initio calculations.For weakly bound complexes (such as most hydrogen-bonded complexes B⋯HX, where B is a simple Lewis base and X is a halogen atom) it is a good approximation to assume that B and HX are rigid and unchanged in geometry on complex formation. Then FB⋯H can be related to the equilibrium centrifugal distortion constant DeJ or ΔeJ (depending on molecular symmetry) of the complex and the various rotational constants of B, HX and B⋯HX, as demonstrated by Novick48 for the case where B is an atom and by Millen49 for a wider range of molecules B. For complexes B⋯MX, where M is a coinage metal atom, the intermolecular bond can be strong and the approximation that the force constant FB⋯M is much smaller than all other stretching force constants is no longer appropriate. To deal with such cases, we have recently described a two-force constant model which relates the quadratic force constants FM–X and FB⋯M (hereafter referred to as F11 and F22, respectively) to either DeJ or ΔeJ under the assumption that the contribution of the cross term F12 is negligible.50 The model applies to all complexes of a Lewis base B with any diatomic molecule (e.g. a hydrogen halide HX, a dihalogen XY, or a coinage metal halide MX) as long as the diatomic molecule lies along a Cn (n ≥ 2) symmetry axis of B in the equilibrium geometry. Note that B is assumed rigid, but can be changed in geometry when subsumed into the complex. During the vibrational motion no further change is assumed, however.
The two-force constant model for a symmetric-top molecule such as H3P⋯AgI leads (with numbering of the Ag and I atoms and internal coordinates r1 and r2 shown in Fig. 2) to the expression50
 | (3) |
 | ||
| Fig. 3 Values of the quadratic intermolecular stretching force constant F22 obtained by fitting the centrifugal distortion constants D0J of the isotopologues H3P⋯107AgI and H3P⋯109AgI using eqn (3) at fixed values of the AgI stretching force constant F11 in the range 130 to 220 N m−1. Eqn (3) is valid only if the off-diagonal force constant F12 is assumed to be zero. The CCSD(T)(F12*)/AVDZ-F12 value of F11, the experimental equilibrium value for the free AgI molecule and the F22 values they correspond to are indicated. | ||
It is also possible to calculate F11 and F22ab initio. At the CCSD(T)(F12*)/AVDZ level of theory the results are F11 = 151.1 N m−1 and F22 = 106.8 N m−1. When the D0J values are fitted by using eqn (3) with F11 fixed at 151.1 N m−1, the result is F22 = 110(5) N m−1, where the error is that implied by the error in the D0J values, and is the best present experimental estimate for this quantity. For free AgI at the same level of theory, F11 = 145.9 N m−1 is obtained, in excellent agreement with the experimental equilibrium value of 145.8 N m−1. Thus. F11 increases by 3.5% when AgI is incorporated into H3P⋯AgI. For comparison, the lower level of theory MP2/aug-cc-pVTZ-PP gives F11 = 168.8 N m−1 and F22 = 130.1 N m−1 when using the GAUSSIAN package.42 The result for free AgI at the same level is F11 = 160.1 N m−1, corresponding to 9.8% overestimation of the experimental equilibrium value. If F11 for H3P⋯AgI were also overestimated by a similar percentage, the corrected value would be F11 = 153 N m−1, which likewise represents a small increase relative to that of the free molecule.
It has been shown that in the limit of rigid, unchanged B and MX geometries, when F11 becomes infinite, eqn (3) reduces to the corresponding Millen expression49
 | (4) |
When B = H3P and MX = AgI, a fit of the centrifugal distortion constants D0J of H3P⋯107AgI and H3P 109AgI (using zero-point rotational constants given in Tables 1 and 2) leads to F22 = 31.3(5) N m−1, which is a very serious underestimate. The reason why becomes clear when the plot of F22 as a function of F11 is extended to cover a wider range of F11 values and unphysical solutions for which F22 is negative are included. The result is the rectangular hyperbola shown in Fig. 4. The horizontal asymptote (F11 = ∞) gives F22 = 31.26 N m−1 and corresponds to the solution when AgI is rigid and unperturbed when within H3P⋯AgI. The vertical asymptote (108.39 N m−1) corresponds to the lowest possible value of F11 consistent with the observed D0J. Clearly, any reasonable F11 must lead to a F22 value that is considerably greater than that given by eqn (4).
| Property | H3Pa | Property | 107AgIb | 109AgIb |
|---|---|---|---|---|
| a Ref. 44. b Ref. 55. c Calculated by fitting the zero-point rotational constants using the program STRFIT (ref. 45). d Calculated from the equilibrium vibrational wavenumber ωe given in ref. 51 by using the expression FAgI = 4π2ωe2c2μAgI, where μAgI = mAgmI/(mAg + mI). | ||||
| B 0/MHz | 133480.1165(17) | B 0/MHz | 1342.99237(7) | 1329.61831(7) |
| C 0/MHz | 117489.4357(77) | χ aa (I)/MHz | −1062.5299(15) | −1062.5230(14) |
| r 0(P−H)/Å | 1.42000c | r 0(Ag−I)/Å | 2.546627 | 2.546617 |
| ∠(HPH)/° | 93.345c | F AgI/(N m−1) | 145.78(3)d | 145.76(3)d |
 | ||
| Fig. 4 The rectangular hyperbola obtained by following the procedure described in the caption to Fig. 3, but with the range of assumed F11 values extended from −100 to +300 N m−1. The negative values of F22 and F11 are unphysical. The asymptote at F11 = 108.39 N m−1 represents the value of that force constant below which a negative, unphysical value of F22 is required to fit the centrifugal distortion constants D0J. The asymptote at F22 = 31.26 N m−1 is the value of this force constant in the limit F11 = ∞ N m−1, that is when the MX molecule is rigid. It can be shown50 that if both PH3 and AgI were rigid and unperturbed on formation of H3P⋯AgI eqn (3) leads to the Millen eqn (4), when equilibrium spectroscopic constants are used in the latter. | ||
The other measure of the strength of binding is the dissociation energy defined earlier; it takes the value De = 116 kJ mol−1 when calculated at the CCSD(T)(F12*)/AVDZ level of theory, after counterpoise correction.52 The value for AgI = Ag + I at the same level of theory is 230 kJ mol−1. It is therefore clear from the De value and the force constant F22 that the intermolecular bond in H3P⋯AgI is by no means weak. In fact by either measure, the P⋯Ag bond is about an order of magnitude stronger than most hydrogen or halogen bonds, but is only about a factor of two weaker than the Ag–I bond itself.
3.4 Electric charge redistribution on formation of H3P⋯AgI
The iodine nuclear quadrupole coupling constant χaa(I) = eqIaaQI carries information about the electric charge distribution at I through the electric field gradient qIaa along the a-axis direction at the iodine nucleus. According to the Townes–Dailey model53 for interpreting such coupling constants, the ionicity ic (or fractional ionic character) of the free AgI molecule is given by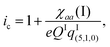 | (5) |
4 Conclusions
The new molecule H3P⋯Ag–I has been synthesized in the gas phase by a laser ablation method in which a pulse of gas mixture consisting of a few per cent each of PH3 and ICF3, with the remainder Ar, interacts with the plasma produced when silver is ablated by a Nd-YAG laser operating at 532 nm. The product was detected and characterised by means of its rotational spectrum, as observed with a chirped-pulse, Fourier-transform microwave spectrometer. The molecule is a symmetric top of C3v symmetry with the atoms P, Ag and I lying in that order on the symmetry axis a. Spectroscopic constants determined by fitting the observed transitions of the isotopologues H3P⋯107AgI and H3P⋯109AgI were interpreted to give the values r0(P⋯Ag) = 2.3488(20) Å and r0(Ag–I) = 2.5483(1) Å for the indicated bond lengths, after assuming changes to the r0 geometry of free PH3 when bound up in the complex were the same as the corresponding changes in the re geometry, as predicted ab initio at the CCSD(T)(F12*)/AVDZ level of theory. It is of interest to note that the value of r0(Ag–I) is increased by only 0.0017 Å relative to the free AgI value of 2.54663 Å (see Table 2).55 Interpretation of the centrifugal distortion constants D0J and the iodine nuclear quadrupole coupling constants led to a value F22 = 110 (5) N m−1 for the quadratic stretching force constant of the P⋯Ag bond and to a value δic = 0.14 for the increase in the Ag–I bond ionicity when H3P⋯AgI is formed. Although the ionicity of AgI increases significantly when subsumed into the complex, we note that the length of the bond and its force constant F11 are effectively unchanged.H3N⋯CuI, synthesized and characterised recently by a similar method,19 is isomorphic with H3P⋯AgI and has r0(N⋯Cu) = 1.9357(13) Å and r0(Cu–I) = 2.3553(5) Å, the latter representing an increase of only 0.0147 Å relative to the free Cu–I value of 2.34059 Å. The N⋯Cu interaction strength, as measured by F22 = 110(30) N m−1, is similar to that 110(5) N m−1 of P⋯Ag in H3P⋯AgI, but the ab initio value for the other measure of binding strength for H3N⋯CuI (De = 168 kJ mol−1) is significantly larger than that (116 kJ mol−1) of H3P⋯AgI. The increase, δic = 0.14, in the ionicity of the Cu–I bond when H3N⋯CuI is formed is identical to that observed for H3P⋯AgI. We conclude that H3P⋯AgI and H3N⋯CuI are very similar in their properties: both are strongly bound, both have similar changes in the ionicity of the M–I bond when the free MI molecule is subsumed into the complex, but the bond length r0(M–I) is effectively unchanged in both by this process.
Several complexes involving hydrogen bonds and halogen bonds to ammonia and phosphine have been described elsewhere, namely H3P⋯HI,25 H3N⋯HI,26 H3P⋯ICl27 and H3N⋯ICl.28 All have C3v symmetry, with all atoms but the three H atoms of PH3 or NH3 lying on the Ca3 axis and therefore all are isomorphic with H3P⋯AgI. The hydrogen-bonded analogues H3P⋯HI and H3N⋯HI have also been discussed in a detailed review,56 where it is concluded, based on several indirect observations, that there is little evidence of significant charge rearrangement or HI bond lengthening in these two complexes. Both are weakly bound, having quadratic force constants F22 = FP⋯H or FN⋯H of 3.4 N m−1 and 7.2 N m−1, respectively. These values are more than an order of magnitude smaller than those of H3P⋯AgI and H3N⋯CuI when FP⋯Ag or FN⋯Cu are calculated from the centrifugal distortion constant D0J by means of eqn (3), the more accurate method for strongly bound complexes. The related halogen-bonded H3P⋯ICl27 and H3N⋯ICl28 have F22 = FP⋯I = 20.8 N m−1 and F22 = FP⋯I 30.4 N m−1, respectively, when obtained by means of eqn (4). As indicated earlier, the larger is F22 relative to F11, the more serious will be its underestimation when eqn (4) is used. This underestimation is likely to be negligible for H3P⋯HI and H3N⋯HI, but it is possible that the values of F22 for H3P⋯ICl and H3N⋯ICl will both be somewhat larger (but only by a few %) than those reported previously. Clearly, the halogen-bonded complexes H3P⋯ICl and H3N⋯ICl are significantly more strongly bound than the hydrogen-bonded species H3P⋯HI and H3N⋯HI (when using the F22 criterion) but less so than H3P⋯AgI and H3N⋯CuI. According to a method of estimating electric charge redistribution from the changes in the I and Cl nuclear quadrupole coupling constants,27,28,57 there is a net movement of 0.15e (where e = electronic charge) from Cl to I in ICl when each of H3P⋯ICl and H3N⋯ICl is formed, thereby suggesting similar charge movement to that observed in each of H3P⋯AgI and H3N⋯CuI.
Acknowledgements
The authors thank the Engineering and Physical Sciences Research Council (UK) for a postgraduate studentship awarded to S. L. S. and project funding (EP/G026424/1). N. R. W. and D. P. T. thank the Royal Society for University Research Fellowships. A. C. L. is pleased to acknowledge the University of Bristol for the award of a Senior Research Fellowship.References
- S. G. Francis, S. L. Matthews, O. K. Poleshchuk, N. R. Walker and A. C. Legon, Angew. Chem., Int. Ed., 2006, 45, 6341–6343 CrossRef CAS PubMed.
- N. R. Walker and M. C. L. Gerry, Inorg. Chem., 2002, 41, 1236–1244 CrossRef CAS PubMed.
- N. R. Walker and M. C. L Gerry, Inorg. Chem., 2001, 40, 6158–6166 CrossRef CAS PubMed.
- S. G. Batten and A. C. Legon, Chem. Phys. Lett., 2006, 422, 192–197 CrossRef CAS.
- N. R. Walker, S. G. Francis, S. L. Matthews, J. J. Rowlands and A. C. Legon, Mol. Phys., 2006, 104, 3329–3337 CrossRef CAS.
- S. L. Stephens, W. Mizukami, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2012, 136, 064306 CrossRef PubMed.
- S. J. Harris, A. C. Legon, N. R. Walker and D. E. Wheatley, Angew. Chem., Int. Ed., 2010, 49, 181–183 CrossRef CAS PubMed.
- V. A. Mikhailov, F. J. Roberts, S. L. Stephens, S. J. Harris, D. P. Tew, J. N. Harvey, N. R. Walker and A. C. Legon, J. Chem. Phys., 2011, 134, 134305 CrossRef PubMed.
- N. R. Walker, D. P. Tew, S. J. Harris, D. E. Wheatley and A. C. Legon, J. Chem. Phys., 2011, 134, 014307 CrossRef PubMed.
- S. L. Stephens, D. P. Tew, N. R. Walker and A. C. Legon, J. Mol. Spectrosc., 2011, 267, 163–168 CrossRef CAS.
- S. L. Stephens, W. Mizukami, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2012, 137, 174302 CrossRef PubMed.
- S. L. Stephens, D. M. Bittner, V. A. Mikhailov, W. Mizukami, D. P. Tew, N. R. Walker and A. C. Legon, Inorg. Chem., 2014, 53, 10722–10730 CrossRef CAS PubMed.
- D. P. Zaleski, S. L. Stephens, D. P. Tew, D. M. Bittner, N. R. Walker and A. C. Legon, Phys. Chem. Chem. Phys., 2015, 17, 19230–19237 RSC.
- J. C. Mullaney, S. L. Stephens, D. P. Zaleski, M. P. Sprawling, D. P. Tew, N. R. Walker and A. C. Legon, J. Phys. Chem. A, 2015, 119, 9636–9643 CrossRef CAS PubMed.
- S. L. Stephens, D. P. Tew, V. A. Mikhailov, N. R. Walker and A. C. Legon, J. Chem. Phys., 2011, 135, 024315 CrossRef PubMed.
- D. P. Zaleski, J. C. Mullaney, D. M. Bittner, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2015, 143, 164314 CrossRef PubMed.
- V. A. Mikhailov, D. P. Tew, N. R. Walker and A. C. Legon, Chem. Phys. Lett., 2010, 499, 16–20 CrossRef CAS.
- D. M Bittner, D. P. Zaleski, S. L. Stephens, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2015, 142, 144302 CrossRef PubMed.
- D. M. Bittner, S. L. Stephens, D. P. Zaleski, D. P. Tew, N. R. Walker and A. C. Legon, Phys. Chem. Chem. Phys., 2016, 18, 13638–13645 RSC.
- G. Margraf, J. W. Bats, M. Bolte, H.-W. Lerner and M. Wagner, Chem. Commun., 2003, 956 RSC.
- M. A. Carvajal, J. J. Novoa and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1465–1477 CrossRef CAS PubMed.
- B. Assadollahzadeh and P. Schwerdtfeger, Chem. Phys. Lett., 2008, 462, 222–228 CrossRef CAS.
- A. C. Legon and D. J. Millen, Chem. Soc. Rev., 1987, 16, 467–498 RSC.
- A. C. Legon, Angew. Chem., Int. Ed. Engl., 1999, 38, 2686–2714 CrossRef PubMed.
- A. C. Legon and G. J. Luscombe, J. Chem. Soc., Faraday Trans., 1991, 87, 507–512 RSC.
- A. C. Legon and D. Stephenson, J. Chem. Soc., Faraday Trans., 1992, 88, 761–762 RSC.
- J. B. Davey, A. C. Legon and E. R. Waclawik, Phys. Chem. Chem. Phys., 2000, 2, 2265–2269 RSC.
- E. R. Waclawik and A. C. Legon, Phys. Chem. Chem. Phys., 1999, 1, 4695–4700 RSC.
- S. L. Stephens and N. R. Walker, J. Mol. Spectrosc., 2010, 263, 27–33 CrossRef CAS.
- D. P. Zaleski, S. L. Stephens and N. R. Walker, Phys. Chem. Chem. Phys., 2014, 16, 25221–25228 RSC.
- Turbomole V7.0 (a development of Universität Karlsruhe (TH) and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007. Available from http://www.turbomole.com, 2015).
- C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102 CrossRef PubMed.
- C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4–74 CrossRef PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. A. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- K. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296 Search PubMed.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- C. Hattig, Phys. Chem. Chem. Phys., 2005, 7, 59–66 RSC.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed.
- E. F. Valeev, Chem. Phys. Lett., 2004, 395, 190–195 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- PGOPHER, a program for simulating rotational structure, designed by C. M. Western, University of Bristol, version 6.0.202, 2010. Available at http://pgopher.chm.bris.ac.uk.
- A. V. Burenin, Mol. Phys., 1992, 75, 305–309 CrossRef CAS.
- Z. Kisiel, J. Mol. Spectrosc., 2003, 218, 58–67 CrossRef CAS.
- C. C. Costain, J. Chem. Phys., 1958, 29, 864 CrossRef CAS.
- C. C. Costain, Trans. Am. Crystallogr. Assoc., 1966, 2, 157–164 CAS.
- S. E. Novick, J. Mol. Spectrosc., 1977, 68, 77–80 CrossRef CAS.
- D. J. Millen, Can. J. Chem., 1985, 63, 1477–1479 CrossRef CAS.
- D. M. Bittner, N. R. Walker and A. C. Legon, J. Chem. Phys., 2016, 144, 074308 CrossRef PubMed.
- F. J. Lovas, E. Tiemann, J. S. Coursey, S. A. Kotochigova, J. Chang, K. Olsen and R. A. Dragoset, NIST Diatomic Spectral Database (created 12 September 2009; updated 12 December 2014), http://www.nist.gov/pml/data/msd-di/.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- C. H. Townes and B. P. Dailey, J. Chem. Phys., 1955, 23, 118 CrossRef.
- W. Gordy and R. L. Cook, in Microwave Molecular Spectra, ed. A. Weissberger, Techniques of Chemistry, Wiley, New York, 1984, ch. XIV, Table 14.5, p. 752 Search PubMed.
- S. G. Batten, A. G. Ward and A. C. Legon, J. Mol. Struct., 2006, 780–781, 300–305 CrossRef CAS.
- A. C. Legon, Chem. Soc. Rev., 1993, 22, 153–163 RSC.
- A. C. Legon, Chem. Phys. Lett., 1999, 314, 472–480 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: All underlying data are provided as electronic supplementary information accompanying this paper. See DOI: 10.1039/c6cp03512d |
| ‡ Present address: Chemistry Department, 360 Parker Building, University of Manitoba, Winnipeg, MB, R3T 2N2, Canada. |
| This journal is © the Owner Societies 2016 |


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 MHz) and 109AgI (∼13
420 MHz) and 109AgI (∼13