Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Peptides@mica: from affinity to adhesion mechanism†
A.
Gladytz
ab,
T.
John
 ab,
T.
Gladytz
b,
R.
Hassert
c,
M.
Pagel
c,
H. J.
Risselada
a,
S.
Naumov
a,
A. G.
Beck-Sickinger
c and
B.
Abel
*ab
ab,
T.
Gladytz
b,
R.
Hassert
c,
M.
Pagel
c,
H. J.
Risselada
a,
S.
Naumov
a,
A. G.
Beck-Sickinger
c and
B.
Abel
*ab
aLeibniz Institute of Surface Modification (IOM), Permoserstrasse 15, 04318 Leipzig, Germany. E-mail: bernd.abel@iom-leipzig.de
bWilhelm-Ostwald-Institute for Physical and Theoretical Chemistry, University of Leipzig, Linnéstrasse 3, 04103 Leipzig, Germany
cInstitute of Biochemistry, University of Leipzig, Brüderstrasse 34, 04103 Leipzig, Germany
First published on 22nd July 2016
Abstract
Investigating the adsorption of peptides on inorganic surfaces, on the molecular level, is fundamental for medicinal and analytical applications. Peptides can be potent as linkers between surfaces and living cells in biochips or in implantation medicine. Here, we studied the adsorption process of the positively charged pentapeptide RTHRK, a recently identified binding sequence for surface oxidized silicon, and novel analogues thereof to negatively charged mica surfaces. Homogeneous formation of monolayers in the nano- and low micromolar peptide concentration range was observed. We propose an alternative and efficient method to both quantify binding affinity and follow adhesion behavior. This method makes use of the thermodynamic relationship between surface coverage, measured by atomic force microscopy (AFM), and the concomitant free energy of adhesion. A knowledge-based fit to the autocorrelation of the AFM images was used to correct for a biased surface coverage introduced by the finite lateral resolution of the AFM. Binding affinities and mechanisms were further explored by large scale molecular dynamics (MD) simulations. The combination of well validated MD simulations with topological data from AFM revealed a better understanding of peptide adsorption processes on the atomistic scale. We demonstrate that binding affinity is strongly determined by a peptide's ability to form salt bridges and hydrogen bonds with the surface lattice. Consequently, differences in hydrogen bond formation lead to substantial differences in binding affinity despite conservation of the peptide's overall charge. Further, MD simulations give access to relative changes in binding energy of peptide variations in comparison to a lead compound.
Introduction
Rational modification of inorganic surfaces with peptides plays a major role for medical, pharmaceutical and technical applications. It is used for the development of biosensors1 or as linkers between inorganic implants and biological tissue to increase cell viability and hence biocompatibility.2–4 Protein coated mesoporous silicates were shown to promote bone regeneration.5–7 These applications benefit from the largely tunable biophysical properties of peptides which enable high affinity binding to the inorganic surface material.8–10Surface binding peptides are often discovered using combinatorial approaches like cell surface11,12 or phage display methods.13,14 Rational strategies however identify the binding motif of a native peptide via structure–activity relationship studies with overlapping peptide sequences and aim to amplify its affinity by multiplying the identified motif.15,16 Both the combinatorial and rational experimental approaches are time and material consuming and thus expensive. Furthermore, the discovery of high affinity binding peptides using these methods does not allow conclusions concerning their binding mechanism. Hence, an improvement of discrete properties of peptide coatings often remains an experimentally challenging task. The use of molecular docking or computer simulation experiments allows insights into the molecular processes during the adsorption and binding of peptides onto surfaces.17–26 The challenge here is that force fields for the description of inorganic surfaces are often either not available or not compatible with the force fields that describe peptides, ions and the solvent.
In this study, the adsorption mechanism of three different peptides to an aluminosilicate was investigated using a combined approach of atomic force microscopy (AFM) and atomistic molecular dynamics (MD) simulations. The wild type peptide RTHKR (see Fig. S2, ESI†) was discovered as the peptide binding sequence for silicon oxide by rational design3 from a weak binding precursor.27 It is a part of the ZnO binding peptide (VRTRDDARTHRK), which was isolated in 2000.28 RTHRK shows a high affinity to metals like zinc and silica, but also to silicates like mica. In addition to RTHRK, we investigated two alternative peptide sequences, which are like RTHRK overall three fold positively charged. In the first variation, RTHRR, the highly localized charge of the amino group in lysine is exchanged with a more diffuse charge distribution of the guanidinium cation (see Fig. S2, ESI†). The second analogue, Ac-RTHRK-NH(CH3), is capped and thus has uncharged termini while restoring the overall charge of the peptide (see Fig. S2, ESI†).
Adsorption–desorption affinities of the different peptide analogues were derived from the concentration dependent adsorption as measured by AFM. In silico free energy calculations using umbrella sampling were applied to validate the observed adsorption–desorption behavior in atomic detail. We propose a method to predict the affinity of any peptide or protein sequence to hydrated multicomponent mineral systems and their interfaces. Our computational approach facilitates the otherwise time consuming and expensive search for suitable new peptide sequences for the various applications shown above.
Experimental details
Peptide synthesis
Peptides were synthesized by automated solid phase peptide synthesis (Syro I peptide synthesizer, MultiSynTech) by standard Fmoc/tBu strategy. RTHRK and RTHRR were synthesized on Wang resin (15 μmol, loading 0.6 mmol g−1). The peptide Ac-RTHRK-NH(CH3) was synthesized on ({3-[(methyl-Fmoc-amino)-methyl]-indol-1-yl}-acetyl AM resin ((15 μmol, loading 0.7 mmol g−1)). A more detailed procedure is given elsewhere.29 Shortly, reactive side chains were protected with Pbf (Arg), Boc (Lys), tBu (Thr), and Trt (His). After elongation, RTHRK-NH(CH3) was N-terminally acetylated with 15 eq. acetic acid and 10 eq. N,N-diisopropylethylamine (DIPEA). Final cleavage of the peptides was performed with trifluoroacetic acid (TFA)/thioanisole/thiocresol (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 v/v) for 3 h shaking at room temperature. The peptides were precipitated and washed with ice-cold diethyl ether. Purification of the peptides was carried out by preparative reversed phase-high performance liquid chromatography (RP-HPLC) on a Phenomenex Jupiter Proteo column (90 Å/4 μm, 22 mm × 250 mm)) using linear gradients of Eluent B in Eluent A (A: 0.1% TFA in H2O, B: 0.08% TFA in acetonitrile (ACN)). Isolated peptides were analytically identified by matrix-assisted laser ionization time of flight mass spectrometry (MALDI-ToF-MS) (Bruker Daltonics) and electrospray ionization (ESI)-ion trap MS (Bruker Daltonics). Observed m/z values were in agreement with calculated molecular weights. Purity and elution properties were checked by analytical RP-HPLC with gradients of Eluent A and B. Final peptide products were obtained with a purity of ≥95% (Table 1).
0.5 v/v) for 3 h shaking at room temperature. The peptides were precipitated and washed with ice-cold diethyl ether. Purification of the peptides was carried out by preparative reversed phase-high performance liquid chromatography (RP-HPLC) on a Phenomenex Jupiter Proteo column (90 Å/4 μm, 22 mm × 250 mm)) using linear gradients of Eluent B in Eluent A (A: 0.1% TFA in H2O, B: 0.08% TFA in acetonitrile (ACN)). Isolated peptides were analytically identified by matrix-assisted laser ionization time of flight mass spectrometry (MALDI-ToF-MS) (Bruker Daltonics) and electrospray ionization (ESI)-ion trap MS (Bruker Daltonics). Observed m/z values were in agreement with calculated molecular weights. Purity and elution properties were checked by analytical RP-HPLC with gradients of Eluent A and B. Final peptide products were obtained with a purity of ≥95% (Table 1).
| Sequence | M [g mol−1] | m/z [M + H]+ | Elution [% ACN] | Purity [%] |
|---|---|---|---|---|
| Peptide sequences are shown by one letter code according to IUPAC. The identity of the peptides was analyzed by MALDI-ToF mass spectrometry and aESI-ion trap mass spectrometry. The m/z ratio of the measured positive ions ([M + H]+) was in agreement with calculated molecular masses. The peptide purity and elution properties (hydrophilicity) were evaluated by two different RP-HPLC systems using different columns and gradients; Gradients of eluent B in eluent A on a bPhenomenex Jupiter Proteo (90 Å, 5 μm), cPhenomenex Jupiter Proteo (300 Å, 4 μm) and VariTide (200 Å, 6 μm), (not shown). Ac (acetylated), –NH(CH3) (N-methylated amide at the C-terminus). | ||||
| RTHRK | 696.4 | 697.4a | 7b | >95 |
| RTHRR | 724.4 | 725.5 | 14b | >95 |
| Ac-RTHRK-NH(CH3) | 751.4 | 752.4 | 14c | >95 |
Sample preparation
The mica substrates (grade V1, Ted Pella, USA) were cut into pieces of about 1 cm × 0.5 cm and cleaved into thin slices with clean, flat surfaces on both sides. The peptides were diluted in TBS buffer (20 mM Tris-HCl, 150 mM NaCl, pH 7.6) to prepare several sample concentrations. The mica substrates were added to the peptide solutions in small tubes and equilibrated at room temperature for two hours. After incubation, the mica substrates were removed from the peptide solution, washed and finally rinsed with ultrapure water. The substrates were gently dried under a nitrogen stream and attached to a microscopic slide for further investigation. All samples were stored in a desiccator under reduced pressure.AFM measurements
Atomic force microscopy (AFM) measurements were performed on the JPK NanoWizard II AFM system with an Olympus IX71 inverted microscope on an isolation platform. Rectangular silicon cantilevers with aluminum coating and pyramidal tips were used in intermittent contact mode (APPNANO ACTA probes, Applied NanoStructures, USA). Its nominal spring constant is 37 Nm and the nominal frequency 300 kHz. Each substrate was analyzed at least two positions with overview scans (10 × 10 μm2) and several detail scans (1 × 1 μm2) within these areas. Ambiguous samples were repeated more often to obtain reliable information about surface coverage and size and shape of peptide clusters. The samples were scanned with a resolution of 512 × 512 data points.AFM data analysis and processing
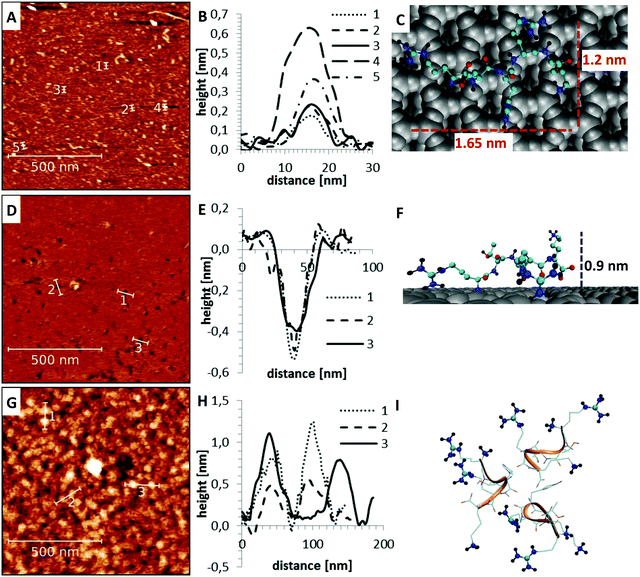
AFM raw data were processed by an automated line-by-line leveling using a polynomial background as implemented in Gwyddion 2.40.30 Characteristic cluster shapes and sizes were extracted by analyzing the line profiles of the images.The degree of peptide coverage of the surfaces was evaluated as a function of peptide concentration. It was necessary to identify a criterion to reliably and quantitatively differentiate between a peptide covered surface and an uncovered surface that was only incubated in pure buffer solution. The number and approximate size of the grains was analyzed using the watershed algorithm as implemented in Gwyddion (see Fig. 2B).30,31 The method delivers the number of grains, their average size and the overall coverage of the surface. The results obtained for surfaces with very low degree of coverage and for fully covered surfaces were in line with the expected behavior. In the intermediate range, the obtained concentration dependence was not satisfactory (see Fig. 1B). The reason is that these samples exhibit many small and closely neighbored peptide clusters which cannot be correctly resolved with the AFM tip (which is large compared to the aggregates and the distance between them). This led to an overestimation of the peptide coverage in the intermediate range (see Fig. 1A).
In order to overcome this problem, the average size of the detected grains was corrected by evaluating the influence of the tip shape. To this end, we first determined the 2D spatial autocorrelation function of each image and obtained the three dimensional line profile of the average grain (Autocor(Δr)) (see Fig. 2C and D). Here, it is important to notice, that the autocorrelation is not time dependent. Instead, the autocorrelation is defined as the sum over all products between an image and its copy translated by the vector Δr in x and y direction. For a mathematical description see eqn (S1) (ESI†). This shape is determined by: (a) the true size of the underlying objects which we aim for, (b) the autocorrelation function of the AFM-tip (especially important for objects which are small compared to the tip size), (c) the autocorrelation of the noise and (d) a constant offset. Accordingly, in order to determine the average grain size, the individual contribution of every parameter was determined by fitting their linear combination to the autocorrelation profile (see eqn (1)).
| Autocor(Δr) = a·Autocorobjects(Δr) + b·Autocortip(Δr) + c·Autocornoise(Δr) + d | (1) |
 | (2) |
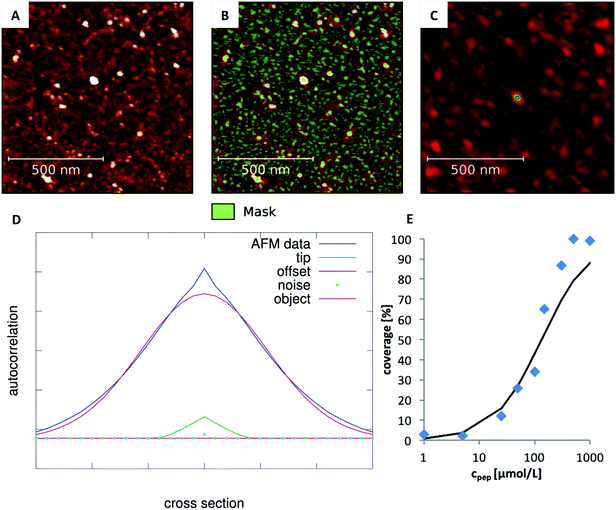 | ||
| Fig. 2 Analysis of the degree of coverage. (A) Recorded AFM image with intermediate degree of coverage (Ac-RTHRK-NH(CH3), 100 μmol L−1). (B) Grains marked by watershed method. The number of grains is correct. However, their average size is overestimated due to the large tip size. (C) Autocorrelation of the image shown in A. The colored spot in the center represents the average grain size of the image (including the lateral broadening). (D) Fit of eqn (1) to the cross section of the autocorrelation function. The FWHM of the deconvoluted contribution of the underlying object (purple Gaussian function) is the diameter of the average grain object. If this is multiplied by the number of grains obtained from the watershed analysis (B), the truly covered area of image A is obtained. Analysis of all images at different concentrations then leads to the adsorption isotherm (E). | ||
After all these contributions were fitted to the autocorrelation function, the only contribution left is the autocorrelation of the underlying peptide aggregates. It can be fitted as a convolution of the autocorrelations of the tip shape and a Gaussian function (for a mathematical definition see S2, ESI†). The full width at half maximum (FWHM) of this Gaussian function then gives the average diameter of the objects (see eqn (3) and (4)).
| Autocorobjects(Δr) = (Autocortip × AutocorGauss)(Δr) | (3) |
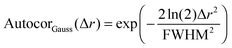 | (4) |
Molecular dynamics (MD) simulations
The simulation setup consists of a 6.2236 × 7.1586 × 11.0000 nm3 cubic box which is periodically multiplied in three dimensions (periodic boundary conditions). The mica layer is six Si/Al layers (labeled ‘A-layer’ in Fig. 3) thick and continuous in the x and y dimension. Varying numbers of overall three fold positively charged peptides (RTHRK, RTHRR or Ac-RTHRK-NH(CH3)) were added at random positions and conformations to the simulation box before the system was solvated with explicit spc water.33 Finally, 0.15 mol L−1 NaCl was included in order to simulate physiological conditions. The system was neutralized by adding additional chloride ions. All MD simulations were run at 300 K (v-rescale coupling34) with the Gromacs 4.5.7 package.35 Electrostatic interactions were calculated using the Particle Mesh Ewald method (PME),36,37 with a 1.2 Å grid and a fourth order spline interpolation. The Lennard-Jones cutoff radius was set to 14 Å. All hydrogen bonds were constraint using the LINCS algorithm.38 Peptides, water and ions were described with the Gromos 45a3 force field parameters.39 The parameters for the mica surface are based on the CLAYFF force field developed by Cygan et al.40 Cygan et al. describe the van-der-Waals interaction EvdW between two atoms i and j which are separated by the distance rij with a Lennard-Jones-potential using the parameters D0 [kcal mol−1] and R0 [Å] according to eqn (5). Gromacs requires the Lennard-Jones-parameters C6 [(kJ nm6) mol−1] and C12 [(kJ nm12) mol−1] according to eqn (6). Therefore, we recalculated the parameters using eqn (7a) and (7b).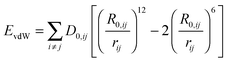 | (5) |
 | (6) |
| C12 = D0R120 | (7a) |
| C6 = 2D0R60 | (7b) |
| Non-bonded parameters | |||||
|---|---|---|---|---|---|
| Atomtype | MW [g mol−1] | Charge [e] | C 6 [(kJ nm6) mol−1] | C 12 [(kJ nm12) mol−1] | Atomtype description, see also Fig. 3 |
| ka | 39.0983 | 1.000 | 2.2985464 × 10−3 | 3.1568567 × 10−6 | K+ |
| si | 28.0855 | 2.100 | 3.9927417 × 10−8 | 5.1755314 × 10−11 | Si |
| alt | 26.9815 | 1.575 | 3.9927417 × 10−8 | 5.1755314 × 10−11 | Al in tetrahedral hole |
| alo | 26.9815 | 1.575 | 1.5402261 × 10−7 | 1.0659356 × 10−9 | Al in octahedral hole |
| oss | 15.9994 | −1.050 | 2.6173456 × 10−3 | 2.6341290 × 10−6 | O on surface |
| oap | 15.9994 | −1.169 | 2.6173456 × 10−3 | 2.6341290 × 10−6 | O apical |
| ohy | 15.9994 | −0.950 | 2.6173456 × 10−3 | 2.6341290 × 10−6 | O hydroxyl |
| hhy | 1.0079 | 0.425 | 0.0000000 × 10 | 0.0000000 × 10 | H hydroxyl |
| Bonded parameters | ||
|---|---|---|
| Atomtype | Ideal bond length [nm] | Force constant [kJ (mol nm2)−1] |
| ohy–hhy | 0.1 | 2.32 × 106 |
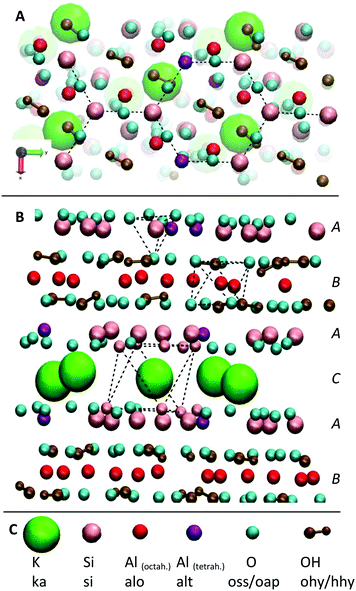
The structure of the mica surface is based on the crystal structure of muscovite mica at 25 °C.41 Muscovite mica K[Si3Al1O8][Al2O2(OH)2] is a monoclinic alumosilicate which belongs to the group of phyllosilicates. Its most important characteristic is an almost perfect basal cleavage which is facilitated by the sheet like arrangement of the Si and Al atoms. Fig. 3 illustrates the structure of muscovite mica and its nomenclature for the MD simulation. A-type layers consist of Si/Al hexagons which are surrounded by corner connected oxygen tetrahedrons. The Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al-ratio in this layer is 3
Al-ratio in this layer is 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Below this is a layer of Al atoms which is octahedrally surrounded by oxygen atoms. After another tetrahedrally surrounded Si/Al layer, a layer of K+ ions follows. The basal cleavage of the surface is facilitated through this plane and leaves two almost perfectly plane Si/Al layers, which are used as clean and fresh substrates for AFM experiments.
1. Below this is a layer of Al atoms which is octahedrally surrounded by oxygen atoms. After another tetrahedrally surrounded Si/Al layer, a layer of K+ ions follows. The basal cleavage of the surface is facilitated through this plane and leaves two almost perfectly plane Si/Al layers, which are used as clean and fresh substrates for AFM experiments.
Despite its complexity, we decided to use the described full atomistic model for the mica surface in order to be able to correctly simulate the hydrogen bond network between the surface and the adsorbing peptides. Simplified models for the mica structure, like a monolayer of SiO2,42,43 are suitable to reproduce the negative surface charge but prevent the analysis of adsorption patterns on the atomic scale (e.g. the hydrogen bond network), which is needed to elucidate affinity differences between adsorbents with identical net charges. Furthermore, pure SiO2 surfaces create a significant electrostatic potential, which is insufficiently shielded.43 In real muscovite mica structures, K+ cations shield the negative surface charge of the oxygen anions very efficiently (see Fig. 3 and Fig. S1, ESI†). Together with additional shielding by dissolved ions and polarization of water molecules, this leads to complete vanishing of the potential within 1.15 nm from the surface (see Fig. S1, ESI†).
The described setup was used to conduct two different types of simulations. First, increasing numbers (1, 5, 10, 15, 20, 25 and 30) of the peptide monomers (for all three peptide sequences) were added to the solution and simulated without constraints for 100 ns each. After 60 ns, a snapshot was taken to add further peptides for the next simulation run. All simulations were run for at least three repetitions to check the reproducibility of the observations. We investigated the concentration dependent adsorption mechanism and identified the main binding motifs and their driving forces.
Second, the desorption free energy was determined using the umbrella sampling algorithm and the results were compared to the adsorption free energy which was determined experimentally. To start the umbrella sampling, the adsorbed final structures of the 100 ns simulation with one peptide monomer in the solvated box were used (see above). After another equilibration of 50 ns on the surface, the peptide was desorbed by pulling it with a constant velocity from the surface in a non-equilibrium simulation run (k = 600 kJ (mol nm2)−1; v = 0.0003 nm ps−1). The force that is needed for this process is larger than it would be in case of an equilibrium process, as stabilizing (solvent) relaxation processes cannot be completed during the fast process. In order to overcome this error, a series of structures from the non-equilibrium simulations was extracted and run with constrained center of mass positions to calculate the potential of mean force from the overlapping umbrella sampling windows.44,45 The force constant of the position restraints for each simulation run was adapted in a way that the average center of mass position did not shift more than 0.15 nm from its input position to ensure a sufficient sampling of the complete desorption process.
For visualization of trajectories and calculation of (bond) distances and angles, the program visual molecular dynamics (VMD) 1.9.1 was used.46 Other properties like temperature, electrostatic potential, electric field, Coulomb and Lennard-Jones interaction or density were evaluated using the tools implemented in Gromacs.
Density functional theory (DFT) calculations
To support and validate the results of the molecular dynamics simulations, density functional theory (DFT) calculations of the adsorbing functional groups of the peptides on a cutout of the mica surface were performed. Namely, we optimized the adsorption geometry of (i) a methylammonium cation (mimicking K and the N-terminus of RTHRK and RTHRR), (ii) a methylguanidinium cation (mimicking R of RTHRK, RTHRR and Ac-RTHRK-NH(CH3)) and (iii) a neutral acetyl methylamine molecule (mimicking the capped N-terminus of Ac-RTHRK-NH(CH3)) (see Fig. S2, ESI†). The mica surface was cutout in a way that one Si/Al hexagon of the a–b-plane (see Fig. S3A (ESI†) and Fig. 3A) was surrounded as realistically as possible. To this aim, we modelled additionally six adjacent Si/Al hexagons in the a–b-plane and one full repetition of the A–B–A–C layer motif in the c-direction (see Fig. S3B (ESI†) and Fig. 3B). In the B-layer (see Fig. 3B), the three fold positively charged Al anions are octahedrally surrounded by oxygen anions, which donate each −0.5e to the central cation. To avoid unbalanced charges at the border of the limited model, we ensured that each Al cation is surrounded by three negative charges donated by oxygen anions. To saturate left over negative charges of oxygen anions at the borders of the model, adjacent positively charged heavy atoms (Si and Al) were replaced by hydrogen atoms.DFT calculations were carried out on the simplified model structures at the PBE0-D3/LAV2P* level of theory as implemented in Jaguar 9.2 program (Jaguar, version 9.2, Schrodinger, Inc., New York, NY, 2016).47 The PBE0-D3 density functional48–50 includes physically and chemically important London dispersion interactions.51 The LAV2P* basis set uses the standard 6-31G(d) basis set for light elements and the LAV pseudopotential52 for heavier elements, such as Al in this case.
Results and discussions
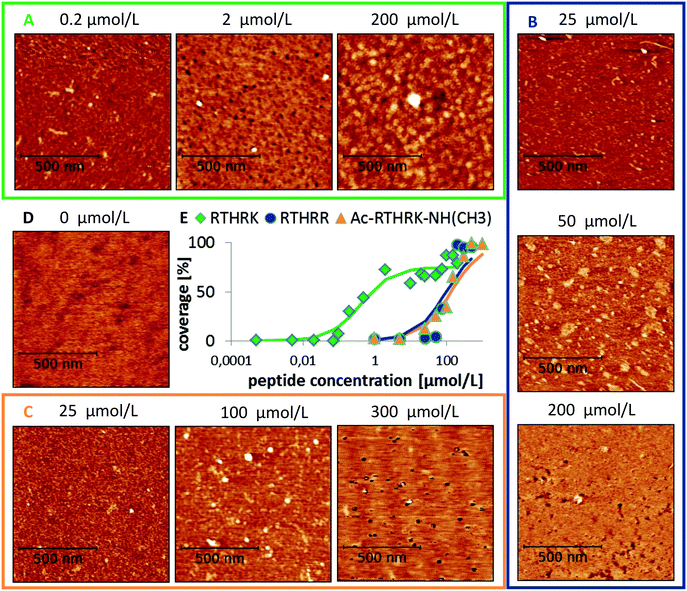
The high charge density of the investigated pentapeptides leads to strong interactions with charged (or polar) surfaces like mica. The surface of muscovite mica is covered with K+ ions, which are partially dissolved upon contact with aqueous solutions, leaving a negatively charged [Si3Al1O8]− surface. The high affinity of the peptide RTHRK to the mica surface led to a full coverage of the surface in the nanomolar concentration range. The same affinity was reached towards a naturally oxidized silicon surface if the peptide sequence is replicated four times ([RTHRK]4).3 Hassert and coworkers showed that modification of the peptide termini with a bioactive integrin binding ligand does not reduce the affinity towards the inorganic surface, but enhances cell spreading and viability of osteoblasts on an oxidized silicon surface.3The affinity to mica surfaces does not only depend on the overall charge of the system. Equally important are the delocalization of the charge distribution within the peptide molecule and the number of available binding sites. To investigate the binding affinity, the degree of surface coverage was measured for mica samples incubated at different peptide concentrations. The EC50 values, the concentration at which half of the surface is covered with peptide, was determined for the three different peptide sequences (see Fig. 4). The original sequence RTHRK has an EC50 value of 0.41 μmol L−1. Delocalization of the charge distribution, namely the exchange of Lys with Arg (RTHRR), led to an increase of the EC50 value to 98 μmol L−1. Capping of the charged termini (Ac-RTHRK-N(CH3)) displayed a similar effect and led to an EC50 value of 133 μmol L−1.
Hasssert et al. additionally measured the binding affinity of the same peptide sequence N-terminally capped with two aminohexanoic acid (Ahx) spacers and biotin (Biotin-(Ahx)2-RTHRK) to an oxidized silicon surface and determined the EC50 value to be 11 μmol L−1.3 In agreement to our observation, this value is significantly higher than the value for the uncapped RTHRK (EC50 = 0.41 μmol L−1). It is however lower than the value for Ac-RTHRK-N(CH3). This might be due to additional polar interactions of the biotin group with the oxidized silicon surface. Hassert et al. determined their values by using both concentration dependent atomic force microscopy and fluorescence microscopy of a dye labelled version of the peptide and obtained very similar results.3 This shows that concentration dependent atomic force microscopy is comparable to well-established fluorescence techniques,53 yielding the additional advantage that topographic information of the surface coverage can be obtained.
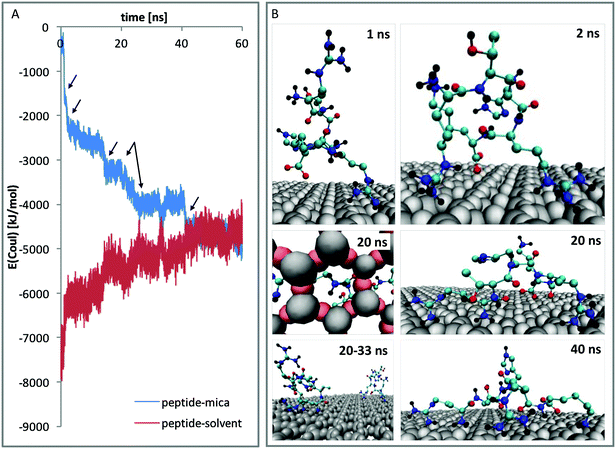
In order to understand these results from a molecular point of view, atomistic molecular dynamics (MD) simulations were performed. An unrestrained simulation of 60 ns revealed a rapid peptide adsorption which was driven by Coulomb interactions between the negatively charged mica surface and the positively charged peptides. Each single contact between a binding site and the mica surface is reflected by a clear change within the Coulomb potential (see Fig. 5A). When the peptides were not sterically hindered by other peptides, they flatly adsorbed on the surface with all positively charged residues and the N-terminus directly bound to the surface. The interaction between the large guanidinium group of the arginine residues and the surface is relatively weak. The peptides could thus diffuse along the surface as long as no other groups are adsorbed. In contrast, the amino groups of lysine and the positively charged N-terminus bound very strongly to the surface. This interaction anchors the molecule and thus completely prevents diffusion along the surface. The strong binding is caused by close Coulomb interactions and the formation of three hydrogen bonds between the amino groups and the hexagonally arranged oxygen atoms of the mica surface (compare Fig. 5B – 20 ns, left).
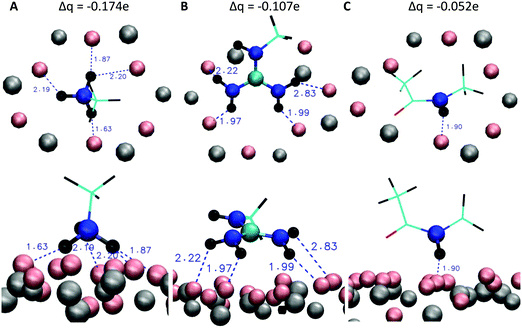
To further investigate the differences of the binding motifs, additional DFT calculations of the binding of functional groups on a cutout section of the mica surface were performed. More specifically, we modelled the adsorption geometry of (i) a methylammonium cation (mimicking K and the N-terminus of RTHRK and RTHRR), (ii) a methylguanidinium cation (mimicking R of RTHRK, RTHRR and Ac-RTHRK-NH(CH3)) and (iii) a neutral acetyl methylamine molecule (mimicking the capped N-terminus of Ac-RTHRK-NH(CH3)). Fig. 6 shows the optimized structures. It is clearly visible that the ammonium group of methylammonium binds with the highest affinity forming four well-localized hydrogen bonds to the adjacent oxygen octahedron (1.63 Å; 1.87 Å; 2.19 Å; 2.20 Å). The calculated partial Mulliken charge of the adsorbed ammonium group is +0.826 (instead of +1 in free solution). Hence, the surface oxygen anions donate −0.174e to the ammonium group. The methylguanidinium cation has a larger distance to the surface (1.97 Å; 1.99 Å; 2.22 Å) and accepts a negative partial charge of only −0.107e from the oxygen anions. Finally, the acetyl methylamine molecule, which is neutral and mimics the capped N-terminus, forms one comparatively weak hydrogen bond of 1.90 Å (receiving −0.052e) and has therefore the lowest adsorption affinity. The observed DFT-optimized geometries and adsorption affinities of the simplified model structures thus confirm and extend the results obtained in the molecular dynamics simulations.
Apart from the differences in surface affinity, the adsorption behavior was similar for all three peptides. Initially, at low peptide concentrations, very small peptide clusters with diameters of roughly 10–20 nm and a height of 0.3–0.8 nm were formed (see Fig. 7A and B). Considering that the tip itself has a diameter of around 10 nm, the true diameter of the peptide aggregates is in the order of 1–4 nm.54 Adsorbed peptide monomers have dimensions of approximately 1.3–1.7 nm along the direction of the backbone, 1.0–1.4 nm between the outer ends of opposing side chains and a height perpendicular to the surface of 0.6–1 nm in the computational model (see Fig. 7C). Accordingly, these observed clusters must correspond to monomers and small oligomers. The number of clusters and their size grew with increasing peptide concentrations. This suggests that monomers assemble to form larger oligomeric clusters. A further increase of the concentration led to a nearly complete coverage of the mica surface with peptide. The peptide layer is extremely homogeneous and flat, except for small defect sites where no peptides were adsorbed. These defects are characterized by 0.2–0.5 nm deep holes in the AFM images (see Fig. 7D and E). Their regular size and pattern suggest that all adsorbed peptides are bound with the same binding sites and in very similar geometries. This is only possible if all adhered peptides are in contact with the surface. This implies that a monolayer was formed which is further supported by the dimensions of the holes (see Fig. 7E and F). Molecular dynamics (MD) simulations validated these assumptions. At low peptide concentrations, oligomers were not formed in solution. Interactions between non-adsorbed peptides and adsorbed peptides remained possible. These interactions were, however, relatively weak and reversible. The dominating peptide–surface interactions typically led to a dissociation of the peptide oligomers at low concentrations. This behavior changed when the monolayer was complete and the concentration was further increased. At very high peptide concentrations, oligomer formation in solution became more likely. The hydrophobic effect led to an assembly of the hydrophobic parts of the peptides in the inner part of the oligomers, while the charged groups were exposed to the solvent. These oligomers can readily adsorb to the surface and form clusters (compare Fig. 7I). This mechanism explains the cluster formation observed in the AFM experiments at higher concentrations (compare Fig. 7G and H).
Next, it was checked if the simulations can reproduce the observed differences in the affinity to mica surfaces of the three peptides. To this aim, the desorption free energy of all three variants was determined using the umbrella sampling technique (see Fig. 8).
The desorption free energy, which is defined as the difference between the equilibrium value in the desorbed state and the potential minimum in the adsorbed state (see Fig. 8D), indeed correlates to the observed adsorption behavior. The original sequence RTHRK shows the highest affinity in the adsorption isotherm measurements and has the largest desorption free energy (ΔRG ≈ 100 kJ mol−1). An exchange of lysine with arginine (RTHRR) led to a decrease of the desorption free energy of around 20 kJ mol−1. On the same order of magnitude, although slightly smaller, is the desorption free energy of the end group capped analogue Ac-RTHRK-NH(CH3).
To directly compare desorption free energies ΔRG of the experiments and the simulations, the equilibrium constants K of the adsorption–desorption reactions were calculated. To fit the experimental data, the classical Langmuir model as given in eqn (9) was applied. The inherent approximations of this simple model (homogeneous and uniform surface; negligible interactions between immobilized, adsorbed peptides; monolayer coverage only) are well fulfilled for the investigated concentration range. The equilibrium constant K is presented as dimensionless quantity in eqn (8).
ΔRG = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K | (8) |
A fit of the data (surface coverage θ depending on the peptide concentration in solution cPep) to the Langmuir model delivers the equilibrium constant with the unit [L mol−1].
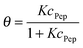 | (9) |
| Pep(aq) + *(ads) ⇄ Pep(ads) + *(aq) | (R1) |
The equilibrium constant K and the coverage degree θads for reaction (R1) are defined in eqn (10) and (11).
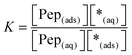 | (10) |
 | (11) |
 | (12) |
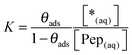 | (13) |
Considering the enormous access of free peptide solution compared to the small number of binding sites on the limited mica surface, it is reasonable to approximate [Pep(aq)] with the input concentration of the peptides: [Pep(aq)] ≈ [Pep]. It can be assumed that *(aq) is equal to the space filled with water in the sample V(*(aq)) ≈ V(H2O). Finally, considering the similar densities of peptide and water the ratio [Pep]/[H2O] can be approximated by the mass fraction wPep. Accordingly, eqn (13) can be simplified as given in eqn (14).
 | (14) |
 | (15) |
ΔRG = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wPep1/2 wPep1/2 | (16) |
| ΔRGads (MD) [kJ mol−1] | ΔRGads (exp.) [kJ mol−1] | |
|---|---|---|
| RTHRK | −103 ± 21 | −37 ± 2 |
| RTHRR | −84 ± 25 | −24 ± 2 |
| Ac-RTHRK-NH(CH3) | −78 ± 20 | −23 ± 3 |
Summary and conclusion
In this work, we investigated the adsorption behavior of the pentapeptide RTHRK and two analogues of it on a mica surface using a combined approach of atomic force microscopy (AFM) and atomistic molecular dynamics (MD) simulations. We experimentally quantified the binding free energy by evaluating the concentration dependent coverage of the surfaces. To correct for a bias introduced by the limited AFM lateral resolution, a novel knowledge-based autocorrelation function was used. In combination with the atomistic simulations, this approach allowed us to quantify the binding affinity and describe the binding mechanism in detail over a large range of peptide concentrations and coverage. All three peptide variations formed homogeneous monolayers. In addition, we identified the main driving force and correctly predicted the differences in the adsorption behavior of the three peptide sequences. Although the adsorption process is driven by Coulomb interactions and the net charge of all investigated peptides is equal, the differences in hydrogen bond formation led to significant differences in the binding affinity.The presented approach is a valuable tool which enables the identification and design of novel silicate binding peptides. Computer simulations will save time and cost and allow a systematic investigation of peptide groups. The simulations also facilitate a more detailed understanding of the interaction motifs of already known high-affinity peptides and their optimization.
Acknowledgements
The authors thank the Deutsche Forschungsgemeinschaft for financial support through the SFB/TRR 102 (B1) and the SFB/TRR 67 (A4). The support of the graduate school BuildMoNa is kindly acknowledged.References
- A. Matsumoto and Y. Miyahara, Nanoscale, 2013, 5(22), 10702 RSC.
- R. Hassert and A. G. Beck-Sickinger, Eur. J. Pharm. Biopharm., 2013, 85(1), 69 CrossRef CAS PubMed.
- R. Hassert, M. Pagel, Z. Ming, T. Häupl, B. Abel, K. Braun, M. Wiessler and A. G. Beck-Sickinger, Bioconjugate Chem., 2012, 23(10), 2129 CrossRef CAS PubMed.
- M. Pagel, R. Hassert, T. John, K. Braun, M. Wießler, B. Abel and A. G. Beck-Sickinger, Angew. Chem., Int. Ed., 2016, 55(15), 4826 CrossRef CAS PubMed.
- D. Lozano, M. Manzano, J. C. Doadrio, A. J. Salinas, M. Vallet-Regí, E. Gómez-Barrena and P. Esbrit, Acta Biomater., 2010, 6(3), 797 CrossRef CAS PubMed.
- M. Manzano and M. Vallet-Regí, J. Mater. Chem., 2010, 20(27), 5593 RSC.
- C. G. Trejo, D. Lozano, M. Manzano, J. C. Doadrio, A. J. Salinas, S. Dapía, E. Gómez-Barrena, M. Vallet-Regí, N. García-Honduvilla, J. Buján and P. Esbrit, Biomaterials, 2010, 31(33), 8564 CrossRef CAS PubMed.
- C. Tamerler and M. Sarikaya, 2nd TMS Symposium on biological materials science, 2007, 3(3), 289.
- C. Vreuls, G. Zocchi, A. Genin, C. Archambeau, J. Martial and C. de van Weerdt, J. Inorg. Biochem., 2010, 104(10), 1013 CrossRef CAS PubMed.
- A. Sengupta, C. K. Thai, M. S. R. Sastry, J. F. Matthaei, D. T. Schwartz, E. J. Davis and F. Baneyx, Langmuir, 2008, 24(5), 2000 CrossRef CAS PubMed.
- S. Brown, Nat. Biotechnol., 1997, 15(3), 269 CrossRef CAS PubMed.
- F. Baneyx and D. T. Schwartz, Protein technologies/Systems biology, 2007, 18(4), 312 CAS.
- S. R. Whaley, D. S. English, E. L. Hu, P. F. Barbara and A. M. Belcher, Nature, 2000, 405(6787), 665 CrossRef CAS PubMed.
- U. O. S. Seker and H. V. Demir, Molecules, 2011, 16(2), 1426 CrossRef CAS PubMed.
- X. Khoo, P. Hamilton, G. A. O'Toole, B. D. Snyder, D. J. Kenan and M. W. Grinstaff, J. Am. Chem. Soc., 2009, 131(31), 10992 CrossRef CAS PubMed.
- B. R. Peelle, E. M. Krauland, K. D. Wittrup and A. M. Belcher, Langmuir, 2005, 21(15), 6929 CrossRef CAS PubMed.
- S. Monti, M. Alderighi, C. Duce, R. Solaro and M. R. TineÌ, J. Phys. Chem. C, 2009, 113(6), 2433 CAS.
- S. Monti and T. R. Walsh, J. Phys. Chem. C, 2010, 114(50), 22197 CAS.
- L. B. Wright and T. R. Walsh, J. Phys. Chem. C, 2012, 116(4), 2933 CAS.
- M. Mijajlovic, M. J. Penna and M. J. Biggs, Langmuir, 2013, 29(9), 2919 CrossRef CAS PubMed.
- C. Wu, A. A. Skelton, M. Chen, L. Vlček and P. T. Cummings, Langmuir, 2012, 28(5), 2799 CrossRef CAS PubMed.
- L. B. Wright and T. R. Walsh, Phys. Chem. Chem. Phys., 2013, 15(13), 4715 RSC.
- M. Hoefling, F. Iori, S. Corni and K.-E. Gottschalk, Langmuir, 2010, 26(11), 8347 CrossRef CAS PubMed.
- M. Hoefling, S. Monti, S. Corni and K. E. Gottschalk, PLoS One, 2011, 6(6), e20925 CAS.
- G. Brancolini, A. Corazza, M. Vuano, F. Fogolari, M. C. Mimmi, V. Bellotti, M. Stoppini, S. Corni and G. Esposito, ACS Nano, 2015, 9(3), 2600 CrossRef CAS PubMed.
- A. Gladytz, E. Lugovoy, A. Charvat, T. Haupl, K. R. Siefermann and B. Abel, Phys. Chem. Chem. Phys., 2015, 17(2), 918 RSC.
- C. K. Thai, H. Dai, M. S. Sastry, M. Sarikaya, D. T. Schwartz and F. Baneyx, Biotechnol. Bioeng., 2004, 87(2), 129 CrossRef CAS PubMed.
- K. Kjærgaard, J. K. Sørensen, M. A. Schembri and P. Klemm, Appl. Environ. Microbiol., 2000, 66(1), 10 CrossRef.
- D. Böhme and A. G. Beck-Sickinger, ChemMedChem, 2015, 10(5), 804 CrossRef PubMed.
- D. Nečas and P. Klapetek, Cent. Eur. J. Phys., 2011, 10(1), 181 Search PubMed.
- P. Klapetek, I. Ohlídal, D. Franta, A. Montaigne-Ramil, A. Bonanni, D. Stifter and H. Sitter, Acta Phys. Slovaca, 2003, 53(3), 223 CAS.
- J. W. Eaton, D. Bateman and S. Hauberg, GNU Octave version 3.0.1 manual: a high-level interactive language for numerical computations, SoHo Books, 2007 Search PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Gunsteren and J. Hermans, in Intermolecular Forces: Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry Held in Jerusalem, Israel, April 13–16, 1981, ed. B. Pullman, Springer Netherlands, Dordrecht, 1981, p. 331 Search PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126(1), 14101 CrossRef PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4(3), 435 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98(12), 10089 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103(19), 8577 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18(12), 1463 CrossRef CAS.
- L. D. Schuler, X. Daura and W. F. van Gunsteren, J. Comput. Chem., 2001, 22(11), 1205 CrossRef CAS.
- R. T. Cygan, J.-J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108(4), 1255 CrossRef CAS.
- M. Catti, G. Ferraris and G. Ivaldi, Eur. J. Mineral., 1989, 1(5), 625 CrossRef CAS.
- K. Kubiak and P. A. Mulheran, J. Phys. Chem. B, 2009, 113(36), 12189 CrossRef CAS PubMed.
- A. Starzyk and M. Cieplak, J. Chem. Phys., 2013, 139(4), 45102 CrossRef PubMed.
- J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6(12), 3713 CrossRef CAS.
- J. M. Rosenbergl, J. Comput. Chem., 1992, 13(8), 1011 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14(1), 33 CrossRef CAS PubMed.
- A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113(18), 2110 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78(7), 1396 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110(13), 6158 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82(1), 284 CrossRef CAS.
- R. L. Willett, K. W. Baldwin, K. W. West and L. N. Pfeiffer, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(22), 7817 CrossRef CAS PubMed.
- I. A. Mastrangelo, M. Ahmed, T. Sato, W. Liu, C. Wang, P. Hough and S. O. Smith, J. Mol. Biol., 2006, 358(1), 106 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp03325c |
| This journal is © the Owner Societies 2016 |