Open Access Article
Open Access ArticleBreathing mode vibrations and elastic properties of single-crystal and penta-twinned gold nanorods†
Yong
Gan
*a,
Zheng
Sun
a and
Zhen
Chen
b
aFaculty of Engineering, Zhejiang University, Hangzhou, Zhejiang 310027, China. E-mail: ganyong@zju.edu.cn
bDepartment of Civil & Environmental Engineering, University of Missouri, Columbia, MO 65211, USA
First published on 22nd July 2016
Abstract
The acoustic vibrations of individual single-crystal and penta-twinned gold nanorods with widths from ∼7 to ∼26 nm are studied using atomic-level simulations and finite element calculations. It is demonstrated that the continuum model in the limit of an infinite rod length could be used to describe the breathing periods of nanorods with an aspect ratio as small as ∼2.5, in combination with bulk material elastic constants. The elastic moduli of gold nanorods are determined via their atomistically simulated extensional periods and the dispersion relation based on long-wavelength approximation. The twinned nanorods become stiffer as the width is reduced, which is in contrast to the size dependence of the modulus in single-crystal nanorods. Further finite element calculations for the breathing periods of nanorods are performed using isotropic elastic constants of bulk gold. We find that the breathing vibrations of the penta-twinned nanorods are more affected by the crystal structure effect than those of single-crystal nanorods, because a smaller range of crystal directions perpendicular to the long axis is involved in the breathing vibrations of twinned nanorods.
1. Introduction
Since their first synthesis in the 1990s,1,2 the fabrication capabilities of gold nanorods have been significantly enhanced in terms of the yield and quality of nanorods,3–5 promoting numerous efforts devoted to exploring their optical, electronic and mechanical properties.5–7 Acoustic vibrations of gold nanorods have been the subject of an increasing amount of research.8–10 This is mainly motivated by the promising potential of vibrating nanorods in the applications of ultrasensitive sensing and nano-optics.11–13 Moreover, vibrational responses of gold nanorods provide accurate information of their mechanical properties,8,10,14 which is of crucial importance, both from a fundamental point of view to understand the effects of sizes and crystal structures on the mechanical properties of nanoobjects, and from a practical viewpoint to design gold nanorod-based sensors and devices.The optical method based on ultrafast time-resolved spectroscopy has been widely used to study the vibrations of gold nanorods.14–16 Many studies have been focused on the measurements of the vibrational responses of ensembles of gold nanorods.16–20 However, ensemble measurements provide the average responses of nanorods, and thus obscure a deeper perspective on the size- and shape-dependent mechanical properties of gold nanorods due to the inevitable inhomogeneity in the size and shape of samples. To overcome this limitation in ensemble measurements, a growing number of time-resolved spectroscopic studies have been conducted on single gold nanorods.21–24 Although single-particle measurements could effectively eliminate the problems resulting from the sample heterogeneity, they suffer from a weaker signal-to-noise ratio as compared with ensemble studies. Thus, it is a challenging task to measure the vibrational responses of single gold nanorods with a small width (e.g., less than 30 nm). Recently, atomistic modeling has been used to study the laser-excited extensional vibrations of individual gold nanorods with widths from ∼7 to ∼24 nm, and shown to be a powerful means complementary to time-resolved spectroscopy for investigating the vibrations of small single nanorods.25,26
So far, the extensional vibration of gold nanorods has been well studied and understood, while there are rare reports on the size and crystal structure dependence of the breathing vibration of gold nanorods. In addition, although the elastic properties of gold nanorods have been intensively investigated, most studies have concentrated on single-crystal nanorods, and there is a lack of a systematic investigation for penta-twinned nanorods. Hence, our understanding is limited with respect to the impact of the crystal structure on the mechanical properties of gold nanorods, especially for small gold nanorods of less than 30 nm width.
Here we study the ultrafast laser-excited breathing vibrations and the elastic properties of different-sized individual single-crystal and penta-twinned gold nanorods, by means of atomistic simulations and finite element (FE) calculations. It is shown that the breathing periods of gold nanorods with an aspect ratio down to ∼2.5 could be well predicted by the continuum elastic model in the limit of an infinitely long rod, with the use of elastic constants of bulk gold. Furthermore, we determine the Young's modulus of penta-twinned gold nanorods through their extensional periods, in combination with a continuum mechanics model, and find that the Young's modulus of penta-twinned nanorods increases as the rod width decreases, which is contrary to the size dependence of elastic modulus of single-crystal nanorods. The FE calculations with isotropic and anisotropic bulk material properties reveal that the breathing vibrations of penta-twinned gold nanorods are more impacted by the crystal structure.
2. Simulation method
The acoustic vibrations of free single gold nanorods in a vacuum induced by femtosecond laser irradiation are considered in this study. By following the previous work,27–29 the ultrafast laser excitation of gold nanorods is simulated using a hybrid method that couples the two-temperature model (TTM)30 into the molecular dynamics (MD) with neglecting energy loss to the surrounding environment and assuming homogeneous laser heating of nanorods. Here we give a brief description of the integrated TTM–MD method, in which the governing equations are27,29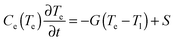 | (1) |
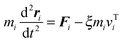 | (2) |
The laser energy source S is expressed as a temporal Gaussian profile28,29
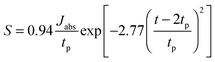 | (3) |
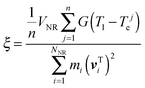 | (4) |
3. Results and discussion
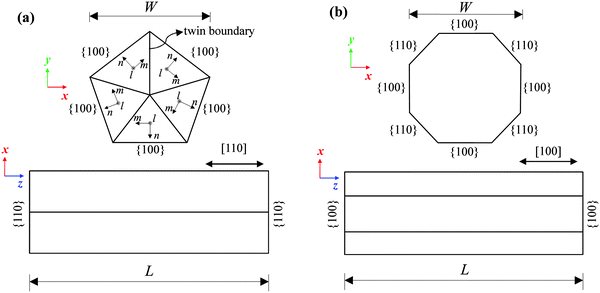
The vibrations of both the single-crystal and penta-twinned gold nanorods are taken into account so that the crystal structure effect can be also examined. The all-atom MD models for gold nanorods are created according to the experimentally analyzed crystal structures,31–33 as schematically illustrated in Fig. 1. For single-crystal nanorods, four {100} and four {110} side facets are parallel to the [100] growth direction, and two {001} facets are located at the ends. Penta-twinned nanorods with a [110] growth direction have five {100} side facets and two {110} end facets. In all nanorod models, the side facets have an approximately equal area. The z-axis is set along the rod axis and the x- and y-axes are positioned in the cross-section plane, as shown in Fig. 1. The vibrations of totally 19 nanorods, with their detailed dimensions as given in Table 1, are investigated.| Sample | L (nm) | W (nm) | Aspect ratio (L/W) |
|---|---|---|---|
| S1 | 24.57 | 7.15 | 3.43 |
| S2 | 42.94 | 12.44 | 3.45 |
| S3 | 57.22 | 16.52 | 3.46 |
| S4 | 71.44 | 20.63 | 3.46 |
| S5 | 85.73 | 24.70 | 3.47 |
| S6 | 17.70 | 7.15 | 2.48 |
| S7 | 40.91 | 16.52 | 2.48 |
| S8 | 20.98 | 7.16 | 2.93 |
| S9 | 49.32 | 16.63 | 2.97 |
| T1 | 26.25 | 7.54 | 3.48 |
| T2 | 39.58 | 11.30 | 3.50 |
| T3 | 52.90 | 15.09 | 3.50 |
| T4 | 69.56 | 19.78 | 3.52 |
| T5 | 79.47 | 22.68 | 3.50 |
| T6 | 92.73 | 26.47 | 3.50 |
| T7 | 19.05 | 7.53 | 2.53 |
| T8 | 38.21 | 15.06 | 2.54 |
| T9 | 22.79 | 7.54 | 3.02 |
| T10 | 45.69 | 15.06 | 3.03 |
The interatomic interactions between gold atoms are described using the embedded atom method (EAM) potential formulated in ref. 34. This EAM potential predicts the elastic constants of c11 = 204.7 GPa, c12 = 170.66 GPa and c44 = 43.39 GPa for bulk single-crystal gold at 298 K,35 which are in good agreement with the experimental values of c11 = 192.34 GPa, c12 = 163.14 GPa and c44 = 41.95 GPa.36 The thermophysical parameters of Ce and G for gold in ref. 37 are used and the free surface conditions are applied in all directions. Once the nanorod models are built, they are equilibrated for 2 ns in the NVT ensemble using the Nosé–Hoover thermostat.38,39 The equilibrated temperature is set at 50 K to achieve a high signal-to-noise level for the vibration responses at ∼298 K. Thereafter, the 100-fs laser irradiation of nanorods is simulated in the NVE ensemble. As suggested in ref. 25 and 26, specific values of Jabs corresponding to the absorbed molar energy of ∼6.3 kJ mol−1 are adopted for attaining a final equilibrium temperature at ∼298 K.
In addition to the modulations in optical responses, the laser-excited vibrations of gold nanorods also result in the oscillations of local displacements and internal pressure as well as the volume changes. Existing experiments generally measured the optical responses of nanorods to identify their vibration periods and damping.9,10,16 It seems that the vibrations of gold nanorods could be investigated via their volume changes. For atomistic nanorods in vibration, however, it is not easy to accurately compute their volumes. Furthermore, at ∼298 K, the thermal oscillations of atoms could lead to a significantly lower signal-to-noise ratio for the volume changes of nanorods as compared with that for the dynamic pressures of nanorods. Alternatively, we study the vibrational responses of nanorods through the internal pressure-related quantities Pαβ, defined as follows:40
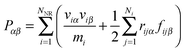 | (5) |
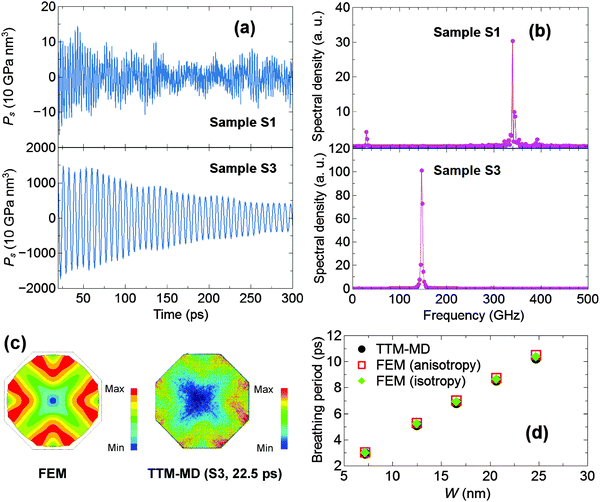
We firstly focus on the breathing mode of single-crystal nanorods S1–S5. Fig. 2a and b present the time-histories and the power spectra of Ps in nanorods S1 and S3, respectively. The dominant peaks with a high amplitude in the power spectra are assigned to the fundamental breathing mode of gold nanorods, as discussed below.
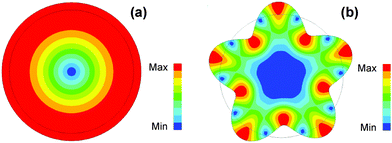
By the FE calculations, the fundamental breathing mode of the octagonal cross-section of single-crystal nanorods characterized by the motion at the vertices is obtained, as shown in Fig. 2c. The cross-sectional dimensions of nanorods in the FE calculations follow those listed in Table 1 and the plain strain assumption is applied. Moreover, the FE calculations are conducted using the material properties for bulk fcc-crystal gold, including the density of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 kg m−3 and the anisotropic elastic constants of c11 = 204.7 GPa, c12 = 170.66 GPa and c44 = 43.39 GPa predicted by the adopted EAM potential. As demonstrated in Fig. 2d, the FE-calculated breathing periods of nanorods agree well with the periods corresponding to the peaks in the power spectrum of Ps.
300 kg m−3 and the anisotropic elastic constants of c11 = 204.7 GPa, c12 = 170.66 GPa and c44 = 43.39 GPa predicted by the adopted EAM potential. As demonstrated in Fig. 2d, the FE-calculated breathing periods of nanorods agree well with the periods corresponding to the peaks in the power spectrum of Ps.
Fig. 2c also presents the top-view atomic pictures of half-cut nanorods S3 at time t = 22.5 ps with the atoms colored by their values of 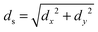 , where dx and dy denote the atomic displacements along the x- and y-axes, respectively, and are computed by the subtraction between the initial and current atomic coordinates. It is evidently seen that the distributions of ds by the atomistic simulations are consistent with the FE-calculated fundamental breathing mode corresponding to the vertex motion. Therefore, not only is the assignment of dominant peaks in the power spectra to the fundamental breathing mode confirmed, but also the use of bulk elastic constants for the breathing mode of single-crystal gold nanorods is validated. Moreover, a lower-frequency peak with much lower amplitude appears in the power spectrum of the smaller sample S1. It actually corresponds to the fundamental extensional mode of the nanorod.
, where dx and dy denote the atomic displacements along the x- and y-axes, respectively, and are computed by the subtraction between the initial and current atomic coordinates. It is evidently seen that the distributions of ds by the atomistic simulations are consistent with the FE-calculated fundamental breathing mode corresponding to the vertex motion. Therefore, not only is the assignment of dominant peaks in the power spectra to the fundamental breathing mode confirmed, but also the use of bulk elastic constants for the breathing mode of single-crystal gold nanorods is validated. Moreover, a lower-frequency peak with much lower amplitude appears in the power spectrum of the smaller sample S1. It actually corresponds to the fundamental extensional mode of the nanorod.
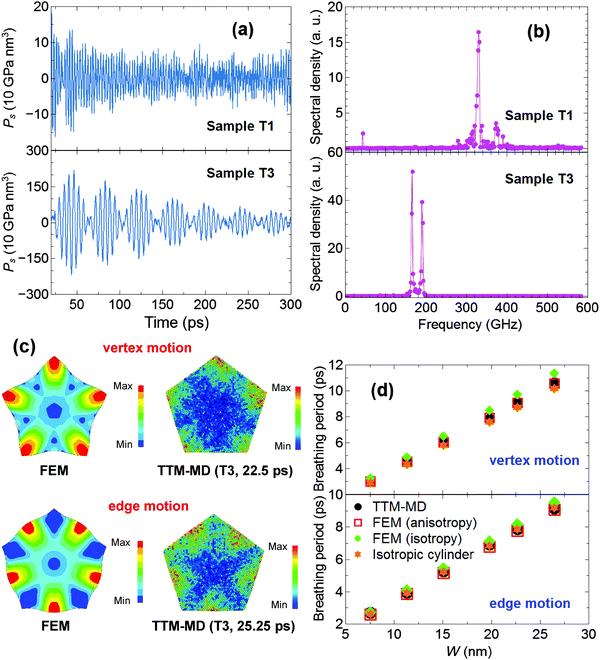
The breathing vibrations of penta-twinned nanorods T1–T6 are further analyzed using the same methodology and procedure. The transient Ps in twinned nanorods T1 and T3 and the corresponding power spectra are separately shown in Fig. 3a and b. Again, the lower-frequency peak for the fundamental extensional mode appears in the power spectrum of the smaller twinned nanorod T1. As can be seen from Fig. 3b, two distinct breathing modes of penta-twinned nanorods with close frequencies are excited. The lower-frequency mode corresponds to the motion at the vertices, while the higher-frequency mode is associated with the motion at the edges of the pentagonal cross-section. These attributions can be proved by Fig. 3c and d, which compare the cross-sectional motions and vibrational periods by the FE and atomistic simulations, respectively.
It is shown in Fig. 3c and d that, in addition to a good agreement in the breathing periods, the atomic displacement patterns in the cross-sectional plane reasonably match two breathing modes with the motions at the vertices and edges of the pentagon as revealed by the FE study. Based on the scheme in Fig. 1a, the FE models for the cross-sections of twinned nanorods are constructed by five triangles with the same material properties. For each triangle, the anisotropic elastic constants in the local l–m–n coordinate system are derived from c11, c12, and c44 of bulk fcc-crystal gold by the tensor transformation41 and used in the FE calculations. It is worth mentioning that these two breathing modes have also been observed in a recent experiment on the vibrations of single gold nanorods with an average width of ∼45 nm.24 In view of the results in Fig. 2 and 3, it is pointed out that the breathing periods of single gold nanorods in either the single-crystal or penta-twinned structure could be well described using the macroscopic elastic model, together with the bulk material elastic constants.
The elastic moduli of penta-twinned gold nanorods are studied next, for which the fundamental extensional periods of gold nanorods Text are required. Basically, the fundamental extensional periods of nanorods can be found through the spectral analysis of Pzz or the quantities containing Pzz. However, the frequency resolution of spectral analysis might not be high enough to guarantee the accuracy of extensional periods, especially for long nanorods. Therefore, the extensional periods of all gold nanorods are obtained by fitting the transient z-axial displacement of the center-of-mass (COM) in a 1.2 nm-thick slab at the sample end, dCOM, to a cosine function, as proposed in our previous work.26
Fig. 4a shows the cosine curves fitted to the transient dCOM data for samples T1 and T3 at the time 20 ps after the laser irradiation, which are calculated by subtracting the averaged z-coordinate of the slab COM over the simulation time period from the transient z-coordinate. It has been proved that the dispersion relation based on the long-wavelength limit is valid for the fundamental extensional vibration of metallic nanorods with an aspect ratio as small as ∼2.4.10,17,26,42 As a result, we determine the elastic moduli of gold nanorods ENR using the dispersion relation of 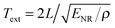 , with density ρ = 19
, with density ρ = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 kg m−3, length L in Table 1, and extensional period Text derived by fitting dCOM. Fig. 4b displays the relationship between the modulus ENR and the rod width W for samples T1–T6. The dependence of the Young's moduli of nanorods S1–S5 on their width is also included in Fig. 4b, for showing the crystal structure effect on the mechanical properties of gold nanorods. In contrast to the size effect in single-crystal nanorods, the penta-twinned gold nanorods become stiffer with the decrease of the width. For example, the Young's moduli of the twinned nanorods T1 (W = ∼7.54 nm), T2 (W = ∼11.3 nm) and T3 (W = ∼15.1 nm) are ∼11%, ∼8% and ∼6% larger than the modulus of bulk gold in the [110] direction E[110], respectively. Indeed, the hardening with the decreasing width is also suggested in the atomistic simulations of penta-twinned metallic nanowires under tension.43 With the increasing W, the elastic modulus of twinned nanorods is closer to the bulk value E[110].
300 kg m−3, length L in Table 1, and extensional period Text derived by fitting dCOM. Fig. 4b displays the relationship between the modulus ENR and the rod width W for samples T1–T6. The dependence of the Young's moduli of nanorods S1–S5 on their width is also included in Fig. 4b, for showing the crystal structure effect on the mechanical properties of gold nanorods. In contrast to the size effect in single-crystal nanorods, the penta-twinned gold nanorods become stiffer with the decrease of the width. For example, the Young's moduli of the twinned nanorods T1 (W = ∼7.54 nm), T2 (W = ∼11.3 nm) and T3 (W = ∼15.1 nm) are ∼11%, ∼8% and ∼6% larger than the modulus of bulk gold in the [110] direction E[110], respectively. Indeed, the hardening with the decreasing width is also suggested in the atomistic simulations of penta-twinned metallic nanowires under tension.43 With the increasing W, the elastic modulus of twinned nanorods is closer to the bulk value E[110].
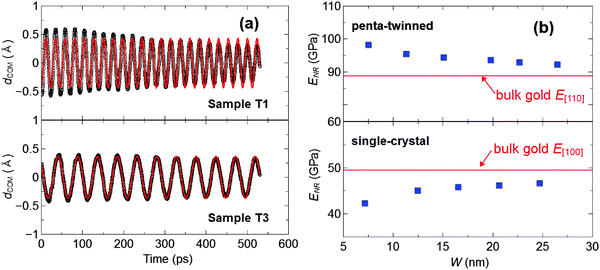 | ||
| Fig. 4 (a) Transient z-axial displacement of the slab COM dCOM for samples T1 and T3. The black circles are the data of dCOM by the combined TTM–MD simulations, and the red curves are the cosine fits to the simulated dCOM. (b) Relationships between the Young's moduli of penta-twinned and single-crystal gold nanorods and their widths. The red lines indicate the Young's moduli of bulk gold along the growth direction of nanorods that are calculated using the EAM potential in the atomistic simulations. The aspect ratios of all nanorods are ∼3.5 (see Table 1). | ||
The stiffening or softening of gold nanorods as shown in Fig. 4 could be, in general, attributed to the constraints by the five-fold twinned structure and/or the nonlinear elasticity of the nanorod core due to surface stress. It has been shown that the nonlinear core elasticity predominantly accounts for the decreasing or increasing Young's modulus of gold nanorods with the decrease of their width, depending on the orientation of nanorods.44,45 Specifically, the softening is exhibited for the 〈100〉 oriented nanorods whereas the 〈110〉 oriented nanorods stiffens. Therefore, the softening of single-crystal gold nanorods ([100] orientation) mainly results from the nonlinear elasticity within the nanorod cores. For the twinned gold nanorods ([110] orientation), in addition to the nonlinear core elasticity influence, the constraints due to the twinned structure also contribute to their stiffening.43 On the other hand, the dispersion relation indicates that the longitudinal wave velocity is proportional to the square root of Young's modulus. The dependence of the atomistically simulated extensional periods of nanorods on their width actually reflects the size-dependent Young's modulus of nanorods due to the constraints by the twinned structure and/or the nonlinear core elasticity, and does not contradict the dispersion relation by the long-wavelength approximation. Furthermore, by the FE calculations (see the ESI†), we find that the dispersion relation based on the long-wavelength limit could be used for the twinned nanorods with an aspect ratio as small as 2.5. The aspect ratios of nanorods in Fig. 4b are all ∼3.5. Thus, a correction analogous to the Rayleigh correction is not required for the dispersion relation.
By fitting the simulated transient P = (Pxx + Pyy + Pzz)/3 to a sum of damped cosine functions (see the ESI†), we have determined the damping time τ of the vibrational motions for nanorods S1–S5 and T1–T6. Tables 2 and 3 give the corresponding intrinsic quality factors Qint calculated by Qint = πτ/T with T being the vibrational period. Except Qint for the extensional mode of twinned nanorods, the other intrinsic quality factors of single-crystal and twinned nanorods are close, and favorably agree with the measured values of 90 ± 29.46 This implies the insignificant crystal-structure effect on the damping for the breathing mode of gold nanorods. The larger Qint for the extensional mode of twinned nanorods is possibly due to the constraints by the five-fold twinned structure. It is worth mentioning that large rod-to-rod variations in the calculated Qint are observed in Tables 2 and 3, and that a single simulation run has been performed for each sample in this work. However, the varying distributions of initial atomic velocities could lead to the changes in the transient pressures of nanorods, which, in turn, would cause the non-negligible variations in the fitted damping times of nanorods. It is suggested that future efforts be made to perform the combined TTM–MD simulations based on different distributions of initial atomic velocities for each nanorod, toward an improved quantitative analysis of the damping of gold nanorods.
| Sample # | Extensional mode | Breathing mode |
|---|---|---|
| S1 | 65.2 | 114.1 |
| S2 | 74.4 | 92.6 |
| S3 | 98.6 | 89.6 |
| S4 | 115.3 | 82.7 |
| S5 | 98.7 | 102.5 |
| Average | 90.4 ± 9 | 96.3 ± 5.5 |
| Sample # | Extensional mode | Breathing mode | |
|---|---|---|---|
| Vertex motion | Edge motion | ||
| T1 | 114.4 | 125.9 | 31.4 |
| T2 | 147.7 | 81.5 | 86.8 |
| T3 | 167.5 | 76.0 | 86.7 |
| T4 | 237.9 | 96.6 | 103.4 |
| T5 | 230.3 | 83.0 | 108.4 |
| T6 | 112.8 | 79.2 | 111.7 |
| Average | 168.4 ± 22.4 | 90.4 ± 7.7 | 88 ± 12.1 |
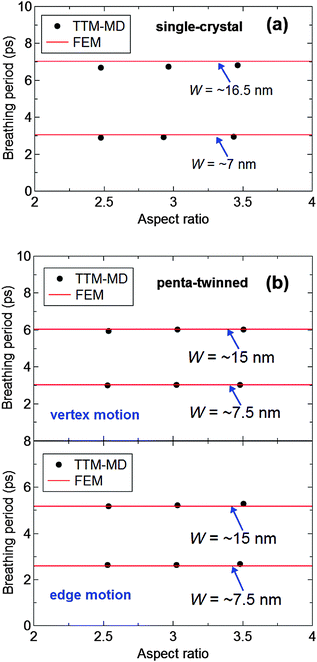
The plane-strain continuum model in our FE analysis strictly holds in the limit of the infinite aspect ratio. The good agreements of breathing periods in Fig. 2d and 3d imply that this model could also be applicable to gold nanorods of finite aspect ratios. The breathing periods of single-crystal (S6–S9) and penta-twinned (T7–T10) nanorods with aspect ratios of ∼2.5 and ∼3 and widths from ∼7 to ∼16.5 nm are further probed by the combined TTM–MD approach, and compared with the FE predictions in Fig. 5. Overall, the FE results are in a good match with the periods by the atomistic simulations (within ∼5%), showing that the adopted continuum model based on the vibrations of an infinitely long rod could be used for gold nanorods with an aspect ratio down to ∼2.5.
It has been reported that there is a trivial crystal structure effect on the breathing mode of metal nanospheres.47 It is interesting to know whether the breathing periods of gold nanorods are also little influenced by the crystal structure. In light of the relations between polycrystalline and monocrystalline elastic constants,48 the Young's modulus E = 78.74 GPa and Poisson's ratio ν = 0.43 for isotropic bulk gold are derived from c11, c12, and c44 for bulk fcc-crystal gold as obtained by the interatomic EAM potential used above. The breathing periods of samples S1–S5 and T1–T6 via the FE calculations with isotropic E and ν are also presented in Fig. 2d and 3d.
As can be found from the above figures, the use of isotropic elastic constants does not significantly affect the FE predictions of the breathing periods of the single-crystal nanorods (∼1.6% difference), suggesting a small crystal structure effect on the breathing mode of the single-crystal nanorods. In comparison, for twinned nanorods, there is some discrepancy between the breathing periods obtained via FE computations with the anisotropic and isotropic bulk elastic constants. Specifically, the differences are ∼7% and ∼5% for the modes with the motion at the vertices and edges of the pentagonal cross-section, respectively. The breathing periods of nanorods depend on the average speed of sound in the crystal directions perpendicular to the long axis of nanorods.21 The penta-twinned gold nanorods are composed of five single-crystal triangular prisms stacked together along a common [110] axis (see Fig. 1a). As compared with single-crystal gold nanorods, penta-twinned nanorods contain a smaller range of crystal directions perpendicular to the long axis, causing a larger deviation of the crystal direction averaged speed of sound from the speed of sound in isotropic polycrystalline gold. Hence, the breathing vibrations of twinned gold nanorods are more influenced by the crystal structure effect than those of the single-crystal nanorods, and the use of isotropic elastic constants is less favorable for twinned gold nanorods.
Finally, we studied the vibrations of infinitely long isotropic elastic cylinders with the same radii as those corresponding to the inscribed circles of the pentagonal cross-sections of nanorods T1–T6. Fig. 6 illustrates the fundamental breathing mode and the five-fold surface mode of an isotropic cylinder, which are similar to the breathing modes of twinned gold nanorods with the edge and vertex motion, respectively. In addition, their periods are found close to those for the breathing modes of the twinned gold nanorods determined by the coupled TTM–MD simulations (less than 5% error), as shown in Fig. 3d. This confirms the claim by Major et al.46 that the two breathing modes of penta-twinned gold nanorods arise from the mixture between the breathing mode of the circular cylinder and the five-fold “whispering-gallery” like surface mode.
4. Conclusions
Ultrafast laser-induced vibrations of individual single-crystal and penta-twinned gold nanorods have been investigated using the continuum and atomistic methods. It is clearly demonstrated that the continuum model based on the vibrations of rods with an infinite length is able to predict well the breathing periods of gold nanorods with a width as small as ∼7 nm and an aspect ratio down to ∼2.5, together with the bulk elastic constants. The Young's moduli of gold nanorods are derived via their atomistically simulated extensional periods and the dispersion relation by the long-wavelength approximation. The elastic modulus of the twinned gold nanorods increases with decreasing width, showing a size effect opposite to that for single-crystal nanorods. In addition, the FE calculations with isotropic and anisotropic elastic constants indicate that the breathing vibrations of the twinned nanorods are more affected by the crystal structure effect than those of the single-crystal nanorods, because less crystal directions perpendicular to the long axis of twinned nanorods are involved in their breathing modes.The present study provides new insights into the breathing vibrations and mechanical properties of single gold nanorods with different sizes and crystal structures, and demonstrates the coupled TTM–MD method as a robust complement to the current experimental approaches for investigating the vibrations of small metallic nanostructures. It is suggested that future efforts utilizing a similar methodology be made to explore the acoustic vibrations of gold nanorods in liquids. The effects of nanoscale solid-fluid interactions on the vibrational period and damping of nanorods and on the non-Newtonian viscoelastic behaviors of high-viscosity liquids would be of particular interest.22–24,49
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 11102185. The atomic snapshots in Fig. 2 and 3 are created using the open-source graphics package OVITO.50Notes and references
- C. A. Foss, G. L. Hornyak, J. A. Stockert and C. R. Martin, J. Phys. Chem., 1992, 96, 7497–7499 CrossRef CAS.
- C. A. Foss, G. L. Hornyak, J. A. Stockert and C. R. Martin, J. Phys. Chem., 1994, 98, 2963–2971 CrossRef CAS.
- N. R. Jana, L. Gearheart and C. J. Murphy, Adv. Mater., 2001, 13, 1389–1393 CrossRef CAS.
- B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15, 1957–1962 CrossRef CAS.
- X. Huang and M. A. El-Sayed, Adv. Mater., 2009, 21, 4880–4910 CrossRef CAS PubMed.
- C. J. Murphy, T. K. Sau, A. M. Gole, C. J. Orendorff, J. Gao, L. Gou, S. E. Hunyadi and T. J. Li, J. Phys. Chem. B, 2005, 109, 13857–13870 CrossRef CAS PubMed.
- J. Kumar and K. G. Thomas, J. Phys. Chem. Lett., 2011, 2, 610–615 CrossRef CAS.
- G. V. Hartland, Annu. Rev. Phys. Chem., 2006, 57, 403–430 CrossRef CAS PubMed.
- A. L. Tchebotareva, P. V. Ruijgrok, P. Zijlstra and M. Orrit, Laser Photonics Rev., 2010, 4, 581–597 CrossRef.
- A. Crut, P. Maioli, N. Del Fatti and F. Vallée, Phys. Rep., 2015, 549, 1–43 CrossRef CAS.
- Y. T. Yang, C. Callegari, X. L. Feng, K. L. Ekinci and M. L. Roukes, Nano Lett., 2006, 6, 583–586 CrossRef CAS PubMed.
- H. Staleva and G. V. Hartland, Adv. Funct. Mater., 2008, 18, 3809–3817 CrossRef CAS.
- K. O’Brien, N. D. Lanzillotti-Kimura, J. Rho, H. Suchowski, X. Yin and X. Zhang, Nat. Commun., 2014, 5, 4042 Search PubMed.
- T. A. Major, S. S. Lo, K. Yu and G. V. Hartland, J. Phys. Chem. Lett., 2014, 5, 866–874 CrossRef CAS PubMed.
- A. Crut, P. Maioli, N. Del Fatti and F. Vallée, Ultrasonics, 2015, 56, 98–108 CrossRef CAS PubMed.
- G. V. Hartland, Chem. Rev., 2011, 111, 3858–3887 CrossRef CAS PubMed.
- M. Hu, P. Hillyard, G. V. Hartland, T. Kosel, J. J. Perez and P. Mulvaney, Nano Lett., 2004, 4, 2493–2497 CrossRef CAS.
- M. Hu, X. Wang, G. V. Hartland, P. Mulvaney, J. J. Perez and J. E. Sader, J. Am. Chem. Soc., 2003, 125, 14925–14933 CrossRef CAS PubMed.
- H. Petrova, J. J. Perez, Z. Y. Zhang, J. Zhang, T. Kosel and G. V. Hartland, J. Mater. Chem., 2006, 16, 3957–3963 RSC.
- M. A. Mahmoud, D. O’Neil and M. A. El-Sayed, Nano Lett., 2014, 14, 743–748 CrossRef CAS PubMed.
- P. Zijlstra, A. L. Tchebotareva, J. W. M. Chon, M. Gu and M. Orrit, Nano Lett., 2008, 8, 3493–3497 CrossRef CAS PubMed.
- P. V. Ruijgrok, P. Zijlstra, A. L. Tchebotareva and M. Orrit, Nano Lett., 2012, 12, 1063–1069 CrossRef CAS PubMed.
- K. Yu, P. Zijlstra, J. E. Sader, Q. H. Xu and M. Orrit, Nano Lett., 2013, 13, 2710–2716 CrossRef CAS PubMed.
- K. Yu, T. A. Major, D. Chakraborty, M. S. Devadas, J. E. Sader and G. V. Hartland, Nano Lett., 2015, 15, 3964–3970 CrossRef CAS PubMed.
- Y. Gan, C. Q. Wang and Z. Chen, Opt. Lett., 2015, 40, 340–343 CrossRef CAS PubMed.
- Y. Gan, Z. Sun and Z. Chen, J. Appl. Phys., 2015, 118, 164304 CrossRef.
- D. S. Ivanov and L. V. Zhigilei, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 064114 CrossRef.
- N. Wang, S. I. Rokhlin and D. F. Farson, J. Nanopart. Res., 2011, 13, 4491 CrossRef CAS.
- Y. Gan and S. Jiang, J. Appl. Phys., 2013, 113, 073507 CrossRef.
- S. I. Anisimov, B. L. Kapeliovich and T. L. Perelman, J. Exp. Theor. Phys., 1974, 39, 375–377 Search PubMed.
- C. J. Johnson, E. Dujardin, S. A. Davis, C. J. Murphy and S. J. Mann, Mater. Chem., 2002, 12, 1765–1770 RSC.
- S.-H. Zhang, Z.-Y. Jiang, Z.-X. Xie, X. Xu, R.-B. Huang and L.-S. Zheng, J. Phys. Chem. B, 2005, 109, 9416–9421 CrossRef CAS PubMed.
- Z. L. Wang, M. B. Mohamed, S. Link and M. A. El-Sayed, Surf. Sci., 1999, 440, L809–L814 CrossRef CAS.
- H. W. Sheng, M. J. Kramer, A. Cadien, T. Fujita and M. W. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134118 CrossRef.
- Y. Zhen and C. Chu, Comput. Phys. Commun., 2012, 183, 261–265 CrossRef CAS.
- J. R. Neighbovrs and G. A. Alers, Phys. Rev., 1958, 111, 707–712 CrossRef.
- Z. Lin, L. V. Zhigilei and V. Celli, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075133 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- M. Allen and D. Tildesley, Computer Simulation of Liquids, Oxford University Press, New York, 1987 Search PubMed.
- A. F. Bower, Applied Mechanics of Solids, CRC Press, Boca Raton, FL, 2010 Search PubMed.
- A. E. H. Love, A Treatise on the Mathematical Theory of Elasticity, Dover Publications, New York, 4th edn, 1944 Search PubMed.
- F. Niekiel, E. Spiecker and E. Bitzek, J. Mech. Phys. Solids, 2015, 84, 358–379 CrossRef CAS.
- H. Liang, M. Upmanyu and H. Huang, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 241403(R) CrossRef.
- Z.-J. Wang, C. Liu, Z. Li and T.-Y. Zhang, J. Appl. Phys., 2010, 108, 083506 CrossRef.
- T. A. Major, A. Crut, B. Gao, S. S. Lo, N. Del Fatti, F. Vallée and G. V. Hartland, Phys. Chem. Chem. Phys., 2013, 15, 4169–4176 RSC.
- V. Juvé, A. Crut, P. Maioli, M. Pellarin, M. Broyer, N. Del Fatti and F. Vallée, Nano Lett., 2010, 10, 1853–1858 CrossRef PubMed.
- A. Crut, P. Maioli, N. Del Fatti and F. Vallée, Phys. Chem. Chem. Phys., 2009, 11, 5882–5888 RSC.
- M. Pelton, D. Chakraborty, E. Malachosky, P. Guyot-Sionnest and J. E. Sader, Phys. Rev. Lett., 2013, 111, 244502 CrossRef PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp03182j |
| This journal is © the Owner Societies 2016 |