Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rate constant calculations of the GeH4 + OH/OD → GeH3 + H2O/HOD reactions using an ab initio based full-dimensional potential energy surface†
J.
Espinosa-Garcia
*,
C.
Rangel
and
J. C.
Corchado
Departamento de Quimica Fisica and Instituto de Computación Científica Avanzada, Universidad de Extremadura, 06071 Badajoz, Spain. E-mail: joaquin@unex.es
First published on 7th June 2016
Abstract
We report an analytical full-dimensional potential energy surface for the GeH4 + OH → GeH3 + H2O reaction based on ab initio calculations. It is a practically barrierless reaction with very high exothermicity and the presence of intermediate complexes in the entrance and exit channels, reproducing the experimental evidence. Using this surface, thermal rate constants for the GeH4 + OH/OD isotopic reactions were calculated using two approaches: variational transition state theory (VTST) and quasi-classical trajectory (QCT) calculations, in the temperature range 200–1000 K, and results were compared with the only experimental data at 298 K. Both methods showed similar values over the whole temperature range, with differences less than 30%; and the experimental data was reproduced at 298 K, with negative temperature dependence below 300 K, which is associated with the presence of an intermediate complex in the entrance channel. However, while the QCT approach reproduced the experimental kinetic isotope effect, the VTST approach underestimated it. We suggest that this difference is associated with the harmonic approximation used in the treatment of vibrational frequencies.
1. Introduction
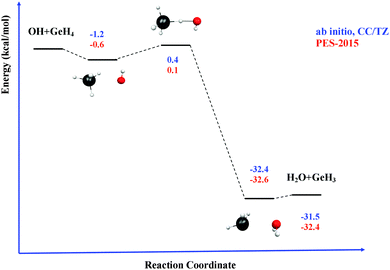
When the size of the molecular reactive system increases, in atom number and/or electron number, the construction of the full-dimensional potential energy surface (PES), representing nuclear motion, becomes increasingly complicated, and with the direct application of ab initio calculations it is practically prohibitive. In these cases, the development of PESs based on functional forms (based on a reduced number of ab initio calculations) acquires greater importance. This is the case studied in the present work, the hydrogen abstraction reactions GeH4 + OH/OD → GeH3 + H2O/HOD, with 45 electrons (as compared with the 19 electrons in the prototype CH4 + OH), where the correlation energy, spin–orbit effects and relativistic energy must be taken into account.GeH4 may be important in plasma-enhanced chemical vapour deposition (DVP) processes,1 while hydroxyl radical reactions have practical applications in both combustion (high temperatures) and atmospheric (low temperature) chemistry. In addition, the GeH4 + OH/OD → GeH3 + H2O/HOD reactions yield water, thus providing an excellent opportunity to study a triatomic molecule in specific quantum states. To the best of our knowledge, no theoretical studies (kinetics and dynamics) have been reported on this reaction, and only one experimental study is available.2,3 Butkovskaya and Setser2,3 studied the infrared chemiluminescence of H2O and HOD products in the reactions of OH and OD radicals with germane at 298 K. They found that: (i) about 50% of the available energy is released as H2O and HOD product vibrational energy, while the other product, GeH3, does not receive much internal energy; (ii) the stretching vibrational distribution was inverted and nearly statistical for the H2O and HOD products, respectively; and (iii) the rate constant was determined, (7.1 ± 1.0) × 10−11 cm3 molecule−1 s−1 at 298 K, relative to the well known rate constant for the similar BrH + OH → Br + H2O, 1.1 × 10−11 cm3 molecule−1 s−1, by measuring the integrated water emission intensity from both reactions.
We have divided the present theoretical study in two parts: (i) the construction of an analytical potential energy surface, named PES-2015, which is based exclusively on high level ab initio calculations and is symmetric with respect to the permutations of the four hydrogen atoms in germane; and (ii) a kinetics study based on this surface, using two approaches, variational transition-state theory (VTST) and quasi-classical trajectory (QCT) calculations, comparing the results with the scarce experimental data, rate constant and kinetic isotope effect (KIE) at 298 K. The present paper is structured as follows. Electronic structure calculations are outlined in Section 2, where the reaction energy, barrier height, stability of the intermediate complexes in the entrance and exit channels, and topology of the reaction from reactants to products are analyzed. Section 3 is devoted to a detailed description of the PES-2015, which describes the hydrogen abstraction reaction on a single surface within the Born–Oppenheimer approximation. Functional form and the fitting process are presented and the results of the final fitting are compared with previous electronic structure calculations. The computational details are presented in Section 4, while Section 5 presents the kinetics results using both approaches, VTST and QCT, and are compared with the only experimental evidence available. Finally, the conclusions are presented in Section 6, focusing on the advantages and disadvantages of the new proposed PES-2015.
2. Electronic structure calculations
The PES-2015 fitting procedure is based exclusively on high level ab initio calculations, and describes the topology of the reaction from the reactants, GeH4 + OH, to the products, GeH3 + H2O. Given the molecular size (45 electrons) we use different levels of calculation.Level I
All stationary points involved in the reaction (reactants, reactant complex, saddle point, product complex and products) were optimized and characterized at the MP2/6-31G(d,p) level of theory. In addition, the minimum energy path (MEP) was constructed at this level, starting from the saddle point geometry in mass-weighted Cartesian coordinates, with some distant points from the reaction path also being calculated. It has been shown that the MP2 method with small basis sets describes reasonably well the reactions of germane with water,4–6 although it is known that this method overestimates the barrier height. To improve the energetic description of the title reaction, single-point calculations were performed at a higher ab initio level, CCSD(T) = FC//cc-pVTZ (coupled-cluster singles and doubles approach, where the connected triple excitations are included using a quasi-perturbative approach, correlating only valence electrons, using the correlation consistent polarized triple-zeta basis set, cc-pVTZ). The level I is then denoted CCTZ//MP2. All calculations were performed using the GAUSSIAN 09 systems of programs.7Level II
Now all stationary points are optimized and characterized at the CCSD(T) = FC/cc-pVTZ level of theory, which is computationally more expensive since at this level the vibrational frequency calculations are numerical. Scuseria and Lee8 showed that the average difference between CCSD(T) and the more expensive CCSDT (where the triple excitations are included in an iterative manner) is small, 0.42 kcal mol−1, in their fourteen test cases.Level III
A serious problem in this reaction is the consideration of the relativistic effects of germanium (32 electrons). This effect is taken into account in the present study by using effective core potentials (ECP) aug-cc-pVTZ-PP basis set for Ge, with the CCSD(T) = FC method, while O and H are described using the aug-cc-pVTZ basis set.9 At this level, single point calculations were performed based on the optimized geometries at the lower MP2/6-31G(d,p) level. In brief, CCPP//MP2.Level IV
Given the expensive computational cost of the optimization and vibrational frequency calculations using ab initio methods, an alternative is the use of density functional theory (DFT) methods. Two approaches were used, MPW60/6-31G(d,p)10 and M062X/6-311++G(d,p),11 which present a balance between quality and cost.Table 1 lists the relative energies (with respect to the reactants) of the stationary points for the title reaction using these methods. In order to test the quality of the electronic structure calculations, and to choose the best method for later use in the fitting procedure, we began by selecting the standard enthalpy of reaction at 298 K, ΔH298r, for comparison. This enthalpy of reaction can be obtained from the respective enthalpies of formation, ΔH298f, for reactants and products. However, in the title reaction, while the enthalpies of formation of OH and H2O are well determined,12 9.40 and −57.8 kcal mol−1, respectively, values available in the literature for GeH4 and GeH3 are widely spread (Table 2), both experimental and theoretical. Using the experimental data, ΔH298r = −40.9 ± 0.3 kcal mol−1, while using the theoretical values ΔH298r ranges from −30.9 to −36.3 kcal mol−1, which are all very far from the experimental data. On the other hand, the enthalpies of reaction at 298 K obtained with the five levels in the present study (Table 1) range from −25.1 to −36.5 kcal mol−1, with the ab initio values in a narrower range, −29.3 and −34.1 kcal mol−1. This comparison evidences the difficulty of the theoretical methods to reproduce the experimental evidence, assuming that these experimental values are correct, since one and only one value has been reported for each species.
| Level | |||||
|---|---|---|---|---|---|
| CCTZ//MP2b | CCTZ | CCPP//MP2c | MPW60 | M062X | |
| a RC, SP, PC and P mean, respectively, reactant complex, saddle point, product complex and products. b CCTZ//MP2 means that the geometry is optimized at the MP2/6-31G(d,p) level while the energy is obtained as a single point calculation at the CCSD(T) = FC//cc-pVTZ level. It corresponds to the level I. c CCPP//MP2 corresponds to the level III. d Relative energy with respect to the products. e Enthalpies of reaction at 298 K, taking into account zero point energy and the thermal corrections at 298 K. | |||||
| RC | −1.18 | −1.94 | −2.60 | ||
| SP | +0.04 | +0.44 | −6.04 | +0.65 | −0.51 |
| PCd | −0.93 | −1.18 | −1.56 | ||
| P | −31.54 | −31.53 | −36.30 | −27.30 | −38.70 |
ΔH0r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
−29.30 | −29.30 | −34.06 | −25.06 | −36.46 |
Next the classical barrier height is analyzed, which is one of the most difficult energy properties to be accurately estimated. The only experimental evidence is an estimation of zero activation barrier.2 Depending on the level used, we obtained values from +0.65 to −6.04 kcal mol−1, with the worst value, −6.04 kcal mol−1, obtained when relativistic effects were considered. Clearly this does not mean that these effects are not important, but that the ECP used is not adequate for this reactive system. The remaining values are close to the zero value.
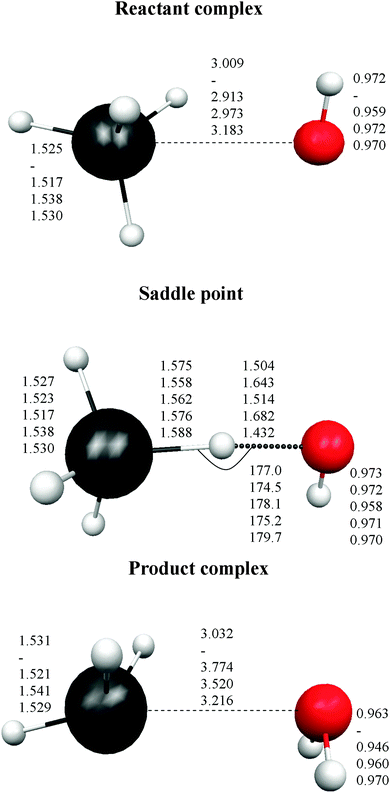
Finally, the intermediate complexes present similar energy stability, regardless of the level used, with differences of about ±1.0 kcal mol−1. In sum, these results show the strong influence of the calculation level used (correlation and basis set) on the correct description of this reactive system. Fig. 1 shows the optimized geometries for the stationary points. In the stabilized reactant complex represented in Fig. 1, the oxygen atom approaches the germanium atom with three hydrogen atoms on the same side, H–O⋯H3Ge–H (face complex). In addition, another reactant complex was located, but now the O atom approaches one H atom of GeH4, forming the structure H–O⋯HGe–H3 (vertex complex). This complex is also stabilized with respect to the reactants, 1.13 kcal mol−1 at the MP2/6-31G(d,p) level, but it presents two imaginary frequencies, and so it is not a true minimum at this level. Similar behaviour was found with other theoretical levels. As with the energy tendency, Fig. 1 shows the different geometrical parameters obtained with the different levels. Thus, the Ge–O distance ranges from 2.913 to 3.009 Å in the reactant complex, and from 3.032 to 3.774 Å in the product complex. In the saddle point the situation is even more confusing, with the Ge–H′ distance larger than the O–H′ distance (H′ being the transferred atom) for two levels, and shorter for the other two levels.
In sum, the energy and structure comparisons showed a dangerous ambiguity when it comes to choosing the more appropriate theoretical method to describe the title reaction.
To finish this section, we consider the possibility of another reaction mechanism. Botkovskaya and Setser2 experimentally studied three very exothermic reactions with hydroxyl radical, BrH, IH and GeH4, which are practically barrierless and present the heavy–light–heavy (HLH) mass combination, with different water product vibrational populations. Based on their experimental results they proposed different reaction mechanisms. So while BrH + OH → Br + H2O presents a direct abstraction reaction mechanism and IH + OH → I + H2O an addition–migration mechanism, for the GeH4 + OH → GeH3 + H2O reaction they proposed two possibilities: (i) the germane may proceed competitively by both ways; or (ii) the reaction shows a direct abstraction mechanism, but the water bending modes appear more vibrationally excited than the stretching modes.
In the direct abstraction mechanism, the oxygen atom approaches the heavy atom (Br or Ge) in linear structure, X⋯H′⋯O, where H′ is the transferred hydrogen atom. For the title reaction, we located and characterized a true saddle point with quasi-linear geometry (Fig. 1). In the addition–migration mechanism, the OH radical forms complexes with I and Ge in the entrance channel, with the quasi-orthogonal structure,  . The posterior migration of the H′ atom through a three-centered transition state explains the water formation. For the title reaction, we located and characterized this complex with Ge in the entrance channel, which is stabilized with respect to the reactants (Fig. 1). However, all attempts to locate the three-centered transition state at different theoretical levels turned out to be fruitless. Therefore, based on these studies, we ruled out the addition–migration mechanism for the title reaction, and we assume that the GeH4 + OH reaction presents a direct abstraction mechanism, similar to the well known BrH + OH or CH4 + OH reactions.
. The posterior migration of the H′ atom through a three-centered transition state explains the water formation. For the title reaction, we located and characterized this complex with Ge in the entrance channel, which is stabilized with respect to the reactants (Fig. 1). However, all attempts to locate the three-centered transition state at different theoretical levels turned out to be fruitless. Therefore, based on these studies, we ruled out the addition–migration mechanism for the title reaction, and we assume that the GeH4 + OH reaction presents a direct abstraction mechanism, similar to the well known BrH + OH or CH4 + OH reactions.
3. Potential energy surface
The development of accurate potential energy surfaces is, in general, a very laborious, tedious and difficult task, where the presence of wells in the entrance and exit channels, the increase in degrees of freedom (the step from atom–diatom to polyatomic systems), and the increase in the number of electrons, complicate this process enormously. In the case of the title reaction, GeH4 + OH, there are further difficulties because it is a very exothermic reaction, with a classical barrier which is practically zero, and consequently the entrance channel is very flat, leading to almost zero gradients of energy. Therefore, the fitting process of the global full-dimensional surface will be very complicated given the energy differences between reactants and products. A similar problem was found in the study of the F(2P) + CH4 reaction and its isotopic variants, which also presents a high exothermicity, −30.0 kcal mol−1, and low barrier height, <1 kcal mol−1. Three full-dimensional PESs were developed for this system by different groups with different strategies,18–21 and it was found that small topology changes in the entrance channel can modify the dynamics (excitation function, vibrational distribution of the products, or the scattering distribution).Taking into account these difficulties and the range of electronic structure values (Section 2), in the present section we develop for the first time a full-dimensional PES for the title reaction, which is based exclusively on ab initio information. We employ an analytical function which is basically a valence bond-molecular mechanics (VB-MM) surface, based on our PES describing the similar CH4 + OH hydrogen abstraction reaction.22 The new PES is widely described as ESI.† In brief, this function is the sum of four terms:
| V = Vstret + Vval + Vop + Vwater | (1) |
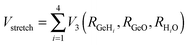 | (2) |
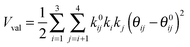 | (3) |
| θ0ij = τ + (τ − π/2)[Sρ(RCHi) − Sρ(RCHj) − 1] + (τ − 2π/3)[Sθ(RCHi) − Sθ(RCHj) − 1] | (4) |
| θ0ij = τ + (τ − τGeH)[Sρ(RGeHi) − Sρ(RGeHj) − 1] + (τ − 2π/3)[Sθ(RGeHi) − Sθ(RGeHj) − 1] | (5) |
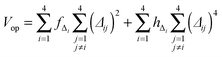 | (6) |
Once the functional form was developed, the 34 parameters were fitted using as input information exclusively electronic structure calculations, describing all the stationary points and the reaction path. Specifically, we used the level I (which is a single point CCTZ//MP2 level), because it represents a compromise between quality and computational economy. Based on our previous experience in the construction of other PESs for polyatomic systems,23–25 in the present study we used a hybrid approach in two consecutive steps, the first trial-and-error hand-made and the second automated to refit the parameters. The first step was based on the fact that most parameters are related to some physical or chemical property, such as geometry and vibrational frequencies of reactants and products, exothermicity, barrier height, etc. So, in the first step we attempted to obtain manually the values of the 34 parameters describing the reaction, from reactants to products. In the second step, we used a recently developed automated multi-beginning least-squares procedure23 which, using Powell's method for local optimization, gives values of the parameters that minimize (locally) the function
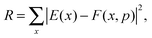 | (7) |
The final parameter set was taken as the best values of this hybrid fitting approach. Finally, it is important to note that the PES presents the advantage that not only the energy, but also the first energy derivatives, i.e., the gradients, are obtained analytically, which is a very desirable feature since it can considerably speed up the kinetics and dynamics calculations.
Next, the quality of PES-2015 was tested against the ab initio information, which represents a test of consistency. The optimized geometries of the saddle point and the intermediate complexes are shown in Fig. 1, and Fig. 2 and 3 show respectively a schematic diagram of the reaction path and an equipotential contour plot. Overall, the new surface reproduces reasonably the ab initio stationary point geometries, where the breaking Ge–H′ bond is larger than the forming H′–O bond, and the approach is practically linear. The imaginary vibrational frequency, 405i cm−1, is close to the CCSD(T) ab initio value, 439i cm−1. The reaction energy and the classical barrier height values are close to the ab initio values. Thus, the reaction is very exothermic, −32.4 kcal mol−1, with a very low barrier, 0.1 kcal mol−1, practically barrierless, suggesting that the tunneling effect is practically negligible. The contour plot (Fig. 3) shows clearly the location of the stationary points, especially the complexes in the entrance and exit channels, and the saddle point. The present comparison with ab initio data shows that the functional form and the fitting process reasonably describe the whole reactive system. The new PES-2015 can be obtained upon request from the authors, prior to its next publication in the POTLIB site.27
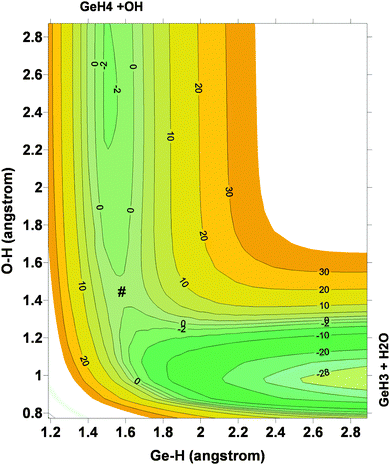 | ||
| Fig. 3 Equipotential contour plot for the GeH4 + OH reaction using the PES-2015 surface. Reactants, products, intermediate complexes and saddle point (#) are clearly represented. | ||
4. Computational details
On the PES-2015 surface, the thermal rate constants at different temperatures in the range 200–1000 K were calculated using two approaches, variational transition-state theory (VTST) and quasi-classical trajectory (QCT) calculations.(a) VTST approach
Using the canonical variational theory,28,29 CVT, the thermal rate constants are given by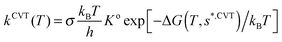 | (8) |
In this heavy–light–heavy mass combination reaction, a priori the tunnelling contribution should play an important role at low temperatures; however, given that this reaction is practically barrierless, the tunnelling effect plays a negligible role.
Note that although VTST includes many approximations, it is a well-validated approach to treat zero-point energy and recrossing34 (also tunnelling, although in the present reaction, as was noted previously, it was not important). For a set of 74 atom–diatom reactions,35 VTST was tested against accurate quantum rate constants, and it was found that in general the agreement was good, with differences of 30–35% and 20–25% when anharmonicity was not and was included, respectively. All kinetics calculations were performed with the POLYRATE-2010 code.36
(b) QCT approach
QCT calculations were carried out using standard procedures implemented in VENUS code37,38 for temperatures in the range 200–1000 K. At each temperature, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories were run with an initial and final Ge–O separation of 15.0 Å, sufficient to ensure that no interaction was present. At each temperature, reactant rotational and vibrational energies were chosen by thermal sampling, while the maximum impact parameter, bmax, was obtained by increasing the value of the impact parameter until no reactive trajectories appeared. The bmax value decreases with temperature, from 10.4 Å at 200 K to 7.8 Å at 1000 K, which is the typical behaviour of barrierless reactions, due to the greater difficulty in compensating the centrifugal energy barrier for the long-range attractive potential.39
000 trajectories were run with an initial and final Ge–O separation of 15.0 Å, sufficient to ensure that no interaction was present. At each temperature, reactant rotational and vibrational energies were chosen by thermal sampling, while the maximum impact parameter, bmax, was obtained by increasing the value of the impact parameter until no reactive trajectories appeared. The bmax value decreases with temperature, from 10.4 Å at 200 K to 7.8 Å at 1000 K, which is the typical behaviour of barrierless reactions, due to the greater difficulty in compensating the centrifugal energy barrier for the long-range attractive potential.39
Using Monte Carlo sampling of the initial conditions, the reaction cross section is given by
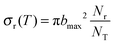 | (9) |
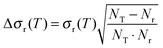 | (10) |
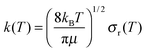 | (11) |
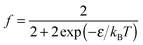 | (12) |
5. Results and discussion
Table 3 lists the VTST and QCT forward rate constants (cm3 molecule−1 s−1) in the temperature range 200–1000 K, and Fig. 4 shows the Arrhenius plots, together with the only experimental value at 298 K for comparison,2 (7.1 ± 1.0) × 10−11 cm3 molecule−1 s−1. First, VTST and QCT rate constants at this temperature, 6.70 × 10−11 and 6.20 × 10−11, respectively, reproduce the experimental data, within the error bar. Moreover, this fast reaction follows the tendency of reactions with OH in the group (XH4):40 CH4 + OH: (7.0 ± 0.2) × 10−15, SiH4 + OH: (1.2 ± 0.2) × 10−11 and GeH4 + OH: (7.1 ± 1.0) × 10−11 cm3 molecule−1 s−1; associated with the weakening of the X–H bond in the series C, Si and Ge:41 103 ± 0.1; 89.6 ± 2.0 and 81.0 ± 3.7 kcal mol−1. Second, the VTST and QCT methods show similar values over the whole temperature range, the QCT values being lower, with differences between 7 and 29%. This agreement is related to the absence of tunneling effects, given the classical character of the QCT calculations. Third, both methods show negative temperature dependence below 300 K. This temperature dependence has also been found in other reactions (involving ions, free radicals or atoms),42–51 and has been associated to the presence of stabilized reactant complexes in the entrance channel.49,52,53 We in fact found a reactant complex (Fig. 1) stabilized by 0.6 kcal mol−1 with respect to the reactants. Unfortunately, no experimental information on the title reaction is available today, and so this negative temperature dependence awaits experimental confirmation. However, hopefully recent QCT calculations50,51 on the similar HBr + OH → Br + H2O reaction (very exothermic and barrierless reaction) which presents a stabilized HBr–OH complex in the entrance channel, also presents negative temperature dependence, in this case below 160 K, thus reproducing the experimental evidence which is available for this reaction. Therefore, for barrierless reactions, where the tunneling effect plays a negligible role, it seems that QCT calculations capture the dynamics of the title reaction, giving a correct answer of the rate constants and their temperature dependence.| T | VTST | QCT | Exp. (ref. 2) |
|---|---|---|---|
| 200 | 9.02 × 10−11 | 7.07 × 10−11 | |
| 250 | 7.32 × 10−11 | 6.50 × 10−11 | |
| 298 | 6.70 × 10−11 | 6.20 × 10−11 | (7.1 ± 1.0) × 10−11 |
| 400 | 6.72 × 10−11 | 6.25 × 10−11 | |
| 500 | 7.46 × 10−11 | 6.73 × 10−11 | |
| 600 | 8.62 × 10−11 | 7.29 × 10−11 | |
| 800 | 1.18 × 10−10 | 8.63 × 10−11 | |
| 1000 | 1.60 × 10−10 | 1.13 × 10−11 |
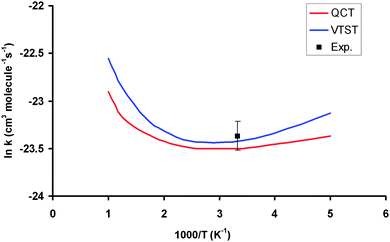 | ||
| Fig. 4 Arrhenius plots of the GeH4 + OH rate constants computed using PES-2015: VTST, blue line; QCT, red line; experimental from ref. 2, black point. | ||
Next we consider the influence of the reactant complex on the rate constants, i.e. the influence of an indirect mechanism, in contraposition to the direct mechanism previously analyzed. Within the equilibrium assumption the mechanism is of the type
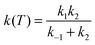 | (13) |
| k(T) = Keq·k2 | (14) |
The phenomenological activation energies for VTST and QCT are respectively −0.31 and −0.10 × 10 kcal mol−1 in the 200–300 K temperature range, and +0.75 and +0.26 kcal mol−1, in the 300–1000 K range. They are obtained by two-point Arrhenius fits at the temperatures indicated, and they represent average values over the corresponding temperature interval. Given that these values are not experimentally available, they represent appropriate quantities for comparison to future experiments.
Next, the kinetic isotope effects (KIEs) are analyzed, thus providing an opportunity to test the theoretical approaches, since they are less sensitive to the accuracy of the surface. These are defined in the usual way, as the ratio of the rate constants for the perprotio reaction to the deuterated reaction, GeH4 + OH/GeH4 + OD. To the best of our knowledge, only one experimental value has been reported at 298 K,2 1.4 ± 0.1, which is very similar to the equivalent HBr + OH/OD reaction,2 1.3 ± 0.2. The calculated KIE at 298 K using the PES-2015 surface are, respectively, 0.80 and 1.37, using VTST and QCT approaches. So, while QCT reproduces the experimental data, VTST gives an inverse KIE. Given that the PES is not responsible for this difference, let us analyze the approximations introduced in the VTST method.
As the barrier height is the same in both isotope variants, in this reaction with a very flat entrance channel the effect of the variation of the vibrational modes along the reaction path will be very important, causing a shift in location of the free energy maximum, ΔG(T,s*,CVT), from the saddle point (s = 0), phenomenon known as variational effect. For the title reaction at 298 K, with a barrier of only 0.1 kcal mol−1, while the ΔG(T,s*,CVT) is 33.008 kcal mol−1 located at s = +0.451 Bohr for the OH reaction, for the OD variant ΔG(T,s*,CVT) = 32.874 kcal mol−1 located at s = +0.469 Bohr. So, the rate constant for the deuterated variant is larger and consequently the KIE(298 K) < 1. We assume that the effect of anharmonicity of the lowest vibrational modes (especially the transitional modes, i.e. modes which are rotations and translations in reactants and products and appear along the reaction path) will be very different for the H and D reactions near the saddle point, and will be the cause of the inverse KIE.
The inclusion of anharmonicity has two effects on the reaction kinetics:29 (i) it produces a greater fall of the lowest vibrational frequencies (transitional modes), diminishing the variational effects and approaching the maximum of ΔG(T,s*,CVT) to the saddle point; and (ii) it produces a decrease of the rate constants, which depends on the reactive system and the temperature. While the anharmonic calculation in polyatomic reactions is not straightforward and is not included in the POLYRATE-2010 code36 when curvilinear coordinates are used, in triatomic atom–diatom reaction its effect has been well studied. For instance, for the Cl + H2 reaction, one of us54 showed that the inclusion of anharmonicity reduces the rate constants between 22 and 55% in the temperature range 150–2100 K, while in other atom–diatom reactions29 the decrease is even larger. For the title reaction, given that anharmonicity is greater for the D variant, we assume a larger decrease of the rate constant and consequently a KIE(298 K) > 1, which would be in agreement with the experiment and the QCT calculations, which are free of this limitation.
6. Conclusions
The present paper presents two different parts, first the development of an analytical full-dimensional potential energy surface for the title reaction and its isotopic variants, and second, the calculation of thermal rate constants and kinetic isotope effects, and their comparison with the only experimental values at 298 K.The overall PES is formulated in terms of VB-MM potentials and fitted to high-level ab initio calculations. Given that it has practically no classical barrier to reaction and is very exothermic, the energy gradients in the entrance channel are practically zero, while in the exit channel they are very high; in this case the fitting procedure was especially complicated. Different tests of the PES show that it reasonably reproduces the ab initio topology of reaction from reactants to products, with special attention to the intermediate complexes in the entrance and exit channels, which can modify the dynamics of reaction.
Based on this PES, thermal rate constants were calculated in the temperature range 200–1000 K using two approaches: VTST and QCT, which present very different fundaments. Both approaches showed negative temperature dependence below 300 K, due probably to the presence of the reactant complex in the entrance channel; although experimental data do not exist for comparison, it reproduces the behaviour for the similar BrH + OH reaction. In addition, both methods reproduce the only experimental data at 298 K, within the experimental error bar. The main discrepancy between the two methods is the KIE. While QCT reproduces the experiment, KIE > 1, VTST gives an inverse KIE. We suppose that this problem of the VTST method is associated with the non-inclusion of anharmonicity in the description of the lowest vibrational frequencies along the reaction path.
In sum, the new PES for the title reaction and its isotopic variants represents a first step in the understanding of this reactive system, and doubtless future improvements will come about, including spin–orbit effects, anharmonicity, relativistic effects, etc., which have only been partly taken into account in the present study. An advantage, however, is that in addition to energy, the new PES provides analytical gradients, i.e., energy first derivatives, and due to the presence of switching functions in the functional form it shows a smooth change from reactants (tetrahedral geometry) to products (pyramidal structure). So, it seems that it correctly describes the kinetics of the reaction, reproducing the only experimental rate constant at 298 K and showing inverse temperature dependence below 300 K, similar to those found in other equivalent reactions, awaiting experimental confirmation. Further dynamics studies on excitation function, product energy disposal or scattering distributions are being planned in our lab and will be presented in a forthcoming paper.
Acknowledgements
This work was partially supported by Gobierno de Extremadura, Spain (Project No. GR15015).References
- A. Lloret, M. Oria, B. Seoudi and L. Abouaf-Marguin, Chem. Phys. Lett., 1991, 179, 329 CrossRef CAS.
- N. I. Butkovskaya and D. W. Setser, J. Chem. Phys., 1997, 106, 5028 CrossRef CAS.
- N. I. Butkovskaya and D. W. Setser, Int. Rev. Phys. Chem., 2003, 22, 1 CrossRef CAS.
- Q. Zhang, D. Zhang, S. Wang and Y. Gu, J. Phys. Chem. A, 2002, 106, 122 CrossRef CAS.
- L. Wang and J. Zhang, J. Phys. Chem. A, 2004, 108, 10346 CrossRef CAS.
- B. Mondal, I. Bhattacharyja, D. Ghost and A. K. Das, Struct. Chem., 2009, 20, 851 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09, Revision A1, Gaussian Inc., Wallinford, CT, 2009 Search PubMed.
- G. E. Scuseria and T.-J. Lee, J. Chem. Phys., 1990, 93, 5851 CrossRef CAS.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099 CrossRef CAS.
- J. Pu and D. G. Truhlar, J. Chem. Phys., 2002, 116, 1468 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2006, 120, 215 CrossRef.
- JANAF Thermochemical Tables, ed. M. W. Chase, Jr., C. A. Davies, J. R. Downey, D. J. Frurip, R. A. McDonald and A. N. Syverud, National Bureau of Standards, Washington, D.C., 3rd edn, 1985, vol. 14 Search PubMed.
- S. R. Gunn and L. G. Green, J. Phys. Chem., 1961, 65, 779 CrossRef CAS.
- P. N. Noble and R. Walsh, Int. J. Chem. Kinet., 1983, 15, 547 CrossRef CAS.
- A. Ricca and Ch. W. Bauslicher, J. Phys. Chem. A, 1999, 103, 11121 CrossRef CAS.
- H. Koizumi, J. Z. Davalos and T. Baer, Chem. Phys., 2006, 324, 385 CrossRef CAS.
- P. R. Duchovicz and C. J. Cobos, J. Phys. Chem. A, 2008, 112, 6198 CrossRef PubMed.
- J. Espinosa-Garcia, J. L. Bravo and C. Rangel, J. Phys. Chem. A, 2007, 111, 2761 CrossRef CAS PubMed.
- G. Czakó, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2009, 130, 084301 CrossRef PubMed.
- J. Palma and U. Manthe, J. Phys. Chem. A, 2015, 119, 12209 CrossRef CAS PubMed.
- J. Espinosa-Garcia, J. Phys. Chem. A, 2016, 120, 5 CrossRef CAS PubMed.
- J. Espinosa-Garcia and J. C. Corchado, Theor. Chem. Acc., 2015, 134, 6 CrossRef.
- J. C. Corchado, J. L. Bravo and J. Espinosa-Garcia, J. Chem. Phys., 2009, 130, 18314 CrossRef PubMed.
- J. Espinosa-Garcia and J. C. Corchado, J. Phys. Chem. A, 2010, 114, 4455 CrossRef CAS PubMed.
- E. Gonzalez, J. C. Corchado and J. Espinosa-Garcia, J. Chem. Phys., 2014, 140, 064310 CrossRef PubMed.
- S. T. Banks and D. C. Clary, Phys. Chem. Chem. Phys., 2007, 9, 933 RSC.
- R. J. Duchovic, Y. L. Volobuev, G. C. Lynch, A. W. Jasper, D. G. Truhlar, T. C. Allison, A. F. Wagner, B. C. Garrett, J. Espinosa-García and J. C. Corchado, POTLIB, http://comp.chem.umn.edu/potlib.
- B. C. Garrett and D. G. Truhlar, J. Am. Chem. Soc., 1979, 101, 4534 CrossRef CAS.
- D. G. Truhlar, A. D. Isaacson and B. C. Garrett, Generalized Transition State Theory, in The Theory of Chemical Reactions, ed. M. Baer, CRC, Boca Raton, FL, 1985, vol. 4 Search PubMed.
- D. G. Truhlar, J. Comput. Chem., 1991, 12, 266 CrossRef CAS.
- C. F. Jackels, Z. Gu and D. G. Truhlar, J. Chem. Phys., 1995, 102, 3188 CrossRef CAS.
- G. A. Natanson, B. C. Garrett, T. N. Truong, T. Joseph and D. G. Truhlar, J. Chem. Phys., 1991, 94, 7875 CrossRef CAS.
- Y. Y. Chuang and D. G. Truhlar, J. Phys. Chem. A, 1997, 101, 3808 CrossRef CAS.
- S. L. Mielke, B. C. Garret, D. G. Fleming and D. G. Truhlar, Mol. Phys., 2015, 113, 160 CrossRef CAS.
- T. C. Allison and D. G. Truhlar, Modern Methods for Multidimensional Dynamics Computations in Chemistry, ed. D. L. Thompson, Word Scientific, Singapore, 1998, p. 618 Search PubMed.
- J. Zheng, S. Zhang, B. J. Lynch, J. C. Corchado,Y. Y. Chuang, P. L. Fast, W. P. Hu, Y. P. Liu, G. C. Lynch, K. A. Nguyen and D. G. Truhlar, POLYRATE-2010-A, University of Minnesota, Minneapolis, MN, 2010 Search PubMed.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014 CrossRef CAS.
- W. L. Hase, R. J. Duchovic, X. Hu, A. Komornicki, K. F. Lim, D.-h. Lu, G. H. Peslherbe, K. N. Swamy, S. R. Vande Linde, A. J. C. Varandas, H. Wang and R. J. Wolf, VENUS96: A General Chemical Dynamics Computer Program, QCPE Bull, 1996, vol. 16, p. 43 Search PubMed.
- A. Rivero-Santamaria, F. Dayon, J. Rubayo-Soneira and M. Mounerville, Chem. Phys. Lett., 2014, 610–611, 335 CrossRef CAS.
- R. Atkinson, D. L. Baulch, R. A. Cox, R. F. Hampson Jr., J. A. Kerr and J. Troe, J. Phys. Chem. Ref. Data, 1992, 21, 1125 CrossRef CAS.
- J. Berkowitz, G. B. Ellison and D. Gutman, J. Phys. Chem., 1994, 98, 2744 CrossRef CAS.
- D. D. Davis, R. E. Huie and J. T. Herron, J. Chem. Phys., 1973, 59, 628 CrossRef CAS.
- J. J. Solomon, M. Meot-Ner and F. H. Field, J. Am. Chem. Soc., 1974, 96, 3727 CrossRef CAS.
- P. Sharkey and I. W. M. Smith, J. Chem. Soc., Faraday Trans., 1993, 89, 631 RSC.
- I. R. Sims, Nat. Chem., 2013, 5, 734 CrossRef CAS PubMed.
- R. J. Shannon, M. A. Blitz, A. Goddard and D. E. Heard, Nat. Chem., 2013, 5, 745 CrossRef CAS PubMed.
- R. J. Shannon, S. Taylor, A. Goddard, M. A. Blitz and D. E. Heard, Phys. Chem. Chem. Phys., 2010, 12, 13511 RSC.
- J. Ree, Y. H. Kim and H. K. Shin, Bull. Korean Chem. Soc., 2013, 34, 2473 CrossRef CAS.
- I. W. M. Smith and A. R. Ravishankara, J. Phys. Chem. A, 2002, 106, 4798 CrossRef CAS.
- A. G. S. Oliveira-Filho, F. R. Ornellas and J. M. Bowman, J. Phys. Chem. Lett., 2014, 5, 706 CrossRef PubMed.
- J. Ree, Y. H. Kim and H. K. Shin, J. Phys. Chem. A, 2015, 119, 3147 CrossRef CAS PubMed.
- D. B. Atkinson, V. I. Jaramillo and M. A. Smith, J. Phys. Chem. A, 1997, 101, 3356 CrossRef CAS.
- A. Persky, Chem. Phys. Lett., 2007, 439, 3 CrossRef CAS.
- J. Sanson, M. L. Sanchez and J. C. Corchado, J. Phys. Chem. A, 2006, 110, 589 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02986h |
| This journal is © the Owner Societies 2016 |