The quest for rationalizing the magnetism in purely organic semiquinone-bridged bisdithiazolyl molecular magnets

Abstract

Semiquinone-bridged bisdithiazolyl-based radicals (XBBO) are appealing purely organic magnetic building blocks for the synthesis of new functional materials. Remarkably, for the phenyl-derivative PhBBO, the rationalization of its magnetism becomes a proof of concept that DFT can dramatically fail to evaluate J_AB magnetic interactions between purely organic radical pairs. Instead, wavefunction-based methods are required. Once J_AB's are fully characterized, the magnetic topology of PhBBO is disclosed to consist of ferromagnetic FM π-stacks that are very weakly coupled (by FM and AFM J_AB interactions). The magnetic susceptibility χT(T) and magnetization M(H) of PhBBO are then calculated using a first-principles bottom-up approach. The study of the unit cell contraction upon cooling from room temperature to zero-Kelvin is relevant to propose a suitable model for the phase transition that occurs at 4.5 K. A simplistic picture tells us that the antiparallel-aligned 1D-FM-chains convert into domains of weakly either FM- or AFM-coupled 1D-FM-chains. Accordingly, the presence of these domains may introduce geometrical spin frustration below 4.5 K.

---

Introduction

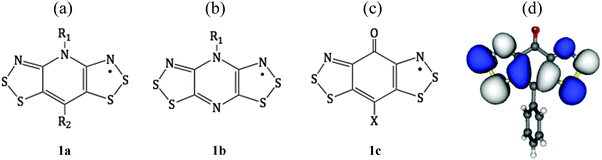
In an attempt to meet the electronic requirements for magnetic performance, namely, spin delocalization and orthogonal orbital overlap, heavy-heteroatom radicals have been widely studied.¹ Interest in the use of thiazyl radicals as building blocks for magnetic and conductive materials has thus grown rapidly, in part because the heavy heteroatom (sulfur) enhances intermolecular magnetic and electronic interactions. N-Alkylated pyridine-bridged bisdithiazolyl radicals (Fig. 1a) have emerged as a new versatile class of radicals for the synthesis of new functional organic materials.² However, they tend to pack in herringbone arrays of slipped π-stacks, which diminish the orbital overlap along the stacking direction.^2,3 The herringbone motif could be avoided using radicals based on N-alkylated pyrazine-bridged bisdithiazolyl (Fig. 1b).⁴ Yet, dimerization is favored, although it can be suppressed by using the right ligands R₁.⁵ In addition to this synthetic strategy, an alternative approach consists of the isoelectronic replacement of the NR₁ moiety in 1a with a carbonyl group to result in a resonance-stabilized semiquinone-bridged bisdithiazolyl radical (denoted XBBO, see Fig. 1c). This replacement intended to be a simple isolobal exchange,⁶ since the incorporation of the carbonyl, CO, group does not perturb the SOMO (see Fig. 1d) with respect to either pyridine- or pyrazine-bridged radicals due to the presence of a nodal plane. However, there is a significant mixing of the CO π*-orbital in the LUMO that results in low-lying open-shell states, whose presence, ultimately, has a major impact on both magnetic and charge-transport properties.⁷ Accordingly, although this new class of radicals has a common molecular framework, the implementation of different exocyclic groups (X = H,^7c,8 F,^7b,9 Me,¹⁰ Ph,^1a,11 Cl^1a) is responsible for XBBO displaying a variety of structural, magnetic, conducting and electronic properties. In general, for XBBO crystals, π-stacked bis-1,2,3-dithiazolyl radicals apparently have good orbital overlap along the stacking direction. Within this context, the phenyl-substituted radical based on the semiquinone-bridged skeleton (Fig. 1c with an exocyclic group X = Ph¹¹) was the first example of this new class of radicals, and is an appealing target for a computational study.

Fig. 1 Structures of (a) an N-Alkylated pyridine-bridged bisdithiazolyl radical, (b) an N-Alkylated pyrazine-bridged bisdithiazolyl radical, (c) a semiquinone-bridged bisdithiazolyl radical XBBO and (d) the SOMO of the PhBBO radical (X = phenyl) at the B3LYP level (visualized with an isovalue of 0.02 a.u.).

The carbonyl oxygen atom in XBBO plays an active structure-making role, giving rise to tightly packed structures linked by short intermolecular S⋯O contacts. These supramolecular synthons afford a rich variety of novel packing motifs, including the head-over-tail motif found for PhBBO (see Fig. 2). The experimental crystal data show that PhBBO crystallizes in the high-symmetry orthorhombic chiral space group P2₁2₁2₁, whose unit cell contains two non-equivalent columns of stacked radicals organized in a head-to-tail disposition.¹¹ Sheets (bc-plane) of approximately coplanar radicals are laced together by a series of intermolecular S3⋯O contacts (2.858 Å) (see Fig. 2a). These bc-sheets are packed in layers to produce alternating ABABAB π-stacks (adjacent radicals are related by the 2-fold screw axis along a) (see Fig. 2b). From an experimental point of view, both the alternating π-stack motif and the paucity of close intercolumn radical–radical contacts suggested an approximately 1D electronic structure.¹¹

Fig. 2 (a) Unit cell of PhBBO viewed perpendicular to the bc-plane, with intermolecular 2.858 Å S3⋯O contacts shown with dashed lines. (b) Two views of the alternating ABAB π-stacks with intra-stack S3⋯S1 contacts d₁ and d₂ along the a-axis.

The available experimental χT(T) data at H = 1 kOe over the range 2–300 K suggested paramagnetic behavior, with strong local ferromagnetic (FM) couplings along the π-stacks.¹¹ These suggested strong FM interactions could be rationalized in terms of the presence of the above-mentioned head-over-tail π-stacking of PhBBO radicals. For temperatures above 100 K, the data are found to be fitted to a Curie–Weiss expression with C = 0.349 emu K mol⁻¹ and θ = +32.8 K. Within the 6–30 K temperature range, the Baker model for a Heisenberg 1D FM-coupled chain (π-stack) of S = ½ centers was used to fit the experimental data with a FM J^chain (+29.5 cm⁻¹) and an antiferromagnetic (AFM) mean field interaction zJ′ (−2.5 cm⁻¹) fitting parameters. According to ZFC–FC experiments at H = 100 Oe, a phase transition occurs at 4.5 K. It was experimentally proposed that below 4.5 K the FM chains become aligned in an antiparallel fashion to form a spin-canted AFM (SC-AFM) state. The AFM ordering was observed to collapse when increasing the magnetic field and the system was experimentally suggested to undergo a spin–flop transition.¹¹

All the above reported experimental data motivate the need for further understanding of the electronic structure of the PhBBO material.

The standard approach for both the interpretation and the simulation of magnetic properties of materials is based on a static perspective. Accordingly, it is assumed that these properties can be obtained with a single static nuclear configuration (usually an X-ray resolved structure or, alternatively, an optimized structure). The magnetic response of the purely organic PhBBO molecular crystal is rationalized here on the basis of a first-principles bottom-up FPBU procedure.¹² One first analyzes the crystal packing to select radical pairs that might be magnetically coupled. Quantum chemistry methods are then used to evaluate all J_AB magnetic couplings. The magnetically significant J_AB interactions define the magnetic topology of the crystal. Full diagonalization techniques are then applied to a properly chosen magnetic model to generate the corresponding energy spectrum. Statistical mechanic tools are fed with those energy levels to simulate the macroscopic properties of interest (χ, C_p, M), which in turn will be compared to the available experimental data.

Summarizing, this work aims at discriminating whether the magnetic topology of PhBBO is mostly one-dimensional, with FM interactions within π-stacks and AFM interactions between π-stacks, by evaluating the magnetic coupling between radicals. The magnetic susceptibility and magnetization of PhBBO will then be calculated in order to validate the computed magnetic topology. Finally, the study of the unit cell contraction upon cooling from room temperature to 0 Kelvin targets at proposing a suitable model for the phase transition that occurs at 4.5 K.

Methodological details

The first-principles bottom-up FPBU procedure was applied to study the magnetism of the target PhBBO system.¹² This working strategy implies the completion of four steps, as summarized herein. First, after inspection of the crystal structure, the symmetry-unique radical pairs that are likely to be magnetically relevant are identified (using a PhBBO⋯PhBBO distance cutoff value of 15 Å). Second, their magnetic exchange interactions, J_AB, are computed and the magnetic topology of the crystal (i.e., the network of connectivity defined by all relevant J_AB values) arises. Third, the Heisenberg Hamiltonian is applied to a model space (a subset of the magnetic topology), which is designed in such a way that, ideally, the resulting set of eigenvalues reproduces those that result from the application of the Heisenberg Hamiltonian to the full, infinite, crystal. Finally, the resulting energies and total spin numbers are introduced into the proper statistical mechanics expressions to calculate the macroscopic properties of the system, such as the magnetic susceptibility χT(T) and magnetization M(H).

The evaluation of the J_AB magnetic coupling between purely organic PhBBO radicals was performed using a dimer and a larger tetramer cluster models. At the DFT level, low spin (LS) broken symmetry (BS)¹³ and high spin (HS) single point energy calculations were performed using Gaussian09¹⁴ for the dimer model and Orca 3.0¹⁵ package for the tetramer model. WFT based multireference CASSCF/PT2 and RASSCF/PT2 energies (E^LS, E^HS)¹⁶ were obtained from Molcas 7.6.¹⁷ The evaluation of J_AB interactions by DFT was performed using the 6-311++g(d,p) basis set,¹⁸ and by WFT methods was performed using the following contraction of the ANO-RCC basis set:¹⁹ (3s2p1d) for N, O and C atoms, (2s) for H, and (4s3p1d) for S atoms. For the latter, the Cholesky decomposition was used to reduce the computational cost associated with the calculation of the two-electron integrals.²⁰ When performing CASPT2 and RASPT2, the standard zero-order Hamiltonian with an IPEA²¹ shift of 0.25 a.u. was applied in the definition of the diagonal Fock matrix elements of the active orbitals. The definition of the different active spaces used is given in ESI,† Section S1. All self-consistent field (SCF) energy convergences have been set up at 10⁻⁷ a.u., thereby allowing an accuracy of 0.05 cm⁻¹ in the evaluation of the magnetic exchange J_AB values.

The unit cell contraction upon cooling from room temperature to zero Kelvin was studied employing plane wave pseudopotential calculations for the variable-cell geometry optimization. This calculation was carried out using the PBE exchange–correlation functional²² within the spin-unrestricted formalism, together with Vanderbilt ultrasoft pseudopotentials,²³ and G-point sampling of the Brillouin zone. In the calculation, the semi-empirical dispersion potential introduced by Grimme²⁴ was added to the conventional Kohn–Sham DFT energy in order to properly describe the van der Waals interactions among all different PhBBO radicals (the so-called DFT-D2). Notice that good predictions for the structure and cohesive energies of molecular crystals are obtained by the use of PBE together with the D2 Grimme correction.²⁵ Our variable-cell optimization, in which the atomic positions and the lattice parameters are optimized simultaneously, was carried out using the QUANTUM ESPRESSO package²⁶ using a plane wave basis set expanded at a kinetic energy cutoff of 70 Ry. The initial atomic positions and lattice parameters for the optimization were taken from the X-ray resolved structures of PhBBO at room temperature (296 K).¹¹ The initial lattice parameters of the supercell are collected in ESI,† Section S2.

Results and discussion

The nature of magnetism of the PhBBO crystal: DFT failure reviewed from a WFT perspective

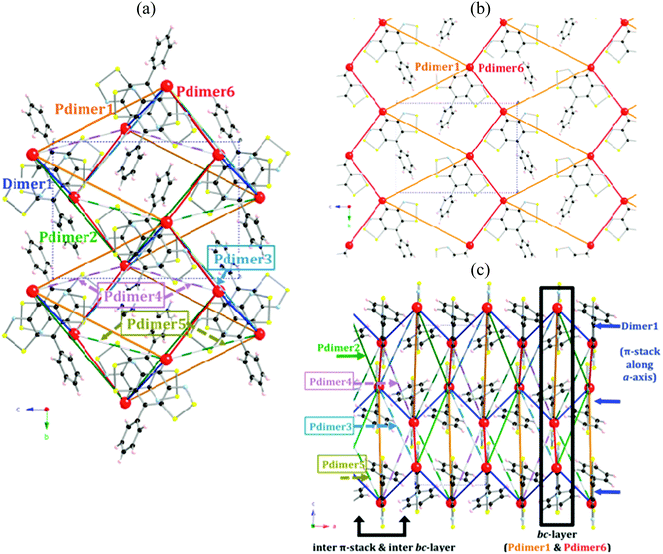
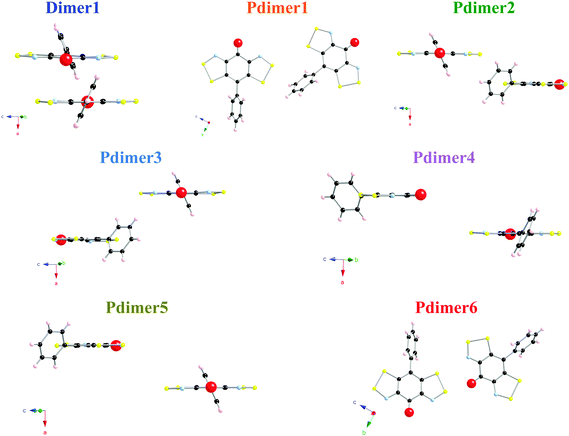
The unit cell of the PhBBO crystal contains two non-equivalent columns of stacked radicals in a head-to-tail disposition: there is one symmetry unique intra-column π-pair (namely Dimer1 along the a-axis) and six different inter-column pairs (Pdimer1–Pdimer6) within a 15.0 Å radius cutoff (Fig. 3a). Pdimer6 and Pdimer1 pairs run along the b-axis forming zigzag chains that are connected in such a way that both dimers alternate along the c-axis (see Fig. 3b). These bc-layers are then laced together by Pdimer2, Pdimer3, Pdimers4 and Pdimer5 contacts (see Fig. 3c). The network of intermolecular interactions within the PhBBO crystal is thus particularly complex (see Fig. 3 for a complete picture of all the intra- and inter-stack radical pairs that have potential to result in non-negligible J_AB magnetic couplings). Accordingly, there is a J_AB magnetic interaction associated with each radical⋯radical contact that has to be evaluated (see the color code in captions of Fig. 3 and 4 for radical pair geometries).

Fig. 3 (a) A bc-view of the PhBBO unit cell indicating all seven non-equivalent radical pairs that have to be evaluated. (b) A bc-layer consisting of chains of Pdimer6 pairs connected through chains of Pdimer1 dimers. (c) The π-stack of bc-layers via Pdimer2-Pdimer5. Color code for radical pairs: Dimer1 (dark blue), Pdimer1 (orange), Pdimer2 (green), Pdimer3 (dashed light-blue), Pdimer4 (dashed pink), Pdimer5 (dashed green), Pdimer6 (red).

The well-known B3LYP hybrid functional,²⁷ which is acknowledged to perform well to compute J_AB magnetic interactions between purely organic radicals,^28a,29,30 and the range-corrected CAM-B3LYP³¹ methods are used to evaluate the J_AB magnetic coupling of the previously selected seven pairs of PhBBO radicals (Fig. 4). The nuclear coordinates were extracted from X-ray data at room temperature.¹¹ The Hamiltonian used is Ĥ = −2∑J_ABŜ_A·Ŝ_B. Thus, for a pair of PhBBO radicals showing a HS triplet state and a LS open-shell BS singlet state, J_AB = E^BS,LS − E^HS at the DFT level within the broken symmetry, BS, approximation.¹³Table 1 shows all calculated J_AB magnetic interactions using the 6-311++G(d,p) basis set.¹⁸ The results obtained indicate that, among all pairs, only Dimer1, Pdimer1, Pdimer2 and Pdimer6 provide a non-zero J_AB. By comparison with the fitted J values (+29.5, −2.5 cm⁻¹), it can be inferred that the values of J_AB for Dimer1 (+343.5/+193.3 cm⁻¹) and Pdimer6 (+24.6/+5.9 cm⁻¹) are highly overestimated at the DFT level.

Fig. 4 Molecular geometry of the intra-π-stack Dimer1, and inter-stack Pdimer1-6 radical pairs, for which the J_AB magnetic exchange values have been evaluated. Notice that the two PhBBO radicals in Pdimer1 and Pdimer6 lay coplanar in the bc-plane.

Table 1 Magnetic exchange couplings calculated for the seven pairs of radicals in the room temperature crystal structure. The calculations were performed at B3LYP and CAM-B3LYP level using the 6-311++g(d,p) basis set, and at CASSCF and RASSCF level using the DZV contraction of the ANO-RCC basis set and different active spaces (see main text and ESI, Section S1). The O⋯O distance between each radical pair is also indicated. See the ‘Methodological details’ section for a description on the basis sets

	O–O dist/Å	B3LYP/cm^−1	CAM-B3LYP/cm^−1	CASSCF/cm^−1	RASSCF-1/cm^−1	RASSCF-2/cm^−1
Dimer1	6.039	343.5	193.3	34.6	44.6	49.7
Pdimer1	12.638	−1.36	−0.9	−0.2	−0.4	−0.3
Pdimer2	12.528	0.6	0.2	0.1	0.1	0.2
Pdimer3	12.668	0.0	0.0	0.0	0.0	0.0
Pdimer4	8.679	0.0	0.0	0.0	0.0	0.0
Pdimer5	8.880	0.0	0.0	0.0	0.0	0.0
Pdimer6	7.162	24.6	5.9	0.3	0.0	0.3

---

An in-depth study of Dimer1 (and Pdimer6) is required in order to disentangle the disagreement between calculated J_AB at the DFT level and fitted J values. While DFT calculations are known to be sometimes insufficient to properly describe inorganic molecule-based magnets,³² our experience indicates that DFT performs correctly with purely organic radical molecule-based magnets.²⁹ As spin density in the PhBBO radical is delocalized over the whole π-system (see the SOMO in Fig. 1d), we focused on the spin density on the nitrogen atoms to monitor whether the radical pair is well described or not.³³ The values obtained in each case are reported in Table 2. For B3LYP and CAM-B3LYP, it can be seen that the spin densities on the N atoms obtained for the monomer are in agreement with the literature (spin densities on N1/N2 are 0.27/0.14 and 0.32/0.21, respectively).^1a,7a,c Regarding Dimer1 in its triplet state, the values again match those obtained for the monomer indicating that the spin distribution is well described. However, the spin density distribution of Dimer1 in the open-shell BS singlet differs from the latter two, since smaller values are obtained for the N2 atom. This can clearly indicate a problem in the spin density distribution of this electronic state. The problem with the open-shell BS singlet state could be related to the radical pair model used to compute the microscopic J_AB magnetic interaction. The effect of the cooperativity between the closest neighboring radicals on the electronic density (and, in turn, on the J_AB values) is evaluated by enlarging³⁴ the pair magnetic model to a tetramer cluster model to include both Dimer1 and Pdimer6 interactions. Using the tetramer model, J_AB(Dimer1) coupling values are calculated to be +336.0 cm⁻¹ and +181.2 cm⁻¹ at B3LYP and CAM-B3LYP levels, respectively (see ESI,† Section S3, for more details). Therefore, there is no J_AB improvement using a larger cluster model. Neither spin–orbit coupling nor anisotropy can be the reason for the DFT failure since a g value of 2.009 was reported for the PhBBO radical.¹¹ We have also evaluated the possible enhancement of the magnetic interactions due to hydrogen interactions by using larger basis sets,³⁵ but with the same outcome. Finally, in PhBBO there are neither counterions nor solvent to be accounted for. Therefore, so far the environment of the radicals has also been properly described.³⁶ Apparently there is no explanation for the failure of B3LYP or CAM-B3LYP functionals when trying to describe the magnetic interaction between Dimer1 (and Pdimer6) semiquinone-bisdithiazolyl radicals. Note that calculations done at the wB97XD level using 6-31+g(d) and 6-311++g(d,p) basis sets give +179.2 and +180.5 cm⁻¹ as J_AB values, respectively, in agreement with our previous CAM-B3LYP results, which was expected since both functionals are range separated hybrids.

Table 2 Mulliken spin densities of the N atoms obtained in the doublet ground state of the PhBBO monomer, and in the triplet and broken symmetry (BS) singlet states of Dimer1. The value of the spin density of the N atoms of the second radical within Dimer1 is indicated in parenthesis. The calculations were performed at B3LYP and CAM-B3LYP levels using the 6-311++g(d,p) basis set

Method	System	Spin state	Spin density N1	Spin density N2
B3LYP	Monomer	Doublet	+0.27	+0.14
	Dimer1	Triplet	+0.27 (+0.27)	+0.13 (+0.13)
		Singlet BS	+0.27 (−0.26)	+0.06 (−0.05)
CAM-B3LYP	Monomer	Doublet	+0.32	+0.21
	Dimer1	Triplet	+0.30 (+0.30)	+0.21 (+0.21)
		Singlet BS	+0.25 (−0.24)	+0.16 (−0.16)

---

We then resorted to WFT based methods, such as CASSCF and RASSCF,¹⁶ to evaluate all J_AB interactions. At the WFT level, J_AB = (E^LS − E^HS)/2 since the Hamiltonian used is the same as for the DFT level (Ĥ = −2∑J_ABŜ_A·Ŝ_B). Several CASSCF and RASSCF spaces (including π-type orbitals and using a DZV basis set,¹⁹ see ESI,† Section S1) were first tested at the X-ray nuclear coordinates of the PhBBO monomer (Table 3), the spin density being the criterion to decide whether the active space was adequate.³³ Indeed, the spin density of the N atoms varies depending on the active space considered. According to Table 3, CASSCF(7,7) and RASSCF(7,2,2;3,1,3) are required for a good description of the PhBBO radical (note that the RASSCF restricted active space is defined as follows: the number of electrons in all RAS space, the maximum number of holes in RAS1, and the maximum number of particles in RAS3; orbitals in RAS1, orbitals in RAS2, and orbitals in RAS3).

Table 3 Mulliken spin densities obtained for the N atoms of the PhBBO monomer in its doublet ground state when using different CASSCF and RASSCF active spaces (see ESI, Section S1, for further discussion on active spaces)

Active space	Spin density N1	Spin density N2
CASSCF(1,2)	0.50	0.00
CASSCF(3,3)	0.43	0.04
CASSCF(5,5)	0.36	0.07
CASSCF(7,7)	0.29	0.17
RASSCF(7,2,2;3,1,3)	0.28	0.12

---

Correspondingly, equivalent CASSCF and RASSCF spaces were tested for Dimer1 and Pdimer1 using two different basis sets (Table 4). The results show that the minimal active spaces are not enough; one must resort to CASSCF(14,14), RASSCF(38,2,2;18,2,6) and RASSCF(38,2,2;16,6,4) to properly describe the spin density. Besides, the DZV to TZV basis set effect is small (see Table 4; for Dimer1: +34.6 to +36.4 cm⁻¹ at the CASSCF level and +44.6 to +43.1 cm⁻¹ at the RASSCF level; for Pdimer1: −0.4 to −0.5 cm⁻¹ at the RASSCF level). Thus, DZV contraction was chosen for the calculation of the J_AB interaction for all remaining radical pairs (Pdimer2–Pdimer6). For Dimer1, we also corroborated that the value of J_AB changes by ca. 8% with the inclusion of dynamic correlation: J_AB = +44.6 cm⁻¹ at the RASSCF(38,2,2;18,2,6) level and J_AB = +48.7 cm⁻¹ at the RASPT2 level. Since RASPT2 calculations are very demanding in terms of computational cost and they imply a small relative improvement (8%) of the J_AB values, our best options to pursue our computational study on the PhBBO crystal are the use of CASSCF(14,14), RASSCF(38,2,2;18,2,6) and RASSCF(38,2,2;16,6,4) (hereafter called CASSCF, RASSCF-1, and RASSCF-2, respectively). Table 1 shows the J_AB values obtained with these active spaces for all unique radical pairs identified in the PhBBO crystal. Notice that, as suggested in the literature,^7b our calculations corroborate that crystals of PhBBO present FM interactions, as also the other members of the XBBO oxobenzo-bridged bisdithiazolyl family do,^7–11 and become a proof of concept that DFT can dramatically fail to evaluate J_AB magnetic interactions between purely organic radical XBBO pairs.

Table 4 Mulliken spin densities of the two non-equivalent N atoms of Dimer1 and Pdimer1 in their triplet state, and magnetic exchange couplings obtained when using different active spaces

Pair	Basis	Active space	J AB/cm^−1	Spin density
				N1	N2
Dimer1	DZV	CASSCF(2,2)	−101.2	0.51	0.00
		CASSCF(6,6)	−25.1	0.42	0.01
		CASSCF(10,10)	24.5	0.37	0.06
		CASSCF(14,14)	34.6	0.30	0.15
		RASSCF(14,2,2;6,2,6)	36.4	0.30	0.07
		RASSCF(38,2,2;18,2,6)	44.6	0.29	0.06
		RASSCF(38,2,2;16,6,4)	49.7	0.29	0.15
	TZV	CASSCF(14,14)	36.4	0.30	0.15
		RASSCF(38,2,2;18,2,6)	43.1	0.29	0.06
Pdimer1	DZV	CASSCF(2,2)	−0.5	0.50	0.00
		CASSCF(14,14)	−0.2	0.29	0.17
		RASSCF(38,2,2;18,2,6)	−0.4	0.27	0.07
		RASSCF(38,2,2;16,6,4)	−0.3	0.29	0.15
	TZV	RASSCF(38,2,2;18,2,6)	−0.5	0.27	0.07

---

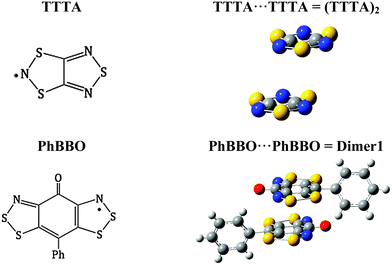
The B3LYP failure was then reviewed from a WFT perspective by comparing the TTTA (1,3,5-trithia-2,4,6-triazapentalenyl) and PhBBO crystals (see Fig. 5). TTTA has been recently shown to be well described at the B3LYP level.^28a Specifically, the high temperature phase of TTTA has a π-stacked pair of radicals whose J_AB value is −143 cm⁻¹ at the B3LYP/6-311++g(d,p) level (see Table 5 for (TTTA)₂). According to Table 5, for the TTTA pair, the WFT based methods require the inclusion of all π-orbitals in the active space as well as dynamic correlation to describe properly the magnetic interaction (J_AB = −162 cm⁻¹ at the CASPT2 level). Notice that this value is in agreement with the result obtained at the B3LYP level, and with the value of −135 cm⁻¹ previously reported at the DDCI level.^37,38 For Dimer1, we have already discussed that, although it is also required to include all π-orbitals in the active space (RASSCF-1), dynamic correlation (RASPT2) hardly affects the resulting J_AB value. However, in the current case, for Dimer1 there is no agreement between J_AB values computed at DFT and WFT levels. The reason for B3LYP performing correctly for the TTTA radical and (TTTA)₂ but not for the PhBBO radical and Dimer1 is, basically, that the latter two show a larger multireference character than the TTTA counterparts (see ESI,† Section S4, for natural molecular orbitals and occupation numbers). Referring to Dimer1, the occupation numbers different from 2.0 vary from 1.83 to 1.94 for doubly occupied natural molecular orbitals and, consequently, they range from 0.18 to 0.06 for virtual natural molecular orbitals. Contrarily, for (TTTA)₂, doubly occupied natural molecular orbitals have occupation numbers (other than 2.0) ranging from 1.90 to 1.94. This means that (TTTA)₂ can be adequately described using a monoreference method, such as DFT, while one has to resort to multireference methods for Dimer1, such as CASSCF and RASSCF. Indeed, this computational evidence is acknowledged in the literature as the multi-orbital effect by experimentalists themselves.^1b,c Analogous to the TTTA dimer, the exchange coupling between N-alkylated (pyridine/pyrazine)-bridged bisdithiazolyl pairs of radicals (see Fig. 1a and b) can be evaluated using DFT-based methods since there is no multi-orbital effect involved. Indeed TTTA and N-alkylated (pyridine/pyrazine)-bridged bisdithiazolyl radicals typify conventional single orbital radicals.^1c Once more it is obvious that DFT-based methods must be used with care depending on the features of the studied system since they might be of no validity^7b,c,10 even for purely organic magnets and lead to misinterpretations.

Fig. 5 Scheme of TTTA and PhBBO radicals, and molecular structures of their π-dimers.

Table 5 Magnetic exchange coupling J_AB (in cm⁻¹) computed with B3LYP/6-311++g(d,p), and CASSCF (CASPT2) and RASSCF-1 (RASPT2) methods using DZV contraction of the ANO-RCC basis set, for TTTA₂ and Dimer1

System	Method	J AB	System	Method	J AB
(TTTA)2	B3LYP	−143.0	Dimer1	B3LYP	+343.0
	CASSCF(2,2)	−4.0		CASSCF(2,2)	−101.2
	CASSCF(22,16)	−17.1		CASSCF(14,14)	+34.6
	CAS(22,16)/PT2	−162.0		RASSCF-1	+44.6
				RASPT2	+48.7

---

Magnetic susceptibility χT(T) and magnetization M(H) simulations of the PhBBO crystal

The computed J_AB magnetic interactions (see Table 1 for J_AB values) show that at room temperature the magnetic topology is three-dimensional (3D), and consists of FM π-stacks that are very weakly coupled (both FM and AFM). We have corroborated that there are FM interactions within π-stacks (Dimer1), as suggested experimentally based on the fitting Baker model (+29.5 cm⁻¹). One can safely say that the head-over-tail π-stacking of PhBBO radicals found in the crystal is responsible for remarkably strong FM interactions along the π-stacks. The main magnetic motif is thus 1D, but there are small AFM (Pdimer1) as well as FM (Pdimer2 & Pdimer6) interactions between π-stacks (see Table 1 for J_AB values). Here we must stress the fact that FM interactions between π-stacks were experimentally not anticipated, since the fitted cumulative inter-stack (mean field) parameter was negative (−2.5 cm⁻¹). Therefore, our results suggest that PhBBO cannot be merely viewed as a spin-canted AFM (SC-AFM) state as proposed experimentally, since the inter-stack interactions are not only AFM in nature. However, the schematic and simplest picture of the α and β spin distribution that emerges from our RASSCF-1 computed magnetic topology (see Fig. 6 and ESI,† Section S5, for full discussion on the choice of J^RASSCF-1_AB values) shows an overall antiparallel alignment of FM chains. This is why it appears to be in a SC-AFM state. From Fig. 6, one realizes that the magnetic topology at room temperature introduces certain small degree of geometrical spin frustration between the radicals connected by Pdimer2 (+0.1 cm⁻¹), which tend to ferromagnetically couple the FM π-stacks (+44.6 cm⁻¹, Dimer1) of the PhBBO crystal, otherwise antiferromagnetically coupled by Pdimer1 (−0.4 cm⁻¹).

Fig. 6 Schematic representation of the magnetic topology at room temperature obtained for the PhBBO crystal at the RASSCF-1 level. Color code for the significant J_AB magnetic coupling: Dimer1 (dark blue, FM), Pdimer1 (orange, AFM), and Pdimer2 (green, FM). The arrows represent the spin propagation according to the J_AB magnetic interaction values to provide a schematic picture of the α and β spin distribution.

In order to explore the dimensionality required by the magnetic model for simulation purposes, a series of χT(T) calculations were performed using the J_AB interactions at the RASSCF-1 level (Fig. 7). The inter-column magnetic interactions were studied using two distinct models: 2 × 4 and 4 × 4 models (see Fig. 7a). It is clear that the χT(T) calculated data are well converged using 2 columns, i.e. the 2 × 4 model (Fig. 7c), since the simulated χT(T) data using either a 2 × 4 or a 4 × 4 model practically overlap. Also, different models were used to check the dependency of the χT(T) calculated data on the magnetic model as it is enlarged along the π-stacking direction (namely, 2 × 4, 2 × 6 and 2 × 8 models in Fig. 7b). According to Fig. 7c, we can conclude that the magnetic interactions along the π-stacking direction are reasonably well described at the 2 × 8 level, i.e. using 16 PhBBO radicals. Indeed, we have confirmed that even at low temperatures the computed χ(T) data agree reasonably well with the available experimental χ(T) data (see ESI,† Section S6). Due to the full diagonalization code we use, we are limited to models up to N = 18 S = ½ radical centers for computer efficiency, the memory required being N!/[(N/2)!(N/2)!]. Although a larger model will reproduce better the numerical χT(T) values, the 2 × 8 model is our best option. Therefore, from this point on, the 2 × 8 magnetic model will be used in all simulations.

Fig. 7 Representation in the (a) bc- and (b) ac-planes of the magnetic exchange models employed in the computation of the χT vs. T curves shown in (c) at an applied field of 1 kOe. The experimental data are also given for comparison purposes.

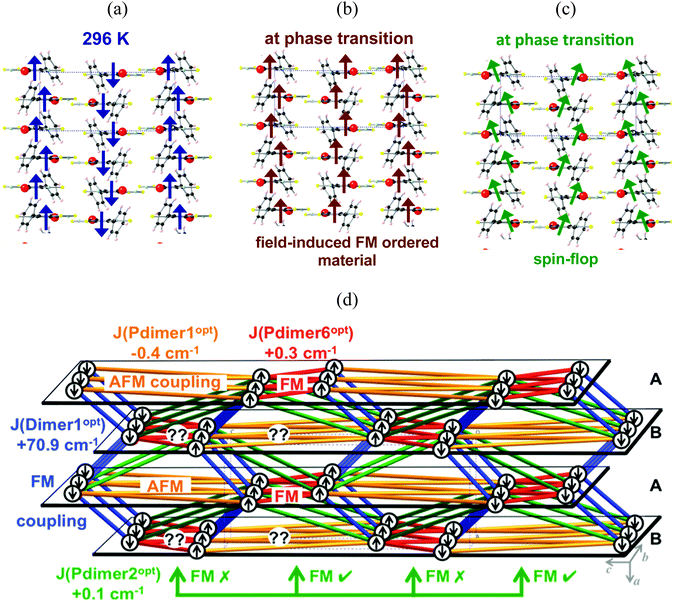
Let us now focus on the phase transition that the PhBBO crystal undergoes at 4.5 K. It was first suggested that, after the phase transition, crystals of PhBBO show metamagnetism,¹¹ which means that the antiparallel alignment of FM ordered π-stacks could be reversed by the field and, in turn, all chains would become aligned in a parallel fashion (see Fig. 8a and b for a schematic representation; notice that Fig. 8a shows a scheme of the ground spin state of Fig. 6). For a metamagnet to be detected, the magnetization as a function of the magnetic field M(H) must show an inflexion, with dM/dH(H) reaching a maximum value at the field at which the magnetic realignment occurs. Nevertheless, experimentally, no inflexion was observed in M(H), nor was any maximum in dM/dH as a function of H prior to saturation, even at T = 2 K. Thus, metamagnetism was ruled out. The available M(H), dM/dH(H) and ZFC–FC data established that AFM ordering collapses above H = 200 Oe. Accordingly, Oakley and coworkers indicated that this behavior was more consistent with a spin–flop transition (see Fig. 8a and c for a schematic representation).

Fig. 8 (a) Schematic representation of the ground spin state obtained using the 296 K PhBBO crystal structure at the RASSCF-1 level. Schematic representation of metamagnetism: (a) to (b); and of a spin–flop transition: (a) to (c). (d) Schematic representation of the magnetic topology obtained using the 0 K PhBBO crystal structure at the RASSCF-1 level. The arrows represent the spin propagation according to the J_AB magnetic interaction values to provide a schematic picture of the α and β spin distribution. Color code for the interactions: Dimer1 (dark blue, FM), Pdimer1 (orange, AFM), Pdimer2 (green, FM), and Pdimer6 (red, FM).

In order to see which is the picture that works out better with the experimental data at the phase transition (4.5 K), we performed the optimization of the PhBBO crystal at zero Kelvin (0 K). Therefore, we will be able to discuss about the effect of the unit cell contraction upon cooling (from room temperature, RT, to 0 K). We performed variable-cell geometry optimization using periodic boundary conditions at the PBE-D2 level^22,24 (see computational details for further discussion). Notice that, although DFT is not capable of calculating the J_AB value for certain PhBBO radical pairs, it is the most sensible choice to undertake geometry optimizations, as already proved in the literature.^7b,25,28b,c The unit cell parameters slightly contract upon cooling from room temperature (X-ray data at 296 K for an orthorhombic space group P2₁2₁2₁: a = 6.801(1) Å, b = 11.378(5) Å, c = 15.625(2) Å) to zero Kelvin (optimized data at 0 K: a = 6.610(1) Å, b = 11.267(5) Å, c = 15.421(1) Å) (see ESI,† Section S2). Despite the small unit cell contraction observed upon cooling, the effect on the J_AB magnetic interactions is clear. Table 6 shows the J_AB values that have been re-evaluated on the optimized nuclear coordinates by means of RASSCF-1/DZV. Notice that the J_AB magnetic coupling for Dimer1 varies from +44.6 cm⁻¹ at room temperature to +70.9 cm⁻¹ at zero Kelvin. Dimer1 is thus another clear example that J_AB can strongly depend on small changes in the interplanar distance between adjacent radicals within a π-stack.^28c Whereas the J_AB magnetic interaction of Pdimer1 and Pdimer2 appears to be invariant upon cell contraction, the J_AB of Pdimer6 is now comparable in absolute value to the magnitude of Pdimer1. It must be stressed that changes in the magnetic properties between radicals, here obtained upon cooling, can also be achieved by means of applying pressure, as has already been reported in the literature.^1c,39 Accordingly, the resulting magnetic topology at 0 K (Fig. 8d) differs significantly from the magnetic topology obtained at room temperature (Fig. 6). An analysis of the spin propagation according to the J_AB values has been performed to provide a schematic and very simplistic picture of the α and β spin distribution at 0 K. Given a PhBBO radical in an A (bc-) layer, its coplanar neighboring radicals are oriented according to the AFM J(Pdimer1^opt) and the FM J(Pdimer6^opt) interactions. The first neighboring B (bc-) layer shows a large amount of geometrical spin frustration since it cannot satisfy either the AFM connection via Pdimer1^opt or the FM connection via Pdimer6^opt. In contrast, the second neighboring A (bc-) layer will again behave accordingly to AFM J(Pdimer1^opt) and FM J(Pdimer6^opt). Notice that an equivalent interpretation follows if a given PhBBO radical from a B (bc-) layer is taken as a reference. Regarding Pdimer2^opt (+0.1 cm⁻¹) at 0 K, it introduces half of the geometrical spin frustration in comparison to that introduced at room temperature. It thus follows that, at the phase transition, the antiparallel-aligned 1D FM chains (Fig. 8a) convert into domains of weakly either FM- or AFM-coupled 1D FM chains (Fig. 8d).

Table 6 Magnetic exchange couplings J_AB (in cm⁻¹) calculated for the seven pairs of radicals in the optimized 0 K crystal structure. The calculations were performed using RASSCF-1 active space (see main text for definition), and the DZV contraction of ANO-RCC basis set. The O⋯O distance (in Å) between each pair of radicals is also indicated

Pair	O⋯O dist	J AB	Pair	O⋯O dist	J AB
Dimer1^opt	6.089	70.9	Pdimer4^opt	8.545	0.0
Pdimer1^opt	12.543	−0.4	Pdimer5^opt	8.649	0.0
Pdimer2^opt	12.542	0.1	Pdimer6^opt	7.036	0.3
Pdimer3^opt	12.612	0.0

---

Let us remind here that, experimentally, no inflexion was observed in M(H), nor was any maximum in dM/dH as a function of H prior to saturation. In fact, at 5 K and more clearly at 2 K, dM/dH(H) showed a minimum at zero applied field that rapidly led to a maximum value at ±10 kOe and ±20 kOe, respectively (see experimental M(H) and dM/dH(H) data in Yu et al.¹¹). Thus, in order to get a deeper insight into the phase transition that experimentally occurs at 4.5 K, M(H) simulations were performed (Fig. 9). The 2 × 8 magnetic model was used together with both X-ray (296 K) and optimized (0 K) J_AB values at the RASSCF-1 level. The magnetization M(H) simulated curves at 2, 5 and 10 K show in all cases a similar shape in comparison to experiment. Note that simulated and experimental M(H) absolute values differ since we are using a finite magnetic model. However, it is dM/dH(H) that can enable us to univocally assign the true nature of the magnetism of the PhBBO purely organic crystal. Fig. 9a and b shows that the set of J_AB magnetic couplings between PhBBO radicals calculated either from X-ray data or using the optimized crystal structure at 0 K cannot produce simulated dM/dH(H) data in agreement with experiment at 2 K and 5 K. The reason for this behavior is that they both share the same energy spectra and, in turn, produce a similar shape of M(H) and dM/dH(H) (see ESI,† Section S7, for details on the energy spectra). For the phase transition to occur, our study reveals that it is required that the AFM J^{inter-π-stack} interactions have an absolute value within the range 10% to 5% of J^π-stack, with J^π-stack being either J^{X-ray,296 K} (+44.6 cm⁻¹) or J^opt,0 K (+70.9 cm⁻¹). According to our microscopic study, the J^{inter-π-stack} estimated value would reasonably agree with the experimentally suggested mean field parameter (−2.5 cm⁻¹). Indeed, we must stress that this cumulative inter-stack fitting value can be interpreted and assigned from first-principles. Thanks to these larger AFM J^{inter-π-stack} interactions, the new energy spectrum has no degenerate lower lying energy states, i.e. it becomes an incommensurate system, which translates into a dM/dH(H) shape in agreement with experimental data (see Fig. 9c and d, and discussion in ESI,† Section S7). Apparently our calculations underestimate the inter-π-stack AFM coupling. The value of J^{inter-π-stack} is rather small compared to the value of the intra-π-stack J_AB interaction. Therefore, the quantitative evaluation of J^{inter-π-stack} might require the inclusion of the electron correlation between the π and σ subspaces (note that the RASSCF-1 space includes only the electron correlation of the π-space). In that case, the DDCI method would be more appropriate as it can consider a larger orbital space to provide highly accurate values for the singlet/triplet energy splitting.^37,38 The resulting J_AB interactions might lead to a better agreement when simulating the dM/dH(H) maximum value. However, these calculations were not performed in this study since they would imply a remarkably large computational effort that will not provide new or different insights into the physical properties of the PhBBO system.

Fig. 9 Simulated dM/dH(H) and M(H) curves obtained using the 2 × 8 magnetic model together with both (a) X-ray (296 K) and (b) optimized (0 K) J_AB values at the RASSCF-1 level, as well as modifying the interstack AFM coupling to a J^{inter-π-stack} = −4.0 cm⁻¹ value in both cases (c and d) respectively.

Conclusions

The π-stacking motif of crystals of purely organic PhBBO at room temperature entails a 3D magnetic topology of FM chains weakly knit together through both FM and AFM couplings, thus resulting in an overall antiparallel alignment of FM 1D π-stacked chains. Therefore, our results suggest that PhBBO cannot be merely viewed as a spin-canted AFM (SC-AFM) state as proposed experimentally,¹¹ since the inter-stack interactions are not only AFM in nature. Upon cooling from room temperature to zero Kelvin, our calculations uncover that there is an enhancement of π-stack and inter-π-stack FM interactions. At the phase transition (4.5 K), a suitable model tells us that there are domains of weakly either FM- or AFM-coupled 1D FM chains. As a result, there is a significant competition between FM chains aligning parallel (FM coupling) or antiparallel (AFM coupling) to each other. This inter-chain coupling competition clearly may lead to a certain degree of geometrical spin frustration upon phase transition at 4.5 K.

A comparison with available experimental magnetic susceptibility data has shown that, for simulation purposes, the inter-π-stack magnetic interactions must be taken into account to adequately calculate the magnetic susceptibility χT(T) and χ(T) data. Besides, in order to reproduce the experimental magnetization M(H) and dM/dH(H) data, our study discloses that the inter-π-stack AFM interactions that couple the FM π-chains should be stronger than those computed in the present study. According to our results, the magnitude of J^{inter-π-stack} should be (in absolute value) as large as 5–10% J^π-stack magnetic coupling.

DFT dramatically fails to calculate the magnetic coupling between purely organic PhBBO radicals. Instead one has to resort to wavefunction-based methods, such as CASSCF and RASSCF. Unlike inorganic molecule-based magnets,³² to our knowledge, this is the first time we encounter that the magnetic coupling between purely organic S = ½ radicals cannot be evaluated by means of DFT-based methods. An exhaustive computational study reveals that the reason behind the DFT failure turns out to be remarkably simple. Purely organic semiquinone-bridged bisdithiazolyl XBBO magnets are multireference systems due to the presence of low-lying open-shell states, unlike other bisdithiazolyl-based systems.^{28,29c,30,34b} This fact is indeed acknowledged in the literature as the multi-orbital effect.^1b,c It is then a must to use DFT with extreme care depending on the features of the studied system since it might be of no validity and lead to misconceptions. As a proof of concept, these limitations are illustrated for the phenyl-substituted semiquinone-bridged bisdithiazolyl PhBBO material.¹¹ We do believe that this conclusion transcends the specific material studied in this work, and is of general validity for the whole family of semiquinone-bridged bisdithiazolyl XBBO functional organic materials.^{1a,7b,c,8–10}

Acknowledgements

The authors thank the Spanish Government for financial support (projects MAT2011-25972 and MAT2014-54025-P), Universitat de Barcelona for a PhD grant to M. F., the Catalan DURSI (2009-SGR-1203 and 2014-SGR-1422) and CESCA and BSC for the allocated computer time. We also acknowledge Prof. Nicolas Ferré and Dr Michael Filatov for fruitful discussions.

References

1. (a) X. Yu, A. Mailman, K. Lekin, A. Assoud, C. M. Robertson, B. C. Noll, C. F. Campana, J. A. K. Howard, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2012, 134, 2264; (b) S. M. Winter, S. Hill and R. T. Oakley, J. Am. Chem. Soc., 2015, 137, 3720; (c) D. Tian, S. M. Winter, A. Mailman, J. W. L. Wong, W. Yong, H. Yamaguchi, Y. Jia, J. S. Tse, S. Desgreniers, R. A. Secco, S. R. Julian, C. Jin, M. Mito, Y. Ohishi and R. T. Oakley, J. Am. Chem. Soc., 2015, 137, 14136.
2. L. Beer, J. L. Brusso, A. W. Cordes, R. C. Haddon, M. E. Itkis, K. Kirschbaum, D. S. MacGregor, R. T. Oakley, A. A. Pinkerton and R. W. Reed, J. Am. Chem. Soc., 2002, 124, 9498.
3. A. W. Cordes, R. C. Haddon, C. D. MacKinnon, R. T. Oakley, G. W. Patenaude, R. W. Reed, T. Rietveld and K. E. Vajda, Inorg. Chem., 1996, 35, 7626.
4. (a) A. A. Leitch, R. W. Reed, C. M. Robertson, J. F. Britten, X. Yu, R. A. Secco and R. T. Oakley, J. Am. Chem. Soc., 2007, 129, 7903; (b) A. A. Leitch, C. E. McKenzie, R. T. Oakley, R. W. Reed, J. F. Richardson and L. D. Sawyer, Chem. Commun., 2006, 1088.
5. (a) C. M. Robertson, D. J. T. Myles, A. A. Leitch, R. W. Reed, B. M. Dooley, N. L. Frank, P. A. Dube, L. K. Thompson and R. T. Oakley, J. Am. Chem. Soc., 2007, 129, 12688; (b) C. M. Robertson, A. A. Leitch, K. Cvrkalj, R. W. Reed, D. J. T. Myles, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2008, 130, 8414; (c) A. A. Leitch, J. L. Brusso, K. Cvrkalj, R. W. Reed, C. M. Robertson, P. A. Dube and R. T. Oakley, Chem. Commun., 2007, 3368; (d) S. M. Winter, K. Cvrkalj, C. M. Robertson, M. R. Probert, P. A. Dube, J. A. K. Howard and R. T. Oakley, Chem. Commun., 2009, 7306.
6. R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1982, 21, 711.
7. (a) J. W. L. Wong, A. Mailman, K. Lekin, S. M. Winter, W. Yong, J. Zhao, S. V. Garimella, J. S. Tse, R. A. Secco, S. Desgreniers, Y. Ohishi, F. Borondics and R. T. Oakley, J. Am. Chem. Soc., 2014, 136, 1070; (b) S. M. Winter, A. Mailman, R. T. Oakley, K. Thirunavukkuarasu, S. Hill, D. E. Graf, S. W. Tozer, J. S. Tse, M. Mito and H. Yamaguchi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214403; (c) A. Mailman, S. M. Winter, J. W. L. Wong, C. M. Robertson, A. Assoud, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2015, 137, 1044.
8. J. W. L. Wong, A. Mailman, S. M. Winter, C. M. Robertson, R. J. Holmberg, M. Murugesu, P. A. Dube and R. T. Oakley, Chem. Commun., 2014, 50, 785.
9. A. Mailman, S. M. Winter, X. Yu, C. M. Robertson, W. Yong, J. S. Tse, R. A. Secco, Z. Liu, P. A. Dube, J. A. K. Howard and R. T. Oakley, J. Am. Chem. Soc., 2012, 134, 9886.
10. X. Yu, A. Mailman, K. Lekin, A. Assoud, P. A. Dube and R. T. Oakley, Cryst. Growth Des., 2012, 12, 2485.
11. X. Yu, A. Mailman, P. A. Dube, A. Assouda and R. T. Oakley, Chem. Commun., 2011, 47, 4655.
12. M. Deumal, M. J. Bearpark, J. J. Novoa and M. A. Robb, J. Phys. Chem. A, 2002, 106, 1299.
13. (a) L. Noodleman, J. Chem. Phys., 1981, 74, 5737; (b) L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131.
14. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
15. F. Neese, ORCA- An ab initio, Density Functional and Semiempirical Program Package, Version 3.0, Max Planck Institute for Bioinorganic Chamistry, Müllheim, 2012.
16. P.-A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477.
17. F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P.-A. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224.
18. (a) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639; (b) K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
19. (a) P.-O. Widmark, P.-A. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291; (b) B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851.
20. H. Koch, A. Sanchez de Meras and T. B. Pedersen, J. Chem. Phys., 2003, 118, 9481.
21. G. Ghigo, B. O. Roos and P.-O. Malmqvist, Chem. Phys. Lett., 2004, 396, 142.
22. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
23. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
24. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
25. T. Bucko, J. Hafner, S. Lebègue and J. Ángyán, J. Phys. Chem. A, 2010, 114, 11814.
26. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 , quantum ESPRESSO v. 4.2.1.
27. (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
28. (a) C. S. Clarke, J. Jornet-Somoza, F. Mota, J. J. Novoa and M. Deumal, J. Am. Chem. Soc., 2010, 132, 17817–17830; (b) S. Vela, F. Mota, M. Deumal, R. Suizu, Y. Shuku, A. Mizuno, K. Awaga, M. Shiga, J. J. Novoa and J. Ribas-Arino, Nat. Commun., 2014, 5, 4411; (c) S. Vela, M. Deumal, M. Shiga, J. J. Novoa and J. Ribas-Arino, Chem. Sci., 2015, 6, 2371.
29. (a) M. Fumanal, S. Vela, J. J. Novoa and J. Ribas-Arino, Chem. Commun., 2015, 51, 15776; (b) M. Fumanal, F. Mota, J. J. Novoa and J. Ribas-Arino, J. Am. Chem. Soc., 2015, 137, 12843; (c) M. Deumal, J. M. Rawson, A. E. Goeta, J. A. K. Howard, R. C. B. Copley, M. A. Robb and J. J. Novoa, Chem. – Eur. J., 2010, 16, 2741; (d) J. Jornet, M. Deumal, J. Ribas-Arino, M. J. Bearpark, M. A. Robb, R. G. Hicks and J. J. Novoa, Chem. – Eur. J., 2006, 12, 3995; (e) M. Deumal, M. J. Bearpark, M. A. Robb, Y. Pontillon and J. J. Novoa, Chem. – Eur. J., 2004, 10, 6422.
30. (a) A. A. Leitch, X. Yu, S. M. Winter, R. A. Secco, P. A. Dube and R. T. Oakley, J. Am. Chem. Soc., 2009, 131, 7112; (b) K. Lekin, J. W. L. Wong, S. M. Winter, A. Mailman, P. A. Dube and R. T. Oakley, Inorg. Chem., 2013, 52, 2188.
31. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51.
32. (a) F. Neese, JBIC, J. Biol. Inorg. Chem., 2006, 11, 702–711; (b) A. Ghosh and P. R. Taylor, J. Chem. Theory Comput., 2005, 1, 597–600.
33. N. Suaud, R. Ruamps, J.-P. Malrieu and N. Guihéry, J. Phys. Chem. A, 2014, 118, 5876.
34. (a) S. Vela, M. Fumanal and M. Deumal, Dalton Trans., 2015, 44, 608; (b) S. Vela, A. Sopena, J. Ribas-Arino, J. J. Novoa and M. Deumal, Chem. – Eur. J., 2014, 20, 7083.
35. S. Vela, J. Jornet-Somoza, M. M. Turnbull, R. Feyerherm, J. J. Novoa and M. Deumal, Inorg. Chem., 2013, 52, 12923.
36. (a) S. N. Herringer, M. Deumal, J. Ribas-Arino, J. J. Novoa, C. P. Landee, J. L. Wikaira and M. M. Turnbull, Chem. – Eur. J., 2014, 20, 8355; (b) J. Jornet-Somoza, N. Codina-Castillo, M. Deumal, F. Mota, J. J. Novoa, R. T. Butcher, M. M. Turnbull, B. Keith, C. P. Landee and J. L. Wikaira, Inorg. Chem., 2012, 51, 6315; (c) J. Jornet-Somoza, M. Deumal, M. A. Robb, C. P. Landee, M. M. Turnbull, R. Feyerherm and J. J. Novoa, Inorg. Chem., 2010, 49, 1750.
37. (a) J. Miralles, J. P. Daudey and R. Caballol, Chem. Phys. Lett., 1992, 198, 555; (b) J. Miralles, O. Castell, R. Caballol and J. P. Malrieu, Chem. Phys., 1993, 172, 33.
38. (a) M. Fumanal, S. Vela, J. Ribas-Ariño and J. J. Novoa, Chem. – Asian J., 2014, 9, 3612; (b) A. Domingo, M. Vérot, F. Mota, C. de Graaf, J. J. Novoa and V. Robert, Phys. Chem. Chem. Phys., 2013, 15, 6982; (c) N. Suaud, R. Ruamps, N. Guihéry and J.-P. Malrieu, J. Chem. Theory Comput., 2012, 8, 4127; (d) N. A. G. Bandeira, D. Maynau, V. Robert and B. Le Guennic, Inorg. Chem., 2013, 52, 7980; (e) J. Jung, B. Le Guennic, M. V. Fedin, V. I. Ovcharenko and C. J. Calzado, Inorg. Chem., 2015, 54, 6891; (f) M. Vérot, J.-B. Rota, M. Kepenekian, B. Le Guennic and V. Robert, Phys. Chem. Chem. Phys., 2011, 13, 6657.
39. A. A. Leitch, K. Lekin, S. M. Winter, L. E. Downie, H. Tsuruda, J. S. Tse, M. Mito, S. Desgreniers, P. A. Dube, S. Zhang, Q. Liu, C. Jin, Y. Ohishi and R. T. Oakley, J. Am. Chem. Soc., 2011, 133, 6051.

---

Footnote

† Electronic supplementary information (ESI) available: (1) CASSCF and RASSCF-1,2 active orbitals and occupation numbers; (2) unit cell contraction upon cooling from 296 K to 0 K; (3) tetramer cluster model calculations; (4) a comparison between (TTTA)₂ and Dimer1 radical pairs; (5) χT(T) comparison using DFT and WFT-based simulations; (6) χ(T) simulation at low temperatures; and (7) energy spectra using 296 K X-ray and 0 K optimized PhBBO crystals. See DOI: 10.1039/c6cp02699k

---