 Open Access Article
Open Access ArticleMetal ion–humic acid nanoparticle interactions: role of both complexation and condensation mechanisms†
Raewyn M.
Town
*a and
Herman P.
van Leeuwen
b
aDepartment of Physics, Chemistry and Pharmacy, University of Southern Denmark, Campusvej 55, 5230 Odense, Denmark. E-mail: raewyn.town@sdu.dk
bPhysical Chemistry and Soft Matter, Wageningen University & Research, Stippeneng 4, 6708 WE Wageningen, The Netherlands
First published on 13th June 2016
Abstract
Purely Donnan type models for electrostatic binding by humic acid (HA) nanoparticles are shown to be physically incomplete. To describe the extent of ion binding by HA, such models need to invoke parameters that are not consistent with experimental observations. These disparate parameters include anomalously high Donnan potentials, as well as intrinsic affinity constants for electrostatically associating ions such as Ca2+. In contrast, the recently introduced counterion condensation – Donnan model (CCD) provides a physicochemically realistic description of the electrostatic contribution to metal ion binding by humic acid nanoparticles. The extent of Ca2+–HA association can be adequately described solely in terms of electrostatics only, including counterion condensation in the intraparticulate double layer in addition to Donnan partitioning in the remainder of the particle body. The binding of Cd(II), Pb, (II) and Cu(II) by HA also involves inner-sphere complex formation leading to intraparticulate metal species distributions with major proportions of condensed and complexed ions.
1 Introduction
Humic acids (HA) are ubiquitous in soils and natural waters and form an important complexant for a wide range of ions and small molecules.1 Accordingly, there is a wealth of literature on the measurement and modelling of its physicochemical association properties.1–3 Aqueous HA can be considered to be composed of soft nanoparticles (NP) that carry a net negative charge at ambient pH.4,5 Indeed, the large number of ionisable functional groups generate a significant particle electric field, which in itself can influence the dynamics and extent of its interactions with oppositely charged ions, Mz+.6 Rigorous interpretation of physicochemical M–HA interactions must therefore take proper account of electrostatic interactions as well as intrinsic chemical contributions to the binding.Conventionally, M–HA complex formation is described in terms of apparent stability constants, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app, that are defined in terms of concentrations of chemical species that are averaged over the entire volume of the solution/dispersion. Furthermore, so-called ‘bound’ M is collectively taken as all forms of M that are associated with the HA entity, including intraparticulate free M and even the excess free M in the extraparticulate interfacial double layer. At this level, various equilibrium models for metal ion speciation have been developed, e.g. the NICA-Donnan2 and WHAM3 models. Generally the electrostatic contribution to Mz+ binding by HA is modeled by assuming Donnan-type partitioning into the HA body or Boltzmann-type accumulation in the extraparticulate zone.3,7–12 The relevant physicochemical parameters then are the effective Donnan volume and the charge density of the HA particle. The various affinities of the functional Mz+ binding sites are modeled either by a number of different types of discrete sites, e.g. WHAM,3 or by a continuous distribution of site affinities, e.g. NICA-Donnan.2 Evidently the meaning of
app, that are defined in terms of concentrations of chemical species that are averaged over the entire volume of the solution/dispersion. Furthermore, so-called ‘bound’ M is collectively taken as all forms of M that are associated with the HA entity, including intraparticulate free M and even the excess free M in the extraparticulate interfacial double layer. At this level, various equilibrium models for metal ion speciation have been developed, e.g. the NICA-Donnan2 and WHAM3 models. Generally the electrostatic contribution to Mz+ binding by HA is modeled by assuming Donnan-type partitioning into the HA body or Boltzmann-type accumulation in the extraparticulate zone.3,7–12 The relevant physicochemical parameters then are the effective Donnan volume and the charge density of the HA particle. The various affinities of the functional Mz+ binding sites are modeled either by a number of different types of discrete sites, e.g. WHAM,3 or by a continuous distribution of site affinities, e.g. NICA-Donnan.2 Evidently the meaning of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app values is not transparent for the case of nanoparticulate complexants in which binding sites are confined to the particle body within which the local conditions are significantly different from those in the bulk aqueous medium. For example,
app values is not transparent for the case of nanoparticulate complexants in which binding sites are confined to the particle body within which the local conditions are significantly different from those in the bulk aqueous medium. For example, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app values increase as the ionic strength of the bulk aqueous medium decreases.13,14 This observation is not due to a significant change in the intrinsic chemical affinity, but rather is a consequence of the greater free M concentration within the HA entity at lower ionic strength. Obviously, a more rigorous description of M–HA complex formation requires detailed knowledge of both electrostatic and intrinsic chemical affinity contributions to the binding and the ensuing consequences for the detailed metal ion speciation inside the HA particle entity.
app values increase as the ionic strength of the bulk aqueous medium decreases.13,14 This observation is not due to a significant change in the intrinsic chemical affinity, but rather is a consequence of the greater free M concentration within the HA entity at lower ionic strength. Obviously, a more rigorous description of M–HA complex formation requires detailed knowledge of both electrostatic and intrinsic chemical affinity contributions to the binding and the ensuing consequences for the detailed metal ion speciation inside the HA particle entity.
Recently the nature of electrostatic binding by HA has been reconsidered.15 The typically high structural charge densities, that prevail within the particle body at ambient pH, invoke cooperative electrostatics effects such as counterion condensation, which features a large preference for the higher valency cations. Such phenomena have been described in detail by Manning for linear polyelectrolytes,16,17 and refer to the tendency of the polyion to condense counterions in its immediate vicinity if the structural charge density is beyond certain limiting values. Counterion condensation is applicable to polyions of any geometry with sufficient charge density, e.g. it has been reported for polyelectrolytes such as DNA,16 soft nanoparticles such as dendrimers,18–20 as well as core–shell NPs with a 3D structural charge in the shell.21 We have observed that counterion condensation in the 3D site distribution structure occurs at charge separations greater than for the 1D case.15 For HA, conductivity data have shown that divalent ions such as Ca2+ and Ba2+ exhibit condensation behavior, whilst monovalent ions do not.22 Notably, it was shown that the extent of electrostatic association of Ca2+ with HA cannot be explained by Donnan-partitioning alone. The CCD model therefore combines counterion condensation in the intraparticulate double layer with Donnan partitioning in the remainder of the particle body. It well describes the extent to which Ca2+ associates with a range of HA samples with different particle sizes at various ionic strengths.15 It has also been applied to the intraparticulate speciation analysis of complexes that involve covalency, i.e. those of Cd(II), Pb(II), and Cu(II).23 Three types of intraparticulate metal species then are distinguished, namely free hydrated ions, electrostatically condensed ions, and inner-sphere complexes. Here we compare the CCD description of M–HA interactions with the results generated by equilibrium speciation models that consider Donnan-type partitioning to be the only electrostatic contribution to the binding. We explore the nature of the fundamental parameters that are relevant for defining the extent of complexation, e.g. the effective Donnan volume and the applicable charge density, and assess the outcomes in terms of the physical consistency.
2 Theory
The equilibrium relationship between the concentrations of the metal ion and the various binding sites of the chemically heterogeneous HA complexant is described by a distributed affinity. The apparent stability constants![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app for the complexes are expressed in terms of smeared-out concentrations and include both electrostatic and intrinsic chemical contributions to the binding between a metal ion M and a reactive site, S. The magnitude of
app for the complexes are expressed in terms of smeared-out concentrations and include both electrostatic and intrinsic chemical contributions to the binding between a metal ion M and a reactive site, S. The magnitude of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app depends on the degree of occupation, θM, of the binding sites by M.1 We define θM as the ratio between the concentrations of inner-sphere metal complexes, MS, and reactive sites, i.e.
app depends on the degree of occupation, θM, of the binding sites by M.1 We define θM as the ratio between the concentrations of inner-sphere metal complexes, MS, and reactive sites, i.e. | (1) |
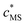 and
and 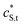 are the smeared-out counterparts.
are the smeared-out counterparts.
2.1 Intrinsic stability constants
The intrinsic stability constant Kint represents the inherent chemical affinity between M and S, not including the long-range electrostatics beyond those on the scale of atom–atom interactions. Kint values may only be obtained from Kapp after applying the appropriate correction for the electrostatic contribution to the binding. For simple ligands, the outer-sphere stability constant, Kos, represents the magnitude of the electrostatic attraction between a negatively charged reactive site and a positively charged metal ion. The extent to which the concentration of the reactant metal ions in the outer-sphere volume is enhanced relative to that in the bulk electrolyte medium, fos, can be computed on the basis of Fuoss–Boltzmann electrostatics.24,25| fos = exp(−Uos/kT) | (2) |
 | (3) |
| Kint = K/fos | (4) |
For the case of soft charged nanoparticulate complexants, the magnitude of the particle's electric field determines the extent to which oppositely charged ions electrostatically associate with the NP entity. The majority of literature for humic acids assumes that this association takes the form of Donnan partitioning into the NP body. The establishment of a Donnan phase requires that the particle radius is much greater than the intraparticulate screening length, κ−1p,33 and that the average structural charge separation, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) C, is sufficiently small so that κp
C, is sufficiently small so that κp![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) C ≪ 1, i.e. high charge density regime.5 When these conditions are met, a Donnan potential difference, ψD, is established between the bulk of the soft phase and the bulk aqueous medium:26
C ≪ 1, i.e. high charge density regime.5 When these conditions are met, a Donnan potential difference, ψD, is established between the bulk of the soft phase and the bulk aqueous medium:26
 | (5) |
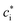 ) according to a Boltzmann factor,
) according to a Boltzmann factor, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B:27
B:27 | (6) |
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int is simply given by:
int is simply given by:![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int = int = ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app/ app/![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B B | (7) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL (with volume VDL and volume fraction φDL).15,23 The justification of a constant Donnan potential throughout the bulk core volume of the particle requires a volume fraction ratio φDL/φD much less than unity, i.e. κprp should be well above unity. In this work we focus on HA entities for which φDL/φD is less than 0.1. In the presence of counterion condensation, the distinction between
DL (with volume VDL and volume fraction φDL).15,23 The justification of a constant Donnan potential throughout the bulk core volume of the particle requires a volume fraction ratio φDL/φD much less than unity, i.e. κprp should be well above unity. In this work we focus on HA entities for which φDL/φD is less than 0.1. In the presence of counterion condensation, the distinction between ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app and
app and ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int encompasses more than the Boltzmann correction of the free metal ion (cf.eqn (7)). Rather, the intrinsic stability constant is defined in terms of intraparticulate (in situ) conditions and reactant concentrations, i.e.
int encompasses more than the Boltzmann correction of the free metal ion (cf.eqn (7)). Rather, the intrinsic stability constant is defined in terms of intraparticulate (in situ) conditions and reactant concentrations, i.e. | (8) |
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int signifies that, for the present case of a heterogeneous complexant, the intrinsic stability represents a weighted average of all the inner-sphere complexes that are formed at the applicable θM. The ensuing metal ion speciation scheme for high charge density soft NP complexants has been published previously,23 and is given in the ESI† (Table S1). We highlight that our approach makes no assumptions about the nature of the charged or reactive sites, nor about the metal binding isotherm.
int signifies that, for the present case of a heterogeneous complexant, the intrinsic stability represents a weighted average of all the inner-sphere complexes that are formed at the applicable θM. The ensuing metal ion speciation scheme for high charge density soft NP complexants has been published previously,23 and is given in the ESI† (Table S1). We highlight that our approach makes no assumptions about the nature of the charged or reactive sites, nor about the metal binding isotherm.
3 Experimental
The experimental details for the data presented herein were reported previously.23 NICA-Donnan computations were performed using Visual Minteq 3.1 and the generic HA parameters.28 The local concentrations were determined from the smeared-out concentrations that were fitted by the model in each computation, together with the generic Donnan volume. For each type of complexing ion, NICA-Donnan assumes a bimodal affinity distribution: for the present comparative purposes, the sum of the complexes with both types of sites was used to compute the proportion of inner-sphere complexes.4 Results and discussion
4.1 Electrostatic contribution to the binding
The physical size of the HA nanoparticle in aqueous dispersion is important for both the Donnan-only and the two-state CCD electrostatic models. A water content of ca. 80% has been reported for several types of HA from viscometric data at pH 7 and ionic strengths of 10 and 100 mol m−3.29 For establishment of the CCD approach, the water content of about 80% provided a consistent description of the Ca2+ association with several types of HA, including Aldrich HA, at ionic strengths of 10 and 100 mol m−3 [see ref. 15 and references therein]. This consistent water content at both ionic strengths is in line with experimental estimates of the particle size of various types of HA by dynamic light scattering, capillary electrophoresis, and fluorescence correlation spectroscopy which confirm that the HA particle size is practically independent of ionic strength in the range 0 to 200 mM.30–32 Due to the presence of a large density of structural charged sites with insignificant local mobility, there is uncertainty about the magnitude of the effective intraparticulate Debye length κ−1p. Duval33 has made some estimations of this crucial parameter which come to approximately 0.6 nm for both 10 and 100 mol m−3 ionic strength in the surrounding medium. The binding of Ca2+ by the HA studied here has been interpreted in terms of a thickness of the electric condensation zone,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL, for which the magnitude was obtained from fitting to agreement with the potential change over the intraparticulate part of the interfacial double layer.15 There should be a close relationship between
DL, for which the magnitude was obtained from fitting to agreement with the potential change over the intraparticulate part of the interfacial double layer.15 There should be a close relationship between ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL and κp but to our knowledge this has not yet been formulated. For the time being we can proceed by accepting the magnitude of
DL and κp but to our knowledge this has not yet been formulated. For the time being we can proceed by accepting the magnitude of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL together with the degree of Ca2+ condensation as the leading numbers for the condensation of any other divalent metal ion. See Section 4.2 below for details. Accordingly, within the total particle volume, Vp, the CCD model distinguishes between an intraparticulate double layer shell with volume VDL, and a Donnan phase with volume VD = Vp − VDL. For the present system with κprp ≫ 1 and both ionic strengths investigated, VD is close to the total particle volume.
DL together with the degree of Ca2+ condensation as the leading numbers for the condensation of any other divalent metal ion. See Section 4.2 below for details. Accordingly, within the total particle volume, Vp, the CCD model distinguishes between an intraparticulate double layer shell with volume VDL, and a Donnan phase with volume VD = Vp − VDL. For the present system with κprp ≫ 1 and both ionic strengths investigated, VD is close to the total particle volume.
The Donnan volume used in the NICA-Donnan model is obtained by fitting a combination of VD and ψD to a so-called mastercurve for protolytic titrations of HA.7 An empirical double logarithmic expression links the Donnan volume to the ionic strength of the bulk medium:12
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VD = b(1 − log VD = b(1 − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I) − 1 I) − 1 | (9) |
In passing we note that the WHAM speciation model assumes Donnan partitioning to occur only within the extraparticulate double layer, irrespective of the particle size.3 The occurrence of extraparticulate “Donnan partitioning” is also allowed in the NICA-Donnan model for fulvic acids and small humic acids for which the fitted Donnan volume is allowed to be greater than the particle size.36 However, the extraparticulate double layer carries a net charge density and does not contain any fixed charges at all, i.e. it is not a true Donnan phase. Rather, Boltzmann accumulation should be expected to occur in such zones. For κprp of order unity and lower, the amount of M2+ in the extraparticulate DL may indeed be significant in the total amount of M associated with the particle. In the CCD, the excess amount of M in the extraparticulate DL is straightforwardly obtained from the Boltzmann accumulation of M2+ as ensuing from the diffuse double layer potential profile37 and included in the mass balance for particle-associated free M.
The approaches for modeling the electrostatic contribution to cation binding by HA are summarized in Table 1 below.
| Model | Electrostatic binding | Donnan volume, VD, relative to particle volume, Vp |
|---|---|---|
| a Irrespective of the physical particle size. b For κprp ≫ 1, in high charge density regime. | ||
| WHAM3 | Donnan partitioninga |
V
D entirely extraparticulate  |
| NICA-Donnan2 | Donnan partitioninga |
V
D may be smaller or larger than the physical Vp. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VD = b(1 − log VD = b(1 − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I) − 1, where b is an empirical factor with generic value of 0.49 for HA I) − 1, where b is an empirical factor with generic value of 0.49 for HA |
| CCD23 | Counterion condensation plus Donnan partitioningb | V D = Vp − VDL |
The equilibrium speciation in a range of M–HA systems has been modeled by the NICA-Donnan approach, with typically good fits to the experimentally measured free metal ion concentrations being reported.38 Despite their very different constituent parameters, the WHAM and NICA-Donnan models predict similar concentrations of free metal ions in the presence of dissolved organic matter.39 This observation points to the empirical nature of the models. The quality-of-fit of the models is assessed on the basis of agreement between the measured and computed ‘free’ versus ‘bound’ M, where ‘bound’ includes all forms of M associated with the HA entities. However, the physical meaning of the various parameters in these equilibrium models is obscured due to the concomitant nature of the fitting process, and the interrelationships between the sub-models for intrinsic chemical and electrostatic binding components.28 Indeed, a recent review of the NICA-Donnan approach stated “The fact that a set of parameter values can be non-unique is first of all due to the large number of parameters in the model. A different way of fitting of the parameters to the data may lead to an equally good description of the data, but different parameter values.”2
4.2 Speciation in the electrostatic Ca2+–HA system
Here we seek to identify the physicochemically most reasonable descriptors for the binding of M2+ by HA. As a straightforward starting point, we consider the case of Ca2+ association with HA. The associative reactions of Ca2+ with negatively charged functional groups are dominated by electrostatics.40–42 The extent to which Ca2+ associates with HA was found to be far greater than that predicted by only Donnan-type electrostatics, with more highly charged HAs exhibiting the greatest amount of Ca2+ association.15 Accordingly, in order to describe the Ca2+–HA data, the NICA-Donnan model resorts to inclusion of intrinsic affinity constants for Ca2+ complexation, together with VD values that are smaller for more highly charged humic acids. For example, the NICA-Donnan VD values fitted to Ca2+–HA binding data follow the inverse order of the HA charge density: e.g. for Elliot soil HA with carboxyl content 4.8 mol kg−1, VD is 0.23 × 10−3 m3 kg−1, with a concomitant protonation constant (K1,H) of 10−0.8 m3 mol−1 significantly lower than the generic value of 10−0.1 mol m−3,43 whilst for a forest soil HA with carboxyl content 2.18 mol kg−1, VD is 2.95 × 10−3 m3 kg−1, using the generic protonation constants.44 An example of the speciation computed by the NICA-Donnan model for the Ca2+–HA system is given in Table 2. The fit to the data invokes a ψD of ca. −100 mV, which is rather negative for the given ionic strength of 82 mol m−3,45 as well as inner-sphere Ca2+ complex formation. As much as 81% of the particle-associated Ca2+ is predicted to be inner-sphere bound, whereas the Kint for CaHA is similar to its purely electrostatic Kos which would hardly suggest any inner-sphere complexes at all. ,
, 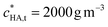 , pH = 8 and I = 82 mol m−3 in bulk electrolyte mediuma
, pH = 8 and I = 82 mol m−3 in bulk electrolyte mediuma
| CCDb | NICA-Donnanc | |
|---|---|---|
a Experimental data from Hering and Morel.46
b Computed using the experimentally measured concentration of free Ca2+ in the bulk medium, together with a condensation factor, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) C, of 0.8 in the intraparticulate double layer with thickness of 2 nm,23 and a volume charge density of −1300 mol e m−3 at pH 8.47
c Computed using the NICA-Donnan generic parameters28 for the given total concentrations of Ca2+ and HA. C, of 0.8 in the intraparticulate double layer with thickness of 2 nm,23 and a volume charge density of −1300 mol e m−3 at pH 8.47
c Computed using the NICA-Donnan generic parameters28 for the given total concentrations of Ca2+ and HA.
|
||
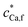 , mol m−3 , mol m−3 |
3.8 × 10−3 | 7.8 × 10−3 |
| c Ca,t, mol m−3 | 38 | 88.5 |
| Fraction free in VDL | 4 × 10−3 | — |
| Fraction free in VD | 0.03 | 0.19 |
| Fraction condensed in VDL | 0.97 | — |
| Fraction inner-sphere MS | — | 0.81 |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B,M in VD
B,M in VD |
250 | 2130 |
In contrast, the CCD model describes the extent of Ca2+–HA association for a range of HA samples, pH and ionic strength values, via inclusion of the mere electrostatic contributions due to counterion condensation within the intraparticulate double layer, together with a more realistic ψD of −70 mV in the bulk of the particle body (Table 2).
4.3 Intraparticulate speciation with inner-sphere complexes M–HA
Here we consider the speciation in M–HA systems in which intrinsic chemical binding is also involved, and compare the results obtained by the CCD and NICA-Donnan approaches. The parameters defining the CCD speciation scheme are given in the ESI.†Table 3 collates the concentrations of the various metal species for the case of a 1–1 background electrolyte (KNO3). In the CCD case, the given intraparticulate![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int values are those derived from local concentrations after accounting for the electrostatic effects (eqn (8)), whilst the NICA-Donnan values are obtained viaeqn (7).
int values are those derived from local concentrations after accounting for the electrostatic effects (eqn (8)), whilst the NICA-Donnan values are obtained viaeqn (7).
 ;
;  ; pH = 6 in bulk electrolyte medium
; pH = 6 in bulk electrolyte medium
| Cd, I = 100 mol m−3 | Cd, I = 10 mol m−3 | Pb, I = 100 mol m−3 | Pb, I = 10 mol m−3 | Cu, I = 100 mol m−3 | Cu, I = 10 mol m−3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CCD | NICAD | CCD | NICAD | CCD | NICAD | CCD | NICAD | CCD | NICAD | CCD | NICAD | |
a The ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int for CCD is given by eqn (8) and for NICA-Donnan by eqn (7). int for CCD is given by eqn (8) and for NICA-Donnan by eqn (7).
|
||||||||||||
| c *M,f, mol m−3 | 1 × 10−3 | 1.8 × 10−3 | 3 × 10−4 | 5.7 × 10−4 | 3 × 10−7 | 4.1 × 10−5 | 6.5 × 10−8 | 9.5 × 10−6 | 7 × 10−7 | 3.6 × 10−6 | 4 × 10−7 | 9.1 × 10−7 |
| c M,t, mol m−3 | 28.6 | 54.4 | 34.1 | 27.2 | 36.5 | 95.0 | 36.5 | 31.1 | 36.5 | 96.2 | 36.5 | 31.2 |
| Fraction free in VDL | 3 × 10−5 | — | 2 × 10−4 | — | 8 × 10−9 | — | 3.5 × 10−8 | — | 2 × 10−8 | — | 2 × 10−7 | — |
| Fraction free in VD | 2 × 10−3 | 0.03 | 0.04 | 0.16 | 4 × 10−7 | 4 × 10−4 | 8 × 10−6 | 2.4 × 10−3 | 9 × 10−7 | 3.5 × 10−5 | 5 × 10−5 | 2.3 × 10−4 |
| Fraction condensed in VDL | 0.7 | — | 0.55 | — | 0.5 | — | 0.5 | — | 0.5 | — | 0.5 | — |
| Fraction inner-sphere MS | 0.3 | 0.97 | 0.41 | 0.84 | 0.5 | 1 | 0.5 | 0.998 | 0.5 | 1 | 0.5 | 1 |
| θ M | 0.014 | 0.018 | 0.02 | 0.026 | 0.026 | 0.03 | 0.026 | 0.036 | 0.026 | 0.033 | 0.026 | 0.035 |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B,M in VD
B,M in VD |
50 | 950 | 5000 | 7700 | 50 | 930 | 5000 | 7700 | 50 | 940 | 5000 | 7800 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int (m3 mol−1)a int (m3 mol−1)a |
−0.52 | −2.0 | −1.8 | −2.2 | 3.2 | −0.1 | 2 | −0.3 | 3 | 1.0 | 1.3 | 0.7 |
The data show that for both approaches the free hydrated metal ions generally are a minor proportion of the total intraparticulate M. The CCD results for Cd(II) at I = 100 mol m−3, show that 70% of the uncomplexed M is condensed in the intraparticulate double layer and 30% is inner-sphere bound, whilst Pb(II) and Cu(II) are approximately equally distributed between these two forms. Furthermore, the total concentration of Cd(II), Pb(II) and Cu(II) associated with the particles is similar at I = 100 and 10 mol m−3. In contrast, in practically all cases considered the NICA-Donnan model predicts that the vast majority of the intraparticulate M is in the form of inner-sphere complexes (Table 3). It also predicts a much greater total concentration in the particle body at an ionic strength of 100 mol m−3 as compared to 10 mol m−3. This outcome is a consequence of the ionic strength dependence of the NICA-Donnan VD value which translates to, for equivalent total mass in the dispersion, the volume fraction of HA being a factor of 6 times lower at an ionic strength of 100 mol m−3 as compared to 10 mol m−3, in contradiction with experimental findings (see Section 4.1).
The extent to which Ca2+ electrostatically associates with HA provides a useful means to probe the consistency of the speciation results for Cd2+, Pb2+ and Cu2+ given in Table 3. That is, the deliberate use of a calcium salt, e.g. Ca(NO3)2, as the background electrolyte, with a concentration of Ca2+ several orders of magnitude greater than that of the target M2+, enables the electrostatic contribution to the binding of M2+ to be eliminated. This feature is a consequence of the purely electrostatic counterion condensation demands of the HA entity being practically totally met by the abundant Ca2+. Accordingly, in terms of the CCD approach the intraparticulate speciation of M2+ will involve only Donnan-type partitioning in VD, Boltzmann accumulation in VDL and inner-sphere complexation in VD and VDL. It should be noted that for a given ionic strength, the effective Donnan potential in the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte is lower than in the standard 1
1 electrolyte is lower than in the standard 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte (cf.eqn (5)). For comparison, computations were performed with the NICA-Donnan model in Ca(NO3)2 media for the same bulk concentrations of HA and M(II) as used in the experiments reported herein.
1 electrolyte (cf.eqn (5)). For comparison, computations were performed with the NICA-Donnan model in Ca(NO3)2 media for the same bulk concentrations of HA and M(II) as used in the experiments reported herein.
Several factors must be taken into account in comparing the ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int values derived for the different ionic strengths in KNO3vs. Ca(NO3)2 electrolyte. As described above, in Ca(NO3)2 there is no counterion condensation of the target M2+ and the Donnan potential is lower than that in KNO3. Accordingly, the intraparticulate environments in KNO3vs. Ca(NO3)2 electrolyte differ in terms of the net charge density and the corresponding ψD, the ensuing magnitude of
int values derived for the different ionic strengths in KNO3vs. Ca(NO3)2 electrolyte. As described above, in Ca(NO3)2 there is no counterion condensation of the target M2+ and the Donnan potential is lower than that in KNO3. Accordingly, the intraparticulate environments in KNO3vs. Ca(NO3)2 electrolyte differ in terms of the net charge density and the corresponding ψD, the ensuing magnitude of ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B,M for the intraparticulate free M2+, and the effective charge screening. In comparing the behavior of Cd(II), Pb(II) and Cu(II), we must also take into account the different chemical affinities of these transition metal ions for the reactive sites as well as the heterogeneous nature of the HA complexant. The chemical affinity of the target M2+ towards the major complexing groups of HA follows the order Cd(II) < Pb(II) ≈ Cu(II), whilst their degree of heterogeneity follows Cd(II) < Pb(II) < Cu(II).1 The overall consequence for each M2+ is that
B,M for the intraparticulate free M2+, and the effective charge screening. In comparing the behavior of Cd(II), Pb(II) and Cu(II), we must also take into account the different chemical affinities of these transition metal ions for the reactive sites as well as the heterogeneous nature of the HA complexant. The chemical affinity of the target M2+ towards the major complexing groups of HA follows the order Cd(II) < Pb(II) ≈ Cu(II), whilst their degree of heterogeneity follows Cd(II) < Pb(II) < Cu(II).1 The overall consequence for each M2+ is that ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int decreases as θM increases, with the magnitude of this effect being governed by the heterogeneity of the complexes. That is, for a given increase in θM, the
int decreases as θM increases, with the magnitude of this effect being governed by the heterogeneity of the complexes. That is, for a given increase in θM, the ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int for Cu(II) is expected to decrease by a greater extent than that for Cd(II).
int for Cu(II) is expected to decrease by a greater extent than that for Cd(II).
With the above features in mind, we consider the physicochemical reasonableness of the CCD and NICA-Donnan results. The case of Cd(II) at I = 100 mol m−3 provides a strong test of the consistency of the two approaches: at the metal-to-site ratio considered, inner-sphere binding is rather weak, and both models show that the total concentration of intraparticulate Cd(II) is significantly reduced in the presence of excess Ca2+ (Tables 3 and 4). The CCD approach generates similar values for both θCd and the intraparticulate concentration of free Cd2+ in the two electrolytes, and consequently similar magnitudes of
in the two electrolytes, and consequently similar magnitudes of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int. The total concentration of intraparticulate Cd(II) in Ca(NO3)2 is lower than in KNO3 by a factor of ca. 1/3, which reflects the absence of the condensed fraction (comprising 70% of the total intraparticulate Cd(II) in KNO3; Table 3). Furthermore, we note that the
int. The total concentration of intraparticulate Cd(II) in Ca(NO3)2 is lower than in KNO3 by a factor of ca. 1/3, which reflects the absence of the condensed fraction (comprising 70% of the total intraparticulate Cd(II) in KNO3; Table 3). Furthermore, we note that the ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int value is comparable to the intrinsic affinity of simple carboxylate ligands, which is physicochemically reasonable for Cd(II) under these conditions, e.g. Kint (eqn (4)) for Cd-acetate is of the order 0.01 m3 mol−1.48,49 The NICA-Donnan derived
int value is comparable to the intrinsic affinity of simple carboxylate ligands, which is physicochemically reasonable for Cd(II) under these conditions, e.g. Kint (eqn (4)) for Cd-acetate is of the order 0.01 m3 mol−1.48,49 The NICA-Donnan derived ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int values for Cd(II) are in broad agreement with the CCD result, being also of order 0.01 mol m−3 in both electrolytes. However, detailed examination reveals discrepancies in terms of the physicochemical reasonableness of the underlying parameters. Firstly, the concentration of intraparticulate free M2+ is a factor of ca. 10 higher in KNO3 than in Ca(NO3)2. As a consequence, the θCd in Ca(NO3)2 electrolyte is much lower, and the derived log
int values for Cd(II) are in broad agreement with the CCD result, being also of order 0.01 mol m−3 in both electrolytes. However, detailed examination reveals discrepancies in terms of the physicochemical reasonableness of the underlying parameters. Firstly, the concentration of intraparticulate free M2+ is a factor of ca. 10 higher in KNO3 than in Ca(NO3)2. As a consequence, the θCd in Ca(NO3)2 electrolyte is much lower, and the derived log ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int value is ca. half a unit higher. In addition, the decrease in the total concentration of intraparticulate Cd(II) in Ca(NO3)2 is much greater than can be explained by electrostatic factors alone, i.e. the reduction in magnitude of the Donnan potential. These outcomes are a consequence of the NICA-Donnan assumption that Ca2+ association involves significant inner-sphere complexation, with consequent displacement of Cd2+ from its inner-sphere complexes with weaker sites.
int value is ca. half a unit higher. In addition, the decrease in the total concentration of intraparticulate Cd(II) in Ca(NO3)2 is much greater than can be explained by electrostatic factors alone, i.e. the reduction in magnitude of the Donnan potential. These outcomes are a consequence of the NICA-Donnan assumption that Ca2+ association involves significant inner-sphere complexation, with consequent displacement of Cd2+ from its inner-sphere complexes with weaker sites.
 ;
;  ; pH = 6 in bulk electrolyte medium
; pH = 6 in bulk electrolyte medium
| Cd, I = 100 mol m−3 | Cd, I = 10 mol m−3 | Pb, I = 100 mol m−3 | Pb, I = 10 mol m−3 | Cu, I = 100 mol m−3 | Cu, I = 10 mol m−3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CCD | NICAD | CCD | NICAD | CCD | NICAD | CCD | NICAD | CCD | NICAD | CCD | NICAD | |
a The ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int for CCD is given by eqn (8) and for NICA-Donnan by eqn (7). int for CCD is given by eqn (8) and for NICA-Donnan by eqn (7).
|
||||||||||||
 , mol m−3 , mol m−3 |
3.2 × 10−3 | 3.8 × 10−3 | 1.1 × 10−3 | 3.4 × 10−3 | 7.7 × 10−4 | 5.2 × 10−4 | 1.5 × 10−5 | 1.9 × 10−4 | 1.2 × 10−3 | 6.1 × 10−5 | 3.5 × 10−4 | 1.7 × 10−5 |
| c M,t, mol m−3 | 11 | 11 | 28 | 8.4 | 30 | 82 | 36 | 30 | 27 | 96 | 34 | 31 |
| Fraction free in VDL | 1 × 10−4 | — | 6 × 10−5 | — | 9 × 10−6 | — | 6 × 10−7 | — | 2 × 10−5 | — | 2 × 10−5 | — |
| Fraction free in VD | 3 × 10−3 | 0.014 | 4 × 10−3 | 0.06 | 3 × 10−4 | 2 × 10−4 | 4 × 10−5 | 9 × 10−4 | 5 × 10−4 | 3 × 10−5 | 1 × 10−3 | 8 × 10−5 |
| Fraction inner-sphere MS | 0.997 | 0.99 | 0.996 | 0.94 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| θ M | 0.016 | 0.004 | 0.04 | 0.009 | 0.043 | 0.033 | 0.052 | 0.034 | 0.039 | 0.038 | 0.048 | 0.035 |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B,M in VD
B,M in VD |
11 | 40 | 105 | 140 | 11 | 40 | 105 | 140 | 11 | 40 | 105 | 140 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int (m3 mol−1)a int (m3 mol−1)a |
−0.35 | −1.6 | −0.46 | −1.7 | 0.73 | 0.2 | 1.5 | 0.2 | 0.48 | 1.2 | 0.15 | 1.2 |
For Cu(II), both the magnitude and the heterogeneity of the intrinsic chemical affinity of its complexes with HA are greater than those for Cd(II). Again, some notable differences in consistency of the interpretation by the CCD and NICA-Donnan models are apparent. At I = 10 mol m−3, the CCD approach shows that both θCu and the intraparticulate concentration of free Cu2+ are significantly higher in Ca(NO3)2 electrolyte than in KNO3. The total concentration of intraparticulate Cu(II) is approximately the same in both electrolytes, whilst the speciation changes from approximately equal amounts of condensed ions and inner-sphere complexes in KNO3 (Table 3) to practically only inner-sphere complexes in Ca(NO3)2 (Table 4). The ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int is ca. an order of magnitude lower in Ca(NO3)2 than in KNO3 which predominantly reflects the ca. one order of magnitude higher θCu. This result reflects the heterogeneity of the HA complexant: a greater proportion of intraparticulate inner-sphere complexes concomitantly means that the average affinity of the complexes is lower. NICA-Donnan derived results for Cu(II) at I = 10 mol m−3 show that the total concentration of intraparticulate Cu(II) and θCu are the same in both electrolytes, and almost all of the particle-associated Cu(II) is predicted to be in the form of inner-sphere complexes in both cases. However, the intraparticulate concentration of free Cu2+ is a factor of ca. 3 lower in Ca(NO3)2. The lower concentration of free Cu2+ within the particle body has the consequence that the
int is ca. an order of magnitude lower in Ca(NO3)2 than in KNO3 which predominantly reflects the ca. one order of magnitude higher θCu. This result reflects the heterogeneity of the HA complexant: a greater proportion of intraparticulate inner-sphere complexes concomitantly means that the average affinity of the complexes is lower. NICA-Donnan derived results for Cu(II) at I = 10 mol m−3 show that the total concentration of intraparticulate Cu(II) and θCu are the same in both electrolytes, and almost all of the particle-associated Cu(II) is predicted to be in the form of inner-sphere complexes in both cases. However, the intraparticulate concentration of free Cu2+ is a factor of ca. 3 lower in Ca(NO3)2. The lower concentration of free Cu2+ within the particle body has the consequence that the ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int values obtained in Ca(NO3)2 are greater than those in KNO3 (by ca. half a log unit). Others have reported that the presence of Ca2+ reduces the extent to which Cd(II) is bound by HA, but has negligible impact on the extent of Cu(II)–HA complex formation.50,51 In the context of the NICA-Donnan model the inconsistent observation was explained by saying that Ca2+ hardly impacts on Cu–HA binding because the inner-sphere complexes of Cu(II) with phenolic type sites are stronger than those of Ca(II), whilst in the case of Cd(II), Ca2+ can compete for inner-sphere complexation of carboxyl groups.50
int values obtained in Ca(NO3)2 are greater than those in KNO3 (by ca. half a log unit). Others have reported that the presence of Ca2+ reduces the extent to which Cd(II) is bound by HA, but has negligible impact on the extent of Cu(II)–HA complex formation.50,51 In the context of the NICA-Donnan model the inconsistent observation was explained by saying that Ca2+ hardly impacts on Cu–HA binding because the inner-sphere complexes of Cu(II) with phenolic type sites are stronger than those of Ca(II), whilst in the case of Cd(II), Ca2+ can compete for inner-sphere complexation of carboxyl groups.50
5 Conclusions and outlook
Over the years a number of models have been developed to describe metal ion binding by HA. Each approach has provided insights into the nature of the association of ions with this charged, chemically heterogeneous complexant. Recent advances in understanding the physicochemical properties of soft, charged nanoparticles cast new light on M–HA complexation phenomena. In accounting for the electrostatic features of soft charged NPs such as HA, a purely Donnan type approach is demonstrated to be a physically incomplete description. Notably, Donnan partitioning by itself greatly underestimates the extent to which Ca2+ associates with HA, and even though covalency is essentially absent in Ca2+ binding, conventional equilibrium speciation models resort to inclusion of chemical affinity parameters to describe the Ca2+–HA association. Taking the NICA-Donnan approach as an example, there are several factors in the model that are out of line with experimental observations.34,35 These include e.g. the values of the protonation constants, the delineation and the ionic strength dependence of the Donnan volume, as well the magnitude of the Donnan potential. Each of the disparities acts to increase the extent of association of oppositely charged ions with the HA entity, thus pointing to possibly missing electrostatic ingredients in the interpretation. It is evident that the Ca2+–HA association involves stronger electrostatic interactions such as counterion condensation, potentially including the possibility for partial formation of inner-sphere ion pairs in which Caaq2+ exchanges some of its inner-sphere water of hydration.52,53 The CCD approach is shown to provide a more satisfactory physicochemical description of the electrostatic contribution to association of M2+ with HA.There are significant differences in the intraparticulate speciation predicted by the CCD and NICA-Donnan approaches. Notably, in 1–1 electrolyte the CCD approach finds a substantial electrostatic contribution to the association of Cd(II), Pb(II), and Cu(II) with HA. It follows that at the level of the ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int values, the CCD and Donnan-only electrostatic models give significantly different results. For the heterogeneous HA complexant,
int values, the CCD and Donnan-only electrostatic models give significantly different results. For the heterogeneous HA complexant, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int is expected to increase as θM decreases. The CCD model retrieves this relationship, whilst the trend in the NICA-Donnan derived values is less systematic. Such differences in intraparticulate speciation are highly significant for e.g. predictions of the lability and bioavailability of the complex species. For example, the present work has shown that for Pb–HA the total concentration of intraparticulate Pb(II) is similar in KNO3 and Ca(NO3)2 electrolyte, yet the lability of the complexes is very different in these two media, as a consequence of effect of the electrostatic environment in the NP body on the reaction rate constants.54 A detailed exploration of the consequences of condensation phenomena on the intraparticulate dynamics of M–HA complexes is underway.
int is expected to increase as θM decreases. The CCD model retrieves this relationship, whilst the trend in the NICA-Donnan derived values is less systematic. Such differences in intraparticulate speciation are highly significant for e.g. predictions of the lability and bioavailability of the complex species. For example, the present work has shown that for Pb–HA the total concentration of intraparticulate Pb(II) is similar in KNO3 and Ca(NO3)2 electrolyte, yet the lability of the complexes is very different in these two media, as a consequence of effect of the electrostatic environment in the NP body on the reaction rate constants.54 A detailed exploration of the consequences of condensation phenomena on the intraparticulate dynamics of M–HA complexes is underway.
Symbols and abbreviations
References
- J. Buffle, Complexation Reactions in Aquatic Systems: An Analytical Approach, Ellis Horwood, Chichester, UK, 1988 Search PubMed.
- L. K. Koopal, T. Saito, J. P. Pinheiro and W. H. van Riemsdijk, Colloids Surf., A, 2005, 265, 40–54 CrossRef CAS.
- E. Tipping, Aquat. Geochem., 1998, 4, 3–48 CrossRef CAS.
- J. F. L. Duval, K. J. Wilkinson, H. P. van Leeuwen and J. Buffle, Environ. Sci. Technol., 2005, 39, 6435–6445 CrossRef CAS PubMed.
- H. P. van Leeuwen and J. Buffle, Environ. Sci. Technol., 2009, 43, 7175–7183 CrossRef CAS PubMed.
- R. M. Town, J. F. L. Duval, J. Buffle and H. P. van Leeuwen, J. Phys. Chem. A, 2012, 116, 6489–6496 CrossRef CAS PubMed.
- P. Warwick, A. Hall, S. J. King, J. Zhu and J. van der Lee, Radiochim. Acta, 1998, 81, 215–221 CrossRef CAS.
- A. P. Robertson and J. O. Leckie, Environ. Sci. Technol., 1999, 33, 786–795 CrossRef CAS.
- R. Marsac, M. Davranche, G. Gruau, M. Bouhnik-Le Coz and A. Dia, Geochim. Cosmochim. Acta, 2011, 75, 5625–5637 CrossRef CAS.
- A. C. Montenegro, S. Orsetti and F. V. Molina, Environ. Chem., 2014, 11, 318–332 CrossRef CAS.
- N. D. Bryan, D. M. Jones, M. Appleton, F. R. Livens, M. N. Jones, P. Warwick, S. King and A. Hall, Phys. Chem. Chem. Phys., 2000, 2, 1291–1300 RSC.
- M. F. Benedetti, W. H. van Riemsdijk and L. K. Koopal, Environ. Sci. Technol., 1996, 30, 1805–1813 CrossRef CAS.
- I. Christl, A. Metzger, I. Heidmann and R. Kretzschmar, Environ. Sci. Technol., 2005, 39, 5319–5326 CrossRef CAS PubMed.
- A. Liu and R. D. Gonzalez, Langmuir, 2000, 16, 3902–3909 CrossRef CAS.
- H. P. van Leeuwen and R. M. Town, Environ. Chem., 2016, 13, 76–83 CrossRef CAS.
- G. S. Manning, Biophys. Chem., 1977, 7, 95–102 CrossRef CAS PubMed.
- G. S. Manning, Q. Rev. Biophys., 1978, 2, 179–246 CrossRef.
- E. Garcia-Fernandez, P. M. R. Paulo and S. M. B. Costa, Phys. Chem. Chem. Phys., 2015, 17, 4319–4327 RSC.
- M. Majtyka and J. Kłos, Phys. Chem. Chem. Phys., 2007, 9, 2284–2292 RSC.
- Q. R. Huang, P. L. Dubin, C. N. Moorefield and G. R. Newkome, J. Phys. Chem. B, 2000, 104, 898–904 CrossRef CAS.
- Z. Li, A. K. van Dyk, S. J. Fitzwater, K. A Fichthorn and S. T. Milner, Langmuir, 2016, 32, 428–441 CrossRef CAS PubMed.
- H. P. van Leeuwen, R. F. M. J. Cleven and P. Valenta, Pure Appl. Chem., 1991, 63, 1251–1268 CrossRef.
- R. M. Town and H. P. van Leeuwen, Phys. Chem. Chem. Phys., 2016, 18, 10049–10058 RSC.
- R. M. Fuoss, J. Am. Chem. Soc., 1958, 80, 5059–5061 CrossRef CAS.
- H. P. van Leeuwen, R. M. Town and J. Buffle, J. Phys. Chem. A, 2007, 111, 2115–2121 CrossRef CAS PubMed.
- H. Ohshima and T. Kondo, Biophys. Chem., 1990, 38, 117–122 CrossRef CAS PubMed.
- L. P. Yezek and H. P. van Leeuwen, Langmuir, 2005, 21, 10342–10347 CrossRef CAS PubMed.
- C. J. Milne, D. G. Kinniburgh, W. H. van Riemsdijk and E. Tipping, Environ. Sci. Technol., 2003, 37, 958–971 CrossRef CAS PubMed.
- M. J. Avena, L. K. Koopal and W. H. van Riemsdijk, J. Colloid Interface Sci., 1999, 217, 37–48 CrossRef CAS PubMed.
- W. F. Tan, L. K. Koopal and W. Norde, Environ. Sci. Technol., 2009, 43, 591–596 CrossRef CAS PubMed.
- J. P. Pinheiro, A. M. Mota, J. M. R. d’Oliveira and J. M. G. Martinho, Anal. Chim. Acta, 1996, 329, 15–24 CrossRef CAS.
- M. Hosse and K. J. Wilkinson, Environ. Sci. Technol., 2001, 35, 4301–4306 CrossRef CAS PubMed.
- J. F. L. Duval, Langmuir, 2005, 21, 3247–3258 CrossRef CAS PubMed.
- T. Lenoir, A. Matynia and A. Manceau, Environ. Sci. Technol., 2010, 44, 6221–6227 CrossRef CAS PubMed.
- E. Companys, J. L. Garcés, J. Salvador, J. Galceran, J. Puy and F. Mas, Colloids Surf., A, 2007, 306, 2–13 CrossRef CAS.
- D. G. Kinniburgh, W. H. van Riemsdijk, L. K. Koopal, M. Borkovec, M. F. Benedetti and M. J. Avena, Colloids Surf., A, 1999, 151, 147–166 CrossRef CAS.
- J. F. L. Duval and H. P. van Leeuwen, J. Phys. Chem. A, 2012, 116, 6443–6451 CrossRef CAS PubMed.
- I. Christl, A. Metzger, I. Heidmann and R. Kretzschmar, Environ. Sci. Technol., 2005, 39, 5319–5326 CrossRef CAS PubMed.
- L. Weng, E. J. M. Temminghoff, S. Lofts, E. Tipping and W. H. van Riemsdijk, Environ. Sci. Technol., 2002, 36, 4804–4810 CrossRef CAS PubMed.
- K. Krishnan and R. A. Plane, J. Am. Chem. Soc., 1968, 90, 3195–3200 CrossRef CAS.
- L. A. Clapp, C. J. Siddons, J. R. Whitehead, D. G. van Derveer, R. D. Rogers, S. T. Griffin, S. B. Jones and R. D. Hancock, Inorg. Chem., 2005, 44, 8495–8502 CrossRef CAS PubMed.
- C. Travers and J. A. Marinsky, J. Polym. Sci., 1974, 47, 285–297 CAS.
- I. Christl, Environ. Chem., 2012, 9, 89–96 CrossRef CAS.
- L. A. Oste, E. J. M. Temminghoff, T. M. Lexmond and W. H. van Riemsdijk, Anal. Chem., 2002, 74, 856–862 CrossRef CAS PubMed.
- J. Buffle, Z. Zhang and K. Startchev, Environ. Sci. Technol., 2007, 41, 7609–7620 CrossRef CAS PubMed.
- J. G. Hering and F. M. M. Morel, Environ. Sci. Technol., 1988, 22, 1234–1237 CrossRef CAS PubMed.
- W.-F. Tan, W. Norde and L. K. Koopal, Geochim. Cosmochim. Acta, 2011, 75, 5749–5761 CrossRef CAS.
- A. Yuchi, H. Wada and G. Nakagawa, Anal. Chim. Acta, 1983, 149, 209–216 CrossRef CAS.
- R. S. Kolat and J. E. Powell, Inorg. Chem., 1962, 1, 293–296 CrossRef CAS.
- D. G. Kinniburgh, C. J. Milne, M. F. Benedetti, J. P. Pinheiro, J. Filius, L. K. Koopal and W. H. van Riemsdijk, Environ. Sci. Technol., 1996, 30, 1687–1698 CrossRef CAS.
- J. Hamilton-Taylor, A. S. Postill, E. Tipping and M. P. Harper, Geochim. Cosmochim. Acta, 2002, 66, 403–415 CrossRef CAS.
- F. J. Millero, F. Gombar and J. Oster, J. Solution Chem., 1977, 6, 269–280 CrossRef CAS.
- L. M. Hamm, A. F. Wallace and P. M. Dove, J. Phys. Chem. B, 2010, 114, 10488–10495 CrossRef CAS PubMed.
- R. M. Town, Environ. Chem., 2015, 12, 130–137 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02634f |
| This journal is © the Owner Societies 2016 |






![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif)