Fragment molecular orbital study of the cAMP-dependent protein kinase catalyzed phosphoryl transfer: a comparison with the differential transition state stabilization method

Abstract

The importance of key residues to the activity of the cAMP-dependent protein kinase catalyzed phosphoryl transfer and to the stabilization of the transition state of the reaction has been investigated by means of the fragment molecular orbital (FMO) method. To evaluate the accuracy of the method and its capability of fragmenting covalent bonds, we have compared stabilization energies due to the interactions between individual residues and the reaction center to results obtained with the differential transition state stabilization method (Szarek, et al., J. Phys. Chem. B, 2008, 112, 11819–11826) and observe, despite a size difference in the fragment describing the reaction center, near-quantitative agreement. We have also computed deletion energies to investigate the effect of virtual deletion of key residues on the activation energy. These results are consistent with the stabilization energies and yield additional information as they clearly capture the effect of secondary interactions, i.e. interactions in the second coordination layer of the reaction center. We find that using FMO to calculate deletion energies is a powerful and time efficient approach to analyze the importance of key residues to the activity of an enzyme catalyzed reaction.

---

Introduction

Fundamental understanding of enzyme catalysis on an atomic level is necessary in order to design new biocatalysts. In order to predict the desired properties needed by the new enzyme to catalyze a targeted reaction, a detailed picture of the role and involvement of the catalytic residues in and near the active site is required. In this respect, computational approaches can play an important role.^1,2 The use of theoretical tools, and quantum chemistry especially, to propose new biocatalyst for practical applications is beneficial in many respects, e.g. time and cost.

To evaluate the importance of key residues for a certain reaction, analysis of both initial (IS) and transition state (TS) properties is essential, since the information on the catalytic performance lies in the difference therein.³ When studying large molecular model systems, such as active site models of enzyme catalyzed chemical reactions, using standard quantum mechanical methods the computational cost is often huge. The fragment molecular orbital (FMO) method⁴ is a considerably faster alternative to full ab initio methods and has previously been applied in studies of enzyme catalysis.^5–8 In the FMO approach the molecule or molecular system is divided into smaller fragments and each fragment is computed fully ab initio in the Coulomb field from the entire molecular system. All interactions between any two fragments (dimers) are considered quantum mechanically as well but only up to a certain cutoff outside of which the fragments are represented by point charges.⁹ Having one residue per fragment (fragmentation is discussed in detail in the FMO section below) one then obtains interaction energies between all residues and the reaction center from only one calculation. Thus, performing FMO calculations on the IS and TS can give information on the TS stabilization effect from all residues considered in the model.

In a recent study by Ito and Brinck,⁸ the contribution of different residues to ketosteroid isomerase catalyzed proton abstraction was investigated using FMO. In addition to considering inter-fragment interaction energies to evaluate the importance of key residues to the activity, the effect on the activation energy of the enzyme-catalyzed reaction by virtually deleting a residue (relative deletion energy) was studied. Also here, the effects of all possible residue deletions are obtained from merely two FMO calculations, the IS and TS. It was found that the relative deletion energy can yield complementary information to that obtained from studying the inter-fragment interaction energies.⁸ The relative deletion energy captured effects arising from secondary interactions, i.e. not direct interactions, with the reaction center, effects that were not captured when analyzing only the interaction energy difference between the TS and IS. While the largest effects from deletion was, not unexpectedly, assigned to Tyr14 and Asp99, which do interact directly with the substrate, a significant increase in activation energy was found also from deleting Tyr55 which have no direct interaction with any of the reactants, but donates a hydrogen bond to Tyr14. This finding elucidated the catalytic effect of Tyr55, which previously was thought of playing just a structural role, as being of electronic character.

Another approach for considering non-covalent interactions in the active site is the differential transition-state stabilization (DTSS) method,^10–12 which is a full ab initio based method, using variation–perturbation partitioning of intermolecular interaction energies. Here, the computed interaction energy can be decomposed into different components in order to isolate certain electronic properties such as delocalization, correlation, exchange and electrostatic effects. To obtain the interaction energy between a residue and the reaction center, the procedure requires an isolated calculation of the two fragments, which means that for a model containing N residues (excluding the reaction center), 2N calculations are required, N calculations each for the IS and TS, in comparison to the two required in FMO. The DTSS interaction energy computed at the MP2 level of theory is denoted ΔE_MP2.

In the present study we are studying the catalytic effects of key residues in the cAMP-dependent protein kinase (PKA) catalyzed phosphoryl transfer reaction using the FMO method. This reaction follows a dissociative mechanism,^13–15 see Fig. 1, during which the Asp166 residue accepts a proton from the substrate peptide. The previous study by Szarek et al.¹⁶ in which the DTSS method was employed to investigate the same properties serves as the base for comparison. The idea is to evaluate the accuracy of the FMO method and its potential as a simpler alternative to the fully ab initio DTSS method to investigate intermolecular interactions important for stabilizing the TS during an enzyme catalyzed chemical reaction. For a given level of theory (in the present study typically MP2/6-31G*), the FMO method is not necessarily faster, but it yields similar and additional information, such as interactions between all residues in the system and the inclusion of polarization effects, due to the electrostatic potential of the surrounding system, on the dimer interaction energy.

Fig. 1 cAMP-dependent protein kinase (PKA) catalyzed phosphoryl transfer following a dissociative mechanism as proposed in previous theoretical studies,^13–15 in which a proton transfer to the Asp166 residue occurs.

In the present study, interaction energies computed with FMO are compared to DTSS MP2-interaction energies calculated in ref. 16. Furthermore, calculated FMO relative deletion energies are shown to strengthen the analysis and provide additional information on catalytic effects of the residues considered in the present model.

Computational details

All calculations have been performed using the FMO method⁴ as implemented in the Gamess-US package.¹⁷ Structures for the IS, shown in Fig. 2a, and TS, the zoom-in of which is visualized in Fig. 2b, of the PKA catalyzed phosphoryl transfer reaction were based on configurations taken from a QM/MM study performed by McCammon and coworkers.¹³ It should be noted that these structures were also employed, after modification, in the study by Szarek et al.¹⁶ in which the differential transition state stabilization (DTSS) methodology was used to investigate intermolecular interactions between the reaction center and key residues. We also compare our results to the DTSS results in the present study. Here, as in ref. 16, the ATP molecule is represented by methyl triphosphate and the substrate peptide by Ser367. While keeping the remaining system frozen, the hydrogen atoms used to saturate all dangling bonds were optimized at the HF/6-31G(d) level of theory. Selected residues (Val44, Lys72, Gln84, Glu91, Lys168, Asn171 and Phe187) were structurally modified as described in ref. 16. Cartesian coordinates for the IS and TS structures used in the FMO calculations can be found in the ESI.† The FMO simulations were performed using the MP2 method in order to facilitate comparison with the DTSS results in ref. 16. Furthermore, the same basis set as employed in ref. 16 was chosen, i.e. 6-31G(d). This choice of basis set may lead to results that are not fully converged in every respect but we choose it nonetheless to avoid drawing conclusions based on basis set difference.

Fig. 2 (a) Active site model used in the FMO simulation of the PKA catalyzed phosphoryl transfer. Cartesian coordinates for the system in the IS and TS can be found in the ESI.† (b) Zoom on the TS configuration, where the dissociation has initiated but the proton shift from the substrate peptide to the Asp166 residue has yet to occur, as indicated by the dashed line.

The fragmentation process is crucial in order to obtain reasonable results. Here, we typically use one residue per fragment. The exception is the fragment containing the reaction center for which the ATP molecule, the substrate peptide (Ser367), the two Mg²⁺ ions and the Asp184 residue were included. Fragmentation of covalent bonds between residues were dealt with according to the procedure described in the FMO section; Thr51, Gly52, Ser53, Phe54 and Gly55 were separated into individual fragments in this way, as were Cys199, Gly200 and Thr201. The fragmentation of covalent bonds along with the reaction center fragment is visualized in Fig. 3.

Fig. 3 Visualization of the fragmentation of the PKA system employed in the FMO calculations. Two backbone chains in the PKA system in the present study required fragmentation across covalent bonds. (a) Fragmentation of the glycine-rich loop (constituted by residues 51–55 in the structure model). (b) Fragmentation of residues 199–201. The dashed lines in (a) and (b) illustrates where the fragmentation occurred. The bond is heterolytically cleaved which means that the electron pair was assigned to the Cα in all cases. (c) The fragment containing the reaction center; the ATP, the Mg²⁺ ions, the substrate peptide represented by Ser367, and the Asp184 residue.

Fragment molecular orbital method

The idea of the fragment molecular orbital (FMO) method¹⁸ relies on the fact that exchange is local, which means that long-range interactions can, approximately, be treated with Coulomb operators only. In the FMO approach, the molecular system is divided into N fragments and molecular orbital (MO) calculations are subsequently performed on each fragment (denoted monomer) and fragment pair (dimer, which is merely the combination of two monomers) in order to obtain electronic structure properties such as the total energy of the system. Note, however, that if the fragments in a dimer are far separated they are treated as point charges. The dominant part of the FMO calculation is the self-consistent field calculations of the dimers within the cutoff radius, the number of which scales linearly with the system size.⁹ Having fragmented the molecular system, the possibility of parallelizing the computations increases significantly. In Gamess-US, the FMO parallelization is efficiently done with the GDDI interface.¹⁹

Typically, the FMO approach yields errors in the total energy of about 2 kcal mol⁻¹ compared to standard MO calculations.¹⁸ To systematically improve the accuracy of the FMO method, trimers can be included⁴ but in the present study the accuracy of the two-body FMO was deemed sufficient.

How the fragmentation is done should be based on chemical understanding of the system. For instance, fractioning should be avoided at bonds with delocalized electron densities.²⁰ If a fragment boundary requires the splitting of a covalent bond, the partition needs to be done heterolytically, i.e. the bond electron pairs should not be separated. As a result of this division of the variational space, one is left with redundant atomic orbitals at the atoms between which the bond is cleaved. Consequently, an operation is required in which these orbitals are projected out.^20,21 For this, a set of hybrid orbitals is needed. In the present study, due to the delocalized nature of the peptide bond, all fragmentation of covalent bonds has, as suggested in⁹ been performed at the Cα. Therefore, it was natural to employ the sp³-hybridized orbital of carbon taken from a calculation of CH₄ using the same basis set as in the FMO calculation.²⁰ Note that as a result of the choice of fragmentation, each fragment residue is shifted by one carboxyl group as compared to the amino acid residue, as can be seen in Fig. 3.

The FMO procedure starts by solving the relevant monomer equations self-consistently after which the dimer equations are solved in the electrostatic potential from the surrounding (N − 2) fragments (or monomers). This electrostatic potential is commonly referred to as the “environmental electrostatic potential” (ESP). The total energy of the molecular system can be expressed in terms of monomer and dimer energies with or without the ESP.

where E_IJ and E_I are the energies including the ESP of fragment pair (or dimer) IJ and fragment (or monomer) I, respectively. We keep in mind the term ΔE_IJ, which is the inter-fragment interaction energy. In the present study, we focus especially on the difference in inter-fragment interaction energy between TS and IS, ΔΔE_IJ, which holds information on the relative stabilization of the TS.

Expressing, instead, the total energy in terms of monomer and dimer energies for which the explicit effects of the ESP have been separated out, we denote the monomer and dimer energies with E_x′ where x = I for fragment I and x = IJ for fragment pair IJ:

Here, ΔD^IJ is the density matrix difference of dimer IJ and the direct sum of the electron densities of monomers I and J (ΔD^IJ = D^IJ − (D^I ⊕ D^J)) and V^IJ the pair ESP.

In the present study, as discussed in the introduction, we compute the energy of the deletion form for which the fragment of interest is virtually deleted from the system. This is achieved by subtracting the monomer energy of the fragment of choice, together with all relevant inter-fragment interaction energies:⁸

E_del can subsequently be computed for each reaction step, although in this study only one is considered, to obtain the effect of deleting a specific residue on the activation energy for that specific step. The relative deletion energy is then defined as the difference in energy of the deletion form between TS and IS for a given reaction step:

ΔE_del = E_del[TS] − E_del[IS] (4)

Computing the relative deletion energy using FMO is fast, and requires but two calculations, the IS and TS of the reaction of interest. One should remember, however, that deleting residues following this approach neglect structural relaxation effects due to the actual residue deletion, which is an assumption that could lead to an overestimation of the effect of the deletion.⁸

Results and discussion

Comparison of FMO interaction energies with DTSS energies

The main objective of the present study was to investigate the use of the FMO method to predict the relative importance of key residues to the activity of the enzyme catalyzed chemical reaction. By comparing inter-fragment interaction energy differences (ΔΔE_IJ = ΔE_IJ[TS] − ΔE_IJ[IS]) to DTSS energies (ΔE_MP2) computed in ref. 16, the accuracy of the FMO method for predicting interactions between individual residues and the reaction center could be evaluated. In addition, calculation of relative deletion energies (defined in the FMO section) was performed to yield information on the effect on the reaction barrier by the deletion of a selected residue.

Gas phase single point FMO calculations were performed on the IS and TS of the PKA active site model, shown in Fig. 2a, at the MP2/6-31G(d) level of theory, for which we obtain an activation energy, defined as E(TS) − E(IS), of 19.5 kcal mol⁻¹. This is slightly higher than obtained in previous studies. In the QM/MM study by Cheng et al., from which the original structures used in the present study were taken, barriers around 7.7–14.3 kcal mol⁻¹, depending on the size of the QM region and method (B3LYP or MP2) of choice, were obtained. In addition, Diaz et al.¹⁵ proposed a barrier of 17.2 kcal mol⁻¹ while Valiev et al. arrived at 11.0 kcal mol^−1 14 and 15 kcal mol^−1 22 (both using B3LYP). The slight overestimate of the activation energy obtained in the present study can be explained by the choice of fragmentation. The FMO activation energy is not fully converged with respect to the size of the fragment containing the reaction center; including also Asp166 brings the activation energy down an additional 1.8 kcal mol⁻¹ to 17.7 kcal mol⁻¹, which is in good agreement with the barrier proposed by Diaz et al.¹⁵ However, in order to make a somewhat direct comparison of stabilization energies with the DTSS results, we choose the fragmentation leading to a barrier of 19.5 kcal mol⁻¹ since interactions with residues not present in the DTSS would arise otherwise.

The difference in inter-fragment interaction energies (ΔΔE_IJ), where I is the fragment containing the reaction center and J any other fragment in the system between the IS and TS, reveals the stabilization (or destabilization) of the TS by fragment J. This can be compared directly to the DTSS energy provided the fragmentation in the FMO method equals partitioning of the system in the DTSS method. In the present study, the fragment containing the reaction center was equal to the chosen reaction complex in ref. 16 with the additional inclusion of both Mg²⁺ ions and also the Asp184 residue. This was done in order to avoid fragmenting the strong electrostatic Asp184–Mg interaction that could lead to unphysical results. In fact, test calculations were performed when including only the Mg²⁺ ions in the reaction center fragment, letting Asp184 be a lone fragment. The opposite charges and the closeness of the two fragments lead to a very high interaction energy between Asp184 and the reaction center fragment. Due to the difference in reaction center complexes, a one-to-one comparison between the DTSS energies and ΔΔE_IJ is not possible. Despite this it turns out that the methods compare rather well, and an almost quantitative comparison is indeed possible. Recalling that the FMO fragmentation is partly done over covalent bonds, this is a very interesting finding.

Looking at Fig. 4, it is rather obvious that ΔΔE_IJ follow the pattern of the DTSS energies. Of the residues constituting the glycine-rich loop (47–57), which has the role of positioning the ATP molecule for the phosphoryl transfer,²³ Thr51, Gly52, Ser53, Phe54, Gly55 and Val57 are considered in the present model. As can be seen in Fig. 4 and Table 1, the largest stabilization/destabilization effects are found for Ser53 and Gly55. The destabilization from Ser53 is slightly smaller with FMO, 3.0 kcal mol⁻¹ compared to 4.7 kcal mol⁻¹ with DTSS. On the other hand, the stabilization from Gly55 is larger with the DTSS method (−4.1 kcal mol⁻¹ compared to −3.6 kcal mol⁻¹) giving a combined stabilization effect from the entire glycine-rich loop that is very similar for both methods; −6.2 kcal mol⁻¹ with DTSS and −6.5 kcal mol⁻¹ with FMO.

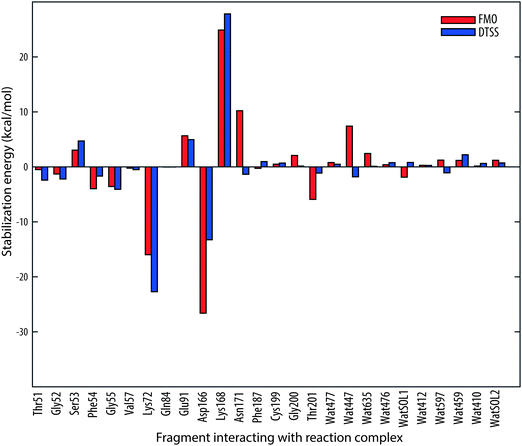Fig. 4 Comparison of transition state stabilization energies for the PKA catalyzed phosphoryl transfer reaction obtained from the DTSS study in ref. 16 (indicated with blue bars) with inter-fragment interaction energy differences (red bars), ΔΔE_IJ = ΔE_IJ [TS] − ΔE_IJ [IS], computed with the FMO method for the same reaction.

Table 1 Interaction energy differences (ΔΔE_IJ) between key residues and the reaction center calculated with the DTSS and FMO methods. The DTSS results are taken from ref. 16

Residue	DTSS	FMO
Thr51	−2.4	−0.5
Gly52	−2.2	−1.3
Ser53	4.7	3.0
Phe54	−1.7	−4.0
Gly55	−4.1	−3.6
Val57	−0.5	−0.2
Lys72	−22.7	−16.0
Gln84	−0.0	−0.0
Glu91	5.0	5.7
Asp166	−13.3	−26.6
Lys168	27.8	24.9
Asn171	−1.4	10.2
Phe187	1.0	−0.3
Cys199	0.7	0.5
Gly200	0.2	2.1
Thr201	−1.1	−5.9
Wat477	0.5	0.8
Wat447	−1.8	7.4
Wat635	0.1	2.5
Wat476	0.8	0.4
WatSOL1	0.8	−1.9
Wat412	0.3	0.3
Wat597	−1.1	1.2
Wat459	2.2	1.2
Wat410	0.6	0.2
WatSOL2	0.7	1.2

---

The residues showing largest stabilization effects are Lys72 and Asp166. The involvement of Asp166 in the catalytic mechanism has been debated in literature. While earlier theoretical studies^24,25 suggested no active participation of any general-base in the phosphoryl transfer, later studies have found that prior to phosphorylation, a proton shift from the substrate peptide serine to Asp166 occurs.^14,15,26,27 This shift is part of the rate-determining step of the reaction, but occurs late in the step. Thus, the bond is not fully formed in the TS, as can easily be seen in Fig. 2b, and the H–O interaction is considered non-covalent in the FMO-analysis. While DTSS predicts a large stabilization effect from Asp166 (−13.3 kcal mol⁻¹) it is even larger with FMO (−26.6 kcal mol⁻¹). The stabilization from Lys72 is on the other hand predicted to be larger with DTSS than FMO, by 6.7 kcal mol⁻¹.

Lys168 has a large destabilizing effect on the TS, by 27.8 kcal mol⁻¹ and 24.9 kcal mol⁻¹ with DTSS and FMO, respectively. The role of Lys168 was investigated thoroughly in ref. 13, in which a large destabilization effect was found as well. In fact, replacing Lys168 with Ala increases K_M significantly.²⁸ The catalytic role of Lys168 is to keep the ATP molecule and substrate peptide in a near-attack conformation.¹³

Asn171 is predicted to have small impact on the stabilization/destabilization of the TS by DTSS. With FMO, however, the effect of destabilization is rather large (10.2 kcal mol⁻¹), a finding which is supported by Cheng et al.¹³ The role of Asn171 is to stabilize the catalytic loop by forming a hydrogen bond to the α-carbonyl of Asp166.²⁸ It also binds to one of the Mg²⁺ ions (Mg1), which, in turn, stabilizes the TS significantly.^13,16 Asn171 reduces the activity but is necessary for the binding of the Mg1 ion.¹³ This feature seems not to be captured by the DTSS. No experimental kinetic studies on the catalytic activity of Asn171 have been performed to our knowledge.

We note a rather large destabilization effect of Wat447 of 7.4 kcal mol⁻¹ that contradicts the small stabilization effect found with DTSS. However, previous theoretical studies¹³ indicate that residues and water (such as Wat447) binding to the Mg²⁺ ions mainly play a structural role and de facto destabilize the TS, which is in line with what FMO predicts. Also, the very large stabilization effect of the Mg²⁺ ions^13,16 leads to a net stabilization contribution to the TS of the entire Mg–ligand complex despite the inhibitory effect of the residues and water that binds the metal ions.

Noteworthy is also the interaction of Thr201 with the reaction center complex, which with FMO is predicted to be −5.9 kcal mol⁻¹ while the DTSS estimate is only −1.1 kcal mol⁻¹.

Since there is a noticeable discrepancy in the interaction energies between DTSS and FMO for some of the residues, especially Asn171, Asp166, Wat447 and Thr201, we studied the effect of excluding also the Asp184 residue from the reaction center fragment. Although the numbers differ slightly, the general trend remains; Asn171 continues to strongly destabilize the TS, as do Wat447. For Asp166, the FMO interaction energy is brought down somewhat to 19.7 kcal mol⁻¹, which is closer to the 13.3 kcal mol⁻¹ obtained with DTSS. The stabilization effect of Thr201 is of similar magnitude as with Asp184 included in the reaction center fragment.

The discrepancy observed for Thr201 is interesting because of the role of the residue in the catalytic process. The main function of Thr201, a residue which is conserved in Ser/Thr-specific protein kinases,²³ is to bridge Asp166 and Lys168;²⁹ Thr201 is at hydrogen bonding distance from Lys168 and Asp166, see Fig. 5. As mentioned in the FMO section, the interaction between any two fragments is considered, meaning we can extract ΔΔE_IJ between Thr201 and the two relevant residues (all other interaction energy differences, except that between Thr201 and the reaction center fragment, are <1 kcal mol⁻¹). The ΔΔE_IJ, presented in Fig. 5, between Thr201 and Lys168 and Asp166, respectively, reveals a balance between stabilizing (−4.4 kcal mol⁻¹) the former and destabilizing (2.2 kcal mol⁻¹) the latter. Indeed, a Thr201Ala mutation renders the enzyme inactive to autophosphorylation.²⁹ This effect is not captured at all in the DTSS calculations since the direct interaction with the reaction center complex is rather weak.¹⁶ In the QM/MM study by Cheng et al. the impact of Thr201 is difficult to interpret since the stabilization effect depends on the model system of choice, although the Thr201 in both models is described with the MM potential.¹³

Fig. 5 Structure of Thr201, Asp166 and Lys168 in which the hydrogen bond distance in the IS and TS (in parenthesis) is marked out together with the FMO interaction energies of Asp166 and Lys168 with Thr201.

It seems the net stabilizing effect from Thr201 comes from secondary interactions with the reaction center, through its direct bonding with Asp166 and Lys168, something that is neglected in the DTSS method; an effect that is clearer when considering the relative deletion energy of Thr201, but we will return to that in the subsequent section.

Deletion energies

In Fig. 6, the computed relative deletion energies are shown. We note that the relative deletion energies for some of the residues are considerably higher than the original activation energy of 19.5 kcal mol⁻¹. A deletion of Lys72 and Asp166 leads to relative deletion energies of 28.4 kcal mol⁻¹ and 32.5 kcal mol⁻¹. In addition, deleting Phe54 and Thr201 increases the activation energy by 4.5 kcal mol⁻¹ and 7.9 kcal mol⁻¹, respectively. These results are correlated to the interaction energy differences in Fig. 4; deleting a residue that stabilizes the TS naturally leads to an increase in activation energy. Analogously, the relative deletion energy of Lys166, which is 2.1 kcal mol⁻¹, can be related to the fact that Lys166 strongly destabilizes the TS.

Fig. 6 Relative deletion energy of activation as a function of the deleted residue. The relative deletion energies are compared to the activation energy without deletion (indicated with a dashed line) computed at the FMO-MP2/6-31g(d) level. If ΔE_del is smaller than the E_act, the bar is blue colored, while if ΔE_del is larger than E_act, the bar is red colored.

As was seen also in ref. 8, the expected behavior of the relative deletion energy should intuitively follow that of the interaction energy differences in Fig. 4, i.e. if ΔΔE_IJ > 0 (destabilization) for a residue at a given reaction step, then ΔE_del < E_act, but not necessarily the magnitude of the energy differences. Typically, the interaction energy difference is larger in magnitude than the relative deletion energy.

To simplify comparison between the properties we compare in Fig. 7 the energy difference E_act − ΔE_del with the FMO interaction energies in Fig. 4. In the case of Thr201, the impact of the virtual deletion on the activation energy exceeds the interaction energy between Thr201 and the reaction center fragment, while for the other key residues the opposite is observed. This is interesting due to the secondary nature of the interaction of Thr201 with the reaction center complex, i.e. Thr201 binds to residues that are directly involved in the reaction through interactions with the substrate. Like in ref. 8, we find that the relative deletion energy is able to capture secondary interactions, i.e. interactions that are not directly considered by ΔΔE_IJ.

Fig. 7 Comparison of FMO calculated interaction energy differences (ΔΔE_IJ), indicated with red bars, with the difference between the activation energy and the relative deletion energy (E_act − ΔE_del) for each deleted residue, visualized with blue bars.

Using the deletion energy to evaluate the importance of key residues to the reaction is clearly powerful since it includes all effects that are captured with ΔΔE_IJ and yields additional information as well, like in the case of Thr201. In addition, the simplicity of using FMO as it requires but two calculations, the IS and TS, makes the approach very efficient. We postulate that this approach can be an interesting tool in rational design of enzyme catalysts as it offers a fast, simple and accurate way of exploring the involvement of all residues in the system of investigation.

Conclusion

Using the FMO method, the PKA catalyzed phosphoryl transfer has been studied. With this method the molecular system is partitioned into fragments, where each fragment is treated ab initio (MP2/6-31G(d) in the present study) and interacts with the others in the electrostatic potential of the entire system. To evaluate the accuracy of the method, transition state stabilization energies due to the interactions between individual residues and the reaction center have been computed and compared to results obtained with the DTSS method in ref. 16. In the FMO approach the fragment describing the reaction center is slightly larger than that used in the DTSS study and contains also the Asp184 residue as well as both the Mg²⁺ ions. Despite this, near-quantitative agreement is obtained between the methods, although some deviations are observed. These deviations seem, however, to arise from the inclusion of polarization effects due to the surrounding system in the FMO interaction energy between a key residue and the reaction center. We note especially the considerable stabilization effect of Thr201 captured with FMO and neglected with DTSS. Since the FMO results in most cases are in near quantitative agreement with the DTSS method, FMO offers a feasible alternative to investigate stabilization effects of the residues in an enzyme system. In addition, the simplicity of requiring but two calculations, one for the IS and one for the TS, makes it computationally efficient and user-friendly, especially since fragmentation across covalent bonds seems not to affect the outcome.

Relative deletion energies, which consider the effect on the activation energy by the virtual deletion of a residue, have also been calculated. Results from these are largely consistent with the conclusions based on the stabilization energies. However, relative deletion energies are found to capture secondary interactions with the reaction center, which typically are neglected when considering stabilization energies based on interaction energies. This finding is in agreement with the results of an earlier study.⁸

Deletion energies in the FMO framework can become an important tool for investigate key residues and their impact on enzyme catalyzed reactions.

Acknowledgements

T. B. acknowledges support from the Swedish Research Council (VR). The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre at Linköping University. We thank Prof. W. Andrzej Sokalski for valuable discussions and Dr Edyta Dyguda-Kazimierowicz for providing the structures used in the present study.

References

1. D. Baker, Protein Sci., 2010, 19, 1817–1819.
2. D. Rothlisberger, O. Khersonsky, A. M. Wollacott, L. Jiang, J. DeChancie, J. Betker, J. L. Gallaher, E. A. Althoff, A. Zanghellini, O. Dym, S. Albeck, K. N. Houk, D. S. Tawfik and D. Baker, Nature, 2008, 453, 190–195.
3. M. Garcia-Viloca, J. Gao, M. Karplus and D. G. Truhlar, Science, 2004, 303, 186–195.
4. D. G. Fedorov and K. Kitaura, J. Chem. Phys., 2004, 120, 6832.
5. I. V. Polyakov, B. L. Grigorenko, A. A. Moskovsky, V. M. Pentkovski and A. V. Nemukhin, Chem. Phys. Lett., 2013, 556, 251–255.
6. T. Nakamura, A. Yamaguchi, H. Kondo, H. Watanabe, T. Kurihara, N. Esaki, S. Hirono and S. Tanaka, J. Comput. Chem., 2009, 30, 2625–2634.
7. T. Ishikawa, R. R. Burri, Y. O. Kamatari, S. Sakuraba, N. Matubayasi, A. Kitao and K. A. Kuwata, Phys. Chem. Chem. Phys., 2013, 15, 3646–3654.
8. M. Ito and T. Brinck, J. Phys. Chem. B, 2014, 118, 13050–13058.
9. D. G. Fedorov, T. Nagata and K. Kitaura, Phys. Chem. Chem. Phys., 2012, 14, 7562–7577.
10. E. Dyguda-Kazimierowicz, W. A. Sokalski and J. Leszcynski, J. Mol. Model., 2007, 13, 839–849.
11. W. A. Sokalski, J. Mol. Catal., 1985, 30, 395–410.
12. B. Szefcyk, A. J. Mulholland, K. E. Ranaghan and W. A. Sokalski, J. Am. Chem. Soc., 2004, 126, 16148–16159.
13. Y. Cheng, Y. Zhang and J. A. McCammon, J. Am. Chem. Soc., 2005, 127, 1553–1562.
14. M. Valiev, R. Kawai, J. A. Adams and J. H. Weare, J. Am. Chem. Soc., 2003, 135, 9926–9927.
15. N. Diaz and J. Field, J. Am. Chem. Soc., 2004, 126, 529–542.
16. P. Szarek, E. Dyguda-Kazimierowicz, A. Tachibana and W. A. Sokalski, J. Phys. Chem. B, 2008, 112, 11819–11826.
17. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
18. K. Kitaura, E. Ikeo, T. Asada, T. Nakano and M. Uebayasi, Chem. Phys. Lett., 1999, 313, 701–706.
19. D. G. Fedorov, R. M. Olson, K. Kitaura, M. S. Gordon and S. Koseki, J. Comput. Chem., 2004, 25, 872.
20. D. G. Fedorov and K. Kitaura, in Modern methods for theoretical physical chemistry of biopolymers, ed. E. B. Starikov, J. P. Lewis and S. Tanaka, Elsevier, Amsterdam, 2006, pp. 3–38.
21. T. Nakano, T. Kaminuma, T. Sato, Y. Akiyama, M. Uebayasi and K. Kitaura, Chem. Phys. Lett., 2000, 318, 614–618.
22. M. Valiev, J. Yang, J. A. Adams, S. S. Taylor and J. H. Weare, J. Phys. Chem. C, 2007, 111, 13455–13464.
23. D. A. Johnson, P. Akamine, E. Radzio-Andzelm, M. Madhusudan and S. S. Taylor, Chem. Rev., 2001, 101, 2243–2270.
24. J. C. Hart, I. H. Hillier, N. A. Burton and D. W. Sheppard, J. Am. Chem. Soc., 1998, 120, 13535–13536.
25. M. C. Hutter and V. Hems, Protein Sci., 1999, 8, 2728–2733.
26. P. F. Cook, E. D. Lowe, E. D. Chrysina, V. T. Skamnaki, N. G. Oikonomakos and L. N. Johnson, Biochemistry, 2002, 41, 7301–7311.
27. M. Y. Yoon and P. F. Cook, Biochemistry, 1987, 26, 4118–4125.
28. M. Madhusudan, E. A. Trafny, N. H. Xuong, J. A. Adams, L. F. Teneyck, S. S. Taylor and J. M. Sowadski, Protein Sci., 1994, 3, 176–187.
29. M. J. Moore, J. R. Kanter, K. C. Jones and S. S. Taylor, J. Biol. Chem., 2002, 277, 47878–47884.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02623k

---