 Open Access Article
Open Access ArticleSelf-assembly behaviours of primitive and modern lipid membrane solutions: a coarse-grained molecular simulation study†
Noriyoshi
Arai
 *a,
Yuki
Yoshimoto
a,
Kenji
Yasuoka
b and
Toshikazu
Ebisuzaki
c
*a,
Yuki
Yoshimoto
a,
Kenji
Yasuoka
b and
Toshikazu
Ebisuzaki
c
aDepartment of Mechanical Engineering, Kindai University, Higashiosaka, Osaka, Japan. E-mail: arai@mech.kindai.ac.jp; Fax: +81 6 6727 2024; Tel: +81 6 4307 3483
bDepartment of Mechanical Engineering, Keio University, Yokohama, Japan
cComputational Astrophysics Laboratory, RIKEN, Wako, Saitama, Japan
First published on 29th June 2016
Abstract
Researchers have studied the origin of life and the process of evolution on early Earth for decades. However, we lack a comprehensive understanding of biogenesis, because there are many stages in the formation and growth of the first cell. We investigate the self-replication processes of coacervate protocells using computer simulations of single-chain lipid and phospholipid aqueous mixtures. Based on a morphological phase diagram, we develop a model of prebiotic self-replication driven by only environmental factors (i.e. temperature and lipid concentrations) without any external force. Moreover, we investigate high concentration structures during the process of self-replication. These structures have an advantage in fusion and repair of cell membranes. Therefore, lipid hot spots may have existed in primordial soup.
1 Introduction
Alexander Oparin came out with “The Origin of Life”1 in 1936. In the book, he proposed the “coacervate theory” to explain the origin of life on the early Earth. A coacervate is a tiny spherical droplet of assorted lipids that spontaneously forms when concentrated mixtures of macromolecules occur at the right temperature, ion, and pH conditions. Since coacervates resemble living cells, Oparin suggested that they were the precursors to the first life. However, in modern theories, coacervates are no longer considered to be direct precursors to the first cells; life is thought to have gone through many intermediate steps before becoming cellular.Sutherland's group discovered that pyrimidine nucleotides can be readily synthesized from ribose, a simple prebiotic molecule, bypassing the more difficult routes.2 This discovery offers persuasive support for the RNA world hypothesis.3 It was a significant step to explain how a complex molecule like a ribonucleic acid (RNA) was formed on the primitive Earth. Alternative models of prebiotic evolution include the peptide nucleic acid (PNA) world hypothesis,4 protein world hypothesis,5 and panspermia hypothesis.6,7
We focus on the self-replication processes of primitive coacervate cells in the primordial soup. All cells are wrapped in membranes that consist mainly of lipids. Cell membranes collect cellular constituents together and prevent the free penetration of large molecules. Modern cell membranes are composed of lipids, cholesterols, and functional proteins. Some proteins are capable of selective water transport,8–10 and have a function of constructing and repairing membranes.11,12 On the other hand, the primitive protocell can accomplish these tasks without proteins. Moreover, it has metabolic and self-replicative functionality. The earliest life may have been simple fatty acid membranes self-replicating in water. Protocells would compete against each other by proliferating, and then adapt to their surroundings. Growth and division are two processes necessary for protocell proliferation.
The study of the fatty acid may lead to the elucidation of the origin of terrestrial life. In the 1990s, Luisi et al.13 added fatty acids to a vesicular solution. These workers observed that when a fatty acid is introduced to the vesicle membrane, the surface area and volume increase. Chen et al.14,15 carried out an experiment on the control of the concentration in a vesicular solution. When a concentration gradient arises across the interior and exterior of a vesicle, water molecules intrude into the vesicle by an osmotic pressure to equalize the concentration between the interior and exterior, and then, tension of the membrane increases. To decrease its membrane tension, the high-tension vesicle grows by competing with nearby vesicles for additional fatty acids.
The nearby vesicles losing their fatty acids shrink and disappear. Zhu et al.16,17 found that spherical vesicles form filament-like shapes with their growth. The filament-like vesicle is fragile; by weak external force, it disaggregates into smaller vesicles, which are spherical protocells. Szostak et al. argued that these processes facilitated many rounds of self-replication.
Self-assembled structures such as micelles, vesicles and bi-layer membranes have already been reported.18–21 Recent studies use functional molecules or heterogeneous lipid mixtures to control self-assembled structures. Morrow et al.19 used a molecular dynamics method to simulate pH-sensitive surfactant solutions. These authors demonstrated pH-dependent morphologies including the formation of a gel-state bilayer at low and intermediate pH, and a spherical micelle at high pH. Chen and Hao20 performed molecular simulations to determine a phase diagram of self-assembly in cationic–anionic surfactant mixtures. This simulation result indicated that the aggregation number, shape, and composition respond to changes in the surfactant ratio. Hu21 used dissipative particle dynamics simulations to investigate the self-assembly in lipid and dendritic molecule mixtures at varying hydrophilic/hydrophobic ratios. Structures characteristic of different mixing ratios include the high-genus vesicle, toroidal vesicle, oblate vesicle, and perforated vesicle. However, the self-assembly behaviour of the fatty acid itself has not been investigated fully.22–24
We investigate the potential for oleic acid and dipalmitoylphosphatidylcholine to have been primitive biomolecules. We present a detailed phase diagram at different vol% of molecules and temperature, using coarse-grained molecular simulations. Based on the result, we discuss the morphological features of a mechanism of self-replication proposed by Szostak et al.14–17
2 Method and models
2.1 Dissipative particle dynamics
Dissipative particle dynamics25–28 (DPD) is a powerful mesoscopic simulation tool enabling the simulation of events occurring in millisecond timescales and on micrometre length scales. DPD particles represent coarse-grained atoms or molecules subject to three types of forces: conservative, dissipative, and random. Since its introduction a decade ago, this method has been used to model various biomolecular systems, including the rupture and reconstruction of the cell membrane,29–31 DNA controlled assembly,32,33 and movement of a molecular motor.34,35 We also employ the DPD method to simulate fatty acid and phospholipid solutions, and to investigate their morphologies depending on the concentration and temperature.The motions of DPD particles obey Newton's equations of motion,
 | (1) |
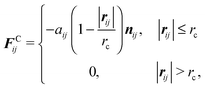 | (2) |
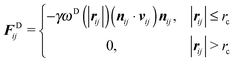 | (3) |
 | (4) |
The dissipative force and the random force are linked by the fluctuation–dissipation theorem,27 thereby one of the two weight functions appearing in eqn (3) and (4) can be chosen arbitrarily with a relation between the amplitude and kBT,
| σ2 = 2γkBT, | (5) |
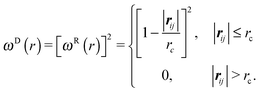 | (6) |
2.2 Simulation model and conditions
We adopted a mesoscopic representation of the molecular components of the system, namely, oleic acid (OA), dipalmitoylphosphatidylcholine (DPPC), and water, as shown in Fig. 1. The OA and DPPC are primitive and modern components of the cell membrane, respectively. The coarse-grained OA model consists of three kinds of beads: hydrophobic head beads, H1, and hydrophobic tail beads, T1 and T2. The coarse-grained DPPC model also uses three kinds of beads: hydrophobic head beads, H2 and H3, and hydrophobic tail beads, T1. A pair of nearest-neighbour beads in the mesoscopic models is connected by a harmonic spring with a spring constant ks of 100 kBT/rc2, and an equilibrium bond length rs of 0.86 rc. The spring force is given by FSij = −ks(|rij| − rs)nij. A single water bead, W, corresponds to four or five water molecules. The interaction parameters aij between bead pairs are shown in Table 1. To determine the interaction parameters of the mesoscopic simulation models, we used J-OCTA simulation software.36 This software estimates the cohesive energy, solubility, the Flory–Huggins parameter, and the equilibrium structures of OA and DPPC. The interaction parameter of the same kind of bead (aii) can be determined from dimensionless compressibility parameters.28,37 In this study, we set aii = 147.71 kBT/rc. On the other hand, the interaction parameter for different kinds of beads (aij) is obtained by the equation aij = aii + 3.268χij where χ is the Flory–Huggins parameter when the number density ρ = 3.0. The noise parameter σ and friction parameter γ are set at 3.0 and 4.5, respectively.| H1 | H2 | H3 | T1 | T2 | W | |
|---|---|---|---|---|---|---|
| H1 | 147.71 | 148.58 | 147.73 | 195.84 | 187.21 | 155.24 |
| H2 | 148.58 | 147.71 | 148.89 | 209.66 | 199.82 | 150.98 |
| H3 | 147.73 | 148.89 | 147.71 | 193.75 | 185.32 | 156.09 |
| T1 | 195.84 | 209.66 | 193.75 | 147.71 | 148.13 | 241.43 |
| T2 | 187.21 | 199.82 | 185.32 | 148.13 | 147.71 | 229.22 |
| W | 155.24 | 150.98 | 156.09 | 241.43 | 229.22 | 147.71 |
We can convert the reduced length unit to SI units by examining the membrane thickness. Usually, the thickness of a DPPC bilayer is about 4.7 nm in vitro.38 Considering that the thickness is about 4.4rc in our simulations, we can yield rc ∼ 1.06 nm.
Two series of computer simulations are carried out in this study. The first series simulates OA solutions and the second series simulates DPPC solutions. To illustrate the phase diagram, we select the concentration c and temperature T as axes. Each initial configuration is random, and the equilibrated systems are simulated in constant-volume and constant-temperature ensembles. A periodic boundary condition is adopted for all directions of the simulation cells. We used cell length (L) values of 15.9, 21.2, 26.5, 31.8, and 42.4 nm. For each L and molecular model, we performed 80 simulations, i.e. four different temperatures ranging from 0.5 to 2.0 kBT and 20 different concentrations ranging from 2.5 to 100%.
To give an estimate of the values of the reduced temperatures T* in terms of physical temperatures T, we have mapped T* onto T according to the linear relation,39i.e. T = aT* + b. The values of the coefficients a and b were obtained using the reduced and physical values of the melting point, and the OA vesicle disruption temperatures.40 The resulting values are a = 21.7 °C and b = 4.3 °C. For the DPPC lipid, we found that a and b are 8.6 °C and 32.6 °C, respectively.
3 Results
3.1 Morphologies of OA solution
Firstly, we studied phase behaviour of OA solutions. In Fig. 2, we show a phase diagram of the system and representative snapshots of equilibrium morphologies. The vertical axis of the phase diagram is the temperature T and the horizontal axis is the concentration c of the OA monomers.As expected, some micelles are formed at very low concentration (c ≤ 20%). Randomly dispersed OA molecules aggregated into several isolated spherical micelles for a short time period. After that the spherical micelles collided with each other, and fused together if they overcame an energy barrier. Eventually, the micelles transitioned to other shapes, depending on the aggregation number. When T ≥ 25 °C, collisions and fusions of micelles occurred frequently. A spherical vesicle (Fig. 2b) is formed at c ∼ 10%. As T increased beyond 45 °C, a tube-like vesicle appeared. The tube-like vesicle was also observed as a filamentous vesicle in vitro.15 On the other hand, at lower T, the collision of micelles occurred rarely. Moreover, the curvature of the aggregated structure decreased at low temperature.41,42 Each micelle had low mean aggregation and low flexibility; accordingly, the vesicle could not form even at c ∼ 20%; however, a disk like micelle emerged (Fig. 2a). As c increased to ∼30%, a cell membrane is formed (Fig. 2c). The membrane stemmed from an opened vesicle, which became more stable than the closed vesicle as c increased.
With further increasing c, a threadlike micelle or a filamentous vesicle composed of excess OAs budded from the membrane, and a bi-layer with a column structure was observed (Fig. 2d). The bud grew up thicker and wider as c increased. A cross bi-layer, which is two bi-layers crossed perpendicularly, emerged at c ∼ 55% (Fig. 2f). However, when the temperature was high (T = 45 °C), the membrane fluctuated rapidly. The column did not develop, but a double bi-layer is formed (Fig. 2e). When c was higher than 60%, the bi-layers intricately intertwined, forming a complex network structure (Fig. 2f). As c increased further, several water domains emerged separately, and a sponge-like phase (Fig. 2h) emerged in the range of 70% < c < 90%. When water was almost exhausted from the system, a gyroid (Fig. 2i) or hexagonal phases emerged at low temperature; at high temperatures, the ordered structure was broken up, and a phase-separated morphology emerged (Fig. 2k).
To confirm the reproducibility of our observations, we carried out five independent simulations for some conditions. Our replicate simulations included conditions for forming a vesicle, bi-layer, and bi-layer with a column. Each simulation was begun with randomized initial parameters; the final morphologies were nearly the same, regardless of the initial parameters.
3.2 Morphologies of DPPC solution
Next, we draw the phase diagram for the DPPC lipid solution in order to show that the above-mentioned argument does not depend on the biomolecule; this argument even applies to a modern phospholipid. In Fig. 3, we show the T versus c phase diagram, and representative snapshots of equilibrium morphologies. The vertical axis of the phase diagram is the temperature T, and the horizontal axis is the concentration of the DPPC monomers c.From low c through moderate c, micelles (Fig. 3a), vesicles (Fig. 3b), and bi-layers (Fig. 3c and d) formed as easily from DPPC as they formed from OA. The bi-layer of DPPC is slightly thicker than that of OA because of the size of the molecule. Whereas the vesicle emerged at T ≥ 25 °C in the OA solution, it emerged at T ≥ 35 °C in the DPPC solution. As c increased to 40%, a bi-layer with a column (Fig. 3d) formed. With further increasing c, water molecules were wrapped in the column, and then it grew thicker. As c continued to increase, the mixture exhibited a network morphology (Fig. 3e), followed by a sponge morphology (Fig. 3f). At c ∼ 85% and T ≤ 45 °C, the body centred cubic (BCC) structure (Fig. 3g) emerged. Eventually, at c ∼ 95%, a disordered and phase-separated morphology emerged at all temperatures (Fig. 3h).
4 Discussion
In our simulations, a phospholipid constituting modern membranes and a primitive fatty acid exhibit various morphologies and phases depending on their concentrations and temperatures in water. In both solutions, a bi-layer membrane is formed at c ∼ 20% (Fig. 2c and 3d). As c increases, a threadlike micelle or a filamentous vesicle, composed of excess lipids, comes out from it (Fig. 2d and 3e). This behaviour corresponds to a “vesicle budding”, in which the excess part is unstable compared to the membrane bi-layer.43–45 Therefore, it is torn easily by an environmental factor or thermophysical property. Actually, it is experimentally observed17 that a long filamentous vesicle is a fragile aggregate, and is easily divided into multiple vesicles by an external shear force.The fluctuations of each lipid increase naturally if the temperature increases. The excess part, such as a tube-like vesicle, is divided from the membrane (Fig. 2d and 3d) when temperature of the aqueous solution increases. After that, the divided parts aggregate to form a spherical vesicle (vesiculation); the exposed hydrophobic groups are surrounded by water, and consequently become a new protocell (Fig. 4).
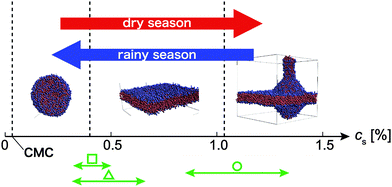 | ||
| Fig. 4 A schematic depicting concentration-dependent transitions in protocell morphology. Red and blue arrows represent increasing and decreasing concentration, respectively. Points are early experimental conditions as follows. Square: The data reported by Zhu et al.,17 circle: the data reported by Budin et al.,51 triangle: the data reported by Zhu et al.16 (CMC: critical micelle concentration and CMC for oleic acid = 0.03%53). | ||
First, fatty acids (or lipids) collected in a puddle on the early Earth. They gathered mutually by a chemical interaction, and as a result, many micelles and vesicles formed (as modelled by the coacervate theory). During the dry season, the concentration of the lipid would increase due to evaporation from the puddle. Accordingly, micelles and vesicles would merge into giant vesicles, which do not have local curvatures, and can be regarded as a flat membrane locally (Fig. 2c). With further increasing concentration, tube-like vesicles would bud from the membranes. After that, as the temperature increased (due to seasonality or a local heat source), bud fission would occur. Then during the rainy season, concentration and temperature would decrease, and the fission products would have become new protocells. This sequence would be repeated over a long period of time.
It is known that morphological phase boundaries depend on the size of the lipid–water system. For example, the simulational concentration (c) of about 30% yields a periodic bilayer when the system size is 15.93 nm3. However, this bilayer forms at c ∼ 18% when the system size is 42.43 nm3. In other words, the concentration at which a particular morphology is observed decreases exponentially with the increasing system size. We used five simulation box sizes to investigate the effect of size on morphology, and estimated a scaling factor for the concentration in our simulations (see the ESI†). The concentration at which the bilayer membrane is formed decreases exponentially with the increasing length of a side of the cubic simulation box. The data are fitted to the function of f(x) = AxB, where A and B are constant. Next, we estimated the scaled physical concentration (cs) on the early Earth by fitting with an actual size by those curves. As a result, in our simulation, the vesicle appears in the cs range of about 0.1–0.8%, consistent with in vitro observations of, 0.28–0.85%.15,17 Actually, the early processes of cell division and growth are thought to be functions of the giant sizes (1 μm order) at which many vesicles probably existed.46,47 If the system sizes were set to 103 μm3, we calculate that the lipid concentrations necessary for bilayer and budding bilayer formation would be 0.55% and 1.05%, respectively. In light of the estimated error arising from our use of a power function fit to five values, the lipid concentration necessary to form a bilayer ranges from 0.48% to 0.62%. Therefore, coacervates proliferate if concentrations change by more than 1% (e.g., due to seasons).
Next, we consider the physical meaning of the fitted curve's constant in Fig. S1 (ESI†). The concentration (CBL) at which the bilayer is formed is attenuated with the box length L (slope factor −0.58). However, the slope factor of CBL for L is generally −1.0. The explanation is as follows. The concentration CBL, density ρ, and area density of the membrane ρa are given by Nl/N, N/L3, and Nl/L2, respectively. Here, Nl is the number of lipid molecules. The concentration can be expressed as
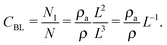 | (7) |
 | (8) |
As shown in Fig. 4, due to slight changes in concentration, various self-assembly structures or phases arise. For that reason, when the concentration of OA is more than 1.05% in the dry-season (concentration-increasing processes), the tubes budding from the bi-layers grow, leading to the cross bi-layer (Fig. 2f) and network (Fig. 2g) morphologies. These structures have many small chambers (water domains separated by a bi-layer). We can regard each small chamber as a small vesicle separated by cell membranes. This transition corresponds to the processes of vesicle fusion. In this state, since the volume of a cell membrane is relatively low, the rate of chemical interaction for a nucleotide and its precursors phosphoric acid, sugar, and amino acid would be enhanced. It is expected that were these materials to have different concentrations between neighbouring chambers, osmolality gaps would facilitate the exchange of chemicals across membranes. Also, these chambers constantly fuse and divide due to thermal fluctuation. In other words, it is expected that self-replication is achieved without external stimuli, for example, shear or electric forces.17,48 Moreover, in this study, to investigate basic processes of cell division, we employed the primitive biomolecule, OA, and simulated simple OA solutions. However, in modern cell membranes, not only a primary lipid, but also steroids, cholesterols, and proteins coexist.49 They have complex structures and functions, and diffuse throughout the modern cell membrane. Therefore, in high-concentration phases (network and sponge), when membrane is damaged, lipids or proteins are easily exchanged for membrane from a neighbouring chamber by translational and flip-flop motions.
To represent the origin of life, several experiments using an oleic acid vesicle have been carried out in recent years.16,17,50,51 The Szostak group proposes that vesicle replication is mediated through cycles of growth and division of vesicles. Zhu et al.16 prepared unilamellar fatty acid vesicles using the dehydration/rehydration method, and applied various shear rates to the solution. As a result, many spherical (daughter) vesicles were formed from long filamentous vesicles with modest shear forces. These authors mention that vesicle pearling and division have important implications for understanding the origin of cellular life.
Budin et al.51 investigated the concentration dependence of fatty acid aggregation. They observed different phases in the fatty acid solutions, including soluble monomers, micelles, and lamellar vesicles, depending on concentration and pH. The micelle–vesicle equilibrium is changed by the concentration: lower concentrations favour smaller micellar aggregates, and higher concentrations favour larger vesicle aggregates. They reported that the micelle–vesicle equilibrium can be used to drive the growth of vesicles upon increasing the amphiphile concentration. Based on this experimental result, they proposed a model for a driven cell cycle.
Zhu et al.17 described an alternative process for protocell division based on simple chemical mechanisms. In their model, protocell division is facilitated by thiol-rich surface environments featuring UV-absorbing polycyclic aromatic hydrocarbons. They suggested that the control of the timing of cell division by the thiol redox state is a mechanism by which an initial dependence on environmental fluctuations could have transitioned to an internally controlled process. The temperature and monomer concentration conditions reported for these in vitro experiments (plotted in Fig. 4) are consistent with the phase boundaries that we observe in silico. This result strongly supports our discussion.
At low OA or DPPC concentrations, a similar vesicle, bi-layer, and bi-layer with column morphologies arise depending on the concentration. However, these self-assembled structures are observed at DPPC concentrations slightly higher than their OA counterparts, because the molecular structure of DPPC is more complex than that of OA. Also, since the 41.3 °C melting temperature of DPPC52 is relatively high, the temperature at which DPPC vesicles form is slightly higher than that for OA vesicles. Therefore, for a modern lipid, prebiotic proliferation proceeds via changing the concentration and temperature, similar to the primitive molecule but at slightly elevated concentrations and temperatures. This observation suggests that the process we report is common to biomolecules, though morphological phase boundary concentrations and temperatures depend on the molecular participants.
5 Conclusions
We modelled the morphological behaviour and temperature–concentration phase diagrams of prebiotic solutions featuring oleic acid and DPPC. A vesicle, membrane (a giant vesicle), and membrane with a vesicle tube are continuously formed at different concentrations and temperatures. Temperature and concentration changes were caused by environmental variations on the early Earth; concentration changes would have resulted from seasonal increases or decreases in the water volume of the primordial soup. Seasonality would have also driven temperature changes, as would have the movement of vesicles across a temperature gradient (perhaps due to geothermal heating).High-concentration structures correspond to states when vesicles are quite close, or in the middle of fusion. These structures have an advantage in the fusion and repair of cell membranes. Hence, during the process of self-replication, locally high concentrations of lipid hot spots may have existed in the primordial soup.
Acknowledgements
We thank Dr T. Ozawa and Mr T. Nakayama (JSOL Corporation) for assistance with the construction of parameters for mesoscopic models.References
- A. I. Oparin, The origin of life, The Macmillan Company, US, 1938 Search PubMed.
- M. W. Powner, B. Gerland and J. D. Sutherland, Nature, 2009, 459, 239–242 CrossRef CAS PubMed.
- W. Gilbert, Nature, 1986, 319, 618 CrossRef.
- P. E. Nielsen, M. Egholm, R. H. Berg and O. Buchardt, Science, 1991, 254, 1497–1500 CAS.
- K. Ikehara, Int. J. Mol. Sci., 2009, 10, 1525–1537 CrossRef CAS PubMed.
- I. S. Shklovskii and C. Sagan, Intelligent life in the universe, Dell, NY, 1966 Search PubMed.
- F. H. Crick and L. E. Orgel, Icarus, 1973, 19, 341–346 CrossRef.
- P. Agre, G. M. Preston, B. L. Smith, J. S. Jung, S. Raina, C. Moon, W. B. Guggino and S. Nielsen, Am. J. Physiol., 1993, 265, F463–F476 CAS.
- P. Agre, L. S. King, M. Yasui, W. B. Guggino, O. P. Ottersen, Y. Fujiyoshi, A. Engel and S. Nielsen, J. Physiol., 2002, 542, 3–16 CrossRef CAS.
- P. Agre, Proc. Am. Thorac. Soc., 2006, 3, 5–13 CrossRef CAS PubMed.
- D. Bansal, K. Miyake, S. S. Vogel, S. Groh, C. C. Chen, R. Williamson, P. L. McNeil and K. P. Campbell, Nature, 2003, 423, 168–172 CrossRef CAS PubMed.
- C. Cai, H. Masumiya, N. Weisleder, N. Matsuda, M. Nishi, M. Hwang, J. K. Ko, P. Lin, A. Thornton, X. Zhao, Z. Pan, S. Komazaki, M. Brotto, H. Takeshima and J. Ma, Nat. Cell Biol., 2008, 11, 56–64 CrossRef PubMed.
- P. L. Luisi, P. Walde and T. Oberholzer, Curr. Opin. Colloid Interface Sci., 1999, 4, 33–39 CrossRef CAS.
- I. A. Chen, R. W. Roberts and J. W. Szostak, Science, 2004, 305, 1474–1476 CrossRef CAS PubMed.
- I. Budin and J. W. Szostak, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5249–5254 CrossRef CAS PubMed.
- T. F. Zhu and J. W. Szostak, J. Am. Chem. Soc., 2009, 131, 5705–5713 CrossRef CAS PubMed.
- T. F. Zhu, K. Adamala, N. Zhang and J. W. Szostak, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9828–9832 CrossRef CAS PubMed.
- N. Arai, K. Yasuoka and Y. Masubuchi, J. Chem. Phys., 2007, 126, 244905 CrossRef PubMed.
- B. H. Morrow, P. H. Koenig and J. K. Shen, Langmuir, 2013, 29, 14823–14830 CrossRef CAS PubMed.
- J. Chen and J. Hao, Phys. Chem. Chem. Phys., 2013, 15, 5563–5571 RSC.
- J.-M. Hu, W.-D. Tian and Y.-Q. Ma, RSC Adv., 2013, 4, 59785–59791 RSC.
- S. M. Sagnella, C. E. Conn, I. Krodkiewska and C. J. Drummond, Phys. Chem. Chem. Phys., 2011, 13, 13370–13381 RSC.
- J. F. D. Liljeblad, E. Tyrode, E. Thormann, A.-C. Dublanchet, G. Luengo, C. M. Johnson and M. W. Rutland, Phys. Chem. Chem. Phys., 2014, 16, 17869–17882 RSC.
- A.-L. Fameau, A. Arnould, M. Lehmann and R. von Klitzing, Chem. Commun., 2015, 51, 2907–2910 RSC.
- P. J. Hoogerbrugge and J. M. V. A. Koleman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- Y. Kong, C. W. Manke, W. G. Madden and A. G. Schlijper, Int. J. Thermophys., 1994, 15, 1093–1101 CrossRef CAS.
- P. Espanõl and P. B. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- X. Li, Y. Liu, L. Wang, M. Deng and H. Liang, Phys. Chem. Chem. Phys., 2009, 11, 4051–4059 RSC.
- N. Arai, K. Yasuoka and X. C. Zeng, Nanoscale, 2013, 5, 9089–9100 RSC.
- T. Yue, X. Zhang and F. Huang, Phys. Chem. Chem. Phys., 2014, 16, 10799–10809 RSC.
- S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, Nature, 2008, 451, 553–556 CrossRef CAS PubMed.
- P. Cigler, A. K. R. Lytton-Jean, D. G. Anderson, M. G. Finn and S. Y. Park, Nat. Mater., 2010, 9, 918–922 CrossRef CAS PubMed.
- N. Arai, K. Yasuoka, T. Koishi and T. Ebisuzaki, ACS Nano, 2010, 4, 5905–5913 CrossRef CAS PubMed.
- N. Arai, K. Yasuoka, T. Koishi, T. Ebisuzaki and X. C. Zeng, J. Am. Chem. Soc., 2013, 135, 8616–8624 CrossRef CAS PubMed.
- J-OCTA, JSOL Corporation, http://www., j-octa.
- R. D. Groot and K. L. Rabone, Biophys. J., 2001, 81, 725–736 CrossRef CAS PubMed.
- A. L. Liu, Advances in Planar Lipid Bilayers and Liposomes, Academic Press, 2006, vol. 3 Search PubMed.
- M. Venturoli, B. Smit and M. M. Sperottoz, Biophys. J., 2005, 88, 1778–1798 CrossRef CAS PubMed.
- P. L. Luisi and P. Stano, The minimal cell: The biophysics of cell compartment, The origin of cell functionality, Springer, Netherlands, 2010 Search PubMed.
- H. J. Risselada and S. J. Marrink, Phys. Chem. Chem. Phys., 2009, 11, 2056–2067 RSC.
- C.-P. Chng, Soft Matter, 2013, 9, 7294–7301 RSC.
- J. S. Bonifacino and B. S. Glick, Cell, 2004, 116, 153–166 CrossRef CAS PubMed.
- S. Yamamoto and S. Hyodo, J. Chem. Phys., 2003, 118, 7937–7943 CrossRef CAS.
- M. Laradji and P. B. S. Kumar, J. Chem. Phys., 2005, 123, 224902 CrossRef PubMed.
- F. Ilhan, T. H. Galow, M. Gray, G. Clavier and V. M. Rotello, J. Am. Chem. Soc., 2000, 122, 5895–5896 CrossRef CAS.
- Y. Yu, J. A. Vroman, S. C. Bae and S. Granick, J. Am. Chem. Soc., 2010, 132, 195–201 CrossRef CAS PubMed.
- H. Terasawa, K. Nishimura, H. Suzuki, T. Matsuura and T. Yomo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 5942–5947 CrossRef CAS PubMed.
- S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731 CAS.
- M. M. Hanczyc, S. M. Fujikawa and J. W. Szostak, Science, 2003, 302, 618–622 CrossRef CAS PubMed.
- I. Budin, A. Debnath and J. W. Szostak, J. Am. Chem. Soc., 2012, 134, 20812–20819 CrossRef CAS PubMed.
- R. Biltonen and D. Lichtenberg, Chem. Phys. Lipids, 1993, 64, 129–142 CrossRef CAS.
- K. Murakami, S. Y. Chan and A. Routtenberg, J. Biol. Chem., 1986, 261, 15424–15429 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02380k |
| This journal is © the Owner Societies 2016 |



