How surface reparation prevents catalytic oxidation of carbon monoxide on atomic gold at defective magnesium oxide surfaces

Abstract

In this contribution, we study using first principles the co-adsorption and catalytic behaviors of CO and O₂ on a single gold atom deposited at defective magnesium oxide surfaces. Using cluster models and point charge embedding within a density functional theory framework, we simulate the CO oxidation reaction for Au₁ on differently charged oxygen vacancies of MgO(001) to rationalize its experimentally observed lack of catalytic activity. Our results show that: (1) co-adsorption is weakly supported at F⁰ and F²⁺ defects but not at F¹⁺ sites, (2) electron redistribution from the F⁰ vacancy via the Au₁ cluster to the adsorbed molecular oxygen weakens the O₂ bond, as required for a sustainable catalytic cycle, (3) a metastable carbonate intermediate can form on defects of the F⁰ type, (4) only a small activation barrier exists for the highly favorable dissociation of CO₂ from F⁰, and (5) the moderate adsorption energy of the gold atom on the F⁰ defect cannot prevent insertion of molecular oxygen inside the defect. Due to the lack of protection of the color centers, the surface becomes invariably repaired by the surrounding oxygen and the catalytic cycle is irreversibly broken in the first oxidation step.

---

1 Introduction

Gold did not receive much attention as a catalyst due to its perfect inertness in the bulk form, until the first evidence for the catalytic activity of small gold clusters was reported in the early 1970s.^1–3 The work of Haruta et al. later confirmed promising catalytic properties of gold in the low-temperature regime for particles up to the nanoscale.^4–6 These findings stimulated a large number of further investigations aiming at explaining the high activity of various gold clusters (see, e.g., special issue,⁷ in particular ref. 8 and 9), resulting in two generally accepted concepts: the catalytic activity depends strongly on the shape and diameter of the gold cluster,¹⁰ and the support material has a large influence on the electronic properties of the gold clusters.¹¹

Experiments in the gas phase revealed that Au₂⁻ is the smallest catalytically active cluster for the CO oxidation reaction.¹² The negative charge of the gold cluster was found to be crucial for weakening the O₂ bond, thus explaining the cluster activity. At surfaces the charge of small supported gold clusters results from the electron redistribution between the cluster and the support, which is very sensitive to their specific interaction.¹³ In particular, the presence of oxygen vacancies in the metal-oxide support^14–16 and the proximity of an underlying metal support on oxide films of various thicknesses¹⁷ have been shown to have a large influence on the charge of deposited gold clusters. Due to its stability and comfortable handling in experiments,¹⁸ MgO is often chosen as a support for fundamental investigations on gold clusters. Experiments for the CO oxidation on selected Au_n clusters deposited on defect-rich MgO(001) films at low temperatures demonstrated high catalytic activity for clusters with more than 8 gold atoms. Limited catalytic activity is also observed for smaller systems such as Au_3–7/MgO(001), but none for Au_1,2/MgO(001).¹⁹

Theoretical investigations based on density functional theory have been performed to shed light on the reaction mechanism at selected clusters, mainly for Au₈@MgO(001) and Au₂₀@MgO(001) (see, e.g., ref. 20). These revealed that the gold clusters bind strongly to electron-rich oxygen vacancies, and that the oxidation reaction can proceed via both Eley–Rideal and Langmuir–Hinshelwood mechanisms. Comparatively little attention has been paid to the smaller, inactive clusters. For one, a joint theoretical-experimental spectroscopic study of the properties of CO on Au_1,2 at various defective sites (e.g., terraces, edges, etc.) has revealed the possibility of the initial formation of a positively charged cluster during the catalytic cycle, in which CO adsorption would precede oxygen adsorption.²¹ In the presence of oxygen, the number of these defective sites is relatively small, which may have led in the past to an overestimation of the role played by color centers as direct catalysts. On the other hand, the importance of color centers in catalysis on larger gold clusters is well established.^14–17 Here, we thus investigate a system in which these vacancies have been covered by gold clusters prior to introduction of the reagents. Arguing that Au_1–3 clusters would be too small to protect an oxygen vacancy in a mixed atmosphere, Amft and co-workers²² demonstrated by means of first principles calculations that catalytic oxidation of CO by Au₃ on defect-free MgO is sustainable.

In this work, we investigate the catalytic CO reaction with O₂ on the smallest possible gold cluster, Au₁, adsorbed on differently charged oxygen vacancies on the MgO(001) surface, in order to provide mechanistic understanding of its catalytic inertness. We aim at confirming by means of unbiased first principles calculations that surface reparation is the origin of this inertness, and explain how oxygen and carbon monoxide interact with gold atoms at defective magnesium oxide surfaces to nullify their catalytic activity. The study is based on density functional theory (DFT) using the periodic electrostatic embedded cluster method (PEECM), where the gold atom and part of the substrate are treated quantum mechanically and embedded into a periodic array of point charges to ensure a proper description of the Madelung potential in the vicinity of the adsorbates.²³ We first investigate the adsorption behavior of the bare gold cluster and the absorption of CO and O₂ thereon to get insights into the bonding properties of the system and to identify possible reaction pathways. In the second part, reaction profiles along minimal energy paths determined by nudged elastic band (NEB) calculations are presented, unambiguously showing that surface reparation by atomic oxygen intercalation will be favored over catalytic oxidation, whenever possible.

2 Computational details

The defective surface systems are studied by means of cluster embedding within a density functional theory (DFT) framework using the B3LYP hybrid functional.^24,25 Following Pacchioni and co-workers, a small symmetric cluster containing the color center, Mg₁₇O₁₂, surrounded by an intermediate pseudopotential region is embedded into a periodic array of point charges (PEECM).²³ The inner local part of the quantum mechanically treated cluster (QM) containing the color center is described using 6-311G and 6-31G* basis sets on Mg and O, respectively. Whenever deemed necessary, a ghost atom with a polarizable basis set (6-311+G*) is added in the vacancy to improve the description of the electron density in the color center. The adsorbate atoms C and O are described using a basis set of valence double zeta quality (6-311+G*), and the Au atom is represented using the valence double zeta basis associated with the 60 electron pseudo potential of Hay & Wadt.²⁶ An intermediate shell in the QM part composed of Mg²⁺ and O²⁻, described by a 10 electron pseudo potential due to Hay & Wadt²⁷ on Mg²⁺ and a point charge of −2 on O²⁻, separates the inner cluster from the periodic array of formal point charges, taking values +2 for Mg²⁺ and −2 for O²⁻. This intermediate shell prevents too strong polarization of the electron density in the QM part by adjacent positive point charges.²³ Convergence tests using the cluster adsorption energy and the HOMO–LUMO energy gap as criteria confirmed that the intermediate shell should count at least one layer between the inner local cluster and the array of point charges.

All calculated adsorption energies are counterpoise corrected, including fragment deformation²⁸ (notation: E^basis_structure(system)):

ΔE^CP_ads(AB) = −E^CP_AB(AB) + E^A_A(A) + E^B_B(B) (1)

The corrected interaction energy ΔE^CP_ads(AB) between fragments A and B is calculated as the difference between the counterpoise corrected energy E^CP_AB(AB) of the cluster AB and the energies of the optimized fragments A and B in their own bases, whereby E^CP_AB(AB) is corrected by the respective difference of the fragment energy in the complete basis and their own in the corresponding cluster conformation with:

E^CP_AB(AB) = E^AB_AB(AB) + (E^A_AB(A) − E^AB_AB(A)) + (E^B_AB(B) − E^AB_AB(B)). (2)

It was shown that, upon relaxation, the ions of the inner local part adjacent to the intermediate shell can lead to severe artifacts, i.e., the ions migrate in the array of point charges in an uncontrolled manner.²³ Consequently, all ions of the MgO slab are kept frozen during structural optimization, apart from the top 8 ions adjacent to the color center. During the numerical frequency analysis, all atoms except Au₁ and the adsorbates are frozen. Furthermore, the harmonic frequencies are scaled with a scaling factor of 0.97 to take into account the anharmonic effects.²⁹ All optimization and single point calculations have been performed using the TURBOMOLE^30,31 program package and the BFGS algorithm. Reaction energy profiles are computed using the Nudged Elastic Band method (spring constant: 0.5 eV Å⁻¹), for which the FIRE algorithm³² implemented in the ATOMIC SIMULATION ENVIRONMENT³³ was used in combination with TURBOMOLE.

3 Results and discussion

3.1 Adsorption behavior

Fig. 1 shows the adsorption energies E_ads of Au₁ and the adsorption height of the gold atom on these differently charged oxygen vacancies. Au₁ is observed to be adsorbed more strongly onto electron-rich oxygen vacancies, probably due to the larger electron charge transfer from the vacancies to the gold cluster. This trend is confirmed by the Mulliken charge of the cluster, which takes the value −0.40 e⁻, −0.03 e⁻, and +0.42 e⁻ for the F⁰, F¹⁺, and F²⁺ color centers, respectively. The pairing of an electron from the single gold atom and from the F¹⁺–MgO(001) surface appears to additionally increase the adsorption strength. The gold atom is also found to be much closer to the surface for the two positively charged cavities. These trends are in good agreement with the literature values, obtained at the periodic DFT/PBE level of theory.¹⁵ Interestingly, enabling the dispersion correction causes an approximately constant shift in the adsorption energy and height, with the literature value lying between both results for the electron-rich cases, F⁰ and F¹⁺. Whereas experimental adsorption energies are unavailable for defective surfaces, an overestimation of the interaction strength between adsorbate and ionic surfaces due to the DFT-D3 dispersion correction has already been reported by Grimme et al.³⁴ From EPR-experiments on clean a MgO(001) surface,³⁵ an activation barrier between 0.2 and 0.3 eV for the diffusion of a single gold atom is found. NEB calculations for the present cluster model using a clean surface result in a single-atom diffusion barrier of 0.45 eV with dispersion correction, and 0.27 eV without. The latter thus appears to yield more reliable energetic properties for reaction at the surface. Furthermore, the choice of functional (PBE vs. B3LYP) and of method (periodic DFT vs. PEECM) seems to affect only marginally the height of the gold atom in the two cases available for comparison. For consistency, we thus choose to calculate the following results without DFT-D3 dispersion correction. Consequently, the energetics of the physisorbed states depending on dispersion interaction should be taken with care.

Fig. 1 Adsorption properties of Au₁ on three differently charged defective terrace sites of MgO(001). Top panel: counterpoise corrected adsorption energy E_ads with (green) and without (blue) dispersion correction, compared to the literature values (red) are obtained from periodic DFT calculation using the PBE functional.¹⁵ Enabling the dispersion correction leads to an increase in the adsorption energy of between 0.98 and 1.11 eV. Bottom panel: height of the gold atom relative to the MgO surface plane (the same color labels as the top panel). The gold atom is found to remain further away from the F⁰–MgO(001) surface than in the positively charged cases. Inset: optimized structure for adsorption on Au₁/F⁰–MgO(001). The cluster favors adsorption on top of the color center in all cases. The lines serve as a guide to the eye.

The counterpoise corrected adsorption energies, various characteristic structural parameters, and internal stretching frequencies for the optimized CO or O₂ structures adsorbed on the three defective surfaces are summarized in Table 1. For each individual reagent, CO and O₂, geometry optimization is initiated by adding the adsorbates starting from slightly asymmetric configurations atop of the Au₁ cluster. The optimized structures, along with the associated adsorption energies on the cluster anchored to the different color centers, can be seen in the top panels of Fig. 2 and 4 for CO and O₂, respectively. The CO is seen to adopt an upright configuration atop the gold atom on the F²⁺ vacancy, with the carbon atom pointing towards the gold. On surface systems bearing a F¹⁺ or F⁰ color center, CO does not preferably adsorb atop Au₁ and the structures are tilted. Furthermore, in the case of the F¹⁺ oxygen vacancy, the structure is found to be a local minimum and the adsorption is slightly unfavorable (E_ads = −0.01 eV). The Mulliken charge analysis (bottom panel of Fig. 2) reveals that CO adsorbs preferentially on cationic Au₁ clusters. In particular, whereas the oxygen atom keeps hold of its electrons on all surfaces, the carbon atom is seen to give away some electron density to the more positively charged gold atom at the F²⁺ vacancy.

Fig. 2 Adsorption energies E_ads (top panel) and Mulliken charges (bottom panel) for CO on Au₁ deposited on the differently charged defect sites of MgO(001). The shown optimized structures are obtained without dispersion correction. The conformation depicted for the F¹⁺ color center corresponds to a meta-stable state. The literature adsorption energy for the F²⁺ color center (top panel, red triangle) is calculated using an embedded cluster at the DFT/B3LYP level of theory.²¹ The lines serve as a guide to the eye.

Table 1 Counterpoise corrected adsorption energies of CO, O₂ and the co-adsorbed CO + O₂ on the respective optimized surface system, as well as characteristic structural parameters and multiplicity (X = C, O). Available literature values appear in parentheses.²¹ All values are calculated without dispersion correction

	E ads(XO), eV	d(X–O), Å	d(Au–X), Å	ν(XO), cm^−1	〈S^2〉	Multiplicity
a Meta-stable state. b First order transition state.
CO + Au1/
F^0–MgO	0.09	1.156	2.504	1838	0.76	Doublet
F^1+–MgO^a	−0.01	1.127	3.310	2146	0.00	Singlet
F^2+–MgO	0.49 (0.21)	1.120 (1.123)	2.183	2205 (2207)	0.75	Doublet
O2 + Au1/
F^0–MgO	1.51	1.329	2.428	1164	0.76	Doublet
F^1+–MgO^b	−0.001	1.206	3.686	1580	2.01	Triplet
F^2+–MgO	0.03	1.204	2.877	1563	1.71	Spin cont.
CO + O2 + Au1/
F^0–MgO^b
CO	0.01	1.129	3.403	2135	0.76	Doublet
O2	1.39	1.328	2.442	1154
F^2+–MgO
CO	0.47	1.120	2.181	2201	1.76	Spin cont.
O2	0.01	1.206	3.573	1580

---

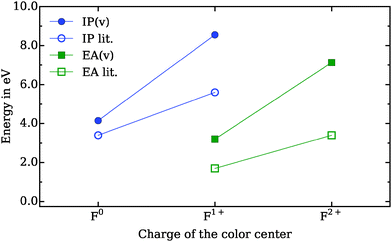Fig. 3 Vertical ionization potential (IP) and electron affinity (EA) of Fⁿ → Fⁿ⁺¹ + e⁻ and Fⁿ + e⁻ → Fⁿ⁻¹, respectively, compared to literature values.³⁶ Due to the restricted size and, as a consequence, restricted ability of polarization of the QM cluster, the deviation to the literature values increases with the number of electron holes. The lines serve as a guide to the eye.

Fig. 4 Adsorption energies E_ads, Mulliken charges and bond distances of O₂ on Au₁ deposited on the differently charged defect sites of MgO(001). The conformation on the F¹⁺ color center corresponds to a first order transition state. The red circle emphasizes a large spin contamination. The lines serve as a guide to the eye.

To assess the quality of the color centers description (F⁰, F¹⁺, F²⁺) located on a MgO(001) terrace sites, vertical ionization potentials (IP) and electron affinities (EA) are compared with literature values³⁶ in Fig. 3. For the F⁰ center the IP is found to be in good agreement with the reference but, although the trends are qualitatively correctly reproduced, deviations increase with the charge of the color center. The reason is twofold: (1) the restricted cluster size of the inner local part inhibits delocalization of the electron hole, and (2) relaxation of only the ions adjacent to the color center does not describe quantitatively the polarization of the lattice. This will affect electron density distribution and adsorption strength of the gold atom and the adsorbates, especially on the positively charged vacancies. In particular, the adsorption energy at the F²⁺ color center is found to be about twice as large (0.49 eV) as other theoretical estimates (0.21 eV, see Fig. 2), obtained using a shell model approach.²¹ The better description of lattice polarization in the latter might create a stronger bond with the gold atom (literature data not available) and modify the interaction strength with the adsorbed CO.

Note that a vast majority (85%) of color centers created by electron bombardment³⁷ are of the F⁰ type, with the remaining 10% and 5% as F¹⁺ and F²⁺ vacancies, respectively.³⁸ To confirm the quality of our embedding for the neutral vacancy, we calculated the adsorption energy atop the Mg²⁺-ion next to Au₁ in the Au₁/F⁰–MgO(001) case. The value (0.09 eV) is found to be similar to the adsorption behavior of CO on clean MgO(001) surfaces (0.14 eV).³⁹ All available structural parameters as well as the calculated C–O stretching frequencies are otherwise found to be in good agreement with previous theoretical work.²¹ The physical trend in frequency observed from F⁰ to F²⁺ (1838 to 2205 cm⁻¹) can be rationalized from the degree of π-back-donation from the gold atom to the adsorbate, which requires an angled conformation of the latter.⁴⁰ The weakening of the CO bond at the F⁰ color center correlates well with the longer bond length and the smaller vibrational frequency compared to the gas phase (2169.8 cm⁻¹).⁴¹ The weak interaction between Au₁ and CO at the F¹⁺ surface system is reflected in the CO stretching frequency similar to the value of the gas phase.

In the top panel of Fig. 4, O₂ is seen to be only weakly adsorbed on the neutral and cationic vacancies, with the preferred configuration lying almost parallel to the surface. For the F⁰ color center, while the molecule also adsorbes at the interface between the cluster and the substrate, one of the oxygen atoms lies almost on top of the gold atom. The result for the adsorption on Au₁ at the F²⁺ vacancy is seen to be highly spin contaminated (denoted by a red circle), pointing at a strong multi-reference character beyond the capabilities of the single-determinant DFT ansatz used here. The weak physisorption interaction of O₂ with the F¹⁺–MgO(001) surface (E_ads = −0.001 eV) is probably also underestimated by the present computational setup, as no dispersion correction has been included. In contrast, the strong interaction between O₂ and Au₁/F⁰–MgO(001) retains the pure doublet character of the electronic ground state (see Table 1). Despite these limitations, it is instructive to look at the relation between the Mulliken charges (bottom panel of Fig. 4) and the adsorption energies. It is seen that a negative charge on the gold atom leads to a much stronger binding of the O₂. Furthermore, the O–O bond is found to be elongated in the negatively charge case (+0.121 Å compared to the gas phase) due to π-back-donation from the cluster to the adsorbate, in agreement with previous theoretical results (1.312 Å for Au₂O₂⁻ with E_ads = 1.06 eV using B3LYP with a similar Gaussian basis set⁴²). The vibrational frequency at the F⁰ vacancy is red-shifted compared to the gas phase value (1580.2 cm⁻¹ for O₂)⁴³ and close to that of the anionic species (1145 cm⁻¹ for O₂⁻vs. 1905.9 cm⁻¹ for O₂⁺),^44,45 which confirms that the bond has been significantly weakened and the adsorbate is negatively charged. This weakening of the O₂ bond is believed to be an important preliminary step for the catalytic oxidation of CO, which qualifies O₂ + Au₁/F⁰–MgO(001) as a promising system for catalysis. In contrast, the bond remains almost at its gas phase value for both positively charge gold atoms (see the inset of the top panel), which should prevent any significant catalytic activity.

The optimized co-adsorbed states, which would correspond to an initial conformation in the catalytic cycle of the Langmuir–Hinshelwood type, retain a structure reminiscent of the superposition of the separate adsorbate reagents. The first structure on the left in Fig. 5 shows an example for the F²⁺ vacancy. In general, the presence of two adsorbates saturates the Au₁ cluster, reducing the adsorption energy (see Table 1). Note that co-adsorption was found to be unstable in the F¹⁺ case, probably due to the weak interaction of both adsorbates with the closed shell Au₁/F¹⁺–MgO(001) system. Since neither CO nor O₂ is strongly adsorbed on this surface system, nor could a co-adsorption state be found, the lack of support from the surface to stretch the O₂ bond is a strong indication that this system will remain catalytically inactive. As was the case for the adsorption of O₂, a high degree of spin contamination is found at the F²⁺ vacancy, while the F⁰ vacancy retains its doublet character. At the F²⁺ center, the distance of the CO molecule to the gold atom remains almost unchanged upon co-adsorption, while the O₂–Au distance increases by about 0.7 Å. The vibrational frequencies parallel this trend, showing a rise towards the gas phase value for O₂, as the bond length is affected by the co-adsorbed species. This system will thus also remain catalytically inactive. In contrast, the O₂ adsorbate retains the same distance to the gold atom on the F⁰ vacancy and it is the CO–Au₁ bond length that increases by 0.9 Å upon co-adsorption. Here, the vibrational frequencies follow the opposite trends as for the F²⁺ color center, since CO is more strongly affected by the co-adsorption. Thus, the preferential adsorption of O₂ on Au₁@F⁰–Mg(001) earmarks this system as the only potentially active catalyst.

Fig. 5 Oxidation pathway of CO on Au₁/F²⁺–Mg(001) determined by NEB calculations. The energy barriers in red suffer from spin contamination of the transition states. The energy differences are given relative to the previous structure.

3.2 CO oxidation on Au₁/Fⁿ⁺–MgO(001)

The rate determining step for the oxidation reaction of CO is believed to be the cleavage of the O₂ bond. In this perspective, the initial weakening of the O₂ bond should lower the activation barrier and, consequently, accelerate the formation of the first CO₂. Based on the adsorption behavior of CO and O₂ in the previous section, various co-adsorbed initial structures are seeded to the optimization algorithm. The structures belonging to local minima then serve as initial conformations for NEB calculations aiming at determining the potential energy profiles of the various possible reaction paths. An optimized reaction path for the formation of CO₂ is depicted in Fig. 5 for the Au₁/F²⁺–Mg(001) system. The initial state is defined as the co-adsorbed conformation identified in the previous section. Manual cleavage of the O₂ bond and subsequent structure relaxation lead to the thermodynamically favored formation of CO₂ (ΔE = −5.06 eV with respect to the initial co-adsorbed structure), while the remaining oxygen atom moves into the vacancy (see the rightmost structure). Using this as a final state, the minimal energy path obtained from NEB calculations using 18 images follows a sequential mechanism: molecular oxygen is first inserted into the vacancy by pushing away the gold cluster (central structure), followed by cleavage of the O–O bond and formation of CO₂. Significant spin contamination of the wave functions is observed at the transition states towards the insertion of molecular O₂ into the vacancy (E_a = 0.27 eV), probably due to the passage from the physisorbed to the chemisorbed species. Note that the gold atom is displaced from the vacancy already in this step, allowing for the molecule to slide into the cavity. Keeping in mind the weak adsorption energy of the Au₁ cluster on F²⁺–Mg(001), this qualitative profile of the insertion reaction should be trusted despite the degree of spin contamination, leading to thermodynamically favored poisoning of the color center (ΔE = −3.21 eV) and effective breaking of the catalytic cycle. The activation barrier for the cleavage of the O₂ bond is very high (2.99 eV) and, under normal reaction conditions, the formation of CO₂ should be kinetically hindered. Despite the spin contamination observed for both transition states, these qualitative conclusions should hold.

On Au₁/F¹⁺–MgO(001), our calculations without dispersion correction predict no stable adsorption conformation for either CO, O₂, or the co-adsorbed state. Thus, no support for the O₂ bond cleavage is observed, leading to even higher activation barriers. With regard to the reparation of the color center, the stronger adsorption state of Au₁ on F¹⁺–MgO(001) compared to the other color centers could inhibit the movement of oxygen into the vacancy. A NEB calculation for the insertion of an O₂ molecule from the gas phase into the vacancy by shifting the Au₁ cluster yields an energy barrier of about 1.10 eV, which is large enough to inhibit the spontaneous reparation of the F¹⁺ color center under normal reaction conditions. In the absence of stable adsorption states, an oxidation reaction at the cluster would be of third order and, thus, statistically highly improbable. Due to the lack of relevance, the reactions at this color center were not further investigated.

The reaction path shown in Fig. 6 for the Au₁/F⁰–MgO(001) system is initiated by the molecular oxygen at the cluster. This choice is motivated by the much more favorable adsorption of the latter (1.51 eV) as compared with CO (0.09 eV), which also has a weak interaction energy in the co-adsorption configuration at the cluster (0.01 eV). The CO molecule was initially placed in the gas phase to force the reactants along an Eley–Rideal path, or at the neighboring magnesium/gold site to simulate a Langmuir–Hinshelwood type mechanism. Both initial structures have a similar energy but the former was found to have an activation barrier above 1 eV, indicating that the most likely reaction path would come upon surface diffusion of a weakly adsorbed carbon monoxide. The structure of the two lowest transition states is shown in the second part of Fig. 6. The proximity of the two reactants can be seen to either preserve the coexistence of the molecular species (E_a = 0.84 eV) or lead to O₂ bond breaking (lowest structure, E_a = 0.60 eV). The latter path further leads to the energetically favored, barrier-less desorption of CO₂ (ΔE = −3.02 eV, central top structure), followed by the lateral displacement of the gold atom to expose the vacancy (E_a = 0.15 eV). The remaining oxygen atom is then seen to intercalate between the gold atom and the defective surface, thereby repairing the vacancy (ΔE = −3.75 eV). The desorption and reparation steps are sequential. The co-adsorbed molecular species follow a similarly favorable reparation path via the formation of a metastable carbonate state (ΔE = −4.43 eV, central bottom structure). A similar carbonate species was also observed on larger gold clusters but it was seen to poison the catalytic cycle due to a high activation barrier for the dissociation of CO₂.⁴⁶ In the present case, displacement of the gold atom has only a small activation barrier (E_a = 0.26 eV) and it leads to the intercalation of an oxygen atom in the vacancy and the barrier-less desorption of carbon dioxide (ΔE = −2.67 eV, rightmost structure). The main difference from the first reaction path is that the desorption and reparation steps are simultaneous here, although leading to similar energetic profiles. Consequently, the catalytic cycle will break after the first formation of CO₂ in both cases.

Fig. 6 Oxidation pathway for CO on Au₁/F⁰–Mg(001) determined using NEB calculations. An adsorbed O₂ (leftmost structure) is approached by a diffusing weakly adsorbed CO. The black path describes the initial formation of unbound CO₂ by dissociation of the O₂ bond, followed by the displacement of the gold atom and intercalation of atomic oxygen in the vacancy (rightmost structure). The gray path describes the transient formation of a metastable carbonate species, followed by the simultaneous dissociation of CO₂ and oxygen intercalation in the vacancy. The energy differences are given relative to the previous structure.

To exclude other competing reactions from being responsible for the catalytic inertness of the Au₁/F⁰–MgO(001) system, alternative pathways were also investigated using the same NEB methodology. The most important ones are summarized in the tentative catalytic cycle in Fig. 7. It can be seen that the intercalation of molecular oxygen in the vacancy is thermodynamically favorable (ΔE = −2.12 eV, top right) while having a large activation barrier (E_a = 1.06 eV). The system shows a marked preference for reacting with the incoming CO molecules, either via a sequential dissociation-reparation process (E_a = 0.60 eV) or via the formation of a carbonate intermediate (E_a = 0.84 eV). The latter preferentially undergoes a simultaneous dissociation-reparation reaction (E_a = 0.26 eV) than the sequential removal of CO₂ (E_a = 1.17 eV) followed by the displacement of the gold cluster and the oxygen intercalation (E_a = 0.15 eV). The reparation event can be seen to effectively terminate the catalytic cycle. Provided that the oxygen atom lives long enough at the interface, reaction with another incoming CO molecule would be energetically favorable (ΔE = −2.43 eV, top left) and kinetically accessible (E_a = 0.20 eV), effectively closing the catalytic cycle. It must be said that, due to the exponential relation between the activation barrier and the reaction rate, this possibility appears to be very hypothetical. Note that summing up the energy differences across the catalytic cycle (ΔE_cycle = −6.15 eV) corresponds approximately to the energy difference of 2CO + O₂ and 2CO₂ in the gas phase, obtained using the current computational setup (ΔE_gas = −6.11 eV). Since the counterpoise correction was observed to over-correct the basis set superposition error in similar systems using bases of double zeta quality,^47,48 the energy of the reactants was obtained using a single calculation by simply placing the molecules far from each other. The remaining discrepancies should be seen as an error estimate for the present computational methodology.

Fig. 7 Catalytic cycle for the oxidation of CO on Au₁/F⁰–Mg(001) and possible termination reactions determined from NEB calculations. Bold arrows denote the most likely reaction paths. The reaction energy is calculated as the difference between the initial and final states used in the NEB calculation, corrected for the adsorption energy of the reactants (i.e., CO, CO₂). All energies are given in eV.

4 Conclusion

In conclusion, we have performed first principles investigations of the CO oxidation reaction for understanding the absence of the catalytic activity of Au₁ on defective MgO(001) surfaces. It was shown that a gold atom deposited on F¹⁺ and F²⁺ color centers interacts only weakly with molecular oxygen, offering little to no support for the O–O bond weakening. The associated lowering of the activation barrier, which is required in the catalytic oxidation process, is found to be insufficient. Furthermore, co-adsorption on Au₁ deposited on F¹⁺–MgO(001) is not supported.

Co-adsorption of CO and O₂ on Au₁/F⁰–MgO(001) was found to be possible, while also leading to significant O–O bond weakening. A first oxidation reaction was found to be thermodynamically and kinetically accessible, with the highest activation energy along the minimal energy path at E_a = 0.60 eV. The latter follows a sequential mechanism for the release of a single CO₂ molecule, followed by the reparation of the color center by intercalation of the remaining oxygen in the vacancy. The vacancy is poisoned during the reaction.

An alternative reaction path leads to the formation of a metastable, adsorbed carbonate intermediate. The ensuing simultaneous release of a CO₂ molecule and reparation of the surface is accessible via a small activation barrier at E_a = 0.26 eV. The lateral mobility of the gold atom above the vacancy was also found to allow for intercalation and binding of molecular oxygen, both in the F⁰ and F²⁺ cases. Summarizing, it appears that the lack of catalytic activity on defective MgO(001) surfaces originates from surface reparation due to insufficient protection of the color centers by the gold atom, which has sufficient lateral mobility because of its relatively low adsorption energy. Our simulations demonstrate unambiguously at an atomistic level how surface reparation prevents catalytic activity: the color center is consumed during the first oxidation step, either via a concerted or a sequential mechanism, and not simply upon dissociative adsorption of an oxygen molecule. This finding can be of great importance for the design of novel, more efficient gold catalysts at defective magnesium oxide surfaces.

References

1. D. Cha and G. Parravano, J. Catal., 1970, 18, 200–211.
2. G. C. Bond, P. A. Sermon, G. Webb, D. A. Buchanan and P. B. Wells, J. Chem. Soc., Chem. Commun., 1973, 444b–445b.
3. H. Huber, D. McIntosh and G. A. Ozin, Inorg. Chem., 1977, 16, 975–979.
4. M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 405–408.
5. M. Haruta, N. Yamada, T. Kobayashi and S. Iijima, J. Catal., 1989, 115, 301–309.
6. M. Haruta, Gold Bull., 2004, 37, 27–36.
7. A. S. K. Hashmi and G. J. Hutchings, Catal. Sci. Technol., 2013, 3, 2861.
8. Y. Y. Wu, N. A. Mashayekhi and H. H. Kung, Catal. Sci. Technol., 2013, 3, 2881–2891.
9. W. Song and E. J. M. Hensen, Catal. Sci. Technol., 2013, 3, 3020–3029.
10. M. Haruta, Catal. Today, 1997, 36, 153–166.
11. P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456.
12. L. D. Socaciu, J. Hagen, T. M. Bernhardt, L. Wöste, U. Heiz, H. Häkkinen and U. Landman, J. Am. Chem. Soc., 2003, 125, 10437–10445.
13. G. Pacchioni, L. Giordano and M. Baistrocchi, Phys. Rev. Lett., 2005, 94, 226104.
14. B. Yoon, H. Häkkinen, U. Landman, A. S. Wörz, J.-M. Antonietti, S. Abbet, K. Judai and U. Heiz, Science, 2005, 307, 403–407.
15. A. Del Vitto, G. Pacchioni, F. Delbecq and P. Sautet, J. Phys. Chem. B, 2005, 109, 8040–8048.
16. P. Frondelius, H. Häkkinen and K. Honkala, New J. Phys., 2007, 9, 339.
17. P. Frondelius, H. Häkkinen and K. Honkala, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 073406.
18. S. Schintke, S. Messerli, M. Pivetta, F. m. c. Patthey, L. Libioulle, M. Stengel, A. De Vita and W.-D. Schneider, Phys. Rev. Lett., 2001, 87, 276801.
19. M. Arenz, U. Landman and U. Heiz, ChemPhysChem, 2006, 7, 1871–1879.
20. U. Landman, B. Yoon, C. Zhang, U. Heiz and M. Arenz, Top. Catal., 2007, 44, 145–158.
21. M. A. Brown, F. Ringleb, Y. Fujimori, M. Sterrer, H.-J. Freund, G. Preda and G. Pacchioni, J. Phys. Chem. C, 2011, 115, 10114–10124.
22. M. Amft and N. V. Skorodumova, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195443.
23. A. M. Burow, M. Sierka, J. Döbler and J. Sauer, J. Chem. Phys., 2009, 130, 174710.
24. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
25. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
26. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
27. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
28. S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
29. N. I. of Standards and Technology, Precomputed vibrational scaling factors, http://cccbdb.nist.gov/vibscalejust.asp, Online, accessed 22/02/2016.
30. O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354.
31. M. Von Arnim and R. Ahlrichs, J. Comput. Chem., 1998, 19, 1746–1757.
32. E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 170201.
33. S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66.
34. S. Ehrlich, J. Moellmann, W. Reckien, T. Bredow and S. Grimme, ChemPhysChem, 2011, 12, 3414–3420.
35. G. Barcaro and A. Fortunelli, New J. Phys., 2007, 9, 22.
36. P. V. Sushko, A. L. Shluger and C. A. Catlow, Surf. Sci., 2000, 450, 153–170.
37. M. Sterrer, E. Fischbach, M. Heyde, N. Nilius, H.-P. Rust, T. Risse and H.-J. Freund, J. Phys. Chem. B, 2006, 110, 8665–8669.
38. G. Pacchioni and H. Freund, Chem. Rev., 2013, 113, 4035–4072.
39. R. Wichtendahl, M. Rodriguez-Rodrigo, U. Härtel, H. Kuhlenbeck and H.-J. Freund, Phys. Status Solidi A, 1999, 173, 93–100.
40. L. Giordano, J. Carrasco, C. Di Valentin, F. Illas and G. Pacchioni, J. Chem. Phys., 2006, 124, 174709.
41. A. L. Floch, Mol. Phys., 1991, 72, 133–144.
42. M. L. Kimble, N. A. Moore, G. E. Johnson, A. W. Castleman, C. Bürgel, R. Mitriç and V. Bonačiç-Koutecký, J. Chem. Phys., 2006, 125, 204311.
43. M. Shimauchi, T. Miura and H. Takuma, Jpn. J. Appl. Phys., 1995, 34, L1689.
44. J. Shamir, J. Binenboym and H. H. Claassen, J. Am. Chem. Soc., 1968, 90, 6223–6224.
45. C. V. V. Prasad, D. Lacombe, W. K. Walker, W. Kong, P. Bernath and J. Hepburn, Mol. Phys., 1997, 91, 1059–1074.
46. M. Stamatakis, M. A. Christiansen, D. G. Vlachos and G. Mpourmpakis, Nano Lett., 2012, 12, 3621–3626.
47. J. Thom H. Dunning, J. Phys. Chem. A, 2000, 104, 9062–9080.
48. K. R. Liedl, J. Chem. Phys., 1998, 108, 3199–3204.

---