Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cooperative enhancement versus additivity of two-photon-absorption cross sections in linear and branched squaraine superchromophores†
Harald
Ceymann
a,
Arnulf
Rosspeintner
b,
Maximilian H.
Schreck
a,
Carina
Mützel
a,
Andreas
Stoy
a,
Eric
Vauthey
*b and
Christoph
Lambert
*a
aInstitut für Organische Chemie, Universität Würzburg, Wilhelm Conrad Röntgen Research Center for Complex Material Systems, Center for Nanosystems Chemistry, Am Hubland, D-97074 Würzburg, Germany. E-mail: christoph.lambert@uni-wuerzburg.de
bDepartment of Physical Chemistry, University of Geneva, 30 Quai Ernest-Ansermet, CH-1211 Geneva 4, Switzerland
First published on 31st May 2016
Abstract
The linear and nonlinear optical properties of a series of oligomeric squaraine dyes were investigated by one-photon absorption spectroscopy (1PA) and two-photon absorption (2PA) induced fluorescence spectroscopy. The superchromophores are based on two indolenine squaraine dyes with transoid (SQA) and cisoid configuration (SQB). Using these monomers, linear dimers and trimers as well as star-shaped trimers and hexamers with benzene or triphenylamine cores were synthesised and investigated. The red-shifted and intensified 1PA spectra of all superchromophores could well be explained by exciton coupling theory. In the linear chromophore arrangements we also found superradiance of fluorescence but not in the branched systems. Furthermore, the 2PA showed enhanced cross sections for the linear oligomers but only additivity for the branched systems. This emphasizes that the enhancement of the 2PA cross section in the linear arrangements is probably caused by orbital interactions of higher excited configurations.
Introduction
In recent years large two-photon-absorption (2PA) cross sections (δ2PA) for quadrupolar-type D–A–D (or similarly in A–D–A, where A is an electron acceptor and D is an electron donor) chromophores have been reported.1,2 The various applications of 2PA, e.g. two-photon fluorescence spectroscopy,3,4 3D microfabrication and optical data storage5 as well as photo dynamic therapy6,7 strongly benefit from high δ2PA values. Furthermore the long wavelengths used in 2PA processes of D–A–D chromophores result in reduced scattering and an improved penetration of the medium, because of the absence of significant linear absorption in the 2PA region.The magnitude of the cross section δ2PA in symmetric systems can be estimated by eqn (1), with Γ02 being the homogeneous linewidth of the 2PA transition, using a three-level model as depicted in Fig. 1.8,9
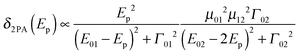 | (1) |
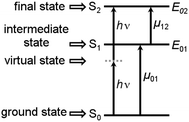 | ||
| Fig. 1 Schematic representation of the 2PA process in the case of the three level model for symmetric systems. | ||
Calculations and experiments have shown that in substituted quadrupolar chromophores the donor end groups have a great influence on the transition moment between the S1 and S2 state μ12 while the extent of conjugation and the strength of the centred acceptor are correlated to μ01.11,12 Webster et al. varied the strength of the acceptor bridge between two identical heterocyclic donor groups by using a polymethine dye, a squaraine dye and a tetraone core. They interpreted the large δ2PA (8200 GM) of the squaraine dye being due to the increase of the density of final states and, thus, to the number of possible electronic transitions between the 1PA state and a state with twice that energy. In addition a large intermediate state resonance enhancement was observed due to the sharply rising low-energy side of the linear absorption spectra.13 These authors also used a squaraine chromophore as the bridge between two zinc porphyrin moieties, leading to very broad 2PA spectra with cross sections of up to 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GM over the region of 1580 to 850 nm.14 Moreshead et al. achieved a high 2PA cross section in molecules that consisted of two squaraines that were bridged by a fluorene moiety.15
000 GM over the region of 1580 to 850 nm.14 Moreshead et al. achieved a high 2PA cross section in molecules that consisted of two squaraines that were bridged by a fluorene moiety.15
Another way to accomplish large 2PA responses is the coupling of several chromophores. The ratio between the 2PA cross section δ(n)2PA of a superchromophore consisting of n monomers and the 2PA cross section δ(1)2PA of the monomer is defined as F(n) in eqn (2). In the literature additive enhancement (F(n) = n), cooperative behaviour (F(n) > n) and weakening (F(n) < n) of the cross sections were reported.16,17 More specific, δ(n)2PA should scale with n2 if full cooperativity is observed.18,19 This is caused by the linear dependence of both μ012 and μ122 on the number of chromophores in eqn (1).20
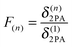 | (2) |
In an older work Scherer et al. together with one of us25 observed an enhancement of the 2PA cross section in a series of thiophene-bridged oligosquaraines (up to pentamers). There, it was concluded that the low-lying 2PA allowed states are the result of conjugational effects which cannot be explained by purely electrostatic exciton coupling. The latter however deliver a reasonable explanation for the shifts of 1PA states.
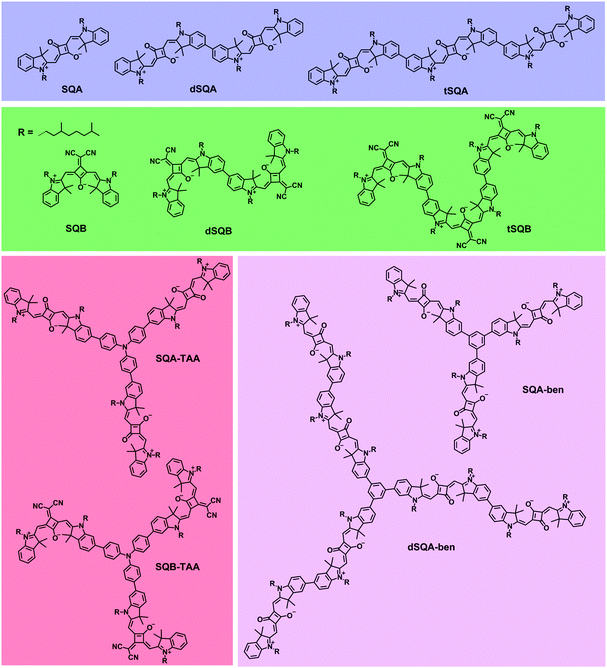
In this work we again focus on the 2PA properties of superchromophores built up from squaraine dyes (see Fig. 2).26–34 Besides linear arrangements we also investigate branched systems with a triarylamine core or a benzene core. In addition to the well-investigated trans-squaraine parent chromophore SQA9,14,15,25,35,36 we also employ the cis-squaraine dye SQB. In the latter system one oxygen atom of the central squaric acid is replaced by a dicyanovinylene group leading to higher acceptor strength and, as a result, to a red shift of the 1PA. In the homodimers dSQA and dSQB and the homotrimers tSQA and tSQB we investigate the effect of direct coupling of dye monomers to yield oligomers on their 2PA properties. In the star-shaped compounds SQA-TAA, SQB-TAA, SQA-ben and dSQA-ben the branching effect is examined. We expect that in all oligomeric superchromophores, the nonlinear optical properties will change as the linear optical properties do because of exciton coupling effects. Thus, it is the goal of this work to examine whether exciton coupling of excited monomer states can be used to increase the 2PA of superchromophores. However, for all the above mentioned dyes one has to take into account that diverse conformers (rotational isomers via the biaryl axis) may be present in solution and the symmetry of compounds might be lower as indicated in Fig. 2.
Results and discussion
Absorption spectra
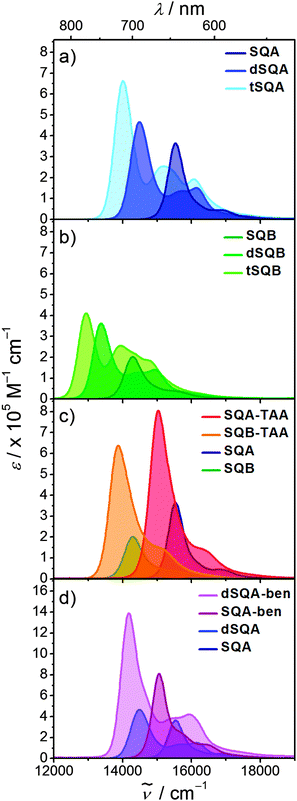
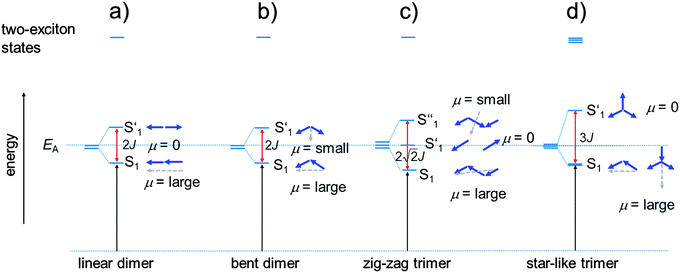
Before we present the results of the 2PA measurements we will first briefly discuss the linear absorption spectra of the monomer dyes and their oligomers. This discussion will be based on the concept of exciton coupling, i.e. the coupling of transition moments of individual chromophores in order to produce the lowest energy excited states of the superchromophores.37–39 In Fig. 3 the 1PA spectra of the investigated squaraines in toluene are presented. The symmetrical monomer SQA (Fig. 3a) shows the typical absorption of a squaraine compound, i.e. one sharp and very intense band in the red region of the visible spectrum, originating from the HOMO → LUMO transition, and a weak shoulder on the high energy side which stems from vibronic progression.For a dimer of SQA (=dSQA) with a head-to-tail orientation we may consider two idealised structures, a bent structure and a more stretched structure both with C2 symmetry. Both structures can be formed by torsion around the biaryl axis. In Fig. 4, the exciton coupling interaction of localised transition moments (blue arrows) with their phase relation (direction of the arrows) for both scenarios is depicted. This theory predicts two possible electronic transitions into two exciton states which are separated by twice the exciton coupling energy J. While for the bent case both transitions are allowed, only the lowest exciton state is an allowed transition in case of the linear structure. In practice, mixtures of at least these two conformers will be present in solution and we expect to observe the lowest exciton state (termed S1 in the following) as a more intense transition and the upper exciton state (termed S1′ because it derives from the S1 state of the monomer) as a less intense peak (shoulder). Fig. 3a shows that for dSQA the more intense maximum at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 is by 1000 cm−1 bathochromically shifted in comparison to SQA, and the weaker peak has an energy of 16
500 cm−1 is by 1000 cm−1 bathochromically shifted in comparison to SQA, and the weaker peak has an energy of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1. The difference of these two absorption maxima can be used to estimate the exciton coupling energy J which is ca. 800 cm−1 (see Table 1).
100 cm−1. The difference of these two absorption maxima can be used to estimate the exciton coupling energy J which is ca. 800 cm−1 (see Table 1).
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) abs/cm−1 (/nm)
abs/cm−1 (/nm) |
ε/M−1 cm−1 | μ abs 2/D2 |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) fl/cm−1
fl/cm−1 |
ϕ
f
(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ex/cm−1) ex/cm−1) |
τ f /ns (TCSPC) |
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) /ns /ns |
μ f 2/D2 | |J|/cm−1 | |
|---|---|---|---|---|---|---|---|---|---|
a Fluorescence quantum yield and excitation wavenumber used for measuring the fluorescence spectra in parentheses. The given error was determined by three independent measurements.
b Multiexponential fit of fluorescence decays measured by TSCPC, excitation at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1. Amplitudes are given in brackets.
c Lifetimes acquired by stretched exponential analysis of fluorescence decays measured by TCSPC, excitation at 15 200 cm−1. Amplitudes are given in brackets.
c Lifetimes acquired by stretched exponential analysis of fluorescence decays measured by TCSPC, excitation at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1. Stretching exponent in brackets.
d Lifetimes acquired by distribution analysis of fluorescence decays measured by TCSPC, excitation at 15 200 cm−1. Stretching exponent in brackets.
d Lifetimes acquired by distribution analysis of fluorescence decays measured by TCSPC, excitation at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1. The distribution is shown in Fig. S1 (ESI).
e This quantum yield deviates from older measurements39 because of the use of an improved set-up. 200 cm−1. The distribution is shown in Fig. S1 (ESI).
e This quantum yield deviates from older measurements39 because of the use of an improved set-up.
|
|||||||||
| SQA | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (643) 500 (643) |
365![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
127 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
0.62 ± 0.033e (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700) 700) |
0.07 (0.03) | 1.64 (0.97)c | 114 | |
| 0.20 (0.10) | |||||||||
| 1.72 (0.87) | |||||||||
| dSQA | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (690) 500 (690) |
466![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
248 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
0.82 ± 0.033 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700) 700) |
0.15 (−0.31) | 1.67d | 172 | 800 |
| 0.25 (0.30) | |||||||||
| 1.82 (0.39) | |||||||||
| tSQA | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (714) 000 (714) |
663![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
410 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
0.85 ± 0.038 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100) 100) |
0.08 (−0.26) | 1.57d | 219 | 743 |
| 1.14 (0.42) | |||||||||
| 1.94 (0.32) | |||||||||
| SQA-TAA | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (665) 000 (665) |
805![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
363 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
0.71 ± 0.009 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700) 700) |
0.05 (−0.13) | 1.79 (0.96)c | 125 | |
| 0.48 (0.12) | |||||||||
| 1.96 (0.75) | |||||||||
| SQA-ben | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 (664) 100 (664) |
811![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
319 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
0.69 ± 0.001 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700) 700) |
0.08 (−0.21) | 1.71 (0.96)c | 123 | 167 |
| 0.23 (0.17) | |||||||||
| 1.84 (0.61) | |||||||||
| dSQA-ben | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 (705) 200 (705) |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 390![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
800 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.80 ± 0.015 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100) 100) |
0.06 (−0.28) | 1.51d | 193 | 167/900 |
| 0.98 (0.27) | |||||||||
| 1.68 (0.45) | |||||||||
| SQB | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 (700) 300 (700) |
202![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
92.7 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.75 ± 0.002e (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400) 400) |
3.45 | 3.46 (1.00)c | 81 | |
| dSQB | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 (747) 400 (747) |
362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
226 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
0.69 ± 0.020 (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) 200) |
2.46 (0.83) | 2.56 (0.93)c | 121 | 800 |
| 4.08 (0.17) | |||||||||
| tSQB | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 (773) 900 (773) |
411![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
339 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
0.58 ± 0.023 (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) 200) |
2.10 (0.89) | 2.05 (0.88)c | 142 | 636 |
| 4.30 (0.11) | |||||||||
| SQB-TAA | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 (721) 900 (721) |
637![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
332 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
0.75 ± 0.020 (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) 200) |
3.06 | 3.02 (0.99)c | 102 | |
For a head-to-tail arrangement of three chromophores as in tSQA we disregard different conformers completely and give only the qualitative solution of exciton coupling theory for a zig-zag arrangement. This is sketched in Fig. 4. Thus, exciton theory predicts three exciton states where the lowest one is highly allowed, the highest one is slightly allowed but the intermediate state is forbidden. The energy splitting of the upper and lower exciton state is 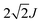 . Again, in practice we expect that these selection rules are lifted because of the presence of different conformers. Indeed, for the trimer tSQAFig. 3a shows three peak maxima with decreasing intensity from lower to higher energy. From the energy difference of the lowest (14
. Again, in practice we expect that these selection rules are lifted because of the presence of different conformers. Indeed, for the trimer tSQAFig. 3a shows three peak maxima with decreasing intensity from lower to higher energy. From the energy difference of the lowest (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) and the highest energy peak (16
000 cm−1) and the highest energy peak (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1) we estimate an exciton coupling energy of ca. 740 cm−1 in good agreement with that of the dimer dSQA.
100 cm−1) we estimate an exciton coupling energy of ca. 740 cm−1 in good agreement with that of the dimer dSQA.
In the superchromophores derived from SQB the substitution of one oxygen atom by a dicyanomethylene group in the central squaric acid moiety leads to increased electron acceptor strength and a lowering of the LUMO energy. This shifts the lowest energy absorption by ca. 1100 cm−1 to the red compared to their SQA analogues (Table 1). The absorption spectra of the dimer dSQB and the trimer tSQB are similar to their SQA analogues but show some variation in peak intensities (Fig. 3b).
The star-shaped trimers SQA-TAA and SQB-TAA with a triarylamine as the connecting core unit essentially show a broadening of the lowest energy absorption band which is indicative of a weak exciton coupling effect (Fig. 3c). The red shift of the absorption relative to their monomers is primarily due to the addition of the propeller-like triarylamine donor to the quadrupole dyes, thus breaking the C2 symmetry of the squaraine moieties and inducing some CT character.40,41 In contrast the trimer SQA-ben with benzene as the connecting bridge displays a small shoulder at ca. 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 on the high energy side of the main absorption band which could be caused by a weak exciton coupling (Fig. 3d). This transition is forbidden for a truly C3 symmetric chromophore as indicated in Fig. 4 and is only visible because of some structural disorder.
700 cm−1 on the high energy side of the main absorption band which could be caused by a weak exciton coupling (Fig. 3d). This transition is forbidden for a truly C3 symmetric chromophore as indicated in Fig. 4 and is only visible because of some structural disorder.
A similar shoulder is observed for the larger dSQA-ben. Here, it is difficult to discriminate between the exciton coupling within the dimer branches and those between the three branches.
The squared transition moments (see Table 1) of the squaraine absorption bands of the superchromophores show nearly additivity to their smaller analogues and thus follow the Thomas–Reiche–Kuhn sum rule.42 This means, that no other electronic transitions with significant oscillator strength contribute to the exciton manifold. In all cases, two-exciton states43,44 can be anticipated as the result of the interaction of two excited chromophores (see Fig. 4). These two-exciton states cannot be reached by 1PA from the ground state but are visible as two consecutive absorption processes from the ground state to the 1PA state and from there to the two-exciton state in e.g. transient absorption spectroscopy experiments.
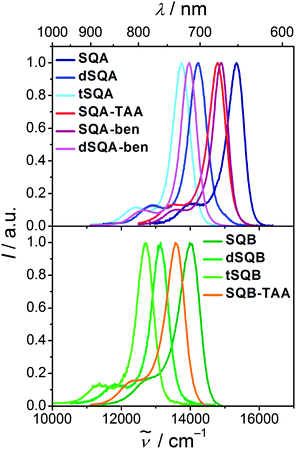
Fluorescence spectra
Upon excitation in the main absorption band the monomeric compounds SQA and SQB show typical squaraine fluorescence emission with a high quantum yield in toluene (Fig. 5). Their fluorescence spectra are the mirror image of the absorption with a small Stokes shift of 200–300 cm−1. The larger superchromophores all show similar behaviour, that is, the fluorescence looks similar to the one of the monomer but shifted to lower energies. Fluorescence lifetimes of all chromophores were measured by TCSPC in toluene. These lifetime measurements gave multiexponential decays in most cases (see Table 1). An alternative decay fit was done using the Kohlrausch equation (stretched exponential, eqn (3)) with exponents β close to 1 which was equally good for most compounds.45I = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(t/ exp(−(t/![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) f)β) f)β) | (3) |
The average lifetimes acquired in this way were used to calculate the transition moment of the fluorescence μf by the Strickler–Berg eqn (4)47 from the fluorescence quantum yield ϕf.
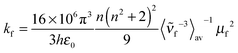 | (4) |
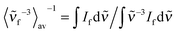 is the average cubic fluorescence energy and kf is the radiative rate constant kf = ϕf/τf.
is the average cubic fluorescence energy and kf is the radiative rate constant kf = ϕf/τf.
The squared fluorescence transition moments of SQA and SQB (see Table 1) are within the experimental uncertainty equal to those of the absorption. Thus, we discuss only relative squared transition moments. Here we observed a less than additive behaviour on going from SQA to dSQA and tSQA but still an increase which proves some microscopic superradiance effect, i.e. collective emission from delocalised states of chromophore aggregates.48–51 A similar effect was observed for dSQB and tSQB but not for all star-like superchromophores which indicates weak exciton coupling in the latter cases and emission from more localised states, that is, symmetry breaking takes place in the excited state.52,53
Two photon absorption induced fluorescence
The 2PAF spectra for the squaraine superchromophores in toluene are presented in Fig. 6 and the cross sections are given in Table 2. The measurement of 2PAF of tSQB was not possible because of the strongly red-shifted fluorescence which interfered with residual stray light from the 800 nm fundamental. Before we discuss the results of the superchromophores we will first present the 2PAF spectra of monomeric squaraines SQA and SQB and compare these results with those from the literature, where available.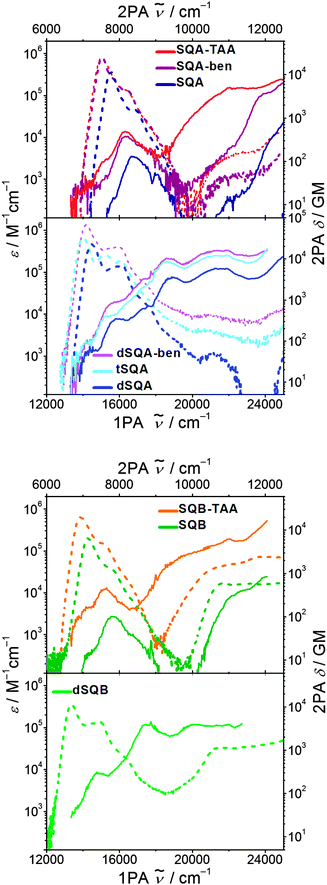 | ||
| Fig. 6 Two photon absorption spectra (solid lines) and one photon absorption spectra (dashed lines) of the investigated squaraines in toluene at rt. | ||
| σ 1PAmax/10−15 cm2 | E 1/cm−1 | δ 2PA1/GM | E 2/cm−1 | δ 2PA2/GM | E 3/cm−1 | δ 2PA3/GM | E 4/cm−1 | δ 2PA4/GM | |
|---|---|---|---|---|---|---|---|---|---|
| a Could not be measured because of red-shifted fluorescence. b The fact that the 2PA cross sections are grouped in columns does not necessarily mean that they derive from similar electronic states. | |||||||||
| SQA | 1.40 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
133 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
800 | ||||
| SQA-TAA | 3.10 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
470 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
4890 | ||||
| SQA-ben | 3.10 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
370 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
3580 | ||||
| dSQA | 1.78 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
340 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
3430 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
5780 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
| tSQA | 2.54 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
415 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
8340 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 240 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
| dSQA-ben | 5.31 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
860 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 170 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 290 |
| SQB | 0.903 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
100 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
400 | ||||
| dSQB | 1.38 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
300 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
3830 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3450 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3880 |
| tSQB | 1.57 | — | — | — | — | — | — | — | — |
| SQB-TAA | 2.44 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
465 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
6220 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 470 |
||
For a centrosymmetric chromophore such as SQA the selection rules for electronic 1PA processes allow transitions from the ground state (Ag) to the excited singlet state with u symmetry while the transitions to g symmetric states are dipole forbidden.54 Indeed, TD-DFT computations (see ESI†) assign Bu symmetry to the lowest singlet excited state. According to this method the two next higher energy excitations are n → π* excitation of the oxygen lone pair electrons into the LUMO. Because of minimal orbital overlap these transitions possess vanishing oscillator strength and can neither be observed by 1PA nor by 2PA spectroscopy. This type of excitation is disregarded in the following. According to the computations the next orbital-overlap allowed state is an Ag state which is 1PA forbidden but 2PA allowed. In our older work of SQA with R = ethyl in CHCl3, the symmetry of this state was confirmed by polarisation dependent 2PAF measurements. This state is at 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 and is also visible by fluorescence excitation anisotropy spectroscopy in viscous media.9 2PAF spectroscopy also showed a weakly allowed transition at 16
200 cm−1 and is also visible by fluorescence excitation anisotropy spectroscopy in viscous media.9 2PAF spectroscopy also showed a weakly allowed transition at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 just above the lowest Bu state at 15
700 cm−1 just above the lowest Bu state at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 (for SQA with R = ethyl in CHCl3). This transition is weakly 2PA allowed because of vibronic coupling to a bu symmetric vibration (Bu × bu = Ag).25 For SQA with R = dimethyloctyl in toluene we can confirm these older results (see Fig. 6) in our present work.
700 cm−1 (for SQA with R = ethyl in CHCl3). This transition is weakly 2PA allowed because of vibronic coupling to a bu symmetric vibration (Bu × bu = Ag).25 For SQA with R = dimethyloctyl in toluene we can confirm these older results (see Fig. 6) in our present work.
For SQB no 2PAF experiments are available in the literature, but, because of its C2v symmetry the 1PA and 2PA allowed states do not show the above mentioned parity selection rules. Thus, in principle all 1PA states are also 2PA allowed. Nevertheless, the 2PA spectrum of SQB is very similar to the one of SQA, showing a weak 2PA (100 GM) at the vibronic shoulder of the S1 absorption at ca. 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 and a much higher 2PA of S2 at ca. 23
700 cm−1 and a much higher 2PA of S2 at ca. 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. According to TD-DFT computations both states have B2 symmetry and are polarised along the long axis of the molecule. S3 is an A1 state and polarised along the molecular C2 axis but is out of reach for the 2PA experiments. This agrees very well with the fluorescence excitation anisotropy (FEA) spectrum (see ESI†).
000 cm−1. According to TD-DFT computations both states have B2 symmetry and are polarised along the long axis of the molecule. S3 is an A1 state and polarised along the molecular C2 axis but is out of reach for the 2PA experiments. This agrees very well with the fluorescence excitation anisotropy (FEA) spectrum (see ESI†).
The 2PAF spectrum of the dimer dSQA shows dramatic differences in comparison to SQA: in addition to the vibronically allowed 2PA peak at the shoulder of the S1 ← S0 transition at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1
500 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 there are pronounced 2PA maxima at ca. 18
55 there are pronounced 2PA maxima at ca. 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 (δ2PA = 3430 GM) and at 21
800 cm−1 (δ2PA = 3430 GM) and at 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 (δ2PA = 5780 GM) which are absent in the monomer SQA. A comparison of the 1PA and the 2PA spectra on a logarithmic scale together with the fluorescence excitation anisotropy (FEA) spectrum allows a more detailed assignment of states (see Fig. 7). The FEA value r = 0.36 around the 0–0 peak of the S1 state proves this transition to be polarised parallel to the emission transition moment (ideally r = 0.4 in this case).56 The FEA drops to ca. 0.2 at the S1(0–1) transition and finally to ca. −0.03 at the S1′ state and to ca. 0.09 for its associated 0–1 transition. The latter values indicate a pronounced angle between the transition moments of these excitations and that of the fluorescence (S1 → S0). Indeed, for the bent dimer case Fig. 4b shows a perpendicular orientation of the S1′ ← S0 transition moment which would ideally give r = −0.2. The following states (termed S1′′ and S1′′′) are visible in the 2PA spectra as pronounced peaks, in the FEA as maxima (r = 0.2) and minima (r = 0.07) but also as weak shoulders and peaks in the 1PA spectrum at ca. 18
800 cm−1 (δ2PA = 5780 GM) which are absent in the monomer SQA. A comparison of the 1PA and the 2PA spectra on a logarithmic scale together with the fluorescence excitation anisotropy (FEA) spectrum allows a more detailed assignment of states (see Fig. 7). The FEA value r = 0.36 around the 0–0 peak of the S1 state proves this transition to be polarised parallel to the emission transition moment (ideally r = 0.4 in this case).56 The FEA drops to ca. 0.2 at the S1(0–1) transition and finally to ca. −0.03 at the S1′ state and to ca. 0.09 for its associated 0–1 transition. The latter values indicate a pronounced angle between the transition moments of these excitations and that of the fluorescence (S1 → S0). Indeed, for the bent dimer case Fig. 4b shows a perpendicular orientation of the S1′ ← S0 transition moment which would ideally give r = −0.2. The following states (termed S1′′ and S1′′′) are visible in the 2PA spectra as pronounced peaks, in the FEA as maxima (r = 0.2) and minima (r = 0.07) but also as weak shoulders and peaks in the 1PA spectrum at ca. 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 and at 21
800 cm−1 and at 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1. While the S1 and S1′ states can easily be derived by exciton coupling theory, S1′′ and S1′′′ cannot. Therefore, assuming a linear dimer situation we construct an orbital interaction diagram as given in the ESI† in which the π–HOMO and the π–LUMO of a monomer interact and give in total four new dimer π-orbitals. With these four orbitals, four singly excited configurations can be generated. Because of their orbital symmetry (either g or u) this gives rise to two allowed and two forbidden transitions from the ground state.57 TD-DFT computations come to the same conclusion (see ESI†).58 Thus, four exited states may be derived from the orbital interaction of two monomers while simple excited state exciton interaction theory predicts only two states. Therefore, it appears that exciton coupling theory is intrinsically insufficient to cover all aspects of 2PA properties. We assume that the four electronic states that we observe experimentally up to 23
400 cm−1. While the S1 and S1′ states can easily be derived by exciton coupling theory, S1′′ and S1′′′ cannot. Therefore, assuming a linear dimer situation we construct an orbital interaction diagram as given in the ESI† in which the π–HOMO and the π–LUMO of a monomer interact and give in total four new dimer π-orbitals. With these four orbitals, four singly excited configurations can be generated. Because of their orbital symmetry (either g or u) this gives rise to two allowed and two forbidden transitions from the ground state.57 TD-DFT computations come to the same conclusion (see ESI†).58 Thus, four exited states may be derived from the orbital interaction of two monomers while simple excited state exciton interaction theory predicts only two states. Therefore, it appears that exciton coupling theory is intrinsically insufficient to cover all aspects of 2PA properties. We assume that the four electronic states that we observe experimentally up to 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 are the four states that we constructed from orbital mixing. Because these states are closely related to S1 of the monomer they are consequently numbered S1 through S1′′′. The relative order of these states is difficult to assign as CI mixing may lead to energy shifts of the simple MO configurations and, furthermore, intensity borrowing between states of same symmetry may alter the observed intensities.59–61
000 cm−1 are the four states that we constructed from orbital mixing. Because these states are closely related to S1 of the monomer they are consequently numbered S1 through S1′′′. The relative order of these states is difficult to assign as CI mixing may lead to energy shifts of the simple MO configurations and, furthermore, intensity borrowing between states of same symmetry may alter the observed intensities.59–61
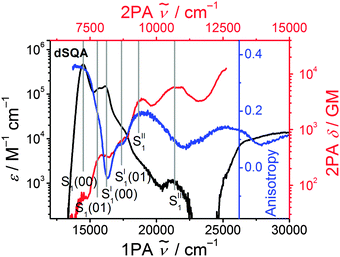 | ||
| Fig. 7 1PA (black) and the 2PA (red) spectra of dSQA in toluene on a logarithmic scale together with the fluorescence excitation anisotropy (FEA) spectrum (blue) in polyTHF at 26 °C. | ||
In the trimer tSQA the 1PA and 2PA allowed states are shifted a little bit towards lower energy (see Fig. 6 and Table 2). More interesting is that the 2PA cross section for the S1′′ and S1′′′ band is about twice that of the dimer (at energies E2 and E3, see Table 2), thus showing a significant cooperative enhancement (see eqn (2)) of δ2PA at very similar state energies. Beyond these general statements it is difficult to draw more specific conclusions about possible n2 dependencies of the 2PA cross sections. This has to do with the fact that one can only compare 2PA cross sections which derive from similar electronic states, this is possible for e.g. the S1′′ and S1′′′ states of dSQA and tSQA but not for SQA where these states are missing. For the former, a relative 2PA cross section of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9.7 is obtained for S1′′ at 18
9.7 is obtained for S1′′ at 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 and of 4
800 cm−1 and of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.5 for S1′′′ at 21
8.5 for S1′′′ at 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1. Both these ratios are very close to the 4
800 cm−1. Both these ratios are very close to the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ratio expected for a dimer and a trimer.
9 ratio expected for a dimer and a trimer.
The dimer dSQB shows a surprisingly similar 2PA spectrum as dSQA with the individual peaks a little bit shifted to lower energies (Fig. 8). The 2PA cross sections are also very similar. This demonstrates that the principal components of the 1PA and 2PA allowed states are in both dimers formed by interaction of the transitions polarised along the molecular long axis and that those polarised perpendicular to the long axis do not play a significant role.62
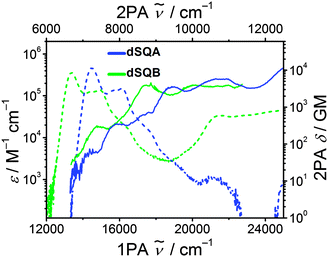 | ||
| Fig. 8 Two photon absorption spectra (solid lines) and one photon absorption spectra (dashed lines) of the dimers dSQA and dSQB in toluene at rt. | ||
The star-like superchromophores SQA-TAA and SQA-ben display qualitatively similar 2PA spectra as SQA. In particular there is a pronounced 2PA at the energy of the vibronic progression at ca. 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (see Table 2). Because of three squaraine chromophores in the star-like systems the 2PA is about three times that of SQA in this energy region. The 2PA at higher energy (>22
000 cm−1 (see Table 2). Because of three squaraine chromophores in the star-like systems the 2PA is about three times that of SQA in this energy region. The 2PA at higher energy (>22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) also rises for the star-like superchromophores, in particular for SQA-TAA. This effect cannot be caused by a double resonance effect with the 1PA state because the lowest 1PA energy is almost the same in SQA, SQA-ben and SQA-TAA. We suppose that it is caused by an increase of density of states because of the enlargement of the π-system, possibly also because of states with CT character in the case of SQA-TAA. This effect is even stronger in the case of SQB-TAA.
000 cm−1) also rises for the star-like superchromophores, in particular for SQA-TAA. This effect cannot be caused by a double resonance effect with the 1PA state because the lowest 1PA energy is almost the same in SQA, SQA-ben and SQA-TAA. We suppose that it is caused by an increase of density of states because of the enlargement of the π-system, possibly also because of states with CT character in the case of SQA-TAA. This effect is even stronger in the case of SQB-TAA.
Much in contrast, the 2PA of dSQA-ben at the S1 to S1′′′ energies is almost exactly three times that of the corresponding 2PA values of dSQA thus showing additivity of the 2PA cross section. Consequently, while there is a cooperative enhancement extending dSQA by one squaraine chromophore to tSQA there is additivity on going from dSQA to dSQA-ben. This demonstrates that the interactions between the branches of the 1,3,5-substituted benzene are negligible but they are strong in the linear arrangement of squaraine dyes.
However, the fluorescence quantum yield is one of the major sources of error in the determination of the 2PA cross section.63 Particularly in case of SQA-ben and dSQA-ben the quantum yields may possess a systematic error because of surface adsorption effects to the cuvette walls. Therefore, the conclusions concerning those chromophores should be taken with care.
For all squaraine superchromophores the 2PA cross section rises strongly when the excitation energy approaches the 1PA energy. This is, as mentioned in the introduction, the consequence of a double resonance effect because for all exciton coupled chromophores, there are biexciton states at about twice the energy of the 1PA states (see Fig. 4). Although the biexciton states cannot simply be characterised as such by 2PA spectroscopy, they may have an indirect influence via the double resonance effect.
Conclusions
In conclusion, all investigated squaraines and squaraine superchromophores displayed sizeable 2PA cross sections. The spectral regions where 2PA resonances occur can be divided into several sections (from low to high energies): (1) for all squaraines the vibronic shoulder at the 1PA energy is 2PA allowed because of vibronic coupling. (2) In the superchromophores dSQA, tSQA, dSQA-ben and dSQB, there is strong 2PA at higher energy states within the exciton manifold. This is caused by symmetry breaking in the superchromophores which lifts the parity rule. (3) For the same superchromophores as above there are low-lying 2PA states which may be understood as being formed by orbital interactions in the linear sequence of squaraine dyes. (4) In case of squaraines with a triarylamine core, the intermediate 2PA allowed states shift to lower energies possibly because of CT character. (5) For all squaraines there is a strong 2PA approaching twice the energy of the 1PA states because of double resonance condition.Besides these findings we found enhancement of 2PA cross sections in linear arrangements of squaraines (dSQA, tSQA, dSQB) but not in those with star-like arrangement (SQA-ben, dSQA-ben) where merely additivity of 2PA cross section is found. The latter is in accord with observations made by Blanchard-Desce et al.22 for other superchromophores with a benzene core. This is surprising given the high oscillator strength of the squaraine dyes. This should lead to a sizable Coulomb coupling between squaraine chromophores even though they are connected by a benzene ring in 1,3,5-position as is evident by comparing the 1PA spectra of SQA and SQA-ben where moderate excitonic couplings were found. Obviously, this is not the case for higher excited states and only additivity of 2PA cross section is therefore observed. Similarly, we found no superradiance effect for branched chromophores but for all linear arrangements. All these observation suggest that the enhancement of 2PA cross section in the linear arrangements of dSQA and tSQA is probably caused by orbital interactions of higher excited configurations.
Experimental
Steady-state absorption spectroscopy
All dyes were dissolved in toluene (Uvasol from Merck) and the UV/vis/NIR-absorption spectra were measured in 1 cm quartz cuvettes from Hellma using a Jasco V-670 spectrometer. The pure solvent was used as reference.The squares of the transition dipole moment were obtained by integration of the main low energy absorption band and calculated as follows64
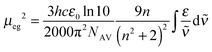 | (5) |
Emission spectroscopy
Steady-state fluorescence measurements were performed with an Edinburgh Instruments FLS980 spectrometer. The compounds were dissolved in toluene (Uvasol from Merck) and purged with argon gas for 30 min prior to each measurement. Fluorescence quantum yields were measured with an integrating sphere and the FLS980 spectrometer applying the method of Bardeen et al.65 to correct for self-absorption. Fluorescence lifetimes were determined by time-correlated single-photon counting (TCSPC) with the FLS980 spectrometer by exciting the samples with a pulsed laser diode at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 (656 nm) under magic angle conditions and using a fast PMT detector (H10720) for fluorescence detection. Deconvolution of the data (4096 channels) was done by measuring the instrument response function with a scatterer (LUDOX). For the fluorescence anisotropy measurement the fluorimeter was equipped with two polarisation filters. The compounds were dissolved in polyTHF (Mn ∼ 650, CAS 25190-06-1, Sigma Aldrich) and measured at 26 °C and 20 °C.
200 cm−1 (656 nm) under magic angle conditions and using a fast PMT detector (H10720) for fluorescence detection. Deconvolution of the data (4096 channels) was done by measuring the instrument response function with a scatterer (LUDOX). For the fluorescence anisotropy measurement the fluorimeter was equipped with two polarisation filters. The compounds were dissolved in polyTHF (Mn ∼ 650, CAS 25190-06-1, Sigma Aldrich) and measured at 26 °C and 20 °C.
Two photon absorption setup
Two-photon cross sections were determined via two-photon excitation spectra using a set-up similar to the one described in ref. 55. In detail, the output of a TOPAS-Prime in combination with a NirUVis frequency mixer (both from Light Conversion) was used as excitation source. The excitation intensity was adjusted using a combination of a broadband zero-order halfwaveplate and a Glan–Taylor polarizer, and the polarization set to vertical. The beam was slightly focused by a (f = 20 cm) lens, which was placed 10 cm before the sample. The pump power was monitored using a powermeter (Thorlabs PM100A) equipped with a thermal sensor (Thorlabs S302C) behind the sample. The fluorescence was focused onto the entrance slit of a monochromator (0.25 m Cornerstone, Oriel, grating 74166 Newport) equipped with a multi-pixel photon-counter avalanche photodiode detector (Hamamatsu S-10362-11-050U) using a spherical mirror (∅ = 75 mm, f = 150 mm). The output signal was preamplified (SR240, Stanford Research Systems), processed with a gated boxcar-integrator and averager module (SR250, SRS), digitized (SR245, SRS) and recorded on a computer.The two photon cross section at a given wavenumber, δ(2)s(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), was calculated as follows66
), was calculated as follows66
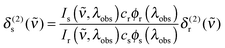 | (6) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ,λobs) is the (two-photon induced) fluorescence intensity at excitation wavenumber ν and observation wavelength λobs for either sample or reference (x ∈ {s,r}). cx and ϕx(λobs) are the concentration and differential fluorescence quantum yield (at the observation wavelength) of sample and reference. LDS698 and Styryl 9 M in chloroform were used as ref. 66 and 67.
,λobs) is the (two-photon induced) fluorescence intensity at excitation wavenumber ν and observation wavelength λobs for either sample or reference (x ∈ {s,r}). cx and ϕx(λobs) are the concentration and differential fluorescence quantum yield (at the observation wavelength) of sample and reference. LDS698 and Styryl 9 M in chloroform were used as ref. 66 and 67.
The power dependence of the fluorescence intensity was monitored throughout the measurement (Fig. S3, ESI†).
Acknowledgements
The Würzburg group thanks the Deutsche Forschungsgemeinschaft for financial support of this work within the Research Group FOR1809. The Geneva group wish to thank the Fonds National Suisse de la Recherche Scientifique through project no. 200020-165890.Notes and references
- S. J. Chung, S. J. Zheng, T. Odani, L. Beverina, J. Fu, L. A. Padilha, A. Biesso, J. M. Hales, X. W. Zhan, K. Schmidt, A. J. Ye, E. Zojer, S. Barlow, D. J. Hagan, E. W. Van Stryland, Y. P. Yi, Z. G. Shuai, G. A. Pagani, J. L. Bredas, J. W. Perry and S. R. Marder, J. Am. Chem. Soc., 2006, 128, 14444–14445 CrossRef CAS PubMed.
- B. Strehmel, S. Amthor, J. Schelter and C. Lambert, ChemPhysChem, 2005, 6, 893–896 CrossRef CAS PubMed.
- W. Denk, J. H. Strickler and W. W. Webb, Science, 1990, 248, 73–76 CAS.
- C. Xu and W. W. Webb, J. Opt. Soc. Am. B, 1996, 13, 481–491 CrossRef CAS.
- D. A. Parthenopoulos and P. M. Rentzepis, Science, 1989, 245, 843–845 CAS.
- J. D. Bhawalkar, N. D. Kumar, C. F. Zhao and P. N. Prasad, Journal of clinical laser medicine & surgery, 1997, 15, 201–204 CAS.
- S. J. Andrasik, K. D. Belfield, M. V. Bondar, F. E. Hernandez, A. R. Morales, O. V. Przhonska and S. Yao, ChemPhysChem, 2007, 8, 399–404 CrossRef CAS PubMed.
- K. Kamada, K. Ohta, I. Yoichiro and K. Kondo, Chem. Phys. Lett., 2003, 372, 386–393 CrossRef CAS.
- J. Fu, L. A. Padilha, D. J. Hagan, E. W. Van Stryland, O. V. Przhonska, M. V. Bondar, Y. L. Slominsky and A. D. Kachkovski, J. Opt. Soc. Am. B, 2007, 24, 67–76 CrossRef CAS.
- M. Drobizhev, A. Karotki, M. Kruk and A. Rebane, Chem. Phys. Lett., 2002, 355, 175–182 CrossRef CAS.
- M. Albota, D. Beljonne, J. L. Bredas, J. E. Ehrlich, J. Y. Fu, A. A. Heikal, S. E. Hess, T. Kogej, M. D. Levin, S. R. Marder, D. McCord-Maughon, J. W. Perry, H. Rockel, M. Rumi, C. Subramaniam, W. W. Webb, X. L. Wu and C. Xu, Science, 1998, 281, 1653–1656 CrossRef CAS PubMed.
- M. Rumi, J. E. Ehrlich, A. A. Heikal, J. W. Perry, S. Barlow, Z. Y. Hu, D. McCord-Maughon, T. C. Parker, H. Rockel, S. Thayumanavan, S. R. Marder, D. Beljonne and J. L. Bredas, J. Am. Chem. Soc., 2000, 122, 9500–9510 CrossRef CAS.
- S. Webster, J. Fu, L. A. Padilha, O. V. Przhonska, D. J. Hagan, E. W. Van Stryland, M. V. Bondar, Y. L. Slominsky and A. D. Kachkovski, Chem. Phys., 2008, 348, 143–151 CrossRef CAS.
- S. Webster, S. A. Odom, L. A. Padilha, O. V. Przhonska, D. Peceli, H. H. Hu, G. Nootz, A. D. Kachkovski, J. Matichak, S. Barlow, H. L. Anderson, S. R. Marder, D. J. Hagan and E. W. Van Stryland, J. Phys. Chem. B, 2009, 113, 14854–14867 CrossRef CAS PubMed.
- W. V. Moreshead, O. V. Przhonska, M. V. Bondar, A. D. Kachkovski, I. H. Nayyar, A. E. Masunov, A. W. Woodward and K. D. Belfield, J. Phys. Chem. C, 2013, 117, 23133–23147 CAS.
- C. Andraud, R. Fortrie, C. Barsu, O. Stéphan, H. Chermette and P. L. Baldeck, in Photoresponsive Polymers II, ed. S. R. Marder and K.-S. Lee, Springer, Berlin, Heidelberg, 2008, vol. 214 Search PubMed.
- F. Terenziani, C. Katan, E. Badaeva, S. Tretiak and M. Blanchard-Desce, Adv. Mater., 2008, 20, 4641–4678 CrossRef CAS.
- E. Collini, Phys. Chem. Chem. Phys., 2012, 14, 3725–3736 RSC.
- M. G. Kuzyk, J. Chem. Phys., 2003, 119, 8327–8334 CrossRef CAS.
- M. Drobizhev, A. Karotki, Y. Dzenis, A. Rebane, Z. Suo and C. W. Spangler, J. Phys. Chem. B, 2003, 107, 7540–7543 CrossRef CAS.
- C. Katan, F. Terenziani, O. Mongin, M. H. V. Werts, L. Porres, T. Pons, J. Mertz, S. Tretiak and M. Blanchard-Desce, J. Phys. Chem. A, 2005, 109, 3024–3037 CrossRef CAS PubMed.
- F. Terenziani, C. Le Droumaguet, C. Katan, O. Mongin and M. Blanchard-Desce, ChemPhysChem, 2007, 8, 723–734 CrossRef CAS PubMed.
- D. Beljonne, W. Wenseleers, E. Zojer, Z. G. Shuai, H. Vogel, S. J. K. Pond, J. W. Perry, S. R. Marder and J. L. Bredas, Adv. Funct. Mater., 2002, 12, 631–641 CrossRef CAS.
- S. J. Chung, K. S. Kim, T. H. Lin, G. S. He, J. Swiatkiewicz and P. N. Prasad, J. Phys. Chem. B, 1999, 103, 10741–10745 CrossRef CAS.
- D. Scherer, R. Dorfler, A. Feldner, T. Vogtmann, M. Schwoerer, U. Lawrentz, W. Grahn and C. Lambert, Chem. Phys., 2002, 279, 179–207 CrossRef CAS.
- L. Beverina and M. Sassi, Synlett, 2014, 477–490 CrossRef CAS.
- L. Beverina and P. Salice, Eur. J. Org. Chem., 2010, 1207–1225 CrossRef CAS.
- A. Ajayaghosh, Chem. Soc. Rev., 2003, 32, 181–191 RSC.
- A. Ajayaghosh, Acc. Chem. Res., 2005, 38, 449–459 CrossRef CAS PubMed.
- S. Sreejith, P. Carol, P. Chithra and A. Ajayaghosh, J. Mater. Chem., 2008, 18, 264–274 RSC.
- P. Anees, S. Sreejith and A. Ajayaghosh, J. Am. Chem. Soc., 2014, 136, 13233–13239 CrossRef CAS PubMed.
- T. Geiger, S. Kuster, J. H. Yum, S. J. Moon, M. K. Nazeeruddin, M. Gratzel and F. Nuesch, Adv. Funct. Mater., 2009, 19, 2720–2727 CrossRef CAS.
- S. Kuster and T. Geiger, Dyes Pigm., 2012, 95, 657–670 CrossRef CAS.
- L. Hu, Z. Q. Yan and H. Y. Xu, RSC Adv., 2013, 3, 7667–7676 RSC.
- S. A. Odom, S. Webster, L. A. Padilha, D. Peceli, H. Hu, G. Nootz, S. J. Chung, S. Ohira, J. D. Matichak, O. V. Przhonska, A. D. Kachkovski, S. Barlow, J. L. Bredas, H. L. Anderson, D. J. Hagan, E. W. Van Stryland and S. R. Marder, J. Am. Chem. Soc., 2009, 131, 7510–7511 CrossRef CAS PubMed.
- S. Ohira, I. Rudra, K. Schmidt, S. Barlow, S. J. Chung, Q. Zhang, J. Matichak, S. R. Marder and J. L. Bredas, Chem. – Eur. J., 2008, 14, 11082–11091 CrossRef CAS PubMed.
- C. Lambert, T. Scherpf, H. Ceymann, A. Schmiedel and M. Holzapfel, J. Am. Chem. Soc., 2015, 137, 3547–3557 CrossRef CAS PubMed.
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CrossRef CAS.
- S. F. Völker, A. Schmiedel, M. Holzapfel, K. Renziehausen, V. Engel and C. Lambert, J. Phys. Chem. C, 2014, 118, 17467–17482 Search PubMed.
- S. F. Völker, T. Dellermann, H. Ceymann, M. Holzapfel and C. Lambert, J. Polym. Sci., Part A: Polym. Chem., 2014, 52, 890–911 CrossRef.
- S. F. Völker, M. Renz, M. Kaupp and C. Lambert, Chem. – Eur. J., 2011, 17, 14147–14163 CrossRef PubMed.
- W. W. Parson, Modern Optical Spectroscopy, Springer, 2009, p. 293 Search PubMed.
- H. v. Amerongen, L. Valkunas and R. v. Grondelle, Photosynthetic Excitons, World Scientific, Singapur, 2002, ch. 3, pp. 73–118 Search PubMed.
- J. Knoester, in Proceedings of the International School of Physics “Enrico Fermi” Course CXLIX, ed. V. M. Agranovich and G. C. La Rocca, IOS Press, Amsterdam, 2002, pp. 149–186 Search PubMed.
- A recently performed fluorescence upconversion measurement of SQA in toluene at 590 nm pump [see ref. 37] was reanalysed using a stretched exponential function and gave τf = 1.57 ns and β = 0.90.
- G. de Miguel, M. Marchena, M. Zitnan, S. S. Pandey, S. Hayase and A. Douhal, Phys. Chem. Chem. Phys., 2012, 14, 1796–1805 RSC.
- S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- R. H. Dicke, Phys. Rev., 1954, 93, 99–110 CrossRef CAS.
- G. L. Celardo, G. G. Giusteri and F. Borgonovi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075113 CrossRef.
- H. Fidder, J. Knoester and D. A. Wiersma, J. Chem. Phys., 1991, 95, 7880–7890 CrossRef CAS.
- We stress that the use of the term “superradiance” in this work differs from the older definition of a “macroscopic superradiance” by Dicke, R. H. Dicke, Phys. Rev., 1954, 93, 99–110 CrossRef CAS see also F. C. Spano and S. Mukamel, J. Chem. Phys., 1989, 91, 683–700 CrossRef.
- E. Vauthey, ChemPhysChem, 2012, 13, 2001–2011 CrossRef CAS PubMed.
- H. Ceymann, M. Balkenhohl, A. Schmiedel, M. Holzapfel and C. Lambert, Phys. Chem. Chem. Phys., 2016, 18, 2646–2657 RSC.
- M. A. C. Nascimento, Chem. Phys., 1983, 74, 51–66 CrossRef CAS.
- We refrain from discussing the relative intensities of these vibronically allowed 2PA bands of the diverse squaraine dyes as intensity borrowing may blur any interpretation in terms of cooperative effects.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, New York, NY, 3. (corr. at 4. print.) edn, 2010 Search PubMed.
- The two g symmetric configurations maybe undergo CI mixing.
- For a comparison of different methods to estimate exciton coupling effects, see W. J. D. Beenken and T. Pullerits, J. Chem. Phys., 2004, 120, 2490–2495 CrossRef CAS PubMed; W. L. Liu, V. Settels, P. H. P. Harbach, A. Dreuw, R. F. Fink and B. Engels, J. Comput. Chem., 2011, 32, 1971–1981 CrossRef PubMed.
- Y. Shibata, S. Tateishi, S. Nakabayashi, S. Itoh and H. Tamiaki, Biochemistry, 2010, 49, 7504–7515 CrossRef CAS PubMed.
- D. Gülen, Photosynth. Res., 2006, 87, 205–214 CrossRef PubMed.
- P. Macak, Y. Luo, P. Norman and H. Ågren, J. Chem. Phys., 2000, 113, 7055–7061 CrossRef CAS.
- Bredas et al. recently pointed out that non-centrosymmetrical cis-squaraines behave essentially as centrosymmetrical trans-squaraines concerning the properties of excited states [see ref. 36].
- Due to the unknown systematic errors of the fluorescence quantum yields we refrain from giving errors for the 2PA measurements, but we estimate those being within 10% relative to each other for the set of compounds studied here.
- J. E. Lewis and M. Maroncelli, Chem. Phys. Lett., 1998, 282, 197–203 CrossRef CAS.
- T. S. Ahn, R. O. Al-Kaysi, A. M. Mueller, K. M. Wentz and C. J. Bardeen, Rev. Sci. Instrum., 2007, 78, 086105 CrossRef PubMed.
- N. S. Makarov, M. Drobizhev and A. Rebane, Opt. Express, 2008, 16, 4029–4047 CrossRef CAS PubMed.
- N. S. Makarov, J. Campo, J. M. Hales and J. W. Perry, Opt. Mater. Express, 2011, 1, 551–563 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic protocols, fluorescence excitation anisotropy spectrum, power dependence of 2PAF, lifetime distributions and TD-DFT calculations. See DOI: 10.1039/c6cp02312f |
| This journal is © the Owner Societies 2016 |