Interaction of water with (silico)aluminophosphate zeotypes: a comparative investigation using dispersion-corrected DFT

Abstract

Porous aluminophosphates (AlPOs) and silicoaluminophosphates (SAPOs) with zeolite-like structures have received considerable attention as potential adsorbents for heat transformation applications using water adsorption/desorption cycles. Since a detailed experimental characterisation of the water adsorption properties has only been performed for some of these materials, such as AlPO-18 (AEI topology) and SAPO-34 (CHA topology), more systematic insights regarding the influence of the pore topology and (for SAPOs) the arrangement of the framework protons on the affinity towards water are lacking. To study the relationships between structure and properties in more detail, the interaction of water with six structurally different AlPOs (with AEI, AFX, CHA, ERI, GIS, RHO topologies) and their SAPO analogues was investigated using dispersion-corrected density-functional theory (DFT-D) calculations. Different possible locations of silicon atoms and charge-balancing protons were considered for the SAPO systems. The calculations for SAPOs at low water loadings (one H₂O molecule per framework proton) revealed that the interaction energies exhibit a considerable variation, ranging from −75 to −100 kJ mol⁻¹ (per water molecule). The differences in interaction energy were rationalised with the different structural environment of the framework protons at which the water molecules are adsorbed. At high water uptakes (near saturation), interaction energies in the range of −65 kJ mol⁻¹ were obtained for all AlPOs, and there was no evidence for a marked influence of pore size and/or topology on the interaction strength. The interaction of water with SAPOs was found to be approximately 5 kJ mol⁻¹ stronger than for AlPOs due to an increased contribution of electrostatic interactions. An analysis of the structural changes upon water adsorption revealed striking differences between the distinct topologies, with the materials with GIS and RHO topologies being distorted much more drastically than the systems based on double six-ring (d6r) units. Moreover, the direct coordination of water molecules to framework aluminium atoms occurs more frequently in these materials, an observation that points towards a reduced structural stability upon hydration.

---

1 Introduction

Microporous aluminophosphates (AlPOs) and silicoaluminophosphates (SAPOs) with zeolite-like structures (zeotypes) currently receive considerable attention as adsorbents for adsorptive heat transformations, with potential applications in the heating or cooling of buildings (adsorption-driven heat pumps, adsorption chillers) and in thermal energy storage (e.g. seasonal heat storage, utilisation of industrial waste heat).^1,2 The use of water as working fluid in such applications is particularly attractive, as water is readily available and environmentally benign. Compared to classical zeolites, which interact more strongly with water, leading to high desorption temperatures (often exceeding 200 °C),³ AlPOs and SAPOs are more promising for processes involving low-temperature waste heat, as only moderate temperatures in the range of 100 °C are needed to desorb water from these systems.^4,5 Since the characteristics of an ideal adsorbent depend strongly on the requirements of the process (such as the desorption temperature that is available from the heat source), there is no “one-size-fits-all” adsorbent for heat transformation applications, but different materials are best suited for different processes.² Therefore, there is considerable scope for the targeted development and testing of novel adsorbents, and for more fundamental research efforts aiming at a better understanding of the relationships between adsorbent structure and water adsorption properties.⁶

AlPOs and SAPOs exhibit a significant structural variability: a review published in 2010 lists more than 25 AlPOs and 16 SAPOs with distinct topologies,⁷ and ongoing research efforts have led to the successful synthesis and structural characterisation of several new systems in the last couple of years.^8–10 While some of the topologies of AlPOs/SAPOs are also found in zeolites, such as the chabazite (CHA) topology of AlPO-34/SAPO-34, others are unique to aluminophosphate-based systems, for example the AEI topology of AlPO-18/SAPO-18. In the absence of structural defects, AlPOs (composition AlPO₄) correspond to a perfect alternating arrangement of Al and P atoms at the tetrahedrally coordinated sites (T sites). The tetrahedral framework of SAPOs has the general composition (Si_xAl_yP_z)O₂, where x is typically in the range of 0.02 to 0.2. If only small amounts of silicon are incorporated in the structure, the Si atoms tend to replace phosphorus atoms at isolated T sites. In this case, y = 0.5 and z = 0.5 − x. The negative framework charge that arises from the replacement of P⁵⁺ by Si⁴⁺ is compensated by framework protons. At higher Si contents, silicon atoms may aggregate in larger assemblies (“silicon islands”), rather than forming isolated Si sites, and the occurrence of such heterogeneities is directly linked to the synthesis conditions.¹¹

Sparked by the potential use of AlPOs and SAPOs in heat transformation applications, a number of researchers have investigated the adsorption of water in these systems. For example, water adsorption experiments using powder samples were performed for AlPO-5 (AFI topology),^12,13 AlPO-17 (ERI),¹³ AlPO-18 (AEI),^12–16 SAPO-34 (CHA),^6,12–14,16 and a triclinically distorted CHA-type system termed AlPO-tric.¹⁶ These materials typically exhibit S-shaped water adsorption isotherms and isobars, a feature that is attractive because a large loading spread can be reached upon a moderate change in pressure and/or temperature (the loading spread corresponds to the difference in water uptake between adsorption and desorption conditions; a larger loading spread leads to a higher attainable energy density). The most promising systems, for example AlPO-18 and SAPO-34, exhibit a loading spread in the range of 300 g kg⁻¹ when assuming H₂O adsorption at 40 °C and desorption in the range of 100 °C, conditions that are relevant for the temporary storage of solar thermal energy.¹⁶ It is worth noting that, in cases where several systems were compared, fairly similar heats of adsorption were measured for different AlPOs and SAPOs, despite the topological (and, in some instances, compositional) differences among the systems studied. For example, Ristic et al. reported heats of adsorption in the range of 55 kJ mol⁻¹ for AlPO-18, AlPO-tric, and SAPO-34.¹⁶ Typically, the heat of adsorption decreases considerably with increasing water loading in SAPO materials, since the first adsorbed water molecules can interact directly with the framework protons, whereas weaker interactions with the framework and other water molecules dominate at higher loadings.¹³ For AlPOs, where such strong interaction sites are absent, it can be expected that the heat of adsorption changes only moderately as a function of the water loading. In addition to the investigation of powder samples, composites of AlPOs or SAPOs and support materials, primarily aluminium sheets or foams,^5,17–20 have been successfully prepared and characterised. The development of stable composites is pivotal for the actual application of these materials in adsorptive heat transformations. This is exemplified by a SAPO-34-coated heat exchanger, which was successfully integrated into a lab-scale adsorption chiller.²⁰

Computational chemistry methods at different levels of theory have been employed to predict and understand the interaction of AlPOs/SAPOs with water at a microscopic level. Henninger and co-workers used grand-canonical Monte Carlo (GCMC) simulations with an empirical force field to predict water adsorption isobars of AlPO-18.¹⁵ Despite rather promising results, this method has not been widely employed for water in AlPOs or SAPOs, whereas there are numerous studies of water adsorption in aluminosilicate zeolites.²¹ A larger number of computational investigations relied on electronic structure methods, especially density-functional theory (DFT). Early periodic DFT studies addressed the interaction of water with the acid sites of SAPO-34.^22,23 It was shown that the adsorption of a single water molecule does not lead to framework deprotonation, but that the interaction with several water molecules can induce the formation of H₃O⁺(H₂O)_n clusters. A later study of the chabazite-type aluminosilicate SSZ-13 showed that the likelihood of framework deprotonation decreases with temperature.²⁴ A number of DFT-based studies addressed the structure and, in some instances, dynamics of water in the pores of several aluminophosphates.^25–28 These studies delivered insights into the interatomic interactions governing water adsorption: For example, the rapid filling of the unit cell of AlPO-34 could be explained with the formation of a collective network of hydrogen bonds,²⁶ and the presence of octahedrally coordinated framework aluminium atoms in water-loaded AlPO-18 was found to be the energetically favoured scenario, in agreement with experimental observations.²⁷ Furthermore, ab initio molecular dynamics (MD) calculations corroborated that the adsorbed molecules have a considerable freedom of motion at room temperature.^25–27 Recent DFT-based studies of water in SAPO-34 have addressed various aspects: a series of investigations by Fjermestad et al. elucidated the role of water during framework desilication and silicon island formation.^29–31 Van Speybroeck and co-workers used ab initio MD calculations to study the proton mobility and framework flexibility in water- and methanol-loaded SAPO-34, as well as the effect of water on methanol-to-olefin conversion reactions.^32,33 Particular attention was paid to the changes in lattice parameters in guest-loaded structures, with the most pronounced change being a contraction of the structure along the c-axis upon water adsorption, in agreement with previous experimental observations.³⁴ Finally, we studied the influence of local heterogeneities (silicon islands, SiAl domains) and defects on the interaction of SAPO-34 with water.³⁵ While a significant effect was observed at low water loadings, the impact on the total interaction strength at high loadings was only modest.

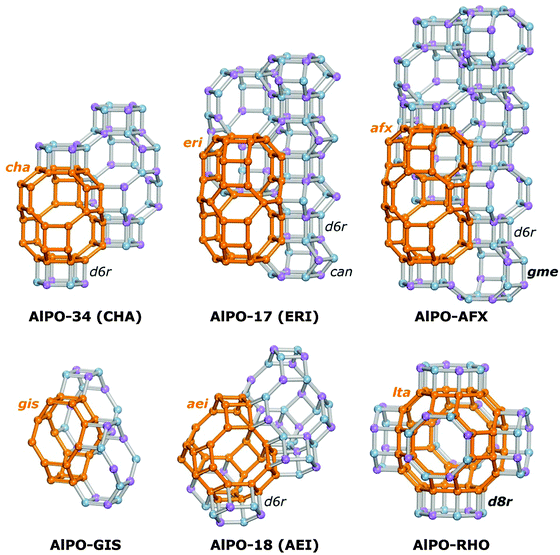
The present work aims at a more systematic computational exploration of the influence of various structural factors (pore size, pore topology, environment of framework protons) on the interaction of AlPOs and SAPOs with water, covering both energetic and structural aspects. Dispersion-corrected density-functional theory (DFT-D) calculations are employed to study the adsorption in six structurally different AlPOs and their SAPO analogues. In addition to AlPO-34/SAPO-34,^36,37 AlPO-17/SAPO-17,^37–40 and AlPO-18/SAPO-18,^38,41,42 pairs where either the AlPO or the SAPO system has already been proposed as adsorbent for heat transformation applications,^{5,6,12–16,20} three other systems are evaluated: AlPO-GIS/SAPO-43,^40,43,44 AlPO-AFX/SAPO-56,⁴⁵ and AlPO-RHO/SAPO-RHO.^9,46,47 With the exception of the last two systems, which so far have only been reported as SAPO materials, not as pure aluminophosphates, all other materials have been successfully synthesised in both AlPO and SAPO form. In all six structures considered, the pores are connected through eight-ring windows. The different structure types were chosen in order to study the influence of pore size and pore geometry: while the main pore systems of AlPO-34, AlPO-17, and AlPO-AFX are formed by elongated cages, AlPO-GIS, AlPO-18, and AlPO-RHO contain more or less isometric pores of different size. The building unit constituting the six structures are visualised in Fig. 1, with one of the main cages being highlighted for each system.

Fig. 1 Visualisation of AlPO structures considered in this work with emphasis on the constituent building units. Distinct building units are labelled with three-letter codes. Labels of those units that are accessible through eight-ring windows are displayed in bold letters. For each system, the outlines of one of the main cages (representing the main portion of the accessible pore volume) are highlighted in orange.

The remainder of this article is organised as follows: after a description of the model systems and the computational methodology, the results of the DFT-D optimisations of guest-free AlPO and SAPO systems are presented. These are followed by a detailed discussion of the DFT-D results for water-containing systems: AlPOs typically exhibit a steep rise of the water adsorption isotherm at a certain relative pressure (corresponding to pore filling). Below this pressure, only very little water is adsorbed due to the absence of preferred adsorption sites. Therefore, only the interaction with large amounts of water (near saturation) is studied for these systems. For SAPOs, initial adsorption at low water pressures will occur at the framework protons, prior to a pore filling at higher relative pressures. Consequently, both the adsorption of small amounts of water (one H₂O per framework proton) and large amounts (near saturation) are considered in the calculations for these materials. Besides reporting the DFT-D interaction energies (averaged over 5 snapshots for high water loadings), the structural changes upon water adsorption are also assessed.

2 Computational details

2.1 Preparation of model systems

DFT-D optimisations were performed for all guest-free systems. These optimisations included a relaxation of the lattice parameters and all atomic coordinates (for some of the SAPOs, constraints were applied to avoid a distortion of the unit cell, see ESI† for more details). Initial models of the AlPO structures were constructed either from published crystallographic data, or by starting from an all-silica model of the framework and replacing the silicon atoms by Al and P in an alternating fashion. For the SAPO systems, the optimised AlPO models were taken as starting point. As it has been established that Si substitution occurs at phosphorus sites of the AlPO matrix,^48,49 isolated phosphorus atoms were replaced by silicon in an ordered fashion, and a hydrogen atom was placed at one of the oxygen atoms surrounding the Si site. This led to a reduction of the symmetry, which is summarised for each system in the Results section (a more detailed description is given in the ESI†). Where applicable, different possible substitution sites, and different available locations of the framework proton were considered in the initial DFT-D optimisations (with the exception of SAPO-34, which has been studied previously). For every possible Si site, only the model with the energetically most favourable proton location was included in the subsequent computations including adsorbed water. It has to be pointed out that, in contrast to our previous work,³⁵ the present study considers only isolated Si atoms, where each Si site requires one proton to balance the charge (N(H) = N(Si)). The possibility of silicon island formation, which may occur at higher Si contents (where N(H) < N(Si)), was not considered.

In order to study the interaction with water, different strategies were pursued for AlPOs and SAPOs: while only high water loadings (near saturation) were considered for AlPOs, both low loadings (one H₂O per framework proton) and near-saturation conditions were included for SAPOs. In the DFT-D calculations for water-loaded systems, all atomic coordinates and the lattice parameters were relaxed. The same constraints as for the guest-free models were applied for systems containing one water molecule per proton, whereas no constraints were invoked at high water loadings.

Starting structures for SAPOs with one molecule of H₂O per proton were prepared by placing the guest molecule in the vicinity of the proton. To investigate AlPOs and SAPOs at high water loadings, preliminary grand-canonical Monte Carlo simulations were performed to determine the approximate saturation uptake of each system. These calculations used the Sorption module of the Accelrys “Materials Studio” suite, with each run comprising five million equilibration steps and five million production steps. The GCMC simulations employed parameters from the Consistent Valence Force Field (cvff).⁵⁰ These parameters were also used in a GCMC study of water adsorption in AlPO-18 by Henninger and co-workers, where reasonable agreement with experimental adsorption isobars was observed.¹⁵ It is worth noting that several of the AlPOs/SAPOs contain smaller cavities bordered by six-rings in addition to the main pore system that is connected by eight-ring windows. As these cavities (d6r and can units shown in Fig. 1) are in principle large enough to accommodate a water molecule, it will depend on the ability of the molecules to pass through the six-ring windows whether the cavities contribute to the total water uptake. In a previous combined MD and experimental study of water in AlPO-34, a water molecule was observed at the centre of the d6r unit.²⁶ On the other hand, these units seem to be inaccessible to water in AlPO-18.²⁷ In any case, the largest part of the adsorbed water will be located in the larger pores, which is why the present study ignores the possibility of adsorption in these small cavities. These areas were blocked by non-interacting spheres in the preliminary GCMC simulations.

The input structures for the DFT-D calculations were generated from fixed-loading Monte Carlo simulations that also used the cvff parameters. The amount of water molecules used in these calculations was always somewhat lower than the saturation uptake predicted from the GCMC simulations (typically ∼15% below the saturation loading). For each system, the fixed-loading MC simulation consisted of at least one million equilibration steps and five million production steps. A total of 200 snapshots were stored throughout the production stage, and five snapshots were randomly selected from the whole production stage. These snapshots were then used as initial configurations in the DFT-D calculations.

One has to bear in mind that the present approach involves one key approximation: for the systems containing large amounts of adsorbed water, the actual interaction energy would correspond to a weighted average over a practically infinite number of possible arrangements of water molecules in the pores. In the approach used here, this is approximated by averaging the interaction energies calculated for a small number of optimised configurations. Admittedly, this is a rather simplistic procedure; however, the findings of our previous work,³⁵ and the fact that the standard deviations arising from the averaging over five snapshots are fairly small (never exceeding ±2.0 kJ mol⁻¹ and being smaller than ±1.0 kJ mol⁻¹ in half of the cases, see below), indicate that one arrives at a reasonable estimate of the interaction energy, especially if the main aim is an identification of trends, rather than a highly accurate quantitative prediction. A more thorough sampling of configuration space (including temperature effects) could be obtained by running a series of ab initio MD calculations starting from different snapshots. However, in the view of the rather large estimated error bars of 10 kJ mol⁻¹ reported in a recent ab initio MD study of water and methanol adsorbed in SAPO-34,³³ it can be anticipated that a computational setup that reduces the error to an acceptable level would be prohibitively expensive, in particular since some of the systems studied have rather large unit cells.

2.2 Details of DFT-D calculations

The DFT-D calculations were performed using the CASTEP code, which employs a combination of plane waves (for valence electrons) and pseudopotentials (for “core” electrons).⁵¹ The calculations used on-the-fly-generated ultrasoft pseudopotentials and an energy cutoff of 700 eV. For all structures, only the gamma-point was used to sample the Brillouin zone. The calculations employed the PBE exchange–correlation functional⁵² in conjunction with the dispersion correction scheme proposed by Tkatchenko and Scheffler,⁵³ termed PBE-TS in the following. In a previous study of water adsorption in SAPO-34 and AlPO-34, good agreement of the PBE-TS interaction energies with experimental heats of water adsorption was observed.³⁵ Furthermore, the PBE-TS functional was employed successfully to predict the structures of sheet silicates,⁵⁴ of molecular crystals and various layered materials,⁵⁵ and of water-containing zeolites.⁵⁶

The PBE-TS interaction energies reported in this study were calculated as follows:

E_int = E_PBE-TS(adsorbent + nH₂O) − E_PBE-TS(adsorbent) − nE_PBE-TS(H₂O)

The first term corresponds to the PBE-TS energy obtained for the adsorbent (AlPO or SAPO) with n water molecules adsorbed, the second term corresponds to the PBE-TS energy of the guest-free adsorbent, and the last term represents an isolated H₂O molecule placed in a large box (edge length 20 Å). Throughout this work, all interaction energies are reported as negative values.

In order to directly compare the calculation results to experimental heats of water adsorption, it would be necessary to explicitly calculate vibrational contributions (zero-point vibrational energy ZPVE and temperature contributions). Since the water-containing AlPO and SAPO models studied in this work contain a large number of non-equivalent atoms in the unit cell, a full vibrational calculation would be computationally very expensive. However, we performed preliminary (PBE) calculations for SAPO-34 with one adsorbed water molecule, obtaining a correction term of ∼+7 kJ mol⁻¹ for temperatures near room temperature. We observed previously that the PBE-TS interaction energies are typically 8 to 10 kJ mol⁻¹ higher than experimental heats of adsorption (in absolute values – interaction energies are negative, whereas heats of adsorption are positive by definition).³⁵ This magnitude is in good accordance with the PBE-based temperature correction. With few exceptions that are mentioned explicitly, only the uncorrected interaction energies are discussed throughout this work. As there is reason to assume that the contribution of vibrations will be similar for all AlPOs/SAPOs studied, the trends identified herein should not be affected by the neglect of vibrational effects.

3 Results and discussion

3.1 Optimisation of guest-free systems

AlPOs. Table 1 reports the lattice parameters of the DFT-D optimised structures of all AlPOs considered in the present work, together with experimental data for calcined AlPOs. These are available for AlPO-34, AlPO-17, and AlPO-18, whereas no experimental structure data have been reported in the publication reporting a gismondine-type pure aluminophosphate AlPO-GIS.⁴³ Finally, as mentioned previously, AlPO-AFX and AlPO-RHO are hypothetical systems, since only SAPOs with this topology have been synthesised so far.^45–47 For AlPO-34, AlPO-17, AlPO-GIS, and AlPO-AFX the conventional setting of the unit cell was used in the calculations. For AlPO-18 and AlPO-RHO, the optimisation was performed in the primitive cell of space groups C2/c and I23, respectively, and the structures were transformed back into the conventional cell for the comparison reported in Table 1.

Table 1 Comparison of lattice parameters of DFT-D optimised AlPO structures to experimental values for calcined systems (where available). Experimental data are taken from ref. 57 for AlPO-34 and AlPO-18, and from ref. 58 for AlPO-17

	Topology	Space group	a/Å	b/Å	c/Å	β/deg
AlPO-34, DFT	CHA	R3̄	13.792		14.972
AlPO-34, Exp			13.744		14.941
AlPO-17, DFT	ERI	P63/m	13.205		15.385
AlPO-17, Exp			13.146		15.350
AlPO-AFX, DFT	AFX	P3̄1c	13.774		20.048
AlPO-GIS, DFT	GIS	Fddd	13.979	13.778	10.349
AlPO-18, DFT	AEI	C2/c	13.802	12.787	18.649	89.82
AlPO-18, Exp			13.746	12.753	18.608	90.00
AlPO-RHO, DFT	RHO	I23	15.123

---

For those three systems for which experimental data for calcined, pure AlPO systems are available, the DFT-D optimised unit cell dimensions agree very well with the experimental cell parameters. There is a consistent tendency to overestimate the lattice parameters slightly, with relative deviations of not more than 0.5%.

After the DFT-D optimisations, geometric calculations using the PoreBlazer code were performed to determine the accessible volume fraction, the diameter of the largest sphere that can be included without overlapping with the framework (d_LS), and the pore limiting diameter (d_PLD).⁵⁹ For the systems with elongated cages, the largest sphere diameter does not fully describe the pore dimensions, as its value depends only on the shortest axis of the cage. To account for this, the length of the longest axis of the cages of AlPO-34, AlPO-17, and AlPO-AFX was estimated from the distance between the centres of the six-rings at the top and the bottom of the cages, subtracting 2 Å to account for the van der Waals radii of the surrounding framework atoms. This quantity, termed d_c because the direction of cage elongation is parallel to the crystallographic c-axis in these systems, is also given in Table 2.

Table 2 Results of geometric calculations using PoreBlazer: accessible volume fraction V_acc, diameter of largest included sphere d_LS, vertical extension of the cage d_c (for systems with elongated cages), and pore limiting diameter d_PLD

	V acc/cm^3 g^−1	d LS/Å	d c/Å	d PLD/Å
AlPO-34	0.376	6.93	9.8	3.57
AlPO-17	0.337	6.53	13.4	3.16
AlPO-AFX	0.378	7.24	14.9	3.50
AlPO-GIS	0.315	4.77	—	2.92
AlPO-18	0.378	7.24	—	3.62
AlPO-RHO	0.412	10.32	—	3.76

---

The accessible volume fractions in the six structures fall in a reasonably narrow range, which leads us to expect that the maximal water uptake should also be similar. In the systems with elongated cages, the largest sphere diameter is fairly similar, which is not surprising given the structural similarities (Fig. 1). The degree of cage elongation in AlPO-34 (d_c ≈ 1.4·d_LS) is considerably smaller than in AlPO-17 and AlPO-AFX (d_c ≈ 2.05·d_LS). In the three systems with isometric cages, the largest sphere diameter increases in the order AlPO-GIS < AlPO-18 < AlPO-RHO. Regarding the pore limiting diameter, which describes the diameter of the largest sphere that can pass through the eight-ring windows, four of the systems have very similar values in the range of 3.5 to 3.6 Å. An inspection of the structures reveals that the eight-ring windows in these systems are almost circular, with typical oxygen–oxygen distances (measured across the cage) of at least 6.5 Å. The exceptions are AlPO-17 and AlPO-GIS: in these systems, the eight-ring windows exhibit an elliptical distortion, which is more pronounced in AlPO-GIS (shortest O–O distance across the cage of 5.72 Å) than in AlPO-17 (shortest O–O distance of 6.0 Å). Due to their small kinetic diameter (2.64 Å), water molecules will be able to diffuse through the windows of all these structures; however, it can be anticipated that an even more drastic elliptical distortion than in AlPO-GIS might impede the diffusion of water through eight-ring windows.

SAPOs. For the SAPO systems, different locations of the Si atoms and the associated protons were considered. These calculations employed models that had a lower symmetry than the parent AlPO structures, without removing the symmetry completely. It has to be conceded that the use of SAPO models retaining an inherent symmetry might introduce a degree of artificial ordering, since Si atoms and associated protons could be distributed over several low-energy sites in real systems. However, the present approach, in which all framework Si atoms are equivalent by symmetry, has the advantage that different possible Si and H locations can be studied in a systematic fashion, permitting the identification of energetically preferred scenarios.

The SAPO models employed for each system are presented in detail in the ESI,† where the silicon and proton locations are also visualised. To distinguish the different models, labels of the form “SAPO-N_SiX_OY” are used, where X designates the location of the silicon atom, and Y labels the oxygen atom to which the framework proton is attached (OY is bonded to SiX). The label SiX is left out if there is only one Si site. Tables S2–S7 of the ESI† report the lattice parameters and relative energies for all models considered. It is apparent that there are many cases where several possible proton locations are very close in energy. To keep the total number of systems tractable, only the lowest-energy proton location for each silicon site was considered in the DFT-D calculations including adsorbed water molecules.

Table 3 gives an overview over the number of different models considered for each structure type, and reports the energetically most favourable scenarios. Due to a lack of available crystallographic data for calcined SAPOs, and the dependence of the DFT-optimised lattice parameters on the distribution of Si and H atoms in the framework, a detailed comparison to experimental data was not attempted for these systems. However, the good agreement for AlPOs found above, together with the previous observation that the PBE-TS optimised lattice parameters of different models of SAPO-34 agree well with experimental values,³⁵ indicate that this functional should provide a realistic prediction of SAPO structures.

Table 3 Overview of SAPO models. The silicon content is reported as atoms per unit cell N(Si) and as molar fraction of all T atoms. Furthermore, the number of distinct Si sites and the number of proton positions (corresponding to the total number of models considered) are given. For SAPO-34, it has been established in previous work that O1 constitutes the most favourable proton position,³⁵ thus, calculations for the other three positions were not repeated in the present study

	Space group	N(T) per u.c.	N(Si) per u.c.	x = N(Si)/N(T)	#(Si sites)	#(H sites)	Energetically preferred model(s)
a Non-conventional setting of space group Cc. b Per primitive cell.
SAPO-34	P32	36	3	0.083	1	4	SAPO-34_O1
SAPO-17	P21	36	2	0.056	2	7	SAPO-17_Si1_O3, SAPO-17_Si2_O5
SAPO-56	Bn	48	2	0.042	2	8	SAPO-56_Si1_O5, SAPO-56_Si2_O4
SAPO-43	P1̄	32	2	0.063	1	4	SAPO-43_O12
SAPO-18	Cn	24^b	2^b	0.083	3	12	SAPO-18_Si1_O12, SAPO-18_Si2_O11, SAPO-18_Si3_O31
SAPO-RHO	I2	24^b	2^b	0.083	1	4	SAPO-RHO_O11

---

A clear trend regarding the energetically preferred proton positions can be identified in those structures in which d6r units are surrounded by four-rings and eight-rings (SAPO-34, SAPO-18, SAPO-56): in these systems, the proton is either bonded to an equatorial oxygen atom of the d6r unit, pointing into an eight-ring window, or it is located at the top of the d6r unit, pointing across a six-ring (ESI,† Fig. S1, S3 and S5). In many instances, the DFT-D energies of these two cases are so close together that a more or less statistical occupation of both positions appears likely for real systems. In SAPO-17, which also contains d6r units, both favoured proton positions are closely associated with six-rings: in SAPO-17_Si1, the proton points across one of the distorted six-ring windows of the can cage, forming a fairly short H⋯O contact of 2.2 Å across the window. If the silicon atom occupies position Si2, the most favourable proton location is located inside the isolated six-ring, which is practically planar (ESI,† Fig. S2). In SAPO-43 and SAPO-RHO, the energetically preferred proton locations are associated with eight-ring windows (ESI,† Fig. S4 and S6). For these systems, a comparison of the most favourable systems to other possible arrangements shows a tendency to maximise the distance between the framework protons. Scenarios in which two protons point into the same eight-ring window are particularly unfavourable, which seems plausible from simple electrostatic considerations.

3.2 Preliminary GCMC simulations

The preliminary GCMC simulations of water adsorption were performed for AlPO and SAPO systems. The approximate saturation uptakes determined from these calculations are listed in Table 4 (while the saturation uptakes of AlPOs and SAPOs with the same topology are not identical, they are sufficiently similar to approximate them by the same value). Unsurprisingly, the four systems with relatively large accessible volumes of more than 0.37 cm³ g⁻¹ also exhibit similar saturation uptakes in the range of 360 g of water per kg of adsorbent. The saturation uptake of AlPO-GIS/SAPO-43 is only slightly lower, despite the fact that its accessible pore volume is considerably smaller (0.32 cm³ g⁻¹). This could point to a rather large difference between the accessible pore volume calculated by PoreBlazer using the kinetic diameter of nitrogen, and the pore volume that is actually accessible to the (smaller) water molecule.

Table 4 Approximate saturation uptakes N_{H2O,saturation} determined from preliminary GCMC calculations and number of H₂O molecules N_H2O per unit cell used in the DFT calculations for high water loadings (p.u.c. = unit cell in primitive setting used for AlPO-18 and AlPO-RHO)

	N H2O,saturation (GCMC)	N H2O (DFT)
AlPO-34/SAPO-34	∼45H2O per u.c. (∼370 g kg^−1)	∼40H2O per u.c.
AlPO-17/SAPO-17	∼35H2O per u.c. (∼290 g kg^−1)	∼30H2O per u.c.
AlPO-AFX/SAPO-56	∼58H2O per u.c. (∼360 g kg^−1)	∼50H2O per u.c.
AlPO-GIS/SAPO-43	∼37H2O per u.c. (∼340 g kg^−1)	∼32H2O per u.c.
AlPO-18/SAPO-18	∼29H2O per p.u.c. (∼360 g kg^−1)	∼25H2O per p.u.c.
AlPO-RHO/SAPO-RHO	∼30H2O per p.u.c. (∼370 g kg^−1)	∼25H2O per p.u.c.

---

While the present study does not aim at an accurate quantitative prediction of the saturation uptake, it is nevertheless insightful to compare the results to available experimental data: Jänchen at co-workers reported a water uptake of 283 g kg⁻¹ for AlPO-17 and 388 g kg⁻¹ for AlPO-18 at room temperature and a relative pressure p/p₀ of 0.3, in good agreement with the values predicted from the GCMC simulations.¹³ On the other hand, they obtained a lower uptake for SAPO-34 than the calculations (279 g kg⁻¹). At a higher relative pressure (p/p₀ = 0.7) and 40 °C, an uptake of ∼320 g kg⁻¹ was reported in a subsequent study of SAPO-34, approaching the value predicted in the present work.¹⁶ Altogether, the reasonable correspondence with experimentally determined uptakes gives confidence that the GCMC simulations provide a sufficiently reliable estimate of the saturation uptake.

3.3 Aluminophosphates: interaction with large amounts of water (near saturation)

Table 5 lists the average DFT-D interaction energies obtained for AlPOs at high water loadings, with the number of water molecules per unit cell being given in the last column of Table 4 for each system. Since the energies were obtained by averaging over five snapshots, the standard deviations are also given. It is quite apparent that the interaction energies are virtually identical for all six systems, falling between −64 and −66 kJ mol⁻¹ with standard deviations in the range of 1 kJ mol⁻¹. The small differences among the interaction energies obtained for different AlPO structures are hardly significant when the magnitude of the standard deviations is considered, therefore, the calculations deliver no indications for an influence of the pore size on the interaction strength. An assessment of the relative contributions of dispersion interactions shows that these are largest for the systems with the smallest pores, as it would be expected based on geometric considerations. In total, however, this contribution appears to be offset by a slightly stronger non-dispersive contribution in the systems with larger pores. It is worth noting that the experimentally determined heats of water adsorption for different aluminophosphates are also very similar, typically amounting to ∼55 kJ mol^−1 13,16 (as discussed above, the systematic difference between DFT results and experimental results can – at least to a large part – be explained with the neglect of vibrational contributions). With regard to the potential application of aluminophosphates in thermal energy storage, there appears to be no possibility to “tune” the interaction strength by judiciously choosing a system with a particular pore size or topology. This finding implies that the energy density will depend virtually exclusively on the amount of water that can be adsorbed in the system. Nevertheless, the pore size will play a crucial role in determining the pressure at which pore filling occurs at a given temperature (with smaller pores leading to filling at lower pressures), an aspect that is of considerable relevance to applications. While the present DFT-based approach is not suitable to study this relationship, it could be investigated with Monte Carlo simulations, with the choice of a sufficiently accurate force field being the main bottleneck.

Table 5 DFT-D results obtained for AlPOs and SAPOs with large amounts of adsorbed water, obtained from an average over five snapshots for each system: interaction energy E_int, relative contribution of dispersion interactions to total interaction E_disp/E_int, and relative volume change ΔV with respect to guest-free system. Standard deviations are also given for E_int and ΔV

	E int/kJ mol^−1	E disp/Eint	ΔV/%		E int/kJ mol^−1	E disp/Eint	ΔV/%
AlPO-34	−65.3 ± 0.5	0.38	−0.6 ± 0.1	SAPO-34_O1	−72.6 ± 0.8	0.34	−1.2 ± 0.4
AlPO-17	−64.0 ± 0.2	0.38	−1.1 ± 0.2	SAPO-17_Si1_O3	−69.7 ± 0.8	0.34	−0.8 ± 0.3
				SAPO-17_Si2_O5	−72.0 ± 1.2	0.33	−1.2 ± 0.1
AlPO-AFX	−66.0 ± 1.1	0.36	−1.1 ± 0.2	SAPO-56_Si1_O5	−69.9 ± 0.6	0.34	−1.2 ± 0.2
				SAPO-56_Si2_O4	−69.2 ± 0.7	0.35	−1.3 ± 0.2
AlPO-GIS	−65.2 ± 0.6	0.43	0.0 ± 0.4	SAPO-43_O12	−71.1 ± 1.6	0.39	−0.3 ± 0.7
AlPO-18	−66.0 ± 1.2	0.36	−1.0 ± 0.3	SAPO-18_Si1_O12	−73.0 ± 0.8	0.33	−1.5 ± 0.3
				SAPO-18_Si2_O11	−72.5 ± 2.0	0.33	−1.5 ± 0.4
				SAPO-18_Si3_O31	−73.3 ± 1.4	0.32	−1.1 ± 0.4
AlPO-RHO	−64.8 ± 1.3	0.34	−2.6 ± 0.7	SAPO-RHO_O11	−70.7 ± 1.1	0.31	−2.8 ± 0.4

---

An assessment of the changes in volume upon water adsorption (changes in individual lattice parameters are supplied in the ESI†), together with a closer inspection of the individual DFT-D optimised snapshots reveals a qualitatively different behaviour for all systems containing d6r units (AlPO-34, -17, -AFX, -18) on the one hand, and those systems that do not contain double six-rings (AlPO-GIS, -RHO) on the other hand. For the AlPOs with d6r units, a slight reduction in volume upon water adsorption is observed, which is typically in the range of −1%. In most cases, the changes in the lattice parameters differ considerably among different snapshots, meaning that no preferred directions of contraction/expansion can be identified. In AlPO-17, however, there is a relatively clear tendency to contract along the c-axis (average change −1.8%), which is partly compensated by an expansion along the a-axis (average change +0.4%). This deformation corresponds to a shortening of the long axis of the eri cage. In the four systems with d6r units, the direct coordination of water molecules to framework aluminium atoms, leading to five-coordinated Al (Al^V), is not observed very frequently (the number of Al^V atoms observed in each snapshot is supplied in the ESI†): while the individual number of Al^V atoms varies between 0 and 3 among different snapshots, there is on average less than one case of Al^V per unit cell. Similar observations were made in a previous study of AlPO-34 and SAPO-34, where models incorporating a somewhat smaller amount of water were studied (30 molecules per unit cell instead of 40).³⁵

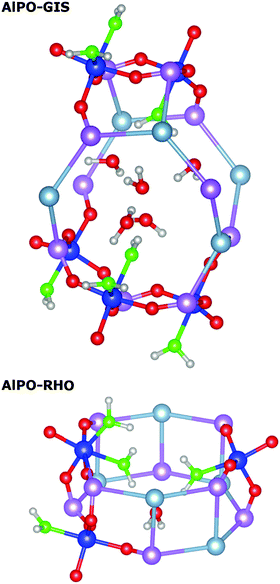
In AlPO-GIS, the volume remains practically constant. However, an evaluation of the changes in individual lattice parameters reveals a significant deformation of the unit cell, despite the negligible change in volume: an expansion by ∼1.8% along a and b is almost exactly compensated by a contraction of ∼−3.5% along the c-axis. As discussed above, the eight-ring windows in guest-free AlPO-GIS are elliptically distorted, with the elongated axis being approximately parallel to the c-axis. Upon water adsorption, this elliptical distortion is considerably reduced. The pronounced change in framework structure coincides with the frequent formation of five-coordinated Al atoms: between two and four of these atoms per unit cell are found in the different snapshots, and there is also one case of six-coordinated Al (Fig. 2).

Fig. 2 Visualisation of the formation of five-coordinated (and six-coordinated) framework aluminium atoms in AlPOs at high water loadings. Top: One gis cage of AlPO-GIS. Bottom: One d8r unit of AlPO-RHO. Only the environment of the five/six-coordinated aluminium atoms (highlighted in blue) is shown in a fully atomistic representation. The oxygen atoms of the coordinated water molecules are shown in light green. Hydrogen bonds are omitted for clarity. Note that the top and bottom of the gis cage are equivalent by translation.

For the case of AlPO-RHO, a pronounced volume reduction of ∼−2.6% is observed, with the volume changes of the snapshots varying between −1.9% and −3.6%. A closer inspection of the lattice parameters after transformation to the pseudo-cubic setting of the cell reveals that this contraction is not isotropic, but that the unit cell shrinks anisotropically along one or two directions (Table S13, ESI†). The contraction is associated with a distortion of the lta cages. Since a considerable degree of flexibility of the RHO structure has been observed and rationalised for the aluminosilicate form,^60,61 it is not surprising that rather large structural changes upon water adsorption are predicted for the AlPO system. As in AlPO-GIS, the formation of five-coordinated framework aluminium atoms is observed quite frequently in AlPO-RHO, with between one and three occurrences (per primitive cell) in the different snapshots, and one occurrence of six-coordinated Al. In the majority of cases, the water molecules which coordinate to the framework Al atoms are located inside the double eight-ring units, as shown exemplarily in Fig. 2.

In those cases where the formation of five-/six-coordinated Al is observed, the Al–O_water distances range from 1.9 to 2.1 Å. The formation of the additional bond(s) causes an elongation of the intra-framework bonds around the aluminium atom to values between 1.75 and 1.9 Å (compared to ∼1.7 to 1.75 Å in guest-free AlPOs).

3.4 Silicoaluminophosphates: interaction with small amounts of water (1H₂O per framework proton)

The results obtained for SAPO materials with one water molecule per framework proton are summarised in Table 6, which reports interaction energies as well as selected interatomic distances. The following discussion groups the systems according to the position of the framework proton at which the water molecule is adsorbed (eight-ring vs. six-ring protons, last column of Table 6).

Table 6 DFT-D results obtained for SAPO models with one adsorbed water molecule per framework proton. In addition to E_int and E_disp/E_int, relevant interatomic distances are also given: d(O–H) refers to the intra-framework O–H bond, d(H⋯O_H2O) represents the hydrogen bond between the framework proton and the water molecule, and d(H_H2O⋯O) corresponds to secondary contacts between H₂O hydrogen atoms and framework oxygen atoms

	E int/kJ mol^−1	E disp/Eint	d(O–H)free/Å	d(O–H)ads/Å	d(H⋯OH2O)/Å	d(HH2O⋯O)/Å	H2O location
SAPO-34_O1	−93.4	0.25	0.974	1.034	1.531	2.21/2.71	Inside 8-ring
SAPO-17_Si1_O3	−74.2	0.23	0.984	1.060	1.467	2.06/2.23	Above 6-ring
SAPO-17_Si2_O5	−78.1	0.30	0.975	1.065	1.446	1.87/1.91	Above 6-ring
SAPO-56_Si1_O5	−88.7	0.23	0.975	1.074	1.419	1.91/1.93	Above 6-ring
SAPO-56_Si2_O4	−97.1	0.24	0.974	1.041	1.503	2.21/2.40	Inside 8-ring
SAPO-43_O12	−101.5	0.24	0.974	1.060	1.450	1.88/2.23	Inside 8-ring
SAPO-18_Si1_O12	−97.5	0.22	0.974	1.045	1.492	1.99/3.01	Inside 8-ring
SAPO-18_Si2_O11	−98.5	0.23	0.974	1.043	1.499	2.11/2.76	Inside 8-ring
SAPO-18_Si3_O31	−89.2	0.20	0.975	1.077	1.415	1.85/1.98	Above 6-ring
SAPO-RHO_O11	−89.4	0.24	0.975	1.033	1.530	2.35/2.83	Above 8-ring

---

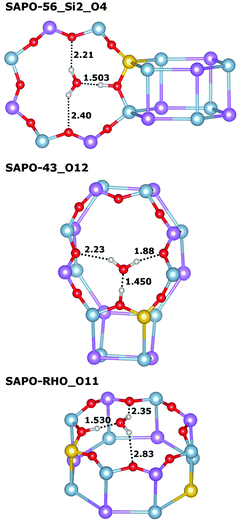
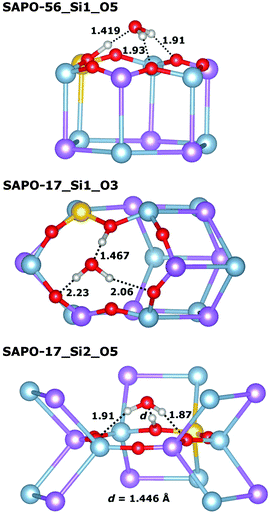
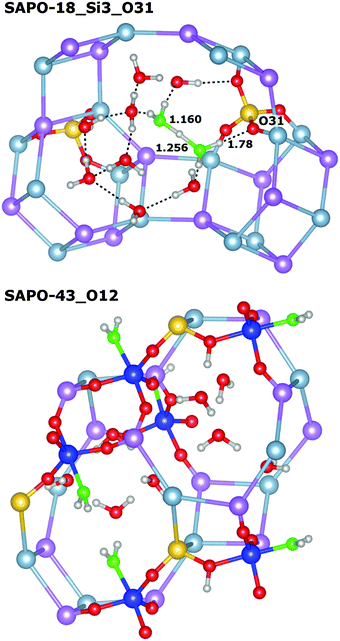
Very similar features are observed for all those systems where the framework proton is attached to an equatorial oxygen atom of a d6r unit, pointing into an eight-ring window (SAPO-34_O1, SAPO-56_Si2_O4, SAPO-18_Si1_O12, SAPO-18_Si2_O11): the interaction with the water molecule inside the eight-ring window is fairly strong, with E_int usually exceeding −95 kJ mol⁻¹ (SAPO-34 is the only exception), while the length of the hydrogen bond d(H⋯O_H2O) between the framework proton and the H₂O oxygen atom is quite long, in the range of 1.5 Å. There are additional (“secondary”) contacts of the H₂O hydrogen atoms to some oxygen atoms surrounding the eight-ring windows. Typically, one secondary contact is significantly shorter than the others (with d(H_H2O⋯O) in the range of ∼2.0 to 2.2 Å), i.e. the molecule assumes an off-centre position inside the window to maximise the interaction with the framework. A representative example (SAPO-56_Si2_O4) is shown in Fig. 3 (top). In SAPO-43_O12, the water molecule is also located inside an eight-ring window. Here, the interaction is even stronger (−101 kJ mol⁻¹) because the distortion of the eight-ring window permits two short secondary contacts (Fig. 3 middle). Of all systems where the water molecule is associated with an eight-ring window, the weakest interaction is observed in SAPO-RHO_O11 (−89 kJ mol⁻¹). The decomposition of the total interaction energy shows that this is primarily due to a reduced non-dispersive contribution. A closer inspection of the local environment reveals that the water molecule is not located inside the eight-ring window, but above it (Fig. 3 bottom). This leads to fairly long secondary contacts, and thus weaker electrostatic interactions between the guest molecule and the framework.

Fig. 3 Visualisation of representative equilibrium structures of water interacting with a proton associated with an eight-ring window in SAPOs. For clarity, the part of the SAPO structures shown is limited to the direct environment of the water molecule, and a fully atomistic representation is used only for the eight-ring window. For the case of SAPO-RHO_O11, a symmetry-equivalent H₂O molecule adsorbed at the bottom of the d8r unit is omitted. Selected interatomic distances are given in Å.

In those cases where the proton is located at the top of a d6r unit (SAPO-56_Si1_O5, SAPO-18_Si3_O31), the water molecule assumes a tripod-like configuration above the d6r unit, with three relatively short hydrogen–oxygen contacts (Fig. 4, top illustrates this for SAPO-56_Si1_O5). Despite these short contacts, the total interaction is comparatively weak, in the range of −89 kJ mol⁻¹, with both the non-dispersive term and the dispersion contribution being smaller than for systems where the water molecule is located inside an eight-ring window. In SAPO-17, the interaction with adsorbed water is weakest among all systems, with interaction energies in the range of −75 kJ mol⁻¹. In both SAPO-17_Si1_O3 and SAPO-17_Si2_O5, the protons point across six-ring windows, with relatively short contacts to the oxygen atoms at the opposite side of the ring. Upon water adsorption, the proton is displaced considerably from its previous equilibrium position in both cases, and the weak overall interaction can be explained with the energetic “penalty” associated with this displacement (Fig. 4 middle and bottom).

Fig. 4 Visualisation of representative equilibrium structures of water interacting with a proton associated with a six-ring window in SAPOs. For clarity, the part of the SAPO structures shown is limited to the direct environment of the water molecule, and a fully atomistic representation is used only for the six-ring window. Selected interatomic distances are given in Å.

In addition to the interatomic distances between the atoms of the water molecule and the closest framework atoms, the length of the intra-framework O–H bond d(O–H) before and after H₂O adsorption is also given in Table 6. In the guest-free structures, the bond lengths d(O–H)_free fall in a narrow range, the only exception being SAPO-17_Si1_O3, where the bond is somewhat elongated due to the interaction between the framework proton and the oxygen atom located at the opposite side of the distorted six-ring. Upon water adsorption, the O–H bonds are elongated to a different extent in different systems, and there is a dependence on the size of the ring with which the framework proton (and, correspondingly, the adsorbed molecule) is associated: in cases where water is adsorbed inside or above an eight-ring window, d(O–H)_ads ranges between 1.03 Å and 1.06 Å, whereas it is increased to 1.06 to 1.08 Å in systems where the water adsorption site is associated with a six-ring. While there is no overall correlation between d(O–H)_ads and the interaction energy, reasonable correlations are observed if systems where H₂O is located inside eight-rings or above six-rings are treated separately (ESI,† Fig. S7). Within each group, an increased elongation corresponds to a stronger interaction, however, the elongation corresponding to a certain interaction energy is much larger if the water molecule is adsorbed at a proton that is associated with a six-ring. These observations provide a possible means for the spectroscopic distinction of different framework protons, as the frequency shift upon water adsorption should be more pronounced in systems where the proton is associated with a six-ring.

For completeness, we also summarise the changes in the unit cell dimensions upon adsorption of small amounts of water in SAPOs: the overall changes in volume are very modest, ranging between virtually no change and a slight volume contraction of up to −0.8%. The typical changes in individual lattice parameters are even smaller (Table S14, ESI†). For the case of SAPO-34, this observation is in accordance with the findings of the previous computational (ab initio MD) study of Van Speybroeck and co-workers, who observed only minimal changes in the lattice dimensions upon addition of small amounts of water.³²

3.5 Silicoaluminophosphates: interaction with large amounts of water (near saturation). The DFT-D interaction energies obtained for SAPOs at high water loadings are included in Table 5. A direct comparison with the corresponding AlPOs shows that the interaction in the SAPO materials is 4 to 7 kJ mol⁻¹ stronger, in the range of −69.5 kJ mol⁻¹ (SAPO-56) to −73 kJ mol⁻¹ (SAPO-34, SAPO-18). For all structure types, the differences in interaction energy between AlPO and SAPO analogues are significantly larger than the calculated standard deviations, which do not exceed 2 kJ mol⁻¹. A closer inspection of the individual results shows that the difference is primarily due to an increased contribution of non-dispersive interactions in the SAPO materials (Tables S15 to S24 of ESI†). It is obvious that the electrostatic interaction of water with charged-framework SAPOs will be stronger than for neutral-framework AlPOs by virtue of the direct interaction of some water molecules with framework protons on the one hand, and due to the increased polarity of the pore wall on the other hand. Conversely, the contribution of dispersive interactions (in absolute terms) should be virtually identical for AlPOs and SAPOs with the same topology, and this is indeed observed. As for the AlPOs, there is no apparent correlation of the interaction energy with the pore size. However, while the differences among the interaction energies obtained for different SAPOs are only slightly larger than the typical standard deviation, a correlation of the interaction energy with the Si content (which is equal to the content of framework protons) can be inferred: the systems in which the interaction is strongest, SAPO-34 and SAPO-18, have the highest Si content x = N(Si)/N(T) of all models, with x = 0.083 (along with SAPO-RHO, where an intermediate interaction strength is found). Consequently, the interaction is weakest in SAPO-56, where x = 0.042. This is in line with the above explanation that an increase of the framework charge tends to enhance the affinity towards water.

For those systems where different Si distributions were considered, particularly SAPO-56 and SAPO-18, the variations among the interaction energies obtained for different models are minimal, so it can be concluded that, in contrast to the pronounced differences at low water loadings, the actual location of silicon atoms and framework protons hardly affects the interaction with water at near-saturation conditions. The same observation was made in our earlier study of SAPO-34, where the interaction energies obtained for a model with eight-ring protons (SAPO-34_O1) was practically the same as for a model with six-ring protons (SAPO-34_O3).³⁵ For this particular SAPO, the DFT-D interaction energy after applying an approximate correction for vibrational effects of +7 kJ mol⁻¹ compares very favourably with experimentally measured heats of adsorption at high water loadings, which are in the range of 65 kJ mol⁻¹.⁶

An analysis of the changes in volume (and in individual lattice parameters) upon water adsorption shows that the SAPOs behave very similarly to their AlPO counterparts, with the deformations being on average somewhat larger: SAPO-34, -56, and -18 exhibit a slight shrinkage upon water adsorption without preferential orientation, whereas a shortening of the longest axis of the eri cage is observed in SAPO-17. In SAPO-43, an expansion along a and b is offset by a contraction along c, and for the case of SAPO-RHO, a pronounced volume shrinkage in the range of ∼−3% is observed, which is often (though not always) fairly anisotropic.

An inspection of the individual snapshots of water-loaded SAPOs shows that the majority of the framework protons have left their initial position after the DFT-D optimisation, forming H₃O⁺ ions or, less frequently, H₃O⁺(H₂O) clusters (Fig. 5 top). The charged species in the final configurations are often, but not always, located in the vicinity of the original position of the framework proton. It has been established in previous computational work that framework deprotonation does not occur when only one or a few water molecules are adsorbed per proton, while it becomes energetically favourable when larger water clusters (e.g. tetramers) interact with one proton.^22–24 A recent ab initio MD study of water-loaded SAPO-34 emphasised the high mobility of the protons in this system at a temperature of 350 K.³² While the present work, which is based on static DFT optimisations, cannot quantify the effect of temperature on the mobility, the observation that framework deprotonation occurs in the large majority of cases is in accordance with these previous findings. The removal of framework protons from their initial positions is observed frequently in all SAPOs studied, regardless of the topology (or silicon content).

Fig. 5 Top: H₃O⁺(H₂O) cluster in SAPO-18_Si3_O31. The framework oxygen atom to which the proton was originally bonded (O31) is deprotonated, but interacts with the H₃O⁺(H₂O) cluster through a hydrogen bond. A portion of the network of hydrogen bonds is included for illustrative purposes. Only the relevant part of the SAPO structure is shown, and selected interatomic distances are given in Å. Bottom: Two adjacent gis cages in SAPO-43_O12, showing the formation of five-coordinated Al atoms in the vicinity of the silicon atoms. Five-coordinated Al atoms are highlighted in blue, and the oxygen atoms of the coordinated water molecules are shown in light green. Only the environment of the five/six-coordinated aluminium atoms is shown in a fully atomistic representation, and hydrogen bonds are omitted for clarity. Note that the top and bottom of the gis cages are equivalent by translation.

In the SAPOs, the formation of five-coordinated framework atoms occurs with a similar frequency as in their AlPO counterparts, with relatively few occurrences in SAPO-34, -17, -56, and -18, and a larger number of Al^V atoms in SAPO-43 and SAPO-RHO. There are two examples where no Al^V atoms are observed in any of the snapshots (SAPO-34_O1, SAPO-18_Si3_O31), however, this does not necessarily reflect a reduced tendency of these systems to form five-coordinated Al due to the limited number of configurations sampled (in this context, it is worth noting that Al^V atoms were found in several snapshots of water-loaded SAPO-34_O1 in our previous study).³⁵ As discussed previously, ab initio MD simulations would be very helpful to study the formation of five-coordinated Al in a more quantitative fashion, especially with regard to the influence of temperature. Another interesting observation from the present investigation is the preferential occurrence of five-coordinated aluminium in the direct vicinity of the silicon atoms, which is most pronounced in SAPO-43_O12 (Fig. 5 bottom).

4 Conclusions

The dispersion-corrected DFT calculations employed in this study have delivered detailed insights into the energetic and structural aspects of water adsorption in AlPOs and SAPOs with different topologies, which can be summarised as follows:

(1) Due to the absence of strongly preferred adsorption sites in AlPOs, the interaction with small amounts of water was investigated only for SAPOs. The interaction is markedly stronger when the framework proton points into an eight-ring than in situations where the proton is located above a six-ring. If it was possible to fully control the proton locations in a real material, the interaction energy could be “tuned” in a certain range, with eight-ring protons leading to higher energy densities, and six-ring protons allowing for lower desorption temperatures. However, since the different proton sites are often extremely close in energy (e.g. in SAPO-18), such a control is unlikely to be possible in real materials. Moreover, the considerable mobility of the protons would lead to a rearrangement during water adsorption/desorption cycles. Nevertheless, further insights could be expected from a comparative study of zeotypes that contain eight-rings, but no six-rings on the one hand (e.g. SAPO-43), and systems with six-rings and larger rings, but no eight-rings, on the other hand (e.g. SAPO-5 [AFI topology, twelve-rings + six-rings] or SAPO-11 [AEL topology, ten-rings + six-rings]).⁴⁰ It would be interesting to see whether the conclusions of the present study also hold for a wider range of structure types.

(2) At high water loadings, there is no evidence for a significant effect of the topology on the material's affinity towards water. When accounting for the contribution of thermal motion in an approximate fashion, heats of adsorption in the range of 55 to 60 kJ mol⁻¹ can be expected for AlPOs, whereas somewhat higher values between 60 and 65 kJ mol⁻¹ will be attained in SAPOs due to stronger electrostatic interactions. In SAPOs, the interaction with water can be enhanced by increasing the silicon content, which is directly correlated with the amount of framework protons as long as no silicon islands are formed. While no effect of the pore size on the interaction strength is observed, it has to be noted that a smaller pore diameter will lead to a pore filling at lower relative pressures. Therefore, the pore size may still determine the suitability of a certain adsorbent for given operating conditions.

(3) Unlike the adsorption energetics, the structural response of the adsorbents to water shows a considerable variation among the different topologies: while the systems that contain d6r units undergo only a moderate contraction, a much stronger deformation of the framework is observed in the zeotypes with GIS and RHO topologies (regardless of the composition). Moreover, the coordination of water molecules to framework aluminium atoms is observed more frequently in these materials. In this context, it is worth noting that a correlation between the strong binding of water to framework Al atoms and irreversible loss of crystallinity upon hydration of SAPOs has been found in a comparative MAS-NMR study of SAPO-34 (stable) and SAPO-37 (FAU topology, decomposes upon hydration at room temperature).⁶² Due to the severe structural changes observed for water-loaded GIS- and RHO-type AlPOs and SAPOs, it can be hypothesised that irreversible transformations might occur during water adsorption/desorption cycles. Such changes are likely to have a detrimental effect on the long-term performance of an adsorbent, rendering it unsuitable for heat transformation applications.

Altogether, the DFT-D computations permit us to conclude that the adsorption energetics in AlPOs and SAPOs are hardly influenced by the topology. There is thus little scope to “tune” the interaction strength – which is directly related to the amount of thermal energy that can be stored – by a judicious choice of a certain framework type. More promising strategies that can be envisaged are the variation of the silicon content in SAPOs and the incorporation of other elements in the framework (metal-containing aluminophosphates [MeAPOs]).⁴⁰ On the other hand, the topology determines the structural response of the material to water, which is why rather large variations in long-term stability have to be expected for AlPOs and SAPOs having different framework types. In this context, the present results, and possible future studies using ab initio MD simulations, may provide useful information that will facilitate the identification of suitably stable adsorbents.

Acknowledgements

I am grateful to Prof. Dr Andreas Lüttge and Dr Rolf Arvidson (Marum, Bremen) for generous access to the Asgard cluster, on which the DFT calculations were run. Funding was provided by the Central Research Development Fund (CRDF) of the University of Bremen (Funding line 04 – Independent Projects for Post-Docs).

References

1. A. Hauer, Adsorption, 2007, 13, 399–405.
2. Y. I. Aristov, Appl. Therm. Eng., 2013, 50, 1610–1618.
3. H. Demir, M. Mobedi and S. Ülkü, Renewable Sustainable Energy Rev., 2008, 12, 2381–2403.
4. S. Shimooka, K. Oshima, H. Hidaka, T. Takewaki, H. Kakiuchi, A. Kodama, M. Kubota and H. Matsuda, J. Chem. Eng. Jpn., 2007, 40, 1330–1334.
5. J. Bauer, R. Herrmann, W. Mittelbach and W. Schwieger, Int. J. Energy Res., 2009, 33, 1233–1249.
6. J. Jänchen and H. Stach, Sol. Energy, 2014, 104, 16–18.
7. S. Kulprathipanja, Zeolites in Industrial Separation and Catalysis, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2010.
8. Z. Han, A. L. Picone, A. M. Z. Slawin, V. R. Seymour, S. E. Ashbrook, W. Zhou, S. P. Thompson, J. E. Parker and P. A. Wright, Chem. Mater., 2010, 22, 338–346.
9. P. Tian, X. Su, Y. Wang, Q. Xia, Y. Zhang, D. Fan, S. Meng and Z. Liu, Chem. Mater., 2011, 23, 1406–1413.
10. R. Martínez-Franco, M. Moliner, Y. Yun, J. Sun, W. Wan, X. Zou and A. Corma, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3749–3754.
11. R. Vomscheid, M. Briend, M. J. Peltre, P. P. Man and D. Barthomeuf, J. Phys. Chem., 1994, 98, 9614–9618.
12. F. M. Bobonich, V. N. Solomakha and L. A. Chubirka, Theor. Exp. Chem., 2001, 37, 116–120.
13. J. Jänchen, D. Ackermann, E. Weiler, H. Stach and W. Brösicke, Thermochim. Acta, 2005, 434, 37–41.
14. S. K. Henninger, F. P. Schmidt and H.-M. Henning, Appl. Therm. Eng., 2010, 30, 1692–1702.
15. S. K. Henninger, F. P. Schmidt and H.-M. Henning, Adsorption, 2011, 17, 833–843.
16. A. Ristić, N. Zabukovec Logar, S. K. Henninger and V. Kaučič, Adv. Funct. Mater., 2012, 22, 1952–1957.
17. H. van Heyden, G. Munz, L. Schnabel, F. Schmidt, S. Mintova and T. Bein, Appl. Therm. Eng., 2009, 29, 1514–1522.
18. S. K. Henninger, G. Munz, K.-F. Ratzsch and P. Schossig, Renewable Energy, 2011, 36, 3043–3049.
19. L. Bonaccorsi, L. Calabrese, A. Freni and E. Proverbio, Microporous Mesoporous Mater., 2013, 167, 30–37.
20. A. Freni, L. Bonaccorsi, L. Calabrese, A. Caprì, A. Frazzica and A. Sapienza, Appl. Therm. Eng., 2015, 82, 1–7.
21. D. Bougeard and K. S. Smirnov, Phys. Chem. Chem. Phys., 2007, 9, 226–245.
22. V. Termath, F. Haase, J. Sauer, J. Hutter and M. Parrinello, J. Am. Chem. Soc., 1998, 120, 8512–8516.
23. Y. Jeanvoine, J. G. Ángyán, G. Kresse and J. Hafner, J. Phys. Chem. B, 1998, 102, 7307–7310.
24. M. V. Vener, X. Rozanska and J. Sauer, Phys. Chem. Chem. Phys., 2009, 11, 1702–1712.
25. E. Fois, A. Gamba and A. Tilocca, J. Phys. Chem. B, 2002, 106, 4806–4812.
26. G. Poulet, P. Sautet and A. Tuel, J. Phys. Chem. B, 2002, 106, 8599–8608.
27. G. Poulet, A. Tuel and P. Sautet, J. Phys. Chem. B, 2005, 109, 22939–22946.
28. R. S. Pillai and R. V Jasra, Langmuir, 2010, 26, 1755–1764.
29. T. Fjermestad, S. Svelle and O. Swang, J. Phys. Chem. C, 2013, 117, 13442–13451.
30. T. Fjermestad, S. Svelle and O. Swang, J. Phys. Chem. C, 2015, 119, 2073–2085.
31. T. Fjermestad, S. Svelle and O. Swang, J. Phys. Chem. C, 2015, 119, 2086–2095.
32. K. De Wispelaere, B. Ensing, A. Ghysels, E. J. Meijer and V. Van Speybroeck, Chem. – Eur. J., 2015, 21, 9385–9396.
33. K. De Wispelaere, C. S. Wondergem, B. Ensing, K. Hemelsoet, E. J. Meijer, B. M. Weckhuysen, V. Van Speybroeck and J. Ruiz-Martínez, ACS Catal., 2016, 6, 1991–2002.
34. D. S. Wragg, R. E. Johnsen, P. Norby and H. Fjellvåg, Microporous Mesoporous Mater., 2010, 134, 210–215.
35. M. Fischer, Phys. Chem. Chem. Phys., 2015, 17, 25260–25271.
36. M. M. Harding and B. M. Kariuki, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1994, 50, 852–854.
37. B. M. Lok, C. A. Messina, R. L. Patton, R. T. Gajek, T. R. Cannan and E. M. Flanigen, J. Am. Chem. Soc., 1984, 106, 6092–6093.
38. S. T. Wilson, B. M. Lok, C. A. Messina, T. R. Cannan and E. M. Flanigen, J. Am. Chem. Soc., 1982, 104, 1146–1147.
39. J. J. Pluth, J. V Smith and J. M. Bennett, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 283–286.
40. E. M. Flanigen, B. M. Lok, R. L. Patton and S. T. Wilson, Pure Appl. Chem., 1986, 58, 1351–1358.
41. A. Simmen, L. B. McCusker, C. Baerlocher and W. M. Meier, Zeolites, 1991, 11, 654–661.
42. J. Chen, J. Thomas, P. Wright and R. Townsend, Catal. Lett., 1994, 28, 241–248.
43. J.-L. Paillaud, B. Marler and H. Kessler, Chem. Commun., 1996, 1293–1294.
44. M. Helliwell, V. Kaučič, G. M. T. Cheetham, M. M. Harding, B. M. Kariuki and P. J. Rizkallah, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 413–420.
45. S. T. Wilson, R. W. Broach, C. S. Blackwell, C. A. Bateman, N. K. McGuire and R. M. Kirchner, Microporous Mesoporous Mater., 1999, 28, 125–137.
46. X. Su, P. Tian, J. Li, Y. Zhang, S. Meng, Y. He, D. Fan and Z. Liu, Microporous Mesoporous Mater., 2011, 144, 113–119.
47. X. Su, P. Tian, D. Fan, Q. Xia, Y. Yang, S. Xu, L. Zhang, Y. Zhang, D. Wang and Z. Liu, ChemSusChem, 2013, 6, 911–918.
48. W. H. Baur, W. Joswig, D. Kassner, J. Kornatowski and G. Finger, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 290–294.
49. G. Sastre, D. W. Lewis and C. R. A. Catlow, J. Phys. Chem. B, 1997, 101, 5249–5262.
50. J.-R. Hill, A. R. Minihan, E. Wimmer and C. J. Adams, Phys. Chem. Chem. Phys., 2000, 2, 4255–4264.
51. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
52. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
53. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
54. D. Tunega, T. Bučko and A. Zaoui, J. Chem. Phys., 2012, 137, 114105.
55. T. Bučko, S. Lebègue, J. Hafner and J. G. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 064110.
56. M. Fischer, Z. Kristallogr. – Cryst. Mater., 2015, 230, 325–336.
57. M. Amri and R. I. Walton, Chem. Mater., 2009, 21, 3380–3390.
58. M. P. Attfield and A. W. Sleight, Chem. Mater., 1998, 10, 2013–2019.
59. L. Sarkisov and A. Harrison, Mol. Simul., 2011, 37, 1248–1257.
60. J. B. Parise, T. E. Gier, D. R. Corbin and D. E. Cox, J. Phys. Chem., 1984, 88, 1635–1640.
61. S. R. G. Balestra, J. J. Gutiérrez-Sevillano, P. J. Merkling, D. Dubbeldam and S. Calero, J. Phys. Chem. C, 2013, 117, 11592–11599.
62. A. Buchholz, W. Wang, A. Arnold, M. Xu and M. Hunger, Microporous Mesoporous Mater., 2003, 57, 157–168.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02289h

---