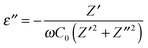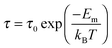Dielectric characteristics of fast Li ion conducting garnet-type Li5+2xLa3Nb2−xYxO12 (x = 0.25, 0.5 and 0.75)
Received
6th April 2016
, Accepted 9th May 2016
First published on 24th May 2016
Abstract
Here, we report the dielectric characteristics of Li-stuffed garnet-type Li5+2xLa3Nb2−xYxO12 (x = 0.25, 0.5 and 0.75) in the temperature range about −53 to 50 °C using AC impedance spectroscopy. All the investigated Li-stuffed garnet compounds were prepared, under the same condition, using conventional solid-state reaction at elevated temperature in air. The Nyquist plots show mainly bulk contribution to the total Li+ ion conductivity for Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb) and Li6La3Nb1.5Y0.5O12 (Li6–Nb), while both bulk and grain-boundary effects are visible in the case of Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) phase at ∼−22 °C. Non-Debye relaxation process was observed in the modulus AC impedance plots. The dielectric loss tangent of Li5+2xLa3Nb2−xYxO12 are compared with that of the corresponding Ta analogue, Li5+2xLa3Ta2−xYxO12 and showed a decrease in peak intensity for the Nb-based garnet samples which may be attributed to a slight increase in their Li+ ion conductivity. The relative dielectric constant values were also found to be higher for the Ta member (>60 for Li5+2xLa3Ta2−xYxO12) than that of the corresponding Nb analogue (∼50 for Li5+2xLa3Nb2−xYxO12) at below room temperature. A long-range order Li+ ion migration pathway with relaxation time (τ0) 10−18–10−15 s and an activation energy of 0.59–0.40 eV was observed for the investigated Li5+2xLa3Nb2−xYxO12 garnets and is comparable to that of the corresponding Ta-based Li5+2xLa3Ta2−xYxO12 garnets.
Introduction
Currently, lithium ion batteries (LIBs) attain much attention because of their high volumetric and gravimetric energy densities, which make them suitable for possible applications from portable devices to electric vehicles and grid scale to support the peak power demand. However, there is a long-term remaining safety concern related to the presently used organic polymer-based Li+ ion electrolytes in LIBs and they must be replaced with thermally stable fast Li+ ion conductors. To this end, several families of inorganic metal oxides and non-oxides have been investigated, of which recently discovered, Li-stuffed garnet-type metal oxides are a potential class of solid-state Li+ ion conductors for all-solid-state LIBs due to their excellent physical and chemical properties.1–7 Briefly, the garnet structure is known to accommodate Li content ranging from 24 to 56 ions per unit cell. Increasing the Li content in Li-stuffed garnets decreases the occupation of tetrahedral Li+ ions and increases the population of octahedral coordinated Li+ ions in the cubic garnet-type structure.8 Except Li3-phase, Li3Ln3Te2O12 (Ln = Y, Pr, Nd, Sm–Lu), the Li+ ions in tetrahedral and octahedral sites are partially filled in all other known Li-stuffed garnets, which make unique structural disorders for fast ion conduction.9 Doping Ba2+ for La3+ and Zr4+ for Nb5+/Ta5+ showed an increase in the conductivity of the parent Li5La3M2O12 (M = Nb, Ta).10,11 To date, the garnet with the nominal chemical formula Li6.4La3Zr1.4Ta0.6O12, exhibits the highest bulk Li+ ion conductivity of 10−3 S cm−1 at room temperature with an activation energy 0.35 eV (25–157 °C).12 Zr and Ta-based garnets were found to be chemically stable towards reaction with Li anodes and showed an electrochemical stability window up to 6 V per Li.13,14 The highly dense crystal structure makes it harder to understand the role of chemical doping at Li, La and M or M′ sites in Li-stuffed Li5La3M2O12, Li6La2AM2O12 (M = Ta, Nb; A = Ca, Sr, Ba), and Li7La3M′2O12 (M′ = Zr, Sn) garnets on Li+ ion transport properties.15,16 Creating oxide ion vacancies by aliovalent doping at Nb-sites in Li5La3Nb2O12 decreased the bulk Li+ ion conductivity.17
It is important to understand the Li+ ion conduction mechanism in garnets to further improve Li+ ion conduction for advanced all-solid-state Li ion battery. It was predicted that the Li+ ions at octahedral sites in the garnet structure mainly attribute to the fast ionic conduction, and tetrahedral site Li+ ions seem to be responsible for maintaining the stability of the garnet framework structure.8 Solid-state 7Li magic angle spinning nuclear magnetic resonance (MAS NMR) and density functional theory (DFT) studies further support the above proposed Li+ ion conduction mechanism in the garnet structure.18,19 Furthermore, several studies have been carried out to understand the chemical composition and Li+ ion dynamics relationship in these Li-stuffed garnets using neutron diffraction, NMR, electrochemical AC impedance spectroscopy and DFT calculations.8,10,19–31 The present study is focused on analyzing the dielectric properties of Li5+2xLa3Nb2−xYxO12 (x = 0.25, 0.5 and 0.75) using electrochemical AC impedance spectroscopy to better understand the Li+ ion conduction mechanism in the Li-stuffed garnets.
Experimental
Single phase cubic structured garnet-type Li5+2xLa3Nb2−xYxO12 (x = 0.25, 0.5 and 0.75 which are represented as Li5.5–Nb, Li6–Nb and Li6.5–Nb, respectively) were prepared by solid-state reaction at elevated temperature.32 The stoichiometric amount of the precursors of high purity LiNO3 (99%, Alfa Aesar), La2O3 (99.99%, Alfa Aesar, preheated at 900 °C for 24 h), Nb2O5 (99.5%, Alfa Aesar), and Y(NO3)3 (99.9%, Alfa Aesar) were ball milled to ensure homogeneity. 10 wt% excess LiNO3 was added to compensate the loss of lithium oxide while sintering. Heating at different stages were carried out at 700 °C/6 h, 900 °C/24 h and 1100 °C/6 h. The dielectric analyses were carried out using the AC impedance spectroscopy employing a Solartron 1260 impedance/gain-phase analyzer (0.01 Hz to 1 MHz) in the temperature range of −53 to 50 °C in air. The temperature was controlled below room temperature using dry ice.33 The pellet garnet samples for AC impedance measurements were painted with Au paste on both sides and were cured for 1 h at 600 °C.
Results and discussion
AC impedance spectroscopy
Typical AC impedance spectra of cubic structured garnet-type Li5+2xLa3Nb2−xYxO1232 (x = 0.25, 0.5 and 0.75 which are represented as Li5.5–Nb, Li6–Nb and Li6.5–Nb, respectively) at −22 °C are shown in Fig. 1. The Li5.5–Nb and Li6–Nb phases of Li5+2xLa3Nb2−xYxO12 show a single semicircle, which corresponds to bulk (b) contribution at higher frequency range and a spike at the low-frequency range due to polarization resistance. The line spacing through the data points is fitted using an equivalent circuit consisting of (RbCPEb)(CPEe) for Li5.5–Nb and Li6–Nb (where Rb is the bulk resistance, CPEb is the constant phase element due to bulk and CPEe is the constant phase element due to electrode). The Rb is the low-frequency intercept to real axis and the bulk capacitance was found to be in the order of ∼10−11 F. The Li6.5–Nb phase shows an additional distorted semi-circle corresponding to grain-boundary (gb) contribution (capacitance ∼ 10−8 F) at low-frequency and it can be described using an equivalent circuit (RbCPEb)(RgbCPEgb)(CPEe) (where Rgb is the grain-boundary resistance, CPEgb is the constant phase element due to gb). The electrode capacitance was found to be in the order of 10−7 F. As reported earlier,32 the density of Li5+2xLa3Nb2−xYxO12 garnet was found to be increasing with increase in Y and Li content. Also, there are some impurity peaks observed in the PXRD spectra of highly doped Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) phase. These factors might be contributing to the presence of grain-boundary impedance in Li6.5–Nb compared to Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb) and Li6La3Nb1.5Y0.5O12 (Li6–Nb). The total resistance (R) (bulk + grain-boundary) was used to estimate the total Li+ ion conductivity (σ) from the low-frequency intercept point of Z′′ (imaginary part of impedance) to the X-axis (Z′, real part of the impedance) (Fig. 1). The Li+ ion conductivity was calculated using the eqn (1):| |  | (1) |
where l is the sample thickness and a is the area of current collector. The Li+ ion conductivity dependence on temperature was represented as the Arrhenius plots (Fig. 2) and they can be described using the eqn (2):| |  | (2) |
where T is the temperature, A is the pre-exponential factor, Ea is the activation energy, and k is the Boltzmann's constant (1.38 × 10−23 J K−1). The Li+ ion conductivity of samples increases from Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb) to Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb), which is consistent with the increase in cell parameter (a) calculated from powder X-ray diffraction (PXRD). The cell constant was found to be 12.8582(5) Å, 12.9136(4) Å and 12.9488(11) Å for Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb), Li6La3Nb1.5Y0.5O12 (Li6–Nb), and Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb), respectively.32 The activation energy calculated for Li5.5–Nb, Li6–Nb and Li6.5–Nb phases are 0.59, 0.58 and 0.42 eV, respectively, in the temperature range of −53 to 50 °C (Table 1) which is in agreement with the Li+ ion conductivity trend.
 |
| | Fig. 1 Typical complex impedance spectra obtained using Li+ ion blocking Au electrodes for Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb), Li6La3Nb1.5Y0.5O12 (Li6–Nb) and Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) at about −22 °C. The line spacing through the data points is fitted using an equivalent circuit consisting of (RbCPEb)(CPEe) for Li5.5–Nb and Li6–Nb and (RbCPEb)(RgbCPEgb)(CPEe) for Li6.5–Nb. | |
 |
| | Fig. 2 Arrhenius plots of bulk Li ion conductivity of Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb), Li6La3Nb1.5Y0.5O12 (Li6–Nb), and total (bulk + grain-boundary) Li+ ion conductivity of Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb). The line passing through the data points is the fitted line using eqn (2). | |
Table 1 The bulk (except bulk + grain-boundary for Li6.5–Nb) conductivity of Li5+2xLa3Nb2−xYxO12 at −22 and 25 °C and the activation energy calculated from the Arrhenius plot (Fig. 2) at temperature range −53 to 50 °C
| Sample |
σ
−22°C (S cm−1) |
σ
25°C (S cm−1) |
E
a (eV) |
| Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb) |
1.50 × 10−6 |
7.18 × 10−5 |
0.59 |
| Li6La3Nb1.5Y0.5O12 (Li6–Nb) |
4.20 × 10−6 |
1.87 × 10−4 |
0.58 |
| Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) |
1.27 × 10−5 |
2.99 × 10−4 |
0.42 |
The relationship of conductivity (σ) and frequency is expressed by the Jonscher universal power law34i.e.,:
where
ω is the angular frequency,
σdc is the dc conductivity,
A is the proportionality constant, and
n is the power factor which varies from 0 to 1. Shown in
Fig. 3 is the Li
+ ion conductivity as a function of frequency for Li
5+2xLa
3Nb
2−xY
xO
12 in the temperature range from −53 to 50 °C. The dispersion region seen at lower frequency range is due to the polarization due to Li
+ ion-blocking electrode. The frequency independent dc plateau region is seen at intermediate frequency range followed by a dispersion region. This could be explained by jump relaxation model which indicates that at intermediate frequencies, the ions hop from one site to the neighboring vacancy site contributing to the dc conductivity, and at higher frequencies the correlated alternative hopping along with the relaxation of ions contribute to the conductivity relaxation at the dispersion region.
35,36 For garnet-type oxide, the jumping of Li
+ ions from one octahedral site to another octahedral-site (for
e.g., 48g-site to the 96h-site) followed by the readjustment of surrounding ions causes the conductivity relaxation.
25
 |
| | Fig. 3 The electrical conductivity of (a) Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb), (b) Li6La3Nb1.5Y0.5O12 (Li6–Nb) and (c) Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) as a function of frequency at different temperatures obtained using AC impedance spectroscopy with Li+ ion blocking Au electrodes. | |
The real (ε′) and imaginary (ε′′) part of permittivity (ε) was computed using the eqn (4) and (5) as shown below:37
| |  | (4) |
| | 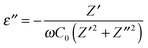 | (5) |
where
C0 is the vacuum capacitance of the cell which is represented as
C0 =
ε0(
a/
l) (where
ε0 is the permittivity of free space = 8.854 × 10
−14 F cm
−1).
Fig. 4 shows the relation between the real part of permittivity (
ε′) and frequency at different temperatures. It is noticeable that the dielectric constant decreases with frequency showing a constant minimum value. The upturn at the lower frequency region may be due to the blocking electrode–electrolyte polarization at the interface. When the frequency is increased, the periodical reversal of the field is increased and as a result the oscillating charges do not contribute to the dielectric constant. This causes a decrease in dielectric constant with increase in frequency. Dipolar polarization leads to formation of a plateau at the low-frequency region at higher temperature, which is clearly visible in the case of Li
6.5–Nb phase and also in the Ta series, Li
5+2xLa
3Ta
2−xY
xO
12 (
x = 0.25, 0.5 and 0.75).
25 Shifting of the plateau towards high frequencies with increasing temperature indicates the increase in frequency of dipolar rotations, as Li
+ ion mobility is enhanced due to the thermal activation.
38
 |
| | Fig. 4 Estimated real part of permittivity (ε′) as a function of frequency of (a) Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb), (b) Li6La3Nb1.5Y0.5O12 (Li6–Nb) and (c) Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) at different temperatures from AC impedance spectroscopy data collected using Li+ ion blocking Au electrodes. | |
The plot of imaginary part of the dielectric permittivity (ε′′) against frequency is illustrated in Fig. 5a–c. ε′′ is the dielectric loss factor which could be the combination of dipolar loss and conduction loss. The conduction loss is predominant at lower temperatures and appears as a straight line and shows inverse relationship to the angular frequency (ω) especially for Li5.5–Nb and Li6–Nb phases (Fig. 5a and b). In all the cases, the peak/plateau at lower frequencies due to dipolar polarization was observed (Fig. 4).
 |
| | Fig. 5 Imaginary part of permittivity (ε′′) as a function of frequency of (a) Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb), (b) Li6La3Nb1.5Y0.5O12 (Li6–Nb) and (c) Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) at different temperatures. | |
The dielectric loss tangent as a function of frequency of Li5+2xLa3Nb2−xYxO12 is shown in Fig. 6. The peak observed in Li5.5–Nb and Li6–Nb phases can be attributed to the dielectric loss due to Li–Li dipolar rotations under the applied electrical field.25 There seem to be two relaxation peaks for Li6.5–Nb phases at intermediate frequencies, suggesting that an additional polarization loss occurs when compared to the Li5.5–Nb and Li6–Nb phases. The higher frequency peak may be attributed to the dielectric loss due to Li–Li dipolar rotation in the bulk.39 The lower frequency peak in Fig. 6c seems to be due to the dielectric loss, as a result of grain-boundary polarization. This is consistent with the appearance of a grain-boundary arc in the AC impedance spectrum of Li6.5–Nb phase (Fig. 1). The shift in loss tangent peaks towards higher frequencies with increase in temperature, similar to the real part of permittivity (ε′) as a function of temperature, indicates that both grain-boundary space charge polarization and Li–Li dipolar interaction in bulk are thermally activated processes.
 |
| | Fig. 6 Dielectric loss tangent (δ) as a function of frequency of (a) Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb), (b) Li6La3Nb1.5Y0.5O12 (Li6–Nb) and (c) Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) at different temperatures. | |
In Fig. 7, the loss tangent of both Nb with Ta members of Li5+2xLa3M2−xYxO12 (M = Nb, Ta) at different temperatures is compared. A similar plot is observed, except for Li6.5–Nb phase of Nb series Li5+2xLa3Nb2−xYxO12, corresponding to bulk and grain-boundary contribution.32 However, very small values of peak intensity of Li5+2xLa3Nb2−xYxO12 (Fig. 7b and c) compared to that of the Ta series Li5+2xLa3Ta2−xYxO12 indicated that either there are fewer dipoles in the Nb garnets than in the Ta garnets or the mobility of the ions is higher in the presently investigated Nb garnets leading to a quick response of Li–Li dipoles to external electric field and resulting in less dielectric loss. Overall, the dielectric relaxation can be considered due to the main-body interactions as is common for the ionic conductor.34 The relative permittivity/dielectric constant (εr) of Li5+2xLa3M2−xYxO12 (M = Nb, Ta32) were calculated using the capacitance (C), as given in eqn (6) and the results are summarized in Fig. 8.
| |  | (6) |
 |
| | Fig. 7 Comparison of dielectric loss tangent (δ) as a function of frequency of (a) Li5.5-, (b) Li6-, and (c) Li6.5-phases of both Ta and Nb members of Li5+2xLa3M2−xYxO12 (M = Nb and Ta25) at different temperatures. | |
 |
| | Fig. 8 The relative permittivity of Li5.5-, Li6-, and Li6.5-phases Li5+2xLa3M2−xYxO12 (M = Nb and Ta) at different temperatures. | |
The dielectric constant slightly increases with an increase in the Li content in the Ta series materials, although there is no trend in variation of εr with the Li content in the Nb series. With the increase in temperature, the value of the dielectric constant is increased in both Nb and Ta based garnets. The dielectric constant of the Nb garnets is found to be relatively higher than that of the Ta garnets. Generally, the higher the dielectric constant, the greater is the polarizability of the medium. Thus, the higher dielectric constant (Fig. 8) and lower dielectric loss (Fig. 7) in the Nb series materials seems to indicate that their Li+ ion mobility is higher compared to that of the Ta garnets since both Nb and Ta oxides exhibit similar ionic radius and electronic structure. A comparison of Li+ ionic conductivity of both Nb and Ta phases of Li5+2xLa3M2−xYxO12 at specific temperatures is shown in Table 2.7,25,32
Table 2 Comparison of ionic conductivity of both Nb and Ta phases of Li5+2xLa3M2−xYxO12 at specific temperatures7,25,32
| |
Li5+2xLa3Nb2−xYxO12 |
Li5+2xLa3Ta2−xYxO12 |
|
T (°C) |
σ (S cm−1) |
T (°C) |
σ (S cm−1) |
| Li5.5-phase |
−33 |
4.52 × 10−7 |
−35 |
5.94 × 10−8 |
| −40 |
2.10 × 10−7 |
−40 |
3.32 × 10−8 |
| |
| Li6-phase |
−33 |
1.21 × 10−6 |
−35 |
5.84 × 10−8 |
| −40 |
5.48 × 10−7 |
−40 |
3.34 × 10−8 |
| |
| Li6.5-phase |
−21 |
1.60 × 10−5 |
−20 |
9.85 × 10−6 |
| −25 |
1.18 × 10−5 |
−25 |
7.29 × 10−6 |
Using modulus analysis, it is possible to understand the bulk relaxation properties in detail by suppressing the lower frequency phenomena, especially the electrode effect.30 The complex dielectric modulus is expressed as eqn (7):
where the real and imaginary parts can be separated as
M′ =
ωC0Z′ and
M′′ = −
ωC0Z′′. The electric modulus accounts for the electric field relaxation in the material at a constant electric displacement.
40 The modulus spectra of Li
5.5–Nb, Li
6–Nb and Li
6.5–Nb phases of Li
5+2xLa
3Nb
2−xY
xO
12 samples, measured at a temperature range of −53 to −21 °C as a function of frequency is shown in
Fig. 9. The electric modulus (
M′′) shows a frequency independent behavior at the lower frequency region for all the samples. This indicates that the electrode polarization does not contribute to the electric modulus and the long-range migration of Li
+ ion by hopping from one site to the neighboring site.
30 The presence of a peak in the modulus spectra has been ascribed to the relaxation associated with Li
+ ion mobility.
25,30 The appearance of a high frequency side peak at lower temperatures could be due to the Li
+ ion re-orientation relaxation as Li
+ ion moves from one octahedron to another octahedron around the immobile tetrahedral site.
25 The shift in peak position towards higher frequencies with increase in temperature indicates that Li
+ ion relaxation re-orientation is a thermally activated phenomenon. Also, it is noticeable that the peak tend to disappear in the Li
6.5–Nb phase which can be explained in terms of long-range order migration of the Li
+ ion instead of local migration as seen in other members.
25
 |
| | Fig. 9 Electric modulus M′′ as a function of frequency of (a) Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb), (b) Li6La3Nb1.5Y0.5O12 (Li6–Nb) and (c) Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) at different temperatures. | |
The relaxation time, τ is related to the frequency maximum in the modulus plots, fM′′ as shown in eqn (8):
| |  | (8) |
which can actually reveal the short range and/or the long range migration of Li
+ in the crystal structure.
Fig. 10 shows the Arrhenius behavior of the relaxation time,
τ for the local motion of Li
+ according to the
eqn (9):
| | 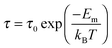 | (9) |
where
τ0 is the relaxation time at infinite temperature and
Em is the migration energy. The migration energy calculated for Li
5.5–Nb, and Li
6–Nb and Li
6.5–Nb phases are 0.59, and 0.52, and 0.40 eV, respectively which is close to the theoretically calculated activation energy. The calculated relaxation time,
τ was in the range of 10
−15–10
−18 s which decreases with Li content and is comparable with that of Ta family, Li
5+2xLa
3Ta
2−xY
xO
12.
25 The AC impedance or NMR analysis of some of the ionic conductors is mentioned here to get an idea of how the relaxation time varies in different electrolytes. In the polymer nano-composites of polyethylene oxide and lithium perchlorate, Li
+ ions show relaxation times of micro seconds (10
−6 s).
41 The fastest Na ion conducting, Na β-alumina, has exhibited a relaxation time
τ0 of 10
−12 s.
42 Solid-state
7Li NMR analysis of Li
1.3Al
0.15Y
0.15Ti
1.7(PO
4)
3 showed a relaxation time in the order of 10
−12 s.
43 For (BiI
3)
0.4–(Ag
3PO
4)
0.6 electrolyte, the mobile Ag
+ ions showed a relaxation time of 10
−7–10
−11 s.
44
 |
| | Fig. 10 Arrhenius plots of relaxation time of (a) Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb), (b) Li6La3Nb1.5Y0.5O12 (Li6–Nb) and (c) Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb). | |
Conclusions
The transport mechanism of Li5+2xLa3Nb2−xYxO12 (x = 0.25, 0.5 and 0.75) was studied in terms of their dielectric behavior at below room temperature. The bulk Li+ ion conductivity of the samples increases with an increase in the Li content and follows the trend, Li5.5La3Nb1.75Y0.25O12 (Li5.5–Nb) < Li6La3Nb1.5Y0.5O12 (Li6–Nb) < Li6.5La3Nb1.25Y0.75O12 (Li6.5–Nb) and also follows the cell constant trend. The Li+ ion conductivity as a function of frequency was found to follow the Jonscher universal power law. The modulus plots indicate a non-Debye behavior for Li+ ion relaxation. Relatively higher dielectric constants for the Nb members compared to that of the Ta members of Li5+2xLa3Nb2−xYxO12 (M = Nb, Ta) could be explained in terms of the higher dipole moments and greater Li+ ion mobility. The calculated relaxation time, τ was 10−18, 10−17 and 10−15 s and the activation energy observed was 0.59, 0.52 and 0.40 eV for Li5.5–Nb, Li6–Nb and Li6.5–Nb, respectively, of Li5+2xLa3Nb2−xYxO12 from the relaxation profile.
Acknowledgements
The funding support from the Natural Sciences and Engineering Research Council of Canada (NSERC) through Discovery Grants (DG) program is acknowledged for this work.
References
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC.
- V. Thangadurai, D. Pinzaru, S. Narayanan and A. K. Baral, J. Phys. Chem. Lett., 2015, 6, 292–299 CrossRef CAS PubMed.
- L. Cheng, W. Chen, M. Kunz, K. Persson, N. Tamura, G. Chen and M. Doeff, ACS Appl. Mater. Interfaces, 2015, 7, 2073–2081 CAS.
- A. Gupta, R. Murugan, M. P. Paranthaman, Z. Bi, C. A. Bridges, M. Nakanishi, A. P. Sokolov, K. S. Han, E. W. Hagaman, H. Xie, C. B. Mullins and J. B. Goodenough, J. Power Sources, 2012, 209, 184–188 CrossRef CAS.
- Y. Li, C.-A. Wang, H. Xie, J. Cheng and J. B. Goodenough, Electrochem. Commun., 2011, 13, 1289–1292 CrossRef CAS.
- S. Narayanan, G. T. Hitz, E. D. Wachsman and V. Thangadurai, J. Electrochem. Soc., 2015, 162, A1772–A1777 CrossRef CAS.
- S. Narayanan, F. Ramezanipour and V. Thangadurai, Inorg. Chem., 2015, 54, 6968–6977 CrossRef CAS PubMed.
- E. J. Cussen, J. Mater. Chem., 2010, 20, 5167 RSC.
- E. J. Cussen, Chem. Commun., 2006, 412–413 RSC.
- S. Narayanan, V. Epp, M. Wilkening and V. Thangadurai, RSC Adv., 2012, 2, 2553 RSC.
- A. Ramzy and V. Thangadurai, ACS Appl. Mater. Interfaces, 2010, 2, 385–390 CAS.
- Y. Li, J.-T. Han, C.-A. Wang, H. Xie and J. B. Goodenough, J. Mater. Chem., 2012, 22, 15357 RSC.
- V. Thangadurai and W. Weppner, Adv. Funct. Mater., 2005, 15, 107–112 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef CAS PubMed.
- V. Thangadurai, H. Kaack and W. J. F. Weppner, J. Am. Ceram. Soc., 2003, 86, 437–440 CrossRef CAS.
- J. Percival, E. Kendrick, R. I. Smith and P. R. Slater, Dalton Trans., 2009, 5177–5181 RSC.
- S. Narayanan and V. Thangadurai, J. Power Sources, 2011, 196, 8085–8090 CrossRef CAS.
- L. van Wullen, T. Echelmeyer, H. W. Meyer and D. Wilmer, Phys. Chem. Chem. Phys., 2007, 9, 3298–3303 RSC.
- M. Xu, M. S. Park, J. M. Lee, T. Y. Kim, Y. S. Park and E. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 052301 CrossRef.
- E. J. Cussen and T. W. S. Yip, J. Solid State Chem., 2007, 180, 1832–1839 CrossRef CAS.
- M. P. O’Callaghan and E. J. Cussen, Chem. Commun., 2007, 2048–2050 RSC.
- M. P. O’Callaghan, D. R. Lynham, E. J. Cussen and G. Z. Chen, Chem. Mater., 2006, 18, 4681–4689 CrossRef.
- A. Kuhn, V. Epp, G. Schmidt, S. Narayanan, V. Thangadurai and M. Wilkening, J. Phys.: Condens. Matter, 2012, 24, 035901 CrossRef CAS PubMed.
- A. Kuhn, S. Narayanan, L. Spencer, G. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094302 CrossRef.
- A. K. Baral, S. Narayanan, F. Ramezanipour and V. Thangadurai, Phys. Chem. Chem. Phys., 2014, 16, 11356–11365 RSC.
- M. M. Ahmad, Nanoscale Res. Lett., 2015, 10, 58 CrossRef PubMed.
- M. M. Ahmad, Ceram. Int., 2015, 41, 6398–6408 CrossRef CAS.
- C. Deviannapoorani, L. Dhivya, S. Ramakumar and R. Murugan, J. Power Sources, 2013, 240, 18–25 CrossRef CAS.
- L. Dhivya, N. Janani, B. Palanivel and R. Murugan, AIP Adv., 2013, 3, 082115 CrossRef.
- S. Ramakumar, L. Satyanarayana, S. V. Manorama and R. Murugan, Phys. Chem. Chem. Phys., 2013, 15, 11327–11338 RSC.
- S. Ramakumar, N. Janani and R. Murugan, Dalton Trans., 2015, 44, 539–552 RSC.
- S. Narayanan, F. Ramezanipour and V. Thangadurai, J. Phys. Chem. C, 2012, 116, 20154–20162 CAS.
- A. M. Phipps and D. N. Hume, J. Chem. Educ., 1968, 45, 664 CrossRef CAS.
- A. K. Jonscher, Nature, 1977, 267, 673–679 CrossRef CAS.
- J. C. Dyre, J. Appl. Phys., 1988, 64, 2456–2468 CrossRef.
- K. Funke, Solid State Ionics, 1997, 94, 27–33 CrossRef CAS.
- J. E. Diosa, R. A. Vargas, I. Albinsson and B. E. Mellander, Solid State Ionics, 2006, 177, 1107–1110 CrossRef CAS.
- A. Orliukas, A. Dindune, Z. Kanepe, J. Ronis, E. Kazakevicius and A. Kežionis, Solid State Ionics, 2003, 157, 177–181 CrossRef CAS.
- K. P. Padmasree, R. A. Montalvo-Lozano, S. M. Montemayor and A. F. Fuentes, J. Alloys Compd., 2011, 509, 8584–8589 CrossRef CAS.
- P. B. Macedo, C. T. Moynihan and R. Bose, Phys. Chem. Glasses, 1972, 13, 171–179 CAS.
- S. Choudhary and R. J. Sengwa, Indian J. Eng. Mater. Sci., 2014, 21, 7–15 CAS.
- K. L. Ngai and U. Strom, Phys. Rev. B, 1988, 38, 10350–10356 CrossRef CAS.
- T. Šalkus, E. Kazakevičius, A. Kežionis, A. Dindune, Z. Kanepe, J. Ronis, J. Emery, A. Boulant, O. Bohnke and A. F. Orliukas, J. Phys.: Condens. Matter, 2009, 21, 185502 CrossRef PubMed.
- A. Saleem and S. A. Suthanthiraraj, Chem. Sci. Trans., 2014, 3, 847–853 Search PubMed.
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article