 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The reaction of CF2Cl2 with gas-phase hydrated electrons†
Jozef
Lengyel
*a,
Christian
van der Linde
a,
Michal
Fárník
b and
Martin K.
Beyer
 *a
*a
aInstitut für Ionenphysik und Angewandte Physik, Leopold-Franzens-Universität Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria. E-mail: jozef.lengyel@uibk.ac.at; martin.beyer@uibk.ac.at
bJ. Heyrovský Institute of Physical Chemistry v.v.i., Czech Academy of Sciences, Dolejškova 3, 18223 Prague, Czech Republic
First published on 3rd August 2016
Abstract
The reaction of dichlorodifluoromethane (CF2Cl2) with hydrated electrons (H2O)n− (n = 30–86) in the gas phase was studied using Fourier transform ion cyclotron resonance (FT-ICR) mass spectrometry. The hydrated electron reacts with CF2Cl2, forming (H2O)mCl− with a rate constant of (8.6 ± 2.2) × 10−10 cm3 s−1, corresponding to an efficiency of 57 ± 15%. The reaction enthalpy was determined using nanocalorimetry, revealing a strongly exothermic reaction with ΔHr(CF2Cl2, 298 K) = −208 ± 41 kJ mol−1. The combination of the measured reaction enthalpy with thermochemical data from the condensed phase yields a C–Cl bond dissociation enthalpy (BDE) ΔHC–Cl(CF2Cl2, 298 K) = 355 ± 41 kJ mol−1 that agrees within error limits with the predicted values from quantum chemical calculations and published BDEs.
Introduction
Since the discovery of the atmospheric ozone hole chlorofluorocarbons (CFCs) have been recognized as one of the important players in ozone depletion.1,2 The most common CFC is dichlorodifluoromethane (CF2Cl2) that was used in refrigerants due to its high latent heat, non-toxicity and inertness. The other factors in these processes are ice particles in polar stratospheric clouds (PSCs).3 Thus the chemistry, which involves not only the CFC in the gas phase, but also the environment of the ice particles, needs to be investigated.The processes involved in ozone depletion are mostly driven by sunlight. Besides photochemistry on ice particles,4 electron-induced reactions have also received significant interest. The most prominent example is dissociative electron transfer (DET) on ice surfaces5–7 where electron transfer to CFCs was greatly enhanced by several orders of magnitude upon adsorption on ice. The mechanism was explained by the presence of a ‘self-trapped’, solvated excess electron in a polar medium such as water or ammonia. Based on the large enhancement of Cl− generation from the DET to CFCs on ices, Lu and Sanche8,9 proposed the cosmic-ray-driven electron reaction model for ozone depletion, short CRE mechanism, as an additional potential source of Cl˙ radicals. This mechanism initiated a controversial debate.8,10–15
Cl− enhancement was also observed in other experiments16,17 and it was interpreted as an attachment of low energy secondary electrons to CF2Cl2 solvated in a polar medium. CF2Cl2 is then decomposed and Cl− is generated due to tunnelling of the solvated electron. In contrast to this interpretation, the dissociative electron attachment (DEA) cross-sections of mixed CF2Cl2/NH3 clusters did not exhibit any enhancement for electron energies in the range of 0–20 eV.18 In condensed phase electrochemistry, DET of carbon–halogen bonds has been extensively studied.19 A sticky DET mechanism with the Cl− and CCl3˙ fragments bound by a solvent cage was established by Pause et al.20 for DET of CCl4 in N,N′-dimethylformamide, but the strength of the interaction was found to decrease with increasing polarity of the solvent.21
DEA to gas-phase CF2Cl2 is an efficient process due to the high electron affinity of halogen atoms.22 Illenberger et al.23,24 observed that DEA to CF2Cl2 at electron energies close to 0 eV occurs viareaction (1), with large cross-sections.
| CF2Cl2 + e− → CF2Cl2*− → Cl− + CF2Cl˙ | (1) |
However, there are very few free electrons in the atmosphere below 50 km altitude,25 because they are quickly captured by abundant molecules, in particular O2.26 Therefore, in the CRE mechanism it is assumed that the PSC particles are able to stabilize solvated electrons generated by ionizing radiation within a condensed phase particle. If CF2Cl2 is also condensed in the particle, DET with formation of Cl− may take place. For the liquid phase, it has been shown already in 1971 by pulse radiolysis studies in bulk aqueous solution that thermalized hydrated electrons react rapidly with CFCs to produce Cl− ions.27
Previous studies in our group have shown that reductive cleavage of carbon–halogen bonds, i.e. DET, competes with the first step of Birch reduction in reactions of chlorobenzene as well as di- and trifluorobenzenes with gas-phase hydrated electrons (H2O)n−.28,29 In order to test whether fully thermalized solvated electrons are capable of inducing DET in CFCs, we examine the reaction of CF2Cl2 and hydrated electrons (H2O)n− in the cluster size range n = 30–86. We report a systematic study on the reaction kinetics. Applying nanocalorimetry, we extract the reaction enthalpy from the experimental data. In combination with literature thermochemistry from the condensed phase, the C–Cl bond dissociation enthalpy (BDE) of gas-phase CF2Cl2 is derived and compared with literature values as well as high-level quantum chemical calculations. We discuss the observed results in comparison with DET studies in bulk ice and photodissociation experiments in water clusters.
Experiment
The experiments are performed using a modified Bruker/Spectrospin CMS47X FT-ICR mass spectrometer, equipped with a 4.7 T superconducting magnet, a Bruker infinity cell, and an APEX III data station.30,31 Hydrated electrons (H2O)n− are generated in a home built external source31,32 by laser vaporization of a solid zinc target and supersonic expansion of the hot plasma in a helium/water gas pulse.33,34 The skimmed (H2O)n− cluster beam is transferred via an electrostatic lens system through differential pumping stages into the ultra-high vacuum (UHV) region of the mass spectrometer, with a background pressure below 5 × 10−10 mbar, and stored in the ICR cell. CF2Cl2 is introduced into the UHV region of the mass spectrometer as a gas through a leak valve at constant pressures in the range of 0.5–1.1 × 10−8 mbar. The purity of the reactant is checked using electron ionization and high resolution mass spectrometry directly in the ICR cell.To determine the rate constant, reactions are monitored by recording mass spectra as a function of time. The intensities of reactant and product clusters in the mass spectra are summed over all cluster sizes. While the experiments are conducted at room temperature, the internal temperature of (H2O)n− clusters is a result of the interplay between radiative heating by black-body radiation and evaporative cooling.35 In combination with the caloric curves measured by Hock et al.36 this places the internal temperature of the clusters in the range of 90–120 K.
Thermochemistry is investigated using nanocalorimetry.30,37 The heat released during the reaction is extracted by quantitative modelling of the average size of reactant and product clusters as a function of time, taking into account blackbody radiation induced dissociation (BIRD).35,38–41 The method was introduced by Höckendorf et al.30 in reactions of (H2O)n− with O2 and CO2.
To extract the reaction enthalpy from the mass spectra, the average cluster size of reactant and product species is calculated. The results are fitted with a genetic algorithm with the following differential equations:
| dNR = −kf(NR − N0,R)dt | (2) |
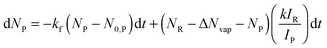 | (3) |
Eqn (2) and the first term in eqn (3) describe BIRD of water clusters, with kf describing the linear dependence on cluster size. N0,R, N0,P account for the contribution of the ionic core to the IR absorption cross-sections. The second term in eqn (3) describes the evaporation of water molecules due to the reaction enthalpy released in the water cluster. The average number of evaporated water molecules ΔNvap is the key result of the fit.
The experiments are assisted by quantum chemical calculations at the Gaussian-4 (G4) level42 using the Gaussian09 program package43 to support the experimentally observed BDE of the CF2Cl2 molecule. In general, G4 level calculations exhibit an average absolute deviation from experiment of 3.5 kJ mol−1.
Results
Fig. 1 shows the mass spectra of the reaction of CF2Cl2 with (H2O)n−. The reaction leads to the formation of hydrated chloride ions and CF2Cl˙ radicals, which evaporate from the water cluster, reaction (4).| CF2Cl2 + (H2O)n− → (H2O)mCl− + CF2Cl˙ + (n − m) H2O | (4) |
To elucidate the reaction rate, the total intensities are plotted as a function of time. The intensities of reactant and product clusters in the mass spectra are summed over all cluster sizes and normalized. The reaction kinetics is quantitatively analysed for the first 4–8 s, depending on the initial cluster size. For n < 30, blackbody radiation induced electron detachment occurs, which interferes with the quantitative analysis.33,44 Thus all quantitative fits are stopped when the lower end of the cluster size distribution reaches n = 30. Fig. 2a shows the kinetic fit using a pseudo-first-order rate law. The resulting first order rate constant krel[s−1] is converted to a pressure corrected absolute rate constant. A relative error of ±25% is determined by the uncertainty of the pressure gauge. Since the CF2Cl2 pressure is a critical parameter for the absolute rate constant determination, the measurements were performed at different pressures repeatedly on different days to minimize any uncertainty. The results of each measurement are shown in Table 1. The measured experimental rate constants kabs are compared with the calculated collision rates to determine the reaction efficiency. We have shown previously that average dipole orientation (ADO) theory,45–48 which describes the ion as a point charge, underestimates the collision rate of clusters with more than 10 water molecules (kADO = 6.1 × 10−10 cm3 s−1 for reaction with CF2Cl2). We therefore use models that account for the geometric size of the water cluster, in particular the hard sphere average dipole orientation, kHSA = 1.0 × 10−9 cm3 s−1, and the surface charge capture model, kSCC = 2.0 × 10−9 cm3 s−1.49 Earlier studies in our group indicate that the actual collision rate of ionic water clusters lies between the two models.50–54 The reaction efficiency can thus be determined using eqn (5).
| Φ = 2kabs/(kHSA + kSCC) | (5) |
| (H2O)n−n = | p(CF2Cl2)/10−9 mbar | k abs/10−10 cm3 s−1 | k HSA/10−9 cm3 s−1 | k SCC/10−9 cm3 s−1 | k ADO/10−10 cm3 s−1 | Φ (%) | ΔNvap | ΔEraw/kJ mol−1 |
|---|---|---|---|---|---|---|---|---|
| 31–47 | 7.2 | 7.1 | 0.9 | 1.8 | 6.2 | 53 | 4.99 | −216 |
| 30–47 | 11 | 6.5 | 0.9 | 1.8 | 6.2 | 48 | 5.39 | −233 |
| 36–50 | 4.7 | 6.6 | 0.9 | 1.9 | 6.2 | 47 | 6.02 | −261 |
| 34–54 | 9.0 | 7.5 | 0.9 | 1.9 | 6.2 | 54 | 4.18 | −181 |
| 35–58 | 8.1 | 7.4 | 0.9 | 1.9 | 6.2 | 53 | 3.41 | −148 |
| 50–82 | 9.0 | 9.4 | 1.0 | 2.1 | 6.0 | 61 | 5.21 | −226 |
| 51–82 | 11 | 10 | 1.0 | 2.1 | 6.0 | 65 | 5.13 | −222 |
| 51–84 | 11 | 12 | 1.1 | 2.1 | 6.0 | 75 | 6.92 | −300 |
| 51–84 | 8.3 | 9.5 | 1.1 | 2.1 | 6.0 | 59 | 2.57 | −111 |
| 46–86 | 9.3 | 10 | 1.0 | 2.1 | 6.0 | 65 | 5.57 | −241 |
| Average | — | 8.6 | 1.0 | 2.0 | 6.1 | 57 | 4.94 | −214 |
The mass spectra reveal that the (H2O)mCl− ions have a slightly lower mean cluster size than the hydrated electrons (H2O)n−. This difference indicates that water molecules are lost due to exothermic reaction. Nanocalorimetry is employed, in which the average number of evaporated water molecules is determined.30 The mean cluster sizes for reactants and products as well as their difference were plotted as a function of time (Fig. 2b and c). A nanocalorimetric fit reveals that the reaction leads to the evaporation of 4.9 ± 0.9 water molecules. The energy required to evaporate a single water molecule from the cluster is ΔEvap = 43.3 ± 3.1 kJ mol−1.36,55 The total energy release is almost identical to the absolute value of the room temperature reaction enthalpy, with minor corrections and a small contribution to the uncertainty.30,50 Then ΔEraw can be calculated using eqn (6), which is converted to room temperature enthalpy ΔHr(CF2Cl2, 298 K) as detailed in the accompanying ESI.†
| ΔEraw = −ΔNvapΔEvap = −214 ± 41 kJ mol−1 | (6) |
| ΔHr(CF2Cl2, 298 K) = −208 ± 41 kJ mol−1 | (7) |
To compare the measured results with literature thermochemistry, we use the observed ΔHr in combination with reaction enthalpies from the condensed phase to calculate the BDE of Cl–CF2Cl bond cleavage. The same approach was successfully used previously on SF6 as a benchmark for nanocalorimetry.50 BDE is calculated from established data, namely the hydration energy of the electron,56 the dissociation enthalpy of HCl,57 the solution enthalpy of gaseous HCl,58 and the ionization energy of the hydrogen atom.59 A thermochemical cycle including all reaction steps is summarized in Table 2. BDE as the enthalpy change of the overall reaction is calculated as the sum of the reaction enthalpies of the partial equations. This results in the C–Cl BDE of CF2Cl2, ΔHC–Cl(CF2Cl2, 298 K) = 355 ± 41 kJ mol−1.
| Reaction | ΔHr (298 K)/kJ mol−1 | Ref. |
|---|---|---|
| H+(g) + e−(g) → H+(aq) + e−(aq) | −1261.9 | 56 |
| H+(aq) + Cl−(aq) → HCl(g) | 74.48 | 58 |
| HCl(g) → H(g) + Cl(g) | 431.58 | 57 |
| H(g) → H+(g) + e−(g) | 1318.4 | 59 |
| CF2Cl2(g) + e− (aq) → CF2Cl(g) + Cl−(aq) | −208 | Our work |
| CF2Cl2(g) → CF2Cl(g) + Cl(g) | 355 | Sum |
In addition, the thermochemistry of the C–Cl bond cleavage of CF2Cl2 is derived by G4 calculations, in which BDE is obtained from the total enthalpies at 298.15 K. The calculated BDE amounts to 337 kJ mol−1. This lies within 18 kJ mol−1 of the experimental value. Both values agree within error limits with the published BDE of 346.0 ± 13.4 kJ mol−1 that was calculated from the standard enthalpies of formation.60,61
Discussion
At first sight, the high exothermicity of reaction (4) may be surprising, given that the C–Cl bond dissociation energy of 355 ± 41 kJ mol−1 is close to the electron affinity of the Cl atom, 348 kJ mol−1. However, the additional energy is supplied by the much stronger interaction of the Cl− ion with the solvent environment compared to the hydrated electron. Essentially, hydration promotes DET.The mechanism of the reaction is straightforward. In the first step, the solvated electron moves to the σ* orbital of one of the C–Cl bonds, reducing the bond order from 1 to 0.5. Water molecules rearrange to solvate the incipient chloride ion, which further weakens the bond until it is broken and the CF2Cl˙ radical is released. Whether a local bound minimum between the Cl− and CF2Cl˙ exists, i.e. whether the DET corresponds to a sticky DET in aqueous solution,19 cannot be determined on the basis of our experiments. We therefore depicted potential curves for both scenarios in Fig. 3. This mechanism can be discussed in connection with two other experiments mentioned in the introduction: the photodissociation of CF2Cl24,62 and the DET mechanism to CFCs on ices.5–9
 | ||
| Fig. 3 Schematic potential energy curves for sticky (dashed) or non-sticky (dotted) DET of a hydrated electron to CF2Cl2. | ||
First, we discuss the photodissociation of CF2Cl2; it is a similar process to DET in the sense that the electron is promoted by a UV photon to the antibonding σ* orbital on one of the C–Cl bonds.62 In our recent study of this process on large water clusters4 we have not seen any evidence for free Cl fragments. Accompanying theoretical calculations revealed a halogen bond63 between Cl and O atoms of water molecules. Thus the CF2Cl2 molecule was bound to the ice nanoparticles with the Cl atoms oriented towards the cluster and the Cl fragment was caged by the cluster after photodissociation.4 This is consistent with the present observation that the Cl− fragment of DET on water clusters remains with water clusters generating the observed (H2O)mCl− products, thus further supporting our previous proposal of halogen bonding between the CF2Cl2 molecule and water clusters. It also matches the observed efficiency of 57%, if one assumes that CF2Cl2 has to collide with the water cluster with the chlorine atoms facing the water network.
Concerning the DET mechanism to CFCs (and other molecules) on ices, it was proposed to proceed via so-called presolvated electrons with binding energies of about 1.3 eV below the vacuum level.8,64–67 The vertical detachment energy of solvated electrons in water clusters strongly depends on the cluster size. In the size range studied here, the VDE of (H2O)n−, n = 30–86, ranges from 1.46 eV to 2.00 eV.68 Extrapolation of cluster values to the bulk yields VDEs ranging from 3.3 eV to 4.0 eV in the literature.68–71 The VDE of bulk water is directly accessible from liquid jet measurements, where values of 3.3 eV have been reported.72,73 No adiabatic values are available for neat water clusters, but Donald et al. studied the hydration of free electrons in La(H2O)n3+, n = 42–160.74 From this study, they extrapolated a bulk hydration enthalpy of −1.3 eV for the electron, identical to the value suggested for the presolvated electron. Direct measurements of the adiabatic hydration enthalpy of an electron in bulk water usually refer to the absolute hydration enthalpy of a proton, which is not precisely known. Taking for example the value reported by Shiraishi et al.56 referenced to ΔHhyd(H+) = −1090 kJ mol−1, which is the textbook standard, results in ΔHhyd(e−) = −172 kJ mol−1 or −1.8 eV. It should be noted that the thermochemical analysis presented here does not rely on the absolute hydration enthalpy of a proton or an electron, but only on their combined value, which should be very reliable. Since hydrated electrons in the excited state relax within 400 fs (n = 25) to 1 ps (bulk) to the electronic ground state,75 we can safely conclude that in our clusters, the electrons are in the electronic ground state. This implies that dissociative electron transfer to CF2Cl2 in the condensed phase does not require a presolvated state, which is in agreement with the earlier results from pulse radiolysis in bulk aqueous solution.27
Conclusions
As previously observed in pulse radiolysis studies in bulk aqueous solution, our results with gas-phase hydrated electrons confirm that fully thermalized hydrated electrons in their electronic ground state are able to induce bond cleavage in CF2Cl2, analogous to the DET mechanism proposed for PSCs. The reaction is efficient and very exothermic. Nanocalorimetry combined with condensed phase literature thermochemistry yields thermochemical data that are consistent with literature values, as well as our own quantum chemical calculations. All these arguments together are consistent with the interpretation that CF2Cl2 undergoes DET in condensed aqueous environments, if thermalized hydrated electrons are present. Whether or not this mechanism is actually relevant for stratospheric ozone destruction is a different question, which cannot be answered on the basis of the present laboratory studies.Acknowledgements
J. L. acknowledges support from the Lise Meitner Programme of the Austrian Science Fund (FWF): project No. M1983-N34. M. F. acknowledges the Czech Science Foundation grant No. 14-08937S.References
- F. S. Rowland and M. J. Molina, Rev. Geophys., 1975, 13, 1 CrossRef CAS.
- M. J. Molina and F. S. Rowland, Nature, 1974, 249, 810 CrossRef CAS.
- S. Solomon, R. R. Garcia, F. S. Rowland and D. J. Wuebbles, Nature, 1986, 321, 755 CrossRef CAS.
- V. Poterya, J. Kočišek, J. Lengyel, P. Svrčková, A. Pysanenko, D. Hollas, P. Slavíček and M. Fárník, J. Phys. Chem. A, 2014, 118, 4740 CrossRef CAS PubMed.
- Q.-B. Lu and L. Sanche, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 153403 CrossRef.
- Q.-B. Lu and T. E. Madey, Surf. Sci., 2000, 451, 238 CrossRef CAS.
- Q.-B. Lu and T. E. Madey, J. Chem. Phys., 1999, 111, 2861 CrossRef CAS.
- Q.-B. Lu, Phys. Rep., 2010, 487, 141 CrossRef CAS.
- Q.-B. Lu and L. Sanche, Phys. Rev. Lett., 2001, 87, 78501 CrossRef CAS PubMed.
- J.-U. Grooß and R. Müller, Atmos. Environ., 2011, 45, 3508 CrossRef.
- R. Müller, Phys. Rev. Lett., 2003, 91, 58502 CrossRef PubMed.
- Q.-B. Lu and L. Sanche, Phys. Rev. Lett., 2002, 89, 219804 CrossRef.
- P. K. Patra and M. S. Santhanam, Phys. Rev. Lett., 2002, 89, 219803 CrossRef PubMed.
- Q.-B. Lu and L. Sanche, Phys. Rev. Lett., 2002, 89, 219802 CrossRef.
- N. R. P. Harris, J. C. Farman and D. W. Fahey, Phys. Rev. Lett., 2002, 89, 219801 CrossRef CAS PubMed.
- N. S. Faradzhev, C. C. Perry, D. O. Kusmierek, D. H. Fairbrother and T. E. Madey, J. Chem. Phys., 2004, 121, 8547 CrossRef CAS PubMed.
- S. Solovev, D. O. Kusmierek and T. E. Madey, J. Chem. Phys., 2004, 120, 968 CrossRef CAS PubMed.
- J. Langer, S. Matt, M. Meinke, P. Tegeder, A. Stamatovic and E. Illenberger, J. Chem. Phys., 2000, 113, 11063 CrossRef CAS.
- A. Houmam, Chem. Rev., 2008, 108, 2180 CrossRef CAS PubMed.
- L. Pause, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2000, 122, 9829 CrossRef CAS.
- L. Pause, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2001, 123, 11908 CrossRef CAS PubMed.
- K. Graupner, S. A. Haughey, T. A. Field, C. A. Mayhew, T. H. Hoffmann, O. May, J. Fedor, M. Allan, I. I. Fabrikant, E. Illenberger, M. Braun, M.-W. Ruf and H. Hotop, J. Phys. Chem. A, 2010, 114, 1474 CrossRef CAS PubMed.
- E. Illenberger, Ber. Bunsenges. Phys. Chem., 1982, 86, 252 CrossRef CAS.
- E. Illenberger, H.-U. Scheunemann and H. Baumgärtel, Chem. Phys., 1979, 37, 21 CrossRef CAS.
- J. Kaplan and C. A. Barth, Proc. Natl. Acad. Sci. U. S. A., 1958, 44, 105 CrossRef CAS.
- D. Smith and N. G. Adams, Top. Curr. Chem., 1980, 89, 1 CrossRef CAS.
- R. H. Schuler, T. I. Balkas and J. H. Fendler, J. Phys. Chem., 1971, 75, 455 CrossRef CAS.
- Y. Cao, R. F. Höckendorf and M. K. Beyer, Int. J. Mass Spectrom., 2008, 277, 206 CrossRef CAS.
- R. F. Höckendorf, O. P. Balaj and M. K. Beyer, Phys. Chem. Chem. Phys., 2011, 13, 8924 RSC.
- R. F. Höckendorf, O. P. Balaj, C. van der Linde and M. K. Beyer, Phys. Chem. Chem. Phys., 2010, 12, 3772 RSC.
- C. Berg, T. Schindler, G. Niedner-Schatteburg and V. E. Bondybey, J. Chem. Phys., 1995, 102, 4870 CrossRef CAS.
- S. Maruyama, L. R. Anderson and R. E. Smalley, Rev. Sci. Instrum., 1990, 61, 3686 CrossRef CAS.
- M. K. Beyer, B. S. Fox, B. M. Reinhard and V. E. Bondybey, J. Chem. Phys., 2001, 115, 9288 CrossRef CAS.
- M. Beyer, C. Berg, H. W. Görlitzer, T. Schindler, U. Achatz, G. Albert, G. Niedner-Schatteburg and V. E. Bondybey, J. Am. Chem. Soc., 1996, 118, 7386 CrossRef CAS.
- R. C. Dunbar, Mass Spectrom. Rev., 2004, 23, 127 CrossRef CAS PubMed.
- C. Hock, M. Schmidt, R. Kuhnen, C. Bartels, L. Ma, H. Haberland and B. von Issendorff, Phys. Rev. Lett., 2009, 103, 73401 CrossRef CAS PubMed.
- W. A. Donald, R. D. Leib, J. T. O'Brien, A. I. S. Holm and E. R. Williams, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18102 CrossRef CAS PubMed.
- M. Sena, J. M. Riveros and N. M. M. Nibbering, Rapid Commun. Mass Spectrom., 1994, 8, 1031 CrossRef CAS.
- T. Schindler, C. Berg, G. Niedner-Schatteburg and V. E. Bondybey, Chem. Phys. Lett., 1996, 250, 301 CrossRef CAS.
- P. D. Schnier, W. D. Price, R. A. Jockusch and E. R. Williams, J. Am. Chem. Soc., 1996, 118, 7178 CrossRef CAS PubMed.
- O. Hampe, T. Karpuschkin, M. Vonderach, P. Weis, Y. Yu, L. Gan, W. Klopper and M. M. Kappes, Phys. Chem. Chem. Phys., 2011, 13, 9818 RSC.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 84108 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09: Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- S. T. Arnold, R. A. Morris and A. A. Viggiano, J. Chem. Phys., 1995, 103, 9242 CrossRef CAS.
- T. Su and M. T. Bowers, Int. J. Mass Spectrom. Ion Processes, 1975, 17, 211 CrossRef CAS.
- T. Su and M. T. Bowers, J. Am. Chem. Soc., 1973, 95, 1370 CrossRef CAS.
- T. Su and M. T. Bowers, J. Chem. Phys., 1973, 58, 3027 CrossRef.
- P. Langevin, Ann. Chim. Phys., 1905, 5, 245 CAS.
- G. Kummerlöwe and M. K. Beyer, Int. J. Mass Spectrom., 2005, 244, 84 CrossRef.
- A. Akhgarnusch, R. F. Höckendorf and M. K. Beyer, J. Phys. Chem. A, 2015, 119, 9978 CrossRef CAS PubMed.
- A. Akhgarnusch and M. K. Beyer, Int. J. Mass Spectrom., 2014, 365, 295 CrossRef.
- R. F. Höckendorf, K. Fischmann, Q. Hao, C. van der Linde, O. P. Balaj, C.-K. Siu and M. K. Beyer, Int. J. Mass Spectrom., 2013, 354–355, 175 CrossRef.
- R. F. Höckendorf, Q. Hao, Z. Sun, B. S. Fox-Beyer, Y. Cao, O. P. Balaj, V. E. Bondybey, C.-K. Siu and M. K. Beyer, J. Phys. Chem. A, 2012, 116, 3824 CrossRef PubMed.
- A. Akhgarnusch, W. K. Tang, H. Zhang, C.-K. Siu and M. K. Beyer, Phys. Chem. Chem. Phys., 2016 10.1039/C6CP03324E.
- W. A. Donald, R. D. Leib, M. Demireva, B. Negru, D. M. Neumark and E. R. Williams, J. Phys. Chem. A, 2011, 115, 2 CrossRef CAS PubMed.
- H. Shiraishi, G. R. Sunaryo and K. Ishigure, J. Phys. Chem., 1994, 98, 5164 CrossRef CAS.
- S. J. Blanksby and G. B. Ellison, Acc. Chem. Res., 2003, 36, 255 CrossRef CAS PubMed.
- V. B. Parker, Thermal Properties of Aqueous Uni-Univalent Electrolytes: National Standard Reference Data Series, National Bureau of Standards 2 (Category 5 – Thermodynamic and Transport Properties), Washington, DC, 1965 Search PubMed.
- P. J. Linstrom and W. G. Mallard, NIST Chemistry WebBook: NIST Standard Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg, MD, 2005 Search PubMed.
- Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 1997 Search PubMed.
- E. Tschuikow-Roux and S. Paddison, Int. J. Chem. Kinet., 1987, 19, 15 CrossRef CAS.
- V. Poterya, J. Kočišek, A. Pysanenko and M. Fárník, Phys. Chem. Chem. Phys., 2014, 16, 421 RSC.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478 CrossRef CAS PubMed.
- C.-R. Wang, J. Nguyen and Q.-B. Lu, J. Am. Chem. Soc., 2009, 131, 11320 CrossRef CAS PubMed.
- C.-R. Wang, K. Drew, T. Luo, M.-J. Lu and Q.-B. Lu, J. Chem. Phys., 2008, 128, 41102 CrossRef PubMed.
- S. Ryu, J. Chang, H. Kwon and S. K. Kim, J. Am. Chem. Soc., 2006, 128, 3500 CrossRef CAS PubMed.
- Q.-B. Lu and L. Sanche, J. Chem. Phys., 2004, 120, 2434 CrossRef CAS PubMed.
- J. V. Coe, G. H. Lee, J. G. Eaton, S. T. Arnold, H. W. Sarkas, K. H. Bowen, C. Ludewigt, H. Haberland and D. R. Worsnop, J. Chem. Phys., 1990, 92, 3980 CrossRef CAS.
- L. Ma, K. Majer, F. Chirot and B. von Issendorff, J. Chem. Phys., 2009, 131, 144303 CrossRef PubMed.
- J. R. R. Verlet, A. E. Bragg, A. Kammrath, O. Cheshnovsky and D. M. Neumark, Science, 2005, 307, 93 CrossRef CAS PubMed.
- T. Zeuch and U. Buck, Chem. Phys. Lett., 2013, 579, 1 CrossRef CAS.
- Y. Tang, H. Shen, K. Sekiguchi, N. Kurahashi, T. Mizuno, Y.-I. Suzuki and T. Suzuki, Phys. Chem. Chem. Phys., 2010, 12, 3653 RSC.
- K. R. Siefermann, Y. Liu, E. Lugovoy, O. Link, M. Faubel, U. Buck, B. Winter and B. Abel, Nat. Chem., 2010, 2, 274 CrossRef CAS PubMed.
- W. A. Donald, M. Demireva, R. D. Leib, M. J. Aiken and E. R. Williams, J. Am. Chem. Soc., 2010, 132, 4633 CrossRef CAS PubMed.
- R. M. Young and D. M. Neumark, Chem. Rev., 2012, 112, 5553 CrossRef CAS PubMed.
Footnote |
† Electronic supplementary information (ESI) available: Conversion of ΔEraw to ΔH298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. See DOI: 10.1039/c6cp01976e K. See DOI: 10.1039/c6cp01976e |
| This journal is © the Owner Societies 2016 |


