Analysis of the magnetically induced current density of molecules consisting of annelated aromatic and antiaromatic hydrocarbon rings

Abstract

Magnetically induced current susceptibilities and current pathways have been calculated for molecules consisting of two pentalene groups annelated with a benzene (1) or naphthalene (2) moiety. Current strength susceptibilities have been obtained by numerically integrating separately the diatropic and paratropic contributions to the current flow passing planes through chosen bonds of the molecules. The current density calculations provide novel and unambiguous current pathways for the unusual molecules with annelated aromatic and antiaromatic hydrocarbon moieties. The calculations show that the benzene and naphthalene moieties annelated with two pentalene units as in molecules 1 and 2, respectively, are unexpectedly antiaromatic sustaining only a local paratropic ring current around the ring, whereas a weak diatropic current flows around the C–H moiety of the benzene ring. For 1 and 2, the individual five-membered rings of the pentalenes are antiaromatic and a slightly weaker semilocal paratropic current flows around the two pentalene rings. Molecules 1 and 2 do not sustain any net global ring current. The naphthalene moiety of the molecule consisting of a naphthalene annelated with two pentalene units (3) does not sustain any strong ring current that is typical for naphthalene. Instead, half of the diatropic current passing the naphthalene moiety forms a zig-zag pattern along the C–C bonds of the naphthalene moiety that are not shared with the pentalene moieties and one third of the current continues around the whole molecule partially cancelling the very strong paratropic semilocal ring current of the pentalenes. For molecule 3, the pentalene moieties and the individual five-membered rings of the pentalenes are more antiaromatic than for 1 and 2. The calculated current patterns elucidate why the compounds with formally [4n + 2] π-electrons have unusual aromatic properties violating the Hückel π-electron count rule. The current density calculations also provide valuable information for interpreting the measured ¹H NMR spectra.

---

1 Introduction

Recently, Cao et al. reported about the synthesis and characterization of organic compounds with two pentalene subunits annelated with a benzene or naphthalene moiety.¹ The molecules with 18 π and 22 π electrons could be expected to be aromatic according to the Hückel electron count. However, nuclear magnetic resonance (NMR) spectroscopy measurements suggested that the aromatic character of the synthesized compounds does not follow this expectation, since the detected upfield shift of the pentalene hydrogen atoms suggests that the molecules are antiaromatic. Based on interpretations of nucleus independent chemical shift (NICS) scans,^2,3 Cao et al. estimated the current pathways and the (anti)aromatic character of the studied molecules with the aim of explaining the unexpected experimental observations. However, estimating detailed current pathways of multiring molecules using magnetic shielding functions is challenging. The first attempt to estimate ring-current strength susceptibilities from the spatial dependence of the magnetic response in order to quantify the degree of aromatic or anti-aromatic character of molecular rings was to the best of our knowledge reported in 1999.⁴ A number of studies have since then shown that current strength susceptibilities deduced from magnetic shielding data depend strongly on the underlying assumed current-pathway model. Hence, shielding based approaches are prone to yield significant uncertainties in current strength susceptibilities, current pathways, and the related degree of aromaticity, which have also previously been pointed out by various authors.^4–13 Thus, when adopting the analogy of microscopes one may consider shielding based approaches as working with a lower resolution, whereas explicit calculations of current densities provide a much higher resolution with better reliability and deeper insights.

In the present work, we show that explicit quantum chemical calculations of magnetically induced current densities are needed for understanding why the bispentalene compounds synthesized by Cao et al. do not obey the Hückel rule for aromaticity.¹ A profound understanding of the aromatic properties has been obtained by calculating the magnetically induced current densities, current pathways, and current strengths using the gauge-including magnetically induced current (GIMIC) method,¹⁴ which is known to provide very detailed information about current patterns even in very complicated molecular systems. The computational method was published in 2004 and has since then been employed in a number of current density studies of complex multiring molecules such as fullerene,¹⁵ gaudiene,¹⁶ porphyrins,¹⁷ graphene models,¹⁸ Möbius twisted molecules,¹⁹ silicon-alkyl clusters,^20–22 and toroidal molecules,²³ to mention only a few. References to further current density studies can be found in the perspective article and in the recent review.^24a,b

An important advantage of the GIMIC method as compared to alternative approaches is that current pathways and current strength susceptibilities can be accurately obtained by numerically integrating the current passing selected planes through the studied molecule. The calculated contributions to the current strength susceptibilities can be used for assessing and comparing electron delocalization properties of different molecules.^14,24–26 Here, the integration analysis for the first time has also been applied along common chemical bonds of annelated rings making it possible to distinguish between local, semilocal and global ring currents. The diatropic and paratropic contributions to the current strength susceptibility along the extent of the integration plane are obtained separately by using a stepwise integration procedure that yields information about the strength of atomic currents and the current-strength distribution of bond currents, which provide a very thorough picture of the current pattern in complex molecules such as bispentalene annelated benzene and naphthalene.

The unit of the reported current strengths (susceptibilities) is ampere per tesla, A T⁻¹. Note that it is not possible to determine current strengths by using shielding based methods without introducing a model for the current pathway. Gauge including atomic orbitals (GIAO) are employed in the GIMIC calculations leading to a fast basis-set convergence that renders calculations on large molecules feasible.^27,28 Methods based on continuous transformation of the origin of the current density (CTOCD) can also be used for calculating gauge origin independent current densities.²⁹ In the CTOCD calculations, the basis set requirements are larger, because traditional non-London type orbital basis sets are employed.³⁰

2 Computational methods

The molecular structures of naphthalene (N), pentalene (P) and the investigated bispentalene derivatives (1, 2, and 3) are shown in Fig. 1. The structures were optimized at the density functional theory (DFT) level^31,32 using Becke's three-parameter functional in combination with the Lee–Yang–Parr exchange–correlation functional (B3LYP) as implemented in TURBOMOLE version 6.6.^31–34 Triple-ζ quality basis sets augmented with polarization functions (def2-TZVP) and the m5 grid were employed.^35,36 Nuclear magnetic shielding constants were calculated at the B3LYP/def2-TZVP level using the mpshift module of TURBOMOLE.^37,38 Magnetically induced current densities were calculated at the B3LYP/def2-TZVP level using the GIMIC program,^14,24,25 which is a free-standing program employed to calculate current densities. GIMIC uses the atomic orbital density matrix and the first-order magnetically perturbed density matrices as well as basis-set information as input data.^14,25 The density matrices are obtained in the electronic structure calculation and in the calculation of nuclear magnetic shielding constants, respectively. Gauge-origin independence and a fast basis-set convergence of the current densities are ensured by using GIAOs.^27,28 Graphical visualization was done using GIMP,³⁹ Mayavi2,⁴⁰ and PyNgl.⁴¹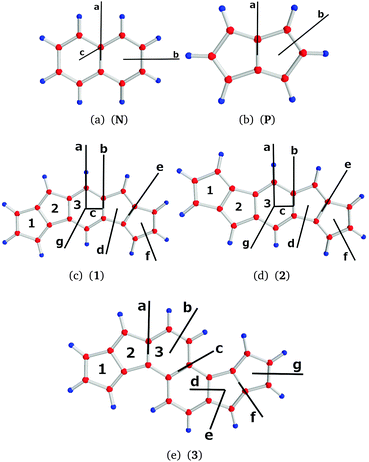

Fig. 1 The molecular structures of the studied molecules with the employed ring (1–3) and plane (a–g) labels. The positions of the integration planes are marked with black bars.

Current strength profiles as shown for plane b of molecule 1 in Fig. 2 are obtained by a stepwise integration procedure. The current strength passing half the molecule through a narrow slice of e.g., 0.05 × 10 Bohr is obtained by numerical integration. The integration is repeated for each slice from the bond center to a very long distance where the current density vanishes. The total current strength is obtained by summing up the contributions from the slices. Different contributions to the current strength can be identified. For example, the diatropic contribution in the interval of about [0,1] in Fig. 2 is the bond current of the C–C bond. The sharp peaks correspond to the atomic current. The strength of the atomic current is most accurately obtained from the diatropic curve, because it is well separated from the other diatropic contributions. The outermost contribution is the diatropic ring current at the outer edge of the molecule. The areas of the diatropic and paratropic curves are almost equal implying that the net strength of the current passing the plane b practically vanishes. The diatropic and paratropic contributions to the atomic current must be equal, because the atomic vortex lies on the integration plane. The paratropic part of the bond current is not seen in Fig. 2, because the bond current returns on the other side of the C–C bond corresponding to negative distances. A first conclusion from the visual inspection of Fig. 2 is that non-local paratropic currents passing plane b of 1 are stronger than the non-local diatropic ones, whereas a comparison of different contributions with the integrated current strengths provides the details.

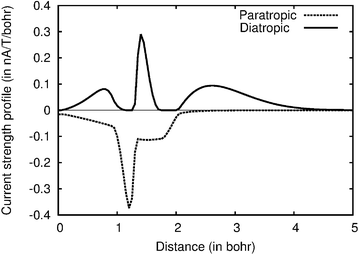Fig. 2 The current strength profile for molecule 2 along the integration plane b. The abscissa begins at the bond center.

3 Results and discussion

3.1 Calculated and measured ¹H NMR chemical shifts

The measured ¹H NMR chemical shifts of the hydrogens of the pentalene and benzene rings are 5.96 ppm and 6.46 ppm for compound 2a as reported in ref. 1, which can be compared to the calculated ¹H NMR chemical shifts for 1 and 2 as well as for the pentalene rings of 3 that are all in the range of 5.49–5.73 ppm. Solvent effects, vibrational effects, and the employed level of electronic structure calculations are some reasons for the deviations between measured and calculated chemical shifts. A previous study showed that the surrounding solvent might significantly stabilize antiaromatic molecules making them less antiaromatic.⁴² The discrepancy can also be assigned to chemical shift contributions from the phenyl groups omitted in the calculation. The contributions to the ¹H NMR chemical shift introduced by the phenyl groups were estimated by calculating the ¹H NMR chemical shifts for compounds 1a and 3a reported in ref. 1 using the molecular structures reported by Cao et al. The obtained phenyl contributions of 0.5–1.6 ppm for compound 1a and 0.2–0.4 ppm for compound 3a are though rather small.

The measured ¹H NMR chemical shifts of the hydrogens of the naphthalene moiety of compound 3a reported in ref. 1 are 5.97 ppm and 6.04 ppm compared to the calculated values of 6.25 ppm and 6.48 ppm for 3. The discrepancy between the calculated and measured ¹H NMR chemical shifts is of the same size as for the aromatic N molecule whose calculated ¹H NMR chemical shifts of 8.18 ppm and 7.80 ppm are about 0.35 ppm larger than the experimental values of 7.81 ppm and 7.46 ppm measured in CDCl₃.⁴³ The calculated ¹H NMR chemical shifts for the antiaromatic pentalene are in the range of 4.82–4.98 ppm. The calculated and experimental ¹H NMR chemical shifts of about 6 ppm suggest that the investigated molecules are most likely antiaromatic, which contradicts the expectation from the Hückel π-electron count, since the molecules 1, 2 and 3 have a perimeter of [4n + 2] π electrons.

3.2 Current density analysis

In this work, we use the term ‘local ring current’ for a closed current circuit, which is mainly localized at one molecular ring, whereas we use ‘semilocal’ and ‘global ring current’ for a flow around a few molecular rings and around the whole conjugated π-electron delocalization pathway of ring-shaped molecules, see Fig. 3. Aihara introduced a similar concept to distinguish between the different current density pathways.⁴⁴ The aromatic, antiaromatic or nonaromatic character of a molecule according to the magnetic criterion can be related to its net current strength susceptibility. In a magnetic field, aromatic molecules sustain diatropic currents, paratropic currents dominate in antiaromatic molecules, while for nonaromatic molecules the strengths of the diatropic and paratropic currents almost cancel.²⁶ Current flows can bifurcate at common bonds between annelated rings in unsaturated organic ring systems. This can be assessed by calculating the current strengths along the in-going and out-going branches at atomic centers.^17,18 Computationally it is possible to determine the local, semilocal and global character of induced ring currents by analyzing the integrated current strengths that pass along the chemical bonds of annelated molecular rings. The profile of the diatropic current passing the integration planes along the common bond of annelated rings yields bond current strengths and the strength of atomic currents. Current density plots reveal the main current flow suggesting where to place the integration planes. The stepwise integration procedure described in Section 2 has been employed for determining bond currents and atomic currents that are needed for obtaining detailed information about the current flow.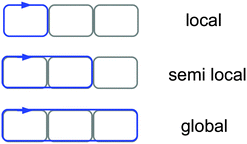

Fig. 3 Schematic illustration of the usage of the terms ‘local’, ‘semilocal’ and ‘global’ current circuits in this work.

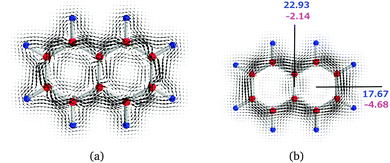
We illustrate the computational approach by first discussing naphthalene (N) as a model example, whose current density has also been studied by other researchers.^45,46 Then, similar analyses are performed on pentalene (P) and the bispentalene derivatives 1–3. Studies of the current density of pentalene have also been reported in ref. 47–49. The placement of the integration planes is shown in Fig. 1. The integrated current strength susceptibilities passing the planes are collected in Table 1. The magnetically induced current densities calculated in planes that are placed 0.5 Bohr and 1 Bohr above the molecular plane of naphthalene are depicted in Fig. 4. The current plots illustrate changes in the current pattern for two planes at different distances from the molecule. The strength of the current that passes along a given chemical bond is determined by placing the integration plane across the bond and perpendicularly to the molecular plane. To consider the whole current strength, the integration plane starts in a current vortex and ends in another current vortex or at a long distance from the molecule where the current density vanishes.

Table 1 The diatropic, paratropic and net current strengths (current strength susceptibility in nA T⁻¹) calculated at the B3LYP/def2-TZVP level. The ring numbering begins at the end of the molecules. The notation 1–2 means the current passing across half the common bond between rings 1 and 2, etc. and 2⊥3 means that the integration plane is placed across the common bond of rings 2 and 3

Molecule	Plane	Ring	Diatropic	Paratropic	Net current
N	a	1–1′	22.93	−2.14	20.80
N	b	1	17.67	−4.68	12.99
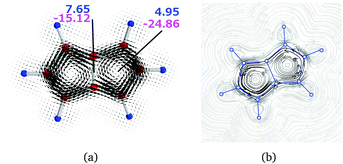
P	a	1–1′	7.65	−15.12	−7.47
P	b	1	4.95	−24.86	−19.91
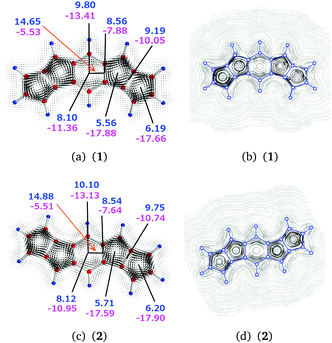
1	a	3	9.80	−13.41	−3.61
1	b	2–3	8.56	−7.88	0.68
1	c	2⊥3	14.65	−5.53	9.12
1	d	2	5.56	−17.88	−12.32
1	e	1–2	9.19	−10.05	−0.86
1	f	1	6.19	−17.66	−11.47
1	g	3	8.10	−11.36	−3.26
2	a	3	10.10	−13.13	−3.03
2	b	2–3	8.54	−7.64	0.90
2	c	2⊥3	14.88	−5.51	9.36
2	d	2	5.71	−17.59	−11.88
2	e	1–2	9.75	−10.74	−0.99
2	f	1	6.20	−17.90	−11.50
2	g	3	8.12	−10.95	−2.83
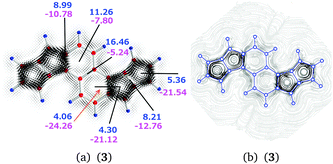
3	a	2–3	8.99	−10.78	−1.79
3	b	3	11.26	−7.80	3.46
3	c	3–3′	16.46	−5.24	11.23
3	d	2⊥3	4.06	−24.26	−20.20
3	e	2	4.30	−21.12	−16.82
3	f	1–2	8.21	−12.76	−4.55
3	g	1	5.36	−21.54	−16.18

---

Fig. 4 The magnetically induced current density of (N) calculated in a plane placed (a) 0.5 Bohr and (b) 1.0 Bohr above the molecular plane. Diatropic currents are assumed to circle clockwise and the paratropic ones circle anticlockwise. The current strength susceptibilities passing the indicated planes were obtained by numerical integration of the current flow. Diatropic current strengths are indicated in blue and the strengths of the paratropic currents are written in magenta. The total current strength susceptibility is the sum of the diatropic and paratropic contributions.

3.2.1 Current strengths and pathways in naphthalene. For N, the integration of the current density passing selected planes shows that a strong diatropic ring current contribution of 22.93 nA T⁻¹ passes through plane a between the two benzene rings as shown in Fig. 4. The paratropic contribution of −2.14 nA T⁻¹ passing the plane originates from the local current around the carbon atom. The rest of the current passing plane a can be assigned to the global diatropic ring current and a local bond current that circles around the central C–C bond. Integration of the current strength passing plane b shows that a local paratropic ring current of −4.68 nA T⁻¹ circles mainly inside the benzene rings. The strength of the paratropic current of −4.22 nA T⁻¹ circling inside the benzene ring can be obtained by integrating the current passing plane c between one of the common carbon atoms and the ring center. The bond current at plane b is then 0.46 nA T⁻¹ yielding a net diatropic current of 17.21 nA T⁻¹ that passes plane b. The total ring current of N is 12.99 nA T⁻¹. The current density analysis for N demonstrates the ability of the integration technique to provide detailed information about the current pathways.

3.2.2 Current strengths and pathways in pentalene. We analogously analyze the magnetically induced current density of a single pentalene P molecule. The diatropic and paratropic currents passing planes a and b are shown in Fig. 5. The strength of the net ring current passing the outer bond of the pentalene rings is −19.91 nA T⁻¹. Thus, P as expected is strongly antiaromatic according to the ring current criterion.²⁶ The current pattern of P is even more complicated than for N requiring a thorough analysis. The current passing plane a can be divided into bond current, atomic current, global paratropic ring current and global diatropic ring current. By studying the diatropic and paratropic currents separately, the current density domains can easily be identified. Integration of the diatropic current passing half the interior C–C bond yielded a current strength of 2.70 nA T⁻¹ for the bond current passing plane a. The diatropic current around the carbon atom at plane a is 1.42 nA T⁻¹. Thus, a global diatropic ring current of 3.52 nA T⁻¹ flows around the outer edge of the whole pentalene molecule and a paratropic current of −13.70 nA T⁻¹ passes from one pentalene ring to the other forming the global net ring current of −10.18 nA T⁻¹. The C–C bond at plane b sustains a local diatropic bond current of 1.43 nA T⁻¹ yielding a local paratropic ring current of −9.73 nA T⁻¹ in the individual pentalene rings.

Fig. 5 The magnetically induced current density of pentalene (a) calculated in a plane placed 1.0 Bohr above the molecular plane and (b) as streamline representation. Diatropic currents are assumed to circle clockwise and the paratropic ones circle anticlockwise. The current strength susceptibilities passing the indicated planes were obtained by numerical integration of the current flow. Diatropic current strengths are indicated in blue and the strengths of the paratropic currents are written in magenta. The total current strength susceptibility is the sum of the diatropic and paratropic contributions.

3.2.3 Current strengths and pathways in 1 and 2. Here, we discuss the integrated current strength susceptibilities of molecules 1 and 2. The current strengths of 2 are given in parenthesis, because the calculated current pathways of compounds 1 and 2 are very similar. The current pathways in 1 and 2 are very complicated requiring separate integration of the diatropic and paratropic contributions passing planes a to f. The labels and placement of the planes and the numbering of the rings are given in Fig. 1. The magnetically induced current density calculated 1 Bohr above the molecular plane and its streamline representation are visualized in Fig. 6.

Fig. 6 The magnetically induced current densities of (a) 1 and (c) 2, calculated in a plane placed 1.0 Bohr above the molecular plane. Diatropic currents are assumed to circle clockwise and the paratropic ones circle anticlockwise. The current strength susceptibilities are obtained by integrating the current flow passing the indicated planes perpendicularly to the molecular plane. Diatropic current strengths are written in blue and the paratropic ones in magenta. The total current strength susceptibility is obtained as the sum of the diatropic and paratropic contributions. The streamlines of the magnetically induced current density of (b) 1 and (d) 2 calculated in the same plane. The atom positions are indicated by blue circles.

The total diatropic current passing plane b is 8.56 (8.54) nA T⁻¹ and the total paratropic current passing it is −7.88 (−7.64) nA T⁻¹. The current strengths passing plane b involves bond currents of the C–C bond and the atomic currents of the carbon atoms. The strength of the bond current of 1.61 (1.62) nA T⁻¹ and the atomic current of 2.32 (2.34) nA T⁻¹ can be obtained from the diatropic contribution to the current passing plane b. The rest of the diatropic current of 4.62 (4.58) nA T⁻¹ is the global ring current that passes plane b mainly on the outside of the central benzene ring. However, we have omitted a small contamination of less than 0.15 nA T⁻¹ from the current density circling around the hydrogen of the benzene ring, which passes back and forth across plane b.

Integration of the current passing plane c yields a positive current of 14.65 (14.88) nA T⁻¹, which is mainly the paratropic current contributions of the pentalene moiety passing between the benzene ring and the pentalene. By considering the bond current of the C–C bond of 1.61 (1.62) nA T⁻¹ one obtains a semilocal paratropic pentalene ring current of −13.04 (−13.26) nA T⁻¹ along the bond. The negative current passing plane c is −5.53 (−5.51) nA T⁻¹. By correcting it for the bond current of 1.61 (1.62) nA T⁻¹, one obtains a paratropic current of −3.92 (−3.89) nA T⁻¹ circling on the inside of the benzene ring.

Integration of the current passing plane a from the molecular center through the central C and H atoms yields an atomic current of 2.42 (2.58) nA T⁻¹ around the carbon atom. A weak diatropic current of 0.24 (0.19) nA T⁻¹ passes inside the carbon and a stronger diatropic current of 7.14 (7.33) nA T⁻¹ passes on the outside of the carbon. By comparing the diatropic current passing outside the carbon with the diatropic current of 4.62 (4.58) nA T⁻¹ passing plane b, one obtains a diatropic current of 2.52 (2.75) nA T⁻¹ that circles around the CH moiety of the benzene ring.

The net paratropic current of −10.99 (−10.55) nA T⁻¹ passing plane a is obtained by correcting the integrated value of −13.41 (−13.13) nA T⁻¹ for the atomic contribution. The net paratropic current passing plane a consists of the paratropic current of the benzene ring of −3.92 (−3.89) nA T⁻¹, the inner part of the local diatropic current of 2.52 (2.75) nA T⁻¹ for the CH moiety, and the paratropic ring current of −4.55 (−3.91) nA T⁻¹ passing the CH moiety to the other pentalene.

Integration of the diatropic current passing plane e yields a bond current of 3.19 (3.38) nA T⁻¹ and an atomic current of 1.41 (1.65) nA T⁻¹. The integrated diatropic and paratropic ring currents passing plane d are 5.56 (5.71) nA T⁻¹ and −17.88 (−17.59) nA T⁻¹, respectively. Since the total diatropic current passing plane e is 9.19 (9.75) nA T⁻¹, the global diatropic ring current of the pentalene moieties is 4.59 (4.72) nA T⁻¹, which agrees well with the value of 4.62 (4.58) nA T⁻¹ obtained at plane b. The difference of 0.97 (0.99) nA T⁻¹ between the diatropic current passing plane d and the global diatropic current is due to local currents in the C–C bond of ring 2. Since the paratropic ring current passing plane d is −16.91 (−16.60) nA T⁻¹ and the sum of the global and semilocal paratropic ring currents of the pentalene moieties passing plane e is −8.64 (−9.09) nA T⁻¹, the difference of −8.28 (−7.51) nA T⁻¹ is the paratropic ring current sustained by ring 2.

The integrated diatropic and paratropic ring currents passing plane f are 6.19 (6.20) nA T⁻¹ and −17.66 (−17.90) nA T⁻¹. By using the same procedure as for ring 2, one obtains a bond current of 1.60 (1.48) nA T⁻¹ for the outer C–C bond of ring 1. The paratropic ring current of ring 1 is −7.42 (−7.33) nA T⁻¹.

The semilocal paratropic current of −8.64 (−9.09) nA T⁻¹ passing the pentalene splits at the benzene ring into the global paratropic ring current of −4.55 (−3.91) nA T⁻¹ and a paratropic current of −4.09 (−5.18) nA T⁻¹ that passes along the common bond of the pentalene and the benzene ring. The strength of the paratropic current passing between the pentalene and the benzene ring is then −12.37 (−12.69) nA T⁻¹, which can be compared with −12.20 (−11.40) nA T⁻¹ that is obtained by adding the two paratropic current contributions passing plane c and correcting them for the bond current of 1.61 (1.62) nA T⁻¹. The agreement between the two values shows the consistency and error bars of the employed approach.

In summary, the current density calculations show that the current flow in 1 (2) consists of local paratropic ring currents of −7.42 (−7.33) nA T⁻¹, −8.28 (−7.51) nA T⁻¹, and −3.92 (−3.89) nA T⁻¹ in rings 1, 2, and 3, respectively. A previous study also showed that benzene rings can sustain a paratropic ring current when they are annelated to two formally antiaromatic rings.⁵⁰ Molecule 1 (2) sustains a global diatropic ring current of 4.62 (4.59) nA T⁻¹, which practically cancels the global paratropic current of −4.55 (−3.91) nA T⁻¹. Thus, the net ring current around the entire molecule is only 0.07 (0.68) nA T⁻¹. The pentalenes sustain a semilocal paratropic ring current of −4.09 (−5.18) nA T⁻¹. Therefore, molecules 1 and 2 according to the ring current criterion can be considered globally nonaromatic with antiaromatic five-membered rings of the pentalenes.

The current density analysis reveals that a diatropic current of 2.52 nA T⁻¹ (2.75) nA T⁻¹ is sustained around the vortex at the benzene C–H moiety introducing a deshielded area in the vicinity of the hydrogens of the benzene ring, which provides a possible explanation for the experimentally observed down-field shift of the ¹H NMR signal as compared to the pentalene hydrogens. The stronger paratropic currents of the individual five-membered rings as compared to the one of the benzene ring also affect the ¹H NMR chemical shifts.

Current density susceptibilities and current strengths were also calculated for the full 1 and 3 molecules including the phenyl substituents. The molecular structures reported in ref. 1 were used. The obtained current strengths for the full molecules given in the ESI† agree qualitatively with the ones obtained for the molecules without phenyl substituents, whose structures were fully optimized in this work.

3.2.4 Current strengths and pathways in 3. In this section, we discuss the integrated current strength susceptibilities of 3 passing integration planes a to g. The labels and placement of the integration planes and the numbering of the rings are given in Fig. 1. The calculated current density obtained in a plane placed 1 Bohr above the molecular plane is depicted in Fig. 7 including a streamline representation.

Fig. 7 (a) The magnetically induced current density of 3 calculated in a plane placed 1.0 Bohr above the molecular plane. Diatropic currents are assumed to circle clockwise and the paratropic ones circle anticlockwise. The current strength susceptibilities obtained by integrating the current flow pass the indicated planes perpendicularly to the molecular plane. Diatropic current strengths are written in blue and the paratropic ones in magenta. The total current strength susceptibility is obtained as the sum of diatropic and paratropic contributions. (b) The streamlines of the magnetically induced current density of 3 calculated in the same plane. The atom positions are indicated by blue circles.

The calculated current pathways for compound 3 significantly differ from those obtained for 1 and 2. The diatropic current of 8.21 nA T⁻¹ passing plane f consists of a bond current contribution of 2.97 nA T⁻¹, an atomic contribution of 1.33 nA T⁻¹, and an outer diatropic current of 3.90 nA T⁻¹, which is the global diatropic current that flows at the exterior of the naphthalene and pentalene moieties.

The semilocal paratropic current around the pentalene is −11.43 nA T⁻¹. Integration of the paratropic and diatropic contributions to the current passing plane g in ring 1 yields a paratropic current contribution of −21.54 nA T⁻¹. By comparing the net diatropic current strength of 5.36 nA T⁻¹ with the outer diatropic current of 3.90 nA T⁻¹, one obtains a bond current of 1.46 nA T⁻¹ in the C–C bond of ring 1. The sum of the strengths of the local and semilocal paratropic ring currents at ring 1 is −20.08 nA T⁻¹ yielding a local paratropic ring current of −8.65 nA T⁻¹ in ring 1.

Analogously, integration of the current strengths passing planes e and f yields a local paratropic ring current of −9.29 nA T⁻¹ for ring 2. The diatropic contribution of 4.30 nA T⁻¹ consists of the global diatropic ring current of 3.90 nA T⁻¹ and a bond current contribution of 0.40 nA T⁻¹.

The current pathways at the naphthalene moiety are complex. Since there is no diatropic current contribution inside the five-membered ring, the positive value of 4.06 nA T⁻¹ consists of contributions from the paratropic currents inside the benzene ring and from the bond current at the common bond between the naphthalene and pentalene moieties. Independent integrations of the diatropic and paratropic contributions to the current passing plane d show that the paratropic ring current inside the benzene ring is −2.42 nA T⁻¹ and the bond current in the common C–C bond is 1.64 nA T⁻¹. To avoid spurious contributions, the integration at plane d is performed from the center of the vortex inside the benzene ring to the vortex center of the five-membered ring.

The diatropic current of 11.26 nA T⁻¹ passing plane b on the outside of the naphthalene branches into three pathways at plane a. One continues on the outside of the pentalene moiety forming the global diatropic ring current of molecule 3. The naphthalene ring current flows along the common bond of the naphthalene and pentalene moieties. The third branch turns back forming the zig-zag current inside the naphthalene.

The paratropic current of −7.80 nA T⁻¹ in plane b inside the naphthalene consists of the local paratropic ring current of the benzene ring of −2.42 nA T⁻¹ and a contribution of −5.38 nA T⁻¹ originating from the diatropic current on the outside of the naphthalene that turns back. The ring current of the naphthalene flowing along the common bond of the naphthalene and pentalene moieties through plane d is 1.90 nA T⁻¹, since the negative current of −24.26 nA T⁻¹ passing plane d consists of the bond current of 1.64 nA T⁻¹ and the paratropic ring current of −20.72 nA T⁻¹ of the pentalene at ring 2. The diatropic and paratropic contributions to the integrated current strength passing plane a are affected by the adjacent hydrogen as the current flow makes a turn passing the plane in both directions. The diatropic contribution increases by 1.62 nA T⁻¹, which is exactly cancelled by a paratropic contribution of −1.62 nA T⁻¹.

The consistency of the calculated currents can be checked by calculating the global diatropic current passing plane a. The obtained value of 3.98 nA T⁻¹ agrees well with the value of 3.90 nA T⁻¹ calculated at the pentalene.

In summary, the current density calculations show that the current flow in 3 consists of local paratropic ring currents of −8.65 nA T⁻¹ and −9.29 nA T⁻¹ in rings 1, and 2, respectively. The molecule sustains a global diatropic ring current of 3.90 nA T⁻¹. The pentalenes sustain a semilocal paratropic current of −11.43 nA T⁻¹ yielding a net semilocal paratropic current of −7.53 nA T⁻¹ around the pentalene moieties. The naphthalene sustains a semilocal ring current of 1.90 nA T⁻¹ and a zig-zag current of 5.38 nA T⁻¹. The benzene rings sustain a local paratropic ring current of −2.42 nA T⁻¹ inside the rings. The naphthalene moiety of 3 can be considered to be very weakly aromatic or nonaromatic, whereas the pentalenes with a net semilocal ring current of −7.53 nA T⁻¹ are antiaromatic. In addition, the five-membered rings of the pentalenes are antiaromatic sustaining strong individual paratropic ring currents. The zig-zag current flow deshields the hydrogens of the naphthalene, which might explain the experimentally observed down-field shift as compared to the pentalene hydrogens. The strong paratropic currents in the pentalenes also contribute to the differences in the measured ¹H NMR chemical shifts.

4 Summary and conclusions

Magnetically induced current densities have been computationally investigated for recently synthesized bispentalene compounds that have been found to violate the Hückel rule for aromaticity.¹ The aromatic character of the molecules and the individual molecular rings have been assigned according to the ring current criterion. The current pathways of the molecules have been calculated providing a plausible explanation for the experimentally observed ¹H NMR chemical shifts. A stepwise integration procedure has for the first time been employed for determining bond current strengths and the strength of the currents circling around atomic centers. The detailed current strength analysis renders the identification of local, semilocal and global ring currents feasible. The obtained current pathways and current strengths of the annelated bispentalene–benzene and bispentalene–naphthalene molecules provide a much more detailed picture of the current patterns as compared to the previously reported one,¹ which was based on a NICS-xy scan approach.³

Cao et al. proposed that 1 and 2 sustain global paratropic currents along the 18 π-electron perimeter and that the benzene ring sustains a local diatropic ring current.¹ Here, the detailed current density analysis leads to a completely different picture: all rings sustain local paratropic ring currents and almost no net current passes from the pentalenes to the benzene ring. The pentalenes sustain a weak semilocal paratropic ring current. The C–H moieties of the benzene ring sustain a local diatropic ring current that deshields the hydrogens of the benzene ring, which may explain the experimentally observed down-field shift of the ¹H NMR signal. According to the magnetic criterion, compounds 1 and 2 are globally nonaromatic, whereas the individual rings and the pentalenes are locally and semilocally antiaromatic, respectively.

For the naphthalene-centered bispentalene (3), Cao et al.¹ concluded that the naphthalene moiety has a more localized diatropic ring current than the benzene ring in the benzene-centered bispentalenes (1 and 2). They also concluded that the paratropic ring current of the individual pentalene rings is stronger in 3 than for 1 and 2.

The current density analysis for 3 shows that the five-membered rings sustain local paratropic ring currents, which are somewhat stronger than for 1 and 2. The net semilocal paratropic ring current around the pentalene moieties is almost as strong as the individual paratropic ring currents of the five-membered rings. The diatropic current passing on the outside of the naphthalene moiety splits into three branches. Almost half the current turns back at the common bond of the naphthalene and pentalenes forming a zig-zag current along the C–C bonds of the naphthalene that are not shared by the pentalenes. About one third of the current continues around the pentalenes forming a global diatropic ring current that partially cancels the very strong paratropic semilocal ring current of the pentalenes. The remaining sixth of the naphthalene current forms a very weak semilocal diatropic ring current around the naphthalene.

Scrutinizing the calculated current density susceptibilities of recently studied thieno-bridged porphyrins reveals that the same kind of zig-zag current also appears in them, where the diatropic current of the annelated thiophene ring also avoids the strong paratropic ring current of the five-membered ring between the thiophene and the porphyrin moieties.⁵¹

The present current density calculations confirm that the aromaticity concept is much more complex than described by the Hückel rule⁵² for aromaticity.^53,54 In annelated multiring molecules, electrons along the electron-delocalization or aromatic pathway can take various routes forming local, semilocal and global ring currents⁴⁴ that can also pass common bonds as shown in this work.

The current pathways can bifurcate and join at annelated rings as in porphyrinoids and graphene fragments.^17,18 For planar π-aromatic molecules dominated by a single ring, such as annulenes, for example, the aromatic character might be estimated by counting the number of π electrons,^52,55,56 whereas for complex multiring molecules with annelated rings, explicit current density calculations including an integration analysis is probably the only means to reliably assess the aromatic properties.^{26,42,57–59}

The present work demonstrates how powerful explicit calculations of current densities are for detailed investigations of the current flow in complex molecules with many annelated conjugated rings. Accurate information about the current pathways and current strengths along different routes is obtained by numerical integration of the current densities, which can be calculated by using accurate computational methods employing gauge including atomic orbitals^14,60,61 or within the ipsosentric approach.^55,56,62,63 The study also shows that the use of magnetic shielding based methods for characterizing the magnetic response of multiring molecular systems leads to significant uncertainties, because they are only an indirect means to determine the current pathways. Similar conclusions have been drawn in a recent study by van Damme et al.⁶⁴

The present study shows that current density plots provide additional and complementary insights, whereas merely a visual inspection is not enough for a reliable detailed analysis. Visualization of the current density in different planes placed parallel to the molecular plane yields an overview of the current pathways and suggests where to place the integration planes, whereas explicit integration of the current strengths is recommended for determining the actual current pathways. The main problem with two dimensional current density plots is that they show the current density in only one or a few planes. The contribution to the current strength might significantly vary with the distance from the molecular plane. Numerical integration of the current strengths takes all contributions into account. The positive and negative contributions can be integrated separately providing additional information about the current pathways and the tropicity of the currents.

Acknowledgements

This work was supported by the Academy of Finland through projects (266227 and 275845). We acknowledge the Magnus Ehrnrooth Foundation for financial support. DS thanks the Swedish Cultural Foundation in Finland, the Alexander von Humboldt Stiftung, and the Fulbright Foundation for financial support. We thank the Norwegian Research Council for financial support through the CoE Centre for Theoretical and Computational Chemistry (Grant No. 179568/V30 and 231571/F20). The computational resources were provided by CSC – the Finnish IT Center for Science – and the Norwegian Supercomputing Program NOTUR (Grant No. NN4654K).

References

1. J. Cao, G. London, O. Dumele, M. von Wantoch Rekowski, N. Trapp, L. Ruhlmann, C. Boudon, A. Stanger and F. Diederich, J. Am. Chem. Soc., 2015, 137, 7178–7188.
2. P. von Ragué Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
3. R. Gershoni-Poranne and A. Stanger, Chem. – Eur. J., 2014, 20, 5673–5688.
4. J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 1999, 1, 3429–3435.
5. P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217–223.
6. S. Pelloni, G. Monaco, P. Lazzeretti and R. Zanasi, Phys. Chem. Chem. Phys., 2011, 13, 20666–20672.
7. P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88.
8. I. Morao, B. Lecea and F. P. Cossío, J. Org. Chem., 1997, 62, 7033–7036.
9. J. O. C. Jiménez-Halla, E. Matito, J. Robles and M. Solá, J. Organomet. Chem., 2006, 691, 4359–4366.
10. S. Pelloni and P. Lazzeretti, J. Phys. Chem. A, 2013, 117, 9083–9092.
11. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, J. Chem. Theory Comput., 2013, 9, 4789–4796.
12. G. Monaco and R. Zanasi, J. Phys. Chem. A, 2014, 118, 1673–1683.
13. D. Du, H. Fliegl and D. Sundholm, J. Chin. Chem. Soc., 2016, 63, 93–100.
14. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.
15. M. P. Johansson, J. Jusélius and D. Sundholm, Angew. Chem., Int. Ed., 2005, 44, 1843–1846.
16. D. Sundholm, Phys. Chem. Chem. Phys., 2013, 15, 9025–9028.
17. H. Fliegl and D. Sundholm, J. Org. Chem., 2012, 77, 3408–3414.
18. M. Kaipio, M. Patzschke, H. Fliegl, F. Pichierri and D. Sundholm, J. Phys. Chem. A, 2012, 116, 10257–10268.
19. H. Fliegl, D. Sundholm and F. Pichierri, Phys. Chem. Chem. Phys., 2011, 13, 20659–20665.
20. R. J. F. Berger, H. S. Rzepa and D. Scheschkewitz, Angew. Chem., Int. Ed., 2010, 49, 10006–10009.
21. K. Abersfelder, A. J. P. White, R. J. F. Berger, H. S. Rzepa and D. Scheschkewitz, Angew. Chem., Int. Ed., 2011, 50, 7936–7939.
22. A. Jana, V. Huch, M. Repisky, R. J. F. Berger and D. Scheschkewitz, Angew. Chem., Int. Ed., 2014, 53, 3514–3518.
23. R. J. F. Berger, Z. Naturforsch., 2012, 67b, 1127–1131.
24. (a) H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518; (b) D. Sundholm, H. Fliegl and R. J. F. Berger, Wires Comput. Mol. Sci., 2016 DOI:10.1002/WCMS.1270.
25. S. Taubert, D. Sundholm and J. Jusélius, J. Chem. Phys., 2011, 134, 054123:1–12.
26. H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676.
27. R. Ditchfield, Mol. Phys., 1974, 27, 789–807.
28. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
29. P. Lazzeretti, M. Malagoli and R. Zanasi, Chem. Phys. Lett., 1994, 220, 299–304.
30. S. Pelloni, P. Lazzeretti and R. Zanasi, J. Phys. Chem. A, 2007, 111, 8163–8169.
31. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
32. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
33. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
34. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, WIREs Comput. Mol. Sci., 2014, 4, 91–100.
35. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
36. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
37. M. Häser, R. Ahlrichs, H. P. Baron, P. Weis and H. Horn, Theor. Chim. Acta, 1992, 83, 455–470.
38. M. Kollwitz, M. Häser and J. Gauss, J. Chem. Phys., 1998, 108, 8295–8301.
39. GIMP: GNU Image Manipulation Program, http://www.gimp.org.
40. P. Ramachandran and G. Varoquaux, Comput. Sci. Eng., 2011, 13, 40–51.
41. PyNgl: Scientific visualization Python program package, http://www.pyngl.ucar.edu.
42. R. R. Valiev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2013, 117, 9062–9068.
43. M. Balci, Basic ¹H- and ¹³C-NMR Spectroscopy, Elsevier Science, Amsterdam, 2005, pp. 1–427.
44. J. Aihara, J. Am. Chem. Soc., 2006, 128, 2873–2879.
45. R. Zanasi and P. Lazzeretti, Mol. Phys., 1997, 92, 609–617.
46. I. G. Cuesta, S. P. A. Sánchez de Merás and P. Lazzeretti, J. Comput. Chem., 2009, 30, 551–564.
47. R. W. Havenith, L. W. Jenneskens, P. W. Fowler and E. Steiner, Phys. Chem. Chem. Phys., 2004, 6, 2033–2039.
48. R. W. Havenith, J. J. Engelberts, P. W. Fowler, E. Steiner, J. H. van Lenthe and P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 289–294.
49. I. G. Cuesta, A. Ligabue, A. Sánchez de Merás and P. Lazzeretti, Phys. Chem. Chem. Phys., 2005, 401, 282–287.
50. J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2008, 10, 6630–6634.
51. H. Fliegl, N. Özcan, R. Mera-Adasme, F. Pichierri, J. Jusélius and D. Sundholm, Mol. Phys., 2013, 111, 1364–1372.
52. E. Hückel, Grundzüge der Theorie ungesättigter und aromatischer Verbindungen, Verlag Chemie, Berlin, 1938.
53. M. Randić, Chem. Rev., 2003, 103, 3449–3606.
54. Y. Tobe, Chem. Rec., 2015, 15, 86–96.
55. E. Steiner and P. W. Fowler, Chem. Commun., 2001, 2220–2221.
56. E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2001, 105, 9553–9562.
57. G. V. Baryshnikov, R. R. Valiev, N. N. Karaush, D. Sundholm and B. F. Minaev, Phys. Chem. Chem. Phys., 2016, 18, 8980–8992.
58. S. Taubert, J. Jusélius, D. Sundholm, W. Klopper and H. Fliegl, J. Phys. Chem. A, 2008, 112, 13584–13592.
59. R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2014, 16, 11010–11016.
60. R. Bast, J. Jusélius and T. Saue, Chem. Phys., 2009, 356, 187–194.
61. S. Pathak, R. Bast and K. Ruud, J. Chem. Theory Comput., 2013, 9, 2189–2198.
62. G. Monaco, R. Zanasi, S. Pelloni and P. Lazzeretti, J. Chem. Theory Comput., 2010, 6, 3343–3351.
63. R. W. A. Havenith and P. W. Fowler, Chem. Phys. Lett., 2007, 449, 347–353.
64. S. Van Damme, G. Acke, R. W. A. Havenith and P. Bultnick, Phys. Chem. Chem. Phys., 2016, 18, 11746–11755.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized Cartesian coordinates and calculated NMR shielding constants are reported for all studied molecules. The current strengths of the phenyl substituted molecules 1 and 3 are also given. See DOI: 10.1039/c6cp01968d

---