CO adsorption on the GaPd(1̄1̄1̄) surface: a comparative DFT study using different functionals

Abstract

CO adsorption on the polar (1̄1̄1̄) surface of the intermetallic compound GaPd is examined within ab initio methods using an all-electron full-potential electronic structure approach. Comparison between the PW-LDA, GGA-PBE, GGA-RPBE, GGA-revPBE, and hybrid HSE06 functionals is considered through bulk, clean surface and CO adsorption calculations. The choice of the functional is found to have a strong influence in the description of single CO adsorption on the surface model proposed in literature. As expected from the so called “CO adsorption puzzle”, differences in the obtained results demonstrate that classic LDA and PBE functionals can only partially describe the complex CO adsorption bonding scenario on a surface containing transition metal elements (in this case Pd atoms), where the energies of the substrate–adsorbate electronic states are shifted, yielding important differences in the absolute values of the adsorption energies, vibrational frequencies and surface–adsorbate interaction. So far the hybrid functional HSE06 correctly retrieves all the tendencies observed experimentally as confirmed by comparing our first-principles results to experimental findings.

---

I. Introduction

The intermetallic compound GaPd is experiencing great interest due to its catalytic properties in the semi-hydrogenation of acetylene, an essential cleaning step for the polyethylene production.^1–3 Recently, different studies about the structure determination and chemical reactivity of the polar surface GaPd(1̄1̄1̄) have been published.^4–9 The work of Rosenthal et al. is an experimental study that joins a variety of surface science techniques.⁴ In particular, results of thermal desorption spectroscopy (TDS) of adsorbed CO molecules indicated that different surface terminations are obtained depending on the preparation temperature (670 K or 870 K). Scanning tunneling microscopy (STM) images revealed flat terraces separated by a unique step height. Low-energy electron diffraction (LEED) together with X-ray photoelectron diffraction (XPD) showed no signs of surface reconstruction or segregation. It was proposed that the surface prepared at 870 K can be explained with an atomistic model derived from a bulk truncation containing in the topmost atomic layer a single protruding Pd atom per surface unit cell. For the surface prepared at 670 K, a denser surface model that could contain either Pd-rich or Ga-rich terminations was proposed. Another study, a joint application of experimental LEED, STM, and plane-wave quantum chemical calculations using the PBE-GGA functional,¹⁰ was performed by Prinz et al.⁵ Calculated relative surface energies and qualitative comparison between experimental and simulated STM images in addition to LEED results, lead the authors to the conclusion that the GaPd(1̄1̄1̄) surface can be explained with a model containing only one protruding Pd atom per surface unit cell, located in the center of 3 Ga atoms, in agreement with the previous findings.⁴ However, a different surface model was proposed in the work of Krajčí et al.⁶ In this study, the determination of the structure of the GaPd(1̄1̄1̄) surface was performed exclusively by plane-wave quantum chemical calculations using the PW91-GGA functional. As the previous publication by Prinz et al. it includes relative surface energy calculations and qualitative comparison of the electronic structure with STM images and photoemission spectroscopy. However, their conclusion points towards a Ga-terminated surface model and not to a Pd-terminated model as in the previous works. The publication of Krajčí et al. includes a study of the CO adsorption in different surface models,⁶ but as in previous ref. 7–9 calculations were performed at the GGA level of theory, thus not addressing the “CO adsorption puzzle”.^11–15

For understanding processes occurring at solid surfaces, the atomic structure determination must be complemented by the analysis of the electronic structure, with both depending on the interplay between the chemical species present at the surface at their corresponding coverages. Thus, to comprehend and predict the behavior of solid surfaces, an atomistic approach is vital. The density functional theory (DFT), offering good accuracy at low computational cost, has become the main tool in the last decades for understanding properties of molecules, aggregates, and materials on the atomic scale.^16,17 DFT is in principle exact.¹⁸ However, since the exact form of the exchange–correlation density functional is not known, approximations must be introduced.¹⁹ The most widely used approximations are the local density approximation (LDA) and the generalized gradient approximation (GGA). In complex and more realistic systems, the choice of the right functional describing the exchange and correlation interactions has a strong impact on the accuracy of the obtained results, sometimes leading to considerable errors in the predicted energies, misleading final interpretations.^{11–15,20–26} Particularly, DFT within the Perdew–Wang parametrization for the LDA (PW-LDA),²⁷ the Perdew–Burke–Ernzerhof (PBE) functional for the GGA,¹⁰ and the modified PBE functional, namely the RPBE,²⁸ fail to predict the correct adsorption site for the CO molecule on most of the surfaces of transition- and noble-metal elements.^11–15 The underlying problem, known as the “CO-adsorption puzzle”, is due to the inherent lack of accuracy of both LDA and GGA to describe at the same time the electronic structure of small molecules, such as CO, the electronic surface structure of metals containing d (and/or f) states, as well as the interactions of the surface and the molecule. This leads to a wrong positioning of the orbitals of the CO molecule upon surface adsorption, causing an overestimation of the adsorption energies.^11,14,15 Additionally, the error also depends on the atomic structure of the adsorption site, which leads to wrong site-preference, i.e. wrong energetic ordering of the different adsorption sites.^{12,14,15,29,30} Thus, the quest for an appropriate DFT method that includes a treatable exchange–correlation term to solve the problems linked to the “CO adsorption puzzle” for intermetallic compounds containing transition-metals at their surfaces must be faced before any comparison with available experimental data. In the present work, a comparative DFT study of the CO adsorption on the Pd₁-terminated model^4,5 of the (1̄1̄1̄) surface of the intermetallic compound GaPd is conducted using different exchange–correlation density-functional approximations. This case study constitutes an excellent opportunity to unveil the effects coming from both surface and sub-surface transition-metal elements on the adsorption of the small, yet very important CO molecule.

II. Computational details

Calculations are conducted using the all-electron full-potential code FHI-aims.³¹ Effects of different approximations in exchange–correlation functional are explored by comparing results obtained with (i) the local density approximation (LDA), (ii) the generalized gradient approximation (GGA) and (iii) the hybrid Hartree–Fock/GGA approximation. Atomic relaxations, electronic structure, and energetics are calculated using the Perdew–Wang parametrization for the LDA (PW-LDA),²⁷ the GGA Perdew–Burke–Ernzerhof (PBE) functional,¹⁰ the modified PBE functional RPBE,²⁸ the revised PBE functional revPBE,³² and the hybrid Hartree–Fock/GGA-PBE Heyd–Scuseria–Ernzerhof functional (HSE06).³³ In the latter, the fraction of the Hartree–Fock exchange α and the screening parameter ω are set to 0.25 and 0.11 bohr⁻¹, respectively, as recommended.³³ FHI-aims employs numeric atomic orbital (NAO) basis sets. Final results are obtained using “tight” numerical settings, basis set level up to tier 1 for Ga and Pd, and up to tier 2 for C and O species.^31,34,35 Relativistic effects are considered for both core and valence electrons employing the scaled zero-order regular approximation (ZORA).^31,36,37 Spin polarization is considered in both bulk and surface calculations, where a fixed quantization (collinear) axis is used to define the spin density. Atomic relaxations are conducted by calculating first energy-derivatives (forces) with respect to the nuclear coordinates, and their minimization using the trust radius method of the Broyden–Fletcher–Goldfarb–Shanno BFGS algorithm.^38,39 For the bulk material, also unit cell size/shape relaxation is considered. In all our calculations, forces are converged to values better than 10⁻⁴ eV Å⁻¹, and total energies and charge densities are converged to values better than 10⁻⁶ eV and 10⁻⁵ e Å⁻³, respectively. A well-converged Γ-centred mesh of 20 × 20 × 20 k-points is used to sample the Brillouin zone in bulk calculations. For the slab calculations an 8 × 8 × 1 k-point mesh was used. Tests in bulk calculations – for all here tested functionals – using an 8 × 8 × 8 mesh and a 20 × 20 × 20 mesh result in energy differences smaller than 10 meV, while no significant differences are found in the calculated bulk and surface atomic and electronic structures.

PBE and HSE06 calculations including both the Tkatchenko–Scheffler (TS) correction⁴⁰ for van der Waals interactions and the modified Tkatchenko–Scheffler (TS^surf) correction that includes short-range screening effects, particularly developed for the study of surface–adsorbate systems,^41–43 have been considered. The results obtained with the HSE06 (PBE) functional show that the dispersion corrections of both TS and TS^surf contribute with ≈0.1 eV (≈0.2 eV) to the final adsorption energies of the studied adsorbate–substrate system. Furthermore, their contribution to the CO adsorption energy differences between the most favoured adsorption sites T₁ and H₁ is <10 meV (<50 meV), for the results obtained with the HSE06 (PBE) functional. Differences between TS- and TS^surf-corrected adsorption energies for the studied adsorbate–substrate system are <10 meV (<20 meV) for the results obtained with the HSE06 (PBE) functional. Since for all the here tested functionals, the CO adsorption energy difference between the sites T₁ and H₁ is ≈1 eV (see Table 4), van der Waals dispersion corrections are found to play only a minor role in the CO adsorption on the GaPd(1̄1̄1̄) surface and are not further considered in the present study. These results are in line with the fact that CO is a very small and stable closed-shell molecule and that Pd is the element that presents the smallest correction for the many-body collective response (screening) of the C₆ coefficients of different metallic surfaces.^41–43

The C–O stretching vibrational frequency of the free molecule (gas phase) together with the vibrational frequencies for CO adsorbed at different surface sites are calculated in the harmonic approximation by diagonalizing the Hessian matrix obtained by finite differences of analytic forces, using “tight” numerical settings and basis set level up to tier 1 for all atomic species. The motion of the C and O atoms, as well as the two topmost atomic layers Pd₁ and Ga₃ is considered, with displacement steps of 0.002 Å for each atom along each Cartesian coordinate. Lower-lying atomic layers of the slab are kept frozen at their corresponding relaxed positions.

Chemical bonding analysis in real space is carried out using the concept of electron localizability indicator (ELI).⁴⁴ The ELI in the ELI-D representation^45,46 is computed by the help of an interface to the FHI-aims code. For both the electron density (ED) and the ELI-D, the attractor locations, basins and the number of electrons contained inside the basins are determined by the DGrid package.⁴⁷

III. GaPd crystal structure and bulk calculations

The intermetallic compound GaPd crystallizes in the cubic FeSi type of structure, space group P2₁3 (No. 198, Pearson symbol cP8), containing 8 atoms per unit cell.⁴⁸ At 295 K and atmospheric pressure, the lattice parameter of GaPd is a = 4.89695(6) Å, with a volume V = 117.4 ų.⁴⁸ The first coordination shell of the Pd (Ga) atoms consists entirely of Ga (Pd) atoms. The shortest inter-atomic distance corresponds to a Pd–Ga distance equal to 2.5399(2) Å, located along the threefold axis, and the closest Pd–Pd distance is 3.0084(1) Å.⁴⁸ Because of the absence of inversion symmetry, two possible enantiomorphic forms of the GaPd compound exist, namely form A and form B.^4,48 The calculations of the atomic and electronic structure of the GaPd compound are initially based on lattice parameters and atomic coordinates from its enantiomorphic form B, as described in ref. 4 and 48 (but accidentally labelled form A in ref. 48). Fig. 1 shows the structure model of form B. Each enantiomorph possesses a characteristic but inverse stacking sequence of four non-equivalent atomic layers along the polar [111] direction. Following the notation developed by Rosenthal et al.,⁴ in the case of form B, the sequence of atomic planes is Pd₁/Ga₃/Pd₃/Ga₁ as shown in Fig. 1.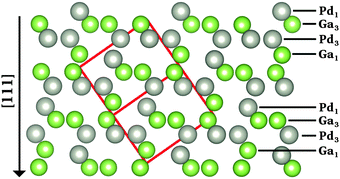

Fig. 1 Projected crystal structure of the enantiomorph B of the intermetallic compound GaPd.⁴⁸ The red box depicts the unit cell, gray (green) spheres represent Pd (Ga) atoms.

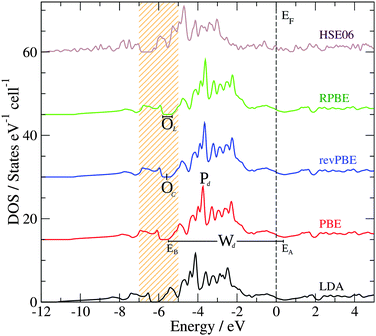
The structural stability of crystals typically correlates with the lattice parameters.⁴⁹ The structural stability of solids is characterized by the enthalpy of formation ΔH_f, which is linked to the cohesive energy and the elasticity of a given compound.⁵⁰ For the intermetallic compound GaPd, a rough approximation of ΔH_f at 0 K, no pressure, and without considering vibrational contributions – here called “formation energy” ΔE_f – can be obtained by calculating the difference between the total energy of bulk GaPd unit cell, and four times the respective bulk energies of elemental Ga and Pd. Table 1 presents the lattice parameter a and the formation energy ΔE_f of GaPd, obtained with different functionals. The relative errors (in %) of the calculated values with respect to the experimentally obtained ones (at room temperature) are given in parenthesis, where a positive (negative) sign indicates an over(under)estimation. To compute ΔE_f, the stable α-modification of Ga and the Cu type of structure of Pd, were considered.^51–53 As expected,⁴⁹ the LDA calculation underestimates the lattice parameter of GaPd with respect to the experimental value, while GGA calculations overestimate it. Bulk calculations using the hybrid functional HSE06 were also conducted. The corresponding optimized lattice parameter is the closest (+0.6%) to the experimental value. The choice of the functional has also an important effect on the obtained values of ΔE_f. Although the latter is negative in all cases, which is in agreement with the high melting point of GaPd (1338 K),⁵⁴ both LDA and GGA calculations overestimate ΔE_f compared to the experimental value of ΔH_f = −5.96 eV.⁵⁵ The RPBE functional gives the highest deviation from the experimental value (+16.38%). In general, all GGA-based calculations give similar results, with the LDA value being this time closer to the experimental ΔH_f (+5.89%) than the GGA values. Although the nearest value to the experimental ΔH_f is the one obtained with the hybrid HSE06 functional (−5.87%), this is not much better than the LDA result.

Table 1 Lattice parameter a and formation energy ΔE_f calculated with different functionals

Functional	a [Å]	ΔEf [eV]
LDA	4.84 (−1.3%)	−5.61 (+5.89%)
PBE	4.96 (+1.2%)	−5.15 (+13.65%)
revPBE	4.99 (+1.9%)	−5.04 (+15.51%)
RPBE	5.00 (+2.2%)	−4.98 (+16.38%)
HSE06	4.93 (+0.6%)	−6.31 (−5.87%)
Experimental	4.90^48	−5.96^55

---

Another important property that can be correlated to the structural stability of a solid is its electronic structure. Fig. 2 presents the bulk density of states (DOS) of GaPd calculated with different functionals, with the lattice parameter relaxed for each functional (see Table 1). Table 2 summarizes the main features of the obtained DOS (defined in Fig. 2), including the opening of the DOS between ≈−5 and ≈−7 eV (position of its center O_C and length O_L), the peak P_d of the Pd 4d band, the Pd 4d bandwidth W_d, and the DOS at the Fermi level n(E_F). In line with previous results, in the valence region the most important partial contribution to the total DOS of GaPd is given by the Pd 4d states, that are shifted below the Fermi level in comparison to pure Pd.^1,56–59 Although the GGA functionals perform similarly, e.g., |ΔP_d| ≤ 0.11 eV, |ΔW_d| ≤ 0.18 eV, the differences between the DOS calculated with LDA and GGA functionals are significant, e.g., ΔW^LDA-RPBE_d = 0.75 eV, ΔP^LDA-RPBE_d = −0.50 eV. However, a PBE calculation at the geometry optimized with the PW-LDA functional (denoted below PBE*) removes almost completely the observed differences, e.g., 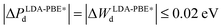. Thus, the differences in the electronic structure obtained with LDA and GGA functionals can partly be tracked down to the differences in their respective optimized geometries. On the other hand, the DOS obtained with LDA and GGA functionals present important differences in comparison to the results obtained with the hybrid HSE06 functional. With respect to the latter, all GGA (LDA) calculations predict both a narrower opening and a smaller Pd 4d bandwidth, i.e., ΔO^HSE06-GGA_L = 0.18 eV (ΔO^HSE06-LDA_L = 0.23 eV) and ΔW^HSE06-GGA_d ≥ 1.03 eV (ΔW^HSE06-LDA_d = 0.46 eV). Furthermore, the DOS is shifted to higher energies in the GGA (LDA) calculations in comparison to the HSE06 results, e.g., |ΔP^HSE06-GGA_d| ≥ 0.95 eV (|ΔP^HSE06-LDA_d| = 0.56 eV). Here, the obtained differences cannot be explained as mainly a geometric effect. The observed differences are due to the self-interaction error present in the LDA and GGA functionals, which is partly removed in hybrid functionals including the HSE06.^{14,33,60–65} As a result, the latter provide a better description of the electronic structure of molecular systems, and have been demonstrated to yield better alignment of the metallic band in solids, but can overestimate its width.^{14,33,60–65} This can explain the difference between the HSE06 and LDA/GGA positions of the Pd 4d band in the bulk GaPd DOS. Since the chemical reactivity of a surface depends on the electronic structure of both the adsorbed molecular species and the surface, the obtained results suggest that the predicted chemical properties of the surfaces of GaPd will be sensitive to the approximations used in the employed exchange–correlation functional.

Fig. 2 Bulk DOS of GaPd calculated with different functionals. The HSE06 DOS calculation was performed using an 8 × 8 × 8 k-point mesh. W_d = E_A − E_B corresponds to the Pd 4d bandwidth, while O_L and O_C depict the length and the center of the opening of the DOS around −6 eV. The zero of the energy scale is set to the Fermi level (E_F, vertical dashed line).

Table 2 Properties of the bulk DOS of GaPd obtained with different functionals (in eV)

Functional	O C	O L	Pd 4d Pd	Pd 4d Wd	n(EF)^a
a Given in states eV^−1 cell^−1.
LDA	−6.22	0.40	−4.12	6.50	0.94
PBE*	−6.19	0.38	−4.10	6.48	0.76
PBE	−5.74	0.45	−3.73	5.93	1.09
revPBE	−5.61	0.45	−3.65	5.80	1.18
RPBE	−5.57	0.45	−3.62	5.75	1.14
HSE06	−6.62	0.63	−4.68	6.96	0.78

---

IV. Pd₁-terminated GaPd(1̄1̄1̄) surface

Following the bulk stacking sequence of atomic planes Pd₁/Ga₃/Pd₃/Ga₁ along [1̄1̄1̄], the construction of the Pd₁-terminated model of the GaPd(1̄1̄1̄) surface is achieved by simple bulk truncation, resulting in a (√3 × √3)Rot30° surface unit cell.^4,5Fig. 3 shows a top view of the Pd₁-terminated model. The topmost atomic layer (Pd₁) consists of only one Pd atom per surface unit cell. The second (third) layer Ga₃ (Pd₃) consists of three Ga (Pd) atoms per surface unit cell – connected with dotted lines in Fig. 3.

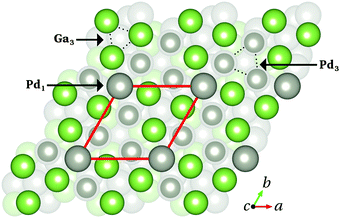Fig. 3 Top view of the Pd₁-terminated model of the GaPd(1̄1̄1̄) clean surface. The red box depicts the surface unit cell. The topmost atomic layers Pd₁, Ga₃ and Pd₃ are highlighted (arrows, dotted lines), while deeper layers appear faded. Color code as in Fig. 1.

The simulation of the Pd₁-terminated model is achieved through asymmetric slabs. In this configuration, the slab is composed of a certain number N_F of atomic layers that are kept fixed at the optimized bulk atomic positions (lying at the bottom of the slab), while another number N_R of atomic layers on top of them (including the surface of interest) can fully relax. The thickness of the vacuum region separating two consecutive slabs is set to 20 Å. The area of the surface unit cell calculated with the LDA, PBE, and HSE06 functionals is 40.6 Ų, 42.6 Ų, and 42.3 Ų, respectively. Calculations conducted with the PBE functional and an 11-layer-thick slab consisting of different N_R and N_F layers – keeping the lattice parameters of the supercell fixed – show that the total energy of the slab changes with the ratio N_F/N_R, decreasing with N_R. The most noticeable differences are between the here tested extreme values N_F/N_R = 1/10 and N_F/N_R = 8/3 (ΔE_slab = 104.5 meV). To determine the thickness of the slab sufficient to simulate the Pd₁-terminated model, surface energy differences and layer-resolved surface density of states (sDOS) calculations were compared for an 11-, a 20-, and a 29-layer-thick slab using the same conditions as described above, but (i) keeping constant the number of fixed layers lying at the bottom (N_F = 4) or (ii) keeping constant the number of atomic layers that can fully relax (N_R = 7), all slabs having identical bottom termination. Thus, the here calculated surface energy differences contain only contributions from the surface of interest (top), since the surface energy of the “frozen” bottom termination is the same for all slabs and cancels out when calculating surface energy differences. The calculations show differences smaller than 1 meV Å⁻² (4 meV Å⁻²) for the surface energy difference between the 20-(11-) and 29-(20-)layer-thick slabs. Furthermore, only negligible changes of the calculated sDOS with the slab thickness were found, all slabs reaching bulk-like behavior in the central layers. Therefore, the 11-layer-thick slab with N_F = 4 at the bottom and N_R = 7 at the top (including the surface of interest) is used in all surface calculations.

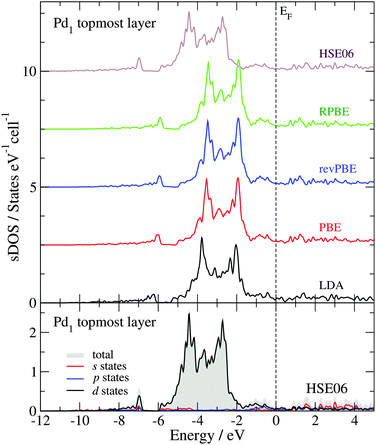
Fig. 4 shows the sDOS of the Pd₁ topmost layer of the clean surface model calculated with different functionals. As for the bulk calculations, the differences between the sDOS calculated with the PBE, revPBE and RPBE functionals, at the geometry optimized with the PBE functional, are negligible (smaller than 0.04 eV for O_C, O_L, P_d and W_d). However, the PW-LDA calculation at the geometry optimized with the PBE functional presents a small shift (0.3 eV) towards lower energies of the opening of the sDOS and the Pd 4d band, in comparison to the PBE results. More significantly, the PBE sDOS shows a shift to higher energies (|ΔO_C| ≈ |ΔP_d| = 0.9 eV) and a reduction of the Pd 4d bandwidth (|ΔW_d| ≈ 1.0 eV), when compared to the HSE06 sDOS, in line with the bulk calculations. The bottom panel in Fig. 4 presents the partial contributions to the total HSE06 sDOS (valence region) of the Pd₁ topmost layer. As expected from a Pd-terminated surface, the analysis shows that its main structure – between −6 and −1.7 eV – is primarily dominated by the Pd 4d states. The total area below the sDOS in this energy window is 4.46 states per cell, where 95% of it corresponds to Pd 4d states. The area under the sDOS between −7 and −6.8 eV is 0.12 states per cell and is also dominated by Pd 4d states, but to a lesser extent (69% Pd d states, 12.5% Pd p states and 18.5% Pd s states). Between −11.6 and −8.4 eV, the number of states in the sDOS is negligible.

Fig. 4 Surface density of states (sDOS) of the topmost atomic layer Pd₁ of the Pd₁-terminated surface model, obtained with different functionals (top panel). The partial contributions to the total sDOS calculated with the HSE06 functional are shown in the bottom panel. The zero of the energy scale is set to the Fermi level (E_F).

Fig. 5 shows the HSE06 sDOS convoluted with a Gaussian function^66–68 (Δε = 0.25 eV) and compared to the He II ultraviolet photoelectron spectra (UPS) of the GaPd(1̄1̄1̄) clean surface recorded at room temperature of the sample prepared at 870 K.⁴ To estimate the contribution of the sub-surface atomic layers, the convoluted surface DOS is calculated considering (a) only the topmost atomic layer Pd₁, (b) both surface and subsurface atomic layers Pd₁ and Ga₃, and (c) the three topmost atomic layers Pd₁, Ga₃ and Pd₃ (emphasized by colored areas in Fig. 5). Moving towards lower energies, the structure of the convoluted sDOS presents two small peaks at 0.2 eV (P₁) and −0.7 eV (P₂), the two main peaks of the Pd 4d band at −3.0 eV (P₃) and −4.3 eV (P₄), and a shoulder-like peak at −5.6 eV (P₅). After an opening at −6.3 eV, a peak at −7.0 eV (P₆) appears together with two subsequent shoulder-like peaks. As can be seen in Fig. 5, there is an excellent agreement between the convoluted HSE06 sDOS and the experimental data.

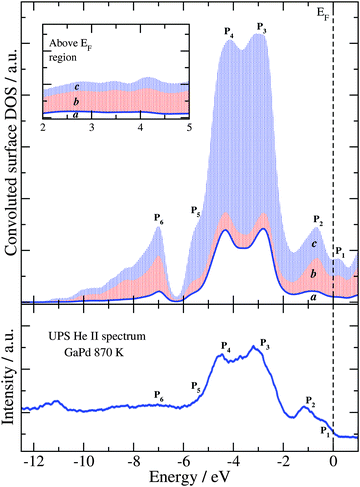Fig. 5 Convoluted sDOS obtained with the HSE06 functional (top panel) and experimental He II UPS spectra of the clean GaPd(1̄1̄1̄) surface (bottom panel).⁴ In the top panel, the blue curve (the envelope of the white area denoted “a”) is the convoluted DOS due to only the top-most layer of the slab. The envelope of the red patterned area (area b) is due to the top and the subsurface layers, while the envelope of the blue patterned area (area c) is due to the three top-most layers of the slab. The inset shows the same three sDOS in the region above the Fermi level (E_F).

V. CO adsorption on the Pd₁-terminated GaPd(1̄1̄1̄) surface

Based on the results and discussion presented above, the CO adsorption on the Pd₁-terminated model of the GaPd(1̄1̄1̄) surface was thoroughly studied applying different functionals. Several starting geometries of the molecule were considered taking into account the atomic structure of the three topmost layers of the Pd₁-terminated surface model. The CO molecule was allowed to fully relax starting from different positions, 3 Å above the initial adsorption site. The initial C–O bond length was set to the calculated value for CO in gas phase (see Table 4). Fifteen crystallographically unique possible adsorption sites can be identified. Fig. 6 summarizes the initial adsorption sites considered in this study: top (T), bridge (B), and hollow (H) sites. In the T_i sites (i = 1 to 3), the CO molecule is initially adsorbed atop one Ga or one Pd atom of the substrate. In the case of B_j sites (j = 1 to 7), the CO molecule initially forms a bridge between two atoms of the substrate, while in the case of H_k sites (k = 1 to 5) the CO molecule is initially located between three substrate atoms.

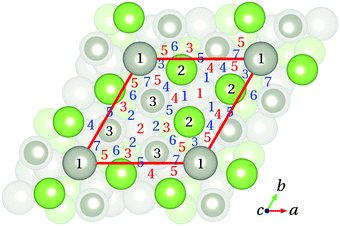Fig. 6 Top view of the Pd₁-terminated model with the initial adsorption sites considered in this study. Top, bridge, and hollow sites are indicated by black (1 to 3), blue (1 to 7) and red (1 to 5) numbers, respectively. Color code is as in Fig. 1 and 3.

Total adsorption energies E_ads(α_β) for the different adsorption sites α_β were calculated using

E_ads(α_β) = E_slab + E_CO − E_slab+CO(α_β), (1)

where E_slab+CO(α_β) is the total energy of the substrate–adsorbate system, i.e., slab plus the CO molecule adsorbed at the site α_β, fully relaxed (α = T, B, H and β = i, j, k, respectively), E_slab is the total energy of the slab before CO adsorption (clean surface), and E_CO is the total energy of the CO molecule in the gas phase.

In calculations based on the HSE06 functional, the most favoured adsorption site is T₁ with CO adsorption energy of 1.07 eV (103.24 kJ mol⁻¹). In this site, the CO molecule relaxes perpendicular to the surface with the C atom pointing towards the topmost Pd atom of the substrate (d(C–Pd₁) = 1.98 Å, see Table 4). When the CO molecule is initially above the sites B₃, B₆, B₇, and H₅ it also relaxes to a position above T₁. In the case of the starting position above T₂, the CO molecule desorbs upon relaxation. Similarly, the CO molecules initially above the hollow sites H₂ and H₃ desorb. On the other hand, the CO molecule initially above T₃ moves towards the hollow site H₁, relaxing perpendicular to the surface, with the C atom pointing towards the substrate (d(C–Ga₃) = 2.88 Å, see Table 4). This is also the case for the CO molecule initially relaxed from above the bridge sites B₁, B₂, B₄, B₅, and hollow sites H₁ and H₄. The site H₁ is composed of a triangle of Ga atoms with a central Pd atom at 2.04 Å below them. In spite of the presence of the accessible Pd atom, the surface Ga atoms make this site unfavourable (E_ads = 0.05 eV = 4.82 kJ mol⁻¹) for the adsorption of the CO molecule.

Summarizing, the HSE06 functional predicts that the CO molecule preferentially adsorbs only at the site T₁, perpendicular to the substrate, with the C atom pointing towards the topmost Pd atom. Furthermore, no CO–Ga interaction is observed. These results are in perfect agreement with the experimental results obtained with the Fourier transform infrared spectroscopy (FTIRS) and the reflection–absorption infrared spectroscopy (RAIRS).^{1,4,7,56–59} The CO adsorption on the GaPd(1̄1̄1̄) surface at room temperature (50 mbar dosage) resulted in the appearance of only one band that was assigned to CO adsorbed on Pd in the on-top position.^{1,4,7,56–59} Moreover, the smaller adsorption energy for CO at the site T₁ of the Pd₁-terminated model of the GaPd(1̄1̄1̄) surface in comparison to CO adsorption on the Pd(111) surface (1.8 eV),⁶⁹ is also in line with the thermal desorption spectroscopy (TDS) results, where the CO desorption from the Pd(111) surface needs a higher energy (desorption at 450 K) than from the GaPd(1̄1̄1̄) surface (desorption at 215 K).⁴ In order to correlate the experimentally obtained desorption temperatures⁴ with the computed adsorption energies, an estimation of the activation energies of desorption E_d is given in Table 3. Considering the results and conditions of the TDS experiments for CO desorption on the GaPd(1̄1̄1̄) and the Pd(111) surfaces given by Rosenthal et al.⁴ and the equation of Redhead for thermal desorption:⁷⁰

E_d ≈ R·T_P [ln(ν₁·T_P/β_H) − 3.64], (2)

where R is the gas constant, ν₁ is the frequency factor for desorption, T_P is the temperature at which the desorption rate is maximum and β_H is the heating rate, a reasonable estimation of E_d is obtained. We have used ν₁ = 1 × 10¹³ s⁻¹, which is a typical value for the estimation of E_d (with ν₁ = 1 × 10¹² s⁻¹ and ν₁ = 1 × 10¹⁴ s⁻¹, the results are essentially the same). In agreement with the computed CO adsorption energy difference (0.7 eV), the estimated difference between the activation energy of desorption of CO on GaPd(1̄1̄1̄) and on Pd(111) is 0.6 eV, signifying a stronger interaction between CO and the surface for Pd(111) than for GaPd(1̄1̄1̄). The here obtained HSE06 CO adsorption energies for the sites T₁ and H₁ are somewhat smaller than previous values obtained with semi-local exchange–correlation functionals. Adsorption energies of 1.19 eV (PW91-GGA),⁶ 1.37 eV (PBE-GGA),⁷ and 1.59 eV (RPBE-GGA)⁸ have been calculated for the T₁ site, and of 0.69 eV (PW91-GGA),⁶ 0.56 eV (PBE-GGA),⁷ and 0.49 eV (RPBE-GGA)⁸ for the H₁ site. All the previous calculations were performed at the GGA level of theory using the pseudopotential plane-wave method,^6,8 and a mixed Gaussian and plane-wave approach.⁷

Table 3 Activation energies of desorption E_d and TDS experimental data from Rosenthal et al.⁴

Surface	T P [K]	β H [K s^−1]	ν 1 [s^−1]	E d [eV]
Pd(111)	450	1.4	1 × 10^13	1.2
GaPd(1̄1̄1̄)	215	1.5	1 × 10^13	0.6

---

(a) Influence of the exchange–correlation functional on adsorption energies and atomic relaxations

To gain further insight into the influence of the exchange–correlation functional on the description of CO adsorption on the GaPd(1̄1̄1̄) surface, LDA- and GGA-based adsorption energies were calculated for CO above the sites T₁ and H₁. In both cases, the CO molecule was allowed to fully relax starting from the final geometries obtained with the HSE06 functional. Table 4 presents the C–O bond length and the interlayer distances of the topmost layers of the Pd₁ surface model before (clean surface, CO in gas phase) and upon CO adsorption on T₁ and H₁, as well as the respective adsorption energies, obtained with LDA, GGA, and hybrid functionals. The adsorption energies E_ads* are calculated at the HSE06 slab geometry, while the adsorption energies E_ads are calculated using slabs built with the lattice parameter optimized with each functional (see Table 1). For the here tested LDA and GGA functionals, the differences between E_ads and E_ads* are smaller than 0.02 eV for CO adsorption on T₁, while they can account for differences up to 0.08 eV (LDA) for CO adsorption on H₁. The results obtained with the HSE06 functional show that, the main effect of the atomic relaxation of the clean surface is the inward relaxation of the topmost Pd atom (0.18 Å), while lower lying atomic planes exhibit much smaller relaxations (<0.04 Å). Upon adsorption of CO on top of a Pd atom (site T₁), the latter relaxes outward again, and the surface interlayer distances become almost the same as the ones from the initial bulk positions (the differences are smaller than 0.02 Å). This indicates a strong interaction between the CO molecule and the topmost Pd atom. On the other hand, when CO relaxes above the site H₁, the interlayer distances relax back to the values calculated for the clean surface (before CO adsorption), as if the CO molecule and the surface acted as two independent systems, corroborating the findings discussed above. Similar to the HSE06 results, the LDA and GGA calculations show an inward relaxation of the topmost Pd atom as main effect of the atomic relaxations on the clean surface. However, deviations in the interlayer distances up to 0.08 Å for LDA and 0.04 Å for the GGA functionals are obtained, when compared to the HSE06 results. After CO adsorption above the site T₁, all tested functionals predict that the CO molecule adsorbs on top of the Pd atom, with the molecule perpendicular to the surface and the C atom pointing towards the surface. The LDA functional predicts a much stronger CO–surface interaction than the GGA and hybrid functionals. Furthermore, while the C–Pd₁ distance d(C–Pd₁) calculated with the different GGA functionals is closer to the HSE06 value than the one obtained with the LDA functional, the latter predicts a C–O bond length d_C–O in better agreement with the HSE06 result. The obtained differences are more pronounced in the case of CO adsorption above H₁. Although for all tested functionals the CO molecule relaxed towards the center of the three Ga atoms of the Ga₃ layer (CO perpendicular to the surface, with the C atom pointing towards the surface), the C–Ga₃ distance changes significantly as function of the exchange–correlation functional. Here, the obtained LDA and PBE final geometries indicate that the CO molecule adsorbs on the site H₁ (d(C–Ga₃)^LDA = 1.55 Å, d(C–Ga₃)^PBE = 1.68 Å), i.e. CO does interact with the surface at the site H₁. However, the adsorption energies E_ads calculated with these two functionals present a difference of 0.55 eV. On the other hand, both the final geometry and the adsorption energy obtained with the revPBE and RPBE functionals indicate that the CO molecule desorbs (in both cases E_ads ≈ 0 eV and d(C–Ga₃) = 3.49 Å), i.e. does not interact with the surface at the site H₁. In line with the “CO-adsorption puzzle”,^11,14,15 the obtained results show significant differences between the LDA, GGA and hybrid functionals. Even though the difference in the adsorption energies for the sites T₁ and H₁ is similar for all tested functionals (≈1 eV), total adsorption energies change significantly with the choice of the functional.

Table 4 Interlayer distances (d(i–j)), C–O bond length (d_C–O) and adsorption energies (E_ads, E_ads*) of CO adsorption on the sites T₁ and H₁, calculated with LDA, GGA and hybrid functionals

Distances [Å]	Clean surface & CO in gas phase					CO above T1					CO above H1
	LDA	PBE	revPBE	RPBE	HSE06	LDA	PBE	revPBE	RPBE	HSE06	LDA	PBE	revPBE	RPBE	HSE06
d C–O	1.13	1.14	1.15	1.15	1.13	1.14	1.15	1.16	1.16	1.13	1.16	1.17	1.14	1.15	1.13
d(C–Pd1)	—	—	—	—	—	1.92	1.96	1.97	1.98	1.98	1.08	1.17	2.94	2.94	2.29
d(Pd1–Ga3)	0.57	0.56	0.56	0.56	0.59	0.75	0.75	0.76	0.76	0.76	0.47	0.50	0.55	0.55	0.59
d(Ga3–Pd3)	0.79	0.88	0.90	0.91	0.87	0.77	0.87	0.90	0.91	0.85	0.90	0.97	0.92	0.93	0.87
d(Pd3–Ga1)	1.00	1.00	1.00	1.01	0.98	0.93	0.93	0.93	0.94	0.92	0.98	0.98	1.00	1.01	0.98
E ads [eV]	—	—	—	—	—	1.74	1.17	0.96	0.93	1.07	0.79	0.24	0.01	0.02	0.05
E ads* [eV]	—	—	—	—	—	1.72	1.18	0.97	0.94	1.07	0.71	0.25	−0.05	0.02	0.05

---

(b) Vibrational frequencies

The calculated C–O stretching frequency is 2247 cm⁻¹ for the free molecule and 2180 cm⁻¹ for the CO molecule adsorbed at the T₁ site, applying the HSE06 functional. The corresponding experimental values are 2143 and 2078 cm⁻¹, respectively.^7,56,58 Thus, the experimentally obtained change in the vibrational frequency of CO upon adsorption (65 cm⁻¹) is in an excellent agreement with the HSE06 calculations (67 cm⁻¹). On the other hand, the calculated C–O stretching frequency is 2137 cm⁻¹ for the free molecule and 1989 (2032) cm⁻¹ for the CO molecule adsorbed at the T₁ site, applying the RPBE (PBE) functional.^7,8 The calculated red shift with the RPBE functional is 148 cm⁻¹, much larger than the experimental value (65 cm⁻¹). Furthermore, the calculated C–O stretching vibration frequency for CO above H₁ is 2241 cm⁻¹, applying the HSE06 functional. Thus, the vibrational frequency difference between the C–O stretching mode of the free molecule and the CO molecule above H₁ is only 6 cm⁻¹, consistent with the nearly-unbounded behavior of the CO molecule above the site H₁ predicted by the HSE06 functional.

(c) Electronic structure of the adsorbate–substrate system

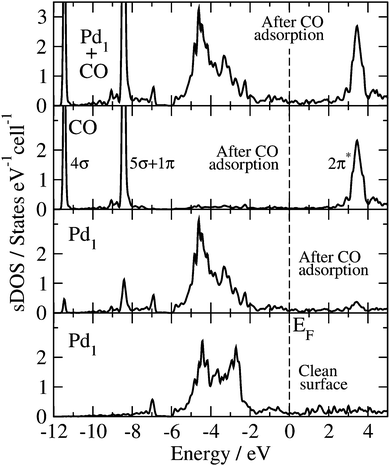
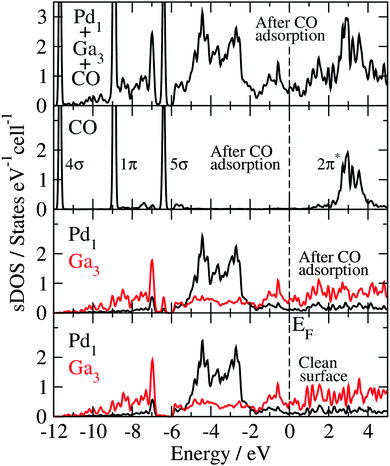
The Blyholder model is generally applied to describe CO adsorption on surfaces containing transition metal (TM) elements.^71–81 According to this model, there is (i) a CO-5σ interaction with the empty TM states of the surface (molecule-to-surface transfer of electrons), that is compensated by (ii) a π-bonding interaction of the filled TM states of the surface with the CO-2π* antibonding states (surface-to-molecule back-donation). The analysis and discussion of the electronic structure of the CO molecule adsorbed at the GaPd(1̄1̄1̄) surface calculated with the HSE06 functional, in the light of the Blyholder model, is given below.

CO–surface interaction on site T₁. The adsorbate–substrate bonding is captured by the emerging features of the sDOS, mainly found in the topmost atomic layer Pd₁, as shown in Fig. 7. Particularly, the sDOS of the clean surface is non-uniformly suppressed between −6 and −1.7 eV, and new structures (peaks), located at −11.5, −8.4 and 3.4 eV, are found upon CO adsorption. These new peaks are also present in the partial sDOS of the adsorbed CO molecule. In agreement with experimental photoemission findings, the peaks at −11.5 and −8.4 eV can be attributed to the interaction of the surface with the 4σ and 5σ + 1π (overlapped) states of the adsorbed CO molecule, respectively.^72–75 On the other hand, the peak at 3.4 eV above the Fermi level can be interpreted as an indication of the surface/CO-2π* interaction.^75,76,78 The integration analysis of the partial contributions to the total sDOS of the Pd₁ topmost layer after CO adsorption shows that the area under the Pd 4d band (between −6 and −1.7 eV) corresponds to 4.25 states per cell, which is 0.21 states per cell less than before adsorption. On the other hand, the areas under the sDOS at energy intervals where the peaks due to the surface/CO-4σ and surface/CO-(5σ + 1π) interactions occur (that were empty before adsorption) correspond to 0.05 states per cell (composed of 73% Pd d states, 8.8% Pd p states and 18.2% Pd s states) and 0.15 states per cell (composed of 80.5% Pd d states, 15.7% Pd p states and 3.8% Pd s states), respectively. Thus, considering that the development of these two peaks comes at the expense of the observed Pd 4d band depletion, the obtained results suggest that a Pd–C σ-bond is created upon CO adsorption, in agreement with the Blyholder mechanism. However, differences with this model are also found. Besides the participation of Pd s and p states to the Pd–C σ-bond as shown above, the C–O bond length d_C–O is almost not affected after the molecule adsorbs on T₁ (differences smaller than 0.01 Å, see Table 4), in line with the small red shift of the CO stretching vibrational frequency upon adsorption (67 cm⁻¹). Thus, the C–O bond is only weakly affected by the adsorption, revealing a rather different (weaker) σ-bonding interaction than the expected from the Blyholder model, as corroborated by thermal desorption and vibrational spectroscopy.^4,7 Additional confirmation of this behavior is obtained when analyzing the possible Blyholder back-donation process. Upon adsorption, the peak assigned to the surface/CO-2π* interaction is mostly dominated by Pd d states (composed of 78.8% Pd d states, 13.9% Pd p states, and 7.3% Pd s states). Previously, the sDOS of the clean surface was dominated by Pd s states (56.3% of the total area), with the total area below the sDOS in this region (between 2.7 and 3.9 eV) being almost the same before and after CO adsorption (0.25 states per cell). However, this somewhat broad peak is shifted well above the Fermi level, i.e., it is empty. This means that in this case the weakening of the C–O bond^11–15,71 does not occur through the back-donation process, because the latter does not take place. The small red shift of the CO stretching vibrational frequency upon adsorption must then be explained through another mechanism, such as, e.g., charge attraction/repulsion between the positively charged C atom and the negatively charged Pd and O atoms.

Fig. 7 Layer-resolved sDOS of the Pd₁ model before and after CO adsorption on T₁. The zero of the energy scale is set to the Fermi level (E_F).

CO–surface interaction on site H₁. Fig. 8 presents the layer-resolved sDOS of the Pd₁ model before and after CO adsorption on H₁. Contrary to the observations of CO adsorption on T₁, in this case the bonding interaction between the molecule and the topmost atomic layers is almost non-existent, confirming the free-molecule-like behaviour of CO above H₁. Here, only one peak around −6.4 eV makes the difference between the sDOS calculated before (clean surface) and after CO adsorption above H₁. The partial CO-contribution to the total sDOS of the adsorbate–substrate system clearly shows that its electronic states exhibit the structure as in the gas phase with the 4σ, 1π, 5σ and 2π* states at −11.7, −8.9, −6.4 and 3.0 eV, respectively.

Fig. 8 Layer-resolved sDOS of the Pd₁ model before and after CO adsorption on H₁. The zero of the energy scale is set to the Fermi level (E_F).

(d) Chemical bonding analysis of the adsorbate–substrate system

Topological analysis of the electron density according to Bader's quantum theory of atoms in molecules (QTAIM)⁸² is used in combination with the electron localizability indicator (ELI-D)^44–46 to characterize the CO–GaPd(1̄1̄1̄) system. The ELI-D is an efficient quantum chemical tool for the analysis of chemical bonding in real space, particularly, in the understanding of the properties of intermetallic compounds and the modeling of the adsorption of atoms and molecules where both covalent and ionic interactions may occur.⁸³

The three known ELI-D basins for the free CO molecule in the valence region⁸³ are retrieved in the surface–adsorbate system: two representing lone pairs – one located at the oxygen atom (4.0 electrons in the free molecule) and one located at the carbon atom (2.5 electrons) – and one basin accounting for the C≡O triple bond with an electron count of 3.3 electrons. Upon adsorption of CO on the site T₁, 0.2 electrons are transferred from the C≡O bonding basin to the oxygen lone pair and the lone-pair at the carbon atom turns into a two-center C–Pd bond with an electron count of 2.8. Here, carbon contributes 2.4 electrons, while 0.4 electrons are coming from the palladium atom. In agreement with the analysis of the electronic structure given above, the formation of a C–Pd σ-bond is also confirmed by the ELI analysis, as proposed in the Blyholder model. In the same line, the back donation of electrons from the metal into the empty C–O antibonding 2π* states does not take place (see Fig. 7). Instead, the negatively charged palladium atom leads to a shift of the electron density to the oxygen lone pair, thus weakening the C–O bond. In this context, the clean GaPd(1̄1̄1̄) surface resembles a charged egg carton, where the “dimples” correspond to the unshielded negatively charged Pd centers, while the positively charged Ga species – shielded by partially dangling bonds – form the “spacers”. Due to the very stable, closed-shell nature of carbon monoxide, strong Pauli repulsion occurs when the CO molecule approaches a dangling bond. Since the dangling bonds shield most of the surface, only two potential adsorption sites out of 15 crystallographically possible (see Fig. 6) are left for the CO molecule: on-top of the Pd₁ atom (T₁ site) and the hollow site at the center of the triangle formed by the Ga₃ atoms (H₁ site). In addition, the orientation of the CO molecule (carbon oriented to palladium) fits the expectations from the charged egg carton model, resulting from the attractive Coulomb interactions of the positively charged C atom (+1.2) and the negative charge on the palladium (−0.4) according to the QTAIM analysis.

In agreement with the much smaller calculated adsorption energy for the H₁ site, no significant chemical interactions between the substrate and the CO molecule are found by ELI-D analysis upon CO adsorption.

VI. Conclusions

The CO adsorption on the (1̄1̄1̄) surface of the intermetallic compound GaPd has been examined using a quantum-chemical all-electron full-potential approach. Comparison of the GaPd bulk, clean surface, and CO adsorption obtained with LDA-, GGA-, and hybrid Hartree–Fock/GGA-based functionals was considered. The choice of the functional was found to have a decisive influence on the bulk and surface electronic structure of GaPd. In particular, bulk calculations using the different functionals lead to differences in the optimized lattice parameter resulting in different bulk electronic structure. Despite the fact that all the here tested methods find the Pd on-top site as the most preferred one for CO adsorption on the GaPd(1̄1̄1̄) surface when compared to the H₁ site, the obtained results demonstrate that classic LDA and GGA functionals cannot retrieve a correct description of the energies of the substrate–adsorbate electronic states, leading to the wrong description of the CO adsorption on a surface containing Pd atoms, including important differences in adsorption energies and surface–adsorbate interaction as reflected in the calculated vibrational frequencies. On the other hand, experimental findings and the results obtained with the hybrid functional HSE06 are in excellent agreement. This holds for the predicted adsorption sites, adsorption energies, as well as vibrational frequencies. This study thus reveals the computational level necessary to derive reliable predictions from DFT calculations regarding the chemical properties of intermetallic surfaces.

Acknowledgements

We thank A. Ormeci for valuable discussions.

References

1. K. Kovnir, M. Armbrüster, D. Teschner, T. V. Venkov, F. C. Jentoft, A. Knop-Gericke, Yu. Grin and R. Schlögl, Sci. Technol. Adv. Mater., 2007, 8, 420–427.
2. J. Osswald, R. Giedigkeit, R. E. Jentoft, M. Armbrüster, F. Girgsdies, K. Kovnir, T. Ressler, Yu. Grin and R. Schlögl, J. Catal., 2008, 258, 210–218.
3. J. Osswald, K. Kovnir, M. Armbrüster, R. Giedigkeit, R. E. Jentoft, U. Wild, Yu. Grin and R. Schlögl, J. Catal., 2008, 258, 219–227.
4. D. Rosenthal, R. Widmer, R. Wagner, P. Gille, M. Armbrüster, Yu. Grin, R. Schlögl and O. Gröning, Langmuir, 2012, 28, 6848–6856.
5. J. Prinz, R. Gaspari, C. A. Pignedoli, J. Vogt, P. Gille, M. Armbrüster, H. Brune, O. Gröning, D. Passerone and R. Widmer, Angew. Chem., Int. Ed., 2012, 51, 9339–9343.
6. M. Krajčí and J. Hafner, J. Chem. Phys., 2013, 138, 124703.
7. J. Prinz, R. Gaspari, Q. S. Stöck, P. Gille, M. Armbrüster, H. Brune, O. Gröning, C. A. Pignedoli, D. Passerone and R. Widmer, J. Phys. Chem. C, 2014, 118, 12260–12265.
8. P. Bechthold, J. S. Ardhengi, A. Juan, E. A. González and P. V. Jasen, Appl. Surf. Sci., 2014, 315, 467–474.
9. J. Prinz, C. A. Pignedoli, Q. S. Stöckl, M. Armbrüster, H. Brune, O. Gröning, R. Widmer and D. Passerone, J. Am. Chem. Soc., 2014, 136, 11792–11798.
10. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
11. P. J. Feibelman, B. Hammer, J. K. Nørskov, F. Wagner, M. Scheffler, R. Stumpf, R. Watwe and J. Dumesic, J. Phys. Chem. B, 2001, 105, 4018–4025.
12. A. Gil, A. Clotet, J. M. Ricart, G. Kresse, M. García-Hernández, N. Rösch and P. Sautet, Surf. Sci., 2003, 530, 71–87.
13. M. Gajdoš, A. Eichler and J. Hafner, J. Phys.: Condens. Matter, 2004, 16, 1141–1164.
14. X. Ren, P. Rinke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045402.
15. L. Schimka, J. Harl, A. Stroppa, A. Grüneis, M. Marsman, F. Mittendorfer and G. Kresse, Nat. Mater., 2010, 9, 741–744.
16. W. Kohn, Rev. Mod. Phys., 1999, 71, 1253–1266.
17. P. Atkins, Molecular Quantum Mechanics, Oxford University Press, Oxford, 1996; R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules (International Series of Monographs on Chemistry), Oxford University Press, Oxford, 1989.
18. P. Hohenberg and W. Kohn, Phys. Rev. B: Condens. Matter Mater. Phys., 1964, 136, 864–871.
19. W. Kohn and L. J. Sham, Phys. Rev. A: At., Mol., Opt. Phys., 1965, 137, 1697–1705.
20. A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320.
21. M. Grüning, O. V. Gritsenko, S. J. A. Van Gisbergen and E. J. Baerends, J. Phys. Chem. A, 2001, 105, 9211–9218.
22. B. Santra, A. Michaelides, M. Fuchs, Al. Tkatchenko, C. Filippi and M. Scheffler, J. Chem. Phys., 2008, 129, 194111.
23. C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816.
24. K. Yang, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2010, 132, 164117.
25. A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792–794.
26. J. P. Perdew, MRS Bull., 2013, 38, 743–750.
27. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
28. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
29. G. Kresse, A. Gil and P. Sautet, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 073401.
30. S. E. Mason, I. Grinberg and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 161401(R).
31. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
32. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
33. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215; J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906; A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
34. T. Auckenthaler, V. Blum, H.-J. Bungartz, T. Huckle, R. Johanni, L. Krämer, B. Lang, H. Lederer and P. R. Willems, Parallel Comput., 2011, 37, 783–794.
35. V. Havu, V. Blum, P. Havu and M. Scheffler, J. Comput. Phys., 2009, 228, 8367–8379.
36. E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792.
37. R. Winkler, Spin-Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems, Springer-Verlag, New York, Berlin, Heildelberg, 2003.
38. W. K. Press, S. A. Teukolsky, W. T. Vetterlin and B. T. Flannery, Numerical Recipes, Cambridge University Press, Cambridge, 2007.
39. J. Nocedal and S. J. Wright, Numerical optimization, Springer-Verlag, New York, Berlin, Heildelberg, 2006.
40. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
41. V. G. Ruiz, W. Liu and A. Tkatchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035118.
42. V. G. Ruiz, W. Liu, E. Zojer, M. Scheffler and A. Tkatchenko, Phys. Rev. Lett., 2012, 108, 146103.
43. G.-X. Zhang, A. Tkatchenko, J. Paier, H. Appel and M. Scheffler, Phys. Rev. Lett., 2011, 107, 245501.
44. M. Kohout, Int. J. Quantum Chem., 2004, 97, 651.
45. M. Kohout, Faraday Discuss., 2007, 135, 43.
46. F. R. Wagner, V. Bezugly, M. Kohout and Yu. Grin, Chem. – Eur. J., 2007, 13, 5724.
47. M. Kohout, Program DGRID, version, 4.6, Radebeul, Germany, 2011. http://www.cpfs.mpg.de/˜kohout/dgrid.html.
48. M. Armbrüster, H. Borrmann, M. Wedel, Y. Prots, R. Giedigkeit and P. Gille, Z. Kristallogr. - New Cryst. Struct., 2010, 225, 617–618.
49. J. L. F. Da Silva, C. Stampfl and M. Scheffler, Surf. Sci., 2006, 600, 703–715.
50. S. Müller, J. Phys.: Condens. Matter, 2003, 15, R1429.
51. B. D. Sharma and J. A. Donohue, Z. Kristallogr., 1962, 117, 293–300.
52. X. F. Li, G. T. Fei, X. M. Chen, Y. Zhang, K. Zheng, X. L. Liu and L. D. Zhang, EPL, 2011, 94, 16001.
53. C. N. Rao and K. K. Rao, Can. J. Phys., 1964, 42, 1336–1342.
54. P. Gille, T. Ziemer, M. Schmidt, K. Kovnir, U. Burkhardt and M. Armbrüster, Intermetallics, 2010, 18, 1663–1668.
55. S. V. Meschel and O. J. Kleppa, Thermochim. Acta, 1997, 292, 13–17.
56. M. Armbrüster, R. Schlögl and Yu. Grin, Sci. Technol. Adv. Mater., 2014, 15, 034803.
57. Yu. Grin, M. Armbrüster, A. I. Baranov, K. Finzel, M. Kohout, A. Ormeci, H. Rosner and F. R. Wagner, Mol. Phys., 2016, 114, 1250–1259.
58. K. Kovnir, M. Armbrüster, D. Teschner, T. V. Venkov, L. Szentmiklósi, F. C. Jentoft, A. Knop-Gericke, Yu. Grin and R. Schlögl, Surf. Sci., 2009, 603, 1784–1792.
59. M. Armbrüster, K. Kovnir, M. Behrens, D. Teschner, Yu. Grin and R. Schlögl, J. Am. Chem. Soc., 2010, 132, 14745–14747.
60. J. Jaramillo, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 1068–1073.
61. J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 124, 154709.
62. A. Stroppa, K. Termentzidis, J. Paier, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 195440.
63. A. Stroppa and G. Kresse, New J. Phys., 2008, 10, 063020.
64. K. Doll, Surf. Sci., 2004, 573, 464–473.
65. M. Neef and K. Doll, Surf. Sci., 2006, 600, 1085–1092.
66. J. J. Markham, Rev. Mod. Phys., 1959, 31, 956–989.
67. M. Iwan and C. Kunz, Phys. Lett. A, 1977, 60, 345–347.
68. D. Ochs, W. Maus-Friedrichs, M. Brause, J. Günster, V. Kempter, V. Puchin, A. Schluger and L. Kantorovich, Surf. Sci., 1996, 365, 557–571.
69. N. M. Martin, M. Van den Bossche, H. Grönbeck, C. Hakanoglu, F. Zhang, T. Li, J. Gustafson, J. F. Weaver and E. Lundgren, J. Phys. Chem. C, 2014, 118, 1118–1128.
70. P. A. Redhead, Vacuum, 1962, 12, 203–211.
71. G. Blyholder, J. Phys. Chem., 1964, 68, 2772–2777.
72. H. Conrad, G. Ertl, J. Küppers and E. E. Latta, Faraday Discuss. Chem. Soc., 1974, 58, 116–124.
73. R. J. Behm, K. Christmann, M. A. Van Hove and G. Ertl, J. Chem. Phys., 1980, 73, 2984–2995.
74. E. Bertel, Appl. Phys. A: Mater. Sci. Process., 1991, 53, 356–368.
75. A. Sandell, O. Björneholm, J. N. Andersen, A. Nilsson, E. O. F. Zdansky, B. Hernnäs, U. O. Karlsson, R. Nyholm and N. Mårtensson, J. Phys.: Condens. Matter, 1994, 6, 10659.
76. T. Anazawa, I. Kinoshita and Y. Matsumoto, J. Electron. Spectrosc. Relat. Phenom., 1998, 88–91, 585–590.
77. G. Tsilimis, J. Kutzner and H. Zacharias, Appl. Phys. A: Mater. Sci. Process., 2003, 76, 743–749.
78. J. Rogozik, J. Küppers and V. Dose, Surf. Sci., 1985, 148, L653–L658.
79. B. Hammer, Y. Morikawa and J. K. Nørskov, Phys. Rev. Lett., 1996, 76, 2141–2144.
80. M. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, 18, C79.
81. J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 2939–2947.
82. R. F. W. Bader, Atoms in Molecules – A Quantum Theory, Clarendon Press and Oxford University Press, Oxford, New York, 1994.
83. Yu. Grin, A. Savin and B. Silvi, The ELF perspective of chemical bonding, The Chemical Bond: Chemical Bonding Across the Periodic Table, Wiley-VCH, 2014, pp. 1–53.

---