 Open Access Article
Open Access ArticleNMR absolute shielding scale and nuclear magnetic dipole moment of 207Pb
Bożena
Adrjan
a,
Włodzimierz
Makulski
a,
Karol
Jackowski
a,
Taye B.
Demissie
b,
Kenneth
Ruud
b,
Andrej
Antušek
c and
Michał
Jaszuński
*d
aLaboratory of NMR Spectroscopy, Department of Chemistry, University of Warsaw, Pasteura 1, 02-093 Warsaw, Poland
bCentre for Theoretical and Computational Chemistry, Department of Chemistry, UiT The Arctic University of Norway, N-9037 Tromsø, Norway
cATRI, Faculty of Materials Science and Technology in Trnava, Slovak University of Technology in Bratislava, Paulinska 16, 917 24 Trnava, Slovak Republic
dInstitute of Organic Chemistry, Polish Academy of Sciences, 01 224 Warszawa, Kasprzaka 44, Poland. E-mail: michal.jaszunski@icho.edu.pl
First published on 24th May 2016
Abstract
An absolute shielding scale is proposed for 207Pb nuclear magnetic resonance (NMR) spectroscopy. It is based on ab initio calculations performed on an isolated tetramethyllead Pb(CH3)4 molecule and the assignment of the experimental resonance frequency from the gas-phase NMR spectra of Pb(CH3)4, extrapolated to zero density of the buffer gas to obtain the result for an isolated molecule. The computed 207Pb shielding constant is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 ppm for the isolated molecule, leading to a shielding of 10799.7 ppm for liquid Pb(CH3)4 which is the accepted reference standard for 207Pb NMR spectra. The new experimental and theoretical data are used to determine μ(207Pb), the nuclear magnetic dipole moment of 207Pb, by applying the standard relationship between NMR frequencies, shielding constants and nuclear moments of two nuclei in the same external magnetic field. Using the gas-phase 207Pb and (reference) proton results and the theoretical value of the Pb shielding in Pb(CH3)4, we find μ(207Pb) = 0.59064 μN. The analysis of new experimental and theoretical data obtained for the Pb2+ ion in water solutions provides similar values of μ(207Pb), in the range of 0.59000–0.59131 μN.
790 ppm for the isolated molecule, leading to a shielding of 10799.7 ppm for liquid Pb(CH3)4 which is the accepted reference standard for 207Pb NMR spectra. The new experimental and theoretical data are used to determine μ(207Pb), the nuclear magnetic dipole moment of 207Pb, by applying the standard relationship between NMR frequencies, shielding constants and nuclear moments of two nuclei in the same external magnetic field. Using the gas-phase 207Pb and (reference) proton results and the theoretical value of the Pb shielding in Pb(CH3)4, we find μ(207Pb) = 0.59064 μN. The analysis of new experimental and theoretical data obtained for the Pb2+ ion in water solutions provides similar values of μ(207Pb), in the range of 0.59000–0.59131 μN.
1 Introduction
The 207Pb nucleus with nuclear spin number 1/2 is very well suited for applications in nuclear magnetic resonance (NMR) spectroscopy. Its NMR signal at the natural abundance (22.6%) is 11.9 times stronger than that obtained by the 13C NMR method.1 The range of 207Pb chemical shifts covers more than 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm, and liquid tetramethyllead, Pb(CH3)4, is recommended as the reference standard,2 while a small addition of benzene-d6 or toluene-d8 serves for the deuterium lock system.3,4 A limited number of chemicals containing lead atoms (mostly inorganic and organometallic compounds) makes 207Pb NMR spectroscopy less popular, but it is obviously a valuable analytical tool for laboratories involved in research on lead.
000 ppm, and liquid tetramethyllead, Pb(CH3)4, is recommended as the reference standard,2 while a small addition of benzene-d6 or toluene-d8 serves for the deuterium lock system.3,4 A limited number of chemicals containing lead atoms (mostly inorganic and organometallic compounds) makes 207Pb NMR spectroscopy less popular, but it is obviously a valuable analytical tool for laboratories involved in research on lead.
The nuclear magnetic dipole moment of the stable isotope of lead, 207Pb, is given in the standard reference tables5 as 0.592583(9) μN, extracted from experimental NMR data6 (we shall discuss systematically the maximum projection of the magnetic moment vector on the axis of the external field, determined in NMR, not the magnitude of the vector itself). The same value is given in the recent IUPAC recommendations.7 Another tabulated value, derived from the optical pumping experiment, is 0.58219(2) μN.8 However, both these reference values are more than 40 years old. Recently, the magnetic dipole moment of 207Pb was studied using different theories for the nuclear structure, the different approximations yielding results in the range of 0.437–0.638 μN9 and 0.582 μN.10
We have determined the nuclear magnetic moments of a large number of nuclei from NMR spectra, and shown that significant improvements in the accuracy compared to older data can be obtained by carefully taking chemical shielding effects into account.11 This requires the simultaneous experimental measurement of NMR resonance frequencies for the nucleus of interest and a reference nucleus (preferably in the same isolated molecule) in combination with quantum chemical calculations. Together, this allows the corresponding absolute shielding constants to be determined. In this work, we apply this approach to the determination of μ(207Pb) by investigating the properties of tetramethyllead, Pb(CH3)4, in the gas phase.
Following our approach, the magnetic dipole moment of a nucleus X may be determined from NMR data using the equation
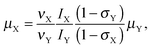 | (1) |
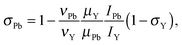 | (2) |
2 NMR experiment
2.1 Gaseous Pb(CH3)4
Tetramethyllead was studied by NMR, measuring the 207Pb, 13C and 1H resonance frequencies in the gas phase. A small amount of tetramethyllead (in each sample ≈0.02 mol L−1, p = 0.2 bar) was mixed with two gases, SF6 (99.8+% from Aldrich) and – in a separate series of measurements – with Xe (99.99% from Messer Griesheim). In different samples, the density of these gaseous solvents varied from 0.44 to 1.4 mol L−1, and the pressure was 11–34 bar.In general, for a binary mixture of gases A and B, a linear approximation for the virial expansion of νA(X), the frequency of the X nucleus in compound A, can be written as (see e.g.ref. 15)
| νA(X) = νA0(X) + νAA1(X)ρA + νAB1(X)ρB | (3) |
| νA(X) = νA0(X) + νAB1(X)ρB | (4) |
The experimental frequencies were linearly extrapolated using eqn (4) to the zero-density limit, allowing the 207Pb, 13C and 1H resonance frequencies for an isolated Pb(CH3)4 molecule to be determined (see Fig. 1 for the 207Pb results). NMR gas samples were prepared according to our standard method described in ref. 17. Liquid benzene-d6 (Aldrich, 99.6% D) was applied as the solvent for the deuterium lock system and the secondary reference standard of 1H and 13C shielding (νD = 76.8464017 MHz and σD = 26.441 ppm14). All the NMR measurements of resonance frequencies were carried out on a Varian-INOVA-500 spectrometer with a switchable probehead (50–500 MHz Varian) at 300 K. The temperature inside the NMR tubes was controlled with pure liquid methanol. The 1H and 207Pb measurements were performed using standard parameters. The decoupled INEPT sequence, optimized for the 1J(13C,1H) = 135.0 Hz constant and proton relaxation times, was applied to increase the strength of the 13C signals. The absolute experimental 1H and 13C shielding constants were obtained following the approach described in ref. 14. The final results, obtained using Xe and SF6, as well as the averaged values which we use in the following, are collected in Table 1.
| Nucleus | Perturber | ν 0/MHz | σ 0/ppm |
|---|---|---|---|
| a For 80% Pb(CH3)4 in toluene ν = 104.729551 MHz. | |||
| 1H | Xe | 500.6062980(3) | 30.075 |
| SF6 | 500.6062972(4) | 30.076 | |
| Average | 500.6062976(4) | 30.075(2) | |
| 13C | Xe | 125.8761536(15) | 194.09 |
| SF6 | 125.8761563(18) | 194.07 | |
| Average | 125.876155(2) | 194.08(2) | |
| 207Pb | Xe | 104.7305736(60) | |
| SF6 | 104.7305642(75) | ||
| Average | 104.730569(8)a | ||
2.2 Pb2+ ions in water solutions
Aqueous solutions of lead(II) perchlorate (Pb(ClO4)2, Sigma-Aldrich, 98%) and lead(II) nitrate (Pb(NO3)2, POCH, 99%) were prepared using double-distilled water (conductivity <0.056 mS cm−1) on the same days as the NMR measurements were carried out. The solutions (conc. 0.02–1.5 M) in 4 mm o.d. glass tubes (Wilmad, 406PP) were placed in standard 5 mm o.d. NMR tubes (Wilmad, 528PP) with benzene-d6 in the annular space for a deuterium lock system. 207Pb NMR spectra were recorded at 298 K using a Bruker AVANCE III HD 500 MHz spectrometer with the 5 mm CPPBBO BB probehead. The observed 207Pb frequency of the Bruker spectrometer was carefully verified with the use of gaseous and reference samples; we obtained a difference of −0.0847151 MHz relative to our Varian spectrometer. This correction was added to all the experimental points for both aqueous solutions, Pb(ClO4)2 and Pb(NO3)2.The reference nucleus for the evaluation of the Pb magnetic moment in this Pb2+ experiment is the deuteron in liquid C6D6, the deuteron magnetic moment is 0.8574382308 μN18.
As shown in Fig. 2, in each solution the Pb frequency can be extrapolated to zero concentration applying a second-order polynomial to fit the results in the 0–0.1 mol L−1 concentration range (r2 > 0.97 for both curves). We note that for Pb(NO3)2 a similar concentration dependence has been observed previously.19 Both experiments, that is Pb(ClO4)2 and Pb(NO3)2, give similar (although not identical) values of the frequency of the hydrated Pb2+ ion, 104.4284576 and 104.4280673 MHz, respectively. The average value, 104.4282624 MHz, is our best estimate of this frequency and gives −2876.8 ppm as the 207Pb chemical shift of the hydrated Pb2+ ion. For comparison, the 207Pb chemical shift of aqueous Pb(NO3)2 solution was earlier given as −2961 ppm3, or −2965.7 ppm (for 1.10 m solution).19
 | ||
| Fig. 2 (A) Upper curve: Pb(ClO4)2 in water; ν = −0.0425043ρ2 + 0.0123594ρ + 104.4284576; (B) lower curve: Pb(NO3)2 in water; ν = 0.0591139ρ2 − 0.0290864ρ + 104.4280673. | ||
A simple check using eqn (1) shows that an error of 0.01 MHz in the Pb frequency leads to a 0.0001 μN change in μ(207Pb). Thus, the ≈0.0004 MHz difference between the extrapolated results for two solutions is negligible, similar to other small effects in our experiment. In particular, two orders of magnitude larger changes of the final Pb magnetic moment arise from variations in the computed Pb shielding constant (see Section 4.2).
A chart illustrating the relative positions of various 207Pb signals on the new shielding scale and the corresponding NMR chemical shifts is given in Fig. 3. Our experiments have shown that the reference nucleus (Pb(CH3)4 liquid in toluene) is 9.72 ppm more shielded than in the isolated Pb(CH3)4 molecule when the reference solution is observed in a cylindrical sample tube placed in a superconducting magnet. As mentioned above, the chemical shift of the hydrated Pb2+ (aq) ion is −2876.8 ppm; the 207Pb chemical shifts of some other simple compounds have been taken from ref. 20.
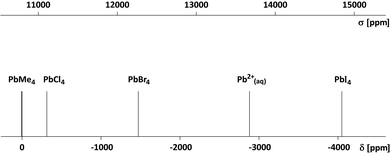 | ||
| Fig. 3 207Pb NMR signals of some simple chemical compounds on the scale of shielding (σ) and the chemical shift (δ). The chemical shift of an isolated Pb(CH3)4 molecule is δ0 = +9.72 ppm. | ||
3 Calculation of the shielding constants
3.1 Nonrelativistic ab initio calculations
We shall limit our discussion to the isotropic shielding constants as there are no experimental data for any of the tensor elements. Unless otherwise stated, all Hartree–Fock (HF) and coupled-cluster singles-and-doubles (CCSD) nonrelativistic results have been obtained using a point nucleus model. The nonrelativistic density-functional theory (DFT) values have also been calculated using a point nucleus, whereas in the relativistic Dirac–Kohn–Sham (DKS) calculations we use a Gaussian nucleus model.21 We have used the experimental geometry of Pb(CH3)4 taken from ref. 22.We begin with an analysis of the nonrelativistic results. We use the coupled-cluster analytic second derivative methods developed by Gauss, Stanton and coworkers23–26 to determine the shielding constants. The nonrelativistic results were calculated using the CFOUR27 program package, which uses gauge-including atomic orbitals (GIAOs28,29) to improve basis set convergence and obtain gauge-origin independent results.
The basis set dependence of the results was investigated at the HF level using the uncontracted version of Dyall's relativistic core-valence double-ζ (cvdz), triple-ζ (cvtz) and quadruple-ζ (cvqz) basis sets.30–33 For Pb(CH3)4, these uncontracted basis sets contain 457, 766 and 1224 functions, respectively. Even though the basis set dependence is found to be weak (see Table 2), the cvqz basis set was used in the final DFT calculations and analyses. The larger basis sets cannot be used at the CCSD level, and we therefore also report the results obtained with the uncontracted Jorge's ADZP basis set,34 which has 348 basis functions.
| Pb | C | H | |
|---|---|---|---|
| a Nonrelativistic GIAO calculations; uncontracted Dyall basis sets unless otherwise stated. | |||
| unc-dyall.cvdz | |||
| CCSD | 5934.0 | 218.92 | 32.833 |
| HF | 6066.7 | 218.75 | 33.138 |
| CGO, CCSD | 5998.5 | 222.22 | 30.934 |
| CGO, HF | 6114.8 | 222.99 | 31.191 |
| unc-dyall.cvtz | |||
| HF | 6053.1 | 217.19 | 32.645 |
| unc-dyall.cvqz | |||
| HF | 6053.6 | 216.96 | 32.510 |
| Jorge, unc-ADZP | |||
| CCSD | 6200.9 | 220.29 | 32.756 |
| HF | 6315.0 | 219.68 | 32.941 |
3.2 Relativistic density-functional theory calculations
The four-component relativistic DFT calculations were performed employing a development version of the program package ReSpect.35 We used the restricted magnetic balance scheme for calculations of the NMR shielding constants36,37 and the restricted kinetic balance scheme for the spin-rotation constants.38 The BP86,39,40 PBE41 and B3LYP42–44 exchange–correlation functionals were used in these DFT calculations.The BP86 and PBE absolute shielding constants were obtained using the GIAO approach. As shown in Table 3, the relativistic DKS/BP86 results are practically converged when extending the basis set. Absolute shielding constants obtained using the largest basis set for the BP86, PBE and B3LYP functionals are also reported for comparison in Table 4. The B3LYP results and the spin–rotation constants were obtained using the common gauge-origin (CGO) approach, where the gauge origin was placed at the center of nuclear mass.38
| Pb | C | H | |
|---|---|---|---|
| a Shielding constants calculated employing the GIAO approach unless stated otherwise. b Shielding constants calculated employing the CGO approach. | |||
| BP86 | |||
| unc-dyall.cvdz | 10247.4 | 190.22 | 31.410 |
| unc-dyall.cvtz | 10210.2 | 189.68 | 30.876 |
| unc-dyall.cvqz | 10200.9 | 189.58 | 30.723 |
| unc-dyall.cvqzb | 10256.3 | 189.56 | 30.526 |
| Pb | C | H | |
|---|---|---|---|
| a Shielding constants calculated employing the GIAO approach (BP86 and PBE) and the CGO approach (B3LYP). Point nuclei at NR, the Gaussian model of the nuclei at the DKS level. | |||
| BP86 | |||
| NR | 5331.7 | 201.26 | 31.959 |
| DKS | 10200.9 | 189.58 | 30.723 |
| Δ(rel) | 4869.2 | −11.68 | −1.238 |
| PBE | |||
| NR | 5360.0 | 201.98 | 31.674 |
| DKS | 10223.4 | 190.18 | 30.699 |
| Δ(rel) | 4863.4 | −11.80 | −0.975 |
| B3LYP | |||
| NR | 5466.3 | 202.80 | 31.864 |
| DKS | 10649.7 | 190.77 | 30.732 |
| Δ(rel) | 5183.4 | −12.03 | −1.132 |
The relativistic corrections, Δ(rel), are estimated as the difference between the relativistic (DKS) and the nonrelativistic (NR) values obtained applying the same exchange–correlation functional and the cvqz basis sets. The Gaussian nucleus model was used at the DKS level, because we have observed that the differences in the relativistic Pb shielding constants computed applying Gaussian and point nucleus are significant – the DKS values of σ(Pb) determined using the Gaussian nuclear model are approximately 350 ppm lower than those obtained for a point nucleus. At the NR level, this difference is less than 1 ppm, whereas for C and H nuclei the differences are below 1 ppm for both levels of theory.
4 Results and discussion
4.1 Pb(CH3)4
The only previous theoretical estimate of σ(Pb) in Pb(CH3)4, 14475.1 ± 500.7 ppm, was obtained by applying a crude approximation relating the Sn and Pb shielding constants.20From the results reported in Table 2 we see that the uncorrelated nonrelativistic results obtained with the unc-dyall.cvqz basis set are close to the basis set limit, as the cvtz and cvqz shielding constants differ by less than 1 ppm for all nuclei at the HF level. As shown in Table 3, at the DKS/BP86/unc-dyall.cvqz level this difference is also smaller than 1 ppm for the C and H nuclei, and smaller than 10 ppm for σ(Pb). Moreover, the GIAO and CGO shielding constants are practically identical for the C and H nuclei, whereas σ(Pb) computed with GIAOs is about 60 ppm (0.6%) smaller than that computed using the CGO approach. Very similar results, showing satisfactory convergence, were obtained with the PBE functional.
To estimate the dependence of the shielding constants on molecular geometry, calculations were performed for two additional structures, determined by contracting and stretching all the bonds in the experimental structure by 1%. The results obtained at the four-component BP86/unc-dyall.cvqz level indicate the very weak dependence of σ(Pb) on the geometry, the values for these contracted or stretched geometries differing at most by 35 ppm from the value obtained at the experimental geometry; this is negligible on the scale of the lead shielding. In contrast, the C and H shielding constants vary significantly, by ≈5 ppm and ≈0.4 ppm, and this geometry dependence may contribute to the difference observed between our best results and experimental data (see Table 5). Since we are primarily interested in the computed shielding of 207Pb, we have not attempted to perform a more detailed study of the geometry dependence of the shielding constants.
| Pb | C | H | |
|---|---|---|---|
| HF, unc-dyall.cvqz | 6053.6 | 216.96 | 32.51 |
| Δ CCSD, unc-dyall.cvdz | −132.7 | 0.17 | −0.31 |
| Δ(rel), BP86 | 4869.2 | −11.68 | −1.24 |
| Total | 10790.1 | 205.45 | 30.97 |
| Δ(rel), PBE | 4863.4 | −11.8 | −0.98 |
| Total | 10784.3 | 205.33 | 31.23 |
| Δ(rel), B3LYP | 5183.4 | −12.03 | −1.13 |
| Total | 11104.3 | 205.10 | 31.07 |
| Experiment | — | 194.08 | 30.07 |
Finally, we can determine from eqn (1) the nuclear magnetic dipole moment of 207Pb. Using the resonance frequencies and σH values given in Table 1, μ(1H) = 2.792847356 μN18 and σPb = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 ppm, we obtain μ(207Pb) = 0.59064 μN. Assuming rather conservative error bars for the computed Pb shielding constant of ±800 ppm, we find that μ(207Pb) is in the range of 0.59016–0.59112 μN (note that in ref. 13 we used erroneous input data to estimate μ(207Pb)). For comparison, using the experimental values of the nuclear magnetic moment of 0.592583 and 0.58219 μN leads (from eqn (2)) to σ(Pb) values of 14
790 ppm, we obtain μ(207Pb) = 0.59064 μN. Assuming rather conservative error bars for the computed Pb shielding constant of ±800 ppm, we find that μ(207Pb) is in the range of 0.59016–0.59112 μN (note that in ref. 13 we used erroneous input data to estimate μ(207Pb)). For comparison, using the experimental values of the nuclear magnetic moment of 0.592583 and 0.58219 μN leads (from eqn (2)) to σ(Pb) values of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 034 and −3576 ppm, respectively. Consequently, the latter experimental value of μ(207Pb) can be excluded.
034 and −3576 ppm, respectively. Consequently, the latter experimental value of μ(207Pb) can be excluded.
Despite the lack of experimental data, we have also computed the spin-rotation constants in Pb(CH3)4, at different levels of approximation. At the relativistic BP86/unc-dyall.cvqz level of theory, we obtain for Pb, C and H −19.778, −0.240 and 0.140 kHz, respectively. The relativistic contribution is significant for Pb, −6.550 kHz, and very small for the C and H nuclei. The PBE results are practically identical to the BP86 data, whereas for B3LYP we find for Pb −18.376 kHz. The nuclear g-factors used in these calculations were taken from ref. 7.
4.2 Pb2+ ions in water solutions
The standard value of the lead magnetic moment has been determined from studies of the Pb2+ ion in a water solution,6 and we have therefore also reproduced the NMR experiment and attempted to compute the corresponding shielding constant. Unfortunately, in the literature there are a variety of different data for the solvation shell structure of the Pb2+ ion in aqueous solution (see e.g.ref. 45–47). EXAFS experiments indicate a hemi-directed, six-coordinated structure with an average Pb–O distance of 2.54(1) Å.46 In contrast, the most recent molecular dynamics study of aqueous lead ions predicts a coordination number between seven and ten, with a strong predominance of an eight-coordination structure, followed by a nine-coordination structure.47 It appears that the observed structure of the Pb2+–water complexes may strongly depend on the timescale of the experiment. Thus, in order to estimate the NMR shielding constant for Pb2+ in aqueous solution, we have considered the Pb2+–water clusters with coordination number nc = 6, 7, 8, 9.The geometries of the complexes were optimized using second-order Møller–Plesset perturbation theory (MP2) using a 60-electron effective core potential cc-pVQZ-PP for Pb48,49 and the corresponding Dunning's cc-pVQZ basis set50 for O and H, keeping the oxygen core electrons frozen. NWChem was used for these structure optimizations.51 The optimized six- and seven-coordinated Pb2+–water clusters were found to be hemi-directed with an average Pb–O distance of 2.55 Å and 2.59 Å, respectively. The eight-coordinated cluster had a square-antiprism geometry and the nine-coordinated cluster a tricapped trigonal prism structure, and the average Pb–O distances were found to be 2.63 Å and 2.67 Å, respectively.
NMR shielding constants were first calculated for a bare Pb2+ ion and for the optimized Pb2+–water clusters at the nonrelativistic HF level of theory using a large GIAO basis set created by combining the uncontracted ANO-RCC basis52 for lead and Dunning's cc-pVTZ basis sets for hydrogen and oxygen, which is expected to give shieldings close to the basis set limit.53 Electron correlation effects were computed using a small double-ζ basis set (Jorge DZP for Pb and cc-pVDZ for O and H). The relativistic corrections were calculated at the DFT/BP86 level in the same manner as the relativistic corrections for Pb(CH3)4. The different contributions as well as the total estimated shielding constant at the optimized geometries are collected in Table 6.
| n c | 0 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|
| a Uncontracted ANO-RCC basis set for Pb; cc-pVTZ for O and H. b Smaller basis set: DZV for Pb; cc-pVDZ for O and H. c Nonrelativistic correlation correction: NR-CCSD – NR-HF, smaller basis set. d Nonrelativistic DFT/BP86 with the unc-dyall.cvqz basis set. e Relativistic DKS/BP86 with the unc-dyall.cvqz basis set. f Relativistic correction. g Nonrelativistic HFa + correlation correctionc + relativistic correctionf. | |||||
| NR-HFa | 10049.1 | 8752.9 | 8952.0 | 9216.4 | 9283.0 |
| NR-HFb | 10023.8 | 9235.8 | 9402.0 | 9613.9 | 9610.0 |
| NR-CCSDb | 10023.1 | 9203.3 | 9344.1 | 9514.3 | 9523.5 |
| Δ(corr)c | −0.7 | −32.5 | −57.9 | −99.6 | −86.5 |
| NR-BP86d | 10049.5 | 8105.0 | 8243.6 | 8449.9 | 8569.9 |
| DKS-BP86e | 17130.5 | 12945.2 | 13402.5 | 14070.6 | 14336.5 |
| Δ(rel)f | 7081.0 | 4840.2 | 5158.9 | 5620.7 | 5766.6 |
| Totalg | 17130.1 | 13560.6 | 14053.0 | 14737.5 | 14963.1 |
We also performed some calculations for solvated Pb2+–water clusters in which additional water molecules have been placed in the second solvation shell. These results indicate that the final theoretical prediction of the Pb2+ shielding in aqueous solution might be lower than our estimates for the first solvation shell structures by several hundred ppm.
The nonrelativistic values of the chemical shift induced by the interaction with water in the Pb2+–water clusters studied here are smaller than those calculated for other ion–water clusters (see e.g.ref. 53). This shift is enhanced by the relativistic effects, reaching 21% and 14% of the bare ion shielding for the six- and eight-coordinated clusters, respectively. The magnitude of the correlation effects, calculated using a small basis set, indicates that electron correlation is not very important for these clusters and thus does not significantly affect the accuracy of the chemical shielding of the water-solvated lead ion.
The Pb(CH3)4 calculations and the NMR experimental investigation, which determined the chemical shift between Pb(CH3)4 and the aqueous Pb2+ ion to be −2876.8 ppm, lead to a shielding of aqueous Pb2+ of 13657.2 ppm. This value is close to the computed shielding of the six-coordinated Pb2+ ion cluster, 13560.6 ppm. It appears that in the NMR experiment, the observed shielding is in agreement with the EXAFS prediction46 that the lead ion will have a six-coordinated solvation structure.
We can now estimate the magnetic dipole moment of 207Pb using the Pb2+ ion experimental data, with deuterium in C6D6 as the reference (see Table 7). However, in this case the computed lead shielding constants are much less reliable than for Pb(CH3)4. We can apply eqn (1) and the Pb2+ shielding constant determined via the experimental chemical shift, 13657.2 ppm, to obtain μ(207Pb) = 0.59065 μN. However, this is not an independent result for μ(207Pb), but instead it indicates the consistency and accuracy of the experimental data for Pb(CH3)4 and Pb2+ ions. Assuming that the error bars of this Pb2+ shielding constant are ±1100 ppm, which means encompassing the new, independently computed 6–8 solvated cluster results, we find that μ(207Pb) is in the range of 0.59000–0.59131 μN. It appears that the old value of the shielding constant, 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 ppm,6 used to determine the literature value of μ(207Pb), 0.592583 μN, was too large (this old value of the shielding constant combined with our new experimental data leads to a similar result, 0.59314 μN).
810 ppm,6 used to determine the literature value of μ(207Pb), 0.592583 μN, was too large (this old value of the shielding constant combined with our new experimental data leads to a similar result, 0.59314 μN).
| μ(207Pb) [μN], source | Reference nucleus, νref [MHz], σref [ppm] | ν Pb [MHz] | σ(Pb) [ppm] |
|---|---|---|---|
| a Calculations, see the text. b Calculated Pb(CH3)4 shielding and the experimental chemical shift between Pb(CH3)4 and aqueous ions, −2876.8 ppm. c IUPAC recommended value; an earlier recommended value was 0.582581 μN.2 | |||
| 0.59064(35) | |||
| NMR, gas-phase Pb(CH3)4 | H in Pb(CH3)4 | 104.730569(8) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 ± 600 790 ± 600 |
| 500.6062976 | |||
| 30.075 | |||
| 0.59059–0.59143 | |||
| NMR, Pb2+ aqueous ion | D in C6D6 | 104.428262(200) | [13560.6–14963.1]a |
| 76.84640167 | |||
| 26.441 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657 ± 600b 657 ± 600b |
||
0.592583(9),5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
|||
| NMR, old value6 | D in D2O | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 810 |
|
| 0.58219(2)5 | |||
| Optical pumping | |||
5 Conclusions
Following the theoretical calculations, we have assumed the 207Pb shielding of an isolated Pb(CH3)4 molecule to be 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 ppm. This shielding constant corresponds to the experimental frequency measured for an isolated molecule; these values lead to a shielding scale for 207Pb NMR spectroscopy in which for liquid Pb(CH3)4 we obtain σ(Pb) = 10799.7 ppm. The fully hydrated Pb2+ ion has, according to our measurements, a much larger shielding of 13657.2 ppm.
790 ppm. This shielding constant corresponds to the experimental frequency measured for an isolated molecule; these values lead to a shielding scale for 207Pb NMR spectroscopy in which for liquid Pb(CH3)4 we obtain σ(Pb) = 10799.7 ppm. The fully hydrated Pb2+ ion has, according to our measurements, a much larger shielding of 13657.2 ppm.
The direct measurement of the shielding constant becomes possible once the magnetic moment of 207Pb has been established.14 Our new value for the 207Pb magnetic moment, obtained from Pb(CH3)4 gas-phase NMR and the corresponding ab initio calculations, is 0.0019 μN smaller than the old value determined from NMR data. This is consistent with our previous experience11,12 – old literature values of magnetic moments determined from NMR are overestimated, because overestimated values of the NMR shielding have been used in their derivation (in the case of Pb2+, 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ppm instead of the more correct value of 13657.2 ppm).
800 ppm instead of the more correct value of 13657.2 ppm).
Acknowledgements
This work was partly financed by the National Science Centre (Poland) grant, according to the decision No. DEC-2011/01/B/ST4/06588 (B. A., W. M., and K. J.). A. A. acknowledges support from the projects APVV-15-0105 and VEGA 1/0279/16 and usage of the resources of HPC Cluster of Slovak University of Technology and Computing Centre of the Slovak Academy of Sciences (projects ITMS 26230120002 and 26210120002). T. B. D. and K. R. acknowledge the support of the Research Council of Norway through a Centre of Excellence Grant (Grant No. 179568/V30). Computer time from the Norwegian Supercomputing program NOTUR is also gratefully acknowledged (Grant No. NN4654K).References
- J. Mason, Multinuclear NMR, Plenum Press, New York, 1987 Search PubMed.
- R. K. Harris, E. D. Becker, S. M. C. de Menezes, R. Goodfellow and P. Granger, Pure Appl. Chem., 2001, 73, 1795–1818 CrossRef CAS.
- B. Wrackmeyer and K. Horchler, Annu. Rep. NMR Spectrosc., 1990, 22, 249–306 CrossRef CAS.
- B. Wrackmeyer, Annu. Rep. NMR Spectrosc., 2002, 47, 1–37 CrossRef CAS.
- N. J. Stone, At. Data Nucl. Data Tables, 2005, 90, 75–176 CrossRef CAS.
- O. Lutz and G. Stricker, Phys. Lett. A, 1971, 35, 397–398 CrossRef CAS.
- E. Cohen, T. Cvitaš, J. Frey, B. Holmström, K. Kuchitsu, R. Marquardt, I. Mills, F. Pavese, M. Quack, J. Stohner, H. Strauss, M. Takami and A. Thor, Quantities, Units and Symbols in Physical Chemistry, IUPAC Green Book, IUPAC & RSC Publishing, Cambridge, 3rd edn, 2nd printing, 2008 Search PubMed.
- H. M. Gibbs and C. M. White, Phys. Rev., 1969, 188, 180–187 CrossRef.
- G. Co', V. D. Donno, M. Anguiano, R. N. Bernard and A. M. Lallena, Phys. Rev. C: Nucl. Phys., 2015, 92, 024314 CrossRef.
- J. Li, J. X. Wei, J. N. Hu, P. Ring and J. Meng, Phys. Rev. C: Nucl. Phys., 2013, 88, 064307 CrossRef.
- M. Jaszuński and K. Jackowski, Lect. Notes Phys., Springer, 2008, vol. 745, pp. 233–260 Search PubMed.
- A. Antušek, K. Jackowski, M. Jaszuński, W. Makulski and M. Wilczek, Chem. Phys. Lett., 2005, 411, 111–116 CrossRef.
- M. Jaszuński, A. Antušek, P. Garbacz, K. Jackowski, W. Makulski and M. Wilczek, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 67, 49–63 CrossRef PubMed.
- K. Jackowski, M. Jaszuński and M. Wilczek, J. Phys. Chem. A, 2010, 114, 2471–2475 CrossRef CAS PubMed.
- K. Jackowski and M. Jaszuński, Concepts Magn. Reson., Part A, 2007, 30, 246–260 CrossRef.
- K. Jackowski, M. Wilczek, W. Makulski and W. Koźmiński, J. Phys. Chem. A, 2002, 106, 2829–2832 CrossRef CAS.
- K. Jackowski, J. Mol. Struct., 2006, 786, 215–219 CrossRef CAS.
- P. J. Mohr, B. N. Taylor and D. B. Newell, Rev. Mod. Phys., 2012, 84, 1527–1605 CrossRef CAS.
- N. Altounian, A. Glatfelter, S. Bai and C. Dybowski, J. Phys. Chem. B, 2000, 104, 4723–4725 CrossRef CAS.
- A. F. Maldonado and G. A. Aucar, J. Phys. Chem. A, 2014, 118, 7863–7875 CrossRef CAS PubMed.
- L. Visscher and K. G. Dyall, At. Data Nucl. Data Tables, 1997, 67, 207–224 CrossRef CAS.
- T. Oyamada, T. Iijima and M. Kimura, Bull. Chem. Soc. Jpn., 1971, 44, 2638–2642 CrossRef CAS.
- J. Gauss and J. F. Stanton, J. Chem. Phys., 1995, 102, 251–253 CrossRef CAS.
- J. Gauss and J. F. Stanton, J. Chem. Phys., 1996, 104, 2574–2583 CrossRef CAS.
- J. Gauss, J. Chem. Phys., 2002, 116, 4773–4776 CrossRef CAS.
- M. Kállay and J. Gauss, J. Chem. Phys., 2004, 120, 6841–6848 CrossRef PubMed.
- CFOUR, a quantum chemical program package written by J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, J. Bomble, L. Cheng, O. Christiansen, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A. Matthews, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see http://www.cfour.de.
- F. London, J. Phys. Radium, 1937, 8, 397–409 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- K. G. Dyall, Theor. Chem. Acc., 1998, 99, 366–371 CAS.
- K. G. Dyall, Theor. Chem. Acc., 2002, 108, 335–340 CrossRef CAS.
- K. G. Dyall, Theor. Chem. Acc., 2006, 115, 441–447 CrossRef CAS.
- K. G. Dyall, Unpublished Basis Sets for 2p–3p Elements, Available from the Dirac web site, http://dirac.chem.sdu.dk.
- A. C. Neto and F. E. Jorge, Chem. Phys. Lett., 2013, 582, 158–162 CrossRef.
- ReSpect, version 3.4.0 (2014) – Relativistic Spectroscopy DFT program of authors, S. Komorovsky, M. Repisky, V. G. Malkin, O. L. Malkina, M. Kaupp, K. Ruud, with contributions from, R. Bast, U. Ekström, M. Kadek, S. Knecht, L. Konecny, I. Malkin-Ondik, E. Malkin, See http://www.respectprogram.org, accessed Mar 15, 2016.
- S. Komorovsky, M. Repisky, O. L. Malkina, V. G. Malkin, I. Malkin Ondik and M. Kaupp, J. Chem. Phys., 2008, 128, 104101 CrossRef PubMed.
- S. Komorovsky, M. Repisky, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2010, 132, 154101 CrossRef PubMed.
- S. Komorovsky, M. Repisky, E. Malkin, T. B. Demissie and K. Ruud, J. Chem. Theory Comput., 2015, 11, 3729–3739 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- K. McQuinn, F. Hof, J. S. McIndoe, X. Chen, G. Wu and A. J. Stace, Chem. Commun., 2009, 4088–4090 RSC.
- I. Persson, Pure Appl. Chem., 2010, 82, 1901–1917 CrossRef CAS.
- A. Bhattacharjee, T. S. Hofer, A. B. Pribil, B. R. Randolf, L. H. V. Lim, A. F. Lichtenberger and B. M. Rode, J. Phys. Chem. B, 2009, 113, 13007–13013 CrossRef CAS PubMed.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- A. Antušek and F. Holka, J. Chem. Phys., 2015, 143, 074301 CrossRef PubMed.
| This journal is © the Owner Societies 2016 |

