Ionic liquid nanostructure enables alcohol self assembly

Abstract

Weakly structured solutions are formed from mixtures of one or more amphiphiles and a polar solvent (usually water), and often contain additional organic components. They contain solvophobic aggregates or association structures with incomplete segregation of components, which leads to a poorly defined interfacial region and significant contact between the solvent and aggregated hydrocarbon groups. The length scales, polydispersity, complexity and ill-defined structures in weakly structured solutions makes them difficult to probe experimentally, and obscures understanding of their formation and stability. In this work we probe the nanostructure of homogenous binary mixtures of the ionic liquid (IL) propylammonium nitrate (PAN) and octanol as a function of composition using neutron diffraction and atomistic empirical potential structure refinement (EPSR) fits. These experiments reveal why octanol forms weakly structured aggregates in PAN but not in water, the mechanism by which PAN stabilises the octanol assemblies, and how the aggregate morphologies evolve with octanol concentration. This new understanding provides insight into the general stabilisation mechanisms and structural features of weakly structured mixtures, and reveals new pathways for identifying molecular or ionic liquids that are likely to facilitate aggregation of non-traditional amphiphiles.

---

Introduction

Surfactants and other amphiphilic species dissolve in water because the hydrophilic head group confers solubility on the hydrophobic tail. The hydrophobic tail disrupts the native hydrogen bond network of water, which is entropically unfavourable. Above the critical micelle concentration (cmc) any added surfactant forms aggregates known as micelles, and beyond this point the monomer concentration remains relatively constant as the micelle concentration increases. In water, micelles are well-defined structures whose shapes depend on the amphiphile packing geometry, which in turn depends on solvent conditions such as temperature, electrolyte and surfactant concentration; the near-spherical structures usually present at low concentrations may become elongated as the concentrations is increased, and then transform into various lyotropic liquid crystals at high concentrations.

Amphiphiles in such strongly structured aggregates exhibit strong segregation of non-polar moieties, which are internalised to minimise contact with the water, surrounded by a layer of head groups oriented towards and in contact with the solvent. The resultant sharp interface minimises contact between water and hydrophobic groups, and leads to a well-defined micelle shape. By contrast, in weakly structured mixtures, the non-polar segregation is less pronounced, amphiphile orientation and aggregate shape are less well-defined, leading to much greater contact between water and hydrocarbon groups. Weakly structured solutions have been identified in microemulsions formed from poorly amphiphilic surfactants,^1–5 and in “surfactant free microemulsions”,^6–11 which are typically ternary mixtures of a hydrotrope (e.g. ethanol), water and a water-insoluble long chain alcohol (e.g. octanol).^6,8,10,11

Such liquids defy detailed structural characterisation. Disordered, strongly-structured mixtures^12–14 and weakly-structured mixtures^{5,6,8,10–12,15} can produce similar small angle scattering patterns that can be fit with a variety of standard models ranging from discrete, polydisperse spheres or other aggregate shapes to bicontinuous structures; small-angle scattering alone thus cannot uniquely determine liquid structure, or differentiate between strongly and weakly structured mixtures. This is because aggregate structures, and their interfaces with the solvent, are so poorly-defined in weakly-structured systems that the low-resolution geometrical approaches and continuum approximations used in small-angle scattering are inadequate.^2,5,16 As a result, the conditions and interactions that produce weakly-structured mixtures are not well understood (compared to strongly structured systems). These mixtures have many attractive characteristics as solvents in formulations for amphiphilic and complex solutes including biomolecules, polymers, and pharmaceuticals, and as liquids for viscosity and lubrication control, and as continuous phases for dispersions, but their utility is as yet under exploited.

Aliphatic alcohols do not self-assemble in water, but are surface active due to their polar alcohol group and hydrophobic alkyl chain.¹⁷ Recently, small- and wide-angle X-ray scattering (SAXS/WAXS) studies have revealed the existence of alkanol aggregates in protic room-temperature ionic liquids (ILs);^18,19 self-assembly of conventional surfactants in ILs is of particular interest, as there are still only a handful of molecular solvents that support this phenomenon,^20–22 but the presence of alkanol aggregates in ILs suggests that a water-centred definition of a surfactant may need revision.²³

Based on trends in the SAXS/WAXS patterns with concentration and alkanol length, Greaves et al. postulated that alkanols form micelle-like aggregates when the alkanol chain length is more than twice that of the IL cation alkyl chain.¹⁸ Subsequently, we examined binary mixtures of even-numbered alkanols from ethanol to dodecanol in 6 different protic alkylammonium ILs by SAXS/WAXS, which showed signatures of a wide variety of self-assembled structures as a function of composition and IL structure.¹⁹ As with weakly-structured ternary mixtures, fits to the scattering patterns were inconclusive, yielding physically plausible best-fit parameters for a range of models including polydisperse micelles and bicontinuous structures.^19,24

Interpretation of the small-angle scattering from these IL–alkanol mixtures is further complicated by the presence of underlying nanostructure in many ionic liquids. IL cations, and sometimes anions, possess distinct apolar and polar groups which render them amphiphilic. As a result, many pure ILs are themselves nanostructured, meaning that the bulk liquid is structurally inhomogeneous on a length scale that exceeds the molecular ionic components.^25–27 IL nanostructure arises due to the solvophobic segregation of cation alkyl chains. Strong Coulombic interactions between charged groups, sometimes reinforced by H-bonding interactions,^25,26,28 cause alkyl chains to form apolar domains segregated from the polar regions. The result is often a bicontinuous sponge-like structure comprised of interpenetrating polar (ionic) and apolar (alkyl) domains. In the IL–alkanol mixtures, the scattering signature of alkanol aggregation was often easily distinguished from the background, which included scattering from the underlying IL nanostructure. However, especially when alkanol and cation alkyl chains were of similar length, alkanol addition altered the solvent nanostructure, and in some cases the aggregate scattering merged with the solvent scattering.¹⁹ This suggests (i) strong coupling or “crosstalk” between IL nanostructure and alkanol aggregates, and (ii) that in binary solutions the IL may play the roles of both the polar solvent and the hydrotrope in weakly-structured ternary aqueous mixtures.

Here we examine the structure in binary liquid mixtures of the IL propylammonium nitrate (PAN) and n-octanol at high resolution by neutron diffraction. The PAN/n-octanol system is particularly significant for liquid nanostructure; shortening the IL cation by one methylene yields ethylammonium nitrate (EAN), which is only partially miscible with n-octanol at room temperature.^29–31 Octanol is also the shortest alkanol that exhibits a small-angle scattering peak, and thus periodic order beyond that of the underlying IL nanostructure. In studies of ternary (and multicomponent) microemulsions, this is an acknowledged signature of amphiphiles³² that form structured liquid mixtures (microemulsions), rather than simply exhibiting critical (Ornstein–Zernike) scattering, although these too may be weakly-structured systems.³³ Indeed Triolo et al. have recently investigated SAXS from EAN/n-pentanol mixtures and interpreted their results within this framework.³⁴ A few binary aqueous systems are also known to exhibit weak structure, which can be difficult to distinguish from, or forms in addition to, critical fluctuations.^35,36

Neutron diffraction accesses molecular length scales as well as those of larger, self-assembled aggregates, allowing the IL nanostructure to be accounted for without relying on the continuum approximations of small-angle scattering. Neutron-beam techniques also enable contrast variation via isotopic substitution that exploits the different scattering cross-sections of hydrogen and deuterium. This allows contributions to the scattering from different components or even individual functional groups in hydrogen-rich and organic mixtures to be amplified or isolated; here, labelling of cation and alkanol alkyl tails and polar groups will be used to establish the liquid nanostructure from the molecular scale up to that of alkanol aggregates. Neutron diffraction is analysed using the atomistic Monte Carlo simulation methodology, empirical potential structure refinement (EPSR) which simultaneously fits scattering patterns with multiple contrasts; this explicitly includes all molecular and ionic components, and provides much higher resolution structural details than is achieved by small-angle scattering. The PAN–octanol system is ideally suited for study by neutron diffraction with EPSR; the aggregates in ternary mixtures such as weakly structured microemulsions and surfactant free microemulsions are too large to be captured in an EPSR simulation box that can be fit in an acceptable time. Additionally, scattering from surfactant free microemulsions is generally weak,^10,11 which would compromise fitting.

Here we seek to determine:

(1) Why n-octanol and other alkanols self-assemble in PAN but not in water.

(2) Whether the PAN–octanol mixture is strongly or weakly structured, and the nature of the interface between octanol-rich and IL-rich domains.

(3) How the nanostructure of the mixture evolves with octanol concentration.

(4) What role the underlying IL nanostructure plays in octanol self-assembly.

There is good evidence that nanostructure influences how ILs solvate and dissolve a range of solutes,^{18,20,37–40} and their ability to support amphiphilic self-assembly.^18,20 Examination of the partitioning of polyoxyethylene alkyl ether surfactants between a non-polar solvent and ethylammonium nitrate (EAN) or PAN⁴¹ has shown that the surfactant alkyl tails experience an average environment in the IL, and are largely insensitive to nanostructure, but that the polar ethoxy moieties are exclusively solvated by the polar domains of the IL.⁴¹ The average solvent environment for the surfactant alkyl chain, which drives micelle formation, is less polar in PAN than EAN. Consequently, while surfactants aggregate in both ILs, critical micelle concentrations (cmcs) are higher in PAN than EAN.^5,15,42,43

IL nanostructure also affects rheology,^44–46 interfacial structure^47–50 and lubrication,^51,52 and can control reaction kinetics and outcomes.^53,54 However, there is frequently ambiguity surrounding the importance of IL nanostructure in determining performance of ILs both as pure liquids and as solvents: when does nanostructure become important compared to the average solvent environment? Here octanol is used as a not-too-simple model solute. Its dissolution and self-assembly in PAN is examined to probe this issue.

Materials and methods

H-PAN was prepared via the drop-wise addition of nitric acid (HNO₃) (Sigma-Aldrich, 70 w/w%) to a chilled aqueous solution (<5 °C) of propylamine (Sigma-Aldrich 98 wt%). Excess water was removed firstly by rotary evaporation for several hours at 45 °C and then purging with dry N₂ at 100 °C. The final water content of the IL was determined to be <0.1% by Karl–Fischer titration. d₃-PAN was synthesised by performing the acid–base reaction in deuterium oxide (D₂O 99% Sigma Aldrich), then dried, and subsequently washed with three molar equivalents of D₂O before the excess D₂O was removed by rotary evaporation for several hours at 45 °C, and then dried a final time following the same procedure as for H-PAN. ¹H-NMR shows that, on average, 2.85 out of 3 amino hydrogen atoms are replaced with deuterium. H-octanol (anhydrous, ≥99%) and d₁₈-octanol (98 atom% D) was purchased from QMX Laboratories Ltd and used as received.

Neutron scattering data were collected using the SANDALS time of flight diffractometer at the ISIS pulsed neutron and muon source at the Rutherford Appleton Laboratory, UK. The instrument has a wavelength range of 0.05–4.95 Å, and covers a Q range of 0.1–50 Å⁻¹. Samples were contained in chemically inert, null scattering Ti_0.68Zr_0.32 flat plate cans of known atomic density (0.0541 atoms per ų) which were sealed with PTFE O-rings during the neutron diffraction experiments. The can dimensions were 35 × 35 mm² with a 1 mm path length and 1 mm wall thicknesses. Prior to loading, diffraction measurements were performed on the empty cans, the empty instrument and a vanadium standard sample for data correction and normalization. The diffraction experiments were conducted at 25 ± 0.1 °C under vacuum. The sample chamber was left to equilibrate for 10 min prior to each measurement. The combined masses of the can and sample for each contrast were measured before and after the diffraction measurement to ensure evaporation had not occurred in the vacuum chamber. The net run time for each system was at least 8 h. For internal consistency, the previously-collected diffraction data of pure PAN⁵⁵ was re-reduced and re-fitted using the same version of GUDRUN and EPSR (see ESI,† Fig. S1).

Data reduction and analysis was carried out using GUDRUN software, as described in the ATLAS manual.⁵⁶ This corrects the raw data by normalisation to the incident neutron flux, for absorption and multiple scattering, Ti–Zr can subtraction and normalisation to absolute units by dividing the measured differential cross section by the scattering of a vanadium standard of known thickness. Corrections for single atom scattering and hydrogen inelasticity were also applied. Fitting to the normalised diffraction data was conducted using EPSR.

Previously published Lennard-Jones parameters for PAN⁵⁷ and octanol⁵⁸ were used as starting parameters for the simulations. The structures of PAN and octanol, and the labels used to identify specific atoms, are shown in Fig. 1.

Fig. 1 Structure of propylammonium nitrate (top) and octanol (bottom). The atoms; carbon (black) oxygen (red) nitrogen (blue) and hydrogen (white) are labelled with the notations used in the EPSR simulation and throughout this paper. Note that equivalent atoms share the same label.

Results and discussion

Fig. 2 shows neutron diffraction patterns (open circles) obtained for 10, 20, 30, 40 and 50 v/v% octanol in PAN with different isotopic substitutions. Unambiguous assignment of diffraction peaks in diffraction patterns of IL systems is complicated by multiple atom–atom correlations (cation–cation, anion–anion, polar–apolar, etc.), which may all contribute positive and negative elements of peaks in the structure factor function, S(Q), particularly for X-ray scattering.⁵⁹ However, for neutron based experiments isotopic substitution provides greater confidence in the fits.⁶⁰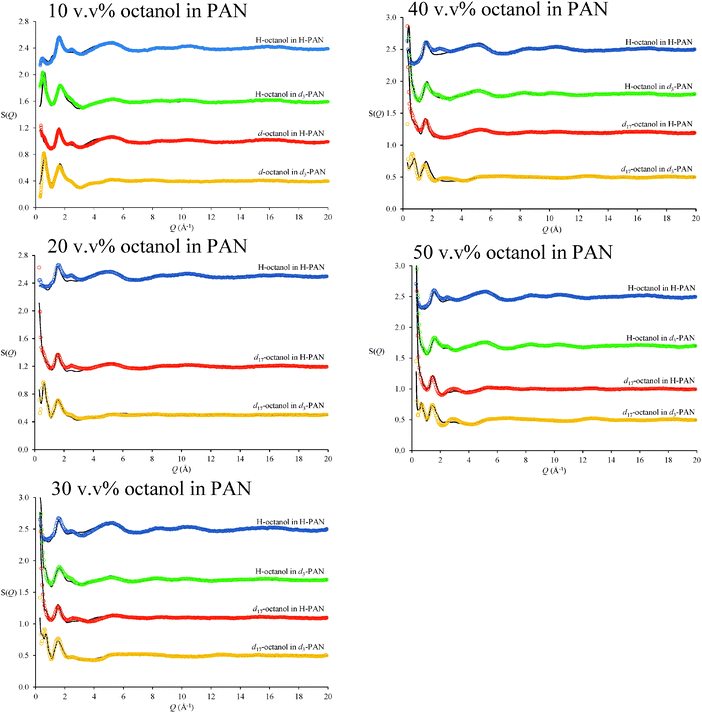

Fig. 2 Measured (coloured data points) and EPSR fitted (black lines) neutron diffraction S(Q) for octanol in PAN isotopomeric mixtures at 298 K. Data are offset for clarity.

EPSR fits for each contrast of the PAN–octanol mixtures are shown as solid lines in Fig. 2. For each mixture, all isotopic substitutions were fit simultaneously using the same EPSR model of the liquid, so different diffraction patterns reflect only the differences in H and D distributions. There are small deviations between the diffraction data and the EPSR fits at wave vectors ≤3 Å⁻¹, but all peak shapes and positions have been captured by the fit. For appropriate contrasts, these scattering profiles are consistent with recent SAXS studies of n-alkanols in protic ILs.¹⁹

In the most dilute (10 v/v%) octanol in PAN mixture, a pronounced low Q peak at 0.485 Å⁻¹ is present in the H-octanol in d₃-PAN contrast (green data in Fig. 2). This peak corresponds to the low Q diffraction peak previously reported for pure d₃-PAN⁶¹ at 0.530 Å⁻¹, which is diagnostic of the underlying nanostructure of PAN.⁶¹ The addition of 10 v/v% octanol shifts the d₃-PAN diffraction peak from 0.530 Å⁻¹ to 0.485 Å⁻¹, indicating swelling of the native PAN nanostructure.⁶¹ At higher octanol concentrations, intense low Q scattering from correlations associated with octanol structures obscures the d₃-PAN diffraction peak.

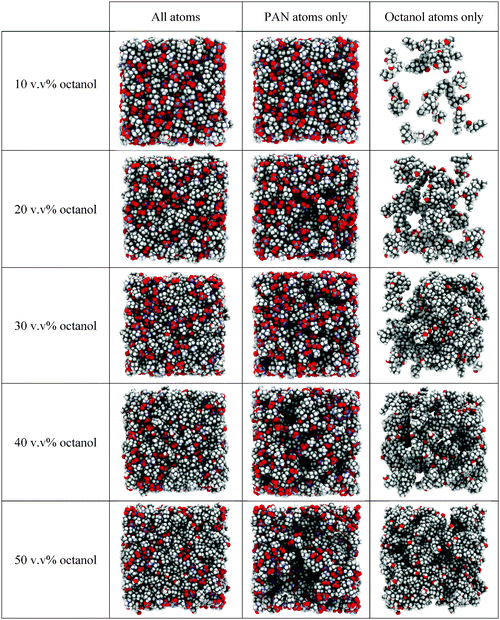
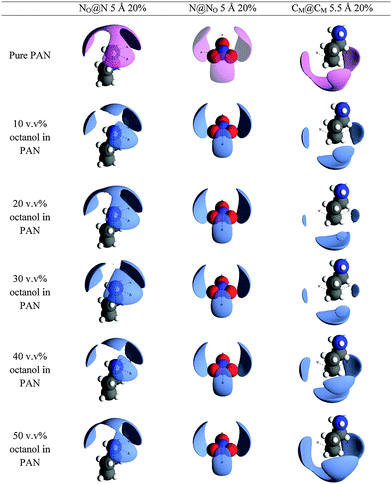
The front faces of snapshots of the converged EPSR simulation boxes corresponding to the neutron diffraction fits are shown in Fig. 3. Examination of the complete simulation boxes (Fig. 3, column 1) reveals structure evolving as a function of octanol concentration. At 10 v/v%, the structure is comparable to pure PAN.⁶¹ A bicontinuous structure comprised of interpenetrating but distinct polar (indicated by the red O and blue N atoms of the nitrate anions and cation ammonium groups) and apolar (grey C atoms and white H atoms) domains is easily seen. As the octanol volume fraction increases, the apolar regions occupy a larger fraction of the box area (volume), but distinct polar domains can still be discerned percolating throughout the liquid.

Fig. 3 Snapshots of the fitted bulk structures of PAN–octanol mixtures equilibrated at 300 K. Each system contains 500 PAN ion pairs and the appropriate number of octanol molecules to produce 10, 20, 30, 40 and 50 v/v% octanol mixtures. Carbon atoms are shown in grey, hydrogen in white, oxygen in red and nitrogen in blue.

Structural features are revealed more clearly when the mixture's components are represented separately. Fig. 3, column 2 displays the PAN ions only, whilst column 3 shows the octanol molecules only. At 10 v/v% the octanol molecules are simply dissolved, and molecularly dispersed throughout the PAN as monomers. At 20 v/v% octanol molecules are associated in clusters. These octanol clusters account for the dramatically increased low Q scattering in the d₁₇-octanol H-PAN contrast at 20 v/v% compared to 10 v/v% (cf.Fig. 2), and are consistent with previous SAXS results for similar mixtures.¹⁹ At an octanol concentration of 30 v/v%, no isolated clusters can be distinguished. The disordered clusters present at 20 v/v% have grown in size and become interconnected. Here, and at higher octanol concentrations, the liquid structure exhibits two percolating bicontinuous networks with two distinct structural length scales: a large scale defined by the dimensions of the aggregated octanol interpenetrated with PAN, and a smaller one defined by the polar/apolar segregation within the IL component itself. This is the equilibrium structure of the liquid mixture, which does not phase separate.

Micelle structures of decyltrimethylammonimum bromide (C₁₀TAB) surfactants in water have been determined by neutron diffraction with EPSR analysis.^62,63 As expected, C₁₀TAB micelles have a well-defined globular structure with alkyl tails internalised and a surface decorated by ammonium headgroups in contact with the water^64–68 and surface-associated Br⁻ counter ions in the micelle Stern layer,⁶² minimising alkyl chain–water contact. This leads to a well-defined micelle aggregation number. This contrasts starkly with the clusters seen in PAN at 20 v/v% octanol in Fig. 3, which are less ordered and quite polydisperse (see below), with large areas of contact between octyl chains and PAN solvent. This is an understandable consequence of both the small hydroxyl “head group” and the relatively small free energy gain from transfer of a methylene (–CH₂–) group from PAN into a nonpolar environment, compared to water.⁴¹ That is, the solvent environment inside an octanol aggregate and bulk PAN are more similar than are the interior of a surfactant micelle and water.

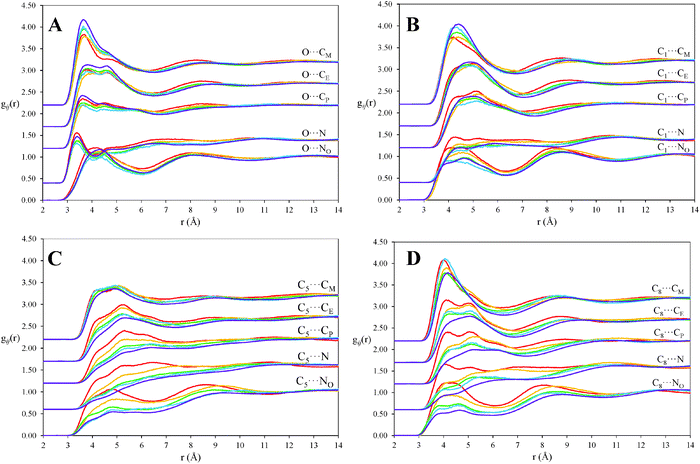
Partial pair correlation functions, g_ij(r), describing the density distributions of particular atom–atom pairs as a function of their separation, normalised to their bulk density, reveal higher resolution features of the liquid structure. The first peak in g_ij(r) corresponds to the first coordination shell of nearest neighbour atoms. Several g_ij(r) functions showing correlations between key octanol atoms with those of propylammonium and nitrate ions are presented in Fig. 4, with corresponding coordination numbers (also normalised to bulk composition) listed in Table 1. Data are shown for correlations between the terminal octanol methyl group (C₈), the carbon atom half way along the alkyl chain (C₅), the carbon atom adjacent to the hydroxyl group (C₁) and the hydroxyl oxygen atom (O) of octanol with each of the cation propyl carbons (C_M, C_E, C_P), the ammonium nitrogen (N), and nitrate centre (N_O) as a function of composition.

Fig. 4 Atom–atom pair correlations, g_ij(r) functions, for select atom–atom pair correlations between octanol molecules to PAN ions in PAN–octanol mixtures. (A) Gives correlations between octanol hydroxyl O atoms and PAN atoms; (B) gives correlations between octanol C₁ atoms (C atoms bearing the hydroxyl group) and PAN atoms; (C) correlations between octanol C₅ atoms (C atom half way along the octanol alkyl chain) and PAN atoms; and (D) octanol C₈ atoms (terminal methyl carbon on the octanol alky chain) and PAN atoms. Red lines indicate data for 10 v/v% octanol in PAN, yellow indicate 20 v/v%, green indicate 30 v/v%, blue indicate 40 v/v% and purple indicate 50 v/v%. Data is offset for clarity.

Table 1 Coordination numbers for key octanol⋯octanol and octanol⋯propylammonium nitrate (PAN) atom–atom pairs, derived from partial radial g_ij(r) distribution data extracted from the EPSR models. All the coordination numbers were numbers were calculated over a radial range of 0.0–4.5 Å, except for the hydrogen bonding interactions in the final 2 rows, which were calculated over 0.0–3.5 Å

		10 v/v%	20 v/v%	30 v/v%	40 v/v%	50 v/v%
HO	O	0.14	0.25	0.45	0.62	0.56
	NO	1.35	1.12	1.02	0.77	0.72
	CM	1.65	1.26	1.32	1.26	1.10
	CE	1.64	1.20	1.27	1.07	0.94
	CP	1.43	1.05	1.03	0.83	0.79
	N	1.25	0.96	0.88	0.67	0.63
O	O	0.12	0.24	0.44	0.62	0.54
	NO	1.23	0.93	0.91	0.71	0.60
	CM	1.59	1.26	1.30	1.20	1.12
	CE	1.58	0.92	1.20	0.91	0.86
	CP	1.33	0.92	0.92	0.69	0.67
	N	0.99	0.77	0.78	0.55	0.49
C1	NO	1.25	0.85	0.75	0.69	0.53
	CM	1.51	1.08	1.38	1.07	0.82
	CE	1.17	0.77	1.08	0.72	0.53
	CP	0.98	0.55	0.91	0.59	0.40
	N	0.98	0.58	0.91	0.55	0.36
C5	NO	0.98	0.47	0.44	0.38	0.28
	CM	0.89	0.65	0.81	0.50	0.58
	CE	0.64	0.44	0.52	0.35	0.32
	CP	0.52	0.26	0.26	0.21	0.20
	N	0.57	0.24	0.21	0.18	0.16
C8	NO	1.39	0.76	0.57	0.57	0.24
	CM	1.48	1.09	0.97	1.08	0.81
	CE	1.30	0.80	0.62	0.68	0.36
	CP	1.09	0.43	0.39	0.46	0.16
	N	0.81	0.43	0.24	0.41	0.07
Hydrogen bonding interactions
O	HN	1.25	0.85	0.81	0.85	0.61
HO	ON	1.78	1.37	1.25	1.19	0.98

---

The most striking feature of these results is the difference between the g_ij(r) functions for the octanol C₅ and C₈ atoms with various IL atoms in the 10 v/v% solution, where octanol molecules are present as monomers (i.e. the red lines in Fig. 4C and D), and those at all higher concentrations. At 10 v/v%, the octyl tails are molecularly dispersed and surrounded by solvent, with little preference for either polar or non-polar atoms. Here the pronounced nearest-neighbour correlation peaks for the hydroxyl O of octanol with each PAN atom is also consistent with it being molecularly dispersed. (The less-pronounced peaks for C₅ correlations simply reflect that it lies at the centre of the chain and can have fewer nearest neighbours.)

At 20 v/v% (yellow lines) the differences in C₅ and C₈g_ij(r) are diminished; this reflects the formation of octanol clusters and represents the average of atoms in dissolved monomers and aggregates. At higher concentrations, the fraction of dissolved monomers is negligible, so the various g_ij(r) are independent of concentration. These reflect the local environment within octanol aggregates. With increasing concentration, the coordination numbers around C₅ and C₈ decrease most markedly for the charged nitrogen centres of PAN, but also for the adjacent carbons C_E and C_P. The C_M coordination number decreases only slightly by comparison. This explains why the aggregates can sustain a large contact area with solvent: the PAN cations form an oriented monolayer with the terminal methyl groups coating exposed octyl tails. Put another way, the PAN nanostructure accommodates exposed octyl chains in a way that water could not.

For octanol C₁ (Fig. 4B), some similar differences between 10 v/v% and higher concentrations can also be discerned, most clearly for correlations the nitrate centre. This is evident too in the C₁–N_O coordination numbers, which decrease with increasing octanol concentration, and to a lesser extent in those of the ammonium N and its adjacent C_P (Table 1). This attenuated effect is consistent with octanol behaving as an amphiphile: as the polar hydroxyl moiety confers solubility on the alkyl tail, it is expected to remain solvated by PAN; C₁ should thus be less affected by octanol aggregation than C₅ or C₈.

The pair correlation functions and coordination numbers for the octanol hydroxyl O are consistent with octanol behaving as a surfactant. Unlike octanol C atoms, there is a pronounced and well-defined peak at small separations between the octanol hydroxyl oxygen and the ammonium centre (O⋯N) g_ij(r) function, and the octanol hydroxyl⋯nitrate (O⋯N_O) g_ij(r) peak is also better defined than the corresponding alkyl chain correlations. These short range correlations are consistent with octanol donating H-bonds to nitrate anions and accepting H-bonds from cation ammonium groups. The O⋯H_N and H_O⋯O_Ng_ij(r) functions (not shown) reveal O⋯H_N and H_O⋯O_N H-bond lengths of 2.70 and 2.65 Å respectively. In the 10 v/v% mixture, coordination numbers for these short range H-bonding interactions (Table 1) indicate each octanol hydroxyl is coordinated by 1.25 ammonium protons (H_N atoms) and 1.78 nitrate O atoms. This means that octanol molecules, on average, accept one H-bond from PAN cations and donate two to nitrate anions via bifurcated H-bonds.^69,70

Although the data indicates H-bonding between the octanol hydroxyl and the polar charged moieties of PAN, this does not equate to exclusive solvation by the polar domains. The coordination numbers show instead that the hydroxyl oxygens are surrounded by both polar and apolar components as nearest neighbours almost without preference (Fig. 4A and Table 1), much like the octanol tail carbons in dilute solution. This contrasts markedly with polyoxyethylene alkyl ether surfactants, where the ethoxy head group moieties are solvated preferentially by the polar domains.⁴¹ This suggests that the hydroxyl is not more solvophilic in PAN than in water.

Increasing the octanol concentration only weakly affects correlations between octanol hydroxyl groups and PAN atoms (cf.Fig. 4A). Coordination numbers decrease by about one-third for cation carbon atoms when the concentration is increased above the aggregation threshold to 20 v/v%, and by a little less for both nitrogen centres. This means octanol hydroxyl solvation in PAN is relatively insensitive to concentration, so it largely retains PAN in its coordination spheres as the octyl chains aggregate. The small differences in the hydroxyl⋯PAN g_ij(r) with further increases in octanol concentration are primarily a consequence of the reduced PAN volume fraction; there are fewer PAN ion pairs available to solvate each hydroxyl. Accordingly, the hydroxyl⋯PAN coordination numbers, and the number of octanol–PAN H-bonds, decrease with concentration, as shown in Table 1.

A complementary picture of octanol aggregation is seen by examining the intermolecular pair correlation functions of C₁, C₅ and C₈ carbons between octanol alkyl chains, shown in Fig. 5. At 10 v/v%, all g_ij(r) functions have very weak or no peaks at nearest-neighbour separations and deviate little from bulk density because octanol is dissolved as isolated monomers. This is clearest for the C₅⋯C₅ correlation, which defines the centre of the octanol tail-group, and which is conspicuously weaker at 10 v/v% than in all other mixtures; its g_ij(r) rises gently with distance towards its bulk density. This is a result of the octyl chain sterically hindering close approach of other C₅ atoms. However, at 20 v/v% octanol and above, cluster formation dramatically increases the extent of octanol alkyl⋯alkyl correlations, particularly in the C₅⋯C₅ distribution at short distances (cf.Fig. 3). Fig. 5 also shows that short-range correlations between C₅ and C₈ atoms also increase markedly at these concentrations, consistent with the aggregation threshold of the octyl chains being reached. As inferred above, intermolecular correlations between C₁ carbons are expected to be least affected by aggregation, and are indeed independent of concentration. Correlations between C₁ and C₅ or C₈ similarly show weak or no concentration dependence.

Fig. 5 Atom–atom pair correlations, g_ij(r) functions, for select atom–atom pair correlations between octanol molecules in PAN–octanol mixtures. Red lines indicate data for 10 v/v% octanol in PAN, yellow indicates 20 v/v%, green indicates 30 v/v%, blue indicates 40 v/v% and purple indicates 50 v/v%. Data is offset for clarity.

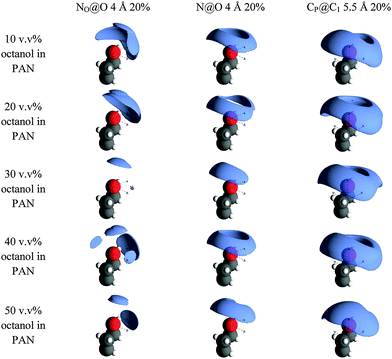
Fig. 6 shows the spatial density functions (SDF) for PAN around the hydroxyl group and three adjacent methylenes of octanol. These are three dimensional surfaces showing the most probable arrangement of the cation and anion nitrogens around the hydroxyl oxygen (N@O and N_O@O, respectively) and the methylene carbons immediately adjacent to the polar head groups of octanol and PAN (C_P@C₁).

Fig. 6 EPSR SDF reconstructions of the g_ij(r) data for key PAN@octanol correlations between PAN ions and octanol molecules. The lobes represent the 20% probability isosurfaces for the orientation of a selected PAN atom on around a central octanol atom.

At 10 v/v%, where octanol is present only as dissolved monomers, N_O@O shows that the first coordination shell of nitrate anions are not isotropically distributed around the hydroxyl O atom, but occupy a lobe preferentially oriented opposite the octanol alkyl chain fragment shown. This is consistent with the nitrate H-bonding to the –OH group while still forming part of the polar H-bonded network of PAN. The N@O distribution forms a torus around and above the hydroxyl oxygen, also consistent with its incorporation into the H-bonded network of the polar domain. C_P@C₁ forms a similar but slightly larger and more diffuse toroidal distribution around the C₁–O axis, centred slightly closer to the alkyl chain. This suggests that the propyl chains of the cation have some preference to orient parallel to the octanol tail even in dilute solution.

As the octanol concentration is increased, the main features of each distribution are retained. The N_O@O and N@O lobes both decrease markedly in size between 10 v/v% and 30 v/v% octanol, indicating a more ordered arrangement of PAN charged groups around the octanol hydroxyl group as the octanol aggregates form. C_P@C₁ lobes increase slightly which, in combination with smaller N@O lobes, suggests greater alignment between octanol and cation chains.

Further increasing octanol concentrations to 40 v/v% and 50 v/v% causes the N@O lobes to grow larger again, while N_O@O develops additional lobes distributed around the hydroxyl oxygen. At such high octanol concentrations, octanol–octanol interactions become more important and the PAN nanostructure must be accommodated within the shrinking voids between the aggregated octanol network.

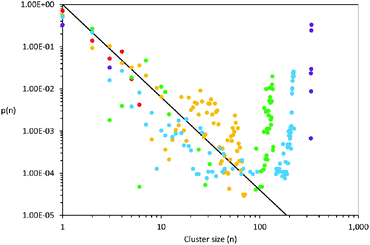
Unlike surfactant micelles in water, the aggregation state of octanol in PAN evolves with concentration from small, discrete clusters into an extended network. This has been assessed via cluster analysis,^71,72 which quantifies the size and continuity of clusters or aggregates. The fitted EPSR simulation boxes were interrogated to determine the probability of finding a cluster of n octanol molecules as a function of cluster size and octanol concentration. In this approach, two molecules are considered to be a part of the same cluster if they are joined by a continuous network of specific atom–atom pairs found within fixed radial limits. The probability distribution for clusters typically follows a power law⁷³ which leads a bicontinuous network when the cluster size distribution crosses the three-dimensional percolation threshold, given by N ∝ n^−2.2 where N is the number of clusters of size n, indicated by the solid line in Fig. 7.^73,74 The presence of percolating structures does not mean that all molecules are contained within a single associated cluster, simply that clusters capable of spanning the bulk can form.

Fig. 7 Cluster analysis of octanol alkyl chain domains. Clusters were identified by a continuous, uninterrupted “chain” of octanol alkyl carbons involving C₈⋯C₈, C₈⋯C₇, C₈⋯C₆ or C₈⋯C₅ atom pairs, where the C atoms were within 7.0, 6.9, 6.8 and 6.4 Å of each other respectively. These chosen distances capture the first coordination shell peaks in the respective g_ij(r) functions for the C⋯C atom pairs. Red dots indicate data for 10 v/v% octanol in PAN, yellow 20 v/v%, green 30 v/v%, blue 40 v/v% and purple 50 v/v%.

Two octanol molecules are considered a part of the same associated cluster if a continuous, uninterrupted “chain” of alkyl chain carbons involving C₈ adjacent to another C₈, C₇, C₆ or C₅ within 7.0, 6.9, 6.8 and 6.4 Å of each other, respectively. C⋯C pairs involving only these carbon atoms were used to ensure that only octanol molecules closely associated are designated as clustered. This same approach has been used previously to determine aggregation numbers for aqueous micelles from EPSR simulations.⁶² The cluster size distributions for the PAN–octanol mixtures at various concentrations are shown in Fig. 7. At 10 v/v% the cluster distribution initially follows the percolation line, before falling below it as expected for a solution that is predominantly dissolved monomer. At 20 v/v%, a broad population of polydisperse aggregates comprising between 20 and 60 octanol molecules forms, again contrasting with the narrow size distribution of aqueous micelles. At concentrations of 30 v/v% and higher, the mixtures contain aggregates that span the simulation box – a bicontinuous structure.

The percentage of octanol monomers are shown in Table 2; for this purpose an octanol molecule is defined as a monomer only if none of its C atoms are within the appropriate radial limits of another octanol molecule.

Table 2 Percentage of octanol monomers in PAN:octanol mixtures determined by cluster analysis

[Octanol] (v/v%)	% Octanol monomers
10	45.4
20	11.4
30	3.3
40	1.1
50	0.1

---

At 10 v/v%, approximately 45% of octanol molecules are monomers. The remainder are associated with 1–3 other octanol molecules, while only a vanishingly small fraction of octanol molecules (∼1–2%) are a part of larger clusters. These small clusters are analogous to the premicellar aggregation observed for conventional surfactants in aqueous solutions.^75–77 This result also suggests that at 10 v/v% the octanol, PAN is approaching its capacity of solvate octanol homogenously without cluster formation.

At 20 v/v% only ∼11% of the octanol molecules are present as monomers. The broad cluster size distribution exceeds the 3D percolation threshold, which means that percolating clusters are beginning to form even at this relatively low alkanol concentration, and polydisperse octanol-rich domains are favoured over discrete structures with well-defined aggregation numbers. The percentage of octanol monomers decreases to just 3% in the 30 v/v% mixture, and continues to fall at higher octanol concentrations. This transition from mostly discrete clusters at 20 v/v% to percolating structures at higher concentrations explains the discontinuous trend in the octanol–octanol g_ij(r) functions in Fig. 5. Irregular octanol alkyl chain packing inside these continuous clusters results in greater variations in octanol C⋯C correlations than in smaller, more discrete clusters where packing is restricted by the energetic drive to maximise internalisation of the alkyl chains. A similar structural evolution has been detected by amplitude modulated atomic force microscope images of near-surface structures of this system.⁷⁸

In previous work we have shown that many solutes^{18,38,39,55,79,80} can alter the underlying sponge-like nanostructure of pure PAN and similar ILs with amphiphilic cations. Recent SAXS/WAXS results suggest that similar effects arise with alkanols,^18,19 but contrast conditions and lower spatial resolution obscure the interpretation. Here we show how monomeric octanol, and octanol clusters, affect the nanostructure of PAN.

Fig. 8 compares partial pair correlation functions between atoms of PAN ions as a function of mixture composition. The pronounced peak in the C_M⋯C_Mg_ij(r) (Fig. 8A), diagnostic for the propyl chain clustering that produces PAN's sponge nanostructure, is markedly decreased in intensity and shifted to larger separations at all octanol contents. Fig. 9 shows the corresponding C_M⋯C_M coordination numbers as a function of octanol concentration. The sharp drop from 2.65 in pure PAN to 1.50 in the 10 v/v% octanol system is due to solvation of monomeric octanol by propylammonium cations, which increases the average spacing between cation methyl groups.

Fig. 8 Atom–atom pair correlations, g_ij(r) functions, for select atom–atom pair correlations in PAN–octanol mixtures. (A) C_M⋯C_M, (B) N_O⋯N, (C) N⋯N, and (D) N_O⋯N_O. Data for Pure PAN are shown by black dashed lines, 10 v/v% octanol by the red lines, 20 v/v% octanol by the yellow lines, 30 v/v% octanol by the green lines, 40 v/v% octanol by the blue lines and 50 v/v% octanol by the purple lines.

Fig. 9 C_M⋯C_M coordination number as a function of octanol concentration derived from the g_ij(r) distribution data extracted from the EPSR models. Coordination numbers were calculated over the range of 0.0–4.5 Å to capture the first g_ij(r) peak.

Increasing the octanol concentration further only weakly affects the C_M⋯C_M peak positions and intensities (Fig. 8), and coordination numbers (Fig. 9) decrease more gradually. This is consistent with the onset of clustering (analogous to a surfactant cmc) occurring between 10 v/v% and 20 v/v% octanol, as suggested by the simulation boxes and cluster analysis. In the presence of clusters, cation chain correlations are only affected by octanol at the interface of the clusters, rather than by every monomer.

In contrast, the correlations between both like and unlike charged centres (i.e. N_O⋯N, N⋯N and N_O⋯N_O), shown in Fig. 8A–C, shift to larger separations in 10 v/v% octanol, then increase markedly and monotonically with the further octanol addition. This increase is an artifact of the reduction in PAN volume fraction and hence average (bulk) atomic density, while local atomic densities are relatively unaltered. This is clearly seen in the coordination numbers in the both the first and second coordination shells (shown in Table 3), which are slightly smaller in mixtures than pure PAN, but which vary little with octanol concentration. This means that a distinct polar ionic domain is present in all mixtures, independent of octanol concentration. The polar domain structure, controlled by strong electrostatic and H-bonding interactions between PAN charge groups, is barely affected by the presence of octanol.

Table 3 Coordination numbers for key propylammonium nitrate (PAN) atom–atom interactions, derived for partial g_ij(r). (α–β) denotes the radius over which the g_ij(r) integration was performed to determine the quoted coordination numbers

	NO–N		ON–HN		N–N		NO–NO		CM–CM
	First shell (0.0–4.4 Å)	Second shell (2.7–6.0 Å)	First shell (0.0–3.0 Å)	Second shell (3.0–4.6 Å)	First shell (0.0–4.4 Å)	Second shell (3.0–6.0 Å)	First shell (0.0–4.0 Å)	Second shell (4.0–7.0 Å)	First shell (0.0–4.5 Å)	Second shell (4.0–6.0 Å)
Pure PAN	4.00	5.70	3.03	7.32	0.56	5.14	0.63	7.24	2.65	4.05
10 v/v% octanol	3.50	5.06	2.43	6.53	0.24	4.04	0.22	6.71	1.56	3.70
20 v/v% octanol	3.39	4.83	2.52	6.30	0.27	3.85	0.26	5.77	1.36	2.88
30 v/v% octanol	3.44	4.94	2.60	6.44	0.31	4.12	0.33	6.09	1.31	2.78
40 v/v% octanol	3.36	4.52	2.50	6.18	0.20	3.72	0.13	5.30	1.21	2.02
50 v/v% octanol	3.60	4.91	2.69	6.72	0.30	4.34	0.31	5.97	0.80	1.99

---

However, there is a slight shift in charge–charge peak positions to higher separations, and the low r peak (at ∼3.4 Å) in the N_O⋯N_O correlation in pure PAN is only a shoulder to the primary peak in the PAN–octanol distributions. Both effects are due to the presence of octanol (hydroxyl) groups between PAN cations.

The three-dimensional probability surfaces for cation around anion and vice versa (N@N_O and N_O@N) are shown as a function of octanol concentration in Fig. 10. Both are remarkably similar across the entire concentration range, consistent with strong electrostatic interactions between these groups and the persistence of polar PAN domains at all compositions studied. The N_O@N distributions have lobes distributed symmetrically around the C₁–N axis adjacent to the three ammonium hydrogens⁶¹ where they form bifurcated H-bonds.⁸¹ The slight variations with concentration are attributed to the presence of octanol molecules solvated between PAN ions. The consistent picture that emerges from g_ij(r), spatial density functions and coordination numbers for PAN polar groups is that the polar domains of PAN resist changes to their structure by octanol addition.

Fig. 10 EPSR SDF reconstructions of the g_ij(r) data for key atom–atom correlations between PAN ions. The lobes represent the 20% probability isosurfaces for the orientation of a selected atom around a central atom.

This conclusion is borne out by cluster analysis of the PAN ionic domains, which is sensitive to the propagation of short range correlations across the EPSR simulation box. Both H_N–O_N (cation–anion H-bonds) and N⋯N_O (cation–anion charge centre) pairs were examined over distances of 3.4 and 5.0 Å, respectively, which were chosen to capture the first coordination shells in the respective g_ij(r) functions. The cluster size distributions obtained showed that ≥99% of the PAN ions are incorporated into a single, continuous cluster at all octanol concentrations; i.e. there is a less than 1% chance of finding a cluster of PAN charged groups, of any size, not continuous with the PAN ionic domain. Even at 50 v/v% added octanol the electrostatic and H-bond polar domain network is still intact and spans the system.

Unlike the PAN charged groups, spatial correlations between the terminal cation methyl carbon atoms (C_M@C_M) are sensitive to octanol concentration, cf.Fig. 10. The coordination numbers are likewise sensitive to concentration, cf.Table 3. In pure PAN a “claw-like” lobe wraps around the C_M carbon, which is the result of tail-to-tail packing of PAN alkyl chains in its native sponge-like nanostructure, with some interdigitation.⁶¹ In the presence of octanol, the probability of chain interdigitation decreases progressively up to 30 v/v%. This is due to the presence of octanol alkyl chains between cation alkyl chains favouring tail-to-tail packing of PAN cations and reducing the C_M⋯C_M coordination number. At 40 v/v%, and 50 v/v% the spatial arrangement reverts towards that seen in pure PAN. This suggests that, as the octanol monomer concentration decreases (Table 2), the packing of cation alkyl chains within the remaining PAN domains more closely resembles the pure IL.

Cluster analysis of the PAN apolar domains reveals the very different roles of the polar and nonpolar components of PAN in these mixtures. Fig. 11 shows the cluster distributions obtained using C_M⋯C_M and C_M⋯C_P atom pairs with radii of 5.0 and 4.8 Å, respectively. Unlike the polar domains, the size and extent of the PAN apolar domain depends strongly on mixture composition. At octanol concentrations 30 v/v% or lower, the PAN apolar domain percolates throughout the simulation box, but at both 40 v/v% and 50 v/v% octanol, only discrete clusters are present. This change explains the increased size of the interdigitation in the C_M⋯C_M SDF plots for the 40 and 50 v/v% mixtures in Fig. 10.

Fig. 11 Cluster analysis of PAN alkyl chain domains. Clusters were identified by a continuous, uninterrupted “chain” of PAN alkyl carbons involving C_M⋯C_M or C_M⋯C_P atom pairs where the C atoms were within 5.0 and 4.8 Å of each other respectively. These distances capture the first coordination shell peaks in the g_ij(r) functions for the respective atom pairs. Red dots indicate data for 10 v/v% octanol in PAN, yellow 20 v/v%, green 30 v/v%, blue 40 v/v% and purple 50 v/v%.

Conclusions

The amphiphilicity and resultant underlying nanostructure of PAN as a solvent enables the self-assembly of the non-surfactant octanol molecule. On the one hand, the strong electrostatic and H-bonding interactions between ammonium and nitrate charged centres responsible for the polar domain network in PAN provide the driving force for the solvophobic segregation of octyl (and even longer alkyl) chains. This local polar domain structure is resilient, and not only persists in PAN up to very high octanol concentrations, but preserves its long-range bicontinuity, suggesting that conductivity and other transport properties will be preserved in such mixtures, at least for polar species.

Octanol is not itself a better amphiphile in PAN than it is in water. It has a higher solubility due to the lower (average) polarity environment. However its aggregates are poorly-defined compared to surfactant micelles, in terms of the low degree of polar/apolar segregation, a lack of well-defined shape, and high polydispersity. Octanol aggregates grow rapidly with increasing concentration, without distinct geometry, and ultimately without bound. The small area of the polar hydroxyl group that is mostly responsible for octanol's inability to form micelles in water remains significant in PAN; the OH group does form H-bonds with both ammonium and nitrate cations, but overall is only weakly solvated by the polar domains of PAN, as its first coordination shell contains atoms of both polar and apolar groups.

Miscibility of octanol is instead conferred by the amphiphilicity of the propylammonium cations. By adapting the PAN bicontinuous nanostructure, they form an oriented monolayer on exposed alkanol chains within clusters, allowing them to be accommodated within swollen and distorted apolar domains; this is sufficient to stabilise aggregates and prevent phase separation. As the octanol concentration increases, it is the propyl tails of the cation that respond and reorganise around the changing aggregates, eventually breaking down their own bicontinuous apolar network into discrete clusters while preserving the polar domain network.

These results illuminate how nanostructured liquids like PAN perform so effectively as solvents for complex solutes and solute mixtures.

In their pioneering studies of alkylpyridinium bromide micelles in ethylammonium nitrate (EAN), Evans et al.⁸² first proposed that the ethylammonium cation acts as a co-surfactant as well as a solvent. Several more recent investigations of amphiphile systems in EAN^5,83,84 and PAN¹⁵ have supported this conclusion. This work, however, points to an even stronger role than a cosurfactant, in which the IL cation is not a cosurfactant incorporated into a pre-existing aggregate, but is essential to the aggregate's very formation and stability.

This behaviour has parallels with weakly structured, ternary “surfactant-free” microemulsions,^6,8 in which octanol aggregates are stabilised by strong adsorption of ethanol onto the aggregate interface.¹¹ This necessarily requires an ethanol composition gradient between the aqueous and octanol “phases” and an excess at the interface. However, in PAN:octanol mixtures, PAN is the solvent, and stabilises aggregates by changes in its local structure.

Ionic liquid nanostructure is readily tunable by simple changes in cation and anion structure, and this shows great promise for controlling the solubility and aggregation behaviour of a diverse range of organic solutes. While octanol is completely miscible with both PAN and ethylammonium formate, it is only partially miscible with EAN, and sparingly soluble in ethanolammonium nitrate and formate.^19,29,30 Like PAN, the polar network in EAN solvophobically excludes octanol above its monomer solubility limit, but its hydrophobic domains comprised of shorter ethyl cation chains less effectively stabilise exposed octanol alkyl chains at the cluster surfaces, and phase separation ensues. This mechanism explains the differences seen in SAXS patterns of alkanols mixed with EAN and PAN.^19,34 Ethylammonium formate has a less pronounced bulk nanostructure than either EAN or PAN,⁸⁵ so we propose that its miscibility with octanol results from a weaker solvophobic driving force, and that fewer, smaller aggregates would form. Ethanolammonium nitrate and formate are both ineffective due to their non-amphiphilic cations and lack of nanostructure.

These results also have implications for other non-aqueous solvent classes. Amphiphilic solvents derived from amides,⁸⁶ diols,²¹ or deep eutectic solvents,^9,87,88 for example, may be used to dissolve amphiphilic solutes, to generate weakly-structured fluids, or may support self-assembly of non-traditional surfactants.

Acknowledgements

RH thanks AINSE for a PGRA. TM thanks the University of Newcastle for a PhD stipend. RA thanks the ARC for a Future Fellowship. This research was supported by an ARC Discovery Project and an ISIS beamtime grant.

References

1. L. Auvray, J. P. Cotton, R. Ober and C. Taupin, J. Phys. Chem., 1984, 88, 4586.
2. M. Kahlweit, R. Strey and G. Busse, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 4197.
3. M. Kahlweit, R. Strey and G. Busse, J. Phys. Chem., 1990, 94, 3881.
4. B. Widom, Langmuir, 1987, 3, 12.
5. R. Atkin and G. G. Warr, J. Phys. Chem. B, 2007, 111, 9309.
6. M. L. Klossek, D. Touraud, T. Zemb and W. Kunz, ChemPhysChem, 2012, 13, 4116.
7. J. Xu, A. L. Yin, J. K. Zhao, D. X. Li and W. G. Hou, J. Phys. Chem. B, 2013, 117, 450.
8. S. Schottl, J. Marcus, O. Diat, D. Touraud, W. Kunz, T. Zemb and D. Horinek, Chem. Sci., 2014, 5, 2949.
9. V. Fischer, J. Marcus, D. Touraud, O. Diat and W. Kunz, J. Colloid Interface Sci., 2015, 453, 186.
10. J. Marcus, D. Touraud, S. Prevost, O. Diat, T. Zemb and W. Kunz, Phys. Chem. Chem. Phys., 2015, 17, 32528.
11. O. Diat, M. L. Klossek, D. Touraud, B. Deme, I. Grillo, W. Kunz and T. Zemb, J. Appl. Crystallogr., 2013, 46, 1665.
12. W. A. Hamilton and L. Porcar, J. Phys.: Conf. Ser., 2010, 251, 012034.
13. B. Angelov, A. Angelova, R. Mutafchieva, S. Lesieur, U. Vainio, V. M. Garamus, G. V. Jensen and J. S. Pedersen, Phys. Chem. Chem. Phys., 2011, 13, 3073.
14. T. Sottmann, R. Strey and S. H. Chen, J. Chem. Phys., 1997, 106, 6483.
15. R. Atkin, S. M. C. Bobillier and G. G. Warr, J. Phys. Chem. B, 2010, 114, 1350.
16. S. Schöttl, D. Touraud, W. Kunz, T. Zemb and D. Horinek, Colloids Surf., A, 2015, 480, 222.
17. J. D. Shaw, Introduction to Colloid and Surface Chemistry, Butterworth-Heinemann Elsevier Science Ltd., Oxford, 4th edn, 1992.
18. T. L. Greaves, D. F. Kennedy, N. Kirby and C. J. Drummond, Phys. Chem. Chem. Phys., 2011, 13, 13501.
19. H. J. Jiang, P. A. FitzGerald, A. Dolan, R. Atkin and G. G. Warr, J. Phys. Chem. B, 2014, 118, 9983.
20. T. L. Greaves and C. J. Drummond, Chem. Soc. Rev., 2013, 42, 1096.
21. A. Ray, Nature, 1971, 231, 313.
22. D. F. Evans, Langmuir, 1988, 4, 3.
23. R. G. Laughlin, The aqueous phase behavior of surfactants, Academic Press, 1994.
24. M. Teubner and R. Strey, J. Chem. Phys., 1987, 87, 3195.
25. R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357.
26. R. Atkin and G. G. Warr, J. Phys. Chem. B, 2008, 112, 4164.
27. T. L. Greaves, D. F. Kennedy, S. T. Mudie and C. J. Drummond, J. Phys. Chem. B, 2010, 114, 10022.
28. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 3237.
29. H. Weingärtner, M. Kleemeier, S. Wiegand and W. Schröer, J. Stat. Phys., 1995, 78, 169.
30. W. Schröer, S. Wiegand and H. Weingärtner, Berichte der Bunsengesellschaft für physikalische Chemie, 1993, 97, 975.
31. H. Weingärtner, T. Merkel, S. Käshammer, W. Schröer and S. Wiegand, Berichte der Bunsengesellschaft für physikalische Chemie, 1993, 97, 970.
32. K. V. Schubert, R. Strey, S. R. Kline and E. W. Kaler, J. Chem. Phys., 1994, 101, 5343.
33. L. S. Ornstein and F. Zernike, Proc. Natl. Acad. Sci. U. S. A., 1914, 17, 793.
34. W. Schroer, A. Triolo and O. Russina, J. Phys. Chem. B, 2016, 120, 2638–2643.
35. G. D'Arrigo, J. Teixeira, R. Giordano and F. Mallamace, J. Chem. Phys., 1991, 95, 2732.
36. R. D. Koehler, K. V. Schubert, R. Strey and E. W. Kaler, J. Chem. Phys., 1994, 101, 10843.
37. A. A. H. Padua, M. F. Gomes and J. Lopes, Acc. Chem. Res., 2007, 40, 1087.
38. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., Int. Ed., 2012, 51, 7468.
39. T. Murphy, R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2014, 16, 13182.
40. T. Murphy, S. K. Callear, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2016.
41. I. L. Topolnicki, P. A. FitzGerald, R. Atkin and G. G. Warr, ChemPhysChem, 2014, 15, 2485.
42. B. Fernandez-Castro, T. Mendez-Morales, J. Carrete, E. Fazer, O. Cabeza, J. R. Rodriguez, M. Turmine and L. M. Varela, J. Phys. Chem. B, 2011, 115, 8145.
43. A. Dolan, R. Atkin and G. G. Warr, Chem. Sci., 2015, 6, 6189.
44. J. A. Smith, G. B. Webber, G. G. Warr and R. Atkin, J. Phys. Chem. B, 2013, 117, 13930.
45. G. L. Burrell, N. F. Dunlop and F. Separovic, Soft Matter, 2010, 6, 2080.
46. A. Takada, K. Imaichi, T. Kagawa and Y. Takahashi, J. Phys. Chem. B, 2008, 112, 9660.
47. J. J. Segura, A. Elbourne, E. J. Wanless, G. G. Warr, K. Voitchovsky and R. Atkin, Phys. Chem. Chem. Phys., 2013, 15, 3320.
48. R. Hayes, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2010, 12, 1709.
49. D. Wakeham, A. Nelson, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 20828.
50. C. Ridings, G. G. Warr and G. G. Andersson, Phys. Chem. Chem. Phys., 2012, 14, 16088.
51. R. A. Asencio, E. D. Cranston, R. Atkin and M. W. Rutland, Langmuir, 2012, 28, 9967.
52. O. Werzer, E. D. Cranston, G. G. Warr, R. Atkin and M. W. Rutland, Phys. Chem. Chem. Phys., 2012, 14, 5147.
53. C. C. Weber, A. F. Masters and T. Maschmeyer, Angew. Chem., Int. Ed., 2012, 51, 11483.
54. C. C. Weber, A. F. Masters and T. Maschmeyer, Green Chem., 2013, 15, 2655.
55. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 13544.
56. A. K. Soper, W. S. Howells and A. C. Hannon, ATLAS: analysis of time-of-flight diffraction data from liquid and amorphous samples, Rutherford Appleton Laboratory, Didcot, 1989.
57. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 3237.
58. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225.
59. H. V. R. Annapureddy, H. K. Kashyap, P. M. De Biase and C. J. Margulis, J. Phys. Chem. B, 2010, 114, 16838.
60. B. Hammouda, S. Krueger and C. J. Glinka, J. Res. Natl. Inst. Stand. Technol., 1993, 98, 31.
61. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 13544.
62. R. Hargreaves, D. T. Bowron and K. Edler, J. Am. Chem. Soc., 2011, 133, 16524.
63. K. J. Edler and D. T. Bowron, Curr. Opin. Colloid Interface Sci., 2015, 20, 227.
64. C. Tanford, J. Phys. Chem., 1972, 76, 3020.
65. C. Tanford, J. Phys. Chem., 1974, 78, 2469.
66. J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525.
67. F. M. Menger, Acc. Chem. Res., 1979, 12, 111.
68. Y. Chevalier and T. Zemb, Rep. Prog. Phys., 1990, 53, 279.
69. I. Rozas, I. Alkorta and J. Elguero, J. Phys. Chem. A, 1998, 102, 9925.
70. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48.
71. L. Dougan, S. P. Bates, R. Hargreaves, J. P. Fox, J. Crain, J. L. Finney, V. Réat and A. K. Soper, J. Chem. Phys., 2004, 121, 6456.
72. J. J. Towey, A. K. Soper and L. Dougan, J. Phys. Chem. B, 2012, 116, 13898.
73. N. Jan, Physica A, 1999, 266, 72.
74. J. J. Towey, A. K. Soper and L. Dougan, Faraday Discuss., 2013, 167, 159.
75. X. H. Cui, S. Z. Mao, M. L. Liu, H. Z. Yuan and Y. R. Du, Langmuir, 2008, 24, 10771.
76. N. D. Gillitt, G. Savelli and C. A. Bunton, Langmuir, 2006, 22, 5570.
77. R. Hadgiivanova and H. Diamant, J. Phys. Chem. B, 2007, 111, 8854.
78. A. Elbourne, S. Cronshaw, K. Voitchovsky, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2015, 17, 26621.
79. O. Russina, A. Sferrazza, R. Caminiti and A. Triolo, J. Phys. Chem. Lett., 2014, 5, 1738.
80. L. M. Varela, T. Méndez-Morales, J. Carrete, V. Gómez-González, B. Docampo-Álvarez, L. J. Gallego, O. Cabeza and O. Russina, J. Mol. Liq., 2015, 210(Part B), 178.
81. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., Int. Ed., 2013, 52, 4623.
82. D. F. Evans, A. Yamauchi, G. J. Wei and V. A. Bloomfield, J. Phys. Chem., 1983, 87, 3537.
83. T. L. Greaves, A. Weerawardena, C. Fong and C. J. Drummond, J. Phys. Chem. B, 2007, 111, 4082.
84. Z. F. Chen, T. L. Greaves, R. A. Caruso and C. J. Drummond, J. Phys. Chem. B, 2015, 119, 179.
85. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, J. Phys. Chem. C, 2014, 118, 13998.
86. T. L. Greaves, A. Weerawardena and C. J. Drummond, Phys. Chem. Chem. Phys., 2011, 13, 9180.
87. A. P. Abbott, D. Boothby, G. Capper, D. L. Davies and R. K. Rasheed, J. Am. Chem. Soc., 2004, 126, 9142.
88. Q. Zhang, K. De Oliveira Vigier, S. Royer and F. Jerome, Chem. Soc. Rev., 2012, 41, 7108.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp01739h

---