Structural investigations on a linear isolated depsipeptide: the importance of dispersion interactions

Abstract

In this paper we present the first investigations on an isolated linear depsipetide CyCO-Gly-Lac-NH-PhOMe (cyclohexylcarbonyl-glycine-lactate-2-anisidine abbreviated as MOC) in a molecular beam experiment. Depsipeptides are a special subclass of peptides which contain at least one ester bond replacing a peptide bond. This leads to a different folding behavior and a different biological activity compared to a “normal” peptide. In order to analyze the folding of an isolated depsipeptide on a molecular level a variety of combined IR/UV methods including IR/IR/UV experiments are applied to MOC. Three different isomers are identified in combination with DFT calculations using the hybrid functional B3LYP-D3 with a TZVP basis set. The most stable structure shows a tweezer-like arrangement between the aromatic chromophore and the aliphatic cyclohexyl ring. A characteristic feature of this structure is that it is stabilized by dispersion interactions resulting from CH/π interactions. If dispersion is not taken into account this structural arrangement is no longer a minimum on the potential energy surface indicating the importance of dispersion interactions.

---

I Introduction

Depsipeptides are an important class of natural products showing diverse biological activity. As a special subclass of peptides they contain at least one ester bond replacing a peptide bond¹ which gives rise to a different folding behavior compared to an ordinary peptide and probably leads to a different biological activity. Many of their linear representatives have strong physiological effects on higher organisms: as a first example dolastatin 15 is found to be a cytostatic anti-cancer agent.² Moreover, linear depsipeptides are not only employed as substructures in chiral dendrons, being widely used as model compounds for natural macromolecules,³ but also serve as Förster resonance energy transfer (FRET) substrates,⁴ representing important biochemical tools e.g. in hepatitis C anti-viral research.⁵ Furthermore, a β-turn forming depsipeptide has been used as a bridge in a porphyrin–quinone donor–acceptor system showing an efficient electron transfer via the hydrogen bond interface where the ester linkages allow the control of the hydrogen-bonding pattern.⁶ Besides the linear depsipeptides, there is a large group of naturally occurring cyclic depsipeptides including beauvericin and valinomycin, which are well-known for their antibiotic and insecticidal effects.^7–9 For both valinomycin and beauvericin their biological activity is attributed to their ability to reversibly bind alkali metal ions and transport them across cell membranes causing apoptosis.¹⁰ In order to explicitly understand the physiological effects induced by these molecules on a molecular level, knowledge on the structure of the isolated neutral molecules is fundamental.

To the best of our knowledge, no spectroscopic investigations on any depsipeptide in a molecular beam experiment have been published so far. Thus we start here with a linear depsipeptide. Fig. 1 shows the investigated molecule which will be referred to as either cyclohexylcarbonyl-glycine-lactate-2-anisidine (CyCO-Gly-Lac-NH-PhOMe) using the peptide nomenclature or [1-[(2-m̲ethoxyphenyl)amino]-1-o̲xopropane-2-yl] 2-(c̲yclohexanecarbonylamino)acetate (MOC) using the IUPAC nomenclature. It contains a glycine residue (Gly) as well as a lactic acid residue (Lac) and therefore represents a depsipeptide whose structural investigation should give basic insights into the preferred conformations of isolated depsipeptides. Furthermore the system contains both an aromatic phenyl ring and an aliphatic cyclohexyl ring. These two groups offer the possibility to interact via CH/π dispersion interactions.

Fig. 1 Schematic illustration of the investigated linear depsipeptide MOC.

With respect to investigations in the condensed phase Gallo and Gellman¹¹ investigated the folding of several depsipeptide models for both β-turns and α-helical turns mediated by hydrogen bonds using molecular mechanics calculations and IR spectroscopy in CH₂Cl₂ solution. The investigated samples include Ac-L-Ala-Glyco-NHMe and Ac-L-Ala-Glyco-NMe₂, the former showing a β-turn and the latter exhibiting no significant hydrogen-bonding in solution. Moreover, Boussard and coworkers¹² published IR spectroscopic studies in CCl₄ solution at room temperature along with theoretical investigations on small depsipeptides. In that study, the molecule t-Bu-Gly-Lac-NH-Me, being most similar to the herein investigated CyCO-Gly-Lac-NH-PhOMe, shows more bands as expected which arise from overlapping absorption bands in the amide A region suggesting the existence of more than one conformer in solution. Further investigations by Boussard et al.¹³ on another set of depsipeptides revealed that in the solid state only van-der-Waals interactions exist between neighboring molecules and consequently the solid state structure is nearly identical to that in solution.

Quantum-mechanics and molecular-mechanics based calculations and simulations on oligodepsipeptides including alternating Gly and Lac residues were published by Zhang and coworkers,¹⁴ concluding that the polyproline II (PPII)-helix leading to a right-handed helical structure is the most stable configuration for the Gly-Lac oligodepsipeptide. A theoretical study on the L-lactic acid residue performed by Kang et al.¹⁵ revealed that the trans orientation of the ester bond is by far the preferred one and the cis population is negligible.

In order to obtain structural information on a molecular level the absence of solvent molecules is a basic premise. Due to the flexible backbone of (depsi)peptides the existence of several almost isoenergetic conformers can be expected, which moreover requires isomer selective techniques. All these requirements can be fulfilled by applying combined IR/UV laser spectroscopy in a molecular beam experiment. These techniques have proven to be useful for investigating “normal” peptides and cyclopeptides, cf. e.g., ref. 16–35.

In this paper we publish the first investigation on a linear depsipeptide in a molecular beam. In the chosen CyCO-Gly-Lac-NH-PhOMe molecule the C- and N-termini of the glycine and lactate units are protected by a cyclohexyl carbonyl and a 2-anisidine group (see Fig. 1). The latter includes an aromatic chromophore which allows the application of the IR/R2PI method^36–38 (see also ref. 16–32, 34 and 35). Therefore, the structurally sensitive NH stretching (amide A) and carbonyl stretching as well as NH bending (amide I/II) vibrations can serve as spectroscopic probes giving direct structural information. In order to distinguish between possible isomers with overlapping electronic resonances the IR/IR/R2PI method^39–41 can be a useful tool.

In order to assign structures, DFT calculations including dispersion corrections were performed and compared with the experimental IR spectra. Dispersion corrections are of significant importance when using DFT calculations not only to investigate folded structures of organic molecules in general, as it was shown e.g. for the hydrated dimer of a coumarin derivative⁴² and several peptides,^29,43–53 but also in particular when CH/π interactions are involved. These interactions play an important role in chemistry and biology, cf. e.g.ref. 54 and are often underestimated. In recent years, several experimental and theoretical investigations on the CH/π interactions have been reported, cf. e.g.ref. 20, 50, 51 and 55–62 including molecular beam measurements on peptides (cf.ref. 20 and 55). In previous investigations Ran and Wong⁶³ analyzed the cooperative CH/π effects between the π face of benzene and the aliphatic CH groups of cyclohexane using high-level ab initio calculations. These results demonstrated that multiple CH/π interactions play an important role in stabilizing the complex. If a deformation of the backbone of the investigated depsipeptide occurs intramolecular CH/π interactions can be formed between aliphatic CH groups of the CyCO unit and an aromatic π system of the NH-PhOMe unit. Therefore this possible CH/π arrangement of MOC is a further interesting feature to be investigated.

II Experimental setup

The used experimental setup is described in detail elsewhere,^16,64 so only a brief description is given here. All spectra were recorded in a molecular beam apparatus consisting of a pulsed valve (General Valve Iota One, 500 μm orifice) for skimmed jet expansion and a differentially pumped time-of-flight mass spectrometer. The investigated sample, purchased from Ambinter, was heated to 120 °C for jet expansion and neon was used as a carrier gas (1.8 bar).

For the IR/IR/R2PI technique three independent laser systems (one UV and two IR laser systems) are required. The UV laser radiation was generated by a frequency-doubled dye laser (Sirah, Cobra Stretch). The two independent IR laser systems have different setups. The first IR laser⁶⁵ generates the IR light (here 3300–3750 cm⁻¹) with a LiNbO₃ crystal by difference frequency mixing (DFM I) of the fundamental (1064 nm) of a seeded Nd:YAG laser (Spectra-Physics, PRO-230) and the output of a dye laser (Sirah, Precision Scan) being pumped by the second harmonic (532 nm) of the same Nd:YAG laser. The obtained IR radiation is amplified in a second LiNbO₃ crystal by an optical parametric amplification (OPA) process using the output of the DFM I process and again the fundamental of the Nd:YAG laser. The spectral region of CO stretching and NH bending vibrations is covered with a further non-linear process (DFM II):⁶⁵ signal and idler radiation from the OPA process are mixed in an AgGaSe₂ crystal to obtain IR light in the relevant region of 1380–1900 cm⁻¹.

The second IR laser generates the IR light in the region of 3300–3750 cm⁻¹ with a recently modified laser system: in a first conversion stage IR light in the region of 5748–6099 cm⁻¹ is generated via the DFM I process in a LiNbO₃ crystal using the fundamental (1064 nm) of a Nd:YAG laser (Innolas, Spitlight 1000) and the output of a dye laser (Sirah, Precision Scan) being pumped by the second harmonic (532 nm) of the same Nd:YAG laser. In a second conversion stage an OPA process via two KTA (KTiOAsO₄) crystals in series generates the amplified DFM I radiation and the IR light in the region of 3300–3750 cm⁻¹ using the DFM I output and again the fundamental of the Nd:YAG laser.

In order to record the IR/R2PI spectra, the IR laser was fired 50 ns prior to the UV laser, whereas for the IR/IR/R2PI measurements the frequency-fixed IR burn laser was fired 100 ns prior to the UV laser. For the IR_fixed/R2PI experiment the frequency-fixed IR laser is fired 50 ns prior to the scanning UV laser.

III Calculations

Possible starting geometries for MOC were derived from molecular dynamics calculations with the consistent force field (CFF) as implemented in the Discovery studio.⁶⁶ (For further details of this procedure, cf. e.g.ref. 24, 29, 48 and 67.) All structural binding motifs obtained from these calculations as well as geometries obtained from further screening with respect to the Φ, Ψ and ω angles are taken as starting geometries for DFT calculations. The DFT calculations were performed with a combination of the two programs Gaussian 09⁶⁸ and Turbomole V6.6⁶⁹ by using the hybrid functional B3LYP with a triple zeta basis set (TZVP) implemented in Turbomole: geometry optimizations were done using the Berny algorithm as implemented in Gaussian 09⁶⁸ whereas energies and gradients were taken from the Turbomole program.⁶⁹ These calculations were realized with the inclusion of Grimme D3 dispersion interactions.⁷⁰ The relative energies including zero-point corrections refer to the most stable isomer.

For the correction of the harmonically calculated vibrational frequencies scaling factors were derived from reference calculations with the well investigated peptide systems (AcPheNHMe)_1,2⁶⁷ and (AcPheOMe)_1,2^16,17 at the same level of theory (DFT/B3LYP-D3/TZVP). The IR/R2PI spectra of different isomers of these species are compared with the calculations leading to appropriate scaling factors. According to these references amide A modes were scaled by a factor of 0.9608 for free NH stretching vibrations, 0.9563 for the vibrations of hydrogen-bonded NH groups and carbonyl stretching and NH bending vibrations were scaled by 0.9850. The application of mode specific scaling factors is further supported by Bouteiller et al.:^71,72 they investigated the correction of the harmonically calculated vibrational frequencies with different MP2 and DFT-(D) methods discussing local and mode specific scaling factors for the interpretation of the IR spectra of biomolecules.

Linear depsipeptides show a high flexibility with respect to the backbone. Based on the Ramachandran plot^73,74 different backbone conformations (Φ and Ψ) and the dihedral angle (ω) describing the relative position of the NH group with respect to the CyCO or NH-PhOMe group (cis or trans orientations) have to be discussed. (For definitions of these dihedral angles, see Fig. 1.) Due to the DFT calculations of MOC 64 different conformers have been found within a relative energy range of 4000 cm⁻¹. Six selected structures are presented in Fig. 2. Further conformers are shown in the ESI† (see Fig. S1 and Table S2). The relative stabilities of these six selected structures obtained at the DFT level (B3LYP-D3/TZVP) and the corresponding dihedral angles based on the Ramachandran plot Φ_Gly, Ψ_Gly, Φ_Lat and Ψ_Lat and ω₁ and ω₂ are listed in Table 1. Important bond lengths and bond angles calculated at the same level of theory are listed in Table 2.

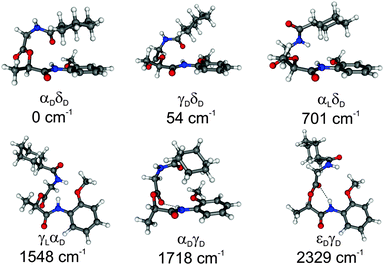Fig. 2 Selected conformers of MOC and their relative energies obtained from DFT calculations (B3LYP-D3/TZVP). For further structures cf. Fig. S1 (ESI†).

Table 1 Geometry parameters of selected structures of MOC (cf.Fig. 2) as obtained from DFT calculations (B3LYP-D3/TZVP). The dihedral angles (in degrees) Φ_Gly, Ψ_Gly, Φ_Lat and Ψ_Lat describing the backbone and the dihedral angles ω₁ and ω₂ describing the amide bond (cis/trans) of the linear depsipeptide are listed (cf.Fig. 1). Furthermore the relative energies (in cm⁻¹) are given

	ΔE	Φ Gly	Ψ Gly	Φ Lat	Ψ Lat	ω 1	ω 2
αDδD	0	64.4	10.7	143.1	−55.6	−167.5	174.0
γDδD	54	94.6	−13.0	151.5	−22.8	−166.5	−177.4
αLδD	701	−71.0	−8.0	159.3	−13.4	164.0	175.9
γLαD	1548	−79.3	26.7	84.8	18.4	−11.4	−178.7
αDγD	1718	87.4	46.1	81.6	−53.0	−169.6	167.5
εDγD	2329	67.2	146.7	91.4	−63.3	22.5	171.6

---

Table 2 Geometry parameters obtained for six different structures of MOC calculated at the DFT/B3LYP-D3/TZVP level of theory. The bond lengths are given in Å and the bond angles in degrees. (For further geometry parameters cf. Table S1, ESI)

	αDδD	γDδD	αLδD	γLαD	αDγD	εDγD
r N1–H1	1.007	1.008	1.007	1.012	1.007	1.012
r N2–H2	1.014	1.011	1.009	1.011	1.014	1.013
r C1–O1	1.224	1.222	1.22	1.223	1.221	1.223
r C3–O2	1.204	1.203	1.202	1.202	1.207	1.209
r C5–O3	1.219	1.220	1.218	1.217	1.220	1.218
r O4–C4	1.457	1.456	1.450	1.452	1.466	1.469
r H2–O2	—	—	—	—	2.071	2.116
θ N1–C2–C3	115.9	115.9	115.1	115.9	112.8	112.4
θ H1–N1–C2	117.9	117.6	117.3	116.6	116.5	115.7
θ H2–N2–C5	117.9	117.0	115.6	116.6	117.5	117.4
θ C2–C3–O4	112.1	112.5	111.3	111.6	112.1	111.5
θ O1–C1–N1	120.9	121.8	121.1	120.0	121.5	119.5
θ O4–C3–O2	125.1	124.6	124.8	125.0	125.4	124.9
θ C4–O4–C3	118.5	117.6	119.5	117.9	123.5	118.6

---

The calculated structures of MOC obtained at the DFT/B3LYP-D3/TZVP level show that folded conformers are significantly more stable than stretched conformers which applies e.g. to the structures α_Dδ_D, γ_Dδ_D and α_Lδ_D. A deformation of the backbone can be energetically compensated for example by the formation of stabilizing hydrogen bonds (see Table 2). However, in the case of the most stable conformer α_Dδ_D a tweezer-like shape without a hydrogen bond is formed. This structure is stabilized by intramolecular CH/π interactions involving the π system of the PhOMe unit and three axial CH bonds of the CyCO residue (cf. Section IV).

For the structures γ_Dδ_D and α_Lδ_D (54 and 701 cm⁻¹ less stable than α_Dδ_D) the tweezer-like shape is more open than in the most stable conformer. Therefore, the stabilization by CH/π interactions is weaker. The isomers γ_Lα_D and ε_Dγ_D are 1548 and 2329 cm⁻¹ less stable than the structure α_Dδ_D. They exhibit a cis orientation of the amide group of the glycine unit (see Table 1ω₁ is about 0°). The stabilization of the basically less stable cis isomers takes place due to dispersion interactions in γ_Lα_D and due to the formation of a hydrogen bond (2.116 Å) in the ε_Dγ_D structure. The structure α_Dγ_D (1718 cm⁻¹ less stable than α_Dδ_D) is stabilized by both the formation of a hydrogen bond (2.071 Å) and dispersion interactions arising from one CH/π interaction of the equatorial CH group of the CyCO unit with the NH-PhOMe residue. (Conformations with multiple CH/π interactions are energetically more favored and CH/π interactions of the equatorial CH groups are less stable than the interaction of the axial CH groups.)⁶³

Furthermore the Gibbs free energies of the six selected isomers are calculated for different temperatures (50, 100, 200 and 298 K), cf. Tables S8–S11 (ESI†). Due to the small energy difference between the α_Dδ_D and γ_Dδ_D structures the different entropy contributions can change the order of energies at a temperature of about 60 K. Nevertheless, these structures are nearly isoenergetic (within temperatures of about 100 K) whereas the hydrogen-bonded structures (like α_Dγ_D) are still less stable and the gain in entropy does not lead to a smaller energy difference with respect to the most stable structures.

Calculations were also performed without the inclusion of dispersion corrections at the same level of theory (B3LYP functional as implemented in Turbomole/TZVP) using Gaussian 09.⁶⁸ A selection of calculated structures without dispersion corrections including the relative stabilities, corresponding dihedral angles based on the Ramachandran plot and geometry parameters, are shown in the ESI† (see Fig. S4 and Tables S6 and S7).

The calculated structures of MOC obtained at the DFT/B3LYP/TZVP level show, in contrast to the calculated isomers including dispersion interactions, that stretched conformers are more stable than folded conformers. Interestingly, the α_Dδ_D structure (cf.Fig. 3a) is only observed if dispersion interactions are taken into account (at least within a relative energy of 4000 cm⁻¹ with respect to the most stable β_Lδ_L structure). This isomer is stabilized by forming intramolecular CH/π interactions between the axial aliphatic CH groups of the CyCO unit and the aromatic π system of the NH-PhOMe unit. This stabilization is much larger than other interactions, especially the tension of the backbone (compared to arrangement β_Lδ_L without dispersion interactions) is compensated by the dispersion interactions.

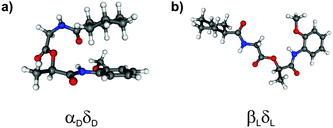Fig. 3 Most stable conformers of MOC obtained from DFT calculations (a) with dispersion corrections and (b) without dispersion corrections.

Furthermore the most stable isomer β_Lδ_L resulting from calculations at the DFT/B3LYP/TZVP level of theory is not observed if dispersion interactions are taken into account (see Fig. 3b). The structures γ_Dδ_D, α_Lδ_D, ε_Dγ_D and α_Dγ_D can also be found as minimum structures without including dispersion interactions (641, 1250, 2757 and 3446 cm⁻¹ less stable than the β_Lδ_L isomer). These isomers are less stable due to the loss of stabilization by dispersion interactions.

IV Results and discussion

An one-color R2PI spectrum of MOC has been recorded in the range of 31 700–37 590 cm⁻¹, cf.Fig. 4a (expansion gas neon). In the vicinity of the electronic origin(s) the spectrum consists of three broadened prominent transitions at 34 637, 35 071 and 35 149 cm⁻¹. It is an interesting effect that no significant change in the broadening is observed by using helium as expansion gas. This is untypical, since usually a better cooling in neon reduces the bandwidths. It should be mentioned that no hydrates of MOC are observed and also fragmentation from hydrates can be excluded (cf. results of the IR/R2PI spectra below, here no vibrational transitions in the OH stretching region above 3600 cm⁻¹ are observed). A possible explanation of the broadening may result from the excited state lifetimes. Excited state lifetime measurements performed by the method of time-correlated single-photon counting (cf. ESI†) in CH₂Cl₂ solution show a mono-exponential lifetime decay. For MOC a lifetime of about 2 ns was obtained, whereas e.g. the well investigated protected amino acid AcPheOMe^16,17 shows an averaged lifetime of about 4 ns (with a long lifetime component of about 12 ns). Although these results are obtained from measurements in solution it can be concluded that the excited sate lifetime of MOC is significantly lower than for AcPheOMe. An indication of a similar behavior in the gas phase might be that no excited state lifetime of MOC could be derived from a two-color R2PI experiment with a time delay between the two ns lasers. Thus in the case of a broadened R2PI spectrum further strategies have to be chosen to figure out if electronic transitions result from an overlap of different isomers. Here e.g. IR/IR methods are ideal applications which are discussed below.

Fig. 4 (a) R2PI spectrum of MOC in the range of 31 700–37 590 cm⁻¹, (b–e) IR_fixed/R2PI spectra of MOC by using different frequency-fixed burn laser frequencies at (b) 3386, (c) 3408, (d) 3414 and (e) 3440 cm⁻¹. The IR_fixed/R2PI spectra are given in red and the corresponding R2PI spectra are given in black.

In order to derive detailed structural information from the IR/R2PI spectra of MOC both the spectral region of the NH stretching vibrations from 3300 to 3750 cm⁻¹ as well as the carbonyl stretching and NH bending modes from 1380 to 1900 cm⁻¹ were measured for the different resonances of the R2PI spectrum (see Fig. 5a–c).

Fig. 5 IR/R2PI spectra of MOC obtained via different resonances of the R2PI spectrum at (a) 34 637, (b) 35 071 and (c) 35 149 cm⁻¹.

The IR/R2PI spectrum in Fig. 5a has been recorded via the first main resonance of the R2PI spectrum at 34 637 cm¹. The spectrum is clearly structured and two vibrations at 3408 and 3466 cm⁻¹ in the region of the NH stretching vibrations are observed. All NH stretching vibrations are located above 3400 cm⁻¹ which indicates that no strong intramolecular hydrogen bonds are formed. (Frequencies of strongly hydrogen-bonded NH groups are usually located below 3400 cm⁻¹.) Furthermore in the carbonyl stretching and NH bending region several characteristic vibrations appear (see below).

As mentioned above, in the R2PI spectrum the UV excitation may not be isomer selective. In order to figure out if more than one isomer corresponds to an IR spectrum and to retain (if necessary) isomer selectivity, IR/IR/R2PI spectroscopy is applied, i.e. the excitation of one isomer with a frequency-fixed IR burn laser has an effect on all IR transitions that belong to the same isomer in the subsequently measured IR/R2PI spectrum. (For more detailed information about the IR/IR/R2PI spectroscopy see ref. 39–41).

In Fig. 6 the IR/IR/R2PI spectroscopy is applied for the first main resonance of the R2PI spectrum at 34 637 cm⁻¹ in order to confirm that the two bands at 3408 and 3466 cm⁻¹ belong to the same isomer. For this measurement the frequency-fixed IR burn laser was set to the transition at 3408 cm⁻¹. The two transitions at 3408 and 3466 cm⁻¹ both show an almost complete depletion in the IR/IR/R2PI spectrum compared to the IR/R2PI spectrum. Therefore, these transitions definitely belong to one isomer. Thus the electronic resonance at 34 367 cm⁻¹ originates from one single isomer and does not overlap with resonances of other isomers.

Fig. 6 IR/IR/R2PI spectrum of MOC via the excitation at 34 637 cm⁻¹ by using a frequency-fixed IR burn laser at 3408 cm⁻¹. The IR/IR/R2PI spectrum is given in red and the corresponding IR/R2PI spectrum is given in black.

A comparison between spectroscopic results obtained via the excitation at 34 637 cm⁻¹ and DFT calculations performed for MOC is shown in Fig. 7. Indeed, among the different possible calculated structures of MOC, the vibrational frequencies calculated at the DFT/B3LYP-D3/TZVP level of the most stable conformer α_Dδ_D are in good agreement with the experimentally obtained frequencies. The experimentally observed vibration at 3408 cm⁻¹ arises from the NH stretching vibration of the NH-PhOMe unit. The IR/R2PI band at 3466 cm⁻¹ can be correlated with the NH stretching mode of the glycine unit. In the range from 1380–1900 cm⁻¹ the calculated frequencies of the α_Dδ_D conformer are also in very good agreement with the experimental bands: the transition at 1767 cm⁻¹ can be assigned to the carbonyl stretching vibration of the glycine unit. The broadened transition at 1698 cm⁻¹ corresponds to two coupled modes between NH bending and carbonyl stretching vibrations. The transition at 1609 cm⁻¹ can be assigned to the NH bending mode of the NH-PhOMe residue and a CH bending transition of the aromatic ring. The position of the frequencies is very well predicted by the calculations, but in contrast to all other transitions in the spectral region from 1400 to 1800 cm⁻¹ the calculated sum of intensities of both transitions is significantly lower than the experimentally observed one at 1609 cm⁻¹. (This is the same for all calculated structures.) This amplification may result from a superposition with combination bands of out-of-plane CH, CC bending and COC (ester) bending vibrations. The experimentally obtained frequency at 1545 cm⁻¹ can be correlated with the NH bending vibration of the NH-PhOMe unit and the vibration at 1495 cm⁻¹ fits to the NH bending mode of the glycine unit as well as a coupled vibration of the NH bending vibrations of the two NH groups of MOC. The remaining transitions in the IR/R2PI spectrum at 1470 and 1442 cm⁻¹ can be correlated with CH bending modes.

Fig. 7 Comparison between the experimental IR/R2PI spectrum of MOC via the R2PI resonance at 34 637 cm⁻¹ (upper trace) and calculated frequencies obtained from DFT calculations (B3LYP-D3/TZVP) of selected isomers of MOC. (For a better illustration the calculated intensities in the amide A region were tripled.)

As pointed out in Section III, a very important result of the DFT calculations is that the most stable structure α_Dδ_D is not formed by neglecting the (CH/π) dispersion interactions (cf. Fig. S4, ESI†). By comparing the positions of IR transitions in the NH stretching region of all structures discussed by including (cf.Fig. 2 and Fig. 7) or excluding (cf. Fig. S4 and Table S6, ESI†) the dispersion only the most stable arrangement (including dispersion) α_Dδ_D fits to the experimental spectrum, i.e. the first electronic resonance at 34 367 cm⁻¹ exclusively refers to structure α_Dδ_D. As mentioned above there are more intense electronic transitions in the R2PI spectrum. The corresponding IR/R2PI spectra (cf.Fig. 5b and c) via the transitions at 35 071 and 35 149 cm⁻¹ partly show similar IR transitions and in both spectra the number of transitions is larger than expected for one isomer in the region of the NH stretching vibrations.

This indicates the presence of isomers with overlapping UV transitions. In order to figure out overlapping electronic excitation energies of different isomers a further strategy is the application of IR_fixed/R2PI spectroscopy, i.e. the UV laser is scanned and the frequency of the IR burn laser is fixed to a vibrational band (cf.Fig. 4b–e). As expected from the discussion above the first UV transition in the IR_fixed/R2PI spectrum at 34 637 cm⁻¹ is well separated, i.e. a depletion effect on this transition is observed if the IR burn laser is fixed at 3408 cm⁻¹ (Fig. 4c) and no effect is observed for the resonances at 3386 cm⁻¹ (Fig. 4b) and 3440 cm⁻¹ (Fig. 4e) (with respect to the transition at 3414 cm⁻¹, see below). In contrast to this, the IR_fixed/R2PI spectra show depletion effects at the electronic transition at 35 071 cm⁻¹ for all fixed IR frequencies at 3386, 3408, 3414 and 3440 cm⁻¹, i.e. different isomers seem to overlap at this electronic transition including the most stable α_Dδ_D arrangement with an IR transition at 3408 cm⁻¹.

Further structural information should be obtained by the IR/IR/R2PI spectroscopy with an UV excitation at 35 071 cm⁻¹ and an IR burn laser fixed at 3440 cm⁻¹ (cf.Fig. 8a). This spectrum indicates a second correlating transition observed at 3470 cm⁻¹. (It should be mentioned that the effect observed at 3470 cm⁻¹ is small, since the transition at 3466 cm⁻¹ referring to the α_Dδ_D isomer is in close vicinity.) Thus from the IR/IR/R2PI spectrum it can be concluded that a further isomer could have transitions at 3440 and 3470 cm⁻¹. Since the combination of transitions at 3408 and 3466 cm⁻¹ has already been assigned to the α_Dδ_D isomer a further pair of transitions at 3386 and 3520 cm⁻¹ remains in IR/R2PI spectrum via 35 071 cm¹ (cf.Fig. 5b). This pair of transitions also appears in the IR/R2PI spectrum via 35 149 cm⁻¹. In order to obtain more information an IR/IR/R2PI spectrum is recorded via 35 149 cm⁻¹ with the frequency-fixed IR burn laser at 3386 cm⁻¹ (cf.Fig. 8b). This spectrum supports the assumption that the transitions at 3386 and 3520 cm⁻¹ belong to a third isomer. With respect to the remaining transition at 3414 cm⁻¹ in the IR/R2PI spectrum via 35 149 cm⁻¹ it should be remarked that it can be interpreted as an overlap of the transitions at 3386, 3408 and 3440 cm⁻¹ (cf. band contour analysis in Fig. S5, ESI†). The IR_fixed/R2PI spectroscopy supports this suggestion: by using an IR burn laser frequency at 3414 cm⁻¹ a depletion on all UV transitions belonging to different isomers can be obtained (see Fig. 4d).

Fig. 8 IR/IR/R2PI spectra of MOC (a) via the UV excitation wavenumber at 35 071 cm⁻¹ by using a frequency-fixed IR burn laser at 3440 cm⁻¹ and (b) via the excitation at 35 149 cm⁻¹ by using a frequency-fixed IR burn laser at 3386 cm⁻¹. The IR/IR/R2PI spectra are given in red and the corresponding IR/R2PI spectra are given in black.

According to this spectroscopic analysis two further isomers of MOC (in addition to the most stable α_Dδ_D isomer) with IR transitions at 3440/3470 cm⁻¹ and 3386/3520 cm⁻¹ are observed.

In order to achieve a structural assignment again the vibrational frequencies of structures of MOC calculated at the DFT/B3LYP-D3/TZVP level (as shown in Fig. 9) are compared with the experimental results. It is obvious that the calculated frequencies of the second most stable conformer γ_Dδ_D are in very good agreement with the experimentally observed ones. The experimentally obtained vibration at 3440 cm⁻¹ arises from the NH stretching vibration of the NH-PhOMe unit; the transition at 3470 cm⁻¹ can be assigned to the NH stretching vibration of the glycine unit. Additionally a good agreement in the NH bending and carbonyl stretching regions is obtained for the γ_Dδ_D isomer with respect to the calculated and experimental observed values. (For detailed assignment of all transitions in this spectral region see Tables S3–S5, ESI†)

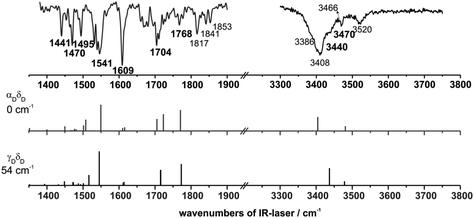Fig. 9 Comparison between the experimental IR/R2PI spectrum of MOC via the R2PI resonance at 35 071 cm⁻¹ (upper trace) and calculated frequencies obtained from DFT calculations (B3LYP-D3/TZVP) of the most stable isomers of MOC. For further isomers cf. Fig. S2 (ESI†). (For a better illustration the calculated intensities in the amide A region were tripled.)

With respect to the remaining pair of vibrational transitions at 3386 and 3520 cm⁻¹ in the NH stretching region, the observation of a transition at 3386 cm⁻¹ seems to indicate a hydrogen-bonded structure. In Fig. 10 the vibrational frequencies calculated at the DFT/B3LYP-D3/TZVP level of a selected number of different possible structures of MOC compared to the IR/R2PI spectrum via the third transition of the R2PI spectrum at 35 149 cm⁻¹ are shown. Unfortunately hydrogen-bonded structures like α_Dγ_D and ε_Dγ_D are much less stable than the other arrangements. However the α_Dγ_D structure is the only one for which the calculated frequencies qualitatively correspond to the experimentally obtained bands in the IR/R2PI spectrum. The transition at 3520 cm⁻¹ can be correlated with the NH stretching vibration of the glycine and the experimentally obtained vibration at 3386 cm⁻¹ arises from the NH group bound to the carbonyl functionality. Thus a very tentative assignment to a hydrogen-bonded structure like the α_Dγ_D arrangement is suggested. In the range of the NH bending and carbonyl stretching modes the calculated frequencies of the α_Dγ_D conformer are also in good agreement to the experimentally observed transitions at 1442, 1470, 1495, 1538, 1609, 1704 and 1768 cm⁻¹ (cf.Fig. 5c). As mentioned above the transition at 1609 cm⁻¹ is not well predicted with respect to its intensity. Again a superposition with combination bands of out-of-plane CH, CC bending and COC (ester) bending vibrations may be a reason for this deviation. It should further be mentioned that in the spectral region of 1400 to 1800 cm⁻¹ the frequencies of all isomers differ only slightly from each other, thus no characteristic assignments could be derived from these bands. On the other hand a clear difference between the discussed isomers α_Dδ_D, γ_Dδ_D and α_Dγ_D is observed in the spectral region from 1800 to 1900 cm⁻¹. In the case of the most stable arrangement (α_Dδ_D) no vibrational transitions are observed whereas the other two assigned isomers show characteristic vibrational signatures at 1817, 1841 and 1853/1855 cm⁻¹ (cf.Fig. 5b and c).

Fig. 10 Comparison between the experimental IR/R2PI spectrum of MOC via the R2PI resonance at 35 149 cm⁻¹ (upper trace) and calculated frequencies obtained from DFT calculations (B3LYP-D3/TZVP), for further isomers cf. Fig. S3 (ESI†). (For a better illustration the calculated intensities in the amide A region were tripled.)

In several former publications, e.g. see ref. 75–78, spectroscopically observed bands above 1800 cm⁻¹ have already been discussed. For benzene a band at 1808 cm⁻¹ was obtained.⁷⁵ Further experiments with different ortho-substituted benzene derivatives revealed vibrations in the region of 1810 to 1870 cm⁻¹.⁷⁷ All these bands were assigned to combination bands arising from the out-of-plane CH deformation fundamentals (of the aromatic ring). In contrast to the most stable isomer α_Dδ_D the out-of-plane CH deformation fundamentals of the aromatic ring in the two isomers γ_Dδ_D and α_Dγ_D are delocalized (cf. Fig. S7, ESI†). This difference might be the reason why intense combination bands above 1800 cm⁻¹ are observed in the IR/R2PI spectrum via the transitions at 35 071 and 35 149 cm⁻¹ (see Fig. 5b and c) but not for the most stable isomer (α_Dδ_D) which is exclusively excited via the transition at 34 637 cm⁻¹ (see Fig. 5a).

Finally another interesting effect that appears in the IR/IR/R2PI spectrum obtained via the UV excitation at 35 149 cm⁻¹ should be mentioned. In this spectrum not only a depletion of the corresponding vibrational transitions at 3386 and 3520 cm⁻¹ is observed it also exhibits further transitions at 3408, 3440 and also at 3466/3470 cm⁻¹ compared to the corresponding IR/R2PI spectrum (cf.Fig. 8b, see also Fig. S6, ESI†). These transitions correlate with the vibrational modes of isomers α_Dδ_D and γ_Dδ_D. After excitation with the first IR photon at 3386 cm⁻¹ the excitation energy will be redistributed over a variety of (low frequency) vibrations. As a consequence it could be feasible that the vibrational frequencies of the high frequency NH stretching frequencies are only slightly or almost not influenced. Thus it may be a possible conclusion that after exciting an isomer with a transition at 3386 cm⁻¹, isomers α_Dδ_D and γ_Dδ_D are formed due to a rearrangement process, i.e. MOC could be an example of IR induced rearrangement in the S₀ state (like the one described for an intramolecular rearrangement in 3HC(H₂O)₁,⁴¹ see also results from IR/UV population transfer spectroscopy on peptides (e.g.ref. 18, 79 and 80)).

V Conclusions

In this paper the first molecular beam investigations on a linear depsipeptide (CyCO-Gly-Lac-NH-PhOMe) are presented. Structural assignments are obtained by applying IR/UV combined spectroscopic techniques in combination with DFT (B3LYP/TZVP) optimized isomers of MOC including dispersion interactions (Grimme D3).

In the region of both the NH stretching vibrations (amide A) and the carbonyl stretching as well as the NH bending vibrations (amide I/II), IR/R2PI experiments (with a scanned UV or IR laser) were performed, showing only one electronic resonance which originates from one single isomer and which does not overlap with resonances of other isomers. Nevertheless, a detailed structural assignment for the IR/R2PI spectra with overlapping excitation energies was possible by using the IR/IR/R2PI spectroscopy. Thus it could be shown that three different isomers of MOC are observed in the molecular beam experiment. Calculations without including dispersion interactions predict a most stable structure which contains completely separated aromatic and aliphatic rings. By including dispersion interactions a folded tweezer-like structure turns out to be the most stable arrangement. This structure is predicted if dispersion interactions are taken into account due to the intramolecular CH/π interactions between the axial aliphatic CH groups of the CyCO unit and the aromatic π system of the NH-PhOMe unit. By comparing experimentally observed IR frequencies and theoretically predicted values the folded tweezer-like structure is clearly assigned. Thus MOC turns out to be an ideal model system to describe the efficiency of dispersion interactions and the necessity to include these interactions in theoretical predictions. In a handy linguistic image this structural formation completely driven by dispersion interaction may be denoted as a “gecko in the gas phase”.

Acknowledgements

The authors thank the Deutsche Forschungsgemeinschaft (DFG: Reference No. GE961/7-2, 9-1) for financial support. This work is part of the PhD thesis of A. S.

References

1. IUPAC Compendium of Chemical Terminology, ed. M. Nič, J. Jirát, B. Košata, A. Jenkins and A. McNaught, IUPAC, Research Triagle Park, NC, 2009.
2. G. R. Pettit, Y. Kamano, C. Dufresne, R. L. Cerny, C. L. Herald and J. M. Schmidt, J. Org. Chem., 1989, 54, 6005–6006.
3. B. Buschhaus, W. Bauer and A. Hirsch, Recent Developments in Dendrimer Chemistry, 2003, 59, 3899–3915.
4. T. Förster, Ann. Phys., 1948, 437, 55–75.
5. M. Taliani, E. Bianchi, F. Narjes, M. Fossatelli, A. Urbani, C. Steinkühler, R. de Francesco and A. Pessi, Anal. Biochem., 1996, 240, 60–67.
6. D. A. Williamson and B. E. Bowler, J. Am. Chem. Soc., 1998, 120, 10902–10911.
7. R. L. Hamill, C. E. Higgens, H. E. Boaz and M. Gorman, Tetrahedron, 1969, 4255–4258.
8. B. C. Pressman, Annu. Rev. Biochem., 1976, 45, 501–530.
9. M. Isaka, P. Kittakoop, K. Kirtikara, N. L. Hywel-Jones and Y. Thebtaranonth, Acc. Chem. Res., 2005, 38, 813–823.
10. H. Sigel, Met. Ions Biol. Syst., 1985, 139.
11. E. A. Gallo and S. H. Gellman, J. Am. Chem. Soc., 1993, 115, 9774–9788.
12. G. Boussard, M. Marraud and J. Neel, Biopolymers, 1977, 16, 1033–1052.
13. C. Lecomte, A. Aubry, J. Protas, G. Boussard and M. Marraud, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1992–1996.
14. J. Zhang, M. King, L. Suggs and P. Ren, Biomacromolecules, 2007, 8, 3015–3024.
15. Y. K. Kang and B. J. Byun, J. Phys. Chem. B, 2008, 112, 9126–9134.
16. M. Gerhards and C. Unterberg, Phys. Chem. Chem. Phys., 2002, 4, 1760–1765.
17. M. Gerhards, C. Unterberg and A. Gerlach, Phys. Chem. Chem. Phys., 2002, 4, 5563–5565.
18. B. C. Dian, A. Longarte and T. S. Zwier, Science, 2002, 296, 2369–2373.
19. P. Carcabal, R. T. Kroemer, L. C. Snoek, J. P. Simons, J. M. Bakker, I. Compagnon, G. Meijer and G. von Helden, Phys. Chem. Chem. Phys., 2004, 6, 4546–4552.
20. A. G. Abo-Riziq, B. Crews, J. E. Bushnell, M. P. Callahan and M. S. De Vries, Mol. Phys., 2005, 103, 1491–1495.
21. W. Chin, I. Compagnon, J.-P. Dognon, C. Canuel, F. Piuzzi, I. Dimicoli, G. von Helden, G. Meijer and M. Mons, J. Am. Chem. Soc., 2005, 127, 1388–1389.
22. A. Abo-Riziq, B. O. Crews, M. P. Callahan, L. Grace and M. S. De Vries, Angew. Chem., Int. Ed., 2006, 45, 5166–5169.
23. V. Brenner, F. Piuzzi, I. Dimicoli, B. Tardivel and M. Mons, Angew. Chem., Int. Ed., 2007, 46, 2463–2466.
24. H. Fricke, A. Funk, T. Schrader and M. Gerhards, J. Am. Chem. Soc., 2008, 130, 4692–4698.
25. E. E. Baquero, W. H. James, S. H. Choi, S. H. Gellman and T. S. Zwier, J. Am. Chem. Soc., 2008, 130, 4784–4794.
26. H. Fricke, A. Gerlach, C. Unterberg, M. Wehner, T. Schrader and M. Gerhards, Angew. Chem., Int. Ed., 2009, 48, 900–904.
27. H. Fricke, K. Schwing, A. Gerlach, C. Unterberg and M. Gerhards, Phys. Chem. Chem. Phys., 2010, 12, 3511–3521.
28. A. M. Rijs, G. Ohanessian, J. Oomens, G. Meijer, G. von Helden and I. Compagnon, Angew. Chem., Int. Ed., 2010, 49, 2332–2335.
29. K. Schwing, C. Reyheller, A. Schaly, S. Kubik and M. Gerhards, ChemPhysChem, 2011, 12, 1981–1988.
30. A. Abo-Riziq, L. Grace, B. Crews, M. P. Callahan, T. van Mourik and M. S. De Vries, J. Phys. Chem. A, 2011, 115, 6077–6087.
31. H. S. Biswal, Y. Loquais, B. Tardivel, E. Gloaguen and M. Mons, J. Am. Chem. Soc., 2011, 133, 3931–3942.
32. E. J. Cocinero, P. Carçabal, T. D. Vaden, J. P. Simons and B. G. Davis, Nature, 2011, 469, 76–79.
33. J. C. Dean, E. G. Buchanan and T. S. Zwier, J. Am. Chem. Soc., 2012, 134, 17186–17201.
34. S. Jaeqx, J. Oomens, A. Cimas, M.-P. Gaigeot and A. M. Rijs, Angew. Chem., Int. Ed., 2014, 53, 3663–3666.
35. M. Alauddin, H. S. Biswal, E. Gloaguen and M. Mons, Phys. Chem. Chem. Phys., 2015, 17, 2169–2178.
36. R. H. Page, Y. R. Shen and Y. T. Lee, J. Chem. Phys., 1988, 88, 4621–4636.
37. C. Riehn, C. Lahmann, B. Wassermann and B. Brutschy, Chem. Phys. Lett., 1992, 197, 443–450.
38. S. Tanabe, T. Ebata, M. Fujii and N. Mikami, Chem. Phys. Lett., 1993, 215, 347–352.
39. V. A. Shubert and T. S. Zwier, J. Phys. Chem. A, 2007, 111, 13283–13286.
40. M. Weiler, K. Bartl and M. Gerhards, J. Chem. Phys., 2012, 136, 114202.
41. A. Stamm, M. Weiler, A. Brächer, K. Schwing and M. Gerhards, Phys. Chem. Chem. Phys., 2014, 16, 21795–21803.
42. A. Stamm, K. Schwing and M. Gerhards, J. Chem. Phys., 2014, 141, 194304.
43. W. Chin, J.-P. Dognon, F. Piuzzi, B. Tardivel, I. Dimicoli and M. Mons, J. Am. Chem. Soc., 2005, 127, 707–712.
44. T. Häber, K. Seefeld, G. Engler, S. Grimme and K. Kleinermanns, Phys. Chem. Chem. Phys., 2008, 10, 2844–2851.
45. E. Gloaguen, B. de Courcy, J.-P. Piquemal, J. Pilmé, O. Parisel, R. Pollet, H. S. Biswal, F. Piuzzi, B. Tardivel, M. Broquier and M. Mons, J. Am. Chem. Soc., 2010, 132, 11860–11863.
46. E. Gloaguen, H. Valdes, F. Pagliarulo, R. Pollet, B. Tardivel, P. Hobza, F. Piuzzi and M. Mons, J. Phys. Chem. A, 2010, 114, 2973–2982.
47. W. H. James, E. G. Buchanan, C. W. Müller, J. C. Dean, D. Kosenkov, L. V. Slipchenko, L. Guo, A. G. Reidenbach, S. H. Gellman and T. S. Zwier, J. Phys. Chem. A, 2011, 115, 13783–13798.
48. K. Schwing, H. Fricke, K. Bartl, J. Polkowska, T. Schrader and M. Gerhards, ChemPhysChem, 2012, 13, 1576–1582.
49. J. J. Lee, M. Albrecht, C. A. Rice, M. A. Suhm, A. Stamm, M. Zimmer and M. Gerhards, J. Phys. Chem. A, 2013, 117, 7050–7063.
50. E. C. Stanca-Kaposta, P. Carçabal, E. J. Cocinero, P. Hurtado and J. P. Simons, J. Phys. Chem. B, 2013, 117, 8135–8142.
51. S. Jaeqx, W. Du, E. J. Meijer, J. Oomens and A. M. Rijs, J. Phys. Chem. A, 2013, 117, 1216–1227.
52. Y. Loquais, E. Gloaguen, S. Habka, V. Vaquero-Vara, V. Brenner, B. Tardivel and M. Mons, J. Phys. Chem. A, 2015, 119, 5932–5941.
53. M. A. Trachsel, P. Ottiger, H.-M. Frey, C. Pfaffen, A. Bihlmeier, W. Klopper and S. Leutwyler, J. Phys. Chem. B, 2015, 119, 7778–7790.
54. M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873–13900.
55. S. Wiedemann, A. Metsala, D. Nolting and R. Weinkauf, Phys. Chem. Chem. Phys., 2004, 6, 2641–2649.
56. K. Shibasaki, A. Fujii, N. Mikami and S. Tsuzuki, J. Phys. Chem. A, 2006, 110, 4397–4404.
57. E. C. Stanca-Kaposta, D. P. Gamblin, J. Screen, B. Liu, L. C. Snoek, B. G. Davis and J. P. Simons, Phys. Chem. Chem. Phys., 2007, 9, 4444–4451.
58. H. S. Biswal and S. Wategaonkar, J. Phys. Chem. A, 2009, 113, 12774–12782.
59. J. J. J. Dom, B. J. van der Veken, B. Michielsen, S. Jacobs, Z. Xue, S. Hesse, H.-M. Loritz, M. A. Suhm and W. A. Herrebout, Phys. Chem. Chem. Phys., 2011, 13, 14142–14152.
60. A. Ciavardini, F. Rondino, A. Paladini, M. Speranza, S. Fornarini, M. Satta and S. Piccirillo, Phys. Chem. Chem. Phys., 2013, 15, 19360–19370.
61. N. A. Seifert, D. P. Zaleski, C. Pérez, J. L. Neill, B. H. Pate, M. Vallejo-López, A. Lesarri, E. J. Cocinero, F. Castaño and I. Kleiner, Angew. Chem., Int. Ed., 2014, 53, 3210–3213.
62. J. Altnöder, S. Oswald and M. A. Suhm, J. Phys. Chem. A, 2014, 118, 3266–3279.
63. J. Ran and M. W. Wong, J. Phys. Chem. A, 2006, 110, 9702–9709.
64. C. Unterberg, A. Jansen and M. Gerhards, J. Chem. Phys., 2000, 113, 7945–7954.
65. M. Gerhards, Opt. Commun., 2004, 241, 493–497.
66. Discovery Studio Client, v2.5.5.9350, Accelrys Software Inc., 2005–2009.
67. M. Gerhards, C. Unterberg, A. Gerlach and A. Jansen, Phys. Chem. Chem. Phys., 2004, 6, 2682–2690.
68. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford CT, 2013.
69. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100.
70. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
71. Y. Bouteiller, J.-C. Gillet, G. Grégoire and J. P. Schermann, J. Phys. Chem. A, 2008, 112, 11656–11660.
72. Y. Bouteiller, J. C. Poully, C. Desfrançois and G. Grégoire, J. Phys. Chem. A, 2009, 113, 6301–6307.
73. G. N. Ramachandran and A. V. Lakshminarayanan, Biopolymers, 1966, 4, 495–497.
74. A. Perczel, J. G. Angyan, M. Kajtar, W. Viviani, J. L. Rivail, J. F. Marcoccia and I. G. Csizmadia, J. Am. Chem. Soc., 1991, 113, 6256–6265.
75. C. R. Bailey, J. B. Hale, C. K. Ingold and J. W. Thompson, J. Chem. Soc., 1936, 931–941.
76. W. R. Angus, C. R. Bailey, J. B. Hale, C. K. Ingold, A. H. Leckie, C. G. Raisin, J. W. Thompson and C. L. Wilson, J. Chem. Soc., 1936, 971–987.
77. D. H. Whiffen, Spectrochim. Acta, 1955, 7, 253–263.
78. D. H. Whiffen, J. Chem. Soc., 1956, 1350–1356.
79. B. C. Dian, J. R. Clarkson and T. S. Zwier, Science, 2004, 303, 1169–1173.
80. B. C. Dian, A. Longarte, P. R. Winter and T. S. Zwier, J. Chem. Phys., 2004, 120, 133–147.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp01675h

---