Partial oxidation of step-bound water leads to anomalous pH effects on metal electrode step-edges

Abstract

The design of better heterogeneous catalysts for applications such as fuel cells and electrolyzers requires a mechanistic understanding of electrocatalytic reactions and the dependence of their activity on operating conditions such as pH. A satisfactory explanation for the unexpected pH dependence of electrochemical properties of platinum surfaces has so far remained elusive, with previous explanations resorting to complex co-adsorption of multiple species and resulting in limited predictive power. This knowledge gap suggests that the fundamental properties of these catalysts are not yet understood, limiting systematic improvement. Here, we analyze the change in charge and free energies upon adsorption using density-functional theory (DFT) to establish that water adsorbs on platinum step edges across a wide voltage range, including the double-layer region, with a loss of approximately 0.2 electrons upon adsorption. We show how this as-yet unreported change in net surface charge due to this water explains the anomalous pH variations of the hydrogen underpotential deposition (H_upd) and the potentials of zero total charge (PZTC) observed in published experimental data. This partial oxidation of water is not limited to platinum metal step edges, and we report the charge of the water on metal step edges of commonly used catalytic metals, including copper, silver, iridium, and palladium, illustrating that this partial oxidation of water broadly influences the reactivity of metal electrodes.

---

Reducing dependence on fossil fuels to address energy security and climate change issues requires new energy sources, more efficient methods of energy conversion, and new methods for energy storage. Electrochemical solutions to these problems, such as fuel cells,^1–3 batteries and super-capacitors, are particularly promising since they are cleaner and more efficient than conventional alternatives such as combustion. Despite considerable efforts to understand and improve fuel cell catalysts, characterizing and fully explaining even basic catalytic reactions in the simplest electrochemical systems is often quite challenging.

Specifically consider platinum, which is central to modern electrochemistry from its industrial applications in fuel cells^1–3 to its academic relevance as a standard for catalytic activity. The Pt(111) surface, in particular, can be prepared reproducibly, exhibits predictable behavior, and forms the basis for understanding platinum electrodes in general. However, polycrystalline platinum, platinum nanoparticles and other faces of platinum display significantly different pH-dependent behavior than Pt(111) for many reactions and processes,^4–10 including the onset of H_upd (hydrogen underpotential deposition),^11–13 the kinetics of the hydrogen evolution/oxidation reactions,^14–16 and the potential of zero total charge.^5,17,18 These deviations from ideal behavior, which can significantly alter the operation of the catalyst,^7,19 are not yet completely understood.

Attempts to explain these individual phenomena separately invoke complicated combinations of adsorbates as a function of pH and potential^5,8,20,21 with proposed explanations almost exclusively presuming that adsorbates with integer charges are most likely. For instance, the Koper group⁵ identified hydroxide adsorption as a possible explanation for the anomalous pH shift for the H_upd peak in the voltammogram. As the authors acknowledge, full coverage of hydroxyl groups would result in a much larger pH effect than experimentally observed. They briefly consider partial charge (in their case, of the adsorbed hydroxyl group), then dismiss this possibility as “somewhat artificial looking”, instead suggesting that coverage of hydroxyl groups on step-edge surfaces change with pH and potential, and are thus responsible for the anomalous pH effect of the onset of H_upd.

While the assumption of integral (or nearly integral) charge appears to be reasonable for many adsorbates on the Pt(111) surface, there is no fundamental reason for adsorbate charge to remain integral since the metal is an electron reservoir. Unsurprisingly, experimental evidence for non-integer adsorbate charges on metal surfaces dates back to as early as 1939.²²

Formally, the quantity of interest is related to the electrosorption valency, defined as the partial derivative of the surface charge density of the metal with respect to the surface concentration of adsorbed species, at constant electrode potential (see ref. 23 for a detailed review). The electrosorption valency can be experimentally measured, and intuitively corresponds to the amount of charge that flows to or from the electrode when an adsorbate moves from solution to the surface.

Few attempts have been made to use ab initio techniques to calculate electrosorption valencies and related quantities,^23,24 primarily because this requires an arbitrary partitioning between adsorbate and electrode of the spatially-continuous electron density in a fixed-charge ab initio calculation, and leads to results dependent on the model for charge partitioning.

Recent developments of fixed-potential DFT methods^25,26 make it possible now to directly calculate the electrosorption valency and related quantities. These calculations employ a grand canonical ensemble of electrons at a fixed chemical potential set by the electrode potential. The average number of electrons changes to minimize the grand free energy and is not restricted to integer values. Exactly as in real electrochemical systems, the net charge of the adsorbate and metal surface is locally compensated by an induced charge density in the electrolyte, treated using continuum solvation methods with ionic screening.^25,27 With fixed-potential DFT methods, the charge changes continuously upon adsorption at fixed potential. The difference in calculated charge of a surface with adsorbate, from those of the solvated surface and adsorbate separately, is equal to the charge that flows to/from the electron reservoir (electrode in experiment), which corresponds precisely to the electrosorption valency.

However, the electrosorption valency as found experimentally, is relative to the solvated surface without the adsorbate. In this context, even if a solvent molecule is specifically bound to the electrode surface and changes the number of electrons at the surface, the electrosorption valency of this solvent is defined to be zero. To separate the effect of the specifically bound solvent which is in this case water, we find the difference in charge between the surface with the specifically adsorbed water, and with a hypothetical solvent that does not specifically bind (a continuum dielectric). Hence, we are able to separate the effect of the specific binding of water from the dielectric contributions of the electrolyte.

Here we directly compute these charge differences for a set of adsorbates, and we find that non-integer charge associated with oxidatively adsorbed water on the step edges of platinum over a wide voltage range provides a simple, universal and fundamental explanation to the apparently disparate non-ideal phenomena on platinum surfaces other than Pt(111).^4–18 We show that moving beyond the assumption of integer charge leads to a more succinct description of electrochemical reactions with greater predictive power. Most importantly, recently developed ab initio methods^25–27 can easily predict the (possibly non-integer) adsorbate charges, as discussed above.

To take a specific example, consider the underpotential adsorption of protons from solution to hydrogen on platinum surfaces (H_upd). At equilibrium,

G_Pt + G_H⁺ + nG_e⁻ = G_Pt–H, (1)

where G_Pt, G_Pt–H, G_e⁻ and G_H⁺ are the Gibbs free energies of the bare platinum electrode, hydrogen adsorbed on the platinum electrode, electrons from the electrode and protons in solution respectively, and n is the number of electrons transferred from the electrode upon adsorption. With changing pH, the proton free energy shifts as ΔG_H⁺ = −RTΔ ln(H⁺ activity), whereas with changing electrode potential, the electron free energy shifts as ΔG_e⁻ = −FΔE, where F is Faraday's constant and E is the electrode potential. Therefore, the electrode potential for proton adsorption changes with pH as −nFΔE = RTΔ ln(H⁺ activity), which corresponds to ΔE/ΔpH ≈ −59 mV/n at room temperature. On the ideal Pt(111) surface, each proton gains one electron upon adsorption as neutral hydrogen and n = 1 yields the observed −59 mV shift per (increasing) pH unit. However, we argue that other Pt surfaces contain oxidatively adsorbed water on the step edges that must be displaced during H_upd, which requires the transfer of n > 1 electrons from the electrode and hence explains the experimentally observed shift of magnitude smaller than 59 mV per pH unit.

The presence of the oxidatively adsorbed water similarly affects the electron count of several reactions on Pt surfaces other than (111) and leads to the anomalous pH dependence of reactivity and the potential of zero total charge. Accounting for non-integer charges, we therefore easily explain all these phenomena without invoking complicated combinations of adsorbates that the conventional analysis with integer charges requires.^5,13,20

The first part of the paper uses computational methods to establish that water binds strongly to step edges on platinum surfaces and is partially oxidized throughout the relevant voltage range. The second part compares computational and experimental data for the anomalous pH dependence of H_upd, and quantitatively demonstrates how that is a direct consequence of H adsorption requiring the displacement of oxidatively bound water. The computational results predict a larger pH dependence of H_upd with increasing ionic strength, which could be experimentally tested. The third part provides evidence that oxidative adsorption of water is a general phenomenon on step edges in several other metals.

Methods

We perform ab initio calculations at fixed electron chemical potential²⁵ using the framework of Joint Density Functional Theory (JDFT)^28,29 as implemented in JDFTx.²⁶ In contrast to conventional fixed-charge calculations, this allows for ready comparison with voltammetric data. The calculations utilize a continuum solvent model (LinearPCM continuum solvation model²⁷ unless otherwise indicated) with ionic screening (1 mol L⁻¹ of cations and anions unless otherwise indicated). This allows us to treat charged slabs with meaningful total free energies and absolute electron chemical potentials (relative to the vacuum level) that quickly converge with simulation cell size, as detailed elsewhere.²⁵ We relate the absolute electron potential to electrode potential using the absolute potential of the standard hydrogen electrode (SHE) as 4.68 V below the vacuum level for the LinearPCM solvation model,²⁷ and 4.55 V for the nonlocal SaLSA solvation model,³⁰ following previous work.³¹

The fixed electron chemical potential calculations directly provide the total number of electrons N in and the grand free energy G of each slab configuration at a specified chemical potential μ. The difference between N for a slab with an adsorbate and the total N for the corresponding bare slab at the same potential and the isolated adsorbate is then exactly the change in electron number due to adsorption, n, that determines if the process is Faradaic or non-Faradaic and the magnitude of anomalous pH shifts, if any. Unlike most recent computational work that focuses on potential-independent surface binding energies or surface state charges,²⁴ our fixed chemical potential approach directly relates to experimental voltammograms.

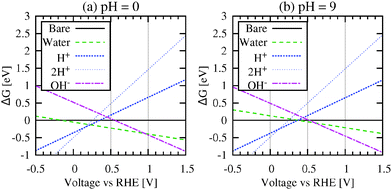
We compare stabilities of various adsorbed species as a function of electrode potential (Fig. 4) by calculating the grand free energy G at one electron chemical potential μ (specifically at 0 V SHE) and extrapolating linearly to nearby potentials μ′ using G′ ≈ G − (μ′ − μ)N. Note that the linearity is valid for specific adsorbate configurations. With changing potential, the most stable adsorbate configuration can change from one to the other, e.g. from H to H₂O adsorbed around 0.25 V SHE in Fig. 3(a), and the overall system free energy tracks the lowest of all configurations and is not assumed to be linear.

Above, G includes vibrational Helmholtz free energy contributions (zero-point energy, finite temperature internal energy and entropy contributions) of the adsorbed configurations. We neglect the vibrational contributions of the Pt atoms in the slab since they do not change appreciably between different adsorbate configurations. Free energies of liquid H₂O and gas-phase H₂ at STP are calculated by adding experimental gas phase entropies³² to solvated and vacuum DFT calculations respectively that include the vibrational zero-point energy. For liquid water, the gas phase entropy conveniently accounts for vibrational, rotational and translational entropy of water molecules, while the solvation model in the DFT calculation accounts for the change in Gibbs free energy between the gas and liquid phases. This directly gives us G_H2O for calculating adsorption free energies of water. For proton adsorption, we calculate at pH = 0 and at the SHE potential using the equilibrium that defines the standard hydrogen electrode, and use the Nernst equation to calculate it for a different pH. For hydroxide adsorption, we use G_OH⁻ = G_H2O − G_H⁺ from the ionic equilibrium in water.

We performed density functional theory calculations with JDFTx,²⁶ with the same methodology as detailed elsewhere,³³ with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional,³⁴ and GBRV ultrasoft pseudopotentials³⁵ with a 20 Hartree kinetic energy cutoff for the plane wave basis. For the free energies of Fig. 4, we included pair-potential DFT+D2 dispersion corrections³⁶ with a C₆ coefficient of 7 J nm⁶ mol⁻¹ for Pt to correctly account for binding energies on its surface.³⁷ We used a 6 × 8 Monkhorst–Pack k-point mesh along the periodic directions, with a Fermi smearing of 0.01 Hartrees for Brillouin zone integration. We used primitive unit cells with 5 layers for the (111) and (100) surfaces, 4 for (533) and (553), and 3 for the (110) surface, along with a minimum separation of 15 Angstrom between periodic images of the slabs (which is then completely isolated using Coulomb truncation³⁸). The bottom layer of each slab is constrained to the calculated bulk lattice structure and the remaining geometry is optimized fully for each calculation.

Results and discussion

We examine the properties of adsorbates on the five experimentally well-studied Pt surfaces shown in Fig. 1, which includes the low-index (111), (100) and (110) surfaces as well as the stepped (533) and (553) surfaces. The (533) surface has four-atom (111) terraces and (100)-like step edges, whereas the (553) surface has five-atom (111) terraces and (110)-like step edges. These stepped surfaces serve as model surfaces for the more common polycrystalline surfaces and nanoparticles which include similar step edges.

Fig. 1 Geometries of water molecules adsorbed at the atop Pt sites on the five surfaces included in this study: (a) (111), (b) (100), (c) (110), (d) (533) and (e) (553). For clarity, we show water molecules from only one unit cell of the surface.

Determining the most stable adsorbate configuration is a difficult problem because of the small energy differences that can be sensitive to the computational method. Various studies differ on the most stable configurations of water, OH, H, and famously CO^39–44 on various Pt surfaces, and even for the seemingly simplest case of H on Pt(111).⁴⁵ Step edges are further complicated with chain-like water structures reported in ultra-high vacuum experiments,⁴⁶ hexagonal and pentagonal arrangements predicted by DFT for partially-covered step edges of Pt(533), and with energy differences less than 0.01 eV for different configurations on fully-covered step edges.⁴⁷ However, the adsorbate charges appear to be robust across various low energy configurations (Table 1) and therefore we leave the exact determination of adsorbate configurations to a future study. We consider the full-coverage adsorption of water to atop platinum sites of step edges, which bind the strongest when available, or terrace sites otherwise, as shown in Fig. 1.

For each of the surfaces of Fig. 1, we plot the change in number of electrons upon adsorption of water molecules, hydroxyl groups, and protons in Fig. 2, with numerical results in Table 1. We report the charges calculated at 0 V relative to SHE, but these charges change by less than 0.05 for electrode potentials between 0 V and 1 V relative to SHE. In all cases, hydroxides and protons transfer approximately one electron to and from the surface respectively, as conventionally expected. Water does not transfer a significant charge on Pt(111) or (100), but adsorption atop the step-edge sites of the other surfaces is accompanied by a loss of 0.3 to 0.4 electrons. The step edge sites on the Pt(110) surface are strongly undercoordinated which makes it favorable for them to strongly adsorb and partially oxidize water, and the water binds closer to the Pt(110) step edge than it does to the terrace sites.

Fig. 2 Adsorption reactions (right) and corresponding change in number of electrons n (left) for different Pt surfaces. Lines indicate the conventionally expected integer charge, while the bars indicate the fractional deviations. See Table 1 for the adsorption sites considered and the corresponding charges.

Table 1 Change in number of electrons, n, for H⁺, OH⁻ and H₂O adsorption on various sites of different Pt surfaces, relative to bare surface in dielectric solvent. ‘Bridge’ denotes bridging site between step edge platinum atoms. For the stepped surfaces, ‘atop’ sites refer to those on the step edge

Species	Surface	Site	n
OH^−	111	atop	−0.99
	100	atop	−1.00
	110	atop	−0.94
	533	atop	−0.92
	553	atop	−0.91
H^+	111	atop	0.97
		fcc	0.97
		hcp	0.97
	100	atop	0.98
	110	atop	1.02
	533	bridge	1.02
	553	atop	1.04
		bridge	1.02
Water	111	atop	−0.03
	100	atop	−0.04
	110	atop	−0.34
	533	atop	−0.37
	553	atop	−0.36

---

The partial oxidation of water on the step edges makes performing fixed-potential calculations over neutral, fixed-charge calculations essential. In fixed-charge calculations of water adsorption on the step edge,⁴⁷ when the cell is constrained to remain neutral, the water binds much more weakly to the surface than the partially-oxidized water does. In particular, we find that the neutral surface with adsorbed water adopts a much lower potential (−1.03 V relative to SHE) than the neutral bare surface (0.41 V relative to SHE), so that the fixed-charge binding-energy is a difference of energies at very different potentials and not relevant for electrochemistry. Given that the water loses a charge equivalent to 0.34 electrons, the fixed-charge (neutral cell) binding energy could therefore underestimate the more electrochemically meaningful fixed-potential value by as much as ∼(0.41 − (−1.03)) × 0.34 ≈ 0.5 eV. In contrast, this issue does not arise for adsorption on the terrace because the water remains approximately neutral regardless. Therefore we find a strong increase of 0.4 eV in the binding energy of water on Pt(110) versus that on Pt(111) at 0 V vs. SHE, compared to that naively expected from neutral fixed-charge calculations of potential-independent binding energies on the two surfaces. This comparison highlights the importance of computing the electrosorption valency of the adsorbates and performing fixed-potential calculations at the potential of interest.

Fig. 3 shows the spatial distribution of the electron density change upon H⁺, water, and OH⁻ adsorption at the Pt(110) step edge. The reductive adsorption of H⁺ leads to an increase in charge density, whereas the oxidative adsorption of both the water and the OH⁻ causes a loss in electron density in the adsorbate and two Pt layers immediately below it. Taking the difference in the Lowdin charges, we find that the charge assigned to the oxygen increases by 0.21 electrons when the water adsorbs to the step edge. This accounts for most of the charge associated with the partial oxidation of the water upon adsorption. Interestingly, the charge associated with the platinum atom is nearly unchanged by the presence of the water. This suggests that the dipole moment of water is not the fundamental reason for the partial oxidation.

Fig. 3 Change in charge density upon adsorption of X = H⁺, H₂O and OH⁻ (from left to right) at the step edge of Pt(110), ρ_surf+X(r⃑) − (ρ_surf(r⃑) + ρ_surf(r⃑)), where the three ρ(r⃑)'s in order are the charge density of the adsorbed configuration, bare surface and isolated adsorbate species. Cyan and yellow indicate the decrease and increase in electron density respectively. The numbers indicate the corresponding changes in Lowdin charges upon adsorption.

Fig. 4 Gibbs free energies of H⁺, water and OH⁻ adsorbed on the atop sites of the step edge of Pt(110), relative to the bare surface in (a) acid conditions, pH = 0 and (b) basic conditions, pH = 9. Free energies are estimated from calculations at 0 V vs. SHE and include vibrational and entropic contributions (see Methods section for details).

Instead, the lone pairs on the oxygen atom on the water molecule appear to play a role in the partial oxidation of the water. The lone pairs are shared with the undercoordinated Pt step edge atoms forming a stronger shorter bond, and in the fixed-potential scenario, the excess electrons on the Pt are transferred to the reservoir resulting in a net loss of electrons from the adsorbate + metal surface. Similar behavior has been observed for weakly chemisorbed neutral adsorbates with lone pairs on undercoordinated surface atoms, such as pyridine on Au(210)⁴⁸ and thiourea on mercury.⁴⁹ In contrast, on the higher coordinated terrace sites, water adsorbs weakly with mostly electrostatic interactions (dipole–induced dipole) and little electron sharing, therefore resulting in negligible oxidation.

Next, we evaluate the prevalence of the oxidatively bound water on step edges by calculating the relative free energies of water, protons and hydroxides adsorbed on the Pt(110) surface over a wide voltage range at low and high pH. Fig. 4 shows that adsorbed water is stable for a significant voltage range at pH = 0 that narrows with increasing pH. Further, water will be displaced by protons at 0.25 V RHE for pH = 0 which increases to 0.4 V RHE for pH = 9.

Our result for water adsorption resolves the long-standing debate regarding the species adsorbed at the step edge, and it suggests that partially oxidized water likely plays a role in many of the reactions happening on the step edge, such as the hydrogen evolution reaction.^14,15,50 Others have suggested that hydrogen binding energy^12,14 changes with pH; this result illustrates that water oxidation rather than hydrogen binding energy explains the unexpected pH dependence.

Fig. 4 also illustrates that the strongly bound, partially oxidized water must be displaced from the step-edge during processes such as H_upd and OH adsorption. This indicates that the H_upd reaction should be written as

yH⁺ + Pt–(H₂O)_x + ne⁻ → Pt–yH + xH₂O, (2)

where y is the number of hydrogen atoms per Pt site, and x is the number of displaced water molecules.

From this equation, the charge transferred per hydrogen atom during H_upd will include both the charge from reduction of water as it is desorbed, and the charge from reduction of H⁺ as it is adsorbed. Therefore hydrogen adsorption on platinum step-edges is not a one-electron process. If n electrons are transferred in H_upd, the electrode potential varies with pH as E = E₀ + RT/(nF)ln[H⁺] by the Nernst equation, where F is the Faraday constant, T is temperature, and R is the gas constant. At room temperature, RT/F ln[H⁺] ≈ −59 mV per pH, so that n > 1 results in a reaction potential relative to an absolute reference electrode that changes by less than 59 mV per pH. Relative to the RHE that shifts 59 mV per pH, this shift will be 59 − 59/n mV per pH.

Table 3 summarizes the predicted anomalous pH effect from experimental data and from DFT calculations at 0 V vs. SHE. The experimental data range from 8 mV per pH to 11 mV per pH, corresponding to n = 1.16 to n = 1.23, rather than the expected 1 electron per proton. The DFT calculations range from n = 1.25 to n = 1.33, corresponding to 12 mV per pH to 15 mV per pH, with the nonlocal SaLSA model results falling closer to the experimental data range. The LinearPCM continuum model overestimates solvation of charged solutes in general, and positively charged species in particular;³⁰ therefore it overestimates the partial oxidation of water here as well.

Table 3 also illustrates the effect of ionic strength. The ionic strengths used in experiment vary, with the experiments for the 110 step edge with 0.1 M ionic strength¹¹ and 0.2 M ionic strength.¹²Fig. 6 illustrates that increasing the ionic strength increases the expected value of n. Increasing ionic strength allows for more charging on the surface, which is known to increase the value of the electrosorption valency.⁵¹ Additionally, one can see that the partial oxidation from water binding changes to nearly zero at low potentials near the potential for water reduction.

Fig. 5 Optimized structure of two water molecules per primitive cell of the Pt(533) step edge, (a) before and (b) after a proton is placed on the step edge. For clarity, we show adsorbates from only one unit cell of the fully-covered step edge.

Fig. 6 Change in charge upon displacement of H₂O adsorbed on Pt(110) by H, as a function of electrode potential, showing the effect of ionic strength.

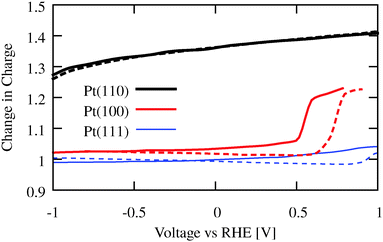
The change in charge upon displacement of H₂O by H is dramatically larger for the Pt(110) surface than the other low-index surfaces, as shown in Fig. 7. This change in charge is nearly constant across a wide voltage range for the three surfaces, illustrating the difference between the stepped surface of the Pt(110) and the other surfaces. At high enough potentials, the water begins to interact more strongly with the Pt(100) surface, but this happens at a potential well beyond that of the underpotential deposition of hydrogen. We note that the transition potentials here should only be qualitatively interpreted, given the limitations of solvation models.

Fig. 7 Change in charge upon displacement of H₂O adsorbed on low-index surfaces by H, as a function of electrode potential. The solid lines include dispersion corrections, while the dashed lines do not. Dispersion corrections negligibly alter results for the strongly-bound water on (110), but change the distance and consequently the charge changes for the weakly bound water on (100) and (110).

To further ensure the reliability of our DFT results, we consider three possible complications: (1) the possibility that the value of y, the number of hydrogen atoms per Pt site, is not one (2) the configuration of water molecules (and the possibility that x, the number of adsorbed water per Pt site, is not one) and neighbor effects between adsorbed water and H (3) accuracy of DFT or the solvation method.

First, we consider the possibility that more than one proton is bound to a given Pt site. DFT studies of Pt(553) surfaces show that hydrogen atoms adsorb most favorably on the atop, fcc hollow, hcp hollow and bridge sites at the step edge with very similar binding energies.²⁰ Identifying the lowest free energy configuration of two protons requires an expansive search,⁴⁵ but the free energy will vary negligibly between configurations due to the similarity in binding energies. Here, we consider one possible configuration of two protons atop the step edge platinum atoms of Pt(110). Free energy calculations shown in Fig. 4 indicate that it is energetically favorable for a single proton to displace water, rather than a two proton (‘2H⁺’) configuration, which only becomes energetically favorable at lower voltages.

Next, the configuration of the water molecules on Pt step edges is likely to change with experimental conditions. To assess how this affects the oxidation state of the adsorbed water, we consider two water molecules per Pt site, with the water molecules occupying both the top and bottom of the step edge as shown in Fig. 5, which is similar to the favorable adsorption structure identified by Kolb et al.⁴⁷ Note that we do not calculate with more water layers because they do not have a single low energy configuration, which necessitates ab initio molecular dynamics with substantially higher computational cost and complexity of analysis. We then added H to the bridge sites, re-optimized the geometries and find that H displaces the water from the step edge with a computed pH shift almost identical to the previous case (Table 2), with the additional water resulting in a change in the pH shift of only 2 mV per pH unit. Therefore, the charge difference is relatively insensitive to coverage and nearest neighbor effects, and the inclusion of further solvent molecules with molecular dynamics is unlikely to substantially alter our predictions.

Table 2 Change in number of electrons n and corresponding anomalous potential shift per pH unit for the displacement of one or two water molecules by a proton

# waters	n	Shift (mV per pH unit, relative to RHE)
1	1.39	17
2	1.34	15

---

Table 3 Observed and predicted H_upd shifts for platinum surfaces and step edges. The Pt(553) and Pt(533) surfaces have 110 and 100 step edges respectively; the rows labeled ‘step’ correspond to experiments on step-edge sites of nanoparticles^11,12

System	Shifts [mV vs. RHE/pH unit]
	Experiment		SaLSA^30		LinearPCM^27
	0.1 M	0.2 M	0.1 M	1 M	0.1 M	1 M
110 step	10^12	11^11
(553)		10^5	14	16	15	17
100 step	8^12	11^11
(533)		10^5	14	16	15	17
(110)			11	13	14	16

---

Further, we examine the variation of the adsorption charge of water on the step edge of Pt(110) with respect to DFT functional and solvation method, at 1 M ionic strength. For the PBE exchange–correlation functional and the LinearPCM solvation model from ref. 27 that we used for much of this paper, the change in electron count is −0.34. With the same solvation method, the local LDA functional and hybrid PBE0 functional yield −0.35 and −0.37 respectively, whereas using the PBE DFT functional with the NonlinearPCM solvation method from ref. 27 yields −0.36 and the nonlocal SaLSA solvation method from ref. 30 yields −0.26. Therefore, the charges we predict are insensitive to the DFT functional with a variation less than 0.02 electrons, and only slightly sensitive to the solvation method.

This insensitivity in the change in charge over a wide voltage range and over differing environmental conditions provides evidence of the robustness of our result that the water oxidizes on step edges throughout a large voltage range. Having identified the source of the H_upd anomalous pH effect, we can explain other effects such as the anomalous potential of zero total charge (PZTC). The partially oxidized water shifts the step-edge H_upd peak, and because the PZTC falls in the H_upd region, this consequentially shifts the PZTC. This explains why the PZTC of Pt is experimentally found to have nearly no shift with pH for the 111 surface (−1 mV per pH unit¹⁷), and a shift of 12 mV per pH unit for the 110 surface.¹⁸

The partially oxidized water that influences many reactions on the platinum step edges is not unique to platinum. We find that water partially oxidizes on step edges more generally, and Fig. 8 reports the change in charge upon water adsorption on pristine 110 surface step edges of metals frequently employed as catalysts. The charge on the water changes somewhat depending on the metal surface, but the phenomenon of partial oxidation is observed for all of these metal step edge sites.

Fig. 8 Change in number of electrons, n, for H₂O adsorption atop pristine 110 metal step edge sites, and corresponding predicted anomalous pH shifts.

Conclusions

We identify the oxidative adsorption of water on step edges in platinum nanoparticles and stepped surfaces as the cause of the anomalous pH effects observed for a number of processes including the potential of zero charge and the onset of H_upd. Although this does not rule out other phenomena such as electrolyte adsorption or water dissociation, it indicates that they are not the cause for these anomalous pH effects. Additionally, we find that the ionic strength is an important parameter, and we find good agreement between our DFT calculations and experimental results when the ionic strength matches that used in experiment. Our results predict that increasing the ionic strength will increase the pH effect for the onset of H_upd for the step edges.

These findings, which are relevant for a large potential and pH range, and for a wide range of catalytic surface compositions, provide the framework for understanding the slowdown of reaction rates (such as HER/HOR) in alkaline media, which we will investigate further in a subsequent paper.

Computationally, these results illustrate the importance of directly calculating electrosorption valencies with fixed-potential DFT methods. These electrosorption valencies can change as a function of potential, leading to large energy differences between extrapolated values from fixed-charge calculations, and those calculated directly from fixed-potential calculations, as we show for the case of water oxidatively adsorbed to step-edges.

Finally, these findings provide an improved way to find the integrated area of a catalyst using the H_upd peaks. Rather than assuming one electron transfer per proton, we suggest a weighting factor of ≈1.2 electrons per proton for the platinum step edge protons for more accurate integrated area estimates.

Acknowledgements

KAS thanks T. P. Moffat for helpful discussions. RS was supported by the Joint Center of Artificial Photosynthesis, a DOE Energy Innovation Hub, supported through the Office of Science of the U.S. Department of Energy under Award Number DE-SC0004993.

References

1. B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 6861.
2. M. K. Debe, Nature, 2012, 486, 7401.
3. A. S. Aricò, P. Bruce, B. Scrosati, J.-M. Tarascon and W. Schalkwijk, Nat. Mater., 2005, 4, 5.
4. S. Daiser and K. Wandelt, Surf. Sci., 1983, 128, L213–L218.
5. M. J. van der Niet, N. Garcia-Araez, J. Hernández, J. M. Feliu and M. T. Koper, Catal. Today, 2013, 202, 105–113.
6. M. J. T. C. van der Niet, A. den Dunnen, L. B. F. Juurlink and M. T. M. Koper, J. Chem. Phys., 2010, 132, 17.
7. M. T. M. Koper, Nanoscale, 2011, 3, 2054–2073.
8. A. den Dunnen, M. J. T. C. van der Niet, C. Badan, M. T. M. Koper and L. B. F. Juurlink, Phys. Chem. Chem. Phys., 2015, 17, 8530–8537.
9. D. C. Skelton, R. G. Tobin, G. B. Fisher, D. K. Lambert and C. L. DiMaggio, J. Phys. Chem. B, 2000, 104, 548–553.
10. M. L. Grecea, E. H. G. Backus, B. Riedmüller, A. Eichler, A. W. Kleyn and M. Bonn, J. Phys. Chem. B, 2004, 108, 12575–12582.
11. R. Gisbert, G. García and M. T. Koper, Electrochim. Acta, 2010, 55, 7961–7968.
12. W. Sheng, Z. Zhuang, M. Gao, J. Zheng, J. G. Chen and Y. Yan, Nat. Commun., 2015, 6, 6848.
13. D. E. Ramaker and C. Roth, ChemElectroChem, 2015, 2, 1582–1594.
14. J. Durst, A. Siebel, C. Simon, F. Hasche, J. Herranz and H. A. Gasteiger, Energy Environ. Sci., 2014, 7, 2255–2260.
15. K. Kunimatsu, T. Senzaki, G. Samjeské, M. Tsushima and M. Osawa, Electrochim. Acta, 2007, 52, 5715–5724.
16. D. Strmcnik, M. Uchimura, C. Wang, R. Subbaraman, N. Danilovic, D. van der Vliet, A. P. Paulikas, V. R. Stamenkovic and N. M. Markovic, Nat. Chem., 2013, 5, 300–306.
17. V. Climent, R. Gomez, J. M. Orts, A. Aldaz and J. M. Feliu, Proc. – Electrochem. Soc., 1997, 97, 222.
18. A. N. Frumkin and O. A. Petrii, Electrochim. Acta, 1975, 20, 347–359.
19. A. Frumkin, O. Petry, A. Kossaya, V. Entina and V. Topolev, J. Electroanal. Chem. Interfacial Electrochem., 1968, 16, 175–191.
20. M. J. Kolb, F. Calle-Vallejo, L. B. Juurlink and M. T. Koper, J. Chem. Phys., 2014, 140, 134708.
21. I. T. McCrum and M. J. Janik, J. Phys. Chem. C, 2016, 120, 457–471.
22. O. A. Esin and B. F. Markov, Zh. Fiz. Khim., 1939, 13, 318.
23. W. Schmickler and R. Guidelli, Electrochim. Acta, 2014, 127, 489.
24. Y.-H. Fang and Z.-P. Liu, ACS Catal., 2014, 4, 4364–4376.
25. K. Letchworth-Weaver and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075140.
26. R. Sundararaman, D. Gunceler, K. Letchworth-Weaver, K. A. Schwarz and T. A. Arias, JDFTx, http://jdftx.sourceforge.net, 2012.
27. D. Gunceler, K. Letchworth-Weaver, R. Sundararaman, K. A. Schwarz and T. A. Arias, Modell. Simul. Mater. Sci. Eng., 2013, 21, 074005.
28. S. Ismail-Beigi and T. A. Arias, Comput. Phys. Commun., 2000, 128, 1.
29. S. A. Petrosyan, A. A. Rigos and T. A. Arias, J. Phys. Chem. B, 2005, 109, 15436–15444.
30. R. Sundararaman, K. A. Schwarz, K. Letchworth-Weaver and T. A. Arias, J. Chem. Phys., 2015, 142, 054102.
31. R. Sundararaman and W. A. Goddard, J. Chem. Phys., 2015, 142, 064107.
32. CRC Handbook of Physics and Chemistry, ed. W. M. Haynes, Taylor and Francis, 93rd edn, 2012.
33. K. A. Schwarz, R. Sundararaman, T. P. Moffat and T. Allison, Phys. Chem. Chem. Phys., 2015, 17, 20805–20813.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
35. K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452.
36. S. Grimme, J. Phys. Chem., 2006, 27, 1787–1799.
37. P. Blonski and N. Lopez, J. Phys. Chem. C, 2012, 116, 15484–15492.
38. R. Sundararaman and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165122.
39. Z. Xu and J. R. Kitchin, J. Phys. Chem. C, 2014, 118, 25597–25602.
40. P. J. Feibelman, B. Hammer, J. K. Nørskov, F. Wagner, M. Scheffler, R. Stumpf, R. Watwe and J. Dumesic, J. Phys. Chem. B, 2001, 105, 4018–4025.
41. B. E. Hayden, K. Kretzschmar, A. M. Bradshaw and R. G. Greenler, Surf. Sci., 1985, 149, 394–406.
42. N. P. Lebedeva, A. Rodes, J. M. Feliu, M. T. M. Koper and R. A. van Santen, J. Phys. Chem. B, 2002, 106, 9863–9872.
43. M. T. M. Koper, R. A. van Santen, S. A. Wasileski and M. J. Weaver, J. Chem. Phys., 2000, 113, 4392–4407.
44. J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674.
45. T. L. Tan, L.-L. Wang, D. D. Johnson and K. Bai, J. Phys. Chem. C, 2013, 117, 22696–22704.
46. M. Morgenstern, T. Michely and G. Comsa, Phys. Rev. Lett., 1996, 77, 703.
47. M. J. Kolb, J. Wermink, F. Calle-Vallejo, L. Juurlink and M. T. M. Koper, Phys. Chem. Chem. Phys., 2016, 18, 3416–3422.
48. D. Yang, L. Stolberg, J. Lipkowski and D. Irish, J. Electroanal. Chem., 1992, 329, 259–278.
49. J. Schultze and D. Rolle, J. Electroanal. Chem., 2003, 552, 163–169.
50. D. Donadio, L. M. Ghiringhelli and L. Delle Site, J. Am. Chem. Soc., 2012, 134, 19217–19222.
51. M. Foresti, M. Innocenti, F. Forni and R. Guidelli, Langmuir, 1998, 14, 7008–7016.

---