Lone-pair–π interactions: analysis of the physical origin and biological implications

Abstract

Lone-pair–π (lp–π) interactions have been suggested to stabilize DNA and protein structures, and to participate in the formation of DNA–protein complexes. To elucidate their physical origin, we have carried out a theoretical multi-approach analysis of two biologically relevant model systems, water–indole and water–uracil complexes, which we compared with the structurally similar chloride–tetracyanobenzene (TCB) complex previously shown to contain a strong charge-transfer (CT) binding component. We demonstrate that the CT component in lp–π interactions between water and indole/uracil is significantly smaller than that stabilizing the Cl⁻–TCB reference system. The strong lp(Cl⁻)–π(TCB) orbital interaction is characterized by a small energy gap and an efficient lp–π* overlap. In contrast, in lp–π interactions between water and indole or uracil, the corresponding energy gap is larger and the overlap less efficient. As a result, water–uracil and water–indole interactions are weak forces composed by smaller contributions from all energy components: electrostatics, polarization, dispersion, and charge transfer. In addition, indole exhibits a negative electrostatic potential at its π-face, making lp–π interactions less favorable than O–H⋯π hydrogen bonding. Consequently, some of the water–tryptophan contacts observed in X-ray structures of proteins and previously interpreted as lp–π interactions [Luisi, et al., Proteins, 2004, 57, 1–8], might in fact arise from O–H⋯π hydrogen bonding.

---

Introduction

The lone-pair–π bonding is a stabilizing interaction between a lone pair (lp) of electrons and a π-system.^1–4 In 1995, Egli and Gessner made the intriguing suggestion that in the d(CpG) steps of Z-DNA, an interaction between an oxygen lp of electrons of the cytidine deoxyribose and the π-face of the guanine base (Fig. 1a) may stabilize the left-handed helix by means of what the authors called “n → π* hyperconjugation”.⁵

Fig. 1 (a) lp–π interaction stabilizing Z-DNA. (b) lp–π interaction suggested to operate between a conserved water molecule and tryptophan W48 in the engrailed homeodomain and its mutants. (c) lp–π interaction observed in the X-ray structure of the charge-transfer complex between Br⁻ and TCP. Reproduced with permission from ref. 5, 26 and 13, respectively.

Not less intriguing was the finding made in 2004 by Luisi et al. who searched the protein data bank (PDB) for water–tryptophan and water–histidine contacts and found hundreds of cases where a water molecule contacts an indole or an imidazole residue along the normal to the ring plane through an endocyclic N atom.⁶ For instance, a specific water–tryptophan contact, interpreted as lp–π interaction, was found to stabilize the engrailed homeodomain and to participate in the recognition of its cognate DNA.^6,7 Since in some of the protein structures, the water molecule was likely to use both H-atoms to donate hydrogen bonds to other neighboring residues, the authors concluded that these water–indole contacts must represent lp–π interactions. An example is shown in Fig. 1b, where the K52E mutant of the engrailed homeodomain (shown in red) binds to the water molecule with two H-bond accepting residues, leaving only the lone pairs of oxygen free for contacting the indole side-chain of tryptophan W48.

Also in 2004, Kochi et al. presented crystal structures of adducts between tetraalkylammonium halides and tetracyanopiperazine (TCP), featuring quite spectacular halide–TCP contacts. Fig. 1c displays the detail of the TCP–(NEt₄Br) 3 : 2 cocrystal.⁸ The bromide⋯ring interactions, oriented roughly along the normals to the TCP planes, show a striking similarity to the O⋯ring interactions shown in Fig. 1a and b.

The TCP–Br⁻ interaction shown in Fig. 1c belongs formally to a subclass of lp–π interactions named anion–π interactions.^4,9–17 Anion–π interactions were theoretically predicted to attract anions such as Cl⁻ or Br⁻ toward the center of substituted/heterocyclic aromatic systems.^18–20 Subsequent experimental and theoretical work^8,10 revealed that in many cases, anions would bind to substituted aromatic systems in a different, “off-center” mode, reminiscent of that seen in Jackson–Meisenheimer σ-complexes.²¹ Accordingly, Hay, Berryman et al. distinguished between three anion–arene binding motifs: (i) noncovalent anion–π interactions, (ii) weakly covalent σ-complexes, and (iii) strongly covalent σ-interactions.^10,12 Some confusion has arisen from the fact that many authors understand that under anion–π interactions the first group can be exclusively found and argue that anion–π interactions are noncovalent interactions, driven by electrostatic, polarization, and dispersion forces (ref. 4, 17, 22, 23 and references therein). A recent IQA analysis by Foroutan-Nejad and Marek challenged this view, indicating that not only the off-center halide–arene complexes but also the symmetric anion–π interactions can profit from significant “multicenter covalency”.²⁴

The TCP–bromide interaction shown in Fig. 1c belongs to the off-center weakly covalent σ-complexes characterized by a substantial lp → π* CT stabilization.¹⁰ Considering the structural similarity between the three interactions shown in Fig. 1, one may wonder whether these interactions could be similar in nature. That is, could the CT component, evidently important in the latter case, contribute significantly also to the stabilization of the two former ones? The present article examines this question. We used a multi-approach theoretical analysis to elucidate the physical origin of water–indole and water–uracil lp–π interactions, in view of their possible role in the stabilization of proteins, nucleic acids, and protein–nucleic acid complexes. To evaluate the influence of the lp donor and that of the lp acceptor on the nature of the interaction, we included in our analysis the chloride–TCB interaction as a reference system with an established significant charge-transfer component.¹⁰ In addition, water–TCB and chloride–indole interactions were investigated as well, which enabled us to make cross-comparisons. Finally, for the water–indole system, we considered also N–H⋯O and O–H⋯π hydrogen bonding orientations, as these binding modes were previously predicted to be more stable than lp–π interactions.²⁵

Results and discussion

General

The model systems investigated in this work are schematically shown in Fig. 2. The structures of the lp–π complexes were idealized so as to place the lp-donating atom on the normal through the N or the C atom, and to orient the lone pair along the normal. This approximately corresponds to the position of the water molecule contacting tryptophan W48 in the engrailed homeodomain mutants (e.g. PDB code 1P7J, Fig. 1b). The geometry was optimized under this constraint, except for the uracil lp–π(M) system, where the lp axis was constrained to coincide with the normal through the centroid of the six-membered ring, in order to model the sugar-base lp–π interactions in Z-DNA (PDB code 1DCG, Fig. 1a). For the Cl⁻–TCB interaction, we considered, apart from the chloride position optimized under the constraint to lie on the normal through the C(H) atom, a second structure which was fully optimized. The unconstrained optimization placed the chloride ion roughly above the midpoint of the C–H bond, corresponding to structures found in halide–arene cocrystals (structures “c” according to Fig. 6 of ref. 10).

Fig. 2 Schematic representation of the model interactions studied in this work. In the lp–π interactions involving water, the water molecule was allowed to move along the normal to the ring plane and to rotate about it so as to minimize the energy. This rotation is, however, not taken into account in the depicted structures. For the chloride–TCB interaction, two structures were considered (see the text).

Both water–indole hydrogen-bonding systems, indole–N (O–H⋯π) and indole–NH (N–H⋯O), were constrained to be perfectly linear, the former aligned with the normal to the indole plane through N, and the latter having the N–H bond coinciding with the axis of one lone pair of the water oxygen atom.

Table 1 lists the components of the interaction energy evaluated using three different decomposition schemes (see Methods). For a comprehensive comparison of the decomposition methods and the definition of the individual components, the reader is referred to the excellent recent review by Phipps et al.²⁷ The most striking observation is that the chloride–TCB system is by far the most stable, its interaction energy being 5 to 10 times larger than that of any of the other systems. The decompositions show, in mutual agreement, that this stabilization arises from larger electrostatic (ES), polarization (POL), charge transfer (CT) and dispersion (DISP) components, which is somewhat balanced by larger Pauli repulsion (PAULI in EDA, included in EX-REP of SAPT and in DEF of NEDA). These individual energy contributions are discussed in the following subsections.

Table 1 Interaction energy components and other descriptors of the model interactions analyzed in this work (see Fig. 2). All energies in kcal mol⁻¹. The last column contains data for the Cl⁻–TCB complex with Cl⁻ on the normal to the TCB ring through the C(H) atom and (after the slash) for the fully relaxed complex. The abbreviations are defined in the text

Method	Lp-donor	H2O						Cl^−
	Arene	Indole–N lp⋯π	Indole–N O–H⋯π	Indole–NH N–H⋯O	Uracil–N lp⋯π	Uracil–M lp⋯π	TCB–C(H) lp⋯π	Indole–N lp⋯π	TCB–C(H) lp⋯π
a Data for the LCP found between water O-atom and uracil N1-atom. Another LCP could be identified between O and C4, with ρ(LCP) = 0.005 e a0^−3, corresponding interatomic DI = 0.018. b Closest atom–atom or atom–centroid distance between the fragments. c van der Waals radii taken from Bondi,^29 correction for H from Rowland and Taylor.^30 d Total interaction energy between fragments relaxed in the complex.
AIM	ρ(rc) [e a0^−3]	0.007	0.014	0.024	0.007	0.005^a	0.008	0.010	0.023/0.034
	DI	0.042	0.041	0.086	0.047	0.030	0.043	0.087	0.158/0.305
SAPT	ES	−2.3	−3.5	−8.3	−3.4	−3.1	−4.1	−4.2	−39.0/−47.3
	EX-REP	3.1	4.6	8.4	3.4	2.8	3.8	10.5	37.8/54.0
	POL	−0.6	−1.4	−2.6	−0.6	−0.6	−0.8	−7.1	−15.6/−24.3
	CT	−0.1	−0.3	−0.7	−0.1	−0.1	−0.1	−0.9	−3.7/−6.5
	DISP	−2.5	−3.3	−2.8	−2.7	−2.7	−2.8	−5.4	−10.9/−12.3
	TOT^d	−2.3	−3.6	−5.4	−3.3	−3.5	−4.0	−6.3	−27.7/−29.8
EDA	ES	−2.1	−3.3	−7.9	−3.6	−3.4	−4.2	−1.5	−33.8/−42.0
	PAULI	0.8	1.8	6.1	1.0	0.4	1.7	1.8	23.0/38.3
	ORB	−0.6	−2.1	−3.2	−0.6	−0.6	−1.0	−5.9	−18.0/−29.2
	TOT^d	−1.8	−3.6	−4.9	−3.2	−3.6	−3.5	−5.6	−28.8/−32.9
NEDA	ES	−2.0	−4.5	−9.5	−3.5	−3.6	−4.1	−3.1	−44.8/−53.0
	POL	−2.6	−2.5	−4.9	−2.3	−3.2	−3.2	−14.8	−9.8/−14.8
	CT	−2.5	−3.8	−13.7	−2.9	−2.2	−1.5	−2.0	−14.3/−36.3
	EX-CORR	−3.7	−3.5	−3.9	−3.2	−4.1	−3.6	−5.9	−7.6/−10.9
	DEF	9.2	10.7	25.5	9.0	9.7	8.9	21.0	52.0/85.4
	TOT^d	−1.6	−3.7	−6.5	−3.0	−3.4	−3.5	−4.8	−24.5/−29.6
NBO		−0.13	−1.68	−7.45	−0.34	−0.29	−0.41	−0.26	−5.3/−21.0
	ε π*/σ*	−3.1	239.8	224.0	−19.5	−21.3	−47.7	80.4	45.0/36.8
	ε lp	−155.0	−152.2	−293.7	−193.3	−264.8	−220.3	5.6	−39.3/−59.0
	ε π*/σ* − εlp	151.9	392.0	517.7	173.8	243.5	172.6	74.8	81.4/95.8
	F lpπ*/σ*	3.1	18.2	44.0	5.6	6.3	5.6	3.1	15.1/32.0
	S lpπ*/σ*	0.03	0.15	0.28	0.05	0.06	0.05	0.03	0.13/0.21
		−0.47	−0.29	−8.25	−0.46	−0.53	−1.01	−1.22	−9.0/−30.1
		−0.38	−1.86	−0.11	−0.05	−0.05	—	—	−0.47/−0.90
	ΔE^(2)total	−0.85	−2.15	−8.36	−0.51	−0.58	−1.01	−1.22	−9.45/−31.00
	q(arene) [e]	−0.003	0.002	−0.021	−0.003	−0.002	−0.006	−0.029	−0.276/−0.358
	d X–Y [Å]	3.12	2.29	1.99	3.07	3.10	3.08	3.25	2.78/2.55
	d X–Y (vdW)^c [Å]	3.07	2.64	2.61	3.07	—	3.22	3.30	3.45

---

Electrostatics

Long-range electrostatics (LRES): effect of the electrostatic potential at the π-surface of the aromatic molecules. In some current energy decomposition methods, including the SAPT, EDA, and NEDA schemes used in this work, the electrostatic energy is defined as the Coulomb energy between the two unperturbed partners. At long distances where orbital overlap is negligible, the ES component can be described in terms of a multipole expansion;²⁸ in the systems studied here it arises from the interaction between the water dipole or the chloride charge with the electrostatic potential (ESP) of the aromatic partner. At decreasing distances, the mutual penetration of the electron shells adds an exponentially increasing negative term called penetration energy to the ES component, vide infra.²⁸

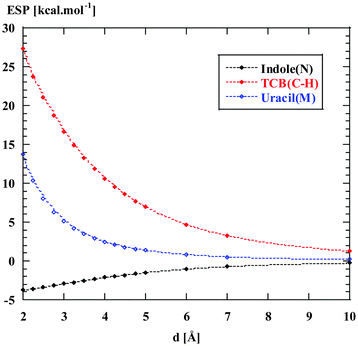
According to Table 1, the Cl⁻–TCB interaction has by far the strongest ES component (−35 to −50 kcal mol⁻¹). For comparison, the Cl⁻–indole interaction is one order of magnitude weaker. In order to estimate the contribution of long-range electrostatics to this difference, we have evaluated the ESP isosurfaces around indole, uracil, and TCB, as shown in Fig. 3. Clearly, TCB has a region of strongly positive ESP at the π-surface of the benzene ring, and especially along the normal to the ring through the C(H) carbon, whereas at the π-surface of indole, the ESP is close to zero or negative. Uracil appears as an intermediate case, with a positive ESP at the π-face, but with a smaller magnitude than in the case of TCB. The difference between the three heterocycles is even more clearly apparent from Fig. 4, where the ESP along the normals through C(H) of TCB, N of indole, and the centroid of the six-membered ring of uracil is plotted as a function of the distance from the ring plane. Fig. 4 shows that the ESP is strongly positive for TCB, slightly positive for uracil, and negative for indole. Thus, the long-range electrostatic forces for the Cl⁻–TCB interaction are attractive, whereas those for the Cl⁻–indole interaction are weakly repulsive. The negative sign of the ES component for the Cl⁻–indole interaction might therefore seem, at first glance, counter-intuitive, and must arise from a small but nonzero contribution from the penetration energy.

Fig. 3 ESP for indole, uracil, and TCB on isosurfaces corresponding to the electron density of 0.04 a.u. The color scale runs from −0.06 to +0.06 a.u.

Fig. 4 Electrostatic potential (in energy units) along the normals to the aromatic systems, through the atoms N of indole, C(H) of TCB, and the centroid of the six-membered ring of uracil, as a function of the distance from the ring plane.

Short-range electrostatics: atomic interpenetration. The origin of the negative ES component for the Cl⁻–indole interaction becomes clear if we consider, in Fig. 5, the distance-dependence of the overall ES component and compare it to the long-range electrostatic energy, approximated as the Coulomb energy of a point charge of −1e in the ESP of the aromatic molecule (designated LRES). As is apparent from Fig. 5, at long distances, the ES energy closely matches the LRES energy, whereas with the onset of orbital overlap (d ≤ 4 Å), the ES energy steeply decreases reflecting the exponential distance-dependence of the penetration energy.^28,31,32 Thus, the ES component for the Cl⁻–indole interaction is positive at long distances but decreases and becomes negative below 4 Å. The ES component of the Cl⁻–TCB complex is negative throughout, in agreement with the positive ESP of TCB, but its extent is substantially enhanced by atomic interpenetration below 4 Å. At the equilibrium distance of ∼2.8 Å, the long-range electrostatic energy (LRES) amounts about one half of the ES component. It is noteworthy that the latter equilibrium distance is ∼0.7 Å below the sum of the van der Waals radii and decreases to a value 0.9 Å below this sum in the fully optimized structure (see the two bottom lines in Table 1). Such a dramatic shortening below the van der Waals distance is not seen in any other analyzed complex.

Fig. 5 Electrostatic energy for binding of a negative unit charge (LRES, closed symbols) and of a chloride anion (calculated using EDA, ES, open symbols) along the normals to the aromatic systems, through the N or the C(H) atom of indole or TCB, respectively. The full and dashed lines join the calculated points using a smoothing fit, and are added for clarity. The arrows indicate the calculated equilibrium distances. Energy scans without geometry relaxation.

Fig. 5 thus demonstrates that both long-range electrostatics and penetration energy contribute to the highly negative ES component characterizing the Cl⁻–TCB complex. The large extent of the short-range electrostatic energy, that is, of the penetration energy, is, in turn, indication that the charge transfer, arising from overlap of occupied orbitals of one partner with unoccupied orbitals of the other partner, operates. Without the charge transfer operating, the increase of the penetration energy upon approaching the partners is counterbalanced by the enhancement of exchange-repulsion (also exponentially increasing), which prevents a further approach. Thus, the large penetration energy involved in the Cl⁻–TCB complex can be related to the efficient charge transfer (see Table 1 and section “Charge transfer” below).

The different ESPs around TCB, indole, and uracil (Fig. 3) are also reflected in the ES energies calculated for the complexes with water (Table 1), although to a smaller extent. The water–TCB lp–π interaction has a larger ES component than the water–uracil and the water–indole lp–π interactions. The negative ESP along the normal to the indole plane through N can be also related to the fact that the ES component is larger for the water–indole O–H⋯π interaction compared to that for the lp⋯π interaction (see the Discussion of hydrogen bonding versus lp⋯π interaction below).

Polarization and dispersion

Polarization and dispersion components derive from polarizability tensors. These two components of the interaction energy depend on the polarizabilities of the partners. The polarizability tensors of the interacting partners, i.e. indole, uracil, TCB, water, and the chloride anion, calculated for the isolated molecules, are given in Table 2. It can be seen that the zz components for the aromatic molecules (z-axis is perpendicular to the mean plane) decrease in the order TCB > indole > uracil. This order is reflected in the POL and DISP components corresponding to complexes with the same partner (H₂O or Cl⁻, see Table 1). The complexes with chloride show a higher polarization component than the corresponding complexes with water, since the net charge of chloride more strongly polarizes the aromatic system than the water dipole. The complexes with chloride show also larger dispersion components, reflecting the larger polarizability of chloride with respect to water (Table 2).

Table 2 Calculated diagonal components of the polarizability tensors

	Polarizability tensor diagonal components [Å^3]
	α xx	α yy	α zz
TCB	210	143	63
Indole	134	104	54
Uracil	72	87	36
Water	9	8	6
Cl^−	10

---

It has to be noted that the efficient charge transfer operating in the Cl⁻–TCB complex and enabling an approach well below the sum of van der Waals radii (Table 1) contributes to a further increase of both POL and DISP components, both increasing with the negative sixth power of the distance.

Charge transfer

All analyses point to a relatively strong CT from Cl⁻ to TCB. The NEDA and SAPT energy decomposition methods quantify the CT component using different procedures, and the numerical CT values determined from NEDA are frequently one order of magnitude higher than those obtained with SAPT,^27,33 an observation that we also make on perusal of Table 1. Nevertheless, both methods agree in indicating that the CT energy of the chloride–TCB system is up to 40 times larger than that of any other lp–π system. The CT character of the chloride–TCB complex is also reflected in the EDA orbital interaction energy component (which includes CT, POL, and, to some extent, DISP, depending on the exchange–correlation functional used). The significant orbital interaction between Cl⁻ and TCB is further evidenced by the shortening of the Cl⋯C distance well beyond the sum of van der Waals radii (Table 1). The magnitude of the CT between Cl⁻ and TCB is also manifest in the second-order perturbation energy, , determined for the charge transfer from the donor lp NBO to the lowest acceptor π* NBO, and in the net charge transferred. That the Cl⁻–TCB interaction has a stronger covalent component than any of the other systems is also apparent from the large ρ(LCP),^34–36 indicating an increase of electron density in the internuclear region (that was already observed in electron density maps¹⁰), and from the interatomic delocalization indices (DI).³⁷

Table 1 shows that the second-order perturbation energy 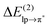, arising from the single lp → π* orbital interaction, makes a dominant contribution to the CT energy of the Cl⁻–TCB lp–π complex. The same statement applies to the indole–water classical N–H⋯O hydrogen bond, where the dominant charge transfer goes from the lp of the water oxygen to the antibonding σ* orbital of the N–H bond of indole.³⁸ All the other lp–π systems have 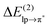energies of the order of a few tenths of kcal mol⁻¹, which are values similar to the 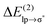stabilization energies of very weak hydrogen bonds, such as CH₄⋯OH₂.³⁸ The energy for chloride–TCB of 21 kcal mol⁻¹, on the other hand, corresponds to 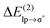values of strong hydrogen bonds, such as FH⋯OH₂.³⁸ The energy for the chloride–TCB interaction is also more than twice as large as the 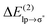energy calculated for the classical indole–water N–H⋯OH₂ hydrogen bond, 7.5 kcal mol⁻¹ (Table 1).

The energy for the fully optimized chloride–TCB complex of 21.0 kcal mol⁻¹ is similar to the value of 21.2 kcal mol⁻¹ obtained by Berryman et al.¹⁰ It is noteworthy that for the symmetrical complex where Cl⁻ approaches the ring centroid of TCB, the ORB component calculated with the EDA method is −9.7 kcal mol⁻¹, about one third of the value of −29.2 kcal mol⁻¹ obtained for the fully optimized off-center complex (Table 1 and Table S1, Fig. S1, ESI†). This indicates that while in the centrosymmetric approach the orbital interaction is somewhat weaker than that in the off-center geometry, it is not neglectable, and classifying this interaction as “non-covalent” or “electrostatic” appears misleading. Our data concurs with the previous finding of a significant global delocalization index for this symmetrical interaction arrangement.²⁴

The second-order CT-stabilization energy calculated for all donor–acceptor orbital pairs, ΔE⁽²⁾_total, can be decomposed into the components corresponding to CT from H₂O/Cl⁻ orbitals to the ring system, , and those corresponding to the CT in the opposite direction, (bottom part of Table 1). For all the lp–π complexes except the water–indole complex, the CT is practically unidirectional, i.e.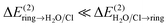. For the water–indole lp–π complex, the and components are of similar magnitude, and ΔE⁽²⁾_total is composed of several small CT interactions in both directions.

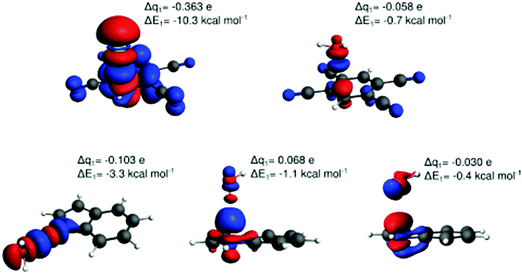
Fig. 6 displays the electron deformation density associated with natural orbitals for chemical valence (NOCV)³⁹ channels with the highest stabilization energy identified for the lp–π interactions Cl⁻–TCB, water–TCB, and water–indole, and for the two water–indole hydrogen-bonded complexes. The identification of the Cl⁻–TCB lp–π CT as the orbital interaction with the highest stabilization orbital energy, followed by the indole–water N–H⋯O hydrogen bond, corresponds to the CT-component ranking in Table 1, confirming again the dominant role of these orbital interactions. We observe that greater stabilization energy goes generally along with a greater amount of transferred charge; however, there is no obvious quantitative correlation. Note that in the two hydrogen-bonding modes of the water–indole interaction the roles of donor and acceptor are inversed, as manifest in the inverse sign of Δq.

Fig. 6 Natural orbitals for chemical valence (NOCV) channels with the largest contributions to the orbital energy for the off-center interactions Cl⁻–TCB lp–π (Cl⁻ on the normal through the C(H) atom, top left), water–TCB lp–π (top right), indole–water N–H⋯O hydrogen bonding (bottom left), water–indole O–H⋯π hydrogen bonding (bottom middle), and water–indole lp–π (bottom right). The NOCV-deformation-density-isosurface threshold used for visualization was 0.0003 a.u. (0.0001 a.u. for water–indole lp–π). Red: depletion, blue: concentration of electron density. The Δq₁ values denote the transferred charge (NOCV eigenvalue) between fragments and ΔE₁ the corresponding stabilizing energy for the first NOCV channel.

Water–indole and water–uracil lp–π interactions involve only a weak CT. All the theoretical analyses presented above are mutually consistent in indicating that biologically relevant lp–π interaction systems water–indole and water–uracil involve relatively weak stabilization due to the charge transfer. In contrast, for the Cl⁻–TCB reference system, our results confirm a stronger CT component, as demonstrated previously.^8,10

Origin of the efficient Cl⁻ → TCB CT. In view of the outstanding CT component of the Cl⁻–TCB lp–π complex, as compared to all the other complexes (Table 1), we may ask about the origin of this difference. According to the second-order perturbation theory, the stabilization energy due to the CT from the lp of water or chloride to a π* orbital of the ring system is proportional to the square of the non-diagonal matrix element, F_lpπ*², and indirectly proportional to the difference in orbital energy between the two interacting orbitals, ε_π* − ε_lp:⁴⁰
The non-diagonal matrix element, in turn, is a function of the overlap integral S_lpπ* (ref. 41, pp. 600–602). The bottom part of Table 1 lists, apart from the second-order perturbation energy, 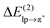, also the corresponding parameters F_lpπ*, S_lpπ*, ε_lp, and ε_π*. As expected, the chloride–TCB interaction profits from a particularly high-energy lp of the chloride anion, making the ε_π* − ε_lp gap significantly smaller than in any of the systems involving water as the lp donor. In addition, the overlap between these two orbitals is rather efficient, resulting in a large F_lpπ* term. Thus, the key characteristics of the chloride–TCB system appears to be the small energy gap between the lp(Cl⁻) and π*(TCB) orbitals and the efficient overlap between them.

Hydrogen bonding versus lp–π interactions between water and indole

Table 1 allows for an interesting comparison between lone-pair–π and hydrogen-bonding interactions involving indole and water, i.e. between the N–H⋯O hydrogen bond in the indole plane, the O–H⋯π hydrogen bond, and the lp–π interaction (see the first three columns of Table 1). The N–H⋯O hydrogen bond is the most stable and the lp–π the least stable interaction in this group. The N–H⋯O hydrogen bond gains its stability both from the strongest electrostatic component and from the strongest CT component. The latter arises from an overlap between the lp and σ* orbitals,^38,42 which is even more efficient than the lp–π* overlap in the Cl⁻–TCB interaction. The lp vs. π* orbital energy difference for the water–indole, ε_σ* − ε_lp, however, is considerably larger than the ε_π* − ε_lp difference for the Cl⁻–TCB interaction, so that the stabilization energy for the latter is larger. The N–H⋯O hydrogen bond also has a stronger polarization component than the O–H⋯π hydrogen bond and the lp–π interaction. This can be related to the in-plane components xx and yy of the polarizability tensor of indole which are larger than the out-of-plane component zz (Table 2). Finally, all the methods indicate that the O–H⋯π hydrogen bond is more stable than the lp–π interaction. This is related to the negative ESP above the indole ring, as has been discussed above (cf. electrostatics). Our calculations indicate therefore that water molecules contacting the π-face of an indole side-chain of tryptophan in proteins have an intrinsic preference for an O–H⋯π orientation with respect to the lp–π orientation. This preference is, however, relatively weak (energy difference of ∼2 kcal mol⁻¹), and can be conceivably overrun by solvation effects and/or the influence of neighboring residues.

Consequences for lone-pair–π interactions in biomolecules

The present investigation was devoted to the evaluation of the physical origin of lp–π interactions in biomolecules¹ and explicitly addressed the participation of CT in these interactions. We used, as a positive control, the Cl⁻–TCB lp–π complex with established CT character.^8,10,24 The hypothesis that we wanted to test stated that the structural similarity between the water–indole lp–π interaction observed in proteins (Fig. 1b), the water–nucleobase lp–π interaction observed in RNA,⁴³ and the halide–π interaction observed with substituted arenes (Fig. 1c) arose from a strong CT component shared by all three interaction types.

In contrast to the above hypothesis, our results, summarized in Table 1, indicate that water–uracil and water–indole lp–π interactions are governed by relatively weak forces, composed of small (≤3.5 kcal mol⁻¹) contributions of ES, POL, CT, and DISP components. On perusal of Table 1, we can see that for all these water–π-ring lp–π interactions, the ES component happens to be of a similar extent as the total interaction energy, that is, all the other components sum up to approximately zero. Such incidental cancelling of energy components can, however, give rise to misinterpretations, and can lead, for instance, to interpretations of hydrogen bonding as either purely electrostatic, or purely covalent.³³ We have already reported such mutual cancelling of non-electrostatic components for other water–π-ring lp–π interactions,⁴⁴ and explained thus previous observations that lp–π interactions involving water, alcohols, or ethers as lp donors can be seemingly described as predominantly electrostatic interactions.⁴⁵ This cancelling of components also explains why classical force-fields are so successful in portraying non-bonding forces in biomolecules, without taking polarization or charge transfer specifically into account.

Particularly interesting is our finding that water associations with the π-face of indole are more likely to occur via O–H⋯π hydrogen bonding than via an lp–π interaction. Although our calculations do not account for solvation or effects of neighboring residues, which may reverse the in vacuo stabilities, this result raises the question whether the out-of-plane (π-surface) contacts between water and tryptophan frequently observed in protein structures may not arise, at least in some cases, from O–H⋯π hydrogen bonding rather than from lp–π interactions, as previously suggested.⁶ In fact, since both the O–H⋯π and the lp–π interactions are relatively weak, it is conceivable that in protein structures, the O–H⋯π and lp–π states constitute a dynamic equilibrium which would provide an entropic advantage for water molecules in such sites.

Concluding remarks

In this paper, we examined the energy components of lp–π interactions, with particular focus on the importance of charge transfer. The analyzed interacting pairs cover a relatively broad spectrum of cases strongly differing both in the total interaction energy and in the magnitude of the individual energetic components. According to the total interaction energy, E_TOT, we can divide the analyzed lp–π complexes into three groups:

(i) At the “strongly-binding” (E_TOT ≈ −30 kcal mol⁻¹) end of the spectrum, we find the Cl⁻–TCB lp–π complex characterized by a considerable shortening of the distance between the closest atoms beyond the sum of van der Waals radii (Δr ≈ 0.9 Å in the fully relaxed complex) and by a high CT contribution, arising from an efficient overlap between the donor lp and acceptor π* orbitals and a small gap between their orbital energies. A significant charge transfer stabilization (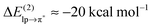) was already found previously for this complex by Berryman et al.¹⁰ Those authors referred to this complex class as “weakly covalent donor to π–acceptor complexes”, as opposed to strongly covalent analogs with F⁻ where 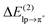is one order of magnitude larger and the interaction energy approaches values typical of covalent bonds.¹⁰ The shortening of the interfragment distance beyond the van der Waals distance is accompanied by an enhancement of penetration energy (contributing about 50% to the ES component) and of Pauli repulsion, both of which increase exponentially with decreasing distance. The close approach of the fragments also causes an increase of the POL and DISP components, corresponding to their dependence on R⁻⁶. It is therefore important to note that the large ES, POL, and DISP components of the Cl⁻–TCB lp–π interaction are, in part, a consequence of the large CT which enables a significant shortening of the interatomic distance beyond the van der Waals contact. However, not the entire extent of the ES, POL, and DISP components is due to the close approach of the fragments induced by the orbital interaction: their long-range parts are significant as well. For the ES component, we have demonstrated in Fig. 5 that the long-range part, LRES, is also greater in magnitude than, for instance, that of the Cl⁻–indole interaction. As for POL and DISP, we can roughly infer the long-range contributions from the zz components of the polarizability tensors (Table 2): at the van der Waals distance, these components for Cl⁻–TCB are expected to be slightly larger than those for Cl⁻–indole, and considerably larger than those for all the other lp–π interactions.

(ii) The intermediate class (−7 kcal mol⁻¹ < E_TOT < −3 kcal mol⁻¹) is represented by the water–uracil lp–π complexes, the water–TCB lp–π complex, and the Cl⁻–indole complex. In this class, the CT component is at least one order of magnitude smaller than that of the first class, and the interfragment separation is within 0.2 Å from the van der Waals distance. Within this group, the Cl⁻–indole complex differs from the others by repulsive long-range electrostatics (Fig. 5), and by larger polarization energy, arising from the polarizing power of the chloride ion.

For the water–uracil and water–TCB lp–π interactions, the stabilization energy is composed of small amounts of ES, POL, CT, and DISP, neither of which exceeds −4.2 kcal mol⁻¹ in any of the three decomposition analyses. The water–uracil(M) lp–π total interaction energy of −3.4 ± 0.2 kcal mol⁻¹ is identical with the value obtained previously from MP2/6-31G* calculations¹ and similar to that determined for the deoxyribose–guanine lp–π interaction energy at the same level of theory.⁴⁶ This suggests that the oxygen lone pairs of electrons of water and deoxyribose interact with π-systems with similar energetics, and our results for the water–uracil lp–π interaction can be thus extrapolated to deoxyribose–nucleobase lp–π interactions.

(iii) At the “weakly-binding” end of the spectrum (E_TOT ≈ −2 kcal mol⁻¹), we find the water–indole lp–π interaction, which combines repulsive long-range electrostatics with relatively low penetration energy, charge-transfer, polarization and dispersion components.

Our calculations show that the lp–π contacts that water forms with the aromatic residues of nucleic acids and proteins correspond to bonding interactions with a very weak CT component. For contacts between water molecules and the π-face of tryptophan, which have been shown to stabilize proteins and protein–DNA complexes,⁶ our calculations suggest that the O–H⋯π hydrogen bonding is the more likely binding mode than the lp–π interaction.

In summary, our work has shown that lone-pair–π interactions can range from weak bonding to relatively strong bonding with a significant CT contribution. A sizeable CT component requires a donor molecule with a high-energy lone pair and a π–acceptor with a relatively low-energy, empty π*-orbital, allowing for efficient overlap with the donor lp-orbital. In agreement with previous results,¹⁰ we found that for TCB an off-center interaction with an anion (chloride) results in better lp–π* overlap and stronger CT. However, our results indicate that even the symmetrical Cl⁻–TCB approach results in a non-neglectable orbital interaction (Fig. S1, ESI†), an effect previously termed “multi-center-covalency”.²⁴ We conclude that considering lone-pair–π or anion–π interactions generally as “non-covalent” (ref. 4, 17, 22, 23 and references therein) does not correspond to reality.

Methods

Geometry optimizations

The lp–π model systems shown in Fig. 2 were constructed by constraining the water O atom or the chloride ion to lie on the normal to the aromatic system through the N or C atom, or through the ring centroid M, using C–X–O or C–X–Cl (X = N, C, or the ring centroid) angle constraints. In the case of the Cl⁻–TCB complex, we also considered the fully optimized geometry. In the lp–π complexes involving water, the X⋯O–H angles were constrained to the value of 111°. This X⋯O–H angle for water was previously determined from a CSD search for neutron diffraction structures of metal complexes coordinating an sp³-hybridized water molecule, as explained in the ESI of ref. 47. Neutron diffraction structures of these metal aqua complexes allow for a relatively precise determination of the directionality of the water lone-pairs. Under the above constraints, the geometries were optimized using the RI-BLYPD3(BJ)/def2-TZVPP level of theory,^48–51 in gas phase, with convergence criteria of 10⁻⁶ Hartree for energy change and 10⁻³ Å for the geometrical gradient. In the case of the indole–N system, we have carried out a control optimization using the RI-MP2/aug-cc-pVTZ level of theory (convergence criteria of 10⁻⁷ Hartree for energy change and 10⁻³ Å for the cartesian gradients) in order to check that the obtained atomic coordinates were very similar (RMSD = 0.024 Å). All calculations used the Turbomole 6.03 package (http://www.turbomole.com). The atomic coordinates of the optimized structures used for theoretical analyses (reported in Table 1) are given in Table S1 (ESI†).

Energy decomposition and other analytical approaches

General. For all the lp–π and hydrogen bonding interactions, we applied three MO-based methods to decompose the interaction energy: the Symmetry-Adapted Perturbation Theory (SAPT),⁵² the Energy Decomposition Analysis (EDA),^53,54 and the Natural Energy Decomposition Analysis (NEDA).⁵⁵ In addition, we have used the Quantum Theory of Atoms in Molecules (QTAIM) theory^56,57 to analyze the electron density at the line critical points (LCP³⁶) and to calculate the interatomic delocalization indices.³⁷ Finally, we employed the Natural Bond Orbitals (NBO) theory⁴⁰ to analyze orbital interactions between lone pairs and π* or σ* orbitals.

Computational details. The AIM analysis used the AIMAll program⁵⁸ and was carried out on wavefunctions obtained in Gaussian 09⁵⁹ at the BLYP-D3/aug-cc-pVDZ computational level, SCF convergence criterion: 10⁻⁸ Hartree. The SAPT calculations were performed at the HF-SAPT2+level (aug-cc-pVDZ basis set, default density-fitting algorithm, SCF convergence criterium: 10⁻⁸ Hartree), as implemented in the PSI4 package.⁶⁰ The EDA decomposition (M06-2X, TZ2P all electron basis set, SCF convergence criterium: 10⁻⁶ Hartree) was performed as implemented in the ADF package.⁵⁴

The orbital interactions were examined within the NBO module Version 6.0⁶¹ implemented in Gaussian 09⁵⁹ at the same level of theory as in the AIM analysis. The total CT energies between partners, 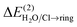and , were calculated considering all possible CTs from occupied to vacant orbitals, with the default threshold for intramolecular orbital transitions set to 0.05 kcal mol⁻¹. The NEDA decomposition analysis⁶² was performed at the M06-2X/6-31G(d,p) level of theory using the NBO module within the GAMESS package.^63,64

Acknowledgements

This work was supported by the Czech Science Foundation (grant no. 14-14654S). We are indebted to Prof. Ben F. Luisi for providing us with results from searches of the pdb database and Dr Jan Vícha for preliminary geometry optimizations. JK thanks Prof. F. Weinhold for helpful discussions. This work was carried out in part under the project CEITEC 2020 (LQ1601) with financial support from the Ministry of Education, Youth and Sports of the Czech Republic under the National Sustainability Program II. Computational resources were provided by the MetaCentrum under the program LM2010005 and the CERIT-SC under the program Centre CERIT Scientific Cloud, part of the Operational Program Research and Development for Innovations, Reg. no. CZ.1.05/3.2.00/08.0144.

References

1. M. Egli and S. Sarkhel, Acc. Chem. Res., 2007, 40, 197.
2. T. J. Mooibroek, P. Gamez and J. Reedijk, CrystEngComm, 2008, 10, 1501.
3. K. A. Wilson, J. L. Kellie and S. D. Wetmore, Nucleic Acids Res., 2014, 42, 6726.
4. S. R. Gadre and A. Kumar, Understanding lone pair-π interactions from electrostatic viewpoint, in Noncovalent Forces, Challenges and Advances in Computational Chemistry and Physics, ed. S. Scheiner, 2015, vol. 19, p. 391.
5. M. Egli and R. Gessner, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 180.
6. E. J. Stollar, J. L. Gelpi, S. Velankar, A. Golovin, M. Orozco and B. F. Luisi, Proteins: Struct., Funct., Bioinf., 2004, 57, 1.
7. E. Fraenkel, M. A. Rould, K. A. Chambers and C. A. Pabo, J. Mol. Biol., 1998, 284, 351.
8. Y. S. Rosokha, S. V. Lindeman, S. V. Rosokha and J. K. Kochi, Angew. Chem., Int. Ed., 2004, 43, 4650.
9. P. Gamez, T. J. Mooibroek, S. J. Teat and J. Reedijk, Acc. Chem. Res., 2007, 40, 435.
10. O. B. Berryman, V. S. Bryantsev, D. P. Stay, D. W. Johnson and B. P. Hay, J. Am. Chem. Soc., 2007, 129, 48.
11. B. L. Schottel, H. T. Chifotides and K. R. Dunbar, Chem. Soc. Rev., 2008, 37, 68.
12. B. P. Hay and V. S. Bryantsev, Chem. Commun., 2008, 2417–2428.
13. O. B. Berryman and D. W. Johnson, Chem. Commun., 2009, 3143.
14. L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808.
15. A. Frontera, P. Gamez, M. Mascal, T. J. Mooibroek and J. Reedijk, Angew. Chem., Int. Ed., 2011, 50, 9564.
16. P. Ballester, Acc. Chem. Res., 2013, 46, 874–884.
17. A. Bauzá, P. M. Deyà, and A. Frontera, Anion–π Interactions in Supramolecular Chemistry and Catalysis, in Noncovalent Forces, Challenges and Advances in Computational Chemistry and Physics, ed. S. Scheiner, 2015, vol. 19, p. 471.
18. M. Mascal, A. Armstrong and M. D. Bartberger, J. Am. Chem. Soc., 2002, 124, 6274.
19. L. Alkorta, I. Rozas and J. Elguero, J. Am. Chem. Soc., 2002, 124, 8593.
20. D. Quinonero, C. Garau, A. Frontera, P. Ballester, A. Costa and P. M. Deya, Chem. Phys. Lett., 2002, 359, 486.
21. J. Meisenheimer, Justus Liebigs Ann. Chem., 1902, 323, 205–226.
22. M. Giese, M. Albrecht and K. Rissanen, Chem. Commun., 2016, 52, 1778.
23. H. Wang, W. Wang and W. J. Jin, Chem. Rev., 2016, 116, 5072–5104.
24. C. Foroutan-Nejad, Z. Badri and R. Marek, Phys. Chem. Chem. Phys., 2015, 17, 30670.
25. T. van Mourik, S. L. Price and D. C. Clary, Chem. Phys. Lett., 2000, 331, 253.
26. E. J. Stollar, U. Mayor, S. C. Lovell, L. Federici, S. M. V. Freund, A. Fersht and B. F. Luisi, J. Biol. Chem., 2003, 278, 43699–43708.
27. M. J. S. Phipps, T. Fox, C. S. Tautermann and C.-K. Skylaris, Chem. Soc. Rev., 2015, 44, 3177.
28. A. J. Stone, The theory of intermolecular forces, Oxford University Press, 2nd edn, 2013, p. 141 ff.
29. A. Bondi, J. Chem. Phys., 1964, 68, 441.
30. R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384.
31. F. L. Hirschfeld and S. Rzotkiewicz, Mol. Phys., 1974, 27, 1319.
32. L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343.
33. A. M. Pendas, M. A. Blanco and E. Francisco, J. Chem. Phys., 2006, 125, 184112.
34. D. Cremer and E. Kraka, Croat. Chem. Acta, 1984, 57, 1259.
35. R. F. W. Bader, T. S. See, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061.
36. C. Foroutan-Nejad, S. Shahbazian and R. Marek, Chem. – Eur. J., 2014, 20, 10140.
37. X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304.
38. F. Weinhold and R. A. Klein, Mol. Phys., 2012, 110, 565.
39. M. P. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576.
40. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
41. F. Weinhold and C. Landis, Valency and Bonding, A natural bond orbital donor–acceptor perspective, Cambridge University Press, 2005.
42. C. Fonseca Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, Chem. – Eur. J., 1999, 5, 3581.
43. S. Sarkhel, A. Rich and M. Egli, J. Am. Chem. Soc., 2003, 125, 8998.
44. Z. Badri, C. Foroutan-Nejad, J. Kozelka and R. Marek, Phys. Chem. Chem. Phys., 2015, 17, 26183.
45. J. Ran and P. Hobza, J. Chem. Theory Comput., 2009, 5, 1180.
46. J. Sponer, H. A. Gabb, J. Leszczynski and P. Hobza, Biophys. J., 1997, 73, 76.
47. S. Rizzato, J. Bergès, S. A. Mason, A. Albinati and J. Kozelka, Angew. Chem., Int. Ed., 2010, 49, 7440.
48. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
49. C. L. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
50. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
51. A. Schafer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1993, 100, 5829–5835.
52. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887.
53. K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340.
54. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 9.
55. E. D. Glendening, J. Phys. Chem. A, 2005, 109, 11936.
56. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1990.
57. P. Popelier, Atoms in Molecules. An Introduction, Prentice Hall, 2000.
58. A. Todd and T. K. Keith, AIMAll, Overland Park KS, USA, 2015.
59. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian 09, Revision D01, Gaussian, Inc., Wallingford, CT, 2013.
60. E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 133, 014101.
61. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis, and F. Weinhold, NBO, Madison, 2013.
62. E. D. Glendening and A. Streitwieser, J. Chem. Phys., 1994, 100, 2900.
63. GAMESS-UK is a package of ab initio programs. See: http://www.cfs.dl.ac.uk/gamess-uk/index.shtml.
64. M. F. Guest, I. J. Bush, H. J. J. van Dam, P. Sherwood, J. M. H. Thomas, J. H. van Lenthe, R. W. A. Havenith and J. Kendrick, Mol. Phys., 2005, 103, 719.

---

Footnotes

† Electronic supplementary information (ESI) available: Fig. S1: Electrostatic and Orbital energy components of the Cl⁻–TCB complex in the symmetrical and off-center geometries; Table S1: EDA analysis of the Cl⁻–TCB complex in the symmetrical and off-center geometries, Table S2: PDB coordinate files of the analyzed complexes. See DOI: 10.1039/c6cp01524g

‡ These authors contributed equally.

§ Present address: Center for Free-Electron Laser Science, DESY, Notkestraße 85, Hamburg, Germany.

---