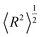Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Is the manifestation of the local dynamics in the spin–lattice NMR relaxation in dendrimers sensitive to excluded volume interactions?
Oleg V.
Shavykin
a,
Igor M.
Neelov
ab and
Anatolii A.
Darinskii
ab
aSt. Petersburg National Research University of Information Technologies, Mechanics and Optics (ITMO University), Kronverskiy pr. 49, St. Petersburg, 197101 Russia. E-mail: kupala-89@mail.ru
bInstitute of Macromulecular Compounds, Russian Academy of Sciences, Bolshoi Prospect 31, V.O., St. Petersburg, 199004 Russia. E-mail: a.darinskii@mail.ru
First published on 17th August 2016
Abstract
The effect of excluded volume (EV) interactions on the manifestation of the local dynamics in the spin–lattice NMR relaxation in dendrimers has been studied by using Brownian dynamics simulations. The study was motivated by the theory developed by Markelov et al., [J. Chem. Phys., 2014, 140, 244904] for a Gaussian dendrimer model without EV interactions. The theory connects the experimentally observed dependence of the spin–lattice relaxation rate 1/T1H on the location of NMR active groups with the restricted flexibility (semiflexibility) of dendrimers. Semiflexibility was introduced through the correlations between the orientations of different segments. However, these correlations exist even in flexible dendrimer models with EV interactions. We have simulated coarse-grained flexible and semiflexible dendrimer models with and without EV interactions. Every dendrimer segment consisted of two rigid bonds. Semiflexibility was introduced through a potential which restricts the fluctuations of angles between neighboring bonds but does not change orientational correlations in the EV model as compared to the flexible case. The frequency dependence of the reduced 1/T1H(ωH) for segments and bonds belonging to different dendrimer shells was calculated. It was shown that the main effect of EV interactions consists of a much stronger contribution of the overall dendrimer rotation to the dynamics of dendrimer segments as compared to phantom models. After the exclusion of this contribution the manifestation of internal dynamics in spin–lattice NMR relaxation appears to be practically insensitive to EV interactions. For the flexible models, the position ωmax of the peak of the modified 1/T1H(ωH) does not depend on the shell number. For semiflexible models, the maximum of 1/T1H(ωH) for internal segments or bonds shifts to lower frequencies as compared to outer ones. The dependence of ωmax on the number of dendrimer shells appears to be universal for segments and bonds in dendrimer models with and without EV interactions.
1 Introduction
Dendrimers are regular hierarchically branched polymers with a wide range of potential applications such as catalysts or nanocarriers for drugs, dye and metal nanoparticle delivery,1–4etc. The dynamical properties of dendrimers are of great importance for many practical applications. Experimentally, dendrimer dynamics is studied by dielectric relaxation, nuclear magnetic resonance (NMR), birefringence measurements and polarized luminescence. In particular, the NMR spin–lattice relaxation method allows us to obtain information about the orientational mobility of NMR active groups by measuring the spin–lattice relaxation rate, 1/T1H. In the case when 1H is used as a marker, 1/T1H is connected with the spectral densities J(ωH) and J(2ωH) by the relation | (1) |
 | (2) |
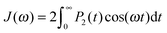 | (3) |
In the majority of theoretical papers on NMR relaxation in dendrimers it is assumed that the dynamics of the NMR active groups reflects the orientation mobility of the segments of the dendrimer. This means that the internuclear vectors in these groups have a component directed along the segment. The theory of NMR relaxation in flexible dendrimers was developed on the basis of the Gaussian model of dendrimers (ref. 12 and 13). In this model, the segments are represented by Gaussian subchains and excluded volume interactions are neglected (phantom model). The reduced dimensionless spin–lattice relaxation rate was considered:
 | (4) |
| P2(t) = exp(−t/τ) | (5) |
| ωmax ≈ 0.616/τ | (6) |
To explain this disagreement, it was assumed13 that the experimentally observed dependence of the NMR signal on the segment position inside a dendrimer is connected with a restricted flexibility (semiflexibility) of the dendrimer. Indeed, calculations have shown that the incorporation of semiflexibility into the Gaussian model of dendrimers leads to the dependence of ωmax on the number of dendrimer layers in the labeled segment.13
The Gaussian dendrimer model is a phantom model, i.e. non-bonded interactions are neglected. But in real dendrimers, the contribution of these interactions is significant. As a result, their size and internal structure differ qualitatively from those predicted by the Gaussian model.
Semiflexibility was incorporated into the Gaussian model through the correlations between the orientations of segments located in different dendrimer shells.
| |〈didj〉| = qk, | (7) |
However, as it was shown by Kumar and Biswas,14,15 the neglect of excluded volume (EV) interactions can be compensated by incorporating semiflexibility into the model, where the restrictions imposed on the segment direction and orientation exactly reproduce the features of EV interactions.
Therefore, the correlations between the orientations of segments are inherent even for dendrimers consisting of flexible elements, and thus there are no real dendrimers without such correlations. Due to excluded volume interactions, there are always correlations between the orientations of segments. Nevertheless, our previous simulation of simple coarse-grained dendrimer models with excluded volume interactions12 shows that the positions of the maximum of 1/T1H coincide for segments located in different dendrimer shells. It means that in this respect the flexible Gaussian and EV models behave similarly. The question arises as to whether this similarity remains when we speak about the effect of semiflexibility on the position of the [1/T1H(ωH)] maximum.
It should be noted that the dependence of the mobility of NMR active groups in poly-lysine dendrimers established experimentally and confirmed by full-atomic molecular dynamics simulations in our recent work9 was interpreted as a manifestation of the restricted flexibility of these dendrimers.
However, a direct comparison of the effect of semiflexibility on the segmental mobility in phantom and excluded volume dendrimer models has not been performed up to now. In the present work, we will perform such a comparison by using computer simulation of simple coarse-grained models. We will show that the shift of the maximum of [1/T1H(ωH)] occurs due to the introduction of an additional angular potential into the EV dendrimer model even if the value of the correlation parameter q remains practically the same.
The remainder of this paper is organized as follows. In Section 2, we briefly describe the model and simulation details. Section 3 is devoted to our results and their discussion. Eventually, Section 4 contains the conclusions.
2 Model and simulation method
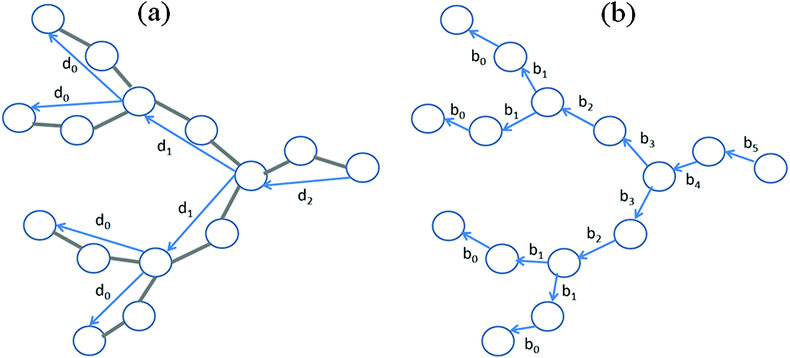
We consider the coarse-grained model of dendrimers depicted in Fig. 1 with different numbers of generations and numbers of beads (Table 1). In the dendrimer models considered earlier in ref. 16 and 17 every segment connecting neighboring branching points consisted of only one bond. In our case, every segment contains two bonds. A similar dendrimer model was simulated in the papers of Karatasos et al.18,19 This model allows monitoring the dendrimer dynamics not only on the segment scale but also on the scale of bonds.| G | N | N t |
|---|---|---|
| 2 | 19 | 6 |
| 3 | 43 | 12 |
| 4 | 91 | 24 |
| 5 | 187 | 48 |
The bonds are considered as springs with the potential
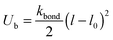 | (8) |
We consider two types of models with the topology shown in Fig. 1. The first type is a phantom (Ph) model, i.e. a model without the excluded volume interactions while the second model includes EV interactions between all beads:
 | (9) |
 . Thus, the potential UR is a purely repulsive potential that represents the short-ranged interactions between non-bonded monomers. It describes dendrimers under good solvent conditions and reproduces the main features of real dendrimers in solutions such as the molecular mass dependence of the gyration radius, density profile, terminal group distribution, etc. The potential parameters σ = 0.8 and ε = 1.0 are similar to those used in ref. 16.
. Thus, the potential UR is a purely repulsive potential that represents the short-ranged interactions between non-bonded monomers. It describes dendrimers under good solvent conditions and reproduces the main features of real dendrimers in solutions such as the molecular mass dependence of the gyration radius, density profile, terminal group distribution, etc. The potential parameters σ = 0.8 and ε = 1.0 are similar to those used in ref. 16.
Semiflexibility is introduced into the dendrimer model through the internal potential which restricts the angle γij between neighboring bonds
 | (10) |
In the previous work,12 we used a free-draining dendrimer model where hydrodynamic interactions (HI) were neglected. As it was shown in ref. 12, the effect of HI interactions appears mainly in global motions, such as the rotation of the dendrimer as a whole. Their effect on internal modes is much weaker. As it was shown in our paper,20 for a flexible dendrimer model with segments consisting of one bond the inclusion of HI does not change the conclusion about the independence of the position of the maximum of the reduced spin–lattice relaxation rate 1/T1H(ωH) from the shell number.
The time evolution of particles in the BD method is described by coupled Langevin differential equations without an inertial term
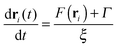 | (11) |
| 〈Γα〉 = 0 | (12) |
| 〈Γα(t1)·Γβ(t2)〉 = 2kBTξδα,βδ(t1 − t2), | (13) |
 and time step Δt = 0.00005τ0. The total simulation time was tsim from 2 × 108Δt = 104τ0 (for the dendrimer of second generation, G = 2) to 32 × 108Δt = 16 × 104τ0 (G = 5). The relaxation time for a single bond (not included in the dendrimer) τb = τ0/4. We measured the dynamic characteristics in τb.
and time step Δt = 0.00005τ0. The total simulation time was tsim from 2 × 108Δt = 104τ0 (for the dendrimer of second generation, G = 2) to 32 × 108Δt = 16 × 104τ0 (G = 5). The relaxation time for a single bond (not included in the dendrimer) τb = τ0/4. We measured the dynamic characteristics in τb.
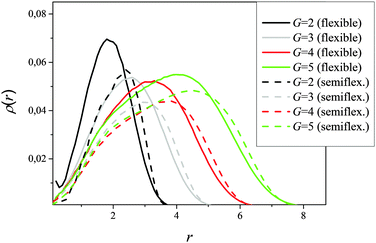
All results were obtained by averaging over the simulation time. In order to ensure that this time is sufficiently large we have studied the dynamics of terminal beads in our models. The density distribution of terminal beads relative to the center of mass (Fig. 4) shows that terminal groups are not only located at the dendrimer periphery but are also distributed along its volume. This well known effect is denoted in the literature as “backfolding” (see, for instance, ref. 22). This distribution is a dynamical one: terminal groups do not remain in definite positions but move to the center and back to the periphery. For an estimation of the time of this exchange we have calculated the mean squared displacement 〈Δr2(t)〉 of terminal beads as a function of time (Fig. 5). 〈Δr2(t)〉 increases initially with time and after some time tmax reaches a plateau. Therefore, tmax can be considered as the time of diffusion of terminal monomers from the inside to the outside of the dendrimer or backwards.
In all cases, the time tmax is much smaller than the simulation time τsim. Therefore, the dendrimer conformation changes many times during the simulation run and the τsim is sufficiently large.
The authors of ref. 12 considered the case when the internuclear vector of NMR active groups has a component directed along the segment and the orientational mobility of segments is displayed in the reorientation of these vectors. In our model, segments consist of two bonds (springs) (Fig. 1) and we will monitor not only the mobility of segments as a whole but also the mobility of constituent bonds.
3 Results of simulation
3.1 Correlations between segment orientations
For the characterization of correlations between segments separated by s shells the average cosine between them was calculated: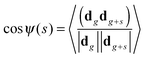 | (14) |
〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ(s)〉 = qs ψ(s)〉 = qs | (15) |
| G | Ph flex. | Ph. semiflex. | EV flex. | EV semiflex. |
|---|---|---|---|---|
| 2 | 0 | 0.2 | 0.2 | 0.3 |
| 3 | 0 | 0.2 | 0.3 | 0.3 |
| 4 | 0 | 0.2 | 0.4 | 0.4 |
| 5 | 0 | 0.2 | 0.5 | 0.5 |
But in the flexible EV model even without the angle potential (10) the correlation parameter q is rather large and its value increases with an increase of the generation number G from q = 0.2 for G = 2 to q = 0.5 for G = 5. The addition of the angle potential (10) to the EV model does not change the value of the correlation parameter q.
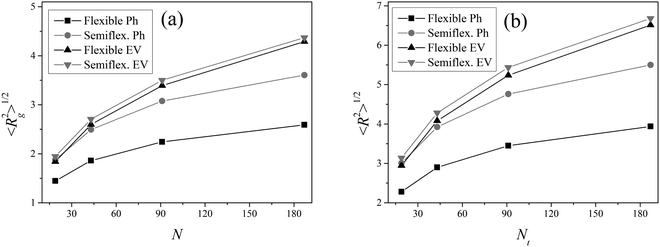
As a result, angular restrictions imposed by the angle potential (10) have only a minor effect on the equilibrium structural characteristics of a dendrimer such as the gyration radius and the core-terminal group distance as well as the density profile (see Appendix A).
| Crot(t) = 〈eg(0)eg(t)〉 | (16) |
 directed along the vector Qg = rt − r0. Here, rt represents the position of an arbitrary terminal monomer and the vector r0 represents the position of the dendrimer core. Averaging in (16) is performed over the simulation time and over all terminal monomers.
directed along the vector Qg = rt − r0. Here, rt represents the position of an arbitrary terminal monomer and the vector r0 represents the position of the dendrimer core. Averaging in (16) is performed over the simulation time and over all terminal monomers.
Autocorrelation functions Crot for different dendrimer models are shown in Fig. 6.
Following the method described in ref. 12 we approximate Crot(t) using two exponents
Crot(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τint) + B exp(−t/τint) + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τrot) exp(−t/τrot) | (17) |
| Model | G = 2 | G = 3 | G = 4 | G = 5 | α |
|---|---|---|---|---|---|
| Ph flexible | 4 | 9 | 22 | 46 | 1.1 |
| Ph semiflexible | 13 | 27 | 81 | 130 | 1.0 |
| EV flexible | 14 | 50 | 280 | 680 | 1.8 |
| EV semiflexible | 18 | 77 | 520 | 910 | 1.8 |
As expected, τrot(G) increases with an increase of G. This time is the largest characteristic time of a dendrimer of the generation G but it is much less than the simulation time τsim which is varied from 104 for G = 2 to 16 × 104 for G = 5. This confirms again that the total simulation times used in these calculations are large enough to obtain the correct data.
The dependence of the orientational correlation time τrot on the overall number of beads N in a dendrimer is shown in Fig. 7. It can be presented in the scaling form
| τrot ∼ Nα | (18) |
 | ||
| Fig. 7 The dependence of the orientational correlation time τrot of the dendrimer rotation as a whole on the overall number of beads N for the models considered. | ||
Note that for the free-draining flexible EV model of a dendrimer with segments consisting of one bond the value of α = 1.6 was obtained earlier.
3.2 Manifestation of the orientational dynamics of segments in NMR relaxation
Eqn (1)–(4) connect the frequency dependence of [1/T1H(ωH)]m or segment belonging to m-th shell in the dendrimer of the generation number G with the second order autocorrelation function (ACF) P2,s(t,G,m) for this segment.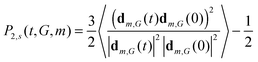 | (19) |
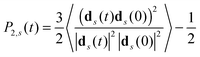 | (20) |
 | (21) |
 .
.
For the flexible Ph model (Fig. 8a) all curves have one maximum located practically at the same frequency for all m. Such a behavior is in agreement with predictions of the theory for the Gaussian dendrimer model.13 The position of this maximum is slightly shifted to lower frequencies as compared to that for a single segment. The curves of [1/T1H(ωH)]m become broader from the side of low frequencies by moving from m = 0 to m = 2.
In the flexible EV model, only the position of the maximum of [1/T1H(ωH)]0 for terminal segments coincides with that for a single segment. The frequency dependence of [1/T1H(ωH)]m for internal segments not only becomes broader but its maxima shift to lower frequencies with an increase of m.
At first glance, such a behavior disagrees with that observed for the Ph model and with theoretical results for the Gaussian model.13 As we will show below, this difference is connected with a different contribution of global dendrimer motion to the segmental dynamics for these models.
The effect of the introduction of semiflexibility is the same for Ph and EV models (Fig. 8). The position of the maximum shifts to lower frequencies by moving from terminal to inner shells in agreement with the predictions of the Gaussian model.
Let us discuss now the origin of the difference between the results obtained for the flexible Ph and EV models. As mentioned above, the rate of reorientation of dendrimer segments is determined both by internal modes and by the overall dendrimer rotation.
Recall that in the theoretical work for the Gaussian model13 only internal modes were taken into account.
For the separation of the contribution of the overall rotation we use the procedure proposed in previous work.12
We start consideration from the first order ACF:
 | (22) |
P1,s(t,G,m) = ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) 1,s(t,m) + am 1,s(t,m) + am![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τrot(G)) exp(−t/τrot(G)) | (23) |
Functions ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) 1,s(t,m) and the factor am for m = 0, 1 and 2 were obtained by fitting simulated P1,s(t,G,m) for dendrimers with G = 2–5, 3–5 and 4–5, respectively (Table 4).
1,s(t,m) and the factor am for m = 0, 1 and 2 were obtained by fitting simulated P1,s(t,G,m) for dendrimers with G = 2–5, 3–5 and 4–5, respectively (Table 4).
| m | Ph flex. | Ph semiflex. | EV flex. | EV semiflex. |
|---|---|---|---|---|
| 0 | 0.01 | 0.02 | 0.10 | 0.10 |
| 1 | 0.01 | 0.04 | 0.35 | 0.40 |
| 2 | 0.03 | 0.09 | 0.46 | 0.50 |
The table shows the values of am for the models considered. As expected am increases with m. For Ph models the contribution of the overall rotation to the orientational dynamics of segments is small in contrast to EV models, where this contribution reaches almost 50% for internal shells. We can introduce the function
 | (24) |
| Pint2,s(t,m) = (Pint1,s(t,m))3 | (25) |
By using Pint2,s(t,m) the frequency dependence of [1/T1H(ωH)]m was calculated for both models (Fig. 9). The results depicted in Fig. 9 demonstrate not only a qualitative but also a quantitative agreement between the results obtained for the Ph and EV model. It means that the internal orientational dynamics of the segments which manifests in spin–lattice NMR relaxation is practically insensitive to excluded volume interactions. Returning to Fig. 9, we can conclude that the observed shift of the peak of [1/T1H(ωH)]m to lower frequencies for inner segments in the flexible EV model is connected with a much stronger contribution of the overall dendrimer rotation to the reorientation of inner segments as compacted in the Ph model. In both models, the introduction of semiflexibility through the angular potential (10) leads to the shift of the maximum to lower frequencies by an increase of the shell number m in agreement with the theoretical predictions for the Gaussian dendrimer model.13 The absolute value of this shift is practically insensitive to excluded volume interactions if the contribution of only internal modes to the segment reorientation is considered. This value is determined by the angular potential (10) which restricts the fluctuations of angles between bonds, wherein the values of the correlation parameter q differ for Ph and EV models.
 | ||
| Fig. 9 Frequency dependence of [1/T1H(ωH)]m calculated on the basis of (25) for segments belonging to different sub-shells for flexible (a) and semiflexible (b) Ph (dotted line) and EV (solid line) models. | ||
3.3 Orientational dynamics of bonds
Now we consider the situation where the internuclear vectors in NMR active groups are directed along bonds inside the dendrimer segments. Every segment consists of two bonds, and therefore every shell can be divided into two subshells numbering from the terminal s = 0 (Fig. 2). As in the case of segments we have calculated the frequency dependence of [1/T1H(ωH)]s for bonds belonging to a subshell with the number s in the dendrimer of generation G on the basis of the second order ACF P2,b(t,G,s). | (26) |
 | (27) |
Similar to segments the introduction of the angle potential (10) for both models leads to the shift of the position of the maximum of [1/T1H(ωH)]s to lower frequencies by the increase of s i.e. by moving from terminal bonds to internal ones (Fig. 10). Fig. 11 presents the dependence of the frequency ωmax,b(s) (reduced to ωmax,b(0)) corresponding to the maximum of [1/T1H(ωH)]s for bonds in the models considered. In the same plot, we also show the dependence of ωmax,s(m) (reduced to ωmax,s(0)) for segments found from Fig. 11 where the effect of the overall dendrimer rotation was excluded.
We see that all points lie on a common line indicating a similar effect of semiflexibility on the internal orientational dynamics of segments and bonds which is insensitive to excluded volume interactions. Note that at the same potential (10) restricting the fluctuations of bond angles, the values of the correlation parameter q for Ph models are smaller than those for EV models (see Table 2).
4 Conclusions
The effect of excluded volume interactions on the manifestation of the local orientational dynamics of segments (or bonds) in spin–lattice NMR relaxation in dendrimers has been studied by using Brownian dynamics simulations. The study was stimulated by the theory developed in ref. 13 for the Gaussian dendrimer model without EV interactions. The theory predicts that for flexible dendrimers the position of the peak of the frequency dependence of the reduced spin–lattice relaxation rate [1/T1H(ωH)] does not depend on the proximity of dendrimer shells to the core by the assumption that the internuclear vectors have a component directed along segments. For semiflexible dendrimers, the peak of [1/T1H(ωH)] shifts to lower frequencies by moving from outer to inner segments. Semiflexibility was introduced into the theory13 through the correlations between the orientations of different segments. However, these correlations exist even in flexible dendrimer models with EV interactions.We have simulated coarse-grained flexible and semiflexible dendrimer models with generation number G = 2–5 with three functional branching points with and without EV interactions. Every dendrimer segment consisted of two rigid bonds. Semiflexibility was introduced through a potential which restricts the fluctuations of angles between neighboring bonds. The potential leads to the appearance of orientational correlations between segments in the Ph models but does not change these correlations in the EV models as compared to the flexible case. The frequency dependence of [1/T1H(ωH)] for segments and bonds belonging to different dendrimer shells was calculated. It was shown that the main effect of EV interactions consists of a much stronger contribution of the overall dendrimer rotation to the dynamics of dendrimer segments as compared to the phantom models. After the exclusion of this contribution the manifestation of internal segmental modes in spin–lattice NMR relaxation appears to be practically insensitive to EV interactions. For the flexible models the position ωmax of the peak of the modified [1/T1H(ωH)] does not depend on the shell number in spite of the orientational correlations between segments in the EV model. For semiflexible models the maximum of [1/T1H(ωH)] for internal segments shifts to lower frequencies as compared to the outer ones. The value of this shift is practically the same for Ph and EV models. For the orientational dynamics of bonds comprising the segments the contribution of the overall dendrimer rotation is much smaller than for segments even with the presence of EV interactions. The contribution of EV interactions is remarkable for dendrimers with segments consisting of one bond and becomes practically negligible for the reorientation of bonds inside two-bond segments. The average concentration of monomer units in a dendrimer decreases with the segment length ls as ls4/5 at the same generation number under good solvent conditions. As a result, the effect of EV interactions will decrease with ls.
It was shown in ref. 13 that the main contribution to the segmental orientational autocorrelation function (ACF) which is fundamental for the frequency dependent [1/T1H(ωH)] is made by local modes which are invariant to the shell number. The introduction of semiflexibility into this model leads to the shift of the maximum to lower frequencies for inner shells. It is explained by the increased contribution of modes with a larger scale (pulsation modes) to the ACF. We show that for flexible and semiflexible models the internal orientational dynamics of segments manifesting in spin–lattice NMR relaxation is not sensitive to the presence or absence of EV interactions.
Thus, our results give additional arguments for the interpretation9 of the experimentally observed difference between the positions of [1/T1H(ωH)] maxima for terminal and inner segments in dendrimers as a manifestation of the restricted flexibility of these macromolecules.
Appendix
A Structural characteristics of flexible and semiflexible dendrimers
The dendrimer size can be characterized by the mean-squared gyration radius | (A.1) |
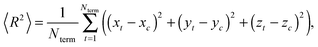 | (A.2) |
The internal structure is characterized by the density profile of all beads (see Fig. 13) in a dendrimer:
 | (A.3) |
It is seen that the introduction of the angular potential (10) does not change practically the structural characteristics of a dendrimer with EV interactions.
Acknowledgements
The reported study was supported by the Supercomputing Center of Lomonosov Moscow State University.25 This work was partly supported by grant 074-U01 of Government of RF and RFBR grants 16-03-00775 and 15-33-20693mol_a_ved.References
- Dendrimers and other Dendritic polymer, ed. M. J. Frechet and D. A. Tomalia, Wiley, England, 1st edn, 2001 Search PubMed.
- A. Patri, I. Majoros and J. Baker, Curr. Opin. Chem. Biol., 2002, 6, 466–471 CrossRef CAS PubMed.
- M. Murat and G. S. Grest, Macromolecules, 1996, 29, 1278–1285 CrossRef CAS.
- Dendrimers in Biomedical Applications, ed. B. Klajnert, L. Peng and V. Cena, RSC Publishing, 2013 Search PubMed.
- C. Malveau, W. E. Baille, X. X. Zhu and W. T. Ford, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2969 CrossRef CAS.
- D. A. Markelov, V. V. Matveev, P. Ingman, E. Lahderanta and N. I. Boiko, J. Chem. Phys., 2011, 135, 124901 CrossRef PubMed.
- F. Pinto, J. Correa, M. Martin-Pastor and R. Riguera, J. Am. Chem. Soc., 2013, 135, 1972–1977 CrossRef PubMed.
- I. M. Neelov, D. A. Markelov, S. G. Falkovich, M. Y. Ilyash, B. M. Okrugin and A. A. Darinskii, Polym. Sci., Ser. C, 2013, 55, 154–161 CrossRef CAS.
- D. Markelov, S. Falkovich, I. Neelov, M. Ilyash, V. Matveev, E. Lahderanta, P. Ingman and A. Darinskii, Phys. Chem. Chem. Phys., 2015, 17, 3214–3226 RSC.
- M. A. Mazo, M. Y. Shamaev, N. K. Balabaev, A. A. Darinskii and I. M. Neelov, Phys. Chem. Chem. Phys., 2004, 6, 1285–1289 RSC.
- R. Kimmich and E. Anoardo, Prog. Nucl. Magn. Reson. Spectrosc., 2004, 44, 257–320 CrossRef CAS.
- D. A. Markelov, S. V. Lyulin, Y. Y. Gotlib, A. V. Lyulin, V. V. Matveev, E. Lahderanta and A. A. Darinskii, J. Chem. Phys., 2009, 130, 044907 CrossRef PubMed.
- D. A. Markelov, M. Dolgushev, Y. Y. Gotlib and A. Blumen, J. Chem. Phys., 2014, 140, 244904 CrossRef PubMed.
- A. Kumar and P. Biswas, J. Chem. Phys., 2011, 134, 214901 CrossRef PubMed.
- A. Kumar and P. Biswas, Phys. Chem. Chem. Phys., 2013, 15, 20294 RSC.
- S. V. Lyulin, A. A. Darinskii, A. V. Lyulin and M. A. J. Michels, Macromolecules, 2004, 37, 4676–4685 CrossRef CAS.
- I. Neelov and D. Adolf, Macromolecules, 2003, 36, 6914–6924 CrossRef CAS.
- K. Karatasos, D. Adolf and G. Davies, J. Chem. Phys., 2001, 115, 5310–5318 CrossRef CAS.
- K. Karatasos and A. V. Lyulin, J. Chem. Phys., 2006, 125, 184907 CrossRef CAS PubMed.
- D. A. Markelov, Y. Y. Gotlib, A. A. Darinskii, A. V. Lyulin and S. V. Lyulin, Polym. Sci., Ser. A, 2009, 51, 331–339 CrossRef.
- D. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352 CrossRef CAS.
- S. Falkovich, D. Markelov, I. Neelov and A. Darinskii, J. Chem. Phys., 2013, 139, 064903 CrossRef CAS PubMed.
- Y. Y. Gotlib, N. K. Balabaev, A. A. Darinskii and I. M. Neelov, Macromolecules, 1980, 13, 602–608 CrossRef CAS.
- Y. Y. Gotlib, A. A. Darinskii, L. I. Klushin and I. M. Neelov, Acta Polym., 1984, 38, 124–129 CrossRef.
- V. Sadovnichy, A. Tikhonravov, V. Voevodin and V. Opanasenko, Contemporary High Performance Computing: From Petascale toward Exascale, Boca Raton, United States, 2013, pp. 283–307 Search PubMed.
| This journal is © the Owner Societies 2016 |