Deuteron quadrupole coupling constants and reorientational correlation times in protic ionic liquids

Abstract

We describe a method for the accurate determination of deuteron quadrupole coupling constants χ_D for N–D bonds in triethylammonium-based protic ionic liquids (PILs). This approach was first introduced by Wendt and Farrar for O–D bonds in molecular liquids, and is based on the linear relationship between the deuteron quadrupole coupling constants χ_D, and the proton chemical shifts δ¹H, as obtained from DFT calculated properties in differently sized clusters of the compounds. Thus the measurement of δ¹H provides an accurate estimate for χ_D, which can then be used for deriving reorientational correlation-times τ_ND, by means of NMR deuteron quadrupole relaxation time measurements. The method is applied to pure PILs including differently strong interacting anions. The obtained χ_D values vary between 152 and 204 kHz, depending on the cation–anion interaction strength, intensified by H-bonding. We find that considering dispersion corrections in the DFT-calculations leads to only slightly decreasing χ_D values. The determined reorientational correlation times indicate that the extreme narrowing condition is fulfilled for these PILs. The τ_c values along with the measured viscosities provide an estimate for the volume/size of the clusters present in solution. In addition, the correlation times τ_c, and the H-bonded aggregates were also characterized by molecular dynamics (MD) simulations.

---

The structure and properties of ionic liquids (ILs) are characterized by a subtle balance between Coulomb interactions, hydrogen bonding and dispersion forces.^1–4 This melange of different types of interaction results in unique properties that make ILs attractive for science and technology.^5,6 Mostly, information about the structure and thermodynamics of this new liquid material has been at the center of interest. However, the characterization and understanding of the molecular motions of ILs is at least equally important as the knowledge of their structure. Translational diffusion of the ions has been extensively studied by NMR Pulsed-Field-Gradient (PFG) and Spin-Echo (SE) techniques. In particular the Watanabe group has provided valuable information about ion self-diffusion in ILs.^7–10 Kremer et al. have shown that the frequency-dependent electrical conductance can be transcribed into ionic self-diffusion coefficients with proper rescaling.¹¹ Although NMR provides information about single particle motions, and enables the characterisation of anisotropic reorientation by site-specific experiments, the knowledge about the rotational dynamics in ILs is surprisingly small.^12–14 This is in particular true for the rotational motions of molecular vectors that are involved in hydrogen bonding.^15–17 If C–H, O–H or N–H bonds of imidazolium or ammonium cations are hydrogen bonded to their counter ions, proton exchange is an issue. Usually, this process is fast compared to the NMR time scale. Hence, a proper distinction between intra- and inter-molecular relaxation contributions to the magnetic dipole–dipole relaxation is often not possible. This problem of fast proton exchange has been addressed earlier for molecular liquids by performing isotopic substitution experiments. For water and alcohols the ¹⁷O-enhanced proton relaxation rates were measured for a series of different ¹⁷O-enriched samples.^18–32 From the separated intramolecular relaxation rates, the reorientational correlation times τ_OH could then be determined. This method has been shown to provide reliable data on the rotational dynamics of hydrogen-bonded molecular liquids and has often been used for the parameterization and validation of force fields employed for molecular dynamics simulations.^33–38 A similar approach has been suggested by Seipelt and Zeidler for the determination of the reorientational correlation times τ_NH in liquid amides.³⁹ However, expensive ¹⁴N/¹⁵N enriched samples needed to be synthesized and characterized. Here, the situation was even more complicated, because both nitrogen isotopes are NMR sensitive with different spins, I = 1 for ¹⁴N and I = 1/2 for ¹⁵N, representing quadrupolar and dipolar nuclei, respectively. For routine measurements, these kinds of NMR relaxation time experiments using isotopic substituted compounds are too complex and prohibitively expensive. Hence, we would like to present an alternative approach for measuring reliable NMR rotational correlation times for protic ionic liquids (PILs) involving N–H/N–D molecular bonds.

The most interesting relaxation mechanism in this respect is based on the interaction of the nuclear quadrupole moment with the main component of the electric field gradient. It is the strongest relaxation mechanism besides spin-rotation, which is not relevant for viscous liquid materials as used here.^40,41 However, before the reorientational correlation times τ_c can be determined from quadrupolar relaxation data, the knowledge of the coupling parameter corresponding to this mechanism, the deuteron quadrupole coupling constant χ_D needs to be known properly. From studies on molecular liquids it is known that χ_D shows significantly different values for the gas, the liquid and the solid phases. χ_D has been shown to be a sensitive probe for hydrogen bonding and is often temperature dependent, despite of what the term ‘coupling constant’ is suggesting.^22,23 In general, the deuteron quadrupole coupling constants for protic ionic liquids as discussed here are not known. However, to provide a solution to this problem, Wendt and Farrar introduced a method for deriving rotational correlation times τ_OH for molecular liquids such as alcohols, which is based on both, quadrupolar relaxation experiments, and a relation between deuteron quadruple coupling constants and proton chemical shifts derived from quantum chemical calculations.^42–45

It is the purpose of this work to show that this approach can be also transferred to N–H bonds in ammonium-based PILs. Our aim is to accurately determine the deuteron quadrupole coupling constants χ_D for those liquids, and to provide reliable reorientational correlation-times τ_c. To demonstrate the reliability of these properties, we have chosen a set of PILs, which we have studied before by using far infrared spectroscopy and DFT calculations of differently sized clusters.^46–50 From these studies we were able to determine the interaction strength between the cations and anions, which should also be reflected in the dynamical properties we would like to investigate here. Three PILs sharing the same cation had been synthesized. The full set of PILs are comprised of triethylammonium bis(trifluoromethylsulfonyl)-imide [(C₂H₅)₃NH][NTf₂] (I), triethylammonium trifluoromethylsulfonate [(C₂H₅)₃NH][CF₃SO₃] (II), and triethylammonium methylsulfonate [(C₂H₅)₃NH][CH₃SO₃] (III). Because we are using the same triethylammonium cation throughout, changes in the interaction strength can only be attributed to the anions. An important feature of the triethylammonium cation is that it exhibits a single proton donor function N–H. The only possible directional interaction ⁺N–H⋯A⁻ provided isolated vibrational bands in the far infrared spectra, which could be clearly attributed to the H-bond enhanced anion–cation interaction. The chosen anions showed increasing interaction strengths in the order [NTf₂] < [CF₃SO₃] < [CH₃SO₃] due to fluorination of the methyl groups.

It is interesting to see how this particular order of anion interaction strengths is reflected in both, the deuteron quadrupole coupling parameters χ_D, as well as in the correlation time τ_NH of the rotational motion of the N–H bond in these PILs. By also measuring the viscosities, we can provide additional valuable information about the validity of the Stokes–Einstein–Debye relation in these ionic liquids.

Results and discussion

First, we measured the proton chemical shifts δ¹H of the N–H proton at the triethylammonium cation in the pure PILs. Using TMS (tetramethylsilane) as an external references, we obtained downfield chemical shifts of about 5.96 ppm for I, 6.81 ppm for II and 8.66 ppm for III at 303 K, respectively. This reflects the expected order for the increasing interaction strength of the anions in the sequence [NTf₂] < [CF₃SO₃] < [CH₃SO₃], as obtained from FIR measurements.^46–50 In addition, the chemical shift differences of about Δ(δ¹H) = 0.85 ppm for II–I and Δ(δ¹H) = 1.84 ppm for III–II clearly indicate that the cation–anion interaction is particularly enhanced in III. Obviously, the inductive effect of the fluorine atoms in [NTf₂] and [CF₃SO₃] strongly weakens the interaction between cation and anion. These chemical shifts are now used for describing the coupling parameters and rotational motion of the cations in all three PILs. For that purpose we measured the NMR deuteron quadrupolar relaxation times T₁.

The PILs I–III were synthesized and characterized as described in earlier studies.^46,48 Then they were deuterated by ¹H/²H exchange in ²H₂O and properly dried. ¹H NMR spectra confirmed that exchange took only place at the N–H position. Longitudinal ²H magnetic relaxation times T₁ were measured using a BRUKER Avance 500 spectrometer at a resonance frequency of ν = ω/2π = 76.7 MHz, employing the inversion recovery (180°–τ–90°) pulse sequence. Results are given in Table 1. The shown values for T₁ are estimated to be accurate to within ±2%.

Table 1 Deuteron relaxation rates 1/T₁ in s⁻¹ for PILs I–III

PILs	293 K	303 K	313 K
I	112.6	93.74	69.98
II	109.78	95.79	71.84
III	124.01	118.88	100.99

---

²H nuclear magnetic relaxation is driven by interaction of the electrostatic quadrupole moment of the ²H-nucleus with the electric field gradient at the ²H-position, generated by the electron distribution surrounding the nucleus along the N–H bond. The relaxation rate 1/T₁ is given by^40,41

where χ_D is the ²H nuclear quadrupole coupling constant, η is the corresponding asymmetry parameter, and τ_c represents the integral reorientational correlation time.

In low-viscosity molecular liquids, the extreme-narrowing condition ω₀τ_c ≪ 1 is commonly fulfilled. However, this is not necessarily guaranteed for ILs, because there is evidence for an extremely stretched orientational dynamics,¹⁴ that may broaden the spectral densities in eqn (1) to extend to the Larmor frequency. We have carefully checked that the relaxation time experiments for all PILs were performed in the extreme narrowing limit. The relaxation rates 1/T₁ increasing with decreasing temperature are showing Arrhenius behaviour (see Table 1). Only for the most viscous PIL III, a frequency dependent relaxation is observed at temperatures well below room temperature, which are not discussed here. We can conclude that the extreme narrowing condition is fulfilled for all PILs at room temperature. We will see later that the largest correlation times τ_c at 303 K are of the order of a few hundred picoseconds. Thus the product ω₀τ_c (76.7 × 10⁶ Hz × 400 × 10⁻¹² s ≈ 0.03) is definitely smaller than 1 and confirms the extreme narrowing condition. Moreover, for the case of the extreme narrowing limit ω₀τ_c ≪ 1, eqn (1) simplifies to

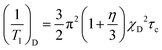eqn (2) shows that we now have access to molecular correlation times τ_c, if the deuteron quadrupole coupling constant χ_D, and the asymmetry parameter η are known.

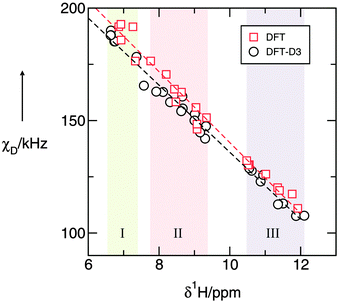
Here we adapt an idea suggested by Wendt and Farrar.^42–45 They could show for pure methanol, as well as for methanol in mixtures with tetrachloromethane, that the correlation time for the reorientation of the O–H bond can be derived from the spin–lattice relaxation rate for the deuteron [eqn (2)]. Due to a strong coupling parameter, the deuteron quadrupole relaxation is entirely an intramolecular process. Other relaxation mechanisms, or the separation of intra- and intermolecular relaxation contributions do not have to be considered. Moreover, since the principal axis of the deuterium electric field gradient is nearly axially symmetric and lies along the direction of the N–D bond,⁵¹ its correlation time is equal to the correlation time for the reorientation of the N–D vector. Experimental data also indicate that there is a negligible isotope effect for the rotational diffusion.^15,16 However, a reasonable deuteron quadrupole coupling constant for the N–D bond in these ILs is not known, neither for the gas phase, nor for the liquid phase. The idea of Wendt and Farrar is based on DFT calculated properties of molecular clusters. They obtained a linear correlation between the calculated proton chemical shifts δ¹H and calculated deuteron quadrupole coupling constants χ_D. The advantage is that δ¹H can be easily measured in the liquid phase, and thus provides reasonable access to χ_D. Huber and co-workers reported that this method provides good agreement between measured and simulated values for water.^51–53 We also used this method previously for estimating χ_D for the liquid phase of pure water and alcohols, as well as their mixtures with organic solvents and ionic liquids.^16,17 Before applying this approach, however, we have to show that the ND bond in PILs can be treated exactly the same way as the OD bond in molecular liquids. For that purpose we determined the proton chemical shifts δ¹H, and the quadrupole coupling constants χ_D from ab initio calculations of PIL clusters including n = 1–4 ion-pairs. The proton chemical shifts were referenced against TMS, as it was done in the experiment. The χ_D = (e²q_zzQ/h) values were derived by multiplying the calculated main components of the electric field gradient tensor q_zz with a calibrated nuclear quadrupole moment eQ for the given theory level and basis set used in the calculations. Similarly to the OD bond in alcohols, the asymmetry parameter of the electric field gradient for ND is found to be negligible and does not need to be considered in [eqn (2)]. This has been shown for molecular systems such as ammonia, formamide, N-methyl formamide and N-methyl acetamide, respectively.^54–59 Throughout, the geometries of the clusters as well as the electric field gradients of the deuterons and the proton chemical shifts were calculated at the B3LYP/6-31+G* level of theory with and without D3 dispersion corrections introduced by Grimme et al.^60–62 This allows us also to quantify the influence of dispersion forces on these two important spectroscopic properties.

In Fig. 1 it is shown that we find a perfect linear behaviour between the deuteron quadrupole coupling constants χ_D, and the proton chemical shifts δ¹H. From linear regression we obtain χ_D = 297.87 kHz − 15.77·δ¹H kHz/ppm and χ_D = 285.06 kHz − 14.92·δ¹H kHz/ppm, if the dispersion correction is taken into account. Enhanced cation–anion interactions, as present in PIL III, lead to larger downfield chemical shifts, and to smaller deuteron quadrupole coupling constants. The weakest interactions, as present in PIL I, are characterized by smaller δ¹H shifts, and larger χ_D values. It does not matter, whether these pairs of properties are calculated for N–H/N–D in varying sized clusters or for different configurations within these clusters, they all show linear dependence. This is not at all surprising, because both properties, δ¹H, as well as χ_D, are sensitive to local and directional interactions, such as hydrogen bonding. In this respect, N–H bonds behave similar to O–H bonds in water and alcohols.^15–17,63 An ultimate test for the reliability of the linear relation between both properties in PILs is carried out by interpolating the chemical shifts to zero ppm, indicating a complete absence intermolecular interactions. For this case we expect the calculated χ_D values to be similar to those measured for the gas phase. And indeed, the estimated value of 297.9 kHz for χ_D in PILs is very close to the measured gas phase and calculated monomer χ_D values for ammonia (290.6 kHz), formamide (292 kHz) and N-methylformamide (294 kHz), respectively.^54–59 Some time ago, Seipelt and Zeidler introduced the ¹⁴N/¹⁵N-method to determine the correlation time τ_NH for N-methylformamide (NMF) and N-methylacetamide (NMA) in the liquid phase.³⁹ Subsequently, they used these correlation times from dipolar relaxation to derive the deuteron quadrupole coupling constants χ_D from quadrupolar relaxation measurements. If we take the measured proton chemical shifts, and the determined deuteron quadrupole coupling constants for the liquid phases of ammonia, NMF, and NMA, we observe that the pairs of spectroscopic properties lie perfectly on our calculated straight line (see Fig. 2). This further supports the reliability of our approach, which allows the determination of quadrupole coupling constants for any state, including the liquid phase, if just the proton chemical shifts can be measured accurately.

Fig. 1 DFT (B3LYP/6-31+G*) calculated deuteron quadrupole coupling constants χ_D, plotted versus calculated proton chemical shifts δ¹H of the N–H groups in different sized clusters of PILs I–III. It is observed that the χ_D values decrease with increasing interaction strength of the PIL anions in the order [NTf₂] > [CF₃SO₃] > [CH₃SO₃]. Including dispersion correction gives slightly lower deuteron quadrupole coupling constants in particular for the weaker interacting anion in PIL I.

Fig. 2 DFT (B3LYP/6-31+G*) calculated deuteron quadrupole coupling constants χ_D, plotted versus calculated proton chemical shifts δ¹H of the N–H groups in different sized clusters of PILs I–III between 0 and 12 ppm. For proving the validity of the relation between both properties we added measured gas phase or calculated monomer values for formamide (FA), N-methylformamide (NMF) and ammonia (NH₃), as well as the liquid phase values for NMF, NH₃ and N-methylacetamide (NMA).^39,54–59 The χ_D values for the molecular liquids show the same linear dependence as the PILs.

Before evaluating the χ_D values for the N–D deuterons for PILs I–III, we would like to briefly discuss the influence of dispersion forces on both spectroscopic properties. In Fig. 1 it is shown that we obtain linear relations between the calculated χ_D and δ¹H values, regardless of whether or not dispersion corrections are taken into account. However, we observe that dispersion forces result in systematically (slightly) smaller quadrupole coupling constants and slightly stronger downfield chemical shifts due to an enhanced interaction between cation and anion in the PILs. The largest difference about 10 kHz is observed for the most weakly interacting PIL I at high χ_D and low δ¹H, whereas for the largest clusters representing the liquid phase, dispersion effects become less important compared to Coulomb interaction and hydrogen bonding. In this liquid region the differences come down to only a few kHz. Here, we can conclude that dispersion correction needs to be considered, in particular for weak cation–anion interaction. Hereby the subtle balance is shifted from Coulomb to dispersion interaction.

Using this linear relation along with the measured proton chemical shifts, we obtain deuteron quadrupole constants χ_D of about 203.9 kHz, 190.5 kHz, and 152.3 kHz for PILs I–III as shown in Fig. 3. The sequence of the χ_D values follows the interaction strength between cation and anion and reflect the frequency shifts in the far infrared spectra.^46–50 The most strongly interacting anion in PIL III, methylsulfonate, forms the strongest hydrogen bond, resulting in the lowest χ_D value of about 152 kHz. Clearly, the quadrupole coupling constant is a sensitive probe for hydrogen bonding in ionic liquids, as it has been previously shown for molecular liquids.^22,23 Unfortunately, there are no N–D deuteron quadrupole coupling constants available from other PILs. Therefore we added χ_D values for related molecular liquids, such as NMF and NMA to Fig. 3.^54–59 Overall, we can conclude that the procedure suggested by Wendt and Farrar for O–H containing molecular liquids, such as methanol, can be successfully applied to N–H bonds in ionic liquids for deriving accurate deuteron quadrupolar coupling constants for the liquid phase.

Fig. 3 Deuteron quadrupole coupling constants χ_D for the N–D deuterons of the triethylammonium cations in PILs I–III as obtained from measured proton chemical shifts δ¹H and the calculated relation between both properties as shown in Fig. 2. For comparison, the known experimental values for molecular liquids NMF and NMA resulting from challenging isotopic substitution experiments are shown.³⁹

The χ_D values derived from the linear relationship are now plugged into eqn (2) for deriving reliable correlation times τ_NH. The resulting reorientational correlation times τ_NH are determined to be 152.3 ps, 178.3 ps and 346.1 ps for PILs I–III (see Fig. 4). With increasing interaction strength of the anions in the order [NTf₂] < [CF₃SO₃] < [CH₃SO₃], the molecular motion of the cation is slowed down. Whereas the change from PIL I to II is moderate, the correlation time τ_NH for PIL III is twice as large as that for I. The same sequence of correlation times is found for the reorientational correlation times τ_NH from MD simulations (for details see the ESI†) and can be attributed to the hierarchy of hydrogen-bond strength observed between the TEA-cation and the varying anions in the different PILs. The correlation times obtained from MD (also included in Fig. 4) are, however, significantly larger than the data obtained from NMR, suggesting that the strengths of the inter-ionic hydrogen bonds are significantly overestimated in the MD-model. It is noteworthy that the best agreement between experiment and simulation can be achieved for PIL I including the NTf₂ anion. For this hydrophobic anion the force field could be properly parameterized in imidazolium-based aprotic ionic liquids.³⁷ Our result here suggests that the interaction strength is mainly overrated for PILs including the triflate and methylsulfonate anions.

Fig. 4 Reorientational correlation times of the N–H molecular vector τ_NH in the PILs I–III (circles) obtained from NMR deuteron quadrupole relaxation time measurements at 303 K and calculated quadrupole coupling constants χ_D. The dotted line is only used as a guideline for the eye. Additionally we show the values obtained from MD simulations at 360 K (triangles) and at 300 K for PIL I (square). Although the same sequence of correlation times is found, the H-bond strength is significantly overestimated in the MD-model.

The long-time behaviour of the computed reorientational correlation function, however, is mostly monoexponential, which is compatible with a Lorentz-shaped spectral density, used in eqn (1). Thus the MD simulations support that the evaluation of the relaxation rates as used here is justified. Moreover, the temperature dependence of simulated correlation times pretty much follows an Arrhenius behaviour.

If we plot the resulting reorientational correlation times τ_cversus measured viscosities η for all liquids, we observe a linear behaviour. This, however, would be expected from the Stokes–Einstein–Debye (SED) relation if the volume/size of the solute are assumed to be similar for all PILs. The SED relation is derived from classical hydrodynamics and simple kinetic theory.^64,65 It provides molecular insight into the dynamical behaviour of liquids and liquid mixtures: in the SED relation⁶⁵ [eqn (3)].

Here τ_c is the reorientational correlation time, η is the viscosity, k_B is the Boltzmann constant, T is the temperature, and V_eff is the effective volume. V_eff is obtained by multiplying the volume V with the so-called Gierer–Wirtz factor f. For neat liquids f has a value of 1/6 ≈ 0.16. The friction factor is only 16% of the value under so-called stick-conditions and we reach the slip limit. From the slope of the plot in Fig. 5, we can estimate the effective volume V_eff to be about 0.1217 nm³. If we assume a spherical shape of the solute particle, we obtain an effective radius r_eff of about 3.07 Å. This radius is in reasonable agreement with the size of the triethylammonium cation, which has been calculated to be 3.22 Å.⁶⁰ Since we use reorientational correlation times of the cation only, which is identical in all three PILs, a linear behaviour between τ_c and η follows. The finding of similar structures for PILs I–III is also consistent with results from recent MD simulations.⁶⁶ In a recent study it could be shown that in the neat PILs all cations are involved in hydrogen bonding, no matter how strong the interaction with the anion is. Moreover, the distribution of H-bonded clusters with anions forming two, one or zero H-bonds was found to be similar for all pure PILs.

Fig. 5 Reorientational correlation times τ_c plotted versus viscosities η. According to the Stokes–Einstein–Debye relation, the linear behavior indicates that the effective volume V_eff is similar for all PILs. And indeed, the calculated size for the solute is that of the triethylammonium cation.

Conclusion

We have shown that a method introduced by Wendt and Farrar for O–D bonds in alcohols can be successfully applied to protic ionic liquids for the accurate determination of deuteron quadrupole coupling constants in N–D bonds. Consequently, the experimentally challenging approach based on complex and expensive isotopic substitution experiments is no longer required for deriving the coupling parameters in hydrogen-bonded ionic liquids. A linear relationship between the deuteron quadrupole coupling constants χ_D and the proton chemical shifts δ¹H for the N–D bonds, computed from DFT calculations of differently sized clusters of three ammonium-based PILs, serves as an internal calibration standard. In addition, also experimentally available χ_D and δ¹H values for molecular liquids, such as ammonia, NMF, and NMA are found to fit perfectly into this linear relationship. Moreover, the gas phase values for χ_D for those molecular liquids are predicted correctly too, suggesting the validity of this relationship. We conclude, that the measurement of δ¹H provides a sufficiently accurate estimate for χ_D, which then can be used for obtaining reorientational correlation-times τ_ND by means of NMR deuteron quadrupole relaxation time experiments. Here we have shown that those correlation times reflect the interaction strength between cation and anion, which is consistent to what has been obtained earlier from far infrared spectra. The rotational dynamics is found to be particularly slowed down for the strongly interacting methylsulfonate anion. However, even the longest correlation time τ_c of about 380 ps is short enough to ensure that the extreme narrowing limit is still valid at room temperature. Finally, we observe that the obtained correlation times for all PILs are proportional to their corresponding viscosities. The Stokes–Einstein–Debye (SED) relation hence suggests the presence of the same type of aggregates in all three PILs. This result corresponds to earlier findings based on molecular dynamics simulations.⁶⁶

Acknowledgements

This work has been supported by the DFG Priority Programme SPP 1807 “Control of London dispersion interaction in molecular chemistry” and partially by the DFG Collaborative Research Center SFB 652 “Strong correlations and collective effects in radiation fields: Coulomb systems, clusters and particles”.

Notes and references

1. H. Weingärtner, Angew. Chem., 2008, 120, 664–682 ( Angew. Chem., Int. Ed. , 2008 , 47 , 654–670 ).
2. P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 125.
3. K. Fumino and R. Ludwig, J. Mol. Liq., 2014, 192, 94–102.
4. K. Fumino, S. Reimann and R. Ludwig, Phys. Chem. Chem. Phys., 2014, 40, 21903–21929.
5. P. Wasserscheid and T. Welton, Ionic Liquids in Synthesis, Wiley-VCH, Weinheim, 2nd edn, 2008.
6. N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150.
7. A. Noda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2001, 105, 4603–4610.
8. H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593–16600.
9. H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2005, 109, 6103–6110.
10. H. Tokuda, K. Ishii, M. A. B. H. Susan, S. Tsusuki, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 2833–2839.
11. J. R. Sangoro, C. Iacob, S. Naumov, R. Valiullin, H. Rexhausen, J. Hunger, R. Buchner, V. Strehmel, J. Kärger and F. Kremer, Soft Matter, 2011, 5, 1678–1681.
12. R. Giernoth and D. Bankmann, Eur. J. Org. Chem., 2005, 4529–4532.
13. Y. Lingscheid, S. Arenz and R. Giernoth, ChemPhysChem, 2012, 13, 261–266.
14. H. Weingärtner, Curr. Opin. Colloid Interface Sci., 2013, 18, 183–189.
15. A. Wulf, R. Ludwig, P. Sasisanker and H. Weingärtner, Chem. Phys. Lett., 2007, 439, 323–326.
16. A. Wulf, K. Fumino, D. Michalik and R. Ludwig, ChemPhysChem, 2007, 8, 2265–2269.
17. E. Herold, M. Strauch, D. Michalik, A. Appelhagen and R. Ludwig, ChemPhysChem, 2014, 15, 3040–3048.
18. D. Lankhorst, J. Schriever and J. C. Leyte, Ber. Bunsenges. Phys. Chem., 1982, 86, 215–221.
19. J. R. C. Van der Maarel, D. Lankhorst, J. De Bleijser and J. C. Leyte, Chem. Phys. Lett., 1985, 122, 541–544.
20. J. R. C. Van der Maarel, D. Lankhorst, J. De Bleijser and J. C. Leyte, J. Phys. Chem., 1986, 90, 1470–1478.
21. R. P. W. J. Struis, J. De Bleijser and J. C. Leyte, J. Phys. Chem., 1987, 91, 1639–1645.
22. R. Ludwig, T. C. Farrar and M. D. Zeidler, J. Phys. Chem., 1994, 98, 6684–6687.
23. R. Ludwig, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1995, 103, 6941–6950.
24. R. Ludwig, Chem. Phys., 1995, 195, 329–337.
25. R. Ludwig, D. S. Gill and M. D. Zeidler, Z. Naturforsch., 1991, 46a, 89–94.
26. R. Ludwig, D. S. Gill and M. D. Zeidler, Z. Naturforsch., 1992, 47a, 857–864.
27. R. Ludwig and M. D. Zeidler, Mol. Phys., 1994, 82, 313–323.
28. R. Ludwig, M. D. Zeidler and T. C. Farrar, Z. Phys. Chem., 1995, 189, 19–27.
29. R. Laenen, K. Simeonidis and R. Ludwig, J. Chem. Phys., 1999, 111, 5897–5904.
30. P. L. Cummins, G. B. Bacskay, N. S. Hush, B. Halle and S. Engström, J. Chem. Phys., 1985, 82, 2002–2013.
31. B. C. Gordalla and M. D. Zeidler, Mol. Phys., 1986, 59, 817–828.
32. B. C. Gordalla and M. D. Zeidler, Mol. Phys., 1991, 74, 975–984.
33. G. Stirnemann, P. J. Rossky, J. T. Hynes and D. Laage, Faraday Discuss., 2010, 146, 263–281.
34. S. J. Bachmann and W. F. van Gunsteren, Mol. Phys., 2014, 112, 2761–2780.
35. Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503.
36. S. J. Bachmann and W. F. van Gunsteren, J. Chem. Phys., 2014, 141, 22D515.
37. T. Köddermann, D. Paschek and R. Ludwig, ChemPhysChem, 2007, 8, 2464–2470.
38. T. Köddermann, D. Reith and R. Ludwig, ChemPhysChem, 2013, 14, 3368–3374.
39. C. G. Seipelt and M. D. Zeidler, Ber. Bunsenges. Phys. Chem., 1997, 101, 1501.
40. A. Abragam, The Principles of Nuclear Magnetism, Oxford Clarendon Press, 1961.
41. T. C. Farrar, An Introduction To Pulse NMR Spectroscopy, Farragut Press, Chicago, 1987.
42. M. A. Wendt and T. C. Farrar, Mol. Phys., 1998, 95, 1077–1081.
43. M. A. Wendt, M. D. Zeidler and T. C. Farrar, Mol. Phys., 1999, 97, 753–756.
44. T. C. Farrar, T. D. Ferris and M. D. Zeidler, Mol. Phys., 2000, 98, 737–744.
45. T. D. Ferris and T. C. Farrar, Mol. Phys., 2002, 100, 303–309.
46. K. Fumino, P. Stange, V. Fossog, R. Hempelmann and R. Ludwig, Angew. Chem., 2013, 125, 12667–12670 ( Angew. Chem., Int. Ed. , 2013 , 52 , 12439–12442 ).
47. P. Stange, K. Fumino and R. Ludwig, Angew. Chem., 2013, 125, 3064–3068 ( Angew. Chem., Int. Ed. , 2013 , 52 , 2990–2994 ).
48. K. Fumino, V. Fossog, K. Wittler, R. Hempelmann and R. Ludwig, Angew. Chem., 2013, 125, 2425–2429 ( Angew. Chem., Int. Ed. , 2013 , 52 , 2368–2372 ).
49. K. Fumino, V. Fossog, P. Stange, K. Wittler, W. Polet, R. Hempelmann and R. Ludwig, ChemPhysChem, 2014, 15, 2604–2609.
50. K. Fumino, A. Bonsa, B. Golub, D. Paschek and R. Ludwig, ChemPhysChem, 2015, 16, 299–304.
51. H. Huber, J. Chem. Phys., 1985, 83, 4591–4598.
52. R. Eggenberger, S. Gerber, H. Huber, D. Searles and M. Welker, J. Chem. Phys., 1992, 97, 5898–5904.
53. D. J. Searles and H. Huber, Accurate Determination of Nuclear Quadrupole Coupling Constants and other NMR Parameters in Liquids from the Combination of Molecular Dynamics Simulations and ab initio Calculations, in Encyclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. K. Harris, Wiley, New York, 2002, vol. 9.
54. R. Ludwig, F. Weinhold and T. C. Farrar, Ber. Bunsenges. Phys. Chem., 1998, 102, 197–204.
55. R. Ludwig, F. Weinhold and T. C. Farrar, Ber. Bunsenges. Phys. Chem., 1998, 102, 205–212.
56. R. Ludwig, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1995, 102, 5118–5125.
57. R. Ludwig, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1995, 103, 3636–3642.
58. R. Ludwig, F. Weinhold and T. C. Farrar, J. Phys. Chem. A, 1997, 101, 8861–8870.
59. R. Ludwig, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1997, 107, 499–507.
60. M. J. Frisch, et al., Gaussian 09 (Revision B.01), 2004, see ESI†.
61. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
62. S. Ehrlich, J. Moellmann, W. Reckien, T. Bredow and S. Grimme, ChemPhysChem, 2011, 12, 3414–3420.
63. A. Wulf and R. Ludwig, ChemPhysChem, 2006, 7, 266–272.
64. A. Einstein, Investigations on the Theory of brownian motion, Dover, New York, 1956.
65. P. Debye, Polar Molecules, Dover, New York, 1929.
66. D. Paschek, B. Golub and R. Ludwig, Phys. Chem. Chem. Phys., 2015, 17, 8431–8440.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp01462c

---