Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Characterization of water dissociation on α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/h2_char_0031_0304.gif) 02): theory and experiment†
02): theory and experiment†
Jonas
Wirth
a,
Harald
Kirsch
b,
Sebastian
Wlosczyk
b,
Yujin
Tong
b,
Peter
Saalfrank
a and
R. Kramer
Campen
 *b
*b
aInstitute of Chemistry, University of Potsdam, Karl-Liebknecht Straße 24-25, D-14476 Potsdam, Germany
bFritz Haber Institute of the Max Planck Society, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: campen@fhi-berlin.mpg.de
First published on 18th April 2016
Abstract
The interaction of water with α-alumina (i.e. α-Al2O3) surfaces is important in a variety of applications and a useful model for the interaction of water with environmentally abundant aluminosilicate phases. Despite its significance, studies of water interaction with α-Al2O3 surfaces other than the (0001) are extremely limited. Here we characterize the interaction of water (D2O) with a well defined α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface in UHV both experimentally, using temperature programmed desorption and surface-specific vibrational spectroscopy, and theoretically, using periodic-slab density functional theory calculations. This combined approach makes it possible to demonstrate that water adsorption occurs only at a single well defined surface site (the so-called 1–4 configuration) and that at this site the barrier between the molecularly and dissociatively adsorbed forms is very low: 0.06 eV. A subset of OD stretch vibrations are parallel to this dissociation coordinate, and thus would be expected to be shifted to low frequencies relative to an uncoupled harmonic oscillator. To quantify this effect we solve the vibrational Schrödinger equation along the dissociation coordinate and find fundamental frequencies red-shifted by more than 1500 cm−1. Within the context of this model, at moderate temperatures, we further find that some fraction of surface deuterons are likely delocalized: dissociatively and molecularly absorbed states are no longer distinguishable.
02) surface in UHV both experimentally, using temperature programmed desorption and surface-specific vibrational spectroscopy, and theoretically, using periodic-slab density functional theory calculations. This combined approach makes it possible to demonstrate that water adsorption occurs only at a single well defined surface site (the so-called 1–4 configuration) and that at this site the barrier between the molecularly and dissociatively adsorbed forms is very low: 0.06 eV. A subset of OD stretch vibrations are parallel to this dissociation coordinate, and thus would be expected to be shifted to low frequencies relative to an uncoupled harmonic oscillator. To quantify this effect we solve the vibrational Schrödinger equation along the dissociation coordinate and find fundamental frequencies red-shifted by more than 1500 cm−1. Within the context of this model, at moderate temperatures, we further find that some fraction of surface deuterons are likely delocalized: dissociatively and molecularly absorbed states are no longer distinguishable.
1 Introduction
α-Alumina surfaces are omnipresent in industrial applications in heterogeneous catalysis, optics and electronics and a useful model for surfaces of more environmentally abundant aluminosilicates.1 Whether in application or the environment, several decades of work have made clear that their properties (e.g. reactivity, polarity and structure) all change dramatically on contact with water.2,3Understanding the molecular mechanism of α-alumina/liquid water interaction is challenging because relevant processes occur over more than ten orders of magnitude in time and space. In principle, studying the interaction of small numbers of water molecules with well-defined α-alumina surfaces in ultra-high vacuum (UHV) should remove much of this complexity. However, even for the most studied α-Al2O3(0001) surface4–11 gaining molecular level insight into water/alumina interaction has proven surprisingly elusive. In fact, while theoretical studies had converged on a common view of the most thermodynamically stable α-Al2O3(0001) surface termination in the absence of water and the molecular mechanism of water/(0001) interaction, it was only in our previous work that clear experimental evidence for the theoretically predicted water dissociation pathways was offered.12
Much previous work has shown that the reactivity of metal oxide surfaces in general, and α-alumina surfaces in particular, is a function of the coordinative undersaturation and density of atoms exposed at the surface.2 A variety of previous theoretical and experimental studies have shown that, in UHV, the α-Al2O3(0001) surface is Al terminated and that this termination results in a layer of Al atoms that are three fold coordinated and a layer of oxygens that are doubly coordinated. While much theory predicts that the (0001) is the most stable of α-alumina's surfaces in UHV, the next most stable surface is generally found to be the stoichiometric (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) (e.g. 0.11 J m−2 less stable than (0001) by the computation of Kurita et al.13). From a computational standpoint a variety of prior workers have found the most stable (1
02) (e.g. 0.11 J m−2 less stable than (0001) by the computation of Kurita et al.13). From a computational standpoint a variety of prior workers have found the most stable (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface structure in UHV in the absence of water to be a stoichiometric oxygen termination that produces a (1 × 1) pattern when probed via low energy electron diffraction (LEED).13–16 This surface is composed of quintuply coordinated surface aluminums and alternating rows of triply and quadruply coordinated surface oxygens. Some prior experimental studies have found a stable surface structure of the (1
02) surface structure in UHV in the absence of water to be a stoichiometric oxygen termination that produces a (1 × 1) pattern when probed via low energy electron diffraction (LEED).13–16 This surface is composed of quintuply coordinated surface aluminums and alternating rows of triply and quadruply coordinated surface oxygens. Some prior experimental studies have found a stable surface structure of the (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface in UHV that produces a (2 × 1) LEED pattern and argued this surface structure is the most stable.17,18 More recent work, however, has found that when oxygen defects are properly filled during sample preparation the thermodynamically stable surface gives a (1 × 1) LEED pattern, consistent with calculation (see ESI† for detailed discussion of this point).3,19,20
02) surface in UHV that produces a (2 × 1) LEED pattern and argued this surface structure is the most stable.17,18 More recent work, however, has found that when oxygen defects are properly filled during sample preparation the thermodynamically stable surface gives a (1 × 1) LEED pattern, consistent with calculation (see ESI† for detailed discussion of this point).3,19,20
While the structure of the α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface in UHV in the absence of H2O thus seems clear, there are to our knowledge no published studies that systematically compare experimental observables of this system with submonolayer concentrations of water and appropriate calculation. Here, we address this shortcoming by following the combined experimental/theoretical approach of our previous study of α-Al2O3(0001)/water interaction.12 We prepare well-defined α-Al2O3(1
02) surface in UHV in the absence of H2O thus seems clear, there are to our knowledge no published studies that systematically compare experimental observables of this system with submonolayer concentrations of water and appropriate calculation. Here, we address this shortcoming by following the combined experimental/theoretical approach of our previous study of α-Al2O3(0001)/water interaction.12 We prepare well-defined α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surfaces in UHV, expose them to submonolayer water coverages and characterize the resulting water/alumina interaction using temperature programmed desorption (TPD) and the interface specific, laser-based technique vibrational sum frequency (VSF) spectroscopy. In parallel we perform a series of density functional theory (DFT) calculations. Collectively the results of this approach allow characterization of the energies and frequencies of all possible surface species as well as the thermodynamics and kinetics of relevant surface processes, especially those of the water dissociation reaction. This combined approach allows us to unambiguously demonstrate that on the (1
02) surfaces in UHV, expose them to submonolayer water coverages and characterize the resulting water/alumina interaction using temperature programmed desorption (TPD) and the interface specific, laser-based technique vibrational sum frequency (VSF) spectroscopy. In parallel we perform a series of density functional theory (DFT) calculations. Collectively the results of this approach allow characterization of the energies and frequencies of all possible surface species as well as the thermodynamics and kinetics of relevant surface processes, especially those of the water dissociation reaction. This combined approach allows us to unambiguously demonstrate that on the (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface in UHV unimolecular water dissociation proceeds through the so-called 1–4 channel, but that the barrier between molecular and dissociative adsorption is quite small: ≈0.06 eV. Explicit calculation of the wavefunction and vibrational eigenvalues for this transition demonstrate that these two states are largely indistinguishable. While all experiments and calculations are conducted with D2O instead of H2O, the deuteron delocalization we describe should only be enhanced when protons are explicitly considered. Such surface deuteron delocalization has not, to our knowledge, been previously described in studies of water/oxide interaction and has significant implications for temperature dependent surface reactivity, physisorption of other solutes and, from a practical point of view, appropriate levels of theory for the description of water/alumina interaction.
02) surface in UHV unimolecular water dissociation proceeds through the so-called 1–4 channel, but that the barrier between molecular and dissociative adsorption is quite small: ≈0.06 eV. Explicit calculation of the wavefunction and vibrational eigenvalues for this transition demonstrate that these two states are largely indistinguishable. While all experiments and calculations are conducted with D2O instead of H2O, the deuteron delocalization we describe should only be enhanced when protons are explicitly considered. Such surface deuteron delocalization has not, to our knowledge, been previously described in studies of water/oxide interaction and has significant implications for temperature dependent surface reactivity, physisorption of other solutes and, from a practical point of view, appropriate levels of theory for the description of water/alumina interaction.
2 Materials and methods
2.1 Experiment
![[1 with combining macron]](https://www.rsc.org/images/entities/b_char_0031_0304.gif) 02) surfaces.
The experiments were performed in an ultra high vacuum (UHV) chamber with a base pressure of 2.5 × 10−10 mbar. Connected to the chamber is a turbo molecular beam source for water dosing and a quadrupole mass spectrometer for determination of surface coverage. For our sample preparation, we adopted a treatment that has been reported previously19 to form a carbon free surface with a well defined (1 × 1)-LEED pattern (see ESI† and our previous study for details of sample preparation and temperature control12). In our hands this procedure also results in a carbon free surface (confirmed by Auger spectroscopy) with a well defined (1 × 1)-LEED pattern (see ESI† for Auger and LEED results).
02) surfaces.
The experiments were performed in an ultra high vacuum (UHV) chamber with a base pressure of 2.5 × 10−10 mbar. Connected to the chamber is a turbo molecular beam source for water dosing and a quadrupole mass spectrometer for determination of surface coverage. For our sample preparation, we adopted a treatment that has been reported previously19 to form a carbon free surface with a well defined (1 × 1)-LEED pattern (see ESI† and our previous study for details of sample preparation and temperature control12). In our hands this procedure also results in a carbon free surface (confirmed by Auger spectroscopy) with a well defined (1 × 1)-LEED pattern (see ESI† for Auger and LEED results).
Given a well-defined α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface, we prepared our sample by setting the sample temperature to 400 K and continually dosing as the sample was cooled to 135 K with a ramp of 20 K min−1. As we show below, this procedure produces a mixed first layer, containing both dissociatively and molecularly adsorbed water, overlain by a layer of ice. The spectral response of the ice layer is used to align our set up before each measurement. Note that this procedure differs significantly from that employed in preparing the α-Al2O3(0001). There, as discussed previously,12 it was necessary to dose continually from 450 K to 300 K by using a ramp of 10 K min−1, followed by staying for 20 minutes at 300 K in order to generate significant coverages of dissociatively adsorbed water. Then the preparation cycle was finished by continually dosing while cooling from 300 K to 140 K with a ramp of 10 K min−1. These qualitative differences clearly suggest the (1
02) surface, we prepared our sample by setting the sample temperature to 400 K and continually dosing as the sample was cooled to 135 K with a ramp of 20 K min−1. As we show below, this procedure produces a mixed first layer, containing both dissociatively and molecularly adsorbed water, overlain by a layer of ice. The spectral response of the ice layer is used to align our set up before each measurement. Note that this procedure differs significantly from that employed in preparing the α-Al2O3(0001). There, as discussed previously,12 it was necessary to dose continually from 450 K to 300 K by using a ramp of 10 K min−1, followed by staying for 20 minutes at 300 K in order to generate significant coverages of dissociatively adsorbed water. Then the preparation cycle was finished by continually dosing while cooling from 300 K to 140 K with a ramp of 10 K min−1. These qualitative differences clearly suggest the (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface is more reactive than the (0001) with respect to water dissociation. This assessment of relative reactivities is consistent with prior work.3
02) surface is more reactive than the (0001) with respect to water dissociation. This assessment of relative reactivities is consistent with prior work.3
Note that all VSF spectra described below were collected at sample temperatures of 135 K. The experimental temperature dependent stability we describe was probed by rapidly annealing a sample from 135 K to the indicated temperature (using a heating ramp of 100 K min−1) and, after reaching the target temperature cooling it at the same rate back to 135 K for analysis.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) with a bandwidth of 8 cm−1 and the emitted sum frequency field detected using an ICCD camera. In our experimental configuration incident IR and VIS beams are coplanar and this plane is normal to the surface. All reported measurements were conducted in the ppp configuration (the polarizations of all beams parallel to the plane of incidence) and incident VIS/IR were at 75/70 degrees with respect to the surface normal. For all experiments we used D2O instead of H2O because our IR source has more energy at OD stretch than OH stretch frequencies. As we discuss in detail below, the novel features of D2O adsorption on this surface, e.g. the small barrier between molecular and dissociated forms, seem likely to be only enhanced in the presence of H2O.
500 cm−1) with a bandwidth of 8 cm−1 and the emitted sum frequency field detected using an ICCD camera. In our experimental configuration incident IR and VIS beams are coplanar and this plane is normal to the surface. All reported measurements were conducted in the ppp configuration (the polarizations of all beams parallel to the plane of incidence) and incident VIS/IR were at 75/70 degrees with respect to the surface normal. For all experiments we used D2O instead of H2O because our IR source has more energy at OD stretch than OH stretch frequencies. As we discuss in detail below, the novel features of D2O adsorption on this surface, e.g. the small barrier between molecular and dissociated forms, seem likely to be only enhanced in the presence of H2O.
| IVSF ∝ |χ(2)|2IVISIIR | (1) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ir is the infrared frequency):
ir is the infrared frequency):| χ(2) ∝ χ(2)NR + χ(2)R | (2) |
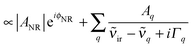 | (3) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) q and 2Γq are the complex amplitude, center frequency and line width of the qth resonance and |ANR| and ϕNR are the nonresonant amplitude and phase. In fitting this model to the data we followed standard procedures.
q and 2Γq are the complex amplitude, center frequency and line width of the qth resonance and |ANR| and ϕNR are the nonresonant amplitude and phase. In fitting this model to the data we followed standard procedures.
Given a measured macroscopic nonlinear susceptibility in a laboratory fixed reference frame (IJK), χ(2) can be written as the sum (N) of molecular responses (β(2)) within a molecular fixed reference frame (ijk) multiplied by the appropriate ensemble average transformation matrix.27
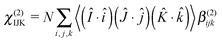 | (4) |
Note that all presented VSF data have been normalized to account for the frequency dependence of the incident infrared energy.
2.2 Theory
Harmonic molecular vibrations were found by means of normal mode analysis, i.e. by diagonalization of the system's dynamical matrix, also including all degrees of freedom of the uppermost substrate layers (details see below); numerical derivatives of the energy with respect to the nuclear coordinates were evaluated using centered finite differences.
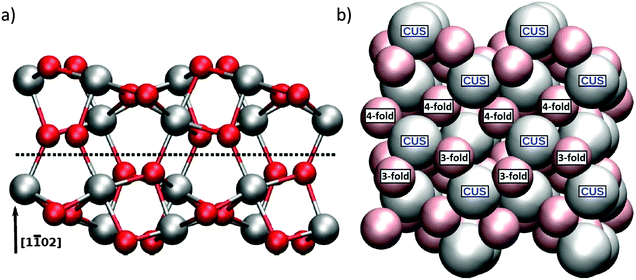
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) plane gives a surface that cannot be repeated by translation along a lattice vector normal to the surface. Because such translation is required for the periodic boundary conditions of our calculation we follow Trainor et al and instead employ a larger (2 × 2) supercell (strictly speaking a pseudo supercell) model.19 The resulting slab shown in Fig. 1a consists of six oxygen and four aluminum layers in the vertical direction, the lower half of which were kept fixed (after initial geometry optimization of the adsorbate-free structure) during optimizations, single point energy calculations and vibrational analyses in the presence of adsorbate species on the top side of the slab. The rectangular cell correctly describing the lateral translational symmetry of the surface structure is defined by two vectors in the directions of the crystallographic [11
02) plane gives a surface that cannot be repeated by translation along a lattice vector normal to the surface. Because such translation is required for the periodic boundary conditions of our calculation we follow Trainor et al and instead employ a larger (2 × 2) supercell (strictly speaking a pseudo supercell) model.19 The resulting slab shown in Fig. 1a consists of six oxygen and four aluminum layers in the vertical direction, the lower half of which were kept fixed (after initial geometry optimization of the adsorbate-free structure) during optimizations, single point energy calculations and vibrational analyses in the presence of adsorbate species on the top side of the slab. The rectangular cell correctly describing the lateral translational symmetry of the surface structure is defined by two vectors in the directions of the crystallographic [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] and [
0] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 101] axes (see Fig. 1b). The calculated corresponding lattice constants were a = 9.60 Å and b = 10.22 Å, and deviated less than 1% from experimental values.19 Consistent with prior work by Kurita et al.,13 vertical relaxation for α-Al2O3(1
101] axes (see Fig. 1b). The calculated corresponding lattice constants were a = 9.60 Å and b = 10.22 Å, and deviated less than 1% from experimental values.19 Consistent with prior work by Kurita et al.,13 vertical relaxation for α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) was found to be less pronounced than in case of the Al terminated (0001). In what follows we describe the surface Al atoms as Coordinatively Unsaturated Sites (CUS). All such CUS sites for the (1
02) was found to be less pronounced than in case of the Al terminated (0001). In what follows we describe the surface Al atoms as Coordinatively Unsaturated Sites (CUS). All such CUS sites for the (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface exhibit the same, albeit rotated, chemical environment: they are each surrounded by 2 three-fold coordinated and 2 four-fold coordinated oxygens.
02) surface exhibit the same, albeit rotated, chemical environment: they are each surrounded by 2 three-fold coordinated and 2 four-fold coordinated oxygens.
| ΔEads = E(H2O + surface) − [E(surface) + E(H2O)] | (5) |
Surface processes such as water dissociation or diffusion were studied using the nudged elastic band (NEB) method (see ref. 41 and references therein) as implemented in the modified VASP version of Jónsson and co-workers. This includes an improved estimate to the band tangent42 as well as a climbing image (CIS) scheme43 for locating the transition state along the minimum energy path (MEP) of the reaction. The NEB procedure used here includes successive linear interpolation steps as described in ref. 39, ending up with eleven images (plus reactant and product image) along the path. Transition states were characterized by a single imaginary frequency corresponding to a vibrational mode that is the coordinate connecting the reactant and product states. Reaction rates were estimated as a function of temperature using the expression,44
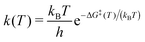 | (6) |
3 Results and discussion
3.1 Experimental UHV results
As described above, we expect our D2O dosing procedure to result in creation of a multilayer of ice. To verify the presence of these multilayers, and their subsequent removal with sample thermal annealing, we performed TPD measurements one example of which is shown in Fig. 2a. The TPD spectrum is clearly dominated by a double peak structure with a long tail to the high temperature side. We and others have previously observed this long tail at higher temperatures in TPD spectra of water adsorption on α-Al2O3(0001)5,12 and assigned it to the recombinative desorption of dissociatively adsorbed water. We follow this assignment here for water adsorption on the α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface. In addition to the tail, two desorption maxima, centered at 162 and 175 K are apparent (see Fig. 2a). Because the 162 K peak increases in magnitude with increasing dosing time while the 175 K does not, we assign the former to the desorption of multilayer water (i.e. ice) and the later to the desorption of surface (<1 monolayer) molecular water.
02) surface. In addition to the tail, two desorption maxima, centered at 162 and 175 K are apparent (see Fig. 2a). Because the 162 K peak increases in magnitude with increasing dosing time while the 175 K does not, we assign the former to the desorption of multilayer water (i.e. ice) and the later to the desorption of surface (<1 monolayer) molecular water.
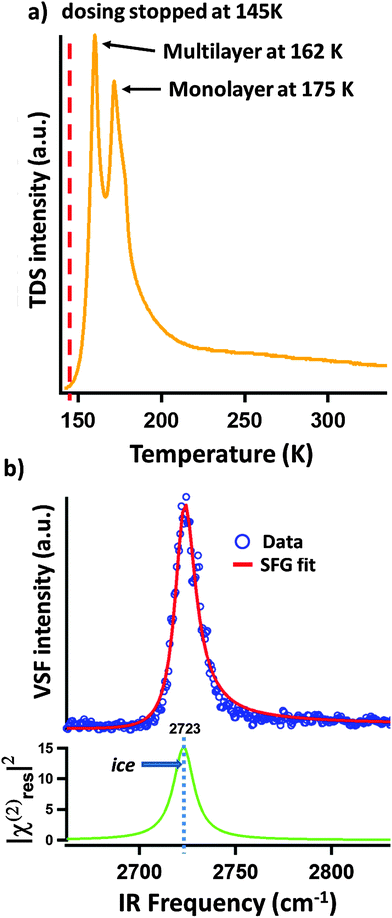 | ||
Fig. 2 (a) The TPD spectrum of mass 20 (D2O) for a sample, prepared as described in the text. To perform the TPD, after stopping D2O dosing at 145 K we applied a heating ramp of 100 K min−1 and detected the desorption of mass 20. The desorption maximum at 162 K is assigned to water desorbing from the weakly bond multilayer of ice (it can be increased in intensity by dosing for longer at low surface temperature). The peak at 175 K is assigned to monolayer desorption. Its amplitude is independent of low temperature dosing time. (b) VSF spectrum of α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface covered by D2O ice and showing the characteristic free-OD peak of the ice/vacuum interface.12 02) surface covered by D2O ice and showing the characteristic free-OD peak of the ice/vacuum interface.12 | ||
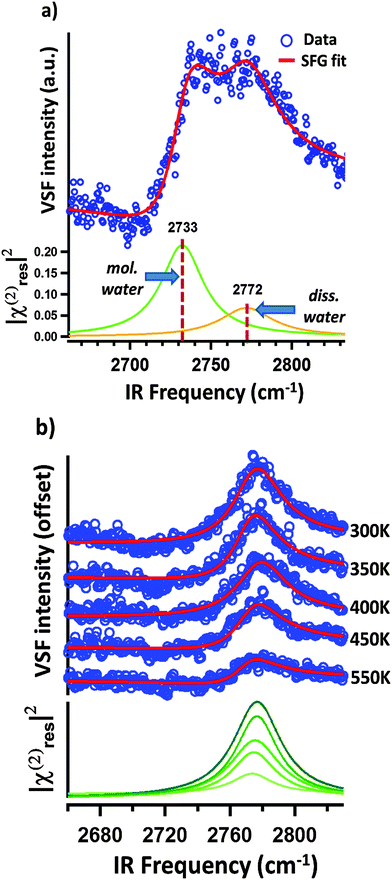
Performing VSF measurements of samples prepared as described above with no subsequent thermal annealing results in a VSF spectrum with a strong single resonance (see Fig. 2b). Using the line shape model discussed above, fitting the data allows us to extract a resonance center frequency of 2723 cm−1 for this feature as expected for the free-OD of D2O ice.12
If our assignment of the TPD data is correct, rapid thermal annealing to temperatures above 175 K should result in a surface that has sub-monolayer D2O coverages. Given that the spectral response shown in Fig. 2b is that of the ice surface one might expect that after evaporating all ice there would be a notable decrease in intensity of the VSF spectrum (the monolayer coverage of adsorbed water is disordered relative to the ice surface) and a change in lineshape (water's local hydrogen bonding environment also changes with respect to that found in ice). As shown in Fig. 3a, our measurements confirm these expectations. Clearly, after annealing to 185 K what was a single intense resonance centered at 2723 cm−1 is now two weaker resonances centered at 2733 and 2772 cm−1. Scanning our IR source over the range 1500–3000 cm−1 and at other polarizations gave no other detectable resonant features.
Because the TPD data (see Fig. 2a) make clear that at 185 K our α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface has only submonolayer coverages of D2O, it seems reasonable to suggest that the two resonances apparent after annealing to 185 K at 2733 and 2772 cm−1 (see Fig. 3a) must be the result of either dissociatively or molecularly adsorbed water. Prior studies have found that some hydroxyl groups resulting from dissociative adsorption of H2O on α-Al2O3(1
02) surface has only submonolayer coverages of D2O, it seems reasonable to suggest that the two resonances apparent after annealing to 185 K at 2733 and 2772 cm−1 (see Fig. 3a) must be the result of either dissociatively or molecularly adsorbed water. Prior studies have found that some hydroxyl groups resulting from dissociative adsorption of H2O on α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) are stable in UHV up to temperatures of ≈700 K.18 This finding suggests that if an observed OD stretch resonance originates from molecularly adsorbed D2O, heating to temperatures >300 K should result in its disappearance while OD stretch modes related to dissociatively adsorbed D2O should still be present.
02) are stable in UHV up to temperatures of ≈700 K.18 This finding suggests that if an observed OD stretch resonance originates from molecularly adsorbed D2O, heating to temperatures >300 K should result in its disappearance while OD stretch modes related to dissociatively adsorbed D2O should still be present.
Fig. 3b shows VSF spectra collected from samples annealed to temperatures above 300 K and rapidly cooled to 135 K for measurement. Clearly the 2733 cm−1 feature apparent at 185 K is now absent (see Fig. 3a) and the intensity of the resonance centred at 2773 cm−1 decreases with increasing maximum temperature.
This data is thus consistent with a scenario in which the 2733 cm−1 resonance is an OD stretch of molecular D2O while the feature centered at 2773 cm−1 is the result of dissociative adsorption. In this scenario, and consistent with the TPD data in Fig. 2a, the decrease in intensity of the 2773 cm−1 feature with increasing temperature is the result of decreasing water coverage with increasing temperature. While consistent with experiment, clearly this understanding of our observed trends still leaves questions: (i) what are the thermodynamics and kinetics that control D2O/α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) interaction? (ii) Relatedly, why do we observe only one spectral feature associated with dissociatively adsorbed D2O (one might expect at least two per energetically plausible dissociation mechanism)? (iii) Why do we observe only one spectral feature associated with molecularly adsorbed D2O? To help answer these questions we turn to theory.
02) interaction? (ii) Relatedly, why do we observe only one spectral feature associated with dissociatively adsorbed D2O (one might expect at least two per energetically plausible dissociation mechanism)? (iii) Why do we observe only one spectral feature associated with molecularly adsorbed D2O? To help answer these questions we turn to theory.
3.2 Computational results
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface is 0.08 Å−2, 60% higher than the 0.05 Å−2 for the (0001) surface.39 To connect to our sub-monolayer experimental results, we here focus on the description of water adsorption, dissociation and diffusion on the α-Al2O3(1
02) surface is 0.08 Å−2, 60% higher than the 0.05 Å−2 for the (0001) surface.39 To connect to our sub-monolayer experimental results, we here focus on the description of water adsorption, dissociation and diffusion on the α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface in the low coverage limit. To our knowledge there is no prior work that has previously explored water reactivity on this surface at these coverages. By placing a single D2O molecule in the (2 × 2) supercell, a surface with 1/8 of a monolayer with respect to the CUS positions results.
02) surface in the low coverage limit. To our knowledge there is no prior work that has previously explored water reactivity on this surface at these coverages. By placing a single D2O molecule in the (2 × 2) supercell, a surface with 1/8 of a monolayer with respect to the CUS positions results.
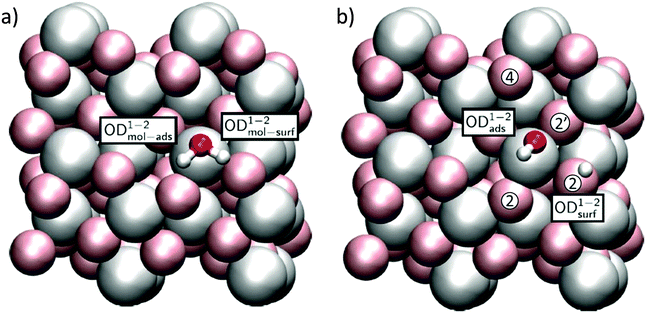
Because the two aluminum CUS atoms per unit cell of the α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface structure have the same, albeit rotated, chemical environment (see Fig. 1b), only two distinct water adsorption geometries are possible. In the first, shown in Fig. 4 the oxygen of an adsorbing D2O sits atop a surface Al. This D2O either adsorbs dissociatively, in which case the OD originating from D2O remains on the surface Al and the extra D is adsorbed by the nearest neighbor three-fold coordinated surface oxygen, labelled a 2 site, or molecularly, in which case it does not. Note that for molecularly adsorbed D2O in this configuration the two OD groups are not equivalent: the OD angles with respect to the surface normal and bond lengths both differ (see Table 1 and ESI† for further structural information). In what follows we refer to the four OD groups shown in Fig. 4a and b using the superscript 1–2. If this molecule dissociatively adsorbs it forms an OD group originating from D2O, denoted by the subscript ads or from bond formation between a surface oxygen and deuterium from D2O, denoted by subscript surf. To refer to the OD in molecularly adsorbed D2O that is ODads if the molecule dissociates we employ the subscript mol-ads and to refer to the D from D2O that forms a bond with surface oxygen when D2O dissociates we use the subscript mol-surf. As shown in Fig. 5, in the second possible set of adsorption geometries an impinging D2O molecule adsorbs on the flank of a surface Al and, when it dissociates, the surface D adsorbs on the next nearest neighbour 3-fold coordinated oxygen (i.e. the 4 site, see Fig. 4b for definition of site labelling convention). The notation used to describe the four possible ODs in this situation is the same as above except a superscript 1–4 is employed. Adsorption of D on 4-fold coordinated oxygens, the 2′ sites, is unfavorable.
02) surface structure have the same, albeit rotated, chemical environment (see Fig. 1b), only two distinct water adsorption geometries are possible. In the first, shown in Fig. 4 the oxygen of an adsorbing D2O sits atop a surface Al. This D2O either adsorbs dissociatively, in which case the OD originating from D2O remains on the surface Al and the extra D is adsorbed by the nearest neighbor three-fold coordinated surface oxygen, labelled a 2 site, or molecularly, in which case it does not. Note that for molecularly adsorbed D2O in this configuration the two OD groups are not equivalent: the OD angles with respect to the surface normal and bond lengths both differ (see Table 1 and ESI† for further structural information). In what follows we refer to the four OD groups shown in Fig. 4a and b using the superscript 1–2. If this molecule dissociatively adsorbs it forms an OD group originating from D2O, denoted by the subscript ads or from bond formation between a surface oxygen and deuterium from D2O, denoted by subscript surf. To refer to the OD in molecularly adsorbed D2O that is ODads if the molecule dissociates we employ the subscript mol-ads and to refer to the D from D2O that forms a bond with surface oxygen when D2O dissociates we use the subscript mol-surf. As shown in Fig. 5, in the second possible set of adsorption geometries an impinging D2O molecule adsorbs on the flank of a surface Al and, when it dissociates, the surface D adsorbs on the next nearest neighbour 3-fold coordinated oxygen (i.e. the 4 site, see Fig. 4b for definition of site labelling convention). The notation used to describe the four possible ODs in this situation is the same as above except a superscript 1–4 is employed. Adsorption of D on 4-fold coordinated oxygens, the 2′ sites, is unfavorable.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface
02) surface
| Configuration | E ads | G ads (T = 0 K) | G ads (T = 135 K) |
|---|---|---|---|
| 1–2-mol. | −1.07 | −1.02 | −0.83 |
| 1–2-diss. | −1.11 | −1.08 | −0.89 |
| 1–4-mol. | −1.48 | −1.45 | −1.25 |
| 1–4-diss. | −1.53 | −1.51 | −1.31 |
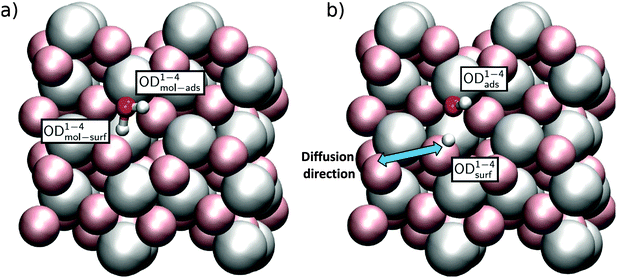 | ||
| Fig. 5 Adsorption geometries for (a) molecular and (b) dissociated water in the 1–4 configuration. The blue arrow indicates a portion of the diffusion channel of the deuteron discussed in the text. | ||
Calculated energies and free energies of each of these configurations are shown in Table 1 along with the angles of each OD group relative to the surface normal. These results suggest that, perhaps counter intuitively, both 1–4 geometries are favoured over the 1–2 geometries by approximately 0.4 eV. This is presumably due to the coordination environment of the CUS atom being tilted with respect to the surface normal in the 1–4 allowing for a stabilizing hydrogen-bond like interaction between the water D and surface O atom (for the molecular structure) or deuteroxyl O atom and the newly formed surface OD group (for the dissociated structure) close to the opposing CUS (see Fig. 5). For both the 1–2 and 1–4 adsorption geometries we note further that the molecular and dissociated forms are ≈ energetically degenerate: within 0.06 eV. We have shown previously that such degeneracy does not occur for the analogous 1–2 water adsorption configuration, but does for the 1–4, on the α-Al2O3(0001) surface.12,39 As we will see below these differences lead to dramatically different surface reactivity.
Much prior work and preliminary studies here strongly suggest that the OD fragment resulting from D2O dissociative adsorption, i.e. ODads, forms a covalent bond to a surface aluminum that is sufficiently strong to be fixed on all relevant timescales.12,39 As a result we here investigate the likelihood of only two types of surface diffusion: (i) diffusion of a water molecule between neighbouring CUS positions each adsorbed in the low energy 1–4 configuration and (ii) migration of the detached water deuteron from the 1–4 position to a neighbouring surface oxygen atom still further away. Because simple thermodynamical considerations dictate that the 1–4 configuration is 107 more probable than the 1–2 (given G1–4 − G1–2 = ΔG = −0.4 eV at T = 300 K, according to Boltzmann statistics e−ΔG/(kBT) ≈ 107 more probable), we did not consider diffusion of the deuteron from the 1–4 to 1–2 positions.
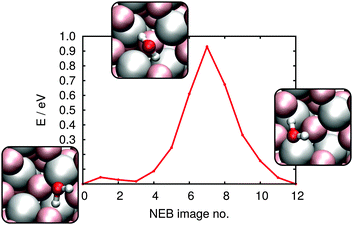
As discussed in the Methods section, we address each of these processes by calculating the relative free energies of the reactant and product states and the reaction coordinate that connects them sampled via the nudged elastic band method. The NEB-derived energy profile for diffusion of a water molecule between two neighboring 1–4 CUS positions is shown in Fig. 6. The process proceeds via rotation of the water molecule through a rather high energy transition state: 0.93 eV. According to eqn (6) at 300 K this results in a rate constant of 2 × 10−3 s−1. At the VSF measurement condition of T = 135 K this rate drops to 9 × 10−23 s−1 suggesting diffusion of molecular water under VSF measurement conditions does not occur. While diffusion between 1–4 configurations would be possible during high temperature annealing clearly such changes do not influence surface energetics, in the low coverage limit all 1–4 configurations are the same.
As discussed above, in either the 1–2 or 1–4 adsorption configuration, the dissociated D forms a covalent bond with a 3-fold coordinated surface oxygen. On the (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface such oxygens form horizontal rows in Fig. 4 and 5 (i.e. in the crystallographic (11
02) surface such oxygens form horizontal rows in Fig. 4 and 5 (i.e. in the crystallographic (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) direction) that are separated by 4-fold coordinated oxygens (i.e. in the crystallographic (
0) direction) that are separated by 4-fold coordinated oxygens (i.e. in the crystallographic (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 101) direction). Because D bond formation with such saturated oxygens is extremely unfavorable, surface structure suggests that D diffusion, if it occurs, should take place along diffusion channels (as shown in Fig. 5). Because, as discussed above, the 1–2 adsorption configuration should exist in extremely small numbers, we here only consider the diffusion of the deuteron from the 4 position in the 1–4 dissociated configuration (Fig. 5(b)) to its nearest neighbour surface oxygen atom. From the resulting NEB-derived energy profile shown in Fig. 7 clarifies that such motion is thermodynamically unfavourable, by 0.73 eV and has a barrier of 1.33 eV. In order to assess the thermodynamic favourability of other product states, a number of different configurations with distances between OD group and deuteron larger than in the 1–2 or 1–4 dissociated geometry were also optimized. No configuration was found in which the new position of deuteron was less than 0.5 eV destabilised, with respect to the initial, stable 1–4 dissociated geometry.
101) direction). Because D bond formation with such saturated oxygens is extremely unfavorable, surface structure suggests that D diffusion, if it occurs, should take place along diffusion channels (as shown in Fig. 5). Because, as discussed above, the 1–2 adsorption configuration should exist in extremely small numbers, we here only consider the diffusion of the deuteron from the 4 position in the 1–4 dissociated configuration (Fig. 5(b)) to its nearest neighbour surface oxygen atom. From the resulting NEB-derived energy profile shown in Fig. 7 clarifies that such motion is thermodynamically unfavourable, by 0.73 eV and has a barrier of 1.33 eV. In order to assess the thermodynamic favourability of other product states, a number of different configurations with distances between OD group and deuteron larger than in the 1–2 or 1–4 dissociated geometry were also optimized. No configuration was found in which the new position of deuteron was less than 0.5 eV destabilised, with respect to the initial, stable 1–4 dissociated geometry.
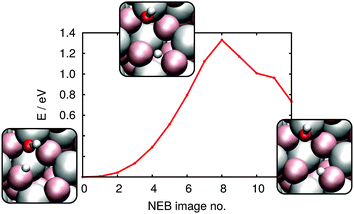 | ||
| Fig. 7 NEB-derived energy profile for diffusion of a proton/deuteron from the 4 position to a neighboring surface oxygen atom; see insets for reactant, product and transition state geometries. | ||
Armed with free energies at each point along the reaction coordinate the rate constant for proton/deuteron “escape” from the 1–4 dissociated configuration is, at 135 K, 4 × 10−34 s−1, at 300 K, 3 × 10−8 s−1 and at 550 K, 70 s−1. This suggests that deuteron diffusion is essentially impossible at the temperatures of VSF analysis and for samples rapidly annealed to 185 K (i.e.Fig. 3a) but that it is significant for samples annealed to temperatures 300–550 K (i.e.Fig. 3b). However, given the 1-D nature of deuteron diffusion and the structural similarity of all 3-fold coordinated surface oxygens, it seems clear that thermodynamic considerations suggest the great majority of deuterons are in the 1–4 configurations (i.e. given a destabilization energy of ΔG = −0.5 eV, at 300 K 1–4 configurations are e−ΔG/(kBT) ≈ 109 more probable). Taken together these calculations suggest that at temperatures from 135–185 K deuteron diffusion does not happen on the timescale of the measurements. While diffusion does occur from 300–550 K, thermodynamics suggests that deuteron locations other than those shown in Fig. 5 are exceptionally uncommon.
| Assignment | Theory | Experiment | |
|---|---|---|---|
| θ (deg) | Freq. (cm−1) | Freq. (cm−1) | |
| OD1–2ads | 41 | 2782 | — |
| OD1–4ads | 34 | 2779 | 2772 |
| OD1–4mol-ads | 49 | 2737 | 2733 |
| OD1–2mol-ads | 67 | 2688 | — |
| OD1–2surf | 37 | 2680 | — |
| OD1–2mol-surf | 84 | 2493 | — |
| OD1–4surf | 50 | 1958 | — |
| OD1–4mol-surf | 112 | 1651 | — |
Considering the well-known GGA-typical overestimation of fundamental frequencies, the nearly perfect overlap between measured and calculated frequencies is likely the result of a fortuitous cancellation between DFT error and anharmonicity. However, much prior work shows that relative harmonic frequencies do not typically suffer from either effect and clearly restating the results in Table 2 in these terms would lead to the same assignment.12 Given this assignment, however, we are still left with the obvious question: why are only two of the possible eight modes apparent in experiment?
Assuming the ratio of 1–2 and 1–4 adsorbed D2O molecules reflects equilibria between all species, the results in Table 1 clearly suggest that the measurable OD stretch spectral response should be dominated by D2O molecules in the 1–4 configuration – as noted above they should be 107 more abundant than 1–2 structures. However, this still leaves four possible species, OD1–4ads, OD1–4mol-ads, OD1–4surf and OD1–4mol-surf, of which only the first two seem to appear in our measurement. Because a D2O molecule in the 1–4 configuration must be either molecularly or dissociatively adsorbed, for every OD1–4ads there must be an OD1–4surf and for every OD1–4mol-ads OD1–4mol-surf. As a result the absence of all such resonance features cannot be the result of thermodynamics.
As discussed above, the measured VSF intensity, given fixed incident beam angles and polarizations, is a function of molecular orientation. Thus one possibility is that the missing resonances exist, but because of the particular combination of incident beam angles and polarizations as well as fragment orientation our VSF measurement is insensitive to their presence. Using the theory discussed earlier (and in more detail in the ESI†) we have calculated the expected relative VSF response for an OD group, given our experimental configuration, as a function of molecular orientation. These results are shown in Fig. 8. Clearly they suggest that, given the calculated orientation of OD1–4mol-surf, i.e. 112(68)° with respect to the surface normal, it should not appear in our results.
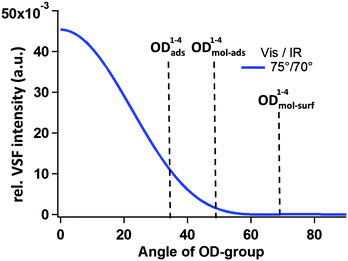 | ||
| Fig. 8 Estimated intensity of the VSF response (using the ppp polarization scheme) as a function of OD orientation given by the angle between OD bond vector and surface normal; details of the underlying model are outlined in the ESI.† The angle for the OD1–4mol-surf is drawn in this scheme at 68 degree, even though given in Table 2 as 112 degree, because the measured IVSF signal is insensitive to changes in OD orientation of 180°. | ||
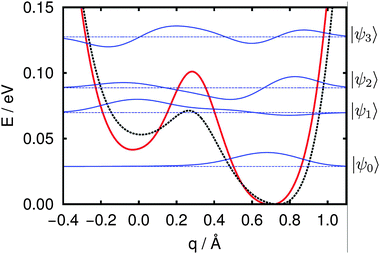
This leaves only the OD1–4surf mode that, if our assignments are correct, we would expect to observe but have not. One possible explanation for this feature's absence is that the uncoupled harmonic oscillator assumption that underlies the frequencies shown in Table 2 does not apply. One scenario in which this approximation would be expected to fail is if the dissociation barrier in the 1–4 configuration is of order one vibrational quanta (1958 cm−1 = 0.24 eV). To evaluate this possibility we calculated the NEB-derived 1–4 dissociation potential using two different exchange–correlation functionals (see Fig. 9).
Here, the linear transit (LT) path between both minima was found to be a suitable coordinate for describing the dissociation reaction:
q = ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) · ·![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) = ( = (![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) − − ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) mol)· mol)·![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) , , | (7) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) denoting any geometry during the course of the reaction,
denoting any geometry during the course of the reaction, ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) mol that of molecularly adsorbed D2O, and with
mol that of molecularly adsorbed D2O, and with ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) as the unit vector pointing from molecularly to dissociatively adsorbed states. Assuming a unitary transformation between the set of N cartesian coordinates {xi} and a set of normal coordinates {qi}, with the above q solely representing the reactive movement of ions during the dissociation process and the other N − 1 coordinates qi being largely constant, the corresponding nuclear LT-Hamiltonian reads:
as the unit vector pointing from molecularly to dissociatively adsorbed states. Assuming a unitary transformation between the set of N cartesian coordinates {xi} and a set of normal coordinates {qi}, with the above q solely representing the reactive movement of ions during the dissociation process and the other N − 1 coordinates qi being largely constant, the corresponding nuclear LT-Hamiltonian reads: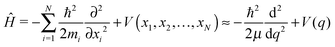 | (8) |
The associated mass μ is then given by the atomic masses mi and the elements ui of the coordinate unit vector:
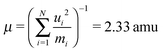 | (9) |
The potential V(q) between molecular and dissociated minimum was again derived using a NEB procedure and extrapolated on both sides to obtain a double-well shape (dotted black line in Fig. 9); further analysis, however, was performed for a potential shape modified according to single-point calculations for the PBE-based geometries but using the HSE06 hybrid functional (solid red line in Fig. 9) in order to improve on the description of the transition state region. The resulting dissociation barrier is only 0.06 eV at the HSE06 level of theory, about three times lower than on the (0001) surface.39
Given this dissociation potential, we found numerical solutions to the vibrational Schrödinger equation by diagonalization of the Hamiltonian according to eqn (8) in a sinc-DVR basis45 (500 grid points on the range [−0.53,1.22] Å). Details of the whole procedure are outlined in ref. 39 (with the only difference that instead of analytic fitting in the present work interpolation of data points was done using cubic splines). The resulting vibrational eigenvalues and wavefunctions are shown in Fig. 9 and clarify why no harmonic OD1–4surf signal can be found in experiment: while the system's ground state is localized, as expected, on the dissociated (right-hand) side of the potential, the first excited state is preferentially molecular in character (localized on the left-hand side of the potential) and the second excited state, has, once again more dissociated. Since the OD1–4surf mode largely corresponds to a change of the system geometry along coordinate q, the calculated eigenvalues strongly suggest the OD stretch vibration of OD1–4surf cannot be described in the normal-mode picture with a frequency of 1958 cm−1 (see Table 2). Instead, it is a transition between a vibrational ground and second excited state, with a frequency of ≈484 cm−1. Clearly a similar failure of the uncoupled harmonic oscillator approximation must also apply to the OD1–4mol-surf mode. Here the lowest transition (first to second excited state) has a frequency of ≈153 cm−1. Two final features are striking about the calculated wavefunctions and eigenvalues: (a) the ground, first and second excited states are sufficiently close in energy that, particularly at the elevated annealing temperatures shown in Fig. 3b, both excited states are likely populated and (b) both excited states are delocalized over the entire width of the potential. If this 1D model of the OD1–4mol-surf and OD1–4surf vibrations captures the surface physical chemistry, this result suggests that during sample thermal treatment a significant portion of interfacial deuterons are spatially delocalized (although this effect is damped at the 135 K temperature of the measurement). Because this delocalization is a result of the anharmonicity of the OD1–4surf potential, and because it would be expected to be larger for protons than deuterons, we expect that for measurements with H2O the degree of delocalization would only increase. We are currently working on addressing both the anharmonicity of these vibrations and their possible delocalization at moderate temperatures experimentally.
We finally note in passing that the exceptionally low dissociation barrier of D2O on the (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface relative to the (0001), in addition to having interesting consequences for surface vibrational spectroscopy, is consistent with our qualitative experimental result that substantially lower dosing times are required to prepare the former surface than the latter.
02) surface relative to the (0001), in addition to having interesting consequences for surface vibrational spectroscopy, is consistent with our qualitative experimental result that substantially lower dosing times are required to prepare the former surface than the latter.
4 Summary and conclusions
We have described water adsorption and dissociation on the oxygen terminated α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface using both experiment, i.e. TPD and VSF spectroscopy, and theory, i.e. periodic-slab DFT calculations. Combining these experimental approaches allows us to produce an oxygen terminated (1
02) surface using both experiment, i.e. TPD and VSF spectroscopy, and theory, i.e. periodic-slab DFT calculations. Combining these experimental approaches allows us to produce an oxygen terminated (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface, adsorb a mixed monolayer of D2O and demonstrate that with increasing temperature molecularly adsorbed D2O appears to desorb while dissociatively, kinetically stabilized, adsorbed D2O remains.
02) surface, adsorb a mixed monolayer of D2O and demonstrate that with increasing temperature molecularly adsorbed D2O appears to desorb while dissociatively, kinetically stabilized, adsorbed D2O remains.
Our DFT based surface model was set up in order to derive a microscopic picture of low water coverage α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) surface chemistry and allows a detailed, microscopic view of this surface speciation. We show that, in the limit of low coverage, D2O adsorption happens via the “1–4” dissociation channel and that this configuration in energetically stabilized by a strong hydrogen bond donated by one OD group to a surface oxygen (while the oxygen in molecular D2O interacts with a surface Al). This stabilization is sufficiently strong that, while the diffusion of molecular D2O or the dissociated deuteron can occur under the conditions of our experiment thermodynamics dictates that other possible configurations should be extremely rare.
02) surface chemistry and allows a detailed, microscopic view of this surface speciation. We show that, in the limit of low coverage, D2O adsorption happens via the “1–4” dissociation channel and that this configuration in energetically stabilized by a strong hydrogen bond donated by one OD group to a surface oxygen (while the oxygen in molecular D2O interacts with a surface Al). This stabilization is sufficiently strong that, while the diffusion of molecular D2O or the dissociated deuteron can occur under the conditions of our experiment thermodynamics dictates that other possible configurations should be extremely rare.
The DFT based model makes it possible to explain why we observe only two, of a possible four, resonances of molecular/dissociated D2O in the 1–4 configuration. Evidently the dissociation barrier, i.e. the barrier separating the OD1–4mol-surf and OD1–4surf species, is sufficiently small, and the OD transition dipole sufficiently parallel to the dissociation coordinate, that both vibrations are strongly anharmonic in character and shifted to frequencies well below our spectral window. To estimate the size of this effect we have solved the vibrational Schrödinger equation along the dissociation coordinate. In addition to quantifying that the fundamental OD stretch transitions of the OD1–4mol-surf and OD1–4surf species should be red shifted by >1500 cm−1 from their frequencies if they were uncoupled harmonic oscillators, this result suggests the deuterons that participate in both species may, at moderate temperatures, be delocalized. Such delocalization, if confirmed by higher level theoretical treatments and experiment, has significant implications for understanding the reactivity of the α-Al2O3(1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02) to water and aqueous phase solutes.
02) to water and aqueous phase solutes.
Acknowledgements
We thank the Deutsche Forschungsgemeinschaft for support of this work through Collaborative Research Center 1109 Understanding of Metal Oxide/Water Systems at the Molecular Scale: Structural Evolution, Interfaces and Dissolution.References
- D. Sparks, Environmental Soil Chemistry, Elsevier Science, 2013 Search PubMed.
- G. E. Brown, Science, 2001, 294, 67–69 CrossRef CAS PubMed.
- J. A. Kelber, Surf. Sci. Rep., 2007, 62, 271–303 CrossRef CAS.
- V. Coustet and J. Jupille, Surf. Sci., 1994, 307–309, 1161–1165 CrossRef CAS.
- J. W. Elam, C. E. Nelson, M. A. Cameron, M. A. Tolbert and S. M. George, J. Phys. Chem. B, 1998, 102, 7008–7015 CrossRef CAS.
- K. C. Hass, W. F. Schneider, A. Curioni and W. Andreoni, Science, 1998, 282, 265–268 CrossRef CAS PubMed.
- P. Liu, T. Kendelewicz, G. E. Brown, Jr., E. J. Nelson and S. A. Chambers, Surf. Sci., 1998, 417, 53–65 CrossRef CAS.
- C. E. Nelson, J. W. Elam, M. A. Cameron, M. Tolbert and S. M. George, Surf. Sci., 1998, 416, 341–353 CrossRef CAS.
- J. Toofan and P. R. Watson, Surf. Sci., 1998, 401, 162–172 CrossRef CAS.
- P. J. Eng, T. P. Trainor, G. E. Brown Jr., G. A. Waychunas, M. Newville, S. R. Sutton and M. L. Rivers, Science, 2000, 288, 1029 CrossRef CAS PubMed.
- C. Niu, C. Shepherd, D. Martini, J. A. Kelber, D. R. Jennison and A. Bogicevic, Surf. Sci., 2000, 465, 163–176 CrossRef CAS.
- H. Kirsch, J. Wirth, Y. Tong, M. Wolf, P. Saalfrank and R. K. Campen, J. Phys. Chem. C, 2014, 13623–13630 CAS.
- T. Kurita, K. Uchida and A. Oshiyama, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155319 CrossRef.
- S. E. Mason, C. R. Iceman, T. P. Trainor and A. M. Chaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125423 CrossRef.
- A. Tougerti, C. Methivier, S. Cristol, F. Tielens, M. Che and X. Carrier, Phys. Chem. Chem. Phys., 2011, 13, 6531–6543 RSC.
- S. Aboud, J. Wilcox and G. E. Brown, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 125407 CrossRef.
- E. Gillet and B. Ealet, Surf. Sci., 1992, 273, 427–436 CrossRef CAS.
- M. Schildbach and A. Hamza, Surf. Sci., 1993, 282, 306–322 CrossRef CAS.
- T. P. Trainor, P. J. Eng, G. E. Brown, I. K. Robinson and M. D. Santis, Surf. Sci., 2002, 496, 238–250 CrossRef CAS.
- M. Sterrer and H.-J. Freund, Catal. Lett., 2013, 143, 375–385 CrossRef CAS.
- X. D. Zhu, H. Suhr and Y. R. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 3047–3050 CrossRef CAS.
- H. Kirsch, X. Zhao, Z. Ren, S. V. Levchenko, M. Wolf and R. K. Campen, J. Catal., 2014, 320, 89–96 CrossRef CAS.
- Y. Tong, J. Wirth, H. Kirsch, M. Wolf, P. Saalfrank and R. K. Campen, J. Chem. Phys., 2015, 142, 054704 CrossRef PubMed.
- C. Hess, M. Bonn, S. Funk and M. Wolf, Chem. Phys. Lett., 2000, 325, 139–145 CrossRef CAS.
- C. D. Bain, P. B. Davies, T. H. Ong, R. N. Ward and M. A. Brown, Langmuir, 1991, 7, 1563–1566 CrossRef CAS.
- B. Busson and A. Tadjeddine, J. Phys. Chem. C, 2009, 113, 21895–21902 CAS.
- H.-F. Wang, W. Gan, R. Lu, Y. Rao and B.-H. Wu, Int. Rev. Phys. Chem., 2005, 24, 191–256 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 124, 154709 CrossRef CAS PubMed.
- Y. Zhao, N. González-Garca and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 2012–2018 CrossRef CAS PubMed.
- B. G. Johnson, C. A. Gonzales, P. M. W. Gill and J. A. Pople, Chem. Phys. Lett., 1994, 221, 100–108 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. Wirth and P. Saalfrank, J. Phys. Chem. C, 2012, 116, 26829–26840 CAS.
- F. Jensen, Introduction to Computational Chemistry, Wiley, 2007 Search PubMed.
- H. Jónsson, G. Mills and K. W. Jacobsen, Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, 1995 Search PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- H. Eyring, Chem. Rev., 1935, 17, 65–77 CrossRef CAS.
- D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96, 1982–1991 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of sample preparation and characterisation, details of VSF spectrometer, review of detailed theory connection measured vibrational sum frequency intensity and molecular orientation and additional parameters describing computed molecular structure. See DOI: 10.1039/c6cp01397j |
| This journal is © the Owner Societies 2016 |