Gas phase complexes of H₃N⋯CuF and H₃N⋯CuI studied by rotational spectroscopy and ab initio calculations: the effect of X (X = F, Cl, Br, I) in OC⋯CuX and H₃N⋯CuX

Abstract

Complexes of H₃N⋯CuF and H₃N⋯CuI have been synthesised in the gas phase and characterized by microwave spectroscopy. The rotational spectra of 4 isotopologues of H₃N⋯CuF and 5 isotopologues of H₃N⋯CuI have been measured in the 6.5–18.5 GHz frequency range using a chirped-pulse Fourier transform microwave spectrometer. Each complex is generated from a gas sample containing NH₃ and a halogen-containing precursor diluted in Ar. Copper is introduced by laser ablation of a solid target prior to supersonic expansion of the sample into the vacuum chamber of the microwave spectrometer. The spectrum of each complex is characteristic of a symmetric rotor and a C_3v geometry in which the N, Cu and X atoms (where X is F or I) lie on the C^a₃ axis. The rotational constant (B₀), centrifugal distortion constants (D_J and D_JK), nuclear spin-rotation (C_bb(Cu) = C_cc(Cu)) constant (for H₃N⋯CuF only) and nuclear quadrupole coupling constants (χ_aa(X) where (X = N, Cu, I)) are fitted to the observed transition frequencies. Structural parameters are determined from the measured rotational constants and also calculated ab initio at the CCSD(T)(F12*)/AVQZ level of theory. Force constants describing the interaction between ammonia and each metal halide are determined from D_J for each complex. Trends in the interaction strengths and geometries of B⋯CuX (B = NH₃, CO) (X = F, Cl, Br, I) are discussed.

---

1. Introduction

Gerry and co-workers demonstrated that B⋯MX complexes, where B is a Lewis base, M is a coinage metal, and X is a halogen atom, can be generated through laser vaporisation of a metal target in the presence of a gas sample undergoing supersonic expansion, then interrogated by microwave spectroscopy.¹ The pure rotational spectra of OC⋯MX (X = F, Cl, Br) were measured and interpreted to determine the geometries of the complexes. An extensive and systematic study of the rotational spectra of B⋯MX complexes, also generated by a combination of laser vaporisation and supersonic expansion, has since been performed. Complexes where the Lewis base is H₂,^2,3 N₂,⁴ CO,^1,5,6 H₂O,⁷ H₂S,⁸ NH₃,^9,10 C₂H₂,^11,12 C₂H₄,^13,14 or c-C₃H₆¹⁵ have been reported. Metal-containing (B⋯MX) complexes have also been investigated by ab initio methods which have explored the nature of bonding interactions and the influence of the halide on the interaction between the metal and the Lewis base.^16–19

This work presents analyses of the rotational spectra of H₃N⋯CuI and H₃N⋯CuF. The structures of the complexes as well as the strengths of interactions between NH₃ and the different CuX (X = F, I) molecules are determined from measured spectroscopic constants and through ab initio calculations. Unlike H₃N⋯CuCl, for which a crystal structure²⁰ was known before its observation in the gas phase, H₃N⋯CuI and H₃N⋯CuF have not been structurally characterised in the condensed phase. The reaction of copper(II) fluoride and copper metal with ammonia has been observed both in gaseous and in anhydrous liquid ammonia.²¹ Among the products obtained were copper(I) fluoride and copper(II) fluoride ammine complexes. It has been suggested that copper(I) fluoride ammine complexes may serve as intermediates that allow the isolation of binary copper(I) fluoride which has not yet been characterized in the solid phase. The results of the present work are compared with those of the previously published reports on H₃N⋯CuCl¹⁰ and OC⋯CuX (X = F, Cl, Br, I).^1,22 Clear trends are identified and described. Legon and co-workers earlier performed systematic studies of hydrogen- and halogen-bonded complexes, B⋯HX²³ and B⋯XY²⁴ (where Y is a halogen atom). The present work compares the properties of H₃N⋯MX with selected H₃N⋯HX and H₃N⋯XY complexes that have been characterised previously.

2. Experimental and theoretical methods

Broadband microwave spectra were measured using a chirped-pulse Fourier-transform microwave (CP-FTMW) spectrometer fitted with a laser ablation source. Detailed descriptions of the spectrometer and laser ablation source are provided in ref. 25 and 26. A gas sample containing ∼4.0% NH₃ and ∼1.5% SF₆ (when generating H₃N⋯CuF) or CF₃I (when generating H₃N⋯CuI) is diluted in argon and prepared at a total pressure of 6 bar. The sample is pulsed (from a Parker-Hannifin Series 9 solenoid valve, using pulse length of 960 μs set using Parker-Hannifin Iota One Valve Driver) into the vacuum chamber of the spectrometer and passes over the surface of a copper rod that is ablated by a Nd:YAG laser pulse (λ = 532 nm, pulse duration of 10 ns, pulse energy of 20 mJ) before undergoing supersonic expansion. A repetition rate of ∼1.05 Hz is employed. The copper rod is continually translated and rotated in order to expose a fresh surface to each laser pulse and to ensure shot-to-shot reproducibility of signal intensities. Isotopically-enriched samples of ¹⁵NH₃ (Sigma-Aldrich, 98% ¹⁵N) and ND₃ (Sigma-Aldrich, 99% D) were used to detect ¹⁵NH₃- and ND₃-containing complexes respectively.

The sequence employed to record broadband microwave spectra involves (i) polarization of the sample by a microwave chirp that sweeps from 6.5 to 18.5 GHz within 1 μs and (ii) recording of the free induction decay of the molecular emission over a subsequent period of 20 μs. The sequence of (i) and (ii) is repeated eight times following each gas sample introduction pulse. The free induction decay (FID) of the polarization is digitized using a 25 Gs s⁻¹ digital oscilloscope after down-mixing against a 19 GHz local oscillator. Frequency domain spectra are obtained through a Fourier transform that uses the high resolution window function (full width at half maximum (FWHM) ∼ 65 Hz) described by Tektronix (details provided as ESI†). The spectra of H₃N⋯^63/65CuF, H₃¹⁵N⋯CuF and D₃N⋯⁶³CuF were averaged for 1500k, 540k and 2520k free induction decays (FIDs) respectively prior to being Fourier transformed. The spectra of H₃N⋯^63/65CuI, H₃¹⁵N⋯CuI and D₃N⋯^63/65CuI were averaged for 660k, 180k and 540k FIDs respectively prior to being Fourier transformed.

Structure optimizations and counter-poise corrected dissociation energies were calculated using the molpro package²⁷ at the CCSD(T)(F12*) level of theory,²⁸ a coupled-cluster method with single and double excitations, explicit correlation,²⁹ and a perturbative treatment of triple excitations.³⁰ Only valence electrons are included in the correlation treatment. A basis set combination consisting of aug-cc-pVQZ on H, N and F atoms and aug-cc-pVQZ-PP on Cu and I atoms was used and will be referred to by AVQZ. ECP-10-MDF^31,32 and ECP-28-MDF^33,34 were used on Cu and I respectively to account for scalar relativistic effects. For the density fitting approximation used to accelerate the CCSD(T)(F12*) calculation, the respective def2-QZVPP basis sets were employed for the MP2³⁵ and Fock³⁶ terms. For the complementary auxiliary basis required for the F12 treatment,³⁷ the def2-TZVPP MP2 density fitting basis sets were used.³⁸ Force constants were calculated from the second derivative of the energy with respect to the internal coordinates using the GAUSSIAN 09 package³⁹ at the MP2 level of theory. A basis set combination consisting of aug-cc-pVTZ on H, N and F atoms, aug-cc-pVTZ-PP on Cu and I atoms was used.

3. Results

3.1 Spectral analysis and assignment

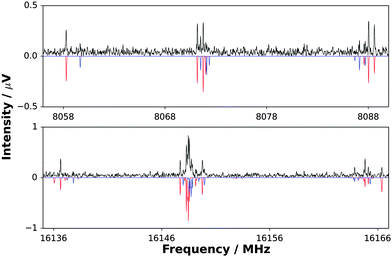
Fig. 1 displays sections of the broadband spectrum measured when probing a gas sample containing CF₃I, NH₃ and argon that interacts with the plasma plume produced by ablation of the copper rod. The most intense transitions are observed for CF₃I⁴⁰ while those of NH₃⋯Ar,⁴¹ CF₃I⋯NH₃,⁴² IF⁴³ and CuI⁴⁴ are also strong. The spectrum of H₃N⋯CuI was identified through the analysis of groups of transitions, significantly weaker in intensity than those of the species listed above, which are separated by frequency increments of ∼2.2 GHz. Distinctive and extensive hyperfine splittings are present in each J′ → J′′ transition as expected for a complex that contains copper and iodine nuclei (which have I = 3/2 and 5/2 respectively). A different range of chemical products was observed, including NH₃⋯SF₆,⁴⁵ NH₃⋯Ar⁴¹ and (NH₃)₂⁴⁶ after exchanging the gas sample for another that contains SF₆, NH₃ and argon. The frequency of the J′ → J′′ = 1 → 0 transition of CuF lies above the upper limit of the spectrometer. Consecutive J′ → J′′ transitions of H₃N⋯CuF, which have lower intensities than those of NH₃⋯SF₆, NH₃⋯Ar and (NH₃)₂, were observed at intervals of ∼8.0 GHz and display hyperfine structure arising from the presence of the copper nucleus (I = 3/2). The J′ → J′′ = 1 → 0 and 2 → 1 transitions of H₃N⋯CuF are shown in Fig. 2. The spectra observed for each of H₃N⋯CuF and H₃N⋯CuI contain only a-type transitions, consistent with the C_3v geometries (Fig. 3) anticipated for each of these complexes and previously observed for each of H₃N⋯AgCl⁹ and H₃N⋯CuCl.¹⁰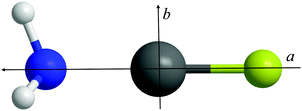

Fig. 1 Top panel: The broadband rotational spectrum (660k FIDs) obtained while using a gas sample containing small concentrations of CF₃I and NH₃ diluted in argon. (a) J′ → J′′ = 7 → 6 transitions of H₃N⋯⁶³CuI. (b) J′ → J′′′ = 4 → 3 transitions of ⁶³CuI. (c) J′ → J′′ = 6 → 5 transitions of H₃N⋯ICF₃. (d) J′ → J′′ = 2 → 1 transition in the Σ_0a state of NH₃⋯Ar.

Fig. 2 Top panel: A section of the broadband spectrum showing J′ → J′′ = 1 → 0 transitions of H₃N⋯CuF (black trace) and a simulation of the transitions of H₃N⋯⁶³CuF and H₃N⋯⁶⁵CuF (red and blue traces respectively). Bottom panel: A section of the broadband spectrum showing J′ → J′′ = 2 → 1 transitions of H₃N⋯CuF (black trace) and a simulation of the transitions of H₃N⋯⁶³CuF and H₃N⋯⁶⁵CuF (red and blue traces respectively).

Fig. 3 The structure of H₃N⋯CuF. N, Cu and F are the blue, grey and green spheres respectively. The a and b principal axes are shown.

Western's PGOPHER⁴⁷ was used to fit parameters in the Hamiltonian shown below to the observed transitions of each complex;

H = H_R − ⅙Q(Cu):∇E(Cu) − ⅙Q(I):∇E(I) − ⅙Q(N):∇E(N) + I_Cu·C_Cu·J (1)

where H_R is the Hamiltonian of a semi-rigid, prolate symmetric rotor. The second, third, and fourth terms on the right hand side describe the coupling of the nuclear electric quadrupole moment with the electric field gradient at each of the Cu, I and N nuclei (respectively). The interaction is given by the scalar (or inner) product of the nuclear quadrupole moment dyadic, Q, and the dyadic of the electric field gradient arising from extra nuclear charges, ∇E. The nuclear quadrupole coupling constants are denoted by χ_aa(X) (where X is Cu, N or I) and can be determined from the nuclear quadrupole hyperfine structure. The last term describes the magnetic hyperfine interaction between the nuclear magnetic moment of Cu and the effective magnetic field generated by the rotation of the molecular framework. An attempt to fit [C_bb(Cu) = C_cc(Cu)] for H₃¹⁴N⋯^63/65CuI yielded a result with uncertainty similar to the value of the parameter. It was therefore not included in the parameter set used in the final fits. The coupling scheme used for H₃¹⁴N⋯^63/65CuI and D₃¹⁴N⋯⁶³CuI is F₁ = J + I_I, F₂ = F₁ + I_Cu and F = F₂ + I_N. For H₃¹⁴N⋯^63/65CuF and D₃¹⁴N⋯⁶³CuF, the coupling scheme is F₁ = J + I_Cu and F = F₁ + I_N. Given that I_N = 1/2 for ¹⁵N and that the described experiments do not resolve any hyperfine splittings introduced by the ¹⁵N nucleus, the term of eqn (1) that applies to the nitrogen atom is omitted when fitting the spectra of isotopologues containing ¹⁵N. Hyperfine splittings introduced by the hydrogen and fluorine nuclei were also not resolved by the present experiments. In every case, the A₀ rotational constant is fixed to the value of C₀ for free ammonia for the purpose of simulating intensities. The results of spectroscopic fits are provided in Tables 1 and 2 for H₃N⋯CuF and H₃N⋯CuI respectively.

Table 1 Determined spectroscopic constants of 4 isotopologues of H₃N⋯CuF

	H3N⋯^63CuF	H3N⋯^65CuF	D3N⋯^63CuF	H3^15N⋯^63CuF
a Numbers in parentheses are one standard deviation in units of the last significant figure. b Value in square brackets is fixed to the result for H3N⋯^63CuF. c The value in square brackets has been determined by scaling Cbb = Ccc for H3N⋯^63CuF by the ratio of the magnetic moments of the ^65Cu and ^63Cu nuclei. d N is the number of fitted transitions, σr.m.s. denotes the r.m.s. deviation of the fit.
B 0/MHz	4037.4554(19)^a	4037.513(10)	3570.3874(16)	3926.6944(36)
D J /kHz	1.20(25)	2.9(13)	[1.20]^b	1.04(48)
χ aa (Cu)/MHz	66.196(12)	61.183(61)	66.441(68)	66.212(21)
χ aa (N)/MHz	−2.717(15)	−2.787(90)	−2.776(41)	—
[Cbb(Cu) = Ccc(Cu)]/kHz	18.9(12)	[20.2]^c	21.7(54)	17.3(23)
N	18	8	8	7
σ r.m.s. /kHz	7.4	23.8	15.8	9.1

---

Table 2 Determined spectroscopic constants of 5 isotopologues of H₃N⋯CuI

	H3N⋯^63CuI	H3N⋯^65CuI	D3N⋯^63CuI	D3N⋯^65CuI	H3^15N⋯^63CuI
a Numbers in parentheses are one standard deviation in units of the last significant figure. b Numbers in square brackets have been fixed. c N is the number of fitted transitions. d σ r.m.s. denotes the r.m.s. deviation of the fit.
B 0/MHz	1162.03613(67)^a	1153.4533(19)	1064.91348(73)	1058.27044(50)	1135.26715(70)
D J /kHz	0.1289(73)	0.097(17)	0.0907(72)	[0.097]^b	0.1048(63)
D JK /kHz	12.96(26)	9.73(80)	9.66(54)	10.91(95)	14.15(47)
χ aa (Cu)/MHz	62.943(95)	58.70(44)	63.75(17)	58.99(41)	62.55(29)
χ aa (N)/MHz	−2.28(11)	−2.18(41)	−2.59(19)	−2.82(18)	—
χ aa (I)/MHz	−613.99(28)	−613.62(77)	−612.86(49)	−614.32(77)	−614.25(43)
N	71	35	46	14	32
σ r.m.s. /kHz	13.2	20.3	21.0	14.6	12.2

---

All spectra were measured using a copper sample containing ⁶³Cu and ⁶⁵Cu isotopes in their natural abundances. The intensities of the spectra of all isotopologues are consistent with the natural fractional abundances of ⁶³Cu and ⁶⁵Cu which are 69% and 31% respectively. Isotopically-enriched samples were used to allow measurement and assignment of the spectra of D₃N⋯^63/65CuI, H₃¹⁵N⋯⁶³CuI, D₃N⋯⁶³CuF and H₃¹⁵N⋯⁶³CuF. Given that only one isotope of each of fluorine and iodine is available, isotopic substitution was not possible at the halogen atom. Confirmation that the molecular carriers of the observed spectra contain copper was obtained through comparison of the nuclear quadrupole coupling constants, χ_aa(Cu) = eQq_aa(Cu), for the various isotopologues. This nuclear quadrupole coupling constant provides a measure of the strength of the coupling of the electric field gradient (q_aa) at the Cu nucleus along the axis a with the ‘conventional’ nuclear electric quadrupole moment eQ, defined as eQ = 〈I,I|Q_zz|I,I〉. Note that both the dyadic Q and its element Q_zz contain the nuclear charge density while the constant Q does not; hence multiplication by the charge of a proton e on the left-hand side of the definition. For any given isotopologue, the electric field gradient is invariant to isotopic exchange (to a very good first approximation) even in the zero-point state so the ratio of the values of χ_aa(⁶³Cu) in B⋯⁶³CuX and χ_aa(⁶⁵Cu) in B⋯⁶⁵CuX should be equal to the ratio of the nuclear electric quadrupole moments of ⁶³Cu and ⁶⁵Cu. This condition is satisfied with the required level of precision for each pair of isotopologues for which the ratio can be calculated. The fitted rotational constant of H₃N⋯⁶³CuF is slightly smaller than that of H₃N⋯⁶⁵CuF. This implies that the Cu atom is sufficiently close to the centre of mass of this complex that any decrease in rotational constant (which would be required under the assumption of a rigid molecular framework, if Cu is not exactly at the centre of mass) is compensated by zero point effects. The rotational constant of H₃N⋯⁶³CuI is greater than that of H₃N⋯⁶⁵CuI by about 10 MHz. For H₃N⋯⁶³CuI, comparing the intensities of transitions having K = 1 with those having K = 0, the former are observed to be significantly more intense than would be expected at a rotational temperature of 2 K. This enhanced population of K = 1 states has been discussed previously¹⁰ and is explained by a reduced efficiency of collisional relaxation when the symmetry of a complex allows for hydrogen atoms to be exchanged by a C₃ rotation about the inertial a axis. K = 0 and K = 1, 2 transitions belong to different symmetry species with relaxation taking place only within the two stacks, such that K = 0 and K = 1 transitions become equal in intensity because K = 0 transitions have twice the statistical weight of each of K = 1, 2. This is consistent with the ratio of the observed intensities of K = 0 and K = 1 transitions of H₃N⋯CuI. Transitions having K = 2 were not observed for either H₃N⋯CuF or H₃N⋯CuI. Transitions having K = 1 were not observed for H₃N⋯CuF for which only J′ → J′′ = 1 → 0 and 2 → 1 transitions are within the frequency range probed by the spectrometer.

3.2 Molecular geometry

By analogy with the geometries previously determined for the H₃N⋯AgCl⁹ and H₃N⋯CuCl¹⁰ complexes, it will initially be assumed that H₃N⋯CuX (X = F, I) adopt a C_3v symmetry in which N, Cu and X are located on the inertial a axis while interconnected in the geometry shown in Fig. 3. This assumption is consistent with the observations of a-type transitions and of a copper atom positioned close to the centre of mass in each of H₃N⋯CuF and H₃N⋯CuI. From this starting point, effective ground state (r₀) and substitution (r_s) geometries will be determined by fitting parameters in the model geometry (Fig. 3) to the experimentally-measured rotational constants. Ab initio calculations have been performed to establish equilibrium (r_e) geometries and other molecular properties.

The STRFIT⁴⁸ program is used to fit the r₀ geometries. The experimental results do not allow independent determination of the N–H bond length, r(N–H), and the angle defining the positions of the hydrogen atoms, ∠(H–N–Cu). For this reason, r(N–H) is held fixed while the r(Cu–X), r(Cu–N) and ∠(H–N–Cu) structural parameters are fitted. The assumed values of r(N–H) in the r₀ geometries of H₃N⋯CuF and H₃N⋯CuI are established by; (1) calculating the difference between the r₀ value of r(N–H) in isolated NH₃ and the r_e value of the same parameter calculated at the CCSD(T)(F12*)/AVQZ level; (2) adding the result of (1) to the r_e value calculated for r(N–H) in each of H₃N⋯CuF and H₃N⋯CuI respectively. Large zero point changes occur in isolated NH₃ upon substitution of hydrogen atoms for deuterium. A shrinkage of 0.0011 Å in r(N–H) and an enlargement of 0.04 degrees in ∠(H–N–Cu) are observed. These changes are assumed to occur in H₃N⋯CuF and H₃N⋯CuI and are accounted for when fitting structural parameters. Fixing the r(N–H) distance as described above allows r(Cu–X), r(Cu–N) and ∠(H–N–Cu) to be determined with reasonable accuracy. Given that no isotopic substitution is available at either halogen atom, the uncertainties listed in Table 3 will be underestimated but the results agree satisfactorily with the results of the ab initio calculations.

Table 3 r _s, r₀ and ab initio r_e structures and the corresponding principal axis coordinates of H₃N⋯CuF and H₃N⋯CuI

	r 0		r s		r e(CCSD(T)(F12*)/AVQZ)
	H3N⋯CuF	H3N⋯CuI	H3N⋯CuF	H3N⋯CuI	H3N⋯CuF	H3N⋯CuI
a Numbers in parentheses are one standard deviation in units of the last significant figure. b Numbers in square brackets have been fixed at values determined as described under “Molecular Geometry”. c An imaginary number was obtained as the Kraitchman coordinate.
r(Cu–X)/Å	1.74919(55)^a	2.35525(46)	—	—	1.7372	2.3574
r(Cu–N)/Å	1.89276(61)	1.9357(13)	1.89(5)	1.9361(13)	1.8804	1.9226
r(H–N)/Å	[1.0187]^b	[1.0185]	[1.0180]	[1.0178]	1.0145	1.0143
∠(H–N–Cu)/°	111.462(26)	111.430(54)	111.500(50)	111.535(30)	111.746	111.811
a Cu/Å	−0.00124(20)	1.28011(37)	0.00(5)^c	1.27874(121)	0.0014945	1.2825
a X/Å	−1.75043(35)	−1.07511(9)	—	—	−1.7387	−1.0750
a N/Å	1.89152(41)	3.21585(88)	1.89128(79)	3.21480(47)	1.8789	3.2051
a H/Å	2.26426(12)	3.58797(26)	—	—	2.2548	3.5819
b H/Å	0.94806(17)	0.94809(34)	—	—	0.94230	0.94170

---

The a-axis coordinates of Cu and N can also be determined by a (r_s) substitution method.⁴⁹ The equation shown below is appropriate for an atom located on the symmetry axis of a symmetric rotor;

ΔI_b is the change in the moment of inertia about the b inertial axis upon substitution, μ is the reduced mass for the isotopic substitution and is given by where M is the mass of the isotopologue selected as parent and Δm is the change in mass upon substitution. The signs assigned to coordinates are those yielding bond lengths consistent with the ab initio calculations within acceptable precision limits.

When using eqn (2) the a coordinate is defined with respect to the principal axis system of the parent isotopologue and ∠(H–N–Cu) and r(N–H) cannot be independently determined for either H₃N⋯CuF or H₃N⋯CuI. The scaling procedure applied earlier to fix r(N–H) when fitting an r₀ geometry is now used to fix an r_s value. In this case, the difference between the r_s and r_e values of r(N–H) in free NH₃ is added to the r_e value calculated for r(N–H) in H₃N⋯CuX to establish the value of r(N–H) in the r_s geometry. Thus, a value of ∠(H–N–Cu) is determined using the equation provided in ref. 50. The uncertainties of r_s coordinates are calculated using δa = 0.0015/|a| as recommended by Costain.⁵¹ All structural parameters and nuclear coordinates are provided in Table 3 alongside those of H₃N⋯CuCl. The lack of an isotopic substitution at the halogen atom prevents the determination of an r_s coordinate for the halogen atom. r_s coordinates determined from Kraitchman's equations⁵² are typically closer to r_e structural parameters than r₀ values owing to partial cancellation of zero point effects when r_s coordinates are calculated.⁵³ From Table 3 it can be seen that r(N–Cu) increases with increasing mass of the halogen atom of H₃N⋯CuX. The value of ∠(H–N–Cu) is essentially independent of the halogen atom.

3.3 Interaction strength and ionicity

The strength of the interaction between NH₃ and CuX can be assessed with reference to the dissociation energy for the H₃N⋯CuX → NH₃ + CuX reaction and also the force constant of the N⋯Cu bond. Ab initio calculations of both these quantities have been performed. As shown in Table 4, the dissociation energy of H₃N⋯CuX decreases with increasing mass of the halogen atom with the highest result being 197 kJ mol⁻¹ for the H₃N⋯CuF complex.

Table 4 Experimental and ab initio calculated force constants k_σ, and ab initio calculated dissociation energies

	F 22 = kσ(exp.)/[N m^−1]	k σ(MP2/AVTZ)/[N m^−1]	D e(CCSD(T)(F12*)/AVQZ)/[kJ mol^−1]
a Determined from DJ of the H3N⋯^63CuF isotopologue. b Determined from DJ of the D3N⋯^63Cu^35Cl isotopologue. c Determined from DJ of the H3N⋯^63CuI isotopologue.
H3N⋯CuF	210(70)^a	242	197
H3N⋯CuCl	170(60)^b	219	183
H3N⋯CuI	111(33)^c	201	168

---

The results of the ab initio calculations of the force constants, k_σ, follow the same trend with k_σ(N⋯Cu) of H₃N⋯CuF found to be 242 N m⁻¹. The ab initio results for the k_σ(N⋯Cu) can be compared with others determined from the experimental data as shown in Table 4. The experimentally-determined force constants are calculated by applying a model⁵⁴ which accounts for contributions to the centrifugal distortion constants from both the Cu–X and N⋯Cu bonds. The force constants appropriate to the Cu–X and N⋯Cu bonds are denoted by F₁₁ and F₂₂ respectively in eqn (3);

where m₁ and m₂ are the masses of the halogen and copper atoms respectively. The principal axis coordinates of the halogen and copper atoms are a₁ and a₂ respectively. This model allows the calculation of either F₁₁ or F₂₂ provided the other is known. Even where neither parameter is accurately known, a good estimate of one will allow an approximate value and uncertainty limits to be assigned to the other.

For each of H₃N⋯CuF, H₃N⋯CuCl and H₃N⋯CuI, it can initially be assumed that F₁₁ is equal to k_σ of the appropriate, isolated metal halide diatomic.^44,55,56 The r₀ coordinates and moments of inertia (I_bb) calculated from the ground state rotational constants (B₀) of the various complexes are then used to determine the F₂₂ values. In the limit of a rigid Cu–X bond, F₁₁ tends to infinity and F₂₂ approaches an asymptotic value. Where F₁₁ ≫ F₂₂, any change in the assumed value of F₁₁ induces only a very small change in the determined value of F₂₂. As shown in Fig. 4, the assumption that the various F₁₁ are reasonably approximated by k_σ for the isolated metal halides (k_σ(Cu–F) = 333 N m⁻¹; k_σ(Cu–I) = 172 N m⁻¹), implies that the bond between the metal and halogen atoms is significantly more rigid than that between the metal and the nitrogen atoms, in each of H₃N⋯CuF and H₃N⋯CuI. After propagating the uncertainty in the measured value of D_J, the assumption that F₁₁ of H₃N⋯CuI = 172 ± 5 N m⁻¹ implies F₂₂ = 111(33) N m⁻¹ for H₃N⋯CuI where the dominant contribution is the uncertainty in D_J. An assumed value of F₁₁ for H₃N⋯CuF of 333 ± 10 N m⁻¹ would imply that F₂₂ falls within a narrow range between 202 and 213 N m⁻¹. However, the uncertainty in the measured value of D_J again makes the dominant contribution and F₂₂ = 210(70) N m⁻¹ after propagation of the uncertainty in D_J. The level of agreement between the experimentally-determined results and those calculated ab initio is closest for H₃N⋯CuF and H₃N⋯CuCl which possess the most rigid MX bonds. It is apparent from both the force constants and the dissociation energies that the strengths of N⋯Cu bonds formed between NH₃ and MX are in the order H₃N⋯CuF > H₃N⋯CuCl > H₃N⋯CuI.

Fig. 4 Plot to illustrate the variation of F₂₂ as a function of the assumed value of F₁₁ for each of H₃N⋯CuF and H₃N⋯CuI. The values of k_σ for the isolated CuF and CuI molecules, assumed equal to F₁₁ in the respective H₃N⋯CuF and H₃N⋯CuI complexes, are marked with a cross (X).

Two types of hyperfine interaction have been included in the Hamiltonian. These are the nuclear quadrupole coupling and nuclear spin-rotation interactions. The former allows the determination of the nuclear quadrupole coupling constant, eQq(X), for X = ¹⁴N, ^63/65Cu and I as appropriate for each isotopologue. The term in eQq_aa(X) represents the electric field gradient with respect to the symmetry axis at atom X. Applying the Townes–Dailey model^57,58 to interpret the eQq(I) value of H₃N⋯CuI, the ionicity (i_c) of the Cu–I bond is calculated to be 0.73 from , where eQq_(5,1,0)(I) is the coupling constant that would result from the presence of an unpaired electron in the 5p_z orbital of the isolated atom and has a value of 2292.71 MHz.⁵⁹ The Townes–Dailey model cannot be readily applied to the analysis of eQq values of Cu and N.

4. Conclusions

The spectra of H₃N⋯CuF and H₃N⋯CuI are each consistent with the C_3v geometry illustrated in Fig. 3. Quantitative details of the geometries and measured nuclear quadrupole coupling constants of the H₃N⋯CuX series are compared with results from other B⋯CuX in Table 5. The r(Cu–N) distances determined for H₃N⋯CuF and H₃N⋯CuI are consistent with expectations following the earlier study of H₃N⋯CuCl and also with the trend established for OC⋯CuX. r(Cu–N) lengthens on substituting a lighter by a heavier halogen atom and is longer in H₃N⋯CuI than in H₃N⋯CuF by 0.043(2) Å. A very similar difference is observed between r(Cu–C) in OC⋯CuF and the same parameter in OC⋯CuI. The trend observed earlier for the Ar⋯CuX⁶⁰ series involved greater incremental changes on substitution of the halogen atom. r(Cu–Ar) in Ar⋯CuF is 0.077(3) Å shorter than the same parameter in Ar⋯CuBr. The attachment of an isolated CuX species to either CO or NH₃ to form B⋯CuX causes a change in r(Cu–X). The Cu–F bonds of H₃N⋯CuF and OC⋯CuF shrink slightly on formation of these complexes from the isolated NH₃/CO and CuX sub-units. In contrast, r(Cu–X) in the analogous B⋯CuCl, B⋯CuBr and B⋯CuI species extend slightly on complex formation. The difference between r(Cu–X) in B⋯CuX and in the corresponding CuX diatomic is denoted by Δr in Table 5 for H₃N⋯CuX and OC⋯CuX. For both B = CO and B = NH₃, Δr is greatest for the iodide. Recent works have described significant changes in the geometry of C₂H₂ when it attaches to MX to form a T-shaped C₂H₂⋯MX complex. Much smaller changes in the bond length of carbon monoxide were identified where OC⋯CuX and OC⋯AgX form from their constituent sub-units. At the level of precision of the present experiments and a previous work, the bond angle within NH₃ does not change significantly when the molecule attaches to MX to form either H₃N⋯CuX or H₃N⋯AgX.

Table 5 χ _aa (⁶³Cu), χ_aa(X), r₀(Cu–N/O) and Δr for OC⋯CuX, H₃N⋯CuX and CuX

	H3N⋯MX		OC⋯MX		MX^a
	χ aa (M)/MHz	χ aa (X)/MHz	χ aa (M)/MHz	χ aa (X)/MHz	χ aa (M)/MHz	χ aa (X)/MHz
a Ref. 44, 55, 56 and 61–64. b Ref. 24 and references therein. c Δr denotes the change in r(Cu–X) when B⋯MX form from isolated B and MX units.
CuF	66.196(12)	—	75.406(19)	—	21.956	—
CuCl	66.629(24)	−23.041(34)	70.8323(210)	−21.4735(22)	16.169	−32.127
CuBr	—	—	67.534(12)	171.600(18)	12.851	261.180
CuI	62.943(95)	−613.99(28)	64.504(3)	−593.465(9)	7.901(1)	−938.377(1)
HCl	—	−47.607(9)^b	—	−52.086(9)^b	—	−67.6189(5)
HI	—	−1324.891(8)^b	—	−1346.238(18)^b	—	−1828.286(9)
ICl	−3073.118(6)^b	−68.927(3)^b	−2953.798(10)^b	−79.837(6)^b	−2927.859(2)	−85.887(3)
BrCl	915.55(2)^b	−86.05(1)^b	875.835(5)^b	−97.615(3)^b	875.309(1)	−102.450(2)

---

	r 0(Cu–N)/Å	Δr/Å	r 0(Cu–C)/Å	Δr/Å
CuF	1.89282(63)	−0.0071(6)^c	1.7639(4)	−0.0198(3)^c
CuCl	1.9183(16)	0.0073(7)	1.796(1)	0.0017(7)
CuBr	—	—	1.8022(9)	0.006(4)
CuI	1.9357(13)	0.0147(5)	1.8154(9)	0.0157(4)

---

Trends in the OC⋯CuX and H₃N⋯CuX series can also be examined from the perspective of the measured nuclear quadrupole coupling constants. Changes in χ_aa for the metal and halogen atoms provide insight into the extent of electric charge redistribution when a complex forms from its component units. The determined χ_aa of OC⋯CuX and H₃N⋯CuX are compared with those for isolated MX species and for selected hydrogen- and halogen-bonded complexes in Table 5. The fractional changes in χ_aa(M) and χ_aa(X) on formation of the complex from the isolated sub-units, B and MX, are greater for OC⋯CuX than for H₃N⋯CuX or Ar⋯CuX. The opposite trend is observed for the hydrogen-bonded complexes, OC⋯HX and H₃N⋯HX. The described differences between the B⋯MX, B⋯HX²³ and B⋯XY²⁴ series arise because the properties of hydrogen- and halogen-bonded complexes are governed mainly by electrostatic interactions whereas the binding between OC or NH₃ and CuX has a significant covalent component. It has been shown that the ionicity of the Cu–X bond of OC⋯CuX decreases with increasing mass of the halogen atom. An ionicity of 0.73 is determined for H₃N⋯CuI during the present work. This is lower than the ionicity of 0.79 determined for H₃N⋯CuCl and therefore consistent with the trend identified earlier for the OC⋯CuX series.

Acknowledgements

The authors thank the EPSRC and the School of Chemistry at Newcastle University for the award of a DTA postgraduate studentship to D. M. B., the European Research Council for the postdoctoral fellowships awarded to S. L. S. and D. P. Z., and for project funding (Grant No. CPFTMW-307000). D. P. Z. also thanks Newcastle University for a SAgE Research Fellowship. A. C. L. thanks the University of Bristol for a Senior Research Fellowship and Newcastle University for a Visiting Professor award. D. P. T. is pleased to acknowledge the Royal Society for the award of a University Research Fellowship. We are also grateful to the EPSRC UK National Service for Computational Chemistry Software (NSCCS) at Imperial College London.

References

1. N. R. Walker and M. C. L. Gerry, Inorg. Chem., 2001, 40, 6158–6166.
2. D. J. Frohman, G. S. Grubbs, Z. Yu and S. E. Novick, Inorg. Chem., 2013, 52, 816–822.
3. G. S. Grubbs, D. A. Obenchain, H. M. Pickett and S. E. Novick, J. Chem. Phys., 2014, 141, 114306.
4. S. G. Francis, S. L. Matthews, O. K. Poleshchuk, N. R. Walker and A. C. Legon, Angew. Chem., Int. Ed., 2006, 45, 6341–6343.
5. N. R. Walker and M. C. L. Gerry, Inorg. Chem., 2002, 41, 1236–1244.
6. C. J. Evans, L. M. Reynard and M. C. L. Gerry, Inorg. Chem., 2001, 40, 6123–6131.
7. V. A. Mikhailov, F. J. Roberts, S. L. Stephens, S. J. Harris, D. P. Tew, J. N. Harvey, N. R. Walker and A. C. Legon, J. Chem. Phys., 2011, 134, 134305.
8. N. R. Walker, D. P. Tew, S. J. Harris, D. E. Wheatley and A. C. Legon, J. Chem. Phys., 2011, 135, 014307.
9. V. A. Mikhailov, D. P. Tew, N. R. Walker and A. C. Legon, Chem. Phys. Lett., 2010, 499, 16–20.
10. D. M. Bittner, D. P. Zaleski, S. L. Stephens, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2015, 142, 144302.
11. S. L. Stephens, W. Mizukami, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2012, 137, 174302.
12. D. P. Zaleski, S. L. Stephens, D. P. Tew, D. M. Bittner, N. R. Walker and A. C. Legon, Phys. Chem. Chem. Phys., 2015, 17, 19230–19237.
13. S. L. Stephens, D. M. Bittner, V. A. Mikhailov, W. Mizukami, D. P. Tew, N. R. Walker and A. C. Legon, Inorg. Chem., 2014, 53, 10722–10730.
14. S. L. Stephens, D. P. Tew, V. A. Mikhailov, N. R. Walker and A. C. Legon, J. Chem. Phys., 2011, 135, 024315.
15. D. P. Zaleski, J. C. Mullaney, D. M. Bittner, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2015, 143, 164314.
16. Q. Wang, B. Zhang and Z. Huang, Chem. Phys. Lett., 2014, 614, 5–9.
17. G. Zhang, H. Yue, F. Weinhold, H. Wang, H. Li and D. Chen, ChemPhysChem, 2015, 16, 2424–2431.
18. G. Zhang, X. Zhao and D. Chen, J. Phys. Chem. A, 2013, 117, 10944–10950.
19. H. Li, Q. Li, R. Li, W. Li and J. Cheng, J. Chem. Phys., 2011, 135, 074304.
20. G. Margraf, J. W. Bats, M. Bolte, H.-W. Lerner and M. Wagner, Chem. Commun., 2003, 956–957.
21. P. Woidy, A. J. Karttunen, M. Widenmeyer, R. Niewa and F. Kraus, Chem. – Eur. J., 2015, 21, 3290–3303.
22. S. G. Batten and A. C. Legon, Chem. Phys. Lett., 2006, 422, 192–197.
23. A. C. Legon and D. J. Millen, Faraday Discuss. Chem. Soc., 1982, 73, 71–87.
24. A. C. Legon, Angew. Chem., Int. Ed., 1999, 38, 2686–2714.
25. S. L. Stephens, W. Mizukami, D. P. Tew, N. R. Walker and A. C. Legon, J. Chem. Phys., 2012, 136, 064306.
26. D. P. Zaleski, S. L. Stephens and N. R. Walker, Phys. Chem. Chem. Phys., 2014, 16, 25221–25228.
27. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253,  DOI:10.1002/wcms.82.
28. C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102.
29. C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4–74.
30. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
31. A. K. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296.
32. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872.
33. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
34. I. S. Lim, P. Schwerdtfeger, B. Metz and H. Stoll, J. Chem. Phys., 2005, 122, 104103.
35. C. Hattig, Phys. Chem. Chem. Phys., 2005, 7, 59–66.
36. F. Weigend, J. Comput. Chem., 2008, 29, 167–175.
37. E. F. Valeev, Chem. Phys. Lett., 2004, 395, 190–195.
38. A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597.
39. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
40. S. L. Stephens and N. R. Walker, J. Mol. Spectrosc., 2010, 263, 27–33.
41. D. D. Nelson, G. T. Fraser, K. I. Peterson, K. Zhao, W. Klemperer, F. J. Lovas and R. D. Suenram, J. Chem. Phys., 1986, 85, 5512–5518.
42. S. L. Stephens, N. R. Walker and A. C. Legon, Phys. Chem. Chem. Phys., 2011, 13, 20736–20744.
43. H. S. P. Müller and M. C. L. Gerry, J. Chem. Phys., 1995, 103, 577–583.
44. S. G. Batten, A. G. Ward and A. C. Legon, J. Mol. Struct., 2006, 780–781, 300–305.
45. D. M. Bittner, D. P. Zaleski, S. L. Stephens, N. R. Walker and A. C. Legon, ChemPhysChem, 2015, 16, 2630–2634.
46. D. D. Nelson, G. T. Fraser and W. Klemperer, J. Chem. Phys., 1985, 83, 6201–6208.
47. C. M. Western, PGOPHER, a Program for Simulating Rotational, Vibrational and Electronic Structure, University of Bristol, http://pgopher.chm.bris.ac.uk.
48. Z. Kisiel, J. Mol. Spectrosc., 2003, 218, 58–67.
49. C. C. Costain, J. Chem. Phys., 1958, 29, 864–874.
50. A. Chutjian, J. Mol. Spectrosc., 1964, 14, 361–370.
51. C. Costain, Trans. Am. Crystallogr. Assoc., 1966, 2, 157–164.
52. J. Kraitchman, Am. J. Phys., 1953, 21, 17–24.
53. J. K. G. Watson, A. Roytburg and W. Ulrich, J. Mol. Spectrosc., 1999, 196, 102–119.
54. D. M. Bittner, N. R. Walker and A. C. Legon, J. Chem. Phys., 2016, 144, 074308.
55. R. J. Low, T. D. Varberg, J. P. Connelly, A. R. Auty, B. J. Howard and J. M. Brown, J. Mol. Spectrosc., 1993, 161, 499–510.
56. J. Hoeft, F. J. Lovas, E. Tiemann and T. Törring, Z. Naturforsch., A: Phys. Sci., 1970, 25, 35–39.
57. C. H. Townes and B. P. Dailey, J. Chem. Phys., 1949, 17, 782–796.
58. B. P. Dailey and C. H. Townes, J. Chem. Phys., 1955, 23, 118–123.
59. W. Gordy and R. L. Cook, Microwave Molecular Spectra, Wiley, New York, 1984.
60. C. J. Evans and M. C. L. Gerry, J. Chem. Phys., 2000, 112, 9363–9374.
61. F. H. de Leeuw and A. Dymanus, J. Mol. Spectrosc., 1973, 48, 427–445.
62. E. Herbst and W. Steinmetz, J. Chem. Phys., 1972, 56, 5342–5346.
63. R. E. Willis and W. W. Clark, J. Chem. Phys., 1980, 72, 4946–4950.
64. F. A. Van Dijk and A. Dymanus, Chem. Phys. Lett., 1968, 2, 235–236.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp01368f

‡ Current address: Chemistry Department, University of Manitoba, Winnipeg, MB R3T 2N2, Canada.

§ Current address: Argonne National Laboratory, Chemical Sciences & Engineering, 9700 S. Cass Ave., Bldg. 200, Lemont, IL 60439, USA.

---