Assessing covalency in equatorial U–N bonds: density based measures of bonding in BTP and isoamethyrin complexes of uranyl

Abstract

Calculations performed at the density functional level of theory have been used to investigate complexes of uranyl with the expanded porphyrin isoamethyrin and the bis-triazinyl-pyridine (BTP) ligands, the latter of which is well-known to be effective in the separation of trivalent lanthanides and actinides. Analysis has been performed using a range of density-based techniques, including the Quantum Theory of Atoms in Molecules (QTAIM), the Electron Localisation Function (ELF) and the reduced density gradient (RDG). The effects of peripheral alkyl substituents on UO₂-isoamethyrin, known to be vital for proper replication of the experimental geometry, are considered. Evidence for comparable amounts of covalent character has been found in the largely ionic U–N bonds of UO₂-isoamethyrin and [UO₂(BTP)₂]²⁺ and examination of the variation in the electronic characteristics of the uranyl unit upon complexation in both of these cases reveal striking similarities in the nature of the U–N bonding and the effect of this bonding on the U–O_yl interaction, as well as evidence of donation into the U–N bonding region from the uranyl unit itself.

---

Introduction

The understanding of bonding in molecular complexes of the f-elements, which exhibit pronounced relativistic effects and strongly correlated valence electronic structure,^1,2 is a major challenge to both the experimental and theoretical research communities. The coordination chemistry of the actinides is rich and varied,^3–7 and the improved characterisation of bonding in actinide complexes is of significant fundamental importance and may help in the identification of novel synthetic targets. Equatorial coordination of uranyl by monodentate ligands has been the subject of many studies,^8–15 and the uranyl unit is known to be highly sensitive to changes in its coordination environment.^16–18 The pronounced weakening of the U–O_yl bond upon complexation with monodentate ligands has been theoretically investigated^14,19,20 and attributed to various, sometimes contradictory, factors. In our recent study of uranyl complexes with monodentate first row ligands,²⁰ we found evidence to support this weakening as being due to covalent interactions in the equatorial plane causing a reduction of the covalent component of the U–O_yl interaction, with the weakening of the U–O_yl bond proportional to the degree of equatorial electron sharing. Moving from simple mono- to bi- and tridentate ligands, uranyl has been observed to form complexes with, for example, bipyridine and various derivatives,^21,22 with some species demonstrating interesting luminescent properties,²³ and the terpyridine ligand has been observed to coordinate uranyl^21,22 as well as U(III),²⁴ acting to bind the latter selectively over the trivalent lanthanides. UO₂Cl₂-3(THF) reacts with another tridentate ligand, 2,6-bis(2-benzimidazolyl)pyridine (H₂BBP) to produce three complexes:²⁵ [(UO₂)(H₂BBP)Cl₂], [(UO₂)(HBBP)(Py)Cl], and [(UO₂)(BBP)(Py)₂], with the effects on the uranyl dication in terms of U–O_yl bond lengthening and deviation of the uranyl unit from linearity found to increase with shorter U–N bonds and increased planarity of the BBP ligand. There are also several examples of uranyl complexation by multidentate and macrocyclic ligands, resulting in, for example, ‘Pacman’ complexes allowing access to unusual oxidation states and resultant novel chemistry,²⁶ crown ether complexes serving as potential extractants for uranyl²⁷ and expanded porphyrins acting as colourimetric actinide sensors.²⁸

A deeper understanding of actinide bonding is also of relevance to the nuclear industry, where current approaches to the remediation of spent nuclear fuel involve the chemical separation of its component radionuclides. This approach allows for the extraction of reusable uranium and plutonium from the uranium fission products. These fission products, which are considered as high level nuclear waste (HLW), include the long-lived minor actinides (MAs), primarily comprised of neptunium, americium and curium isotopes with half-lives >10⁶ years, and the majority of the lanthanides, with half-lives typically on the order of decades.

Current research is focussed upon ligands suitable for the selective extraction of these minor actinides, the reasons being twofold. Firstly, separation of long- and short-lived radioisotopes can provide more economically viable waste storage and management strategies. Secondly, the minor actinides can be transmuted into usable nuclear fuel via neutron bombardment, but only if separated from the lanthanides, which have large neutron-absorption cross-sections. The chemistry of the MAs is very similar to that of the lanthanides, being dominated by the trivalent oxidation state,⁵ rendering selective extraction an exceedingly difficult challenge. The 5f shell of the actinides has a greater radial extent than the contracted, core-like, chemically inert 4f-shell of the lanthanides and current opinion^29–32 suggests that this increased radial extent leads to enhanced covalent interactions which can be exploited to produce An(III) complexes with increased thermodynamic stability of over Ln(III) analogues. Sulphur-, phosphorus- and nitrogen-donor ligands have been demonstrated to preferentially coordinate An(III) (see ref. 29 and references therein) and, of these, the N-donors have received perhaps the most attention, partly due to the fact that they often satisfy the ‘CHON principle’: ligands composed only of carbon, hydrogen, nitrogen and oxygen can be fully combusted to environmentally safe gaseous products after use, minimising secondary waste. Of these N-donor ligands, 2,6-bis(1,2,4-triazine-3-yl)pyridine (BTP) was the first to be shown to exhibit excellent selectivity,³³ although the related ligands 6,6′-bis(1,2,4-triazin-3-yl)-2,2′-bipyridine (BTBP) and 2,9-bis(1,2,4-triazin-3-yl)-1,10-phenanthroline (BTPhen) have since demonstrated improved selectivity, stability and kinetics.^34,35 The origin of this selectivity, however, remains elusive: covalency in complexes of the lanthanides and later actinides is weak,^32,36 and variation in covalency is consequently very slight,^37,38 making quantitative assessments extremely difficult. For this reason, uranium complexes are often considered as model systems^39–43 in studies of actinide covalency, since there is a growing body of evidence that these complexes often exhibit increased covalent bonding when compared to those of other actinides.^{36–38,41,44,45}

In this contribution we theoretically compare the bonding of two uranyl complexes, namely [UO₂(BTP)₂]^2+ 22 and UO2IA,⁴⁶ where IA = [24]hexaphyrin(1.0.1.0.0.0), commonly referred to as isoamethyrin (see Fig. 1). Isoamethyrin is a hexadentate nitrogen donor ligand that has previously been demonstrated to coordinate uranyl, neptunyl and plutonyl cations,^28,47 suggesting its use as a potential colorimetric sensor for actinides in aqueous environments. It is anticipated that by examining in detail the electronic structure of uranyl as one moves from coordination by monodentate ligands²⁰ to coordination by multidentate and macrocyclic ligands, so the effect of the equatorial coordination environment on the uranyl unit can be better understood. Here, we investigate two six-coordinate complexes of uranyl: one which features two tridentate ligands and a second which comprises a single hexadentate macrocyclic ligand. Although the electronic structure of uranyl, with its formally empty 5f-shell, differs significantly from that of lower oxidation state later actinides, we propose that if U–N bonding in UO₂IA is of similar character to that in [UO₂(BTP)₂]²⁺, then there is scope for future investigations of IA as a potential separation ligand for the trivalent minor actinides.

Fig. 1 Molecular structure of (a) BTP and (b) the isoamethyrin dianion, the two ligands considered in this study. Symmetry-distinct coordinating nitrogens are labelled.

We aim to avoid the ambiguity which can arise from orbital based methods of characterising bonding³² by focussing solely on properties of the experimentally observable electron density. To this end we employ the Quantum Theory of Atoms in Molecules (QTAIM).⁴⁸ QTAIM analysis partitions a molecule into a contiguous set of space-filling atomic basins, Ω_i, the surfaces of which satisfy the condition ∇ρ(r)·n(r) = 0, where n(r) is the vector normal to the atomic surface. Evaluation of ∇ρ(r) = 0 reveals the set of critical points associated with the molecule. Each atomic basin (typically) contains a single nuclear critical point (NCP) at the position of the nuclear centre. A bond critical point (BCP) is found when the uniquely defined line of maximum density between two atoms has its minimum at the interatomic surface joining the two atomic basins: in this situation, the atoms are considered to be bonded to one another.⁴⁹ The bond can be characterised by the values of the electron density and its Laplacian at the BCP: as a general rule, ρ_BCP > 0.20 a.u. and ∇²ρ_BCP < 0 for a covalent bond, whilst ρ_BCP < 0.10 a.u. and ∇²ρ_BCP > 0 indicates an ionic bond. More broadly, increasing values of ρ_BCP indicate increasing covalent character within a bond. Additional information can be obtained from the atomic partitioning by integrating one- and two-electron properties over the resulting basins. In this way, atomic populations N(i) as well as localisation λ(i) and delocalisation indices δ(i,j) can be defined. While λ(i) gives the number of electrons localised in the atomic basin Ω_i, δ(i,j) gives the number of electrons shared between basins Ω_i and Ω_j, and so can be considered a quantitative measure of covalency. We have recently employed this approach in order to gain detailed insight into the variation in uranyl bonding due to equatorial bond covalency.²⁰

We complement the QTAIM analysis with studies of the Electron Localisation Function (ELF).⁵⁰ The ELF provides a measure of the likelihood of finding a localised pair of electrons at a given point in space. Of particular relevance to this study are the values at which the ELF isosurface bifurcates. The higher the ELF value at the bifurcation point, the higher the degree of electron sharing between the two spatial regions separated by the bifurcation.⁵¹ We also consider an approach to identifying regions of weak interaction⁵² which relates the density, ρ(r), to the reduced density gradient (RDG), defined as s(r) = |∇ρ(r)|/2(3π²)^1/3ρ(r)^4/3. Finally, we compare these results to explicit electron density differences resulting from complexation.

Computational details

Geometrical structures were optimised at the density functional theoretical level using version 6.4 of the TURBOMOLE quantum-chemical software package,⁵³ employing the Ahlrichs basis sets⁵⁴ of polarised triple-zeta quality: def2-TZVP (H, C, N) and def-TZVP (U). For U, 60 core electrons were replaced with a Stuttgart–Dresden–Bonn relativistic effective core potential (RECP).^55,56 Analytical and numerical frequency analysis was performed in order to confirm the optimized structures as local energetic minima.‡ Based on these structures, all-electron single point energy calculations were performed, replacing the def-TZVP basis set and RECP on the U centre with the corresponding segmented all-electron relativistically contracted (SARC) basis set⁵⁷ of polarised triple-zeta quality, and accounting for relativistic effects with the 2nd order Douglas–Kroll–Hess Hamiltonian.^58,59 In order to investigate the exchange–correlation (xc-)functional dependence of the simulations, as well as the effect of including exact exchange, two xc-functionals were used, namely the PBE functional⁶⁰ based on the generalised gradient approximation (GGA) and the popular hybrid-GGA functional, B3LYP.^61,62 Solvent effects were incorporated using the COSMO continuum solvation model⁶³ using a relative permittivity of 8.9 to simulate solvation in dichloromethane, for which there is experimental data.²⁸ All-electron densities were subsequently employed in the QTAIM analysis, which was performed using the AIMAll code.⁶⁴ ELF and RDG analysis were performed using version 3.3.6 of the Multiwfn code,⁶⁵ which was also employed in order to generate density difference data. RDG, ELF and density difference data were visualised using the VMD code.⁶⁶

Results and discussion

Structural characterisation

Gas phase molecular geometries, optimised using the PBE functional, are shown in Fig. 2. [UO₂BTP₂]²⁺ was found to be non-planar, in agreement with crystallographic data,²² optimising to a structure with C_2h symmetry with two distinct U–N bond lengths. In contrast, UO₂IA was found to be planar, exhibiting C_2v symmetry with three distinct U–N bond lengths and the uranium ion sitting slightly off-centre. These qualitative characteristics were also found when employing the B3LYP functional. Omission of peripheral alkyl substituents is a relatively common simplification in theoretical chemistry but in the case of UO₂IA, this omission results in significant deviations from the experimentally characterised complex, which exhibits a non-planar geometry leading to a significant reduction in U–N bond-length when compared to our simplified structure, with this difference being most pronounced for the longer U–N_B and U–N_C bonds. Our theoretical bond lengths for unsubstituted UO₂IA are, however, in excellent agreement with those obtained previously at the same level of theory.⁶⁷ In this previous study, it was found that the presence of alkyl substituents induced the non-planarity structure observed experimentally. The macrocyclic core is believed to be too large for the uranyl unit, and the stability gained by this formally Hückel aromatic system adopting a planar geometry is presumably smaller than that gained by the distortion, which allows shorter, stronger U–N bonds to form and minimises steric effects among the alkyl groups, although it is worth noting that non-planarity can also arise as a direct result of ligand–ligand repulsion.²² Reintroducing the alkyl groups, generating the complex hereby referred to as UO₂IA′, and reoptimising without symmetry constraints resulted in bond lengths in better agreement with those found experimentally and a non-planar structure.

Fig. 2 Top- and side-views of PBE-optimised gas-phase structures of (a) [UO₂BTP₂]²⁺, (b) UO₂IA and (c) UO₂IA′. For clarity, substituents have been omitted from (c). U = yellow, O = red, N = blue, C = grey, H = white.

U–O and U–N bonds lengths are summarised in Table 1. Calculated U–O bond lengths are in good agreement with experimental values and, in the gas phase, show an elongation of ∼0.07 Å (∼0.06 Å) compared to uncoordinated uranyl when employing the PBE (B3LYP) functional: this elongation indicates a weakening of the U–O bond, and will be investigated in subsequent sections.

Table 1 Comparison of U–O and U–N bond lengths (in Å) with experimental values and previous work

		PBE		B3LYP		Exp^a^,^b	PBE/TZP^c
		GP	DCM	GP	DCM
a Ref. 22 (averaged values). b Ref. 46. c Ref. 67.
[UO2(BTP)2]^2+	U–O	1.778	1.786	1.756	1.764	1.758	—
	U–NT	2.634	2.612	2.657	2.635	2.565	—
	U–NP	2.655	2.636	2.676	2.656	2.602	—
		2.641	2.62	2.663	2.642	2.577	—
UO2IA	U–O	1.777	1.787	1.758	1.767	—	1.79
	U–NA	2.625	2.614	2.633	2.619	—	2.627
	U–NB	2.915	2.908	2.91	2.903	—	2.906
	U–NC	2.799	2.792	2.796	2.788	—	2.786
		2.78	2.771	2.78	2.770	—	2.773
UO2IA′	U–O	1.787	1.799	1.766	1.777	1.760	1.799
	U–NA	2.586, 2.587	2.573, 2.573	2.602, 2.601	2.586	2.566	2.590
	U–NB	2.772, 2.765	2.702, 2.693	2.790, 2.785	2.773, 2.766	2.677	2.773
	U–NC	2.713, 2.705	2.755, 2.747	2.726, 2.724	2.716, 2.710	2.644	2.714
		2.688	2.674	2.704	2.689	2.631	2.692

---

In the case of [UO₂(BTP)₂]²⁺, U–N bond lengths are slightly overestimated by ∼0.07 Å (∼0.09 Å) when employing the PBE (B3LYP) functional in the gas phase. Agreement with experiment is slightly improved when solvent effects are taken into account, reducing the calculated difference to ∼0.04 Å (∼0.07 Å) when using the PBE (B3LYP) functional. This demonstrates that the different model chemistries employed here are both capable of adequately modelling the relevant uranyl–ligand interactions. The U–N bonds lengths in UO₂IA, however, are overestimated by up to 0.24 Å (0.23 Å) at the PBE (B3LYP) level. Inclusion of solvent effects slightly reduces this overestimation to 0.23 Å (0.23 Å) at the PBE (B3LYP) level of theory and introduces a very slight degree of non-planarity in the IA complex, but made no substantial qualitative difference to any complex considered here. We find that the shortest U–N bonds occur when the pyrolle unit lacks any meso-carbon bridging. These meso-carbons appear to give flexibility to the macrocycle, allowing the 2-2-bipyrrole subunit incorporating the N_C-donors to approach closer than the groups incorporating the N_B-donors, which exhibit maximum deviation from the experimental value. In UO₂IA′, however, the presence of the peripheral alkyl substituents causes the ligand to distort slightly from planarity, allowing all U–N bonds to shorten. This low symmetry distorted complex exhibits six distinct U–N bond lengths. It remains the case that the shortest U–N bonds occur when the pyrolle unit lacks meso-carbon bridges. The U–N_A bonds shorten by around 0.04 Å (0.03 Å) with the PBE (B3LYP) functional when compared to the UO₂IA complex, bringing them into good agreement with experimental bond length of 2.566 Å. The U–N_B bonds are significantly reduced by up to 0.15 Å (0.11 Å) with the PBE (B3LYP) functional, bringing them into better agreement with the experimental values of 2.677 Å, although these bonds are still overestimated by up to ∼0.10 Å (∼0.13 Å). Although inclusion of the alkyl groups improves the overall agreement with experiment, the overestimation of the U–O bond length is slightly increased, by ∼0.01 Å (∼0.02 Å) with the PBE (B3LYP) functional in the gas phase. Geometries obtained using the PBE xc-functional have slightly improved agreement with experiment than those obtained with B3LYP.

QTAIM analysis

In order to investigate the electronic structure of the complexes in detail we have analysed the electron density using the Quantum Theory of Atoms in Molecules (QTAIM). Tables 2 and 3 present various properties of the electron density at the U–O and U–N bond critical points (BCPs), as well as delocalisation indices. Due to the similarity of data obtained in the gas phase and in the presence of a continuum solvent, only the former is presented here: the latter can be found in the ESI.† The large values of ρ, along with the large negative values of the energy density, H, found at the U–O BCP in both complexes (Table 2) are indicative of a covalent interaction, as has been found previously.^20,68 This is further supported by the high degree of electron sharing between the U and O ions. When comparing [UO₂BTP₂]²⁺ with UO₂IA and UO₂IA′, the similarity in QTAIM properties, in conjunction with the very similar bond lengths presented in Table 1, indicate strong similarities in the equatorial coordination environments of all complexes.

Table 2 QTAIM-derived properties of the U–O bond of the three complexes considered in this study. ρ_BCP = electron density at BCP. ∇²ρ_BCP = Laplacian of ρ_BCP. H_BCP = energy density at BCP. δ(U,O) = delocalisation index between U and O centres. All reported quantities are in atomic units

		[UO2(BTP)2]^2+	UO2IA	UO2IA′
a Average over both U–O bonds.
ρ BCP	PBE	0.307	0.307	0.299
	B3LYP	0.325	0.323	0.317
∇^2ρBCP	PBE	0.314	0.314	0.315
	B3LYP	0.264	0.263	0.265
H BCP	PBE	−0.283	−0.283	−0.270
	B3LYP	−0.318	−0.263	−0.303
δ(U,O)	PBE	1.992	2.011	1.971
	B3LYP	1.961	1.968	1.936^a

---

Table 3 QTAIM-derived properties of the U–N bond of the three complexes considered in this study. ρ_BCP = electron density at BCP. ∇²ρ_BCP = Laplacian of ρ_BCP. H_BCP = energy density at BCP. δ(U,N) = delocalisation index between U and N centres. All reported quantities are in atomic units

		[UO2(BTP)2]^2+		UO2IA			UO2IA′
		U–NT	U–NP	U–NA	U–NB	U–NC	U–NA	U–NB	U–NC
ρ BCP	PBE	0.048	0.045	0.049	0.026	0.034	0.052, 0.052	0.035, 0.036	0.039, 0.400
	B3LYP	0.045	0.043	0.048	0.026	0.033	0.050, 0.050	0.034, 0.034	0.038, 0.039
∇^2ρBCP	PBE	0.117	0.113	0.117	0.065	0.081	0.128, 0.129	0.088, 0.089	0.099, 0.100
	B3LYP	0.116	0.111	0.118	0.068	0.085	0.127, 0.128	0.087, 0.088	0.099, 0.100
H BCP	PBE	−0.005	−0.004	−0.005	−0.000	−0.002	−0.005, −0.005	−0.002, −0.002	−0.002, −0.003
	B3LYP	−0.004	−0.003	−0.004	−0.000	−0.002	−0.005, −0.005	−0.001, −0.001	−0.002, −0.002
δ(U,N)	PBE	0.305	0.290	0.348	0.221	0.264	0.354, 0.352	0.268, 0.272	0.283, 0.290
	B3LYP	0.272	0.262	0.313	0.198	0.241	0.318, 0.317	0.238, 0.240	0.256, 0.260

---

As expected, values of ρ_BCP are much lower for U–N bonds in all complexes (Table 3). The magnitude of these values, along with the near-zero energy densities, indicate largely ionic interactions, as might be expected. One trend can, however, be still be observed: shorter U–N bonds correspond to larger values of ρ_BCP and greater degrees of electron sharing, supporting the intuitive view that shorter, stronger bonds exhibit higher covalency, with a commensurate reduction of covalent character in the U–O bond. The effect of peripheral alkyl substituents on the QTAIM and structural parameters of the U–N bonds in the IA′ complex is far greater than the choice of exchange–correlation functional or solvation. The choice of functional does, however, appear to have small but noticeable effects on QTAIM parameters: use of the B3LYP functional results in a significant increase in ρ_BCP in the U–O bond in both complexes, along with a small reduction in electron sharing. Topological properties of the U–N bonds are largely unaffected by the change in functional, although there is a small systematic reduction in all properties. This implies that the hybrid functional, which includes a proportion of exact Hartree–Fock exchange, leads to increased electron localisation. The effect of solvation on QTAIM parameters is very small and implies a very slight weakening of the U–O bonds, accompanied by a minor strengthening of the U–N bonds, in agreement with structural parameters. However, since the dependence of these properties on the choice of exchange–correlation functional and solvation is small, from hereon we only report details of our analyses of gas-phase PBE results. Corresponding data obtained using the B3LYP functional, along with those obtained via the inclusion of a continuum solvent model, can be found in ESI.†

The lengthening of the U–O bond upon complexation may provide evidence that, whilst the degree of U–N electron sharing is small, it has a non-negligible effect on the U–O bond. To investigate this effect in more detail, the QTAIM parameters of the uranyl unit in isolation and when complexed by BTP and IA/IA′ have been evaluated (see Table 4). To enable comparison, the isolated uranyl calculations were performed at the complexed uranyl geometries. To further aid analysis, we define two new parameters:

where N(UO₂) gives the uranyl electronic population (from which the charge q(UO₂) can be derived) and λ(UO₂) the number of electrons localised on the uranyl unit. In the case of isolated UO₂²⁺, N(UO₂) = λ(UO₂) = 106.

Table 4 QTAIM-derived properties of isolated and complexed uranyl. Isolated uranyl simulated at the complexed geometry. Δ gives the difference between isolated and complexed values. Properties derived from PBE/def(2)-TZVP densities. All quantities are in atomic units

	[UO2(BTP)2]^2+			UO2IA			UO2IA′
	UO2^2+	Complex	Δ	UO2^2+	Complex	Δ	UO2^2+	Complex	Δ
a Values averaged over both O centres.
N(U)	88.92	89.21	+0.28	88.92	89.16	+0.23	88.94	89.17	+0.24
N(O)	8.54	8.81	+0.27	8.54	8.83	+0.29	8.53	8.85	+0.31
N(UO2)	106	106.82	+0.82	106	106.81	+0.81	106	106.86	+0.86
λ(U)	86.61	86.14	−0.47	86.61	86.18	−0.43	86.62	86.14	−0.48
λ(O)	7.31	7.62	+0.31	7.31	7.67	+0.36	7.31^a	7.69^a	+0.38
λ(UO2)	106	105.47	−0.53	106	105.64	−0.36	106	105.56	−0.44
δ(U,O)	2.32	1.99	−0.33	2.32	2.01	−0.31	2.32^a	1.97^a	−0.35

---

The data in Table 4 gives considerable insight into the effect of equatorial complexation on U–O bonding. As can be seen from the calculated difference in properties upon complexation, the three complexes exhibit strong qualitative similarities. Firstly, approximately 0.8–0.9 a.u. of electronic charge is donated onto the uranyl unit. Of this donated charge, approximately equal amounts (0.2–0.3 a.u.) populate the uranium and each of the oxygen ions. This additional electronic charge on all ions increases electrostatic repulsion between them. Secondly, we can consider that, to a first approximation, the electronic charge localised on each centre dictates the degree of ionic interaction. In all complexes, electron localisation increases on the oxygen centre and decreases on the uranium centre, implying a more ionic U–O interaction upon complexation. Finally, there is a corresponding reduction in δ(U,O), indicating a reduction in covalent interaction. These three factors combine to explain the lengthening, and hence weakening, of the U–O interaction in the complexes.

Further insight into the U–N interactions can also be obtained. Whilst N(UO₂) increases by approximately 0.8–0.9 a.u. upon complexation, λ(UO₂) reduces to a value below that of the isolated dication, with this reduction more pronounced in the BTP complex (0.53 a.u. compared to 0.36 a.u. in UO₂IA and 0.44 a.u. in UO₂IA′). This is consistent with our previous studies of uranyl coordination by nitrogen donors.²⁰ Since λ(UO₂) takes into account U–O delocalisation, any differences between N(UO₂) and λ(UO₂) must therefore be due to electron sharing between the uranyl unit and the ligand, i.e. covalency in the U–N bonds. This difference is 1.35 a.u., 1.17 a.u. and 1.30 a.u. for the BTP, IA and IA′ complexes, respectively. Since the increase in electron localisation on the oxygen ions, λ(O), is approximately equal in magnitude but opposite in sign to the decrease in electron sharing in the U–O bond, δ(U,O) (+0.33 versus −0.33, +0.36 versus −0.31 and +0.38 versus −0.35 a.u. in the BTP, IA, and IA′ complexes, respectively), we can deduce that the increase in λ(O) is almost exclusively due to donation from the U–O bond. The reduction in electron localisation on the uranium centre, λ(U), is therefore almost entirely due to electron sharing in the U–N bond. Put simply, the ∼0.8–0.9 a.u. of charge donated upon complexation is contributed almost entirely into U–N bonding and also induces a donation of ∼0.4–0.5 a.u. of charge from the uranyl unit into the bonds. This donation cannot be back-bonding in the traditional sense, since U(VI) is formally 5f⁰6d⁰. Nevertheless, this is clear evidence of a significant uranium contribution to the bonds.

Electron localisation function

The variation in U–N bond lengths combined with the previously discussed QTAIM parameters provides evidence of weak but non-negligible covalent interactions. Such interactions should also be detectable by analysis of the electron localisation function, n(r). Whilst a strongly covalent interaction would be characterised by a local maximum in n(r) along the bond direction in the bonding region (associated with a disynaptic ELF basin between the two centres), a predominately ionic interaction would instead exhibit a local minimum,§ and an absence of any disynaptic basin. The value of n(r) at this minimum, which formally corresponds to a critical point, should however give a measure of electron-pair localisation and hence covalent character. Bonds with a greater degree of electron sharing would be expected to exhibit higher values of n(r) at the critical points. These critical values, n_C, correspond to isosurface values at which n(r) bifurcates. Table 5 gives the critical values of n(r) for the U–N bonds of all complexes considered in this study and Fig. 3 shows n(r) evaluated at isosurfaces above and below these critical values, illustrating the bifurcation.

Table 5 Critical values of the ELF, n_C, calculated in the U–N bonding regions

	[UO2(BTP)2]^2+		UO2IA			UO2IA′
	U–NT	U–NP	U–NA	U–NB	U–NC	U–NA	U–NB	U–NC
n C	0.197	0.183	0.204	0.112	0.150	0.210, 0.209	0.149, 0.151	0.166, 0.170

---

Fig. 3 ELF isosurfaces of (a) ([UO₂(BTP)₂]²⁺), visualised at n(r) = 0.17 (left) and 0.24 (right), (b) UO₂IA, visualised at n(r) = 0.10 (left) and 0.24 (right), (c) UO₂IA′, visualised at n(r) = 0.14 (left) and 0.24 (right). Distinct localisation domains are indicated by colour.

Fig. 3 shows that, for n(r) below the lowest value of n_C, the ELF surface consists of a single localisation domain. Above the highest value of n_C, bifurcation occurs, resulting in three ([UO₂(BTP)₂]²⁺) or two (UO₂IA/UO₂IA′) localisation domains, corresponding to the uranyl unit and the ligand(s). This indicates that in both complexes the U–N bonding region exhibits the lowest degree of electron sharing, as expected in the otherwise covalently bonded complexes. In the case of the isoamethyrin complex, bifurcation occurs at a very low value, due to the long, weak, U–N_B bond. Table 5 shows that the critical value associated with the U–N_T bond is marginally higher than that of the U–N_P bond, suggesting higher electron delocalisation and therefore covalency. This is commensurate with our other analyses, which show the U–N_T bonds to be slightly shorter, with larger values of both ρ_BCP and δ(U,N), when compared to the U–N_P bonds. This is more pronounced in UO₂IA and UO₂IA′. Here, the critical values associated with the U–N bonds are ordered as follows: U–N_B < U–N_C < U–N_A. This ordering is in complete agreement with our structural and topological analysis which show the U–N_A (U–N_B) bonds to be shortest (longest) and most (least) covalent.

Regions of weak interaction

It has previously been demonstrated that in regions of both covalent and predominately noncovalent interactions, the reduced density gradient s(r) assumes very small values.⁶⁹ However, while ρ(r) can be large in covalent bonding regions, it is small but non-zero in regions of largely noncovalent interaction, such as might be expected in the U–N bonding regions of the complexes considered here. Plots of s(r) against ρ(r) therefore exhibit spikes at low densities, indicating the presence of such interactions.⁵² These plots can be complemented by visualisations of the s(r) isosurface, revealing the spatial regions in which these interactions are taking place. Since such interactions can be both attractive and repulsive, s(r) isosurfaces are typically mapped with values of ρ(r)sgn(λ₂), where sgn(x) is the signum function, returning −1 if x < 0 and 1 if x > 0, and λ₂ is the second largest eigenvalue of the Hessian of ρ(r): λ₂ is typically negative (positive) for attractive (repulsive) interactions.⁷⁰ Scatter plots of s(r) against ρ(r)sgn(λ₂) are given in Fig. 4 for all complexes, the data are evaluated over the entire molecule, but we have also focussed on the bonding regions in the equatorial plane in order to generate data of higher fidelity. For all complexes, there are several points at which s(r) falls to zero. Formally, these correspond to critical points in the electron density, as can be verified by comparing those occurring at negative values of ρ(r)sgn(λ₂)to the values of ρ(r) at the U–N BCPs given in Table 3. s(r) also falls to zero at ρ(r)sgn(λ₂) ∼ −0.01 (a.u.) and at small positive values indicating other weak interactions. In order to investigate the spatial regions associated with the interactions we have plotted isosurfaces of s(r), colour-mapped with ρ(r)sgn(λ₂). These isosurfaces can be seen in Fig. 5. As would be expected the red regions, associated with the zeroes of s(r) and negative values of ρ(r)sgn(λ₂), correspond to attractive U–N interactions. The similarity in size and shape of these regions between the three systems is striking, and supports the assertion that U–N bonding is very similar in these complexes. Regions of weak interaction, coloured green, can be seen between ligand nitrogens: in [UO₂(BTP)₂]²⁺ this is an interligand interaction, whereas in UO₂IA and UO₂IA′ this is an interaction between nitrogens on either side of the bridging carbon. These regions may be indicative of steric repulsion or, alternatively, of weak attraction. All repulsive interactions are N–N interactions, and can be interpreted as weak steric repulsion.

Fig. 4 Scatter plots of s(r) against ρ(r)sgn(λ₂) in (a) [UO₂(BTP)₂]²⁺, (b) UO₂IA and (c) UO₂IA′.

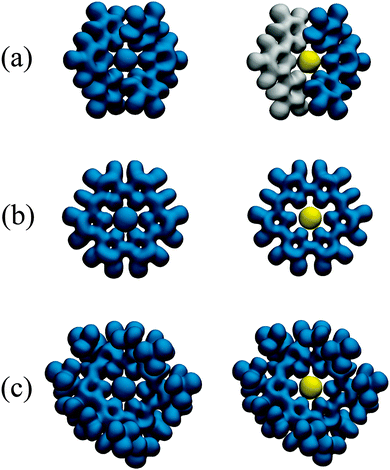
Fig. 5 Isosurfaces of the reduced density gradient, s(r), mapped with values of ρ(r)sgn(λ₂) for (a) [UO₂(BTP)₂]²⁺, (b) UO₂IA and (c) (b) UO₂IA′. Red regions indicate attractive interactions with weakly covalent character. Isosurfaces are rendered at s(r) = 0.35 a.u., corresponding to the horizontal lines in Fig. 4.

Density differences upon complexation

We complete our analysis with a consideration of the difference in electron density distribution which occurs upon complexation. We have generated this data by calculating the density of the complexes, and comparing these to the densities of the uranyl and ligand fragments held at the geometries found in the complexes. The density difference can be seen in Fig. 6. Again, the [UO₂(BTP)₂]²⁺, UO₂IA and UO₂IA′ complexes exhibit similar characteristics, and these strongly support our previous assertions regarding U–N bonding and the effect on the uranyl U–O bond. There is a clear accumulation of electron density in the U–N bonding region and, in keeping with previous measures, this is more pronounced in [UO₂(BTP)₂]²⁺ than UO₂IA, presumably due to the (typically) shorter U–N bonds in the former. UO₂IA′ has somewhat more pronounced accumulation in the U–N bonding region than UO₂IA, consistent with both the shorter U–N bonds and our QTAIM analysis which indicates greater covalency. The size of the isosurfaces in the U–N bonding region of both UO₂IA and UO₂IA′ (although easier to observe in the former) follows the order previously identified in (i) the value of ρ(r) at the U–N BCP, (ii) the magnitude of δ(U,N), (iii) the ordering of the critical values of n(r) for the U–N bonds and (iv) the magnitude of ρ(r)sgn(λ₂) in the regions of weak interaction found via analysis of the reduced density gradient. This charge density is contributed partly from the C–N bonds on the ligands and partly from the uranyl unit itself. The isosurfaces show characteristics of both σ- and π-donation, in keeping with the ability of uranyl to act as both a σ- and π-acceptor. The density difference plots also clearly show the charge transfer from the U–O bonding region onto the uranyl oxygens as discussed at length during our QTAIM analysis, and observed by us previously.²⁰ This serves to further justify our assertion that ligand complexation results in reduced covalent character in the U–O bond, leading to the bond lengthening found in the present calculations, as well as throughout the literature.

Fig. 6 Electron density differences in (a) [UO₂(BTP)₂]²⁺, (b) UO₂IA and (c) UO₂IA′ upon complexation. Blue regions indicate charge accumulation and yellow areas charge depletion. All densities visualised using an isosurface of ρ = 0.005 a.u.

Summary and conclusions

We have performed a series of density functional theory calculations on the complexation of uranyl with three multidentate nitrogen-donor ligands. As part of these calculations, we have investigated the effects of exchange–correlation functional and solvation on a series of properties. We have found that, in agreement with a previous theoretical study,⁶⁷ the gas phase structure of UO₂IA is planar, with a very slight degree of non-planarity introduced by solvation. This is in contradiction to the experimentally synthesized alkyl substituted complex and so we conclude that, since the dianionic IA ligand is formally Hückel aromatic, the energetic stability afforded by a planar geometry is sufficient to outweigh the penalty associated with the unusually long U–N bonds found in the unsubstituted complex. When the substituents are included, we find that, in improved agreement with experiment, the steric effects associated with alkyl substitution are more substantial than the stability gained by planarity, leading to a distorted complex in which shorter, stronger U–N bonds are able to form.

We have considered four different methods for studying the bonding in these complexes, all based on analysis of the experimentally observable electron density. These analyses focus on the nature of U–N bonding in these complexes and the consequent effects on the highly covalent U–O bond of uranyl. These measures involve the use of the Quantum Theory of Atoms in Molecules and the Electron Localisation Function. We have also investigated regions of weak covalent interaction through analysis of the reduced density gradient, and complemented these studies with visualisation of the electron density difference induced via complexation of the uranyl unit by the IA, IA′ and BTP ligands. These four analyses were found to be in complete agreement: all demonstrated weak, but non-negligible, covalent character in the U–N bonding region of both complexes. As might be expected, the covalent character of the bonds was found to increase as the U–N bond length shortened. We have found that use of the B3LYP exchange–correlation functional leads to slightly increased electron localisation when compared to results obtained using the PBE functional. The B3LYP functional incorporates a degree of exact exchange, and it is known that this results in localisation of the electron density in the valence shell of transition metals and f-elements.⁷¹ This effect is sometimes used to reduce the well-known self-interaction error present in approximate exchange–correlation functionals. This spurious self-interaction leads to an overestimate of electron delocalisation, especially in strongly correlated systems. Nevertheless, our B3LYP-derived results still demonstrate substantial electron-sharing. We have also performed an in-depth analysis of the effect of removing peripheral alkyl substituents from isoamethyrin, a common simplification in computational chemistry, which, in this case, has a pronounced effect on both geometry and QTAIM parameters. Inclusion of solvent effects has small consistent effects in all complexes. U–N bond lengths are found to slightly decrease by around ∼0.01 Å and there is a corresponding increase in electron sharing. Similarly, there is a small lengthening of U–O bonds when solvent effects are considered, and correspondingly, a small decrease in electron sharing.

Our analyses revealed a strong effect on the uranyl U–O bonds upon complexation, namely a noticeable reduction in electron sharing in the U–O bonding region, with charge instead localising on the oxygen centres. This leads to an increase of ionic character in the U–O bond. This, of course, also corresponds to a reduction in covalency. Since the covalent interaction is stronger, this reduction explains the increased U–O bond lengths found in our structural analysis.

We have also demonstrated that the uranyl unit itself donates electronic charge into the U–N bonding region. This cannot be traditional back-bonding, since the U(VI) centre is formally 5f⁰6d⁰, but instead is a contribution that is localised on the uranium centre in the isolated uranyl dication. This uranium donation appears to be a general feature of equatorial bonding in uranyl complexes.²⁰

Finally, the results presented here show that, from an electronic perspective at least, multidentate expanded porphyrin ligands provide interesting model systems for investigating An–N bonding characteristics. The similarity in bonding character to that of BTP complexes supports the possibility of using such macrocycles as model systems in the investigation of the origins of selectivity of nitrogen donor ligands for trivalent actinides over lanthanides: we intend to explore these possibilities further in future work.

Acknowledgements

AK thanks the EPSRC for the award of a career acceleration fellowship (grant EP/J002208/2). We also acknowledge UCL research computing, Lancaster University and the National Service for Computational Chemistry Software (NSCCS) for access to the Legion, HEC and Columbus/Slater HPC facilities, respectively. All data created during this research are openly available from the Lancaster University data archive at DOI: http://10.17635/lancaster/researchdata/66.

References

1. M. Seth, M. Dolg, P. Fulde and P. Schwerdtfeger, J. Am. Chem. Soc., 1995, 117, 6597–6598.
2. M. Dolg, in Encyclopedia of Computational Chemistry, ed. H. F. Schaefer, Wiley, Chichester, 2002.
3. A. E. V. Gorden, M. A. DeVore and B. A. Maynard, Inorg. Chem., 2013, 52, 3445–3458.
4. D. Patel and S. T. Liddle, Rev. Inorg. Chem., 2012, 32, 1–22.
5. N. Kaltsoyannis and P. Scott, The f elements, Oxford University Press, Oxford, 1999.
6. S. T. Liddle, Angew. Chem., Int. Ed., 2015, 54, 8604–8641.
7. G. Schreckenbach and G. A. Shamov, Acc. Chem. Res., 2010, 43, 19–29.
8. P. G. Allen, J. J. Bucher, D. K. Shuh, N. M. Edelstein and T. Reich, Inorg. Chem., 1997, 36, 4676–4683.
9. U. Wahlgren, H. Moll, I. Grenthe, B. Schimmelpfennig, L. Maron, V. Vallet and O. Gropen, J. Phys. Chem. A, 1999, 103, 8257–8264.
10. C. E. Rowland, M. G. Kanatzidis and L. Soderholm, Inorg. Chem., 2012, 51, 11798–11804.
11. J.-C. Berthet, P. Thuéry and M. Ephritikhine, Chem. Commun., 2007, 604–606.
12. V. Vallet, U. Wahlgren, B. Schimmelpfennig, H. Moll, Z. Szabó and I. Grenthe, Inorg. Chem., 2001, 40, 3516–3525.
13. M. Straka, K. G. Dyall and P. Pyykkö, Theor. Chem. Acc., 2001, 106, 393–403.
14. K. I. M. Ingram, L. J. L. Häller and N. Kaltsoyannis, Dalton Trans., 2006, 2403–2414.
15. J. L. Sonnenberg, P. J. Hay, R. L. Martin and B. E. Bursten, Inorg. Chem., 2005, 44, 2255–2262.
16. F. Quilès and A. Burneau, Vib. Spectrosc., 2000, 23, 231–241.
17. F. Quilès, C. Nguyen-Trung, C. Carteret and B. Humbert, Inorg. Chem., 2011, 50, 2811–2823.
18. C. Nguyen-Trung, D. A. Palmer, G. M. Begun, C. Peiffert and R. E. Mesmer, J. Solution Chem., 2000, 29, 101–129.
19. S. Tsushima, Dalton Trans., 2011, 40, 6732–6737.
20. P. Di Pietro and A. Kerridge, Inorg. Chem., 2016, 55, 573–583.
21. I. A. Charushnikova and C. Den Auwer, Russ. J. Coord. Chem., 2004, 30, 511–519.
22. J.-C. Berthet, P. Thuéry, J.-P. Dognon, D. Guillaneux and M. Ephritikhine, Inorg. Chem., 2008, 47, 6850–6862.
23. Z. Hnatejko, S. Lis, P. Starynowicz and Z. Stryła, Polyhedron, 2011, 30, 880–885.
24. J.-C. Berthet, M. Nierlich, Y. Miquel, C. Madic and M. Ephritikhine, Dalton Trans., 2005, 269–379.
25. R. Copping, B. Jeon, C. D. Pemmaraju, S. Wang, S. J. Teat, M. Janousch, T. Tyliszczak, A. Canning, N. Grønbech-Jensen, D. Prendergast and D. K. Shuh, Inorg. Chem., 2014, 53, 2506–2515.
26. J. B. Love, Chem. Commun., 2009, 3154–3165.
27. Y. K. Agrawal, P. Shrivastav and S. K. Menon, Sep. Purif. Technol., 2000, 20, 177–183.
28. J. L. Sessler, P. J. Melfi, D. Seidel, A. E. V. Gorden, D. K. Ford, P. D. Palmer and C. D. Tait, Tetrahedron, 2004, 60, 11089–11097.
29. H. H. Dam, D. N. Reinhoudt and W. Verboom, Chem. Soc. Rev., 2007, 36, 367–377.
30. J.-H. Lan, W.-Q. Shi, L.-Y. Yuan, J. Li, Y.-L. Zhao and Z.-F. Chai, Coord. Chem. Rev., 2012, 256, 1406–1417.
31. L. E. Roy, N. J. Bridges and L. R. Martin, Dalton Trans., 2013, 42, 2636–2642.
32. N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413.
33. Z. Kolarik, Solvent Extr. Ion Exch., 2003, 21, 381–397.
34. M. G. B. Drew, M. R. S. J. Foreman, C. Hill, M. J. Hudson and C. Madic, Inorg. Chem. Commun., 2005, 8, 239–241.
35. F. Lewis, L. Harwood, M. J. Hudson, M. G. B. Drew, J. Desreux, G. Vidick, N. Bouslimani, G. Modolo, A. Wilden, M. Sypula, T.-H. Vu and J.-P. Simonin, J. Am. Chem. Soc., 2011, 133, 13093–13102.
36. S. A. Kozimor, P. Yang, E. R. Batista, K. S. Boland, C. J. Burns, D. L. Clark, S. D. Conradson, R. L. Martin, M. P. Wilkerson and L. E. Wolfsberg, J. Am. Chem. Soc., 2009, 131, 12125–12136.
37. A. Kerridge, Dalton Trans., 2013, 42, 16428–16436.
38. A. Kerridge, RSC Adv., 2014, 4, 12078–12086.
39. M. Mazzanti, R. Wietzke, J. Pécaut, J.-M. Latour, P. Maldivi and M. Remy, Inorg. Chem., 2002, 41, 2389–2399.
40. D. Guillaumont, J. Phys. Chem. A, 2004, 108, 6893–6900.
41. D. Guillaumont, THEOCHEM, 2006, 771, 105–110.
42. L. Petit, C. Adamo and P. Maldivi, Inorg. Chem., 2006, 45, 8517–8522.
43. M. A. Denecke, P. J. Panak, F. Burdet, M. Weigl, A. Geist, R. Klenze, M. Mazzanti and K. Gompper, C. R. Chim., 2007, 10, 872–882.
44. I. Kirker and N. Kaltsoyannis, Dalton Trans., 2011, 40, 124–131.
45. M. J. Tassell and N. Kaltsoyannis, Dalton Trans., 2010, 39, 6576–6588.
46. J. L. Sessler, D. Seidel, A. E. Vivian, V. Lynch, B. L. Scott and D. W. Keogh, Angew. Chem., Int. Ed., 2001, 40, 591–594.
47. J. L. Sessler, A. E. Gorden, D. Seidel, S. Hannah, V. Lynch, P. L. Gordon, R. J. Donohoe, C. Drew Tait and D. Webster Keogh, Inorg. Chim. Acta, 2002, 341, 54–70.
48. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
49. R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396.
50. A. Savin, A. D. Becke, J. Flad, R. Nesper, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1991, 30, 409–412.
51. P. Fuentealba, E. Chamorro and J. C. Santos, in Theoretical Aspects of Chemical Reactivity, ed. A. Toro-Labbé, Elsevier B.V., Amsterdam, 2007, pp. 57–85.
52. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
53. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
54. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
55. X. Cao and M. Dolg, J. Chem. Phys., 2001, 115, 7348.
56. W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535.
57. D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684.
58. M. Douglas and N. Kroll, Ann. Phys., 1974, 155, 89–155.
59. B. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748.
60. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
61. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
62. P. Stephens, F. Devlin, C. Chabalowski and M. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
63. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
64. T. A. Keith, AIMAll (Version 14.11.23), TK Gristmill Software, Overl. Park KS, USA, 2014.
65. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
66. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
67. G. A. Shamov and G. Schreckenbach, Inorg. Chem., 2008, 47, 805–811.
68. A. E. Clark, J. L. Sonnenberg, P. J. Hay and R. L. Martin, J. Chem. Phys., 2004, 121, 2563–2570.
69. A. Zupan, K. Burke, M. Ernzerhof and J. P. Perdew, J. Chem. Phys., 1997, 106, 10184.
70. R. F. W. Bader and H. Essén, J. Chem. Phys., 1984, 80, 1943.
71. R. Beekmeyer and A. Kerridge, Inorganics, 2015, 3, 482–499.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp01273f

‡ Frequency analysis was not performed on the UO₂IA′ complex when using the B3LYP xc-functional due to computational expense.

§ Technically, this point is a saddlepoint on the ELF surface, characterised as a (3,−1) critical point in terms of the topology. It is only a minimum along the bond.

---