The role of halide ions in the anisotropic growth of gold nanoparticles: a microscopic, atomistic perspective

Abstract

We provide a microscopic view of the role of halides in controlling the anisotropic growth of gold nanorods through a combined computational and experimental study. Atomistic molecular dynamics simulations unveil that Br⁻ adsorption is not only responsible for surface passivation, but also acts as the driving force for CTAB micelle adsorption and stabilization on the gold surface in a facet-dependent way. The partial replacement of Br⁻ by Cl⁻ decreases the difference between facets and the surfactant density. Finally, in the CTAC solution, no halides or micellar structures protect the gold surface and further gold reduction should be uniformly possible. Experimentally observed nanoparticle's growth in different CTAB/CTAC mixtures is more uniform and faster as the amount of Cl⁻ increases, confirming the picture from the simulations. In addition, the surfactant layer thickness measured on nanorods exposed to CTAB and CTAC quantitatively agrees with the simulation results.

---

1 Introduction

Anisotropic metal nanoparticles have been and still are the subject of great attention and investigation due to their shape and size-dependent physical and chemical properties.¹ The rational control of their size and shape during the synthesis process is one of the main targets of ongoing research.² The gold nanorods are usually prepared using a seed mediated growth technique. In this technique, ascorbic acid (a mild reducing agent) is added to an aqueous cetyltrimethylammonium bromide (CTAB) solution of HAuCl₄ for the selective reduction of Au³⁺ to Au⁺ (growth solution), followed by the addition of small gold seeds that catalyze the reduction of Au⁺ on their surface.^3–5 The addition of silver nitrate to the growing solution can increase the yield of short gold nanorods (aspect ratio circa 6) to nearly 100%.⁴ In most of the synthesis recipes for gold nanoparticles, halide ions (chloride, bromide or iodide) are present in water in addition to stabilizing surfactants or polymers.^6–20 In fact, halide anions significantly influence the morphology of gold nanoparticles,^21,22 thanks to their strong tendency to adsorb on metallic surfaces. The growth of the nanoparticles takes place in a rather complex mixture of salts and surfactants in water.²³ A microscopic, atomistic picture of the growing solution would help to understand the mechanism and to rationally control the synthesis. Some recent theoretical studies have tried to rationalize the role of halides. In particular density functional theory (DFT)-based calculations have been used to show that surfactants, bromide, and silver preferentially adsorb on some facets of the seeds.²⁴ This is certainly an interesting first step in the direction of microscopically understanding the role of interfacial interactions in shaping the growth, however the cost of DFT calculations is still preventing us from studying systems including more than a few molecules. Force field-based molecular dynamics (MD) simulations have proven to be an effective tool to consider larger systems at the nanometric scale, including the electrolyte solution and therefore accounting for the effect of temperature and dynamics on the nano- to microsecond timescale.

In particular MD simulations have been used to address metal nanoparticle/liquid interfaces and to accurately describe the adsorption of peptides and organic molecules.^25–27 A recent simulation study on ionic liquids interacting with various facets of gold has shown good correlations with experimentally observed nanorod growth.²⁸ There, the stabilization of the different facets was found to be mediated by ammonium ions which were also acting as the solvent. Walsh and coworkers have also recently shown how peptide sequences can discriminate between gold facets under aqueous conditions offering a promising route to control the growth and organisation of bio-mimetically synthesized gold nanoparticles.²⁷ In our recent work,²⁹ we have performed MD simulations of different gold facets in contact with an electrolyte solution containing CTAB surfactants in order to understand the microscopic/molecular origin of the anisotropic growth. Our simulations showed, for the first time, that on all the surfaces CTAB forms distorted cylindrical micelles spaced by water channels containing bromide ions, which can provide a path for the diffusion of the gold reactants toward the gold surface.²⁹

Here, we want to investigate the influence of the halides on the growth mechanism of gold nanorods in CTAB/CTAC solutions using a combination of simulations and experiments. We aim to understand how the structure of the gold/surfactant/electrolyte interface changes when Cl⁻ replaces Br⁻ at different concentrations. The key question we want to address is how the halides affect the surfactant assembly at the surface and consequently the interface structure and properties of different facets. For this purpose, we built a simple model of the nanorod surface in contact with the growing solution and we simulate the microscopic mechanism of adsorption of CTAB/CTAC surfactant mixtures with different ratios on three gold surfaces namely the native Au(111), Au(110) and Au(100). Our surfaces are treated as infinite planes in the periodic boundary condition, and therefore our analysis is especially relevant to the growth stage in which the different facets of the nanorod are already formed and have sizes of a few nanometers. In this regime it is possible to isolate the role played by the different facets (different planes) with respect to that of the edges. In particular, we analyze the surface passivation by halide ions, the packing density of CTA⁺, the compactness of the surfactant layer and the potential difference between the bulk and the surfactant layer. Our model systems include pure CTAB, pure CTAC, a mixture of 50% CTAB and 50% CTAC and a mixture of 25% CTAB and 75% of CTAC in the growth solution. We want to mention here that, for the moment, we do not include silver cations in our simulation models. Indeed, although it is well established that the addition of a small amount of silver nitrate during the synthesis has an important effect on the growth,⁵ this is a further element of complication that we plan to address in a further study.

We find that the degree of binding of the different halides to the gold surfaces has a strong impact on the structure of the surfactant layer at the interface. Replacing Br⁻ with Cl⁻ causes an important structural rearrangement of the surfactant layer which becomes less compact. Also, the difference between different facets in terms of surface density of surfactants and ions becomes less pronounced as the CTAB/CTAC ratio decreases. Finally when all Br⁻ is replaced by Cl⁻ only a few disordered CTA⁺ molecules can bind to the gold surface, confirming that CTAC is unable to exert a protecting action on the gold surface and is unable to inhibit the growth of any gold surface. The simulations are then compared to the experiments to validate our findings. In particular growth experiments are performed in different CTAB/CTAC mixtures which correspond to the relative concentration of halides as investigated in the simulations. Moreover, a measure of the surfactant layer thickness is provided through measurements of the surface plasmon resonance from nanorods immersed in CTAB or CTAC solutions. The experiments provide a validation of the simulation predictions showing a quantitative accord between the simulated and measured thickness of the surfactant layer. The combined approach of atomistic molecular dynamics simulations and corresponding experiments provides a general framework to investigate the complex processes occurring during nanocrystal formation linking properties at the solid/liquid interface to the morphology of the growing solid.

2 Methods

2.1 Computational section

2.1.1 Models and simulation details. We first studied the adsorption of halides at the gold/water interface without surfactants. A 4 × 4 × 1.26 nm³ gold slab is solvated with a water slab of about 5 nm thickness. The details of the simulation models for the Au(111) surface/water interface in the presence of different halides are reported in Table 1, including box sizes and the number of atoms. We have considered three different halides, namely Cl⁻, Br⁻ and I⁻ in combination with the same number of Na⁺ counterions in order to keep the system neutral. Ions are added to the system randomly replacing water molecules.

Table 1 Model details of the Au(111) surface in contact with a sodium halide solution (1.81 M, 3.87 and 7.78 M)

Name of surfaces	No. of halide ions	No. of water molecules	Box dimensions X [nm], Y [nm] Z [nm]
1.81 M
Au(111)	90 Cl^−	2761	4.02, 4.02, 7.04
Au(111)	90 Br^−	2761	4.02, 4.02, 7.03
Au(111)	90 I^−	2761	4.02, 4.02, 7.04
3.87 M
Au(111)	180 Br^−	2581	4.01, 4.01, 7.03
Au(111)	180 I^−	2581	4.01, 4.01, 7.02
7.78 M
Au(111)	360 Cl^−	2221	4.02, 4.02, 7.03
Au(111)	360 Br^−	2221	4.02, 4.02, 7.03
Au(111)	360 I^−	2221	4.01, 4.01, 7.02

---

In Table 2, the details of the model systems for the gold/electrolyte interface containing different types of surfactants are described. In particular box sizes and the number of atoms for the 100% CTAB, 50% CTAB 50% CTAC, 25% CTAB 75% CTAC and 100% CTAC systems for the three surfaces Au(111), Au(110) and Au(100) are reported. The thickness of the gold slab is 1.26, 1.45 and 1.43 nm for the Au(111), Au(110) and Au(100) surface models, respectively. We would like to mention here that only the native surfaces are considered. The Au(100) surface can reconstruct in the Au(100)-hex, in aqueous solution, while the Au(110) surface can reconstruct in the missing row.³⁰ However this represents a further element of complication which will be addressed in future work along with higher index planes. The 100% CTAB model described here is the same as we have already used in our previous work.²⁹

Table 2 Model details of different concentrations of CTAB/CTAC surfactant in water on the gold(111), (110) and (100) surfaces

Name of surfaces	No. of CTAB/CTAC	No. of water molecules	Box dimensions X [nm], Y [nm], Z [nm]
100% CTAB
Au(111)	180/0	4982	4.07, 4.07, 15.47
Au(110)	180/0	4936	4.08, 4.08, 15.90
Au(100)	180/0	4884	4.1, 4.1, 15.61
50% CTAB	50% CTAC
Au(111)	90/90	4802	4.06, 4.06, 15.44
Au(110)	90/90	4802	4.08, 4.08, 15.54
Au(100)	90/90	4802	4.1, 4.1, 15.61
25% CTAB	75% CTAC
Au(111)	45/135	4982	4.07, 4.07, 15.49
Au(110)	45/135	4936	4.08, 4.08, 15.92
Au(100)	45/135	4884	4.11, 4.11, 15.64
100% CTAC
Au(111)	0/180	4982	4.07, 4.07, 15.47
Au(110)	0/180	5651	4.14, 4.14, 15.75
Au(100)	0/180	4884	4.11, 4.11, 15.65

---

Further details about the initial configuration are reported in the ESI† (see Fig. S5).

All MD simulations have been performed using the GROMACS package (version 4.5.5).^31–34 Periodic boundary conditions were applied in all three directions. Energy minimization was conducted after the addition of water and ions to keep the maximum force on any atom below 1000 kJ mol⁻¹ nm⁻¹. A constant temperature of 300 K and a constant pressure of 1 bar were maintained by the Berendsen and Parrinello–Rahman coupling scheme. A time step of 2 fs was employed and trajectories were stored at every 2 ps. The system was first equilibrated in the NVT ensemble (constant number of particles, volume, and temperature) for 100 ps, and subsequently NPT (constant number of particles, pressure, and temperature) ensemble simulations were performed. MD production runs were extended for at least 200 ns for the 100% CTAB models. Longer simulations up to 1000 ns were considered for the CTAB/CTAC mixtures and for the 100% CTAC systems (Table 2) in order to achieve convergence for the structure of the surfactant layer at the interface. Convergence of the surface density of CTA⁺ and Br⁻ as a function of time has been carefully checked and reported in Fig. S6 of the ESI.† Trajectories from the last 50 ns were used for the calculation of the properties reported in Table 4. In the case of the metal/electrolyte interfaces without surfactants (models in Table 1) a shorter simulation time can already provide good statistical sampling. In this case, MD production runs of 50 ns were performed and trajectories from the last 10 ns were used for analysis.

2.1.2 Force-field parameters. The GROMOS96 53a6 forcefield³⁵ was employed for all our MD simulations. In particular the cetyltrimethylammonium cation (CTA⁺) model proposed and validated by Wang and Larson³⁶ has been used in combination with the SPC water model. The charge assignment for CTA⁺ is such that the three methyl groups in the head group and the methylene group adjacent to the nitrogen carry a partial positive point charge of +0.25e each and the central nitrogen atom is neutral.³⁶ The Lennard-Jones parameters for gold and halide ions are reported in Table 3. The Lennard-Jones parameters for gold from the study of Heinz et al.³⁷ were employed for the metal description. They quantitatively reproduce the density, surface tension, and interface tension with water³⁸ and they have been extensively used also to investigate noncovalent adsorption of organic and biomolecules,³⁸ including also single CTAB surfactant molecules, hexadecylammonium chloride (HDAC), amino acids on Au(111)³⁹ and peptides³⁸ on Au(111) and Au(100) in aqueous solution. The same parameters had been already used in our previous work.²⁹ The combination of the CTAB force field from ref. 36 and the gold parametrization from ref. 37 has been discussed in our previous work.²⁹ In particular we verified that for the CTAB parameters from ref. 36 the single molecule binding geometry and adsorption energy to Au(111) in aqueous solution are in close agreement with those obtained using the all-atom CHARMM-METAL force field. The Lennard-Jones parameters for bromide ions are from ref. 40. The Lennard-Jones parameters for iodide ions are from the study of Reif and Hunenberger.⁴¹ They are compatible with ionic polarizability and are calibrated to reproduce single-ion hydration free energies derived from the experimental conventional hydration free energies along with a standard intrinsic hydration free energy of the proton. A description of the halide solvation structure is reported in the ESI† (Fig. S1).

Table 3 Lennard-Jones parameters of Au, Cl⁻, Br⁻ and I⁻

Name	C6 [kJ mol^−1 nm^6]	C12 [10^−5 kJ mol^−1 nm^12]
Au^37	0.029227046	0.9650000
Cl^− ^35	0.01380625	10.6915600
Br^− ^40	0.027655690	6.5480464
I^− ^41	0.044452000	18.8618000

---

2.2 Experimental section

2.2.1 Materials. Deionized water from a Millipore system (>18 MΩ, Milli Q) was used in all experiments. All chemicals were purchased from Sigma-Alldrich and used without any further purification.

2.2.2 Synthesis of gold nanorods. Gold nanorods were prepared using a two-step process according to the literature.⁵ First, seeds were prepared as follows: 50 μL of 0.1 M tetrachloroauric acid (HAuCl₄) are added to 5.0 mL of Milli Q water and mixed with 5.0 mL of 0.2 M cetyltrimethylammoniumbromide (CTAB) solution. During vigorous shaking, 0.60 mL of ice-cold 0.020 M sodium borohydride (NaBH₄) was added resulting in the formation of a brownish-yellow or yellow suspension of seeds. The seed suspension was kept at 30 °C and used within one day. In a second step, seeds were grown to nanorods in the following way: 10 mL of growth solution containing 5.0 × 10⁻⁴ M HAuCl₄, (0.10-X) M CTAB, X M CTAC, 8.0 × 10⁻⁵ M silver nitrate (AgNO₃) and 5.5 × 10⁻⁴ M ascorbic acid (AA) was prepared. X was varied between 0 and 0.1. AA changes the growth solution from dark yellow to colorless. After the addition of 12 μL of seeds, the solution changes color to blue or grayish-red within 10–20 min.

2.2.3 Growth kinetics. Growth solutions with the same concentrations as for the synthesis of gold nanorods and a reduced total volume of 3 mL were prepared in a cuvette. After the addition of 7.2 μL of seed solution and rapid mixing, UV/VIS transmission spectra were recorded every 3 seconds.

2.2.4 TEM. TEM images were recorded on a Philips EM420 using an operating voltage of 120 kV. TEM samples were prepared from about 1 mL of nanoparticle solution, and centrifuged twice for 10 minutes at 9870g (10 000 rpm). The supernatant solution was first replaced by 1 mL and the second time by 300 μL of fresh water. A drop (5 μL) of this concentrated solution was deposited on a 200 mesh formvar-coated copper grid and dried in air at room temperature. The particle sizes were measured using the TEM image manually and – when possible – using an automatic sizing tool by using the Image Processing Toolbox of MATLAB. We cross-checked the reliability of the automatic count manually for every image series.

2.2.5 Single nanoparticle spectroscopy (NanoSPR). We determined the change in resonance wavelengths Δλ_res of gold nanorods induced by the coverage of CTAB or CTAC to verify the theoretical prediction of a thicker surfactant layer in the presence of bromide ions. This experiment was performed on a homebuilt dark-field microscope system that allows the automatic determination of many single nanoparticle spectra of gold nanorods immobilized at the bottom of a microfluidic flow cell.⁴² The flow cell allows the exposure of the nanoparticles to different solutions. Before immobilizing gold nanorods in the flow cell by the addition of a 1 M sodium chloride solution, we cleaned the cell by rinsing with 300 μL of Hellmanex II, a commercial cleaning concentrate followed by 3 mL of ultrapure water. The plasmon resonance wavelength λ_res (see Fig. 1a) of about 40 individual nanoparticles within the field of view was automatically recorded before and after rinsing with different solutions. Generally, the plasmon resonance wavelength changes to larger wavelength if the particle environment's refractive index increases (due to the adsorption of molecules, cf.Fig. 1b). To confirm the different adsorption properties of CTAB and CTAC predicted by the simulation, we performed the following sequence of experiments: the initial resonance position of the nanoparticles was recorded after extensive washing with pure water. These resonance positions serve as the baseline for the following steps and we display only the shift with respect to this initial position in Fig. 1c and b. In a first step, we flushed in 300 μL of 0.01 M CTAC and recorded the resonance positions again (see Fig. 1c, step 1). On average, the resonance positions shifted towards larger wavelength by about 0.7 nm. In a second step, we washed again with 3 mL of pure water and recorded the resonance positions (Fig. 1c, step 2). The spectral positions shifted towards lower wavelength, as expected for the removal of bound CTAC molecules. However, to our surprise, the resonance position was slightly blue shifted by about 0.4 nm compared to the initial baseline. This blue shift is most likely caused by a charging effect induced by halide ion adsorption. The steps three and four repeat the same procedure as steps one and two – only replacing CTAC with CTAB. Both the redshift and the following blueshift are considerably more pronounced (Fig. 1c). Because our primary interest is to compare the surface coverage of CTAC and CTAB, we corrected the shift caused by the charging effect by using the mean of step 2 as the baseline for step 1 and the mean of step 4 as the baseline for step 3. The resulting corrected plasmon shifts are shown in Fig. 4c and used for the analysis of surface coverage and layer thickness.

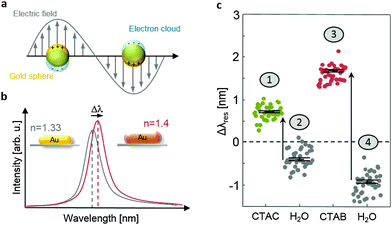Fig. 1 (a) A characteristic of noble metal nanoparticles is the appearance of particle plasmons upon excitation with light: the conduction electrons follow the electromagnetic field of the incoming wave. The resulting surface charges generate a restoring force which causes an oscillation. If excited at the eigenfrequency of this oscillation, the oscillation amplitude becomes very large and causes strong light absorption and/or scattering,⁴³ (b) sketch of the light scattering spectra of a gold nanorod embedded in water (n = 1.33) and with an additional surfactant layer on the surface (n = 1.4, inset). The surfactant layer causes a resonance wavelength shift Δλ_res. (c) Original data (uncorrected) for the measurement shown in Fig. 4 (see the text for details). Each dot represents the spectral shift of the plasmon resonance of an individual nanoparticle.

3 Results and discussion

3.1 Adsorption of halides on the gold surface

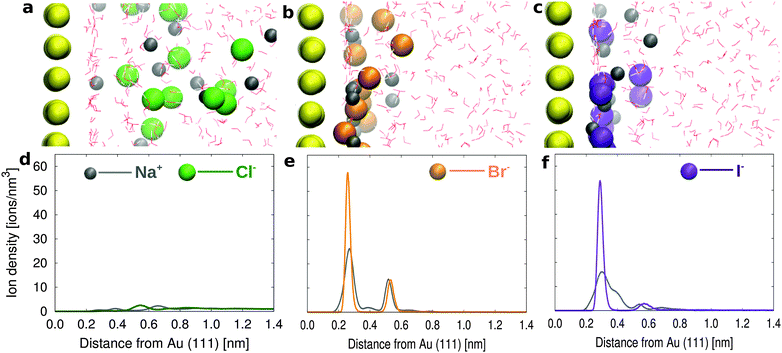
Before describing the more complex electrolyte solution containing the surfactants, we focus on the adsorption of the halide ‘alone’ at the interface. For this purpose, we have simulated the Au(111) surface in contact with a 1.81 M solution containing NaCl, NaBr or NaI, respectively. Snapshots from the simulation trajectories are reported in Fig. 2 (a, b, c for NaCl, NaBr, and NaI solutions, respectively). The simulations reproduce the expected difference in propensity for the gold surface,^44,45 with comparable strong binding for Br⁻ and I⁻.

Fig. 2 Snapshots from simulations for (a) NaCl, (b) NaBr and (c) NaI in water on the Au(111) surface. Ion density as a function of distance from the Au(111) surface for (d) NaCl, (e) NaBr and (f) NaI. Water molecules are represented with sticks, where red and white are used for oxygens and hydrogens, respectively. The different shades of the same color are used to provide a 3D projection.

The likelihood to find the halides on the gold surface can also be expressed in terms of surface concentration, calculated as the number of ions in the first layer divided by the surface area. The number of ions in the first layer is calculated from the integral number (I.N.), namely the integral of the first peak in the ion density profile (see the dotted lines in Fig. S2a–c in the ESI†). The surface concentration of Cl⁻ ions (0.26 ions per nm²) is negligible as compared to that of Br⁻ and I⁻ (2.06 and 2.07 ions per nm²), showing that Cl⁻ ions preferentially remain in the solution, in contrast to Br⁻ and I⁻ ions which are strongly adsorbed on the gold surface. Our data can be compared to the experimental ion adsorption data obtained using the chronocoulometric technique.⁴⁴ In particular, since in our simulation we do not apply any external potential we can assume that we provide a simplified model of the open circuit conditions where, additionally, our model also assumes zero charge density on the gold surface. Under such conditions we quantitatively agree with the experimental data at zero applied voltage, which suggest negligible Cl⁻ adsorption with a surface density of 0.25 ions per nm² and a significant Br⁻ adsorption with a surface density of 2.7 ions per nm².

Looking more in detail, we find that Br⁻ ions form two layers next to the gold surface with a higher number of ions in the first layer. In particular Br⁻ can be directly adsorbed on the gold surface competing with the water molecules in the first adsorbed layer. The ion density profiles are reported in Fig. 2d–f. On the other hand for the NaCl solution, the first adsorbed layer on the gold surface is only formed by water (as can be observed from the water density profile in Fig. S2a–c in the ESI†). The first (weak) peak in the Cl⁻ density profile only appears around the water second layer (see e.g. Fig. S2a in the ESI†). The results for the NaCl solution are in agreement with the pioneering work of Spohr on the molecular simulation of the electrochemical double layer.⁴⁶ The halide propensities at the gold/water interface follow a similar trend to those observed at the air/water interface in the simulations by Jungwirth and Tobias⁴⁷ and at the hydrophobic solid surfaces in the simulations by Horinek and Netz.⁴⁸

3.2 Adsorption of CTAB/CTAC surfactants on Au(111), Au(110) and Au(100)

To understand how the different surface affinity of Cl⁻ and Br⁻ affects the structure of the surfactant layer, we simulate electrolyte solutions containing 100% CTAB (2 M solution), a mixture of 50% CTAB and 50% CTAC (1 M CTAB, 1 M CTAC), a mixture of 25% CTAB and 75% of CTAC (0.5 M CTAB, 1.5 M CTAC) and finally 100% CTAC (2 M solution). Fig. 3a shows a snapshot of a simulation box containing the Au(111) surface, the CTAB layer, and the water layer after 200 ns. The CTAB headgroups favorably attach to the gold surface and form a distorted cylindrical micelle, where the CTAB headgroups arrange in the outer layer of the micelle and the CTAB tails arrange in the core of the micelle. A similar behaviour is observed on Au(110) and Au(100) as well, although with some differences in the ion densities (see ESI,† Fig. S7a–c).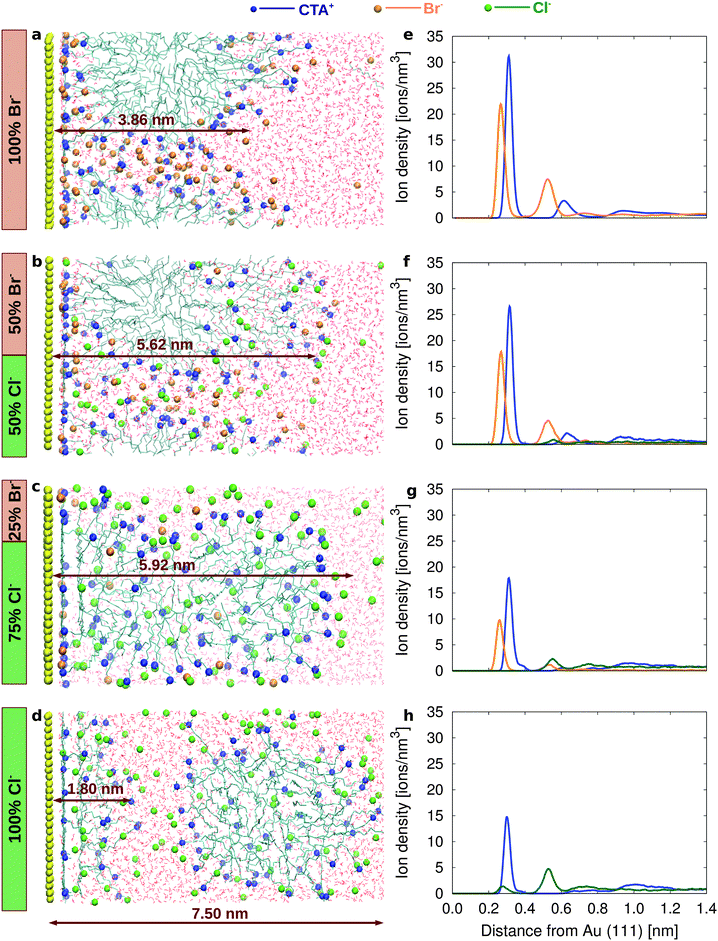

Fig. 3 Snapshots from the simulations for (a) 100% CTAB, (b) 50% CTAB 50% CTAC, (c) 75% CTAB 25% CTAC and (d) 100% CTAC. Ion density as a function of the distance from the Au(111) surface for (e) 100% CTAB, (f) 50% CTAB 50% CTAC, (g) 75% CTAB 25% CTAC and (h) 100% CTAC (see ESI,† Fig. S7–S10 for Au(110) and Au(100)).

The synergic co-adsorption of the anionic and cationic components of a model quaternary ammonium bromide surfactant (although with a shorter hydrophobic tail) had been also experimentally measured using the thermodynamics of an ideally polarized Au(111) or Au(100) electrode.^49,50 The ion density profiles of CTA⁺ and Br⁻ are reported in Fig. 3e as a function of the distance from the Au(111) surface. The surface density of Br⁻ and CTA⁺ is calculated in our simulations as the number of ions in the first layer divided by the surface area (Fig. S7a–c in the ESI†). The surface density of Br⁻ is higher on Au(110) and Au(100) (1.41 and 1.40 ions per nm², respectively) than on Au(111) (1.09 ions per nm²) resulting, in the case of Au(110) and Au(100), in the passivation of a larger surface area (Table 4).

Table 4 Surface density of CTA⁺, Br⁻ and Cl⁻ with different concentration ratios of CTAB/CTAC on different gold surfaces. The maximum standard error in the surface densities is 0.01 ions per nm²

Name of surface	Au(111)	Au(110)	Au(100) [ions per nm^2]
CTA^+ 100% CTAB	1.31	1.49	1.49
CTA^+ 50% CTAB 50% CTAC	1.08	0.90	0.85
CTA^+ 25% CTAB 75% CTAC	0.97	1.18	0.78
CTA^+ 100% CTAC	0.66	0.67	0.65
Br^− 100% CTAB	1.09	1.41	1.40
Br^− 50% CTAB 50% CTAC	0.76	0.74	0.77
Br^− 25% CTAB 75% CTAC	0.56	0.84	0.82
Cl^− 50% CTAB 50% CTAC	0.06	0.03	0.01
Cl^− 25% CTAB 75% CTAC	0.17	0.15	0.12
Cl^− 100% CTAC	0.12	0.07	0.01

---

The lower surface passivation on Au(111) could translate into a higher reduction rate of gold species (such as AuCl₂⁻) on Au(111). The anisotropic Br⁻ density also influences the CTA⁺ surface density, which is higher on Au(110) and Au(100) (1.49 molecules per nm²) than on Au(111) (1.31 molecules per nm²) (Table 4). The less compact surfactant layer on Au(111) could provide easier access to gold species in solution promoting a more efficient growth on such a surface. Additional insight into the interfacial properties can be provided by the interfacial electrostatic potential, defined as the difference in the potential between the bulk solution and the CTAB layer. Such an electrostatic potential difference is higher across the Au(111) interface than across the Au(110) and Au(100) interfaces (see ESI,† Table S4 and Fig. S7e), providing a stronger driving force for the migration of the negatively charged AuCl₂⁻ species toward the gold slab. In turn this could result in an additional factor promoting faster growth of gold nanorods at the Au(111) surface.

In order to study the influence of Cl⁻ on the surface properties we performed new simulations where 50% of Br⁻ are replaced by Cl⁻ (Fig. 3b). The ion density profiles of CTA⁺, Br⁻ and Cl⁻ are reported in Fig. 3f as a function of the distance from the Au(111) surface. The surface density of halides on all the three surfaces is lower than that in the 100% CTAB case (Table 4 and ESI,† Fig. S8a–c), resulting in a reduced surface passivation and possibly in an increased reduction rate. Interestingly, the lower Br⁻ density at the gold/water interface has a remarkable effect on the structure of the surfactant layer, which appears more stretched (and less compact) as compared to the 100% CTAB case (Fig. 3b). The CTA⁺ surface density is reduced and the difference between facets becomes less pronounced (1.08, 0.90 and 0.85 ions per nm² for Au(111), Au(110) and Au(100), respectively). This finding would support the idea that, in the mixture of CTAB/CTAC, the surfactant layer is not capable of significantly blocking the growth along any particular direction, resulting in a more isotropic growth. The interface electrostatic potential between the surfactant layer and the bulk solution (see ESI,† Fig. S8e and Table S4) is also pointing to an isotropic behaviour along the three considered directions.

As the CTAB fraction is further reduced to 25%, the CTA⁺ surface density decreases and the surfactant layer becomes even less compact (ESI,† Fig. S9), and its structure even more stretched along the z direction (Fig. 3c, see Fig. S12 and Table S5 in the ESI†).

The most striking results are certainly obtained for the 100% CTAC solution (Fig. 3d, h and Fig. S10 in the ESI†). For such a system the initial configuration is prepared with a CTAC micelle adsorbed on the gold surface (Fig. S11a in the ESI†). However, as the simulation proceeds, the CTAC micelle becomes more and more stretched in the z direction (which is the direction orthogonal to the surface) (a picture of the system at t = 300 ns is provided in Fig. S11b of the ESI†) and finally detaches from the gold surface moving into the bulk after 600 ns (the final equilibrated system is reported in Fig. 3d). Such a behaviour is certainly driven by the low propensity of Cl⁻ for the surface. In the final configuration (Fig. 3d) a few surfactant molecules, which are left on the gold surface, tend to lay flat so as to maximize the interaction between their hydrophobic tail and the gold surface, while their headgroup orients towards the bulk solution. The thickness of this remaining surfactant layer is about 1.8 nm on Au(111) and Au(100) and 2.4 nm on Au(110) surfaces (Table S5 in the ESI†). In such a scenario, the thin surfactant layer will be unable to inhibit the growth of gold nanoparticles in any direction, explaining an isotropic, faster growth rate.

We would like to comment here that the simulation results which we present for the 50% CTAB and 25% CTAB systems do not possibly represent the most stable equilibrium state for the mixture. They suggest a trend, namely the micellar layer destabilization. The real scenario is certainly more complex and we also expect that some degree of anisotropy would characterize the gold nanorod surface, where the CTAB micellar layer is not uniformly covering the surfaces, but would probably form patches. Larger box dimensions as well as enhanced sampling techniques would indeed be necessary to explore in a more systematic way such a possibility. The case of the 100% CTAC system is certainly more simple. The clear message from the simulations is that the CTAC micelle prefers to be in the solution and does not stick onto gold, although some CTA⁺ molecules can adsorb onto the gold surface. Again the exact details of the CTA⁺ adsorption cannot be directly inferred by a single trajectory. However, in the 100% CTAC system the thickness of the surfactant layer formed by the disordered CTA⁺ adsorbed on gold must certainly be much smaller than the thickness of a full micelle (see Table S5 in the ESI†).

3.3 Validating our prediction: the experimental results

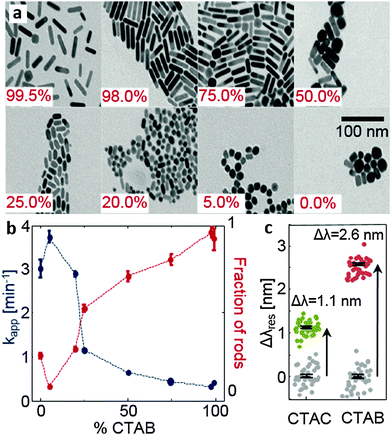
The simulations predict several properties that can be tested experimentally: an increasing amount of chloride ions should lead to faster and more isotropic nanoparticle growth and CTAC should form a considerably thinner layer on gold than CTAB. We tested the first aspect by a series of nanoparticle syntheses where we varied the ratio of CTAC and CTAB in the growth solution. Transmission electron microscopy (TEM) images of the resulting particles are displayed in Fig. 4a. The TEM images show the expected trend towards more isotropic particles with decreasing bromide concentration. A quantitative analysis of many TEM images, where we determined the fraction of rods versus spheres (see Fig. S13 in the ESI†), confirms the trend as well (Fig. 4b). In addition, we monitored the speed of the nanoparticle growth by following the optical absorption in the interband region at 450 nm (see Fig. S14 in the ESI†) which is a measure of the nanoparticle volume. We extract an apparent rate constant from these volume growth curves using a Boltzmann-function (for resource limited growth). The reaction speed decreases when the amount of CTAB is increased (blue dots in Fig. 4b) which confirms again the trend expected from the simulation.

Fig. 4 Experimental data. (a) Representative transmission electron microscopy (TEM) images of gold nanorods synthesized with different percentages of CTAB in the growth solution, keeping the total CTAB⁺ CTAC concentration constant. (b) Quantitative results of the percentage of rods over spheres extracted from TEM images as a function of the CTAB percentage (red dots) and the corresponding apparent reaction rates determined by optical absorption (blue dots), and (c) plasmon resonance wavelength shifts Δλ_res of many individual gold nanoparticles immobilized in a water filled glass capillary, after exposure to 0.01 M CTAC (green dots) and CTAB (red dots). The gray points show the same particles after exposure to water. In the latter case, the observed shifts are an indication of the measurement accuracy. The black symbols show the mean values of their standard error bars (statistics over about 40 particles).

To test the second prediction from the simulation, the thicker surfactant layer on the gold surface in the presence of bromide ions, we exploit the sensitivity of the plasmon resonance frequency of gold nanoparticles to the adsorbed layer of the material.⁴³ Using a homebuilt dark-field microscope in combination with a scanning stage and a spectrometer,⁴² we determine the plasmon resonance position λ_res of about 40 gold nanoparticles before and after exposure to a solution containing either 0.01 M CTAB or CTAC. The exposure to CTAB/CTAC leads to a small but clearly measurable shift Δλ_res in the plasmon resonance (Fig. 4c, see Fig. 1). As expected, the shift for CTAB is much larger than that measured after CTAC exposure (2.6 nm versus 1.1 nm). Since the plasmon resonance shift Δλ_res is a function of layer thickness t and its refractive index, we have converted the measured values to a layer thickness. For this conversion, we use published values for the refractive index of CTAB and CTAC of about n = 1.4^51,52 and simulation results for the plasmon resonance of gold nanoparticles in different media we obtained using the boundary element method⁵³ (see Fig. S15 in the ESI†). This calculation resulted in a layer thickness of t = 1.6 nm and t = 4.2 nm for CTAC and CTAB, respectively. Our results fit nicely with some recent small-angle neutron scattering measurements⁵⁴ of the structure and the size of ligands attached to the surfaces of gold nanorods. They found out that nanorods prepared with CTAC have a lower surfactant layer thickness (<3 nm) than those with CTAB (about 3.6 nm), although they have also used sodium oleate in the growth solution.⁵⁴ Interestingly, the thickness values obtained from the shifts of the plasmonic resonance are in very good agreement with the results from the simulation: 1.8 nm and 3.8 nm (Table S5 in the ESI†).

4 Conclusions

We have presented here a detailed atomistic investigation of the gold nanoparticle surface in contact with the surfactant/electrolyte solution, which addresses the role of the halides in the formation of the protective layer of surfactants. Our simulations show that CTAB is able to form a compact micellar layer on the gold surface which is actually denser on Au(100) and Au(110) with respect to Au(111). The key element in the micelle adhesion to the surface is bromide propensity for the gold surface. When bromide is partially (eventually fully) replaced by chloride the micelles prefer to diffuse into the electrolyte solution leaving the gold surface unprotected. Indeed, for the CTAC system only a few surfactant molecules are sticking to the gold surface, leaving the surface itself more easily accessible to further gold reduction. Two sets of experiments, particle synthesis and plasmon shift measurements, confirm the trends expected from the simulations and agree quantitatively with the predicted values for the surfactant layer thickness. These experimental confirmations let us strongly believe that the atomistic simulations provide an accurate description of the underlying processes. The role of certain halide ions (bromide) in mediating, in a strongly crystal facet dependent way, the adhesion of cationic surfactant molecules, provides a better understanding of the way, additives direct nanocrystal growth towards specific shapes. Moreover, the combined computational and experimental approach provides a template for understanding the nanocrystal growth dynamics in general, which is a major step in the rational design of nanostructure formation from solution. In a next step, this approach should incorporate actual reaction steps to elucidate the intricate electrochemical and diffusive processes in this highly dynamical process.

Acknowledgements

We thank Condensed Matter Theory Group KOMET 331 for providing access to its computational facilities and the Deutsche Forschungsgemeinschaft for financial support under grant no. SU 752/1. All the simulations were performed on the Mogon ZDV cluster. The experiments were supported by the ERC through the project 259640 (SingleSense). We thank Jan-Philipp Günther for help with the conversion of the plasmon shift to the surfactant layer thickness.

References

1. P. D. Howes, R. Chandrawati and M. M. Stevens, Science, 2014, 346, 53–63.
2. M. Grzelczak, J. Pérez-Juste, P. Mulvaney and L. M. Liz-Marzán, Chem. Soc. Rev., 2008, 37, 1783–1791.
3. N. R. Jana, L. Gearheart and C. J. Murphy, J. Phys. Chem. B, 2001, 105, 4065–4067.
4. C. J. Murphy, T. K. Sau, A. M. Gole, C. J. Orendorff, J. Gao, L. Gou, S. E. Hunyadi and T. Li, J. Phys. Chem. B, 2005, 109(29), 13857–13870.
5. B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15(10), 1957–1962.
6. W. Cheng, S. Dong and E. Wang, Angew. Chem., Int. Ed., 2003, 42, 449–452.
7. J. Pérez-Juste, L. Liz-Marzan, S. Carnie, D. Chan and P. Mulvaney, Adv. Funct. Mater., 2004, 14(6), 571–579.
8. T. H. Ha, H.-J. Koo and B. H. Chung, J. Phys. Chem. C, 2007, 111, 1123–1130.
9. J. E. Millstone, W. Wei, M. R. Jones, H. Yoo and C. A. Mirkin, Nano Lett., 2008, 8(8), 2526–2529.
10. M. Grzelczak, A. Sanchez-Iglesias, B. Rodriguez-Gonzalez, R. Alvarez-Puebla, J. Pérez-Juste and L. M. Liz-Marzán, Adv. Funct. Mater., 2008, 18, 3780–3786.
11. D. K. Smith and B. A. Korgel, Langmuir, 2008, 24, 644–649.
12. D. K. Smith, N. R. Miller and B. A. Korgel, Langmuir, 2009, 25(16), 9518–9524.
13. T. Soejima and N. Kimizuka, J. Am. Chem. Soc., 2009, 131, 14407–14412.
14. X. Fan, Z. R. Guo, J. M. Hong, Y. Zhang, J. N. Zhang and N. Gu, Nanotechnology, 2010, 21, 105602.
15. J. Zhang, M. R. Langille, M. L. Personick, K. Zhang, S. Li and C. A. Mirkin, J. Am. Chem. Soc., 2010, 132(40), 14012–14014.
16. Z. Jiao, H. Xia and X. Tao, J. Phys. Chem. C, 2011, 115(16), 7887–7895.
17. J. S. DuChene, W. Niu, J. M. Abendroth, Q. Sun, W. Zhao, F. Huo and W. D. Wei, Chem. Mater., 2013, 25, 1392–1399.
18. M. R. Langille, M. L. Personick, J. Zhangand and C. A. Mirkin, J. Am. Chem. Soc., 2012, 134, 14542–14554.
19. M. G. A. da Silva, M. R. Meneghetti, A. Denicourt-Nowicki and A. Roucoux, RSC Adv., 2014, 4, 25875–25879.
20. A. Kedia and P. S. Kumar, RSC Adv., 2014, 4, 4782–4790.
21. T. K. Sau and C. J. Murphy, Philos. Mag., 2007, 87, 14–15.
22. S. E. Lohse, N. D. Burrows, L. Scarabelli, L. M. Liz-Marzán and C. J. Murphy, Chem. Mater., 2014, 26(1), 34–43.
23. C. J. Murphy, L. B. Thompson, A. M. Alkilany, P. N. Sisco, S. P. Boulos, S. T. Sivapalan, J. A. Yang, D. J. Chernak and J. Huang, J. Phys. Chem. Lett., 2010, 1(19), 2867–2875.
24. N. Almora-Barrios, G. Novell-Leruth, P. Whiting, L. M. Liz-Marzán and N. López, Nano Lett., 2014, 14(2), 871–875.
25. H. Ramezani-Dakhel, L. Ruan, Y. Huang and H. Heinz, Adv. Funct. Mater., 2015, 25, 1374–1384.
26. H. Heinz and H. Ramezani-Dakhel, Chem. Soc. Rev., 2016, 45, 412–448.
27. L. B. Wright, J. P. Palafox-Hernandez, P. M. Rodger, S. Corni and T. R. Walsh, Chem. Sci., 2015, 6, 5204–5214.
28. K. C. Jha, H. Liu, M. R. Bockstaller and H. Heinz, J. Phys. Chem. C, 2013, 117, 25969–25981.
29. S. K. Meena and M. Sulpizi, Langmuir, 2013, 29(48), 14954–14961.
30. L. B. Wright, P. M. Rodger and T. R. Walsh, and S. Corni, J. Phys. Chem. C, 2013, 117, 24292–24306.
31. H. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
32. D. V. D. Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
33. B. Hess, C. Kutzner, D. V. D. Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
34. S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
35. C. Oostenbrink, A. Villa, A. E. Mark and W. F. V. Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676.
36. Z. Wang and R. G. Larson, J. Phys. Chem. B, 2009, 113, 13697–13710.
37. H. Heinz, R. A. Farmer and R. R. Naik, J. Phys. Chem. B, 2008, 112, 17281–17290.
38. H. Heinz, B. L. Farmer, R. B. Pandey, J. M. Slocik, S. S. Patnaik, R. Pachter and R. R. Naik, J. Am. Chem. Soc., 2009, 131, 9704–9714.
39. J. Feng, R. B. Pandey, R. J. Berry, B. L. Farmer, R. R. Naikc and H. Heinz, Soft Matter, 2011, 7, 2113–2120.
40. H. Yu, M. Ramseier, R. Burgi and W. F. van Gunsteren, ChemPhysChem, 2004, 5(5), 633–641.
41. M. M. Reif and P. H. Hunenberger, J. Chem. Phys., 2011, 134, 144104.
42. C. Rosman, J. Prasad, A. Neiser, A. Henkel, J. Edgar and C. Sönnichsen, Nano Lett., 2013, 13(7), 3243–3247.
43. J. Olson, S. Dominguez-Medina, A. Hoggard, L.-Y. Wang, W.-S. Chang and S. Link, Chem. Soc. Rev., 2015, 44, 40–57.
44. J. Lipkowski, Z. Shi, A. Chen, B. Pettinger and C. Bilger, Electrochim. Acta, 1998, 43, 2875–2888.
45. O. M. Magnussen, Chem. Rev., 2002, 102, 679–725.
46. E. Spohr, Electrochim. Acta, 1999, 44, 1697–1705.
47. P. Jungwirth and D. J. Tobias, Chem. Rev., 2006, 106, 1259–1281.
48. D. Horinek and R. R. Netz, Phys. Rev. Lett., 2007, 99, 226104.
49. J. P. Vivek and I. J. Burgess, Langmuir, 2012, 28(11), 5031–5039.
50. J. P. Vivek and I. J. Burgess, Langmuir, 2012, 28(11), 5040–5047.
51. C. Yu, L. Varghese and J. Irudayaraj, Langmuir, 2007, 23, 9114–9119.
52. A. A. Ashkarran and A. Bayat, Int. Nano Lett., 2013, 3, 50–60.
53. U. Hohenester and A. Trügler, Comput. Phys. Commun., 2012, 183, 370–381.
54. M. J. A. Hore, X. Ye, J. Ford, Y. Gao, J. FeiŁ, Q. Wu, S. J. Rowan, R. J. Composto, C. B. Murray and B. Hammouda, Nano Lett., 2015, 15(9), 5730–5738.

---

Footnotes

† Electronic supplementary information (ESI) available: Solvation structure of halides, electrostatic potentials at the interface, halide ions on the Au(111) surface in water, density profiles and electrostatic potential profiles for different CTAB/CTAC systems and conversion of the plasmon shift to the layer thickness. See DOI: 10.1039/c6cp01076h

‡ Present address: Max Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany.

---